Abstract
Objective/Study Question
To estimate and compare sample average treatment effects (SATE) and population average treatment effects (PATE) of a resident duty hour policy change on patient and resident outcomes using data from the Flexibility in Duty Hour Requirements for Surgical Trainees Trial (“FIRST Trial”).
Data Sources/Study Setting
Secondary data from the National Surgical Quality Improvement Program and the FIRST Trial (2014–2015).
Study Design
The FIRST Trial was a cluster‐randomized pragmatic noninferiority trial designed to evaluate the effects of a resident work hour policy change to permit greater flexibility in scheduling on patient and resident outcomes. We estimated hierarchical logistic regression models to estimate the SATE of a policy change on outcomes within an intent‐to‐treat framework. Propensity score‐based poststratification was used to estimate PATE.
Data Collection/Extraction Methods
This study was a secondary analysis of previously collected data.
Principal Findings
Although SATE estimates suggested noninferiority of outcomes under flexible duty hour policy versus standard policy, the noninferiority of a policy change was inconclusively noninferior based on PATE estimates due to imprecision.
Conclusions
Propensity score‐based poststratification can be valuable tools to address trial generalizability but may yield imprecise estimates of PATE when sparse strata exist.
Keywords: Resident duty hours, surgical outcomes, medical education, propensity score methods, generalizability
Randomized controlled trials (RCT) are generally considered the “gold standard” in evidence‐based medicine (Sackett 1989; Guyatt et al. 2000; Wright, Swiontkowski, and Heckman 2003; Tricoci et al. 2009), despite broad recognition that RCT samples may be unrepresentative of inference populations—that is, “real‐world” populations of policy/decision‐making interest. This incongruity arises because homogeneous samples are often selected for purposes of improving statistical efficiency and constant treatment effects. Ethical conduct of trials requires informed consent, which can impart an element of self‐selection that also reduces generalizability (Hennekens and Buring 1998; Storms 2003). Unequal access to information about trials due to socioeconomic disparities and cultural differences can further exacerbate nonrepresentativeness (Gross et al. 2005). Finally, ex‐post discovery of “off‐label” uses for treatment may lead to later discovery of new populations of interest beyond the original study population.
The nonrepresentativeness of samples from major trials is well documented (Murthy, Krumholz, and Gross 2004; Stewart et al. 2007; Humphreys et al. 2013; Kennedy‐Martin et al. 2015). Several studies have found systematic differences between trial participants and nonparticipants with respect to characteristics such as disease severity, race/ethnicity, gender, socioeconomic status, and age (Magee et al. 2001; Rovers et al. 2001; Gross et al. 2005; Zimmerman, Chelminski, and Posternak 2005; Elting et al. 2006). Additional studies applying inclusion criteria to inference populations have found disproportionately low rates of study eligibility among patients in real‐world populations (Gandhi et al. 2005; Blanco et al. 2008a,b; Le Strat, Rehm, and Le Foll 2011; Hoertel et al. 2012, 2013; Wissing et al. 2014; Lamont et al. 2015). This literature provides valuable descriptions of the nature and extent of nonrepresentativeness in major RCT samples, but it leaves an important question unanswered: What might the expected effect of treatment be in the inference population or in a subpopulation of the inference population that may not have been represented in the trial sample?
We demonstrate how this question can be addressed using a propensity score‐based poststratification approach developed by O'Muircheartaigh and Hedges (2014) to estimate population average treatment effects from studies involving nonrepresentative samples. We apply this method to data from the Flexibility in Duty Hour Requirements for Surgical Trainees Trial (“FIRST Trial”) to estimate the average effect of a resident duty hour policy change in the population of general surgery residency programs and affiliated hospitals (of which the FIRST Trial sample was a subset) and the subset of the inference population that did not participate in the FIRST Trial.
Background
Population Average Treatment Effect (PATE) Estimation
Causal attribution in nonrandomized studies is challenging because receipt of intervention may be correlated with observed and unobserved subject characteristics. One established approach for dealing with this problem is propensity score‐based poststratification (Rosenbaum and Rubin 1983, 1984; D'Agostino 1998). Rosenbaum and Rubin (1983) showed that predicted probabilities from models predicting receipt of intervention—that is, “propensity scores,” can be used to balance observables across subjects that received the intervention and those that did not. Stratifying subjects based on propensity scores yields homogeneous subgroups of subjects. The sample average treatment effect (SATE) can then be computed as the weighted average of treatment effects across subgroups using the proportion of subjects in each stratum as weights (Rosenbaum and Rubin 1983, 1984; D'Agostino 1998).
O'Muircheartaigh and Hedges (2014) adapted this method of propensity score‐based poststratification to obtain estimates of the population average treatment effect (PATE) in studies with nonrepresentative samples. A complete motivation and exposition of their approach have been published elsewhere (Tipton 2013a; O'Muircheartaigh and Hedges 2014). Briefly summarized, their procedure involves first estimating a propensity score model to predict study inclusion (Rosenbaum and Rubin 1983, 1984; Brookhart et al. 2006). Second, predicted probabilities of study participation (i.e., propensity scores) are obtained from the propensity model. Third, observations are stratified by propensity scores into k strata (k = 5 has been shown to reduce bias due to confounding on observables by 90 percent; Rosenbaum and Rubin 1984). Fourth, stratum‐specific treatment effects are estimated using data from the study sample. Fifth, an estimate of the PATE is computed as the weighted average of stratum‐specific treatment effects using the proportion of the inference population in each stratum as weights.
Methods
Application—The Flexibility in Duty Hour Requirements for Surgical Trainees Trial (“FIRST Trial”)
Resident work hours in the United States are regulated by the Accreditation Council for Graduate Medical Education (ACGME) with the intent of protecting patients and residents by preventing fatigue‐related errors. However, there is concern that excessive restrictions on work hours may compromise training and education goals. Described extensively elsewhere (Bilimoria et al. 2016a,b), the Flexibility in Duty Hour Requirements for Surgical Trainees Trial (“FIRST Trial”) was a two‐arm, cluster‐randomized pragmatic noninferiority trial of general surgery residency programs in the United States and their hospital affiliates to evaluate the effect of a duty hour policy change on patient and resident outcomes. Programs randomized to “flexible duty hour policy” (intervention) were permitted to waive three ACGME standards: (1) the requirement that interns work no more than 16 hours per shift and residents no more than 28 hours (24 hours plus 4 transitional hours); (2) the requirement that residents have at least 8 (preferably 10) hours between shifts; and (3) the requirement that residents have at least 14 hours off after 24‐hour call duty. Programs randomized to usual care were to adhere to usual ACGME standards. All programs, regardless of study arm assignment, were subject to ACGME's 80 work hours/week cap (averaged over 4 weeks) and requirements to have at least 1 in every 7 days off, and 24‐hour call no more than once every third night.
The FIRST Trial study population comprised all 252 ACGME‐accredited general surgery residency programs and their hospitals as enumerated in 2013–2014. Programs in New York were excluded because of state‐mandated duty hours (27 programs). Programs with unresolved ACGME accreditation issues were also excluded (12 programs). Because the FIRST Trial relied on patient data collection through the American College of Surgeons (ACS) National Surgical Quality Improvement Program (NSQIP), programs that were not affiliated with one or more ACS NSQIP hospitals were ineligible to participate (77 programs). Of the remaining 136 general surgery residents in the population, 12 could not be reached for recruitment and six declined enrollment. A total of 118 programs and 154 hospitals were enrolled and randomized at the beginning of the FIRST Trial. One program and three hospitals withdrew from the study prior to conclusion of the study. Although 86 percent of eligible programs enrolled in the FIRST Trial, the study sample does not encompass the entire policy‐relevant inference population (all ACGME‐accredited general surgery residency programs). Thus, it is an empirical question whether SATEs reported in the FIRST Trial are generalizable to the programs and hospitals that did not participate in the FIRST Trial (nonparticipants) and/or the population of policy interest as a whole (both FIRST Trial participating programs and hospitals and nonparticipants).
Unit of Analysis
Although some hospitals sponsor general surgery residency programs, it is often the case that residency programs are sponsored by an institution that is organizationally distinct from the clinical facility in which residents work. Residency programs enrolled in the FIRST Trial with one or more affiliated hospitals. Programs could not enroll in the FIRST Trial without a hospital affiliate; similarly, a hospital could not enroll in the FIRST Trial without an affiliated residency program. Thus, in our propensity model predicting participation in the FIRST Trial, the unit of analysis was the “program‐hospital pair.” Using the roster of program‐hospital pairs in the FIRST Trial, we identified all program‐hospital pairs in the inference population as either trial participants or nonparticipants.
Inference Population and Subpopulation Defined
We define the total inference population (POP) to include both program‐hospital pairs that participated in the FIRST Trial as well as nonparticipating pairs (N = 1,048 program‐hospital pairs). We define the inference subpopulation of nonparticipants (SubPOP) to refer to the subset of the total inference population that did not participate in the FIRST Trial (n = 896 program‐hospital pairs). We define the FIRST Sample (SAMP) to refer to the subset of the total inference population that participated in the FIRST Trial (n = 152 program‐hospital pairs). In this study, we examine the generalizability of the FIRST Trial with respect to (1) the inference subpopulation of nonparticipants (SubPOP) and (2) the inference population as a whole (POP).
Data
Data for this study came from numerous sources, including the ACGME, the American Board of Surgery (ABS), the American Medical Association (AMA) FREIDA™ database of residency programs, and the American Hospital Association (AHA) Annual Survey (Fiscal Year 2013). Patient‐level data and resident‐level data came from the FIRST Trial and have previously been described in detail (Bilimoria et al. 2016aa; Bilimoria et al. 2016b).
Measures
General Surgery Residency Program Characteristics
From the ABS, AMA, and ACGME, we obtained data on the following general surgery residency program characteristics: program type (academic, community‐based, military); number of approved residency slots; number of postgraduate year (PGY) 5 residents; history of ACGME accreditation issues; mean ABS In‐Training Examination (ABSITE) scores; and geographic location. To characterize program‐level research engagement, we used institutional listings from the National Institute of General Medical Sciences (NIGMS) Medical Scientist Training Program (MSTP) and the Association for Academic Surgery (AAS) to identify program‐hospital pairs that had a MSTP and/or that had representatives serving in the AAS.
Hospital Characteristics
Hospital characteristics obtained from the AHA included bed size; annual admission volume; total annual surgical volume; type of control (not‐for‐profit, for‐profit, other); membership in the Council of Teaching Hospitals (COTH); percent Medicaid discharges; full‐time registered nurses (RN) per bed; level 1 trauma center designation; hospital engagement in health‐related research; and provision of any transplant services (bone marrow, heart, kidney, liver, lung, tissue, and/or other transplant).
Outcomes
The FIRST Trial evaluated the effect of assignment to flexible duty hours on both patient outcomes as well as resident outcomes. We assessed the generalizability of the FIRST Trial in both the subset of the inference population that did not participate in the trial as well as the total inference population with respect to both patient and resident outcomes. However, for parsimony, we present and discuss only those analyses pertaining to patient outcomes and have reserved our analyses of resident outcomes for the Appendices SA2–SA9 that accompany this article. The FIRST Trial 30‐day postoperative patient outcomes were as follows: death or serious morbidity (DSM, primary patient outcome); death; serious morbidity; any morbidity; failure‐to‐rescue; pneumonia; renal failure; unplanned reoperation; sepsis; surgical site infection (SSI); and urinary tract infection (UTI) (Bilimoria et al. 2016a,b).
Propensity Score Model
Program‐hospital propensity to participate in the FIRST Trial was modeled using hierarchical logistic regression with program‐level random intercepts to account for the clustering of program‐hospital pairs within residency programs (some programs participated in the FIRST Trial with more than one hospital affiliate) (Li, Zaslavsky, and Landrum 2013). Covariates included in the propensity model were chosen on the basis of two considerations. First, covariates should predict participation in the FIRST Trial as well as patient outcomes or more specifically, differences in outcomes (i.e., treatment effects). Second, we sought covariates with the most complete data to minimize missing data. Regressors in our final model included program type; number of PGY5 residents; a dichotomous variable indicating any history of ACGME accreditation issues between 2012 and 2015; a dichotomous variable indicating engagement in health‐related research, MSTP institution, and/or presence of AAS representative; annual hospital admission volume; type of hospital control; COTH membership; percent Medicaid discharges; RN‐to‐bed ratio; a dichotomous indicator variable for any transplant services; level 1 trauma designation; and census division. Details of our propensity model are provided in Appendix SA2. Predicted probabilities (including both fixed and random components) obtained from this model constituted the propensity scores in analyses that followed. Program‐hospitals pairs were stratified by quintile of propensity scores.
We constructed a histogram of propensity scores to assess whether the assumption of common support was violated.
It is necessary to demonstrate that the propensity score‐based poststratification (sub)population‐weighted sample is similar to the underlying inference (sub)populations. To this end, for each covariate in the propensity model, we computed absolute standardized mean differences (|SMD|s) between inference (sub)populations, FIRST Sample, and (sub)population‐weighted samples (details in Appendices SA2–SA9).
As benchmarks for judging the size of |SMD|s, we adopted and implemented three criteria proposed by Rubin (2001). First, |SMD|s should be no greater than 0.50. Second, the ratio of propensity score variances in the inference (sub)population and (sub)population‐weighted sample should be within the 0.50–2.00 range, ideally close to 1.00. Third, the ratio of variances in the inference (sub)population and (sub)population‐weighted sample of residuals obtained by regressing each covariate on the propensity score should also be within the 0.50–2.00 range and close to 1.00. Rubin's criteria help characterize how well the propensity score reweighted samples approximate underlying inference (sub)populations of interest and help ensure that estimates of average treatment effects (ATEs) obtained by poststratification methods are not mere extrapolations (King and Zeng 2006).
We also implemented Tipton's (2014) Generalizability Index (β), which uses Bhattacharyya's coefficient to compare the distribution of propensity scores in the inference (sub)population to that in the sample (Tipton 2014; Brown 2015). Bhattacharyya's coefficient is an index that summarizes the similarity of two histograms and ranges from 0 to 1, with the following interpretation suggested by Tipton when applying the coefficient to propensity score distributions: β < 0.50 “low” generalizability of sample; 0.50 ≤ β < 0.80 “medium” generalizability of sample; 0.80 ≤ β < 0.90 “high” generalizability of sample; 0.90 ≤ β “very high” generalizability of sample. Conceptually, Tipton's β describes how close a sample is to approximating a random, probability sample from the underlying population of interest (Tipton 2014; Tipton et al. 2016).
Estimation of Sample Average Treatment Effects
Sample average treatment effects (SATEs) were estimated using the FIRST Trial sample patient‐level NSQIP data, previously described in detail elsewhere (Bilimoria et al. 2016a,b). The basic intent‐to‐treat model in the FIRST Trial regressed patient outcomes on study arm assignment (intervention [“flexible” duty hours] vs. usual care [“standard” ACGME duty hours]) with controls for randomization stratum and random intercepts (program and hospital level). Because study arm assignment was random in the FIRST Trial, the coefficient on study arm assignment identified the intent‐to‐treat estimate of the effect of assignment to flexible duty hour policies on patient outcomes. Each outcome was modeled separately.
Estimation of Stratum‐Specific Treatment Effects
To obtain stratum‐specific estimates in this study, patient outcomes were regressed on study arm assignment, propensity score stratum, and the interaction between study arm assignment and propensity score stratum using hierarchical logistic regression models that included program‐level random intercepts. Each outcome was modeled separately, and all models controlled for randomization stratum. Additional detail on estimating stratum‐specific treatment effects is provided in Appendices SA2–SA9.
Computation of Average Treatment Effects
Weighted averages across stratum‐specific treatment effects and standard errors were computed using methods described in Appendices SA2‐SA9 to obtain estimates of the average “treatment” effect of assignment to flexible duty‐hour policies among the subpopulation of nonparticipants (“SubPATE”) and estimates of the average treatment effect within the total inference population (“PATE”).
Results
At the time of recruitment, the FIRST Trial enumerated 252 ACGME‐accredited general surgery programs in the United States that were affiliated with 771 distinct clinical sites. Due to multiple affiliations, 1,048 unique program‐hospital pairs were enumerated in the total inference population after excluding ineligible programs and clinical sites other than general hospitals. Of the 1,048 program‐hospital pairs in the inference population, 152 (14.50 percent) participated in the FIRST Trial while 896 (85.50 percent) did not participate. Complete data for the propensity score model were available for 951 of the 1,048 (91 percent) program‐hospital pairs, of which 803 were nonparticipants and 148 were participants in the FIRST Trial.
Evaluation of Propensity Score Model and Generalizability of FIRST Trial
Complete estimates from our propensity score model predicting participation of program‐hospital pairs are provided in Appendices SA2–SA9.
Table 1 reports the means and standard deviations (SD) for each variable in the inference population, the inference subpopulation of nonparticipants, the FIRST Sample, the population‐weighted sample, and subpopulation‐weighted sample.
Table 1.
Means and Standard Deviation of Program‐Hospital Characteristics in the Inference Population (POP), Inference Subpopulation of Nonparticipants (SubPOP), the FIRST Sample (SAMP), Population‐Weighted Sample (PWS), and Subpopulation‐Weighted Sample (SubPWS)
| Variable | Mean (SD) | ||||
|---|---|---|---|---|---|
| POP | SubPOP | SAMP | PWS | SubPWS | |
| Propensity score (logit scale) | −2.24 (1.33) | −2.48 (1.22) | −0.96 (1.21) | −2.14 (0.29) | −2.36 (0.26) |
| Program type | |||||
| Academic | 52.79% (49.95%) | 49.94% (50.03%) | 68.24% (46.71%) | 44.82% (37.58%) | 40.49% (37.10%) |
| Community‐based | 41.54% (49.30%) | 43.71% (49.63%) | 29.73% (45.86%) | 46.57% (48.31%) | 49.68% (49.34%) |
| Military | 5.68% (23.15%) | 6.35% (24.40%) | 2.03% (14.14%) | 8.61% (10.73%) | 9.82% (12.25%) |
| Number of PGY5 slots | 5.28 (2.24) | 5.13 (2.16) | 6.06 (2.51) | 4.81 (1.66) | 4.58 (1.57) |
| Any ACGME accreditation issue | 18.09% (38.51%) | 19.30% (39.49%) | 11.49% (31.99%) | 15.06% (36.69%) | 15.72% (37.61%) |
| Research‐oriented | 82.02% (38.42%) | 80.20% (39.87%) | 91.89% (27.39%) | 78.76% (34.66%) | 76.33% (37.02%) |
| 2013 mean ABSITE scores | 502.47 (34.31) | 501.41 (34.97) | 508.20 (29.97) | 505.55 (32.81) | 505.01 (33.33) |
| Annual hospital admissions (in 1000s) | 22.21 (17.04) | 21.00 (17.22) | 28.77 (14.40) | 22.85 (10.36) | 21.75 (9.86) |
| Type of control | |||||
| Not‐for‐profit | 68.45% (46.49%) | 67.00% (47.05%) | 76.35% (42.64%) | 72.89% (45.05%) | 72.25% (45.45%) |
| For‐profit | 5.36% (22.54%) | 5.85% (23.49%) | 2.70% (16.27%) | 3.19% (12.89%) | 3.27% (12.72%) |
| Other | 26.18% (43.99%) | 27.15% (44.50%) | 20.95% (40.83%) | 23.92% (41.92%) | 24.47% (42.16%) |
| COTH membership | 51.63% (50.00%) | 47.70% (49.98%) | 72.97% (44.56%) | 50.49% (43.94%) | 46.34% (44.77%) |
| Percent Medicaid discharges | 0.22 (0.17) | 0.23 (0.17) | 0.20 (0.11) | 0.20 (0.13) | 0.20 (0.13) |
| Full‐time RN/bed | 1.99 (0.86) | 1.99 (0.87) | 2.01 (0.76) | 1.99 (0.76) | 1.98 (0.76) |
| Any transplant services | 49.32% (50.02%) | 45.33% (49.81%) | 70.95% (45.56%) | 44.16% (40.65%) | 39.21% (41.31%) |
| Level 1 trauma designation | 44.16% (49.68%) | 40.72% (49.16%) | 62.84% (48.49%) | 39.43% (38.14%) | 35.11% (37.37%) |
| Census division | |||||
| 1—New England | 6.94% (25.43%) | 5.60% (23.01%) | 14.19% (35.01%) | 9.07% (21.86%) | 8.12% (20.37%) |
| 2—Mid‐Atlantic | 19.56% (39.69%) | 21.30% (40.96%) | 10.14% (30.28%) | 18.55% (38.21%) | 20.10% (40.05%) |
| 3—East North Central | 16.51% (37.15%) | 16.69% (37.31%) | 15.54% (36.35%) | 19.35% (39.25%) | 20.05% (39.88%) |
| 4—West North Central | 6.41% (24.51%) | 5.85% (23.49%) | 9.46% (29.36%) | 4.58% (12.87%) | 3.68% (10.45%) |
| 5—South Atlantic | 16.93% (37.52%) | 16.81% (37.42%) | 17.57% (38.18%) | 21.08% (32.89%) | 21.73% (32.43%) |
| 6—East South Central | 5.57% (22.95%) | 5.23% (22.28%) | 7.43% (26.32%) | 5.23% (17.22%) | 4.82% (15.82%) |
| 7—West South Central | 9.36% (29.14%) | 9.59% (29.46%) | 8.11% (27.39%) | 7.26% (19.63%) | 7.10% (18.59%) |
| 8—Mountain | 4.84% (21.47%) | 5.11% (22.03%) | 3.38% (18.13%) | 3.38% (13.70%) | 3.38% (13.15%) |
| 9—Pacific | 13.88% (34.59%) | 13.82% (34.54%) | 14.19% (35.01%) | 11.50% (28.37%) | 11.00% (27.29%) |
Total inference population (POP) N = 951 program‐hospital pairs with complete data for our analyses; subpopulation of FIRST Trial nonparticipants (SubPOP) n = 803 pairs; FIRST Trial sample = 148 pairs.
Inference Population versus FIRST Sample
Table 2 shows |SMD|s between the inference population and FIRST Sample for each covariate in the propensity model. None of the |SMD|s between the population and sample were >0.5 (Rubin Criteria 1) for any of the covariates in the propensity model. Most of the variance ratios of residuals between the inference and sample were close to one, with only two lying outside the prescribed 0.50–2.00 range: proportion program‐hospital pairs that were military based, and percent of Medicaid discharges.
Table 2.
Inference Population (POP), FIRST Sample (SAMP), and Population‐Weighted Sample (PWS) Comparisons
| Variable | POP vs. SAMP | POP vs. PWS | ||
|---|---|---|---|---|
| |SMD| | Rubin Criterion 3 σ 2 POPRESID/σ 2 SAMPRESID a | |SMD| | Rubin Criterion 3 σ 2 POPRESID/σ 2 PWSRESID a | |
| Propensity score (logit scale) | 0.96b | — | 0.08 | — |
| Program type | ||||
| Academic | 0.31 | 1.03 | 0.16 | 1.17 |
| Community‐based | 0.24 | 1.02 | 0.10 | 0.91 |
| Military | 0.16 | 5.09a | 0.13 | 1.56 |
| Number of PGY5 slots | 0.35 | 0.83 | 0.21 | 1.34 |
| Any ACGME accreditation issue | 0.17 | 0.83 | 0.08 | 0.91 |
| Research‐oriented | 0.26 | 1.35 | 0.08 | 0.85 |
| 2013 mean ABSITE scores | 0.17 | 1.26 | 0.09 | 1.05 |
| Annual hospital admissions (1000s) | 0.39 | 1.50 | 0.04 | 2.14a |
| Type of control | ||||
| Not‐for‐profit | 0.17 | 1.03 | 0.10 | 1.01 |
| For‐profit | 0.12 | 1.34 | 0.10 | 1.21 |
| Other | 0.12 | 1.02 | 0.05 | 1.04 |
| COTH membership | 0.43 | 1.04 | 0.02 | 0.96 |
| Percent Medicaid discharges | 0.11 | 2.21a | 0.12 | 1.51 |
| Full‐time RN/bed | 0.02 | 1.28 | 0.00 | 1.12 |
| Any transplant services | 0.43 | 1.14 | 0.10 | 1.06 |
| Level 1 trauma designation | 0.38 | 1.17 | 0.10 | 1.29 |
| Census division | ||||
| 1—New England | 0.29 | 0.85 | 0.08 | 0.51 |
| 2—Mid‐Atlantic | 0.24 | 1.09 | 0.03 | 0.90 |
| 3—East North Central | 0.03 | 0.94 | 0.08 | 0.79 |
| 4—West North Central | 0.12 | 1.11 | 0.07 | 2.04a |
| 5—South Atlantic | 0.02 | 0.99 | 0.11 | 0.97 |
| 6—East South Central | 0.08 | 1.08 | 0.01 | 1.26 |
| 7—West South Central | 0.04 | 1.07 | 0.07 | 1.25 |
| 8—Mountain | 0.07 | 1.17 | 0.07 | 1.29 |
| 9—Pacific | 0.01 | 1.03 | 0.07 | 1.18 |
Additional tests: Rubin (2001) Criterion 2: ratio of variance of propensity score between groups should be within (0.5, 2) range. This ratio was 1.21 between POP and SAMP and 16.02 between the POP and PWS. Tipton's Generalizability Index (β) was 0.87 (POP vs. SAMP). According to Tipton (2014): β < 0.50 “low”; 0.50 ≤ β < 0.80 “medium”; 0.80 ≤ β < 0.90 “high”; 0.90 ≤ β “very high” generalizability of sample.
Rubin (2001) Criterion 2: ratio of variance of residuals should be within (0.5, 2) range.
Rubin (2001) Criterion 1: |SMD|s > 0.5 SDs may indicate distributional dissimilarity between groups.
The propensity score model was reasonably successful in balancing covariates between the inference population and sample. |SMD|s between the inference population and population‐weighted sample were generally smaller than between the inference population and sample. As before, none of the |SMD|s were greater than 0.50. Variance ratios of residuals between the inference population and population‐weighted sample barely exceeded 2.00 for two covariates: annual hospital admission volume and proportion program‐hospital pairs in the West North Central census division.
Rubin advises that the variance ratio of propensity scores in two groups should be within the 0.50–2.00 range; however, we computed this ratio to be 1.21 between the inference population and the sample and 16.02 between the population and the population‐weighted sample.
Tipton's β comparing the similarity of propensity score distributions in the inference population to that in the sample was 0.87 or “very highly” generalizable. Together, these assessments generally suggest that the population‐weighted sample obtained by propensity score‐based poststratification is adequately similar to the inference population and that ATEs obtained from subclassification procedures may produce valid estimates of PATEs. However, the lone violation of Rubin's second criterion suggests caution.
Inference Subpopulation (Nonparticipants) versus FIRST Sample
Table 3 compares the inference subpopulation of nonparticipants, the FIRST Sample, and the subpopulation‐weighted sample. |SMD|s between nonparticipants and the FIRST Sample exceeded 0.50 SDs (subpopulation) for one covariate: proportion program‐pairs providing transplant services. Variance ratios of residuals exceeded 2.00 for two covariates: proportion military‐based program‐pairs and percent Medicaid discharges.
Table 3.
Inference Subpopulation (SubPOP), FIRST Sample (SAMP), and Subpopulation‐Weighted Sample (SubPWS) Comparisons
| Variable | SubPOP vs. SAMP | SubPOP vs. SubPWS | ||
|---|---|---|---|---|
| |SMD| | Rubin Criterion 3 σ 2 SUBPOPPRESID/σ 2 SAMPRESID a | |SMD| | Rubin Criterion 3 σ 2 SUBPOPRESID/σ 2 SUBPWSRESID a | |
| Propensity score (logit scale) | 2.30b | — | 0.11 | — |
| Program type | ||||
| Academic | 0.35 | 1.03 | 0.17 | 1.21 |
| Community‐based | 0.28 | 1.02 | 0.09 | 0.90 |
| Military | 0.16 | 5.83a | 0.17 | 1.57 |
| Number of PGY5 slots | 0.42 | 0.80 | 0.23 | 1.44 |
| Any ACGME accreditation issue | 0.22 | 0.80 | 0.16 | 0.90 |
| Research‐oriented | 0.37 | 1.41 | 0.00 | 0.84 |
| 2013 mean ABSITE scores | 0.20 | 1.30 | 0.11 | 1.05 |
| Annual hospital admissions (1000s) | 0.45 | 1.59 | 0.05 | 2.48a |
| Type of control | ||||
| Not‐for‐profit | 0.21 | 1.04 | 0.12 | 1.02 |
| For‐profit | 0.16 | 1.40 | 0.13 | 1.24 |
| Other | 0.13 | 1.03 | 0.06 | 1.05 |
| COTH membership | 0.49 | 1.05 | 0.01 | 0.95 |
| Percent Medicaid discharges | 0.13 | 2.43a | 0.14 | 1.57 |
| Full‐time RN/bed | 0.04 | 1.33 | 0.02 | 1.14 |
| Any transplant services | 0.55b | 1.16 | 0.08 | 1.06 |
| Level 1 trauma designation | 0.49 | 1.20 | 0.06 | 1.35 |
| Census division | ||||
| 1—New England | 0.31 | 0.82 | 0.08 | 0.46a |
| 2—Mid‐Atlantic | 0.27 | 1.11 | 0.02 | 0.89 |
| 3—East North Central | 0.01 | 0.93 | 0.11 | 0.75 |
| 4—West North Central | 0.16 | 1.13 | 0.10 | 2.47a |
| 5—South Atlantic | 0.01 | 0.99 | 0.11 | 0.95 |
| 6—East South Central | 0.11 | 1.09 | 0.00 | 1.33 |
| 7—West South Central | 0.09 | 1.09 | 0.11 | 1.31 |
| 8—Mountain | 0.06 | 1.20 | 0.06 | 1.35 |
| 9—Pacific | 0.04 | 1.04 | 0.07 | 1.22 |
Additional tests: Rubin (2001) Criterion 2: ratio of variance of propensity score between groups should be within (0.5, 2) range. This ratio was 1.00 between SubPOP and SAMP and 17.23 between the SubPOP and SubPWS. Tipton's Generalizability Index (β) was 0.80 (SubPOP vs. SAMP). According to Tipton (2014): β < 0.50 “low”; 0.50 ≤ β < 0.80 “medium”; 0.80 ≤ β < 0.90 “high”; 0.90 ≤ β “very high” generalizability of sample.
Rubin (2001) Criterion 2: ratio of variance of residuals should be within (0.5, 2) range.
Rubin (2001) Criterion 1: |SMD|s > 0.5 SDs may indicate distributional dissimilarity between groups.
Propensity score reweighting generally appears to have improved covariate balance in the subpopulation‐weighted sample (SubPWS). After reweighting, |SMD|s were generally smaller, and none were >0.50 SD (subpopulation). Variance ratios of residuals fell slightly outside the 0.50–2.00 range for three covariates: annual hospital admission volume, proportion program‐pairs in New England, and proportion program‐pairs in West North Central.
However, Rubin's second criterion was violated once again. The variance ratio of propensity scores in the inference subpopulation and sample was 1.00, but it was 17.23 in the subpopulation and subpopulation‐weighted sample.
Tipton's β was 0.80, indicating “high” generalizability of the sample. Despite violation of Rubin's second criterion, we cautiously conclude that Rubin's 1st and 3rd criteria and Tipton's Index suggest that average treatment effects estimated from the SubPWS may provide estimates of the subpopulation average treatment effect (SubPATE).
Population Average Treatment Effect of Flexible Duty Hour Policies on Patient Outcomes
Figure 1 shows the estimated average effect of assignment to flexible duty‐hour policies on patient outcomes in the FIRST Sample (SATE), inference population (PATE), and inference subpopulation of nonparticipants in the trial (SubPATE). Effects are expressed as odds ratios (OR) contrasting assignment to flexible duty hour policies against standard ACGME duty hour policies. Blue‐shaded regions depict areas within the margin of noninferiority predetermined by FIRST Trial investigators (Bilimoria et al. 2016a,b). Flexible duty hour policies were deemed superior to standard ACGME policies if both the point estimate and upper bound of the 92 percent confidence interval (92 percent UB) were below 1.00. Noninferiority was conclusively established if both the point estimate and the 92 percent UB were below the noninferiority margin. Noninferiority was inconclusive if the point estimate was below the noninferiority margin, but the 92 percent UB confidence interval extended beyond it. Inferiority was inconclusive if the point estimate extended outside the noninferiority margin, but the lower bound of the 92 percent confidence interval (92 percent LB) was contained within the lower bound. Flexible duty‐hour policies were deemed conclusively inferior to ACGME policies if both the point estimate and the 92 percent LB were to the right of the inferiority margin.
Figure 1.
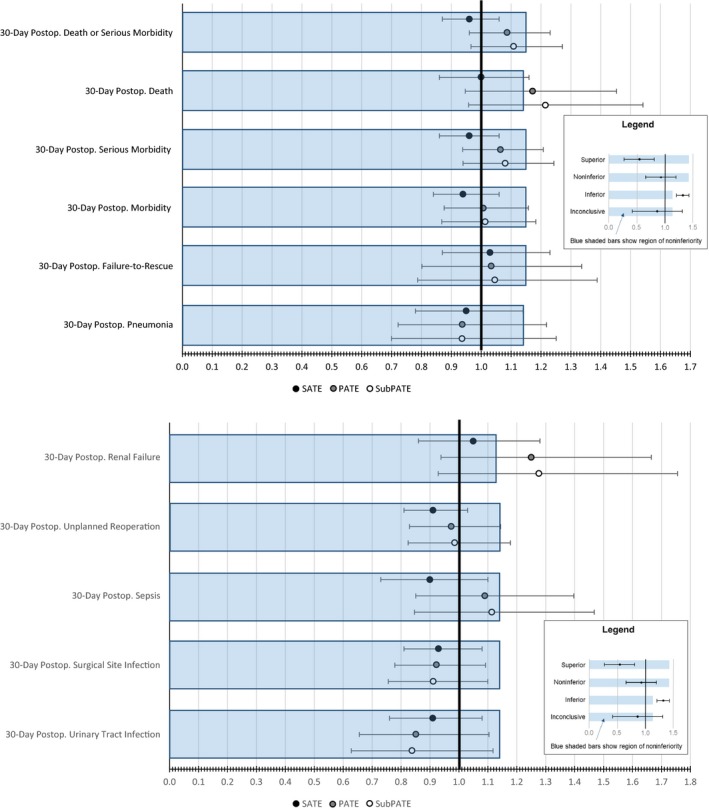
Estimated Sample Average Treatment Effects and Population Average Treatment Effects of Flexible Duty Hour Policies on Patient Outcomes [Color figure can be viewed at http://wileyonlinelibrary.com]
As previously reported and as shown in Figure 1, SATE estimates were either conclusively noninferior (DSM, serious morbidity, morbidity, pneumonia, unplanned reoperation, sepsis, SSI, UTI) or inconclusively noninferior to standard duty hour policy (death, failure‐to‐rescue, renal failure) (Bilimoria et al. 2016a). However, only two PATE estimates were conclusively noninferior (SSI, UTI). For seven outcomes, PATE estimates were inconclusively noninferior (DSM, serious morbidity, morbidity, failure‐to‐rescue, pneumonia, unplanned reoperation, and sepsis). For two outcomes, PATE estimates were inconclusively inferior (death and renal failure). SubPATE estimates were very similar to PATE estimates and were conclusively noninferior for SSI and UTI and inconclusively inferior to standard duty hour policy for death and renal failure. Confidence intervals around PATE and SubPATE estimates were considerably wider than those around SATE.
Discussion
Summary
We demonstrated how propensity score‐based poststratification can be used to estimate the PATE in the FIRST Trial, a cluster‐randomized trial comparing the effect of flexible resident duty hour policies versus standard ACGME duty hour policies on patient outcomes and resident outcomes (Appendices SA2–SA9). Previous work showed that large, academic medical centers and research‐oriented programs were overrepresented in the FIRST Trial due to the eligibility requirement that hospitals participate in ACS NSQIP. Given the nonrepresentativeness of the FIRST Trial sample, it is of policy relevance to assess how generalizable the FIRST Trial results are vis‐à‐vis nonparticipating programs, as well as the inference population taken as a whole.
Confidence intervals around (Sub)PATE estimates were substantially wider than those around SATE estimates. Consequently, while the FIRST Trial found that 30‐day DSM was conclusively noninferior under flexible duty hour policies based on the SATE, our (Sub)PATE estimates suggest that flexible policy was inconclusively noninferior to standard ACGME policies for this outcome.
Limitations
Our study should be considered alongside its limitations. First, propensity score methods only reduce bias due to selection on observables. A mis‐specified propensity score model (such as one with omitted variables) can lead to biased estimates of treatment effects (Drake 1993). Despite the balance in observables achieved following poststratification (Tables 1 and 2), there could have been unmeasured characteristics that determine trial participation and outcomes (or treatment effect) that we could not account for. Because there were no theoretical reasons for including interactions among covariates, we omitted them from the propensity model for parsimony. If there were omitted variables and/or interactions that should have been included in the model, then trial participation would not be strongly ignorable due to unobserved confounders, and (Sub)PATE estimates might be biased (Joffe and Rosenbaum 1999).
A limitation of the propensity score poststratification method is greater imprecision in PATE estimates compared to SATE estimates. Wider confidence intervals around our (Sub)PATE estimates imply greater uncertainty around the potential effects of flexible duty hour policies in the inference (sub)population. In the context of noninferiority or equivalence designs, wider confidence intervals may change conclusions based on SATEs. In our evaluation of the FIRST Trial, seven outcomes for which flexible duty hours were conclusively noninferior based on SATE estimates were inconclusively noninferior based on (Sub)PATE estimates.
Imprecision in our (Sub)PATE estimates may be due to uneven distribution of the FIRST Sample across propensity score strata despite full coverage. Sparse strata may yield highly imprecise stratum‐specific estimates of the treatment effect. If the distribution of the sample across strata poorly matches the distribution of the population across strata, then noisy stratum‐specific estimates will be weighted more heavily and will introduce greater uncertainty in (Sub)PATE estimates. This underscores the importance of planning trial samples with generalization to an inference population in mind (Tipton 2013b; O'Muircheartaigh and Hedges 2014; Tipton et al. 2014).
An alternative approach to estimating average treatment effects was recently proposed by Rudolph et al. (2016), in which stratum weights are defined as the inverse of the variance of the stratum‐specific SATEs divided by the sum across strata of the inverse variances of stratum‐specific treatment effects. Compared to weighting by the proportion of the inference population in each stratum as we did in this paper, Rudolph et al.'s method was shown to yield more precise estimates of ATEs when treatment effects are constant across strata (Rudolph et al. 2016). However, ATEs estimated using Rudolph's approach may not be interpretable as a population average treatment effect because the weights do not correspond to the relative distribution of stratum‐specific units within the overall inference population.
Conclusion
Problems of generalizability in major trials have become increasingly salient, focusing greater attention on the importance of external validity of RCTs in evidence‐based medicine and/or policy (Steckler and McLeroy 2008).
Pragmatic trial designs, population‐based probability sampling, and effectiveness studies have all been advocated as strategies for addressing concerns about external validity in studies (Gotay 2006). In the study design phase, external validity can be addressed through informed sampling designs (Tipton 2013b; Tipton et al. 2014).
After a study has concluded, generalizability can still be assessed through the use of propensity score‐based subclassification approaches such as that developed by O'Muircheartaigh and Hedges (2014) and as we demonstrated in this paper. An advantage of this approach is that it only requires data sufficient to estimate a propensity model of study participation. Data on treatment and outcomes among nonparticipants are not required. The use of propensity score methods to estimate PATEs has been explored by others in the context of propensity score weighting (Stuart et al. 2011; Stuart, Bradshaw, and Leaf 2015). Weighting approaches also begin with a propensity score model to study inclusion, but rather than stratify observations by propensity scores, observations in the study sample are weighted by the inverse probability of study participation. A drawback of inverse probability weighting is the possibility that extreme weights may allow rare observations to distort results (Ellis and Brookhart 2013). In hierarchical data, it may also be unclear at which level a weight should be applied.
We demonstrated the feasibility of using propensity score‐based stratification as a method for estimating population average treatment effects in studies with nonrepresentative samples, such as the FIRST Trial. As applied to the FIRST Trial, we found that PATE estimates of the effects of assignment to flexible duty hour policies (vs. standard ACGME duty hour policies) were consistent with SATE estimates, but they were less efficient due to sparse strata.
Supporting information
Appendix SA1: Author Matrix.
Appendix SA2: Methodological Details.
Appendix SA3: Propensity Score Model for PATIENT OUTCOMES Analyses.
Appendix SA4: Stratum‐Specific Sample Estimates of Effects of Assignment to Flexible Duty Hours on PATIENT OUTCOMES.
Appendix SA5: Overview of Resident Outcomes Analyses.
Appendix SA6: Propensity Score Model for RESIDENT OUTCOMES Analyses.
Appendix SA7: Evaluating Propensity Score Model for RESIDENT OUTCOMES Analyses.
Appendix SA8: Stratum‐Specific Sample Estimates of Effects of Assignment to Flexible Duty Hours on RESIDENT OUTCOMES.
Appendix SA9: Subpopulation and Population Average Effects of Assignment to Flexible Duty Hours on RESIDENT OUTCOMES (SubPATE and PATE).
Acknowledgments
Joint Acknowledgment/Disclosure Statement: Support for the FIRST Trial was provided by the American Board of Surgery (ABS), the American College of Surgeons (ACS), and the Accreditation Council for Graduate Medical Education (ACGME). Additional support from this work was provided by the Department of Surgery, Feinberg School of Medicine, Northwestern University. The authors wish to acknowledge the following individuals for the invaluable contributions to the FIRST Trial: Allison R. Dahlke, M.P.H., Remi R. Love, B.S., Mark E. Cohen, Ph.D., Anthony D. Yang, M.D., John L. Tarpley, M.D., John D. Mellinger, M.D., David M. Mahvi, M.D., Rachel R. Kelz, M.D., M.S.C.E., Clifford Y. Ko, M.D., M.S.H.S., David D. Odell, M.D., M.M.Sc., Frank R. Lewis, M.D., Jonathan Fryer, M.D., Anne Grace, Ph.D., Julie K. Johnson, Ph.D., Lindsey J. Kreutzer, M.P.H., Shari Meyerson, M.D., Emily S. Pavey, M.A., Sean Perry, J.D., Alfred Rademaker, Ph.D., Ravi Rajaram, M.D., Judy Shea, Ph.D., Sameera Ali, M.P.H., Amy Hart, B.S., Emma Malloy, B.A., Brian Matel, B.A., Craig Miller, B.S.E.E., Lynn Modla, M.S., Ajit Sachdeva, M.D., Lynn Zhou, Ph.D., James Hebert, M.D., Michael Englesbe, M.D., M.P.H., Paul Gauger, M.D., Christine V. Kinnier, M.D., Joseph Cofer, M.D., Mitchell Posner, M.D., Eugene Foley, M.D., Thomas Louis, Ph.D., Thomas Biester, M.S., Andrew Jones, Ph.D., Rebecca Miller, M.S., Thomas Nasca, M.D., John Potts, M.D., Margaret M. Class, and all the program directors, program coordinators, surgeon champions, and surgical clinical reviewers at the participating residency programs and hospitals.
Disclosures: None.
Disclaimer: None.
References
- Bilimoria, K. Y. , Chung J. W., Hedges L. V., Dahlke A. R., Love R., Cohen M. E., Hoyt D. B., Yang A. D., Tarpley J. L., Mellinger J. D., Mahvi D. M., Kelz R. R., Ko C. Y., Odell D. D., Stulberg J. J., and Lewis F. R.. 2016a. “National Cluster‐Randomized Trial of Duty‐Hour Flexibility in Surgical Training.” New England Journal of Medicine 374 (8): 713–27. [DOI] [PubMed] [Google Scholar]
- Bilimoria, K. Y. , Chung J. W., Hedges L. V., Dahlke A. R., Love R., Cohen M. E., Tarpley J., Mellinger J., Mahvi D. M., Kelz R. R., Ko C. Y., Hoyt D. B., and Lewis F. H.. 2016b. “Development of the Flexibility in Duty Hour Requirements for Surgical Trainees (FIRST) Trial Protocol: A National Cluster‐Randomized Trial of Resident Duty Hour Policies.” JAMA Surgery 151 (3): 273–81. [DOI] [PubMed] [Google Scholar]
- Blanco, C. , Olfson M., Goodwin R. D., Ogburn E., Liebowitz M. R., Nunes E. V., and Hasin D. S.. 2008a. “Generalizability of Clinical Trial Results for Major Depression to Community Samples: Results From the National Epidemiologic Survey on Alcohol and Related Conditions.” Journal of Clinical Psychiatry 69 (8): 1276–80. [DOI] [PubMed] [Google Scholar]
- Blanco, C. , Olfson M., Okuda M., Nunes E. V., Liu S.‐M., and Hasin D. S.. 2008b. “Generalizability of Clinical Trials for Alcohol Dependence to Community Samples.” Drug and Alcohol Dependence 98 (1–2): 123–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brookhart, M. A. , Schneeweiss S., Rothman K. J., Glynn R. J., Avorn J., and Sturmer T.. 2006. “Variable Selection for Propensity Score Models.” American Journal of Epidemiology 163 (12): 1149–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown, G. K. 2015. “BHATT: Stata Module to Compute Bhattacharyya Coefficient and Bhattacharyya Distance Statistics of Distribution Overlap.” Boston College Department of Economics.
- D'Agostino, R. B. 1998. “Propensity Score Methods for Bias Reduction in the Comparison of a Treatment to a Non‐Randomized Control Group.” Statistics in Medicine 17 (19): 2265–81. [DOI] [PubMed] [Google Scholar]
- Drake, C. 1993. “Effects of Misspecification of the Propensity Score on Estimators of Treatment Effect.” Biometrics 49: 1231–6. [Google Scholar]
- Ellis, A. R. , and Brookhart M. A.. 2013. “Approaches to Inverse‐Probability‐of‐Treatment–Weighted Estimation with Concurrent Treatments.” Journal of Clinical Epidemiology 66 (8 Suppl): S51–6. [DOI] [PubMed] [Google Scholar]
- Elting, L. S. , Cooksley C., Bekele B. N., Frumovitz M., Avritscher E. B. C., Sun C., and Bodurka D. C.. 2006. “Generalizability of Cancer Clinical Trial Results: Prognostic Differences between Participants and Nonparticipants.” Cancer 106 (11): 2452–8. [DOI] [PubMed] [Google Scholar]
- Gandhi, M. , Ameli N., Bacchetti P., Sharp G. B., French A. L., Young M., Gange S. J., Anastos K., Holman S., Levine A., and Greenblatt R. M.. 2005. “Eligibility Criteria for HIV Clinical Trials and Generalizability of Results: The Gap Between Published Reports and Study Protocols.” AIDS (London, England) 19 (16): 1885–96. [DOI] [PubMed] [Google Scholar]
- Gotay, C. C. 2006. “Increasing trial Generalizability.” Journal of Clinical Oncology 24 (6): 846–7. [DOI] [PubMed] [Google Scholar]
- Gross, C. P. , Filardo G., Mayne S. T., and Krumholz H. M.. 2005. “The Impact of Socioeconomic Status and Race on Trial Participation for Older Women with Breast Cancer.” Cancer 103 (3): 483–91. [DOI] [PubMed] [Google Scholar]
- Guyatt, G. H. , Haynes R. B., Jaeschke R. Z., Cook D. J., Green L., Naylor C. D., Wilson M. C., and Richardson W. S.. 2000. “Users' Guides to the Medical Literature: XXV. Evidence‐Based Medicine: Principles for Applying the Users' Guides to Patient Care. Evidence‐Based Medicine Working Group.” Journal of the American Medical Association 284 (10): 1290–6. [DOI] [PubMed] [Google Scholar]
- Hennekens, C. H. , and Buring J. E.. 1998. “Validity Versus Generalizability in Clinical Trial Design and Conduct.” Journal of Cardiac Failure 4 (3): 239–41. [DOI] [PubMed] [Google Scholar]
- Hoertel, N. , Le Strat Y., Blanco C., Lavaud P., and Dubertret C.. 2012. “Generalizability of Clinical Trial Results for Generalized Anxiety Disorder to Community Samples.” Depression and Anxiety 29 (7): 614–20. [DOI] [PubMed] [Google Scholar]
- Hoertel, N. , Le Strat Y., Lavaud P., Dubertret C., and Limosin F.. 2013. “Generalizability of Clinical Trial Results for Bipolar Disorder to Community Samples: Findings from the National Epidemiologic Survey on Alcohol and Related Conditions.” Journal of Clinical Psychiatry 74 (3): 265–70. [DOI] [PubMed] [Google Scholar]
- Humphreys, K. , Maisel N. C., Blodgett J. C., Fuh I. L., and Finney J. W.. 2013. “Extent and Reporting of Patient Nonenrollment in Influential Randomized Clinical Trials, 2002 to 2010.” Journal of the American Medical Association Internal Medicine 173 (11): 1029–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joffe, M. M. , and Rosenbaum P. R.. 1999. “Invited Commentary: Propensity Scores.” American Journal of Epidemiology 150 (4): 327–33. [DOI] [PubMed] [Google Scholar]
- Kennedy‐Martin, T. , Curtis S., Faries D., Robinson S., and Johnston J.. 2015. “A Literature Review on the Representativeness of Randomized Controlled Trial Samples and Implications for the External Validity of Trial Results.” Trials 16: 495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King, G. , and Zeng L. C.. 2006. “The Dangers of Extreme Counterfactuals.” Political Analysis 14 (2): 131–59. [Google Scholar]
- Lamont, E. B. , Schilsky R. L., He Y., Muss H., Cohen H. J., Hurria A., Meilleur A., Kindler H. L., Venook A., Lilenbaum R., Niell H., Goldberg R. M., Joffe S., and O. Alliance for Clinical Trials in . 2015. “Generalizability of Trial Results to Elderly Medicare Patients with Advanced Solid Tumors (Alliance 70802).” Journal of the National Cancer Institute 107 (1): 336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Strat, Y. , Rehm J., and Le Foll B.. 2011. “How Generalisable to Community Samples Are Clinical Trial Results for Treatment of Nicotine Dependence: A Comparison of Common Eligibility Criteria with Respondents of a Large Representative General Population Survey.” Tobacco Control 20 (5): 338–43. [DOI] [PubMed] [Google Scholar]
- Li, F. , Zaslavsky A. M., and Landrum M. B.. 2013. “Propensity Score Weighting with Multilevel Data.” Statistics in Medicine 32 (19): 3373–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magee, L. A. , Bull S. B., Koren G., and Logan A.. 2001. “The Generalizability of Trial Data; A Comparison of Beta‐Blocker Trial Participants with a Prospective Cohort of Women Taking Beta‐Blockers in Pregnancy.” European Journal of Obstetrics, Gynecology, and Reproductive Biology 94 (2): 205–10. [DOI] [PubMed] [Google Scholar]
- Murthy, V. H. , Krumholz H. M., and Gross C. P.. 2004. “Participation in Cancer Clinical Trials: Race‐, Sex‐, and Age‐Based Disparities.” Journal of the American Medical Association 291 (22): 2720–6. [DOI] [PubMed] [Google Scholar]
- O'Muircheartaigh, C. , and Hedges L. V.. 2014. “Generalizing from Unrepresentative Experiments: A Stratified Propensity Score Approach.” Journal of the Royal Statistical Society Series C‐Applied Statistics 63 (2): 195–210. [Google Scholar]
- Rosenbaum, P. R. , and Rubin D. B.. 1983. “The Central Role of the Propensity Score in Observational Studies for Causal Effects.” Biometrika 70 (1): 41–55. [Google Scholar]
- Rosenbaum, P. R. , and Rubin D. B.. 1984. “Reducing Bias in Observational Studies Using Subclassification on the Propensity Score.” Journal of the American Statistical Association 79 (387): 516–24. [Google Scholar]
- Rovers, M. M. , Straatman H., Ingels K., van der Wilt G. J., van den Broek P., and Zielhuis G. A.. 2001. “Generalizability of Trial Results Based on Randomized Versus Nonrandomized Allocation of OME Infants to Ventilation Tubes or Watchful Waiting.” Journal of Clinical Epidemiology 54 (8): 789–94. [DOI] [PubMed] [Google Scholar]
- Rubin, D. B. 2001. “Using Propensity Scores to Help Design Observational Studies: Application to the Tobacco Litigation.” Health Services & Outcomes Research Methodology 2 (3–4): 169–88. [Google Scholar]
- Rudolph, K. E. , Colson K. E., Stuart E. A., and Ahern J.. 2016. “Optimally Combining Propensity Score Subclasses.” Statistics in Medicine 35 (27): 4937–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sackett, D. L. 1989. “Rules of Evidence and Clinical Recommendations on the Use of Antithrombotic Agents.” Chest 95 (2 Suppl): 2S–4S. [PubMed] [Google Scholar]
- Steckler, A. , and McLeroy K. R.. 2008. “The Importance of External Validity.” American Journal of Public Health 98 (1): 9–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart, J. H. , Bertoni A. G., Staten J. L., Levine E. A., and Gross C. P.. 2007. “Participation in Surgical Oncology Clinical Trials: Gender‐, Race/Ethnicity‐, and Age‐Based Disparities.” Annals of Surgical Oncology 14 (12): 3328–34. [DOI] [PubMed] [Google Scholar]
- Storms, W. 2003. “Clinical Trials: Are These Your Patients?” Journal of Allergy and Clinical Immunology 112 (5 Suppl): S107–11. [DOI] [PubMed] [Google Scholar]
- Stuart, E. A. , Bradshaw C. P., and Leaf P. J.. 2015. “Assessing the Generalizability of Randomized Trial Results to Target Populations.” Prevention Science 16 (3): 475–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart, E. A. , Cole S. R., Bradshaw C. P., and Leaf P. J.. 2011. “The Use of Propensity Scores to Assess the Generalizability of Results from Randomized Trials.” Journal of the Royal Statistical Society Series a‐Statistics in Society 174: 369–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tipton, E. 2013a. “Improving Generalizations from Experiments Using Propensity Score Subclassification: Assumptions, Properties, and Contexts.” Journal of Educational and Behavioral Statistics 38: 239–66. [Google Scholar]
- Tipton, E. . 2013b. “Stratified Sampling Using Cluster Analysis a Sample Selection Strategy for Improved Generalizations from Experiments.” Evaluation Review 37 (2): 109–39. [DOI] [PubMed] [Google Scholar]
- Tipton, E. . 2014. “How Generalizable Is Your Experiment? An Index for Comparing Experimental Samples and Populations.” Journal of Educational and Behavioral Statistics 39 (6): 478–501. [Google Scholar]
- Tipton, E. , Hedges L., Vaden‐Kiernan M., Borman G., Sullivan K., and Caverly S.. 2014. “Sample Selection in Randomized Experiments: A New Method Using Propensity Score Stratified Sampling.” Journal of Research on Educational Effectiveness 7 (1): 114–35. [Google Scholar]
- Tipton, E. , Hallberg K., Hedges L. V., and Chan W.. 2016. “Implications of Small Samples for Generalization: Adjustments and Rules of Thumb.” Evaluation Review. [DOI] [PubMed] [Google Scholar]
- Tricoci, P. , Allen J. M., Kramer J. M., Califf R. M., and Smith S. C. Jr. 2009. “Scientific Evidence Underlying the ACC/AHA Clinical Practice Guidelines.” Journal of the American Medical Association 301 (8): 831–41. [DOI] [PubMed] [Google Scholar]
- Wissing, M. D. , Kluetz P. G., Ning Y. M., Bull J., Merenda C., Murgo A. J., and Pazdur R.. 2014. “Under‐Representation of Racial Minorities in Prostate Cancer Studies Submitted to the US Food and Drug Administration to Support Potential Marketing Approval, 1993‐2013.” Cancer 120 (19): 3025–32. [DOI] [PubMed] [Google Scholar]
- Wright, J. G. , Swiontkowski M. F., and Heckman J. D.. 2003. “Introducing Levels of Evidence to the Journal.” Journal of Bone and Joint Surgery American Volume 85‐A (1): 1–3. [PubMed] [Google Scholar]
- Zimmerman, M. , Chelminski I., and Posternak M. A.. 2005. “Generalizability of Antidepressant Efficacy Trials: Differences Between Depressed Psychiatric Outpatients Who Would or Would Not Qualify for an Efficacy Trial.” American Journal of Psychiatry 162 (7): 1370–2. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix SA1: Author Matrix.
Appendix SA2: Methodological Details.
Appendix SA3: Propensity Score Model for PATIENT OUTCOMES Analyses.
Appendix SA4: Stratum‐Specific Sample Estimates of Effects of Assignment to Flexible Duty Hours on PATIENT OUTCOMES.
Appendix SA5: Overview of Resident Outcomes Analyses.
Appendix SA6: Propensity Score Model for RESIDENT OUTCOMES Analyses.
Appendix SA7: Evaluating Propensity Score Model for RESIDENT OUTCOMES Analyses.
Appendix SA8: Stratum‐Specific Sample Estimates of Effects of Assignment to Flexible Duty Hours on RESIDENT OUTCOMES.
Appendix SA9: Subpopulation and Population Average Effects of Assignment to Flexible Duty Hours on RESIDENT OUTCOMES (SubPATE and PATE).


