Sequence diversity of tubulin isotypes in regulation of the mitochondrial voltage-dependent anion channel

Abstract

The microtubule protein tubulin is a heterodimer comprising α/β subunits, in which each subunit features multiple isotypes in vertebrates. For example, seven α-tubulin and eight β-tubulin isotypes in the human tubulin gene family vary mostly in the length and primary sequence of the disordered anionic carboxyl-terminal tails (CTTs). The biological reason for such sequence diversity remains a topic of vigorous enquiry. Here, we demonstrate that it may be a key feature of tubulin's role in regulation of the permeability of the mitochondrial outer membrane voltage-dependent anion channel (VDAC). Using recombinant yeast α/β-tubulin constructs with α-CTTs, β-CTTs, or both from various human tubulin isotypes, we probed their interactions with VDAC reconstituted into planar lipid bilayers. A comparative study of the blockage kinetics revealed that either α-CTTs or β-CTTs block the VDAC pore and that the efficiency of blockage by individual CTTs spans 2 orders of magnitude, depending on the CTT isotype. β-Tubulin constructs, notably β3, blocked VDAC most effectively. We quantitatively described these experimental results using a physical model that accounted only for the number and distribution of charges in the CTT, and not for the interactions between specific residues on the CTT and VDAC pore. Based on these results, we speculate that the effectiveness of VDAC regulation by tubulin depends on the predominant tubulin isotype in a cell. Consequently, the fluxes of ATP/ADP through the channel could vary significantly, depending on the isotype, thus suggesting an intriguing link between VDAC regulation and the diversity of tubulin isotypes present in vertebrates.

Introduction

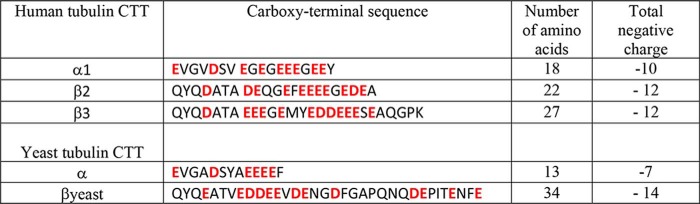
Tubulin is an abundant cytosolic protein known primarily as the building block of microtubules. It is a heterodimer with α- and β-subunits forming an acidic, water-soluble, compactly folded 110-kDa protein with a well-defined crystal structure (1). Each subunit of human tubulin has a highly negatively charged unstructured carboxyl-terminal tail (CTT)³ composed of 10–27 amino acids (2) exposed at the protein surface. The data on the exact length of individual CTTs vary slightly in different sources, depending on which residue is chosen as the beginning of the CTT (e.g. compare Refs. 1–4). Here, we follow the Nogales et al. (1) definition of the beginning of the CTT as the end of the H12 helix at residue 430 (Table 1). In vertebrates, tubulin possesses significant variability due to the expression of several tubulin genes. Seven α- and eight β-tubulin isotypes in the human tubulin gene family vary mostly in the length and primary sequence of the CTTs (5). By contrast, lower eukaryotes have fewer tubulin genes (e.g. yeast tubulin has just two α-tubulin isotypes and one β-tubulin isotype) (6). The highest sequence variability in CTTs is found in the β-tubulin isotypes. In addition, β-isotypes have different expression levels in different tissue types. For instance, β2 is enriched in the brain, where it constitutes 58% of the total β-tubulin (7), whereas β3 is found exclusively in neuronal cells and in large numbers of cancer cells of nonneuronal origin (8). However, the role of tubulin genetic diversity remains largely unknown (9). Mutations in various tubulin isotypes have been associated with a broad spectrum of human pathologies ranging from blood clotting to oncology and neurological disorders (10). Another puzzling phenomenon is that CTTs act as primers for multiple tubulin post-translational modifications (PTMs), so that most of the isotype sequence variation occurs in the CTT (∼50% sequence identity between tubulin CTTs, compared with 80–95% for the tubulin body) (11). The physiological reason for such striking molecular diversity in CTTs is also not entirely clear, leading to the proposed “tubulin-code” hypothesis, where the numerous tubulin genes together with PTMs have the potential to encode information on microtubules and their associated cellular effectors (12). The main limitation to experimental studies of the sequence–function relationships for the tubulin CTTs is the difficulty of determining the dynamics and conformational ensembles of the intrinsically disordered CTTs.

Table 1.

CTT sequences of human and yeast α- and β-tubulin isotypes, starting from the end of helix 12

The negatively charged residues are highlighted. The total negative charge in the CTT includes the carboxyl group from the final amino acid.

In addition to their important functions involving interactions with motor proteins and other microtubule-associated proteins, tubulin CTTs appear to play a role in regulating permeability of the mitochondrial voltage-dependent anion channel (VDAC) (13–16). As the major transport channel and most abundant protein in the mitochondrial outer membrane, VDAC is responsible for most of the metabolite flux in and out of mitochondria. VDAC was shown to be involved in a wide variety of mitochondria-associated pathologies, from various forms of cancer to neurodegeneration (17–19). The uniqueness of this large, weakly selective β-barrel channel arises mainly from its location at the interface between the mitochondria and the cytosol (20), where it serves as a pathway for all mitochondrial water-soluble respiratory substrates, such as ATP and ADP, and for small ions (21–24). Dimeric tubulin was shown to reversibly and partially block VDAC reconstituted into planar lipid membranes with nanomolar efficiency and thereby control the fluxes of mitochondrial metabolites through VDAC (15, 16). In these experiments, a single VDAC channel spans a planar lipid bilayer that separates and electrically isolates two buffer-filled compartments (25). The ionic current through the VDAC channel is induced by the applied transmembrane potential and is monitored for changes induced by the addition of dimeric tubulin, as illustrated in Fig. 1, A and B.

Figure 1.

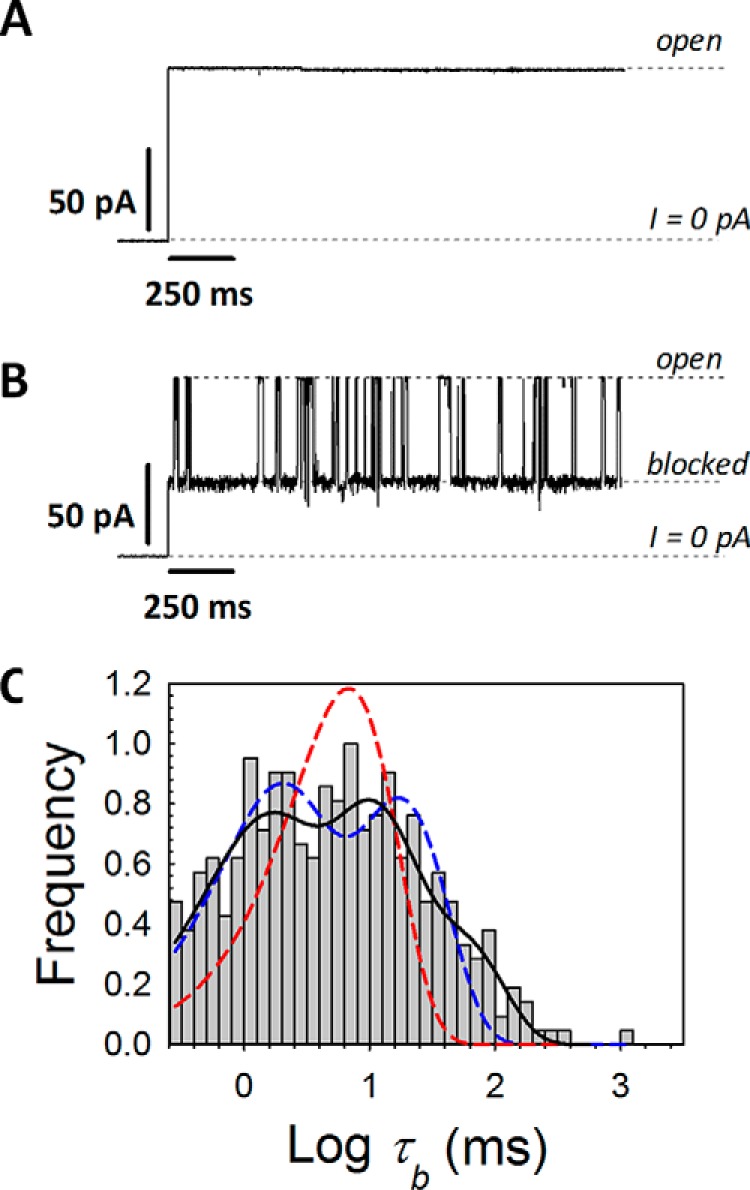
Mammalian tubulin induces VDAC blockage events characterized by a wide distribution of blockage (dwell) times. A and B, representative records of the current through the same single VDAC channel before (A) and after (B) the addition of 20 nm WT mammalian tubulin (isolated from porcine brain), at −27.5 mV of applied voltage. The membrane-bathing solutions contained 1 m KCl buffered with 5 mm HEPES at pH 7.4. Here and in Fig. 3, dashed lines indicate VDAC open and tubulin-blocked states and zero current. For clarity of presentation, the current records were inverted and smoothed with a 33-point boxcar digital filter using pClamp version 10.3. C, log-binned distribution of blockage times, τ_b, fit by a single exponent (dashed red line) or a sum of two exponents (dashed blue line). The maximum statistically significant number of exponential components (p < 1 × 10⁻⁵ using χ² test) is three (solid black line), using a Simplex optimization algorithm and maximum likelihood minimization. The total number of events in the histogram is 459. The position of the left vertical axis corresponds to the time resolution of experimental setup, which is about 0.2 ms.

Dimeric tubulin blocks VDAC conductance measurably only when a negative potential is applied from the side of tubulin addition (25). When the sign of the potential is reversed, no blockage events are observed, and the channel open-state conductance is as steady as in a control experiment without tubulin addition (25). This observation and the fact that tubulin with proteolytically cleaved CTTs does not induce characteristic blockages (15) indicate that the negatively charged CTTs are responsible for the VDAC blockage. On the other hand, synthetic peptides of α- and β-tubulin CTTs did not block the channel either, up to 10 μm (m = mol/l) concentration (15), thus suggesting that CTTs must be attached to the main tubulin body to induce the characteristic VDAC blockages.

Based on these observations, a model of VDAC–tubulin interaction was suggested, in which the negatively charged tubulin CTT partially blocks the positively charged VDAC pore, causing a decrease of the pore dimensions by steric obstruction and a reversal of ionic selectivity (15, 16, 26). Equilibrium and nonequilibrium MD simulations, together with a Rosetta protein–protein docking algorithm, allowed further tests of the structural rearrangements of the VDAC–tubulin complex (27). It was found that the unstructured α-tubulin CTT in the murine VDAC1 pore decreases the pore conductance by >40% and, even more importantly, switches its selectivity from anionic to cationic, in excellent agreement with experiments on reconstituted channels (28).

The most important physiological consequence of VDAC's reversible blockage by the tubulin CTT for mitochondria is that the tubulin-blocked state of the channel is essentially impermeable to ATP, as shown by direct channel-reconstitution experiments (26) and by MD simulations (27). The presence of the negatively charged tubulin CTT in the pore creates an ∼8–12-kJ/mol barrier for ATP translocation, due to the strong electrostatic repulsion between ATP and the negative charges on the CTT. Unlike small anions such as Cl⁻, the bulkier and more negatively charged ATP molecule cannot overcome the steric and electrostatic barriers created by the CTT lodged inside the pore. Thus, tubulin can be a potent regulator of the flux of respiratory substrates (most of which are negatively charged) across the mitochondrial outer membrane and, consequently, of mitochondrial respiration. Experiments with isolated mitochondria (15, 29) and intact cancer cells (13, 14) confirmed that the VDAC–tubulin interaction is functionally important in maintaining mitochondrial potential and, therefore, for regulating mitochondrial respiration in cancer cells. It was proposed that tubulin's interaction with VDAC contributes to suppression of mitochondrial metabolism in the Warburg phenomenon (30).

The biochemical evidence of the VDAC–tubulin interaction was first obtained by Carre et al. (31) in experiments showing co-immunoprecipitation of VDAC with tubulin. Interestingly, in that study, α-tubulin and β-tubulin were found at comparable levels in mitochondria, suggesting that mitochondrial tubulin is a heterodimer. The so-called “mitochondrial membrane tubulin” is enriched in the β3 isotype compared with the rest of the cellular tubulin and represents about 2% of total cellular tubulin (31).

Considering the wide heterogeneity of tubulin CTT isotypes, it seems natural to ask whether different CTTs could differently affect ATP permeability through VDAC and thus regulate mitochondrial respiration. However, biophysical dissection of the interaction of the individual tubulin CTT isotypes with the VDAC pore has been hindered by the massive inhomogeneity of the WT tubulin purified from native sources, such as bovine, murine, or porcine brains, that has been used in all previous experiments with reconstituted VDAC. Tubulin isolated from brain contains a mixture of α-tubulin and β-tubulin isotypes that is further complicated by PTMs. Distributions of the blockage times (such as the one shown in Fig. 1C) induced by native dimeric tubulin isolated from brain and added to a single VDAC channel are typically rather broad and cannot be described by a single exponent, suggesting that multiple species, presumably different tubulin CTT isotypes, block the channel. The differences in length and charge between α-tubulin and β-tubulin CTTs and heterogeneity within different β-CTTs are essential (4) (Table 1). However, the question of which CTT exactly, that of α-tubulin or β-tubulin or both, blocks VDAC and with what efficiency remained unanswered until now.

Highly homogeneous recombinant tubulin constructs with one or two specific CTTs have recently became available (3, 32–35), opening a new opportunity to answer this longstanding question. Both types of recombinant tubulins, yeast-based (3) and human-based (32–35), were fully functional and able to polymerize and form microtubules suitable for motor protein motility and processivity (3, 33–35). The recombinant human homogeneous microtubules showed different rates of polymerization compared with WT (32, 35). Kinesin-1 velocities on recombinant yeast–human CTT tubulin constructs were very similar to the yeast and porcine brain microtubules, but the average run length for kinesin-1 was different on yeast and recombinant constructs. The results of these studies (3, 32–35) demonstrate that recombinant tubulins are a reliable means to study tubulin isotype-specific effects in vitro and to dissect the role of individual tubulins' CTTs.

Here we use the previously described recombinant yeast α/β-tubulin constructs with CTTs from various human tubulin isotypes (3). Each of the five engineered tubulin constructs was tested for its interaction with reconstituted VDAC and compared with isolated native yeast and mammalian tubulins. We found that individual tubulin CTTs block the VDAC pore with dramatically distinct characteristic dwell times and different effective “gating charges.” VDAC blockage by different tubulin CTTs can be explained entirely by electrostatic and entropic interactions of the acidic tubulin tail with the positively charged VDAC pore and the transmembrane field. Our results show that regulation of VDAC permeability and, consequently, fluxes of ATP/ADP through the channel depend strongly on the identity of the tubulin CTT, suggesting a novel role of the diverse tubulin isotypes in vertebrates.

Results

Tubulin–VDAC colocalization in mitochondria

Whereas biophysical and biological consequences of tubulin binding to VDAC have been extensively studied, a visual assessment of this interaction in situ in cells using conventional confocal approaches is challenging due to high expression levels of both tubulin and VDAC. To override these limitations, we used in situ proximity ligation assay (PLA), a powerful method that allows assessment of the presence of two proteins at close distances with a resolution up to 30 nm (36), without requiring tenuous protein engineering or particular imaging techniques (37). Fig. 2 illustrates the results of PLA performed in human neuroblastoma cells, where the β3 isoform is found in close proximity to VDAC1. Notably, interaction between the two proteins, indicated in the image (Fig. 2A) by a red positive reaction, follows the characteristic pattern of mitochondria (also following VDAC localization) in neuroblastoma cells, thus confirming the mitochondrial localization of β3 tubulin and hence its availability for interaction with VDAC.

Figure 2.

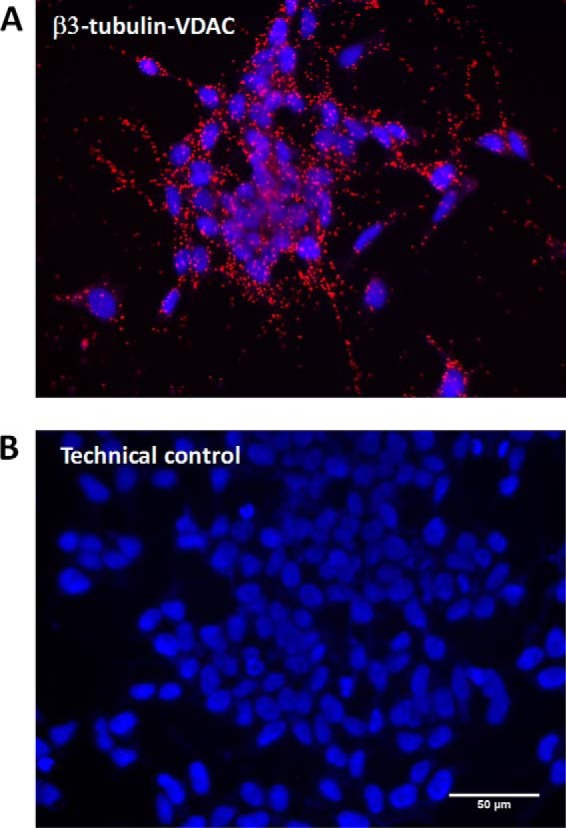
β3 tubulin is found in close proximity to VDAC in neuroblastoma cells. A, representative image of Duolink in situ proximity ligation assay using anti-β3 tubulin and anti-VDAC antibodies in human neuroblastoma cells. Interaction between molecules is indicated by a red positive reaction. B, no reaction was detected in the negative control, in which no primary antibodies were added. Scale bar, 50 μm. Nuclei are visualized using DAPI.

The off-rates of VDAC blockages by tubulin constructs

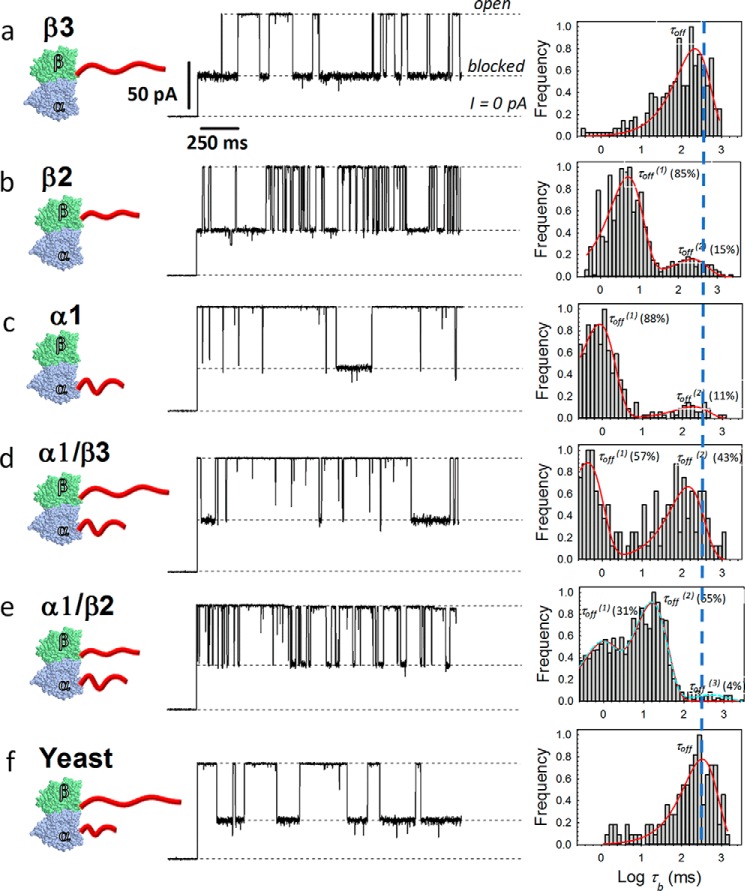
To evaluate molecular details of the CTT–VDAC interaction, we examined five previously described yeast tubulin-human CTT recombinant constructs (3) (schematically shown in Fig. 3, left column) for their ability to interact with VDAC reconstituted into planar lipid membranes formed from diphytanoyl-phosphatidylcholine. We chose to test three tubulin constructs with individual human β3, β2, or α1 CTTs (Table 1) bound to the corresponding β-tubulin or α-tubulin yeast subunits with their natural α-CTT and β-CTTs removed (TUBB2A-CTT, TUBB2A-CTT, and TUBA1A-CTT) and two constructs with both α- and β-CTTs, α1/β3 and α1/β2, bound (TUBA1A/TUBB2A and TUBA1A/TUBB3, following the HUGO (Human Genome Organization) Gene Nomenclature Committee (71).

Figure 3.

Kinetic analysis of VDAC blockage by individual tubulin constructs. Left column, a–f, cartoons illustrating recombinant tubulins with human β3, β2, α1, α1/β3, α1/β2, and yeast CTTs (red). Middle column, representative traces of ion currents through a single VDAC channel in the presence of 8–10 nm recombinant tubulin construct shown at the left. All records were taken at −27.5 mV of applied voltage; constructs were added to the cis compartment. Other experimental conditions are as in Fig. 1. Right column, corresponding log-binned distributions of blockage times, τ_b, calculated from statistical analysis of current records, fragments of which are shown in the middle. Red solid lines are the single exponential fits with characteristic time τ_off = 〈τ_b〉 equal to 242 and 330 ms for β3 and yeast tubulin WT (a and f) or double exponential fits with characteristic times τ_off⁽¹⁾ and τ_off⁽²⁾ equal to 5 and 229 ms for β2 (b), 0.9 and 184 ms for α1 (c), 0.4 and 142 ms for α1/β3 (d), and 0.8 and 16 ms for α1/β2 (e). The best fit (p < 1 × 10⁻⁵ using χ² test) for the α1/β2 construct (e) is achieved with three exponents (dashed cyan line), where the minor third component (τ_off⁽³⁾ = 488 ms) accounts for 4% of events. The occurrence (%) of blockage times in the log-binned distribution of blockage times is shown in brackets for all double and triple exponential fits. The total number of events represented by histograms in a, b, c, d, e, and f are 362, 778, 618, 269, 1488, and 288, respectively.

Representative experiments with single VDAC channels are shown in Fig. 3 (current traces in the middle), where the addition of an 8–10 nm concentration of an individual recombinant tubulin construct to one side of the membrane (cis side, the side of the VDAC addition) causes rapid time-resolved downward (toward zero current) transitions between the high-conducting open state and low-conducting blocked state. These blockages are also characteristic for WT mammalian tubulin (isolated from porcine brain; see “Experimental procedures”) (Fig. 1B). Conductance of the open state in the presence of tubulin constructs remains the same as in control (Fig. 1A), and the conductance of the blocked state is ∼40% of the open-state conductance (compare traces in Fig. 3 with Fig. 1B and traces elsewhere (15, 16, 26)). Notably, the VDAC behavior in the presence of any tubulin, WT or recombinant, is drastically different from the steady-state current through the channel in the absence of tubulin (at the same applied voltage of −27.5 mV), as illustrated in Fig. 1A.

Despite the similarity in the tubulin-blocked conductance level and the overall character of tubulin-induced fast current transitions, the kinetics of the blockage events are strikingly different among the five tubulin constructs. Distributions of dwell times or blockage times, τ_b, are quantitatively different for each construct (Fig. 3, right column). First, the blockage events induced by the construct with only the β3 CTT are described by a single-exponential function at all applied voltages (Fig. 3, right column, row a). The characteristic time the channel spends in the blocked state, τ_off = 〈τ_b〉, calculated at −27.5 mV, as shown in Fig. 3 (row a), is equal to 240 ms. Second, the majority of the blockage times (85–88% of the total blockage events) obtained with two other single-CTT constructs, β2 and α1, can also be described by single-exponential functions, but with characteristic times orders of magnitude smaller than those obtained for the β3 construct: τ_off = 5 and 0.9 ms for β2 and α1 tubulin, respectively (Fig. 3, right column, rows b and c). There is an apparent positive correlation between the length of the CTT (and, correspondingly, the number of negative charges it bears (Table 1)) and the duration of blockage times. The longest β3 CTT (27 amino acids long and 12 negative charges, following a definition of the CTT as starting from the end of helix 12 (1)) causes ∼100 times longer blockages than the shortest α1 CTT (18 amino acids and 10 negative charges) (Fig. 4B). Third, the distributions of blockage times induced by tubulin constructs with two CTTs, α1/β3 and α1/β2, require two-exponential fitting with almost equal contributions of each exponent to the total distribution (∼40–60% events for τ_off⁽¹⁾ and τ_off⁽²⁾) but with distinctly different mean dwell times; τ_off⁽¹⁾ is equal to 0.43 and 0.8 ms, and τ_off⁽²⁾ is equal to 142 and 16 ms for α1/β3 and α1/β2, respectively (Fig. 3, right column, rows d and e). Two-tailed tubulins induce two-component distributions of τ_b that are noticeably distinct from the single-tailed constructs, for which the τ_b distributions are dominated by a single exponent. These results suggest that each CTT blocks the VDAC pore with a characteristic residence time. The α1/β3 construct, for which the two CTTs are very different in length and charge (Table 1), induces blockages with τ_off⁽¹⁾ and τ_off⁽²⁾ that differ by 2 orders of magnitude (Fig. 3, right column, row d). Accordingly, the α1/β2 construct, comprising two CTTs with less pronounced length and charge differences (Table 1), induces blockages with ∼20 times different characteristic times and partially overlapping τ_b distributions (row e).

Figure 4.

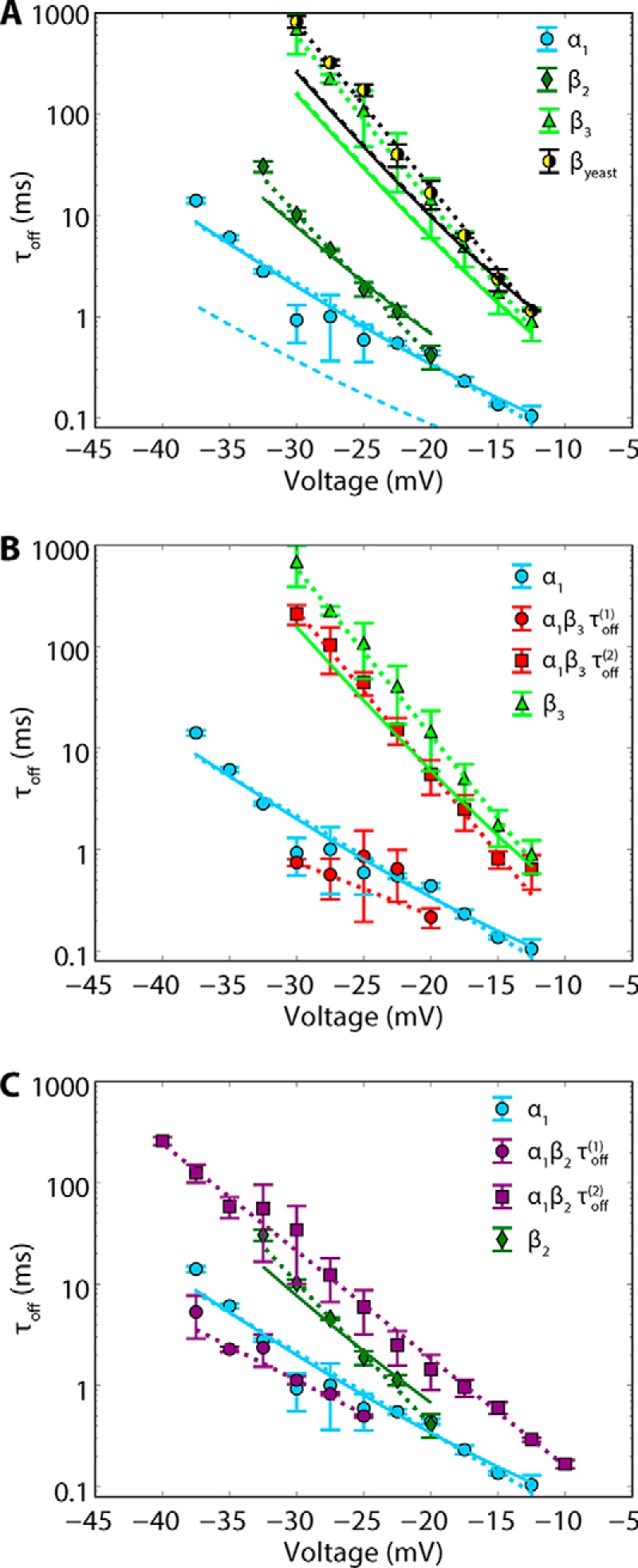
Mean dwell times of tubulin blockage are exponentially voltage-dependent. A, voltage dependences of τ_off⁽¹⁾ obtained for α1, β2, and β3 tubulin constructs and β_yeast. B and C, voltage dependences of τ_off⁽¹⁾ and τ_off⁽²⁾ obtained for the α1/β3 construct compared with β3 and α1 constructs (B) and for the α1/β2 construct compared with β2 and α1 constructs (C). Dotted lines, fits to the Arrhenius equation (Equation 1); solid lines, fits to the drift-diffusion model (see “Appendix”) with optimized parameters l_t^α = 1.43 nm and l_t^β = 2.01 nm; dashed lines are initial estimates using l_t^α = l_t^β = 2 nm as reasonable values of the drift-diffusion model. Each data point is a mean of 3–5 independent experiments ± S.D. (error bars).

A clue about the nature of the minor (occurrence <15%) and longer-lasting τ_off⁽²⁾ components in blockages induced by α1 and β2 CTTs comes from the comparison of these two τ_b distributions with the τ_b distribution obtained with yeast tubulin. Yeast tubulin induces blockages with the distribution dominated by a single-exponential function with τ_off = 330 ms (Fig. 3, row f). For the α1/β2 construct (Fig. 3e), a third minor component (occurrence ∼4%) characteristic of yeast tubulin can also be observed. The best fit using a maximum likelihood estimate is achieved with three exponents (p < 1 × 10⁻⁵) (e, dashed cyan line), although a two-exponent fit also gives significant results (p < 1 × 10⁻⁵). The vertical dashed line in Fig. 3 (right column) aligns the peak from yeast tubulin with the minor components from the α1, β2, and α1/β2 constructs. This suggests that blockages characterized by τ_off⁽²⁾ in α1 and β2 CTTs and τ_off⁽³⁾ in α1/β2 distributions arise from a minor fraction (4–15%) of native yeast tubulin retained in the recombinant tubulin samples (as reported in Ref. 3). The presence of a small amount of “foreign” tubulin in an otherwise homogeneous sample of recombinant tubulin is easily sufficient to be detected by the VDAC pore. This is possible as long as the two tubulins induce blockages with significantly different τ_off, because tubulin in concentrations as low as 1 nm already induces resolvable VDAC blockages (38), making the VDAC pore an extremely sensitive single-molecule sensor. We cannot rule out the presence of small amounts of WT yeast tubulin in the β3 and α1/β3 samples; however, their presence is not detectable with the VDAC pore because the τ_b distribution of WT yeast tubulin overlaps with the β3 distribution (Fig. 3, rows a and f).

To further test VDAC blockage by individual CTTs, we compared the voltage dependences of τ_off for all tubulin constructs (Fig. 4). We followed our assignment of the minor long-lasting components to the “foreign” yeast tubulin and considered only the major τ_off components (occurrence >20%). The exponential increase of τ_off with voltage found for all five constructs (Fig. 4) corresponds to the mechanism of tubulin-induced blockage, as the restricted permeation block suggested earlier for the WT mammalian tubulin-induced blockage (16). Importantly, not only does the absolute value of τ_off for different single-tailed tubulins measured at the same voltage differ by 2 orders of magnitude, but τ_off changes with voltage at a different rate (Fig. 4A), indicating that blockage by each CTT involves movement of a different number of charges through the pore under the applied field. The voltage dependences for the β3 construct and WT yeast tubulin are very similar (Fig. 4A), with τ_off for β-yeast tubulin systematically higher than for β3. The comparison of τ_off voltage dependences for the two-tailed tubulins with corresponding single-tailed constructs shows the overlap of the τ_off⁽¹⁾ values for α1/β3 and α1/β2 tubulins with τ_off for α1 tubulin at all applied voltages (Fig. 4, B and C). Likewise, the values of τ_off⁽²⁾ obtained for α1/β3 and α1/β2 tubulins overlap with τ_off for β3 and β2 tubulins, respectively (Fig. 4, B and C). These results show that each tubulin CTT blocks the VDAC pore with a unique characteristic blockage time and voltage dependence and that both α- and β-CTTs block the VDAC.

Ion selectivity of the tubulin-blocked state

For the CTTs used in our study, the conductance of the tubulin-blocked state (∼40% of the open-state conductance) is found to be independent of the CTT structure. It was shown previously in channel experiments (26) and by MD simulations (27) that the small-ion selectivity of the tubulin-blocked state is cationic, which is reversed relative to the anionic selectivity of the open state. Here, we compare ion selectivities of the blocked state induced by recombinant and WT mammalian tubulins. Fig. 5 shows I/V plots obtained on the same channel in 200 mm (cis) versus 1 m (trans) gradient of KCl for the open state and for the blocked states induced by the α1/β3 tubulin construct added to the cis side of the membrane or by mammalian tubulin added to the trans side. In this experiment, we used the ability of tubulin to block the channel measurably only when negative potential is applied from the side of tubulin addition, driving the negatively charged CTT into the pore (16, 25). Therefore, the negative potential at the cis side drives the CTT of the α1/β3 construct added to the cis side of the membrane into the channel, and positive potential (negative at the trans side) drives the WT mammalian tubulin added to the trans side of the membrane. The open state (black triangles in Fig. 5) has anionic selectivity with reversal potential (the potential at which the ionic current is zero) ψ_rev = −9.4 ± 0.5 mV, as indicated by a black arrow. The blocked states induced by the α1/β3 construct or mammalian tubulin (red and blue circles, respectively) have cationic selectivity with ψ_rev = 8.4 ± 0.4 and 9.5 ± 0.6 mV, respectively (indicated by corresponding red and blue arrows in Fig. 5). Therefore, blockage of VDAC by either recombinant or native tubulin (which is essentially a mixture of tubulin isotypes with PTMs) reverses the open-state anionic selectivity to cationic, confirming that the mechanism of VDAC blockage is the same for WT mammalian tubulin and the recombinant constructs.

Figure 5.

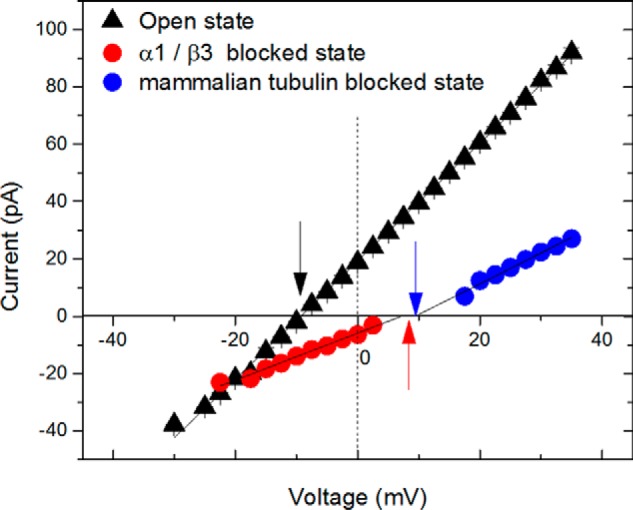
Ionic selectivity of the tubulin-blocked state of VDAC is cationic for both a recombinant construct and WT mammalian tubulin. Current–voltage relationships for a single VDAC channel in a membrane separating 200 mm (cis) and 1 m (trans) KCl solutions (2 mm HEPES, pH 7.4) are shown. Open state (black triangles) has anionic selectivity with the reversal potential ψ_rev = −9.4 ± 0.5 mV, marked by the black arrow. Currents for the tubulin-blocked states are denoted by red circles for the α1/β3 tubulin construct and by blue circles for WT mammalian tubulin. To be able to measure the reversal potential for the two tubulins on the same single channel, we added the recombinant tubulin to the cis side and WT tubulin to the trans side of the membrane, in concentrations of 10 and 20 nm, respectively. As indicated by the arrows, blockage of VDAC by either tubulin similarly reverses the original anionic selectivity of the channel to the cationic one with ψ_rev = 8.4 ± 0.4 mV and 9.5 ± 0.6 mV for α1/β3 and the WT mammalian tubulin, respectively.

The on-rate of tubulin construct blockages

The on-rate of tubulin blockages of VDAC is always characterized by a single-exponential function (15) and is concentration-dependent (38). The measured on-rates normalized to the tubulin bulk concentration [C], k_on = 1/τ_on[C], do not significantly differ between tubulin constructs except for the difference between β2 and α1/β2 (p < 0.05, one-way ANOVA) (Fig. 6). However, the statistical significance between the k_on of these two constructs vanishes if the increased rate of blockage events induced by two-tailed constructs compared with single-tailed constructs is divided by the number of CTTs per molecule. When k_on values obtained for α1/β2 and α1/β3 were normalized by the number of CTTs in this manner, the on-rates of all constructs were found to be statistically indistinguishable (p > 0.05). As was previously shown, the on-rate of VDAC blockage depends on the concentration of tubulin bound to the membrane in close proximity to VDAC and is therefore extremely sensitive to the tubulin membrane-binding efficiency (39), which varies with membrane lipid composition (38). Because all of the tubulin constructs were derived from the yeast α/β heterodimer and the lipid composition of planar membranes was the same in all experiments, the properly normalized on-rates for the constructs are expected to be of the same order of magnitude, as observed (Fig. 6). Importantly, this contrasts with the spread of 2 orders of magnitude among the observed off-rates (Fig. 4).

Figure 6.

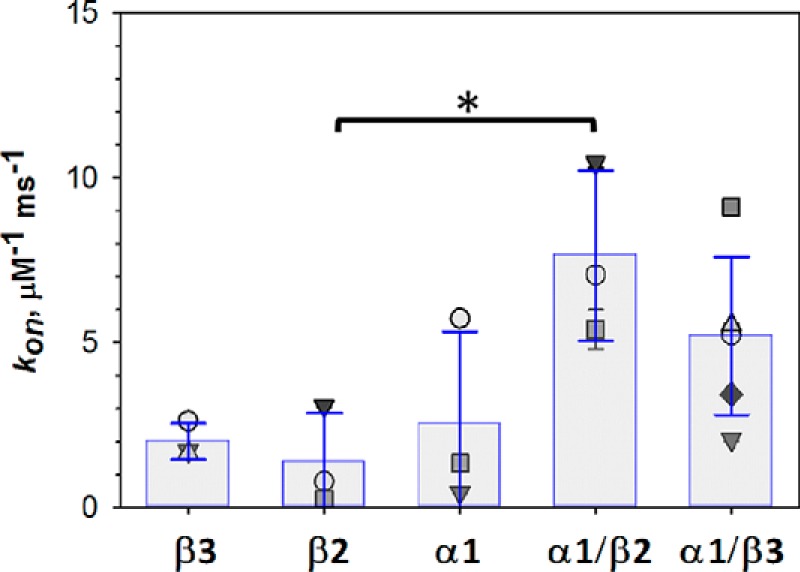
The on-rate constants of VDAC blockage by different tubulin constructs. There is no significant difference between the on-rate constants of VDAC blockages except for the difference between β2 and α1/β2 (*, p < 0.05 one-way ANOVA). Data were analyzed by one-way ANOVA (F_4,14 = 5.33, p = 0.01) followed by a pairwise multiple Holm–Sidak comparison test. Applied voltage was −25 mV. Each symbol corresponds to an individual experiment; bars are the mean values of 3–5 independent experiments ± S.D. (error bars). When the on-rate constants are normalized by the number of CTTs per construct, the differences between β2 and α1/β2 lose statistical significance (F_4,14 = 1.29, p = 0.32, one-way ANOVA).

Discussion

A model of the tubulin CTT–VDAC interaction

The off-rates, calculated from the residence time of a CTT inside the pore at a given voltage, showed a pronounced sensitivity to the CTT isotype. The voltage dependence of the off-rate provides information about the number of charges moving through the pore under the applied field in terms of an effective “gating charge” n. This quantity can be determined by fitting the voltage-dependent τ_off to an Arrhenius-type rate equation, with elementary charge e and transmembrane potential V,

$${\tau }_{\text{off}}\left(V\right)\hspace{0.17em}\propto \hspace{0.17em}\exp \left(\frac{ne\left|V\right|}{k_{B}T}\right)$$ (Eq. 1)

where k_B is the Boltzmann constant and T is absolute temperature.

The kinetic analyses of the off-rates showed that individual tubulin CTTs block the VDAC pore with distinct characteristic blockage times, which span 2 orders of magnitude and are characterized by different n, depending on the CTT isotype (Fig. 4 and Table 2). There is an apparent positive correlation between the length and total negative charges of an individual CTT and its VDAC blockage parameters τ_off (at −27.5 mV) and n (Tables 1 and 2).

Table 2.

Physical parameters of the tubulin CTTs, characteristic blockage time, τ_off, obtained at −27.5 mV of applied voltage, and effective “gating charge” n of VDAC blockage calculated from the measured τ_off voltage dependences using Equation 1

τ_off and n values are expressed as a mean of 3–5 independent experiments ± S.D.

Tubulin CTT	CTT length	CTT center chargea	τoff at −27.5 mV	n
	nm		ms
βyeast	13.6	−11	322 ± 22	9.7 ± 0.1
β3	9.2	−11	227 ± 22	9.9 ± 0.3
β2	7.2	−8	4.6 ± 0.1	8.4 ± 0.2
α1	5.6	−5	1.3 ± 0.6	4.7 ± 0.1

^a CTT center charge is equal to total CTT charge excluding first five and last three amino acids.

Another interesting result is the single-exponential distribution of τ_b obtained with yeast tubulin (Fig. 3f), which contrasts with the broad distribution of τ_b obtained with mammalian tubulin (Fig. 1C). The single characteristic blockage time obtained with yeast tubulin indicates that all measured blockage events are induced by one yeast CTT, whereas its relatively large blockage time suggests that the longer β-CTT (34 amino acids and −14 charges) is responsible (Table 1). Most likely, the blockages induced by the short yeast α-CTT (13 amino acids and −7 charges) are too fast to be resolved in our experimental setup. It is easily seen that the blockages induced by the human α1 CTT, which is 5 amino acids longer than the yeast α-CTT, are close to the limit of our setup resolution of ∼0.2 ms (Fig. 3c). An alternative explanation is that the yeast α-CTT is too short to reach the center of the pore, where a constriction zone is formed by the α-helical N terminus of VDAC (Fig. 8).

Figure 8.

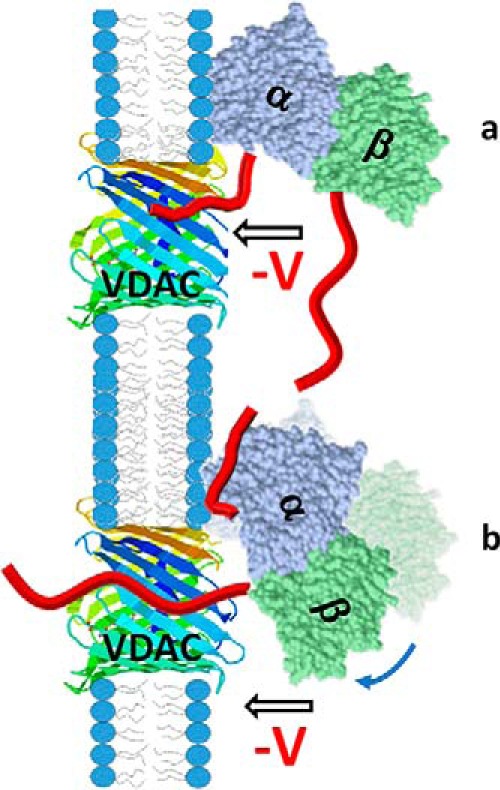
Cartoon of a model of VDAC pore blockage by the α-CTT or β-CTT of tubulin. The orientation of membrane-bound tubulin dimer is adopted from Ref. 39 with α-tubulin as the membrane-bound subunit. In such alignment, the contribution of the length and especially the first amino acids of the CTT to the blocking kinetics should be different for α-CTTs (a) and β-CTTs (b). There is some degree of rotational dynamics for the stably bound α-tubulin shown in (b) with the arrow and shadow image, which could also affect the kinetics of pore blockage by the β-CTT.

The yeast β-CTT is even longer than human β3 and bears two extra negative charges, but its effective gating charge and τ_off are very similar to those obtained with β3 CTT (Fig. 4A and Table 2). Mammalian tubulin, by contrast, is a mixture of the 13 possible CTT isotypes with massive variations due to PTMs (5) that gives the observed range of τ_b spanning up to 3 orders of magnitude at 27.5 mV (Fig. 1C). This is in sharp contrast to the τ_b distributions obtained for recombinant tubulins with a highly homogeneous CTT content. Disregarding the minor components that we attribute to the unavoidable presence of small amounts of native yeast tubulin, only for the recombinant constructs with a single CTT is a single exponential distribution observed, confirming that each of the four individual CTTs studied, α1, β2, β3, and β_yeast (but not α_yeast), blocks the pore.

The restricted permeation block hypothesis does not discriminate between different mechanisms of CTT interaction with the VDAC pore. In particular, it does not specify whether CTT retraction involves dissociation of specific CTT residues from the putative binding sites in the pore lumen. To test this, we constructed a physical model that does not account for specific binding interactions and incorporates only the steric and charge properties of the CTT–VDAC system. This model assumes that the observed τ_off corresponds to the average escape time from an interaction potential well that depends only on the electrostatic energy landscape defined by the positions of the charged amino acids in the CTT, the transmembrane potential, and the geometry of the system (membrane-bound tubulin with the CTT lodged in the VDAC pore, as shown in Fig. 7A). The exponential dependence of the blockage time on voltage suggests a Kramers-type escape problem (40, 41) that is dominated by electrostatic effects; essentially, the role of the model is to calculate the height of the energy barrier to CTT retraction from the pore. For details of the model, which involves constructing the interaction potential to be used in a first-passage time calculation in a drift-diffusion framework (41–43), see “Appendix.” The only free parameters are the distances between the tubulin body, where the CTT is tethered, and the pore constriction. These tether lengths, l_t, might be different for α-tubulin and β-tubulin CTTs (see the model in Fig. 8) and are correspondingly denoted l_t^α and l_t^β. Note that the β-tubulin tail is tethered further away from the pore (Fig. 8), as expected from the finding that tubulin binds to lipid membrane via the α-tubulin subunit (39).

Figure 7.

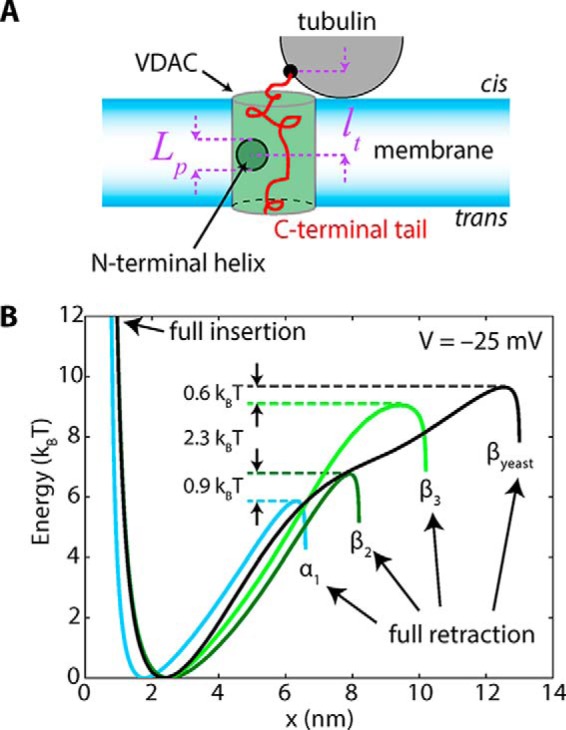
Physical model of CTT/pore interaction. A, geometry of the model showing the definitions of pore length l_p and tethering distance l_t. B, potentials corresponding to the escape of each CTT from the pore, calculated using optimized parameters l_t^α = 1.43 nm and l_t^β = 2.01 nm. Differences in escape times are described almost entirely by the heights of the barrier and not by residue-specific interactions between the CTT and the pore lumen.

The dashed curves in Fig. 4A show the model calculation for the simple case where the tails are assumed to be tethered at a distance equal to half the membrane thickness away from the pore constriction (l_t^α = l_t^β = 2 nm). The agreement is already reasonable; optimizing these two parameters, we obtain the solid curves in Fig. 4A, which are parametrized by l_t^α = 1.4307(69) nm and l_t^β = 2.0128(47) nm, where the brackets denote 95% confidence intervals. The interaction potentials corresponding to the optimized curves are shown in Fig. 7B for V = −25 mV. The parameter x is a distance corresponding to the penetration of the CTT into the pore from full extension at x = 0 to full retraction at x = L, where L is the length of the CTT. For clarity, the energy scale is referenced to the potential minimum near x = 2 nm. That the difference between the α- and β-CTT tethering distances is only ∼0.6 nm is not very surprising, given the flexibility of the bound tubulin on the surface (Fig. 8) observed with microsecond all-atom MD simulations (39). The simulations show some degree of rotational dynamics for the stably bound α-tubulin (illustrated in Fig. 8b with arrow and shadow image) that could also affect the kinetics of pore blockage by β-CTT.

The unambiguous determination of tubulin's orientation at the membrane surface, with the α-tubulin subunit stably bound (39) aids our understanding of the detailed mechanism of tubulin's interaction with VDAC and the roles of the α-CTTs and β-CTTs. It is clear from Fig. 8 that the relatively short α-tubulin CTT attached near one end of the dimer can be captured into the VDAC pore only when the α-tubulin subunit is membrane-bound. For other surface configurations, including nearly all in which the β-tubulin subunit is bound, this would be impossible. Conversely, the longer β-tubulin CTT, which is attached near the dimer interface (Fig. 8), is pore-accessible when tubulin is bound via the α-tubulin subunit.

The success of our simple physical model in predicting the lifetimes of the CTT–VDAC interaction has an important consequence. It appears that the different lifetimes observed experimentally do not arise from interactions of CTT-specific residues with complementary residues in the VDAC lumen, but rather from basic physical properties of the blocker: the total amount of charge and its distribution on the CTT. The total CTT charge is the most important of these properties and is responsible for the orders-of-magnitude separation between the times of blockage by α- and β-tubulin CTTs. In distinguishing between the three β-tubulin tails, however, the distribution of charges is also crucial (Tables 1 and 2). Indeed, the charged residues adjacent to the tubulin body do not contribute to the effective gating charge, as they cannot reach the pore. Charged residues near the end of the CTT also have a limited effect on the blockage time because they pass the pore, and hence contribute to the interaction potential, after the retraction process is nearly complete. Near full retraction, the CTT has already surmounted the maximum of the interaction potential (Fig. 7), which is largely entropic in origin, such that the effect of the charged residues near the end of the CTT on the potential maximum (and thus on the blockage times) is diminished. Thus, the β_yeast and β3 CTTs have very similar dynamics, despite β_yeast having additional charges at the beginning and at the end. Likewise, the blockage times of β2 and β3 differ by an order of magnitude, despite the same nominal number of charges, because the electrical forces from the charges near the end of the β2 CTT are much smaller than the large entropic forces experienced by a CTT that is almost completely retracted. By contrast, none of the charges in the β3 CTT are located at the tail end. These effects account for the strong correspondence between the effective gating charge n and the number of charges in the middle of the CTT (Table 2). Interestingly, the length of the CTT does not have a strong effect on the induced blockage time. Together, these phenomena give rise to a new type of specificity, in which the charge distribution in a CTT has a predominant effect on the blockage efficiency.

It should be noted that short-lived, residue-specific interactions were observed in short (10-ns) molecular dynamics simulations between the anionic α1 tubulin CTT and basic residues in the VDAC N-terminal α-helix (27). The CTT was not observed to pass the N-terminal helix of VDAC, but the duration of the simulations was insufficient to characterize the lifetime of the CTT–VDAC interaction or to assess whether the CTT passes through the channel (which has been observed experimentally with other polypeptides (44)) on experimental (ms) time scales.

The model allows the estimation of the expected escape time for other CTT constructs, such as the yeast α-tubulin CTT, as well as the effect of polyglutamylation, the most common PTM of brain tubulin (45). For example, the height of the barrier to escape for the yeast α-tubulin's CTT at 25 mV is 2.52 k_BT smaller than that calculated for mammalian α-tubulin. Thus, we expect the escape time to be exp(2.52) = 12 times smaller. This is below the time resolution of our experimental setup, so we cannot decisively resolve these CTT blockage events, as postulated earlier. A similar estimation for polyglutamylation yields an increase in barrier height of 3.37 k_BT at 25 mV if 6 glutamic acid residues are added to the end of the β3 CTT. This corresponds to an increase in blockage time by a factor of 30, to more than 2 s. More polyglutamylation or higher membrane potentials would therefore result in essentially permanent blockage on molecular time scales. Note that significant polyglutamylation can also result in very long blockage times even for very low transmembrane potentials. At 10 mV and with the addition of 20 glutamic acid residues, the average blockage time for the β3 CTT is also expected to be nearly 1 s. The effect of branched polyglutamate structures (observed in adult brains (5)) on VDAC blockage is unclear and cannot be predicted by the physical model for linear polypeptide CTTs. The additional charge carried by multiple strands in branched polyglutamate structures may result in very efficient blocking of VDAC; on the other hand, the increased steric effects may inhibit VDAC blockage by these structures. Future experimental and simulation work will be crucial to understand these effects.

VDAC blockage by tubulin, as characterized by the on- and off-rates, is impressively voltage-dependent (15). Far from its saturation, the voltage dependence of the on-rate reports on the exponential increase in the number of CTT captures per second with voltage. The on-rate strongly depends on the α-tubulin subunit domain membrane-binding efficiency (38, 39). In this respect, the obtained results expectedly differ from those of a recent study of VDAC blockage by CTT–albumin chimeras synthesized using the methods of click chemistry (46). The major difference between these two constructs, albumin-based and yeast tubulin-based, is that water-soluble albumin does not bind to the membrane surfaces and, therefore, does not belong to the class of peripheral membrane proteins (47, 48). Consequently, the CTT–albumin chimeras showed orders of magnitude lower blockage on-rates and quite different relationships between the CTT structure and blockage parameters, thus highlighting the critical importance of tubulin–membrane interactions proposed earlier (39, 49–51).

Physiological implications

The in situ PLA data confirm the abundance of tubulin β3 isotype interaction with VDAC in cells (Fig. 2). However, at this point, we can only speculate about the physiological relevance of our finding that β3 isotype is the most effective VDAC blocker. Compared with other β-tubulin isotypes, the TUBB3 gene is the most conserved across all vertebrate species, suggesting critical functional roles of this isotype (52). However, the distribution is quite narrow; absent from most tissues, it is abundantly expressed in specific neurons of the brain and in the peripheral nervous system (53). Although adaptive advantages conferred by this isotype to neurons are still a matter of debate, the β3 isotype is generally considered to be a neuronal marker whose nonmicrotubule functions remain totally unexplored. The β3 isotype is the most comprehensively examined isotype across a variety of cancers (54). Coupled with evidence of its aberrant expression levels in a wide range of tumors of neuronal and nonneuronal origin and disease aggressiveness and resistance to chemotherapy, β3 tubulin is thought to be a survival factor. Interaction between this tubulin isotype and VDAC was evoked to explain modulation of metabolic stress and mitochondrial functions in cancer cells (55). Future research will verify the preferential tubulin isotype interaction with VDAC in cells and potential modifications of these interactions under chemotherapeutic treatment.

Conclusions

Using five different recombinant tubulin constructs that present, individually and in combination, human β3, β2, and α1 CTTs to the VDAC pore, we found that either α-CTTs or β-CTTs individually block the pore. The blockage lifetime spans 2 orders of magnitude, depending on the CTT isotype, with the β3 CTT blocking VDAC most effectively. VDAC blockage by different tubulin CTTs can be explained entirely by electrostatic and entropic interactions of the acidic tubulin tail with the positively charged VDAC pore and the transmembrane electric field. The different blockage lifetimes observed experimentally arise from basic physical properties of the CTT, such as the total amount of charge and its distribution along the tail. We suggest that these phenomena constitute a distinct form of specificity in which the one-dimensional charge distribution within the CTT sequence, rather than the three-dimensional conformation of the CTT or specific interactions between the CTT and pore-lining residues, predominantly determines the blockage efficiency. These results, in combination with the previously determined α/β-tubulin dimer orientation at the membrane surface (39), advance our understanding of the detailed mechanism of tubulin interaction with VDAC and the roles of the α-CTTs and β-CTTs.

Our results also suggest a novel role for the diversity of tubulins in vertebrates, which is due to the extraordinary sensitivity of VDAC regulation to the tubulin CTT sequence. Depending on the expression levels and PTMs of the various tubulin isotypes, the effectiveness of this regulation may vary significantly between different cell and tissue types, between normal and cancer cells, or between mature and developing cells (2), thus suggesting a mechanism of fine-tuned regulation of mitochondrial metabolism through VDAC–tubulin interaction.

Experimental procedures

Expression and purification of recombinant tubulin

The five engineered recombinant tubulin dimers constructed of yeast α/β-tubulin heterodimer with distinct human carboxyl-terminal tails, α1 (TUBA1A, following HUGO nomenclature in Ref. 3), β2 (TUBB2A), β3 (TUBB3), α1/β2 (TUBA1A/TUBB2A), or α1/β3 (TUBA1A/TUBB3), were generated as described previously (3). The yeast expression system used for purifying recombinant tubulin was adapted from Ref. 56. This method overexpresses the recombinant yeast α/β-tubulin from two yeast 2-μm galactose-inducible expression plasmids. The recombinant tubulin (yeast α-int-His/β-tubulin) was separated from the native one using metal-affinity chromatography as described previously (56). The estimated endogenous yeast β-tubulin component was <3% (3). The His₆ tag was placed in a luminal loop in α-tubulin as described (3). The His₆ tag located in the luminal surface does not interfere with interaction of tubulin CTTs with the VDAC pore, as previous studies have shown that amino acids inserted into this luminal loop do not disrupt tubulin function, such as assembling into microtubules (72) or affect the velocity of kinesin-1 movement on recombinant, His₆-tagged yeast microtubules (3). The purified recombinant tubulin heterodimers (∼10 μm) were stored in 80 mm PIPES, pH 6.8, 2 mm MgCl₂, 1 mm EGTA, and 200 μm GTP buffer at −80 °C. Yeast WT tubulin was isolated following a procedure described previously (56).

Protein purification

Lyophilized porcine brain tubulin was purchased from Cytoskeleton Inc. (Denver, CO); dissolved at 1 mg/ml in 0.1 mm PIPES buffer, pH 7.0, with 0.5 mm MgCl₂; aliquoted and snap-frozen in liquid nitrogen; and then stored at −80 °C. Each aliquot of mammalian or recombinant tubulin was used once in channel experiments, thus avoiding repeated freezing/thawing. VDAC was isolated from frozen mitochondrial fractions of rat liver that were a generous gift of Dr. Marco Colombini (University of Maryland, College Park, MD) following the standard method (57) and purified on a hydroxyapatite/celite (2:1) column as described previously (58).

Proximity ligation assay

Human neuroblastoma cells (SH-SY5Y, catalog no. CRL-2266, ATCC, Manassas, VA) were grown in 8-well chamber slides (Thermo Scientific Nunc^TM Lab-Tek^TM II Chamber Slide^TM system) for 24 h in RPMI 1640 supplemented with 10% (v/v) fetal bovine serum (Gibco). Then cells were fixed with 3.7% paraformaldehyde and 0.05% glutaraldehyde (Sigma), followed by permeabilization with 0.05% Triton X-100 (Sigma) and denaturation with 6 n guanidine HCl (Invitrogen). The cells were then incubated with blocking solution provided with the Duolink in situ red kit (mouse/rabbit; Sigma-Aldrich, DUO92101) according to the manufacturer's instructions. Primary antibodies used were rabbit against human VDAC (Abcam 15895) and mouse against either human α-tubulin (clone DM1A, Sigma-Aldrich). Cells were washed twice using Wash Buffer A (Duolink in situ reagents, Sigma) and incubated with the appropriate anti-species secondary antibodies to which oligonucleotides had been conjugated (anti-rabbit PLA probe PLUS and anti-mouse PLA probe MINUS, Sigma-Aldrich) for 1 h at 37 °C. The cells were then treated with Duolink ligation ligase solution for 30 min at 37 °C. Finally, cells were incubated with the Duolink amplification polymerase solution for 60 min at 37 °C, followed by washing and mounting on slides with Duolink Mounting Medium with DAPI. Images were acquired using a EVOS® FL Auto Imaging system (Thermo Scientific) with light cubes for DAPI and Texas Red, under ×40 magnification. Each fluorochrome image was collected separately and then merged using NIH ImageJ software (version 1.49).

Channel reconstitution

Planar bilayer membranes were formed from lipid monolayers across a ∼70–90-μm orifice in a 15-μm Teflon film separating two ∼1.2-ml reconstitution cell compartments, as described previously (25, 59). A 5 mg/ml solution of diphytanoyl-phosphatidylcholine (Avanti Polar Lipids, Alabaster, AL) in pentane was used for bilayer formation. The membrane potential was maintained using Ag/AgCl electrodes with 2 m KCl and 15% (w/v) agarose bridges. Channel insertion was achieved by adding purified VDAC in a 2.5% Triton X-100 solution to the aqueous phase of 1 m KCl buffered with 5 mm HEPES at pH 7.4 in the cis compartment while stirring. Potential is defined as positive when it is greater at the side of VDAC addition (cis) (25). Tubulin was added to the membrane-bathing solutions in the cis compartment after VDAC reconstitution and collection of control recordings of the channel current in tubulin-free solution. Conductance measurements were performed as described previously (59), using an Axopatch 200B amplifier (Axon Instruments, Inc., Foster City, CA) in the voltage clamp mode. Data were filtered by a low-pass 8-pole Butterworth filter (model 900, Frequency Devices, Inc., Haverhill, MA) at 15 kHz and a low-pass Bessel filter at 10 kHz and directly saved into computer memory with a sampling frequency of 50 kHz. The effective time resolution of the setup was ∼200 μs. For data analysis by Clampfit version 10.3, no digital filtering was applied. Individual events of current blockages were discriminated, and kinetic parameters were acquired by fitting logarithmic single, double, or triple exponentials to logarithmically binned histograms (60) as described previously (61). All lifetime histograms used 10 bins/decade. The number of blocking events for each analyzed current fragment was in the range from 250 to 2500. Four different logarithmic probability fits were generated using different fitting algorithms, and the mean and S.D. of the fitted time constants were used as mean and S.D. for the characteristic open and blockage times.

Statistics

Each channel experiment was repeated at least three times on different membranes. Concentration of tubulin was varied in the range of 8–30 nm to achieve the number of blockage events sufficient for statistical analysis. Records for analysis were obtained no less than 40 min after each tubulin addition to ensure a steady state. Because blockage time histograms do not depend on event rate, blockage time histograms for each experiment include data from current records corresponding to the same transmembrane voltage but a range of tubulin concentrations. Fits to histograms such as those in Figs. 1 and 3 used the maximum likelihood estimator with the simplex algorithm in Clampfit version 10.3. For fitting with multiple exponential functions, the number of exponents n was chosen so that the improvement in fitting with n + 1 exponentials was not statistically significant at the p < 0.001 level. To accept an n + 1-exponential fit, the natural logarithm of the ratio of the n + 1 likelihood/n likelihood was required to exceed 13. This ratio follows a χ² distribution with 2 degrees of freedom. A value of 13 corresponds to a probability of <0.001 that the n + 1 fit is better by chance than the n fit. For the statistical analysis of mean values as in Figs. 4 and 6, the differences between two groups of data were analyzed by a two-tailed t test using p < 0.05 as the criterion of significance. Differences between many groups were analyzed by one-way analysis of variance.

Modeling and optimization

The model was implemented using custom Python code. Optimization was performed on the Bridges (62, 63) high performance computing system using the DREAM Markov chain Monte Carlo algorithm (64) implemented in the software package Bumps (65). Confidence intervals on parameters and model predictions are calculated from the last 28,616 of 308,000 total DREAM samples.

Author contributions

T. K. R., P. A. G, and S. M. B. conceptualized the study, designed experiments, and interpreted results. P. A. G. and A. R. acquired the data and analyzed the results. D. P. H. developed the models and performed model optimizations. M. S. produced and characterized recombinant proteins. T. K. R. and D. P. H. analyzed the data and drafted the article. All authors contributed to writing, editing the article, and revising it critically for important intellectual content.

Appendix

The measured average escape time can be approximated by a first-passage time in a drift-diffusion framework (41–43). We parameterize the penetration of the carboxyl-terminal tail into the VDAC channel by a distance parameter x, which corresponds to the distance from the tubulin body to the VDAC channel constriction along the contour of the CTT. For tubulin, this calculation is quite straightforward, as the CTT can exit the nanopore only by retracting to the cis side of the membrane. Mathematically, this constraint is implemented as a reflecting boundary condition on the stochastic drift-diffusion equation at x = 0, and the corresponding solution for the average first passage time of retraction is as follows (41).

$$\tau \left(x_0\right)=D^{-1}{\displaystyle {\int }_{x_0}^L\exp \frac{U\left(x\right)}{k_{B}T}}\hspace{0.17em}dx{\displaystyle {\int }_0^x\exp \left(-\frac{U\left(x\prime \right)}{k_{B}T}\right)dx\prime }$$ (A1)

Here, U(x) is the sequence- and voltage-dependent interaction potential, whereas D is a diffusion constant. x₀ is the so-called “injection” point representing the initial position of the CTT and is taken to be at the minimum of the potential.

The interaction potential can be written as the sum of an electrical contribution U_E(x) and an entropic (geometric) component U_S(x).

$$U\left(x\right)=U_E\left(x\right)+U_S\left(x\right)$$ (A2)

U_E(x) is constructed from the known amino acid sequence of the CTT,

$$U_E\left(x\right)=eV{\displaystyle {\sum }_{i=1}^N{z}_i\Theta \left(x-x_i\right)}$$ (A3)

where e is the elementary charge, V is the transmembrane potential, z_i is the charge state of the ith amino acid, and Θ(x) is the Heaviside step function. If we introduce l_aa as the contour length per amino acid and N is is the number of amino acids, then L = Nl_aa is the total length of the CTT, and x_i = il_aa is the position of the ith amino acid along the contour of the CTT. This function is then smoothed by convolution with a Gaussian with full width at half-maximum equal to the pore length L_p. The amino acids are counted from the first residue after helix H12 in the tubulin crystal structure (1).

U_S(x) can be estimated from the known statistical properties of polymers. When the CTT is in the VDAC pore, it can be divided into two domains: the transmembrane domain, which has already passed through the pore, has length L − x − L_p/2, and can be treated as a polymer tethered to an impenetrable infinite wall (the membrane); and the cis domain, which has length x − L_p/2 and can be considered to be tethered to both the membrane and the tubulin body. In both cases, for simplicity, we describe the space of possible polymer conformations as a non-self-avoiding random walk of a polymer tethered to an impenetrable infinite wall, for which the Green's function (in cylindrical coordinates ρ, φ, z) is calculated from the method of images (66, 67).

$$G\left(r,\hspace{0.17em}r\prime ,\hspace{0.17em}\text{n}\right)={\left(\frac{2\pi n{b}^2}{3}\right)}^{-3/2}\hspace{0.17em}\exp \left(-\frac{3{\rho }^2}{2n{b}^2}\right)\left(\exp \left(-\frac{3{\left(z-\delta \right)}^2}{2n{b}^2}\right)-\exp \left(-\frac{3{\left(z+\delta \right)}^2}{2n{b}^2}\right)\right)$$ (A4)

Here, r = (ρ, φ, z) and r′ = (0, φ, δ), n is the number of segments of Kuhn length b connecting the two points, and δ is a small offset from the surface that can be taken to be arbitrarily small (10⁻³ was used for these calculations). The number of states available to the polymer is proportional to the volume integral of the Green's function over the unprimed variables (68), ω ∝ ∫∫∫G(r, r′, n)dV. For the transmembrane domain, this integral yields ω_T(x) ∝ erf(√(3/2n_T) × δ/b), where n_T = (L − x − L_p/2)/b.

For the cis domain, we assume that the molecule is tethered at a single point r = (0, φ, l_t) directly above the pore, where l_t is the distance between the attachment point and pore constriction. Ignoring the volume occupied by the tubulin body, we find the following.

$${\omega }_c\left(x\right)\hspace{0.17em}\propto \hspace{0.17em}{\left(\frac{2\pi n_c{b}^2}{3}\right)}^{-\frac{3}{2}}\left(\exp \left(-\frac{3{\left(l_t-\delta \right)}^2}{2n_c{b}^2}\right)-\exp \left(-\frac{3{\left(l_t+\delta \right)}^2}{2n_c{b}^2}\right)\right)$$ (A5)

Here, n_C = (x − L_p/2)/b. The entropic contribution to the potential is then simply U_S(x) = −k_BTlnω_Cω_T to within an additive constant that does not affect the escape time calculation. Based on atomic force microscopy studies, the Kuhn length b is 0.6 nm (69), whereas l_aa = 0.4 nm.

Inspection of the energy profiles in Fig. 7B shows that a large entropic contribution at small x (corresponding to full extension of the tail) prevents the system from ever reaching x = 0, justifying the use of the reflecting boundary condition in calculating the average escape time. The longest CTT, from yeast β-tubulin, is 34 amino acids long, so the radius of gyration is approximately R_g ≈ √(Lb/6) = 1.2 nm. This is approximately the radius of the VDAC lumen, so the confinement of the CTT in the pore is limited to the 1.4-nm diameter constriction at the center of the VDAC channel coming from VDAC's N-terminal α-helix (70). Thus, we have L_p = 1.2 nm (the approximate outer diameter of an α-helix). The diffusion constant of a polypeptide in VDAC has previously been determined to be about 0.4 μm²/s (43). The only unknowns are thus the tether lengths l_t, which might be different for α- and β-tubulin and are correspondingly denoted l_t^α and l_t^β. These are expected to be ∼2 nm, which is half the thickness of the membrane (i.e. the distance from the membrane surface to the VDAC center constriction).