Do TFSA Anions Slither?

Abstract

Multi-nuclear (¹H, ²H, and ¹⁹F) magnetic resonance spectroscopy techniques as functions of temperature and pressure were applied to the study of selectively deuterated 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)amide (EMIM TFSA) ionic liquid isotopologues and related ionic liquids. For EMIM TFSA, temperature-dependent ²H T₁ data indicate stronger electric field gradients in the alkyl chain region compared to the imidazolium ring. Most significantly, the pressure dependences of the EMIM and TFSA self-diffusion coefficients revealed that the displacements of the cations and anions are independent, with diffusion of the TFSA anions being slowed much more by increasing pressure than for the EMIM cations, as shown by their respective activation volumes (28.8 ± 2.5 cm³/mol for TFSA vs. 14.6 ± 1.3 cm³/mol for EMIM). Increasing pressure may lower the mobility of the TFSA anion by hindering its interconversion between trans and cis conformers, a process that is coupled to diffusion according to published molecular dynamics simulations. Measured activation volumes (ΔV^‡) for ion self-diffusion in EMIM bis(fluoromethylsulfonyl)amide and EMIM tetrafluoroborate support this hypothesis. In addition, ²H T₁ data suggests increased ordering with increasing pressure, with two T₁ regimes observed for the MD₃ and D₂ isotopologues between 0.1–100 and 100–250 MPa respectively. The activation volumes for T₁ were 21 and 25 (0–100 MPa) and 11 and 12 (100–250 MPa) cm³/mol for the MD₃ and D₂ isotopologues, respectively.

Graphical Abstract

¹H and ¹⁹F self-diffusion coefficients for EMIM TFSA as functions of pressure.

Introduction

There is great interest in studying ionic liquids (ILs) on a fundamental level as models for the transport properties of complex liquid systems, as well as for possible applications in several industries, including textiles, energy and nuclear waste recycling. With regards to energy, ILs comprised of imidazolium-based cations and their counter anions have formed the basis of many research projects geared towards the development of alternative electrolyte materials for energy storage devices such as batteries^1–4 and supercapacitors.^5–8 This is because of their useful combination of chemical, thermal and physical properties such as low volatility, combustion resistance and ionic conductivity. Another attractive feature of ILs is their tunability. Depending on the application, desired performance can be achieved by combining the right cation and anion to produce the required properties. Theories for controlling properties by design have been advanced based on trends observed in particular classes of ILs.^9–11 For example, it has been proposed that if one desires better transport properties, the choice should be ions of small size, greater charge delocalization and multiple conformations that differ slightly in energy. However, experience has shown that empirical relationships are poor predictors of what properties will result from particular pairings for many cations and anions. Nevertheless, the bis(trifluoromethylsulfonyl)amide (TFSA, (CF₃SO₂-N-SO₂CF₃)⁻) anion has become very popular in ionic liquid science for its tendency to form lower melting, lower viscosity and higher conductivity salts than many other anions. When combined with imidazolium cations, TFSA can produce fluid room temperature ILs with high ionic conductivity.¹¹

Various techniques have been applied towards understanding the factors that control the fluid properties of ILs, including molecular dynamic simulations,^12–14 conductivity,^15,16 viscosity,^15–17 Raman spectroscopy^18–20 and nuclear magnetic resonance (NMR).^{12,16,21–26} As a tool, NMR is able to provide nucleus-specific microscopic and macroscopic translational and rotational dynamics through determination of the spin-lattice relaxation time T₁ and the self-diffusion coefficient D, over a wide temperature and frequency range. Most NMR studies have been done as a function of temperature, which causes both changes in energy and density. However, when done as a function of pressure, NMR allows separation of the density effects from energy-related ones, which oftentimes control the transport dynamics of mobile systems, especially ones in which viscosity effects play a role. In this study we report multi-nuclear NMR (¹H, ²H, and ¹⁹F) T₁ relaxation and (¹H and ¹⁹F) self-diffusion data as functions of temperature and pressure for the deuterated isotopologues of 1-ethyl-3-methylimidazolium (EMIM) cation with the TFSA anion, and for comparison, EMIM bis(fluoromethylsulfonyl)amide (FSA, also known as FSI) and EMIM tetrafluoroborate (BF₄). The selective deuteration allows us to analyze the fundamental dynamics of the cation through ¹H (I = ½) and ²H (I = 1) probe nuclei. The quadrupole ²H nucleus is extremely sensitive to rotational dynamics and reflects the interaction between the nuclear quadrupole moment and its electric field gradient. The advantage of determining both T₁ and D data comes from the fact that analysis of T₁ data and associated correlation times often require an assumption about the relaxation mechanism and its relation to the translational motion of the probe species, while D data provides a direct determination of the translational motion.

Variable pressure has been used in vibrational spectroscopic studies of ILs^27–31 comprised of various anions and cations including EMIM and TFSA^18–20 and results show several behaviors, including conformational changes, enhancement of cation-anion hydrogen bonding interactions and shifts of vibrational frequencies to higher values. In this manuscript we present our findings of variable pressure and temperature NMR T₁ and D studies for EMIM TFSA, and pressure studies on EMIM FSA and EMIM BF₄. To the authors knowledge there have been no published variable-pressure NMR studies on these ILs. The initial objective for this study was to use selective deuteration to probe the local environment of each segment of the EMIM cation to identify each contribution to the transport properties of the IL. One question of interest was whether the motion of the anion is coupled to that of the cation at higher pressures. As increasing pressure is expected to affect the packing (molecular order) and possibly screening – two factors that affect the structure of ILs,³⁰ we expected to see these changes in both the short- and long-range dynamics of the system. Remarkably, as will be explained below, we found that the conformational dynamics of the TFSA anion dominate the effects of pressure on self-diffusion in EMIM TFSA.

One of the key molecular interactions in ILs is hydrogen bonding^30,32 through the C-H•••X and C-H•••O groups. Although weak in comparison with Coulombic interactions, hydrogen bonding plays a role in the structure and therefore dynamics of ILs. In general, strong hydrogen bonding can produce order in systems and one example of this are the O-H•••O bonds in water. Because of this, numerous efforts has been directed towards determining its precise nature. While it is not the intention of this manuscript to explore explicitly the hydrogen bonding in the EMIM TFSA system, we will use it to explain our results where applicable. As hydrogen bonds are known to increase in strength with increasing pressure, our reasoning of their effect on the system’s dynamics is applicable.

Experimental Section

Sample Preparation

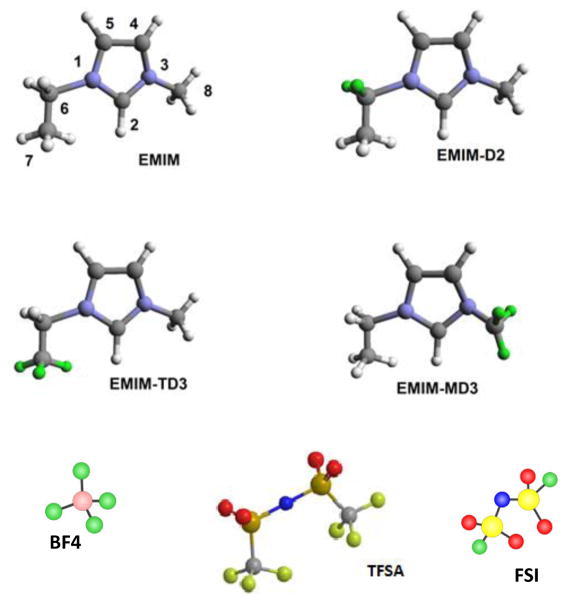
Three partially-deuterated 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)amide ILs were prepared by reaction of 1-methylimidazole with the appropriately deuterated ethyl bromide or the reaction of 1-ethylimidazole with methyl iodide-d₃, followed by metathesis to the TFSA salts using aqueous Li TFSA. Complete details regarding the synthesis can be found in the Supporting Information of Shkrob, et al.³³ Their structures are shown in Figure 1. The syntheses of EMIM FSI and EMIM BF₄ are reported in the Supporting Information. The samples were dried in a vacuum oven until their water content was below 200 ppm and stored in a dry argon-filled glove box to avoid absorption of atmospheric moisture.

Figure 1.

Structures of the deuterium-labeled (indicated in green) EMIM cations and the BF₄, FSA and TFSA anions (cis conformation shown).

Nuclear Magnetic Resonance

The ¹H spectra for EMIM TFSA were recorded using a Bruker Avance III 400 MHz SB spectrometer, using CDCl₃ as the ²H lock and a small amount of TMS (¹H δ = 0 ppm) as the chemical shift reference.

The T₁ and D measurements were conducted on a Chemagnetics CMX-300 spectrometer as a function of temperature from 296 to 373 K and pressure (up to 2.5 kbar) with a 7.3T superconducting magnet. For this magnetic field, ¹H, ²H and ¹⁹F resonances occur at frequencies of 309, 47 and 283 MHz respectively. For both the ¹H and ¹⁹F variable temperature T₁ and D measurements, the ILs were inserted into a 5 mm NMR tube. The experiments were performed in a 5mm Nalorac gradient probe and a current amplifier provided by Magnetic Resonance Instruments, Inc. The NMR spectra were obtained by collecting free induction decay following π/2 pulse and Fourier transforming the data.

Multinuclear spin-lattice relaxation measurements (T₁) were determined using the inversion recovery (180°-τ-90°-Acq) sequence for about 15 values of τ. At least five T₁s were allowed between repetitions of the pulse sequence and uncertainties were ~5%. Self-diffusion coefficients (D) can be obtained by using either static or pulsed field gradients with the Hahn spin-echo pulse sequence (π/2 - τ - π). For the pulsed field gradient technique, D values were obtained using the Hahn spin-echo pulse sequence with square-shaped gradient pulses of equal amplitude g, duration δ and separation Δ after the rf pulses. The values of δ and Δ are chosen to allow sufficient attenuation of the echo amplitude. The resulting attenuation depends on the change in positions and associated frequencies of the spins during the separation interval Δ and was shown to be represented by the equation:

$$A(g)=A_{0}exp[-2\tau /T_2]exp[-D{(\gamma \delta g)}^2(\mathit{\Delta }-\delta /3)]$$ 1

Here γ is the magnetogyric ratio, g is the gradient strength (dB/dz) and A₀ is the value of the echo amplitude at zero gradient. The values of both Δ and δ were adjusted at each new temperature setting and once optimized, g was varied to measure diffusion. The value of D was obtained by fitting the echo attenuation data for about 15 values of g ranging from ~0.2 – 3 T/m and uncertainties were ~ 5%. For D values determined by the static field gradient method, the echo attenuation profile is determined from:

$$A(\tau )=A_{0}exp[-2\tau /T_2]exp[-2D{(\gamma \tau g)}^2\tau /3]$$ 2

For all D values calculated, single exponential attenuation profiles were obtained.

For the multi-nuclear variable pressure measurements, the ILs were hermetically sealed in a plastic bag, placed in an rf coil and immersed in the pressure transmitting fluid (Fluorinert FC-3283 and vacuum oil for ¹H and ¹⁹F, respectively) inside a copper-beryllium pressure vessel. The pressure was generated using a manual pump that is capable of reaching pressures up to 2.5 kbar. The probe used was home built with a tuning circuit with an effective range of 60–80 MHz, which corresponds to a static field gradient of 27.5–35 T/m. All variable pressure experiments were performed at 80 MHz using a 35 T/m gradient.

Calculation of activation volumes from literature data

Activation volumes for comparison with our experimental results were obtained from analysis of literature data sets of diffusion constants and viscosities measured versus pressure and temperature. Data sets were selected for analysis based on their relevance to the focus of the study and the availability of sufficient data for accurate fitting. All the data used, their sources, and the resulting fits are tabulated in Supporting Information Section 2.

Results and discussion

Ambient pressure experiments

Before presentation of our novel pressure dependence results we shall compare our T₁ relaxation results on the EMIM TFSA isotopologues at ambient pressure with previous reports. The ¹H NMR peak assignments are consistent with those of Hayamizu, et al.²² and are tabulated in Table 1 following the scheme shown in Figure 1. A representative NMR spectrum for the MD₃ EMIM TFSA IL is shown in Figure S1 of Supporting Information Section 1. ¹⁹F and ²H NMR spectra (not shown) had single peaks.

Table 1.

¹H NMR parameters of each proton site of the EMIM cation in neat EMIM TFSA.

H label	2	4	5	6	7	8
δ (ppm)	8.45	7.39	7.32	4.14	1.42	3.84
Multiplicity	Triplet	DxD	DxD	Quadruplet	Triplet	Singlet
	4JH2–H4 = 4JH2–H5 = 1.60Hz 3JH4–H5 = 2.00Hz			3JH6–H7 = 7.34Hz

Variable-temperature diffusion and T₁ relaxation studies

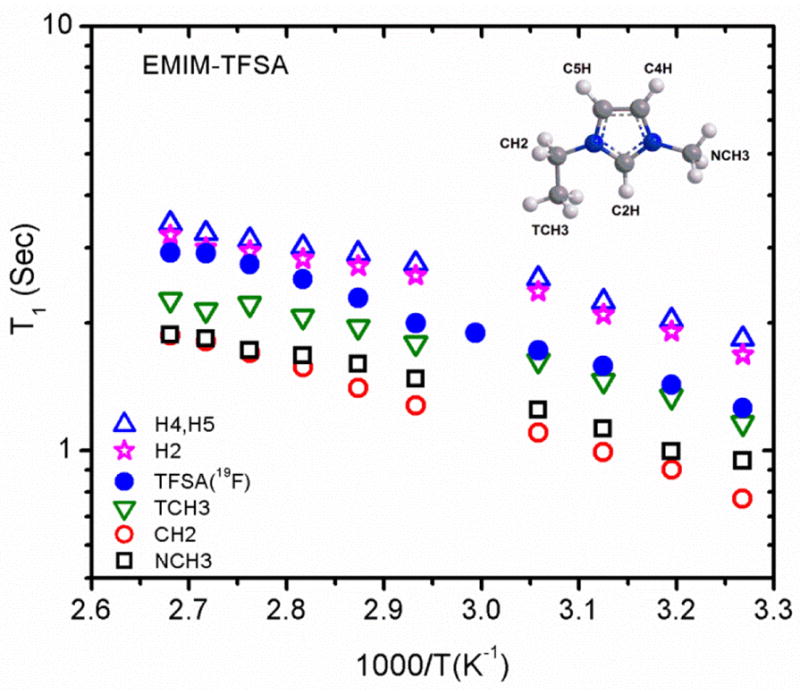
The ¹H and ¹⁹F spin-lattice relaxation times (T₁s) for EMIM TFSA are shown in Figure 2 as functions of inverse temperature. (Similar graphs for three deuterated isotopologues of EMIM are shown in Figures S2–S4 of Supporting Information Section 1.) For a heterogeneous spin I = ½ system, the magnetization recovery can have non-exponential behavior, making it difficult to determine a definitive T₁. Fortunately, for the samples studied all magnetization recoveries were exponential and the general behavior shows increasing T₁ with increasing temperature. The behavior for the adjacent ring protons H4 and H5 are identical and were the longest for all samples, while the NCH₃ and CH₂ protons had the shortest T₁s. The ¹⁹F T₁s for CF₃ groups of TFSA were linear for all the samples. The data observed for the EMIM TFSA sample is consistent with that in the literature.²²

Figure 2.

Arrhenius plots of ¹H and ¹⁹F T₁ relaxation times for the assigned peaks of EMIM TFSA.

Over the temperature range studied, no T₁ minimum was observed. Because of this, it was not possible to determine correlation times associated with the motions. Regardless, for mobile media the dynamics of the diffusing species cause fluctuations of the local fields that, depending on the spin, could be magnetic or electric in nature. In the case of magnetic fluctuations, the fields may be due to dipole-dipole interactions, chemical shift anisotropy, scalar couplings, and spin rotations. All four produce modulations that create mechanisms for relaxation. While the motions may be translational and/or rotational in nature, for viscous media such as ionic liquids where the timescale for viscosity-affected motions are long, the expectation is that the T₁s obtained represent the reorentational motion of the whole molecule. Additionally, for ¹H spins, the dipole-dipole interactions are the main source of relaxation. Since the dipole-dipole interaction depends inversely on the cube of atomic internuclear distances, intramolecular interactions are stronger than intermolecular ones.^34,35 Although this does not however entirely exclude the intermolecular interactions, they shall be considered negligible. This further supports our interpretation of the T₁s as broadly indicative of the rate of motion of molecules bearing nuclei.

Activation energies were determined from the T₁ data for all the samples and the values are summarized in Table 2. Values range from ~8 – 17 kJ/mol, and the all-proteo EMIM IL had lower activation energies compared to D₂, TD₃ and MD₃. The difference in values may be due to the perturbation of the hydrogen bonding by the presence and location of the deuterons. Hydrogen bonding and its effect on ion transport is extremely sensitive to the breakage and formation of bonds, which facilitate ion transport. The placement of a larger moment of inertia within the network affects the rotational motions and rates of formation and breakage, thereby the effective hydrogen bonding.³⁶ Early single crystal studies on the effect of substituting deuterium for hydrogen in O-H•••O hydrogen bonded crystals showed a change in the lattice dimensions, the general trend being an increase.^37,38 Such an increase could reduce the strength of the hydrogen bonding by increasing the distances between the interaction sites on the cations and anions. Disturbance of the hydrogen bonding was also observed by Chang, et al.,³⁹ whose work showed the presence of D₂O affecting the IR vibrational frequencies for the both the alkyl and imidazolium C-H groups.

Table 2.

Activation energies for reorientational motion in EMIM TFSA determined from ¹H, ²H and ¹⁹F T₁ data (kJ/mol).

Position	EMIM-MD3	EMIM-TD3	EMIM-D2	EMIM
H4, H5	11.8 ± 0.8	10.3 ± 0.2	10.0 ± 0.2	8.3 ± 0.5
H2	9.9 ± 0.7	10.3 ± 0.3	10.8 ± 0.3	8.4 ± 0.5
TCH3	12.4 ± 0.4	-	12.3 ± 0.3	9.1 ± 0.5
CH2	16.9 ± 0.8	11.2 ± 0.3	-	12.3 ± 0.2
NCH3	-	10.3 ± 0.3	11.2 ± 0.4	10.1 ± 0.4
TFSA (19F)	11.8 ± 0.2	12.2 ± 0.3	12.6 ± 0.5	12.3 ± 0.3
2H T1 data	15.0 ± 0.3	16.2 ± 0.2	11.6 ± 0.1	-

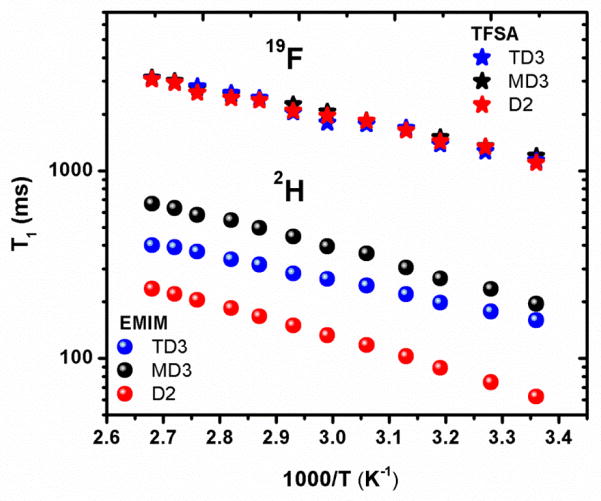
Shown in Figure 3 are the linear Arrhenius plots of ²H and ¹⁹F T₁ relaxation data for the three deuterated isotopologues. The ¹⁹F relaxation times were identical as expected, while the ²H T₁s were in the order MD₃ > TD₃ > D₂ at each temperature, the same pattern observed for the activation energies for ¹H relaxation. The MD₃ and TD₃ had similar activation energies (~15 and 16 kJ/mol) while that for the D₂ group was lower (~12 kJ/mol). Deuterons relax through quadrupolar interactions, which the T₁ results indicate are more efficient in the D₂ isotopologue, meaning the electric field gradient is strongest in the location of CD₂, followed by MD₃. Additionally, the fact that different T₁s are observed for the various deuterated groups suggests asymmetry in the interactions between each group and its surroundings, which is comprised mainly of anions in the first solvation shell. Both the TFSA and EMIM ions are asymmetric with regards to their charge distributions.^40–42 This asymmetry was demonstrated for the TFSA anion by ab initio calculations from which the natural charge was determined and electrostatic potential (ESP) based charge calculated for the various points of interactions (N, O and F).^41,42 While the values of the charges determined by the two methods differed, the pattern observed was the same, with the order N > O > F for favorable interaction locations. The fact that the fluorine atoms had the lowest charge means they are most ‘ionic’, less restricted and therefore more able to effect conformational changes.

Figure 3.

Arrhenius plots of ²H and ¹⁹F T₁ relaxation times for the assigned peaks of deuterated EMIM TFSA samples.

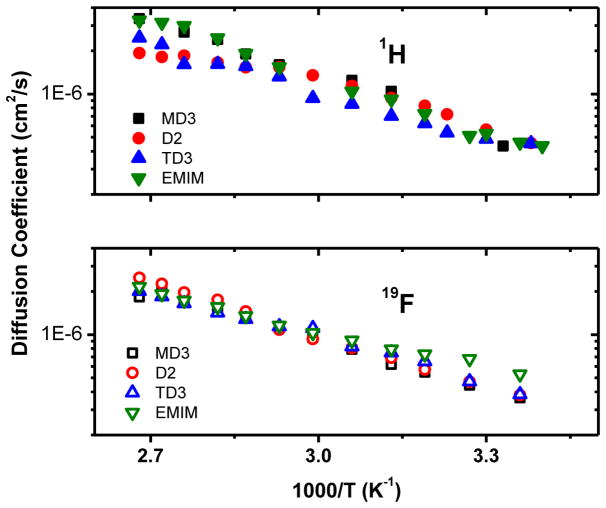
Self-diffusion coefficients D were determined as a function of temperature using the PGSE NMR technique for the cations (¹H) and anions (¹⁹F), and the Arrhenius plots are shown in Figure 4. Slightly faster diffusion was observed for the cations over the entire temperature range and results are comparable with those of Hayamizu et al.,²² Noda et al.¹⁶ and Borodin et al.¹² While acknowledging that the diffusion coefficients are best fit using the Vogel-Tamman-Fulcher equation,^12,16,22 linear fits over the measured temperature range obtain an activation energy for all the ¹H diffusion data taken as one set of 22.5 ± 1.0 kJ/mol and that for all the ¹⁹F data taken as one set is 20.5 ± 0.6 kJ/mol.

Figure 4.

Arrhenius plots of ¹H and ¹⁹F self-diffusion coefficients for all four EMIM TFSA isotopologues.

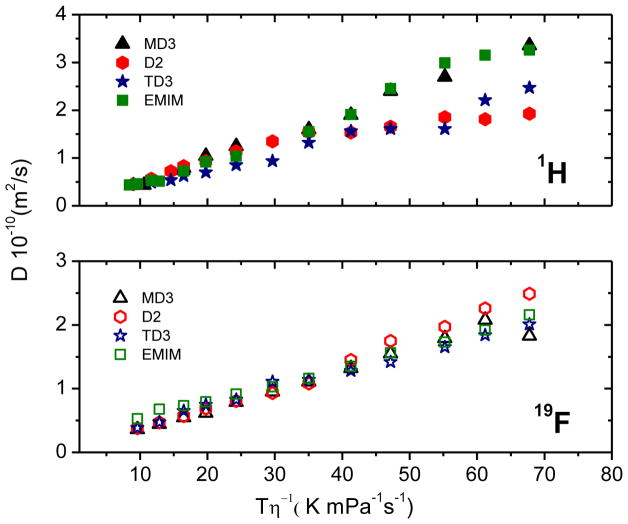
Variable-temperature diffusion studies on EMIM TFSA^16,22 have shown that the diffusion correlates well with the inverse of the viscosity through the Stokes-Einstein relationship: D = kT/πcηr, where k is the Boltzmann constant, T is the absolute temperature, c is a constant (4–6) and r is the effective hydrodynamic radius. As shown in Figure 5, when D is plotted against T/η the result is linear and shows the TFSA anion having a greater hydrodynamic radius than the EMIM cation.¹⁶ The viscosity data used for the figure was taken from Noda et al.¹⁶ and considered the same for all isotopologues.

Figure 5.

¹H and ¹⁹F diffusion constants vs. T/η for the EMIM TFSA isotopoloques.

The dispersion observed at higher temperatures in the ¹H D data in both Figures 4 and 5 may be attributed to three competing factors - the mass difference between ¹H and ²H, the strengths of the electric field gradients and the reduction in hydrogen bonding with increasing temperatures. Increasing temperature is known to break hydrogen bonds and reduce their interactions. As hydrogen bonds break the dominant mode of proton transport becomes the ‘Vehicle mechanism’. Greater mass would further reduce this process, resulting in lower self-diffusion coefficient values. In addition to this is the effect of the electric field gradient, which appears strongest for D₂ compared to both MD₃ and TD₃. When all these points are considered differences in the ¹H D data at higher temperatures seems reasonable, even after accounting for at most a 5% error in the diffusion values.

Variable-pressure diffusion and T₁ relaxation studies

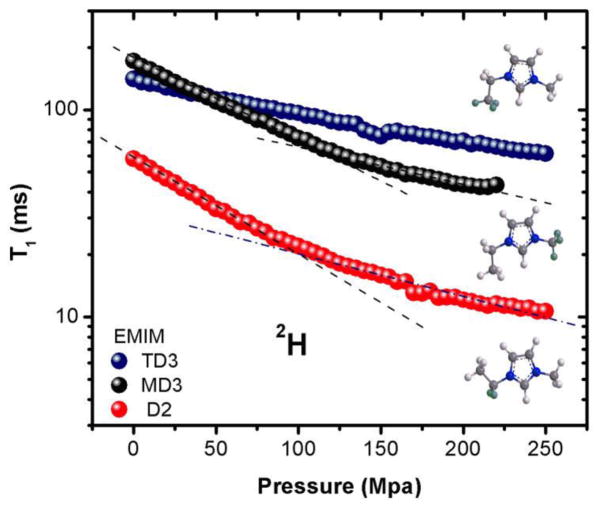
Variable pressure data for T₁ (²H) relaxation and ion (¹H and ¹⁹F) self-diffusion are reported in Tables S19 and S20 of Supporting Information Section 1. The data are depicted in Figures 6 and 7 below, and the relaxation times and diffusion constants both decrease with increasing pressure as expected. The use of pressure as a variable allows the changing of the inter- and intra-molecular interactions without affecting the frequency (temperature) or causing compositional changes. As shown, no saturation was observed for either T₁ or D over the pressure range studied, which suggests that whatever dynamical changes are taking place have not yet reached their limits. While the D data is monotonic, the T₁ plots for the two isotopologues that are deuterated adjacent to the imidazolium ring exhibit two distinct linear regions between the pressure ranges 0.1–100 and 100–250 MPa, which could indicate two different packing arrangements for both the MD₃ and D₂ deuterated samples. It is possible that at the transition point the increasing pressure forces the isotopologues and their anions into a new molecular arrangement and that modest change in their electric field gradients causes corresponding variations in relaxation. The linearity of the TD₃ group could be due to its distance away from the ring, or the fact that the alkyl chain is a less favorable interaction site compared to both MD₃ and D₂ for hydrogen bonded imidazolium cation-anion interactions.^40–42

Figure 6.

²H T₁ relaxation times for deuterated EMIM TFSA isotopologues as functions of pressure.

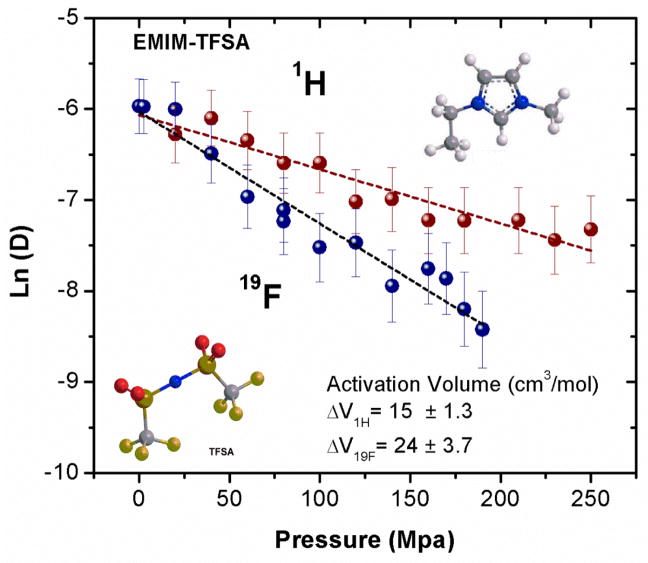
Figure 7.

¹H and ¹⁹F self-diffusion coefficients for EMIM TFSA as functions of pressure.

Activation volumes for relaxation and diffusion as determined by fitting the T₁ or D vs. pressure data according to equation (3) are given in Table 3.

Table 3.

Activation volumes determined from variable-pressure ²H T₁ data at 22 ˚C.

Deuteration site	ΔV (cm3/mol) (0.1–100 MPa)	ΔV (cm3/mol) (100–250 MPa)
MD3	21 ± 1	11 ± 1
D2	25 ± 1	12 ± 1
TD3	8 ± 1 (0.1–250 MPa)

$$\mathrm{\Delta }V=-RT{(\partial \text{ln}\mathrm{\alpha }/\partial \mathrm{P})}_{\mathrm{T}}$$ 3

Here α can be 1/T₁ or D, P is the pressure, T is the temperature and R is the gas constant. There are rearrangements in the local environment to accommodate ion rotation that depend on local density fluctuations. Activation volume is therefore an indicator of the ease of mobility, with higher values oftentimes being attributed to more restricted motion, possibly due to greater interactions between the species. The values obtained for the MD₃ and D₂ isotopologues are similar, with that for the 100–250 MPa region being almost half that of the 0.1–100 MPa region. The TD₃ isotopologue showed the smallest activation volume and monotonic behavior over the entire pressure range.

Figure 7 illustrates a remarkable finding about the pressure-dependent behavior of the EMIM cation and TFSA anion diffusion coefficients. At ambient pressure the self-diffusion coefficients, measured by ¹H and ¹⁹F respectively, are essentially the same. However, with increasing pressure the diffusion of the anion slows faster than for the cation, resulting in an activation volume that is almost twice as large for TFSA compared to EMIM (28.8 vs. 14.6 cm³/mol, respectively, see also Table 4).

Table 4.

Activation volumes for ionic self-diffusion and fluidity for selected ILs, and calculated ionic volumes. All volumes are in cm³/mol and measured at 25 °C unless noted.

Ionic Liquid	ΔV‡cation	ΔV‡anion	ΔV‡fluidity	Vcationa	Vaniona
EMIM TFSA	14.6 ± 1.3 b (22 °C)	28.8 ± 2.5 b (22 °C)	25.9 ± 0.7 d	70.2	95.6
BMIM TFSA i	19.2 ± 1.4 b (27 °C)	22.6 ± 2.7 b (27 °C)	27.3 ± 0.2 e	90.6	95.6
HMIM TFSA i	–	–	27.4 ± 0.2 d 25.4 ± 0.3 d (50 °C)	111.1	95.6
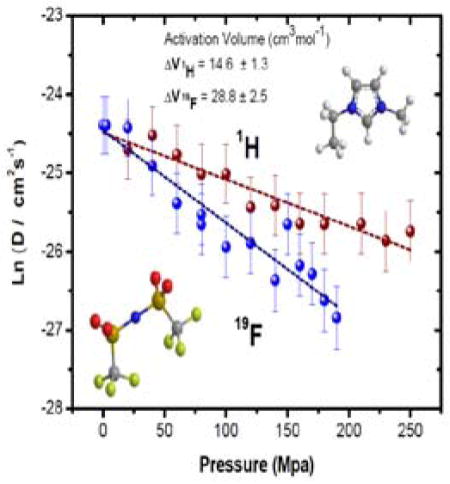
EMIM FSA	12.9 ± 0.9 b (22 °C)	11.0 ± 1.5 b (22 °C)	–	70.2	65.0
EMIM BF4	14.0 ± 1.0 b (22 °C)	15.3 ± 1.4 b (22 °C)	24.4 ± 1.0 (20 °C) f	70.2	30.4
BMIM BF4 i	22.0 ± 0.4 c 19.0 ± 0.2 c (50 °C)	No data at 25 °C 18.9 ± 0.7 c (50 °C)	25.0 ± 0.1 g 21.4 ± 0.2 g (50 °C)	90.6	30.4
HMIM BF4 i	–	–	29.5 ± 0.6 d 23.2 ± 0.2 d (50 °C)	111.1	30.4
OMIM BF4 i	25.3 ± 0.8 c (50 °C)	24.7 ± 0.4 c (50 °C)	29.2 ± 0.2 h 25.5 ± 0.2 h (50 °C)	131.6	30.4

^aRef. 50.

^bThis work.

^cRef. 51.

^dRef. 52.

^eRef. 53.

^fRef. 54.

^gRef. 55.

^hRef. 56.

ⁱBMIM = 1-butyl-3-methylimidazolium, HMIM = 1-hexyl-3-methylimidazolium, OMIM = 1-octyl-3-methylimidazolium.

In fluid (as opposed to crystalline) ionic liquids, the TFSA anion exists in equilibrium between two conformational states about the C-S^···S-C dihedral angles - described as trans or anti (C₂ symmetry) and cis or gauche (C₁ symmetry). (In crystals, typically only one conformer is present although there can be exceptions.) This equilibrium has been studied experimentally by Raman spectroscopy^20,43 and by electronic structure and molecular dynamics (MD) simulations.^12,43–48 Under ambient conditions the trans conformer is slightly favored^20,43 and the enthalpy change from the trans conformer to cis is positive by about 3.5 kJ/mol according to temperature-dependent Raman spectroscopy⁴³ and supported by MD simulations.¹² Pressure-dependent Raman spectroscopy²⁰ on N,N-diethyl-N-methyl-N-(2-methoxyethyl)ammonium (DEME) TFSA showed an increasing trans/cis ratio with increasing pressure, finding that the partial molar volume of the trans-TFSA anion conformer is 0.7 cm³/mol smaller than that of the cis one for that system.

Molecular dynamics simulations by Borodin et al.¹² showed that artificially increasing the barrier for trans-cis conversion of the anion in EMIM TFSA and N-methyl-N-propylpyrrolidinium TFSA by 12.5 kJ/mol resulted in slowing down of the anion and cation transport by 40–50%. No similar effect was found in the case of the smaller FSA anion. They showed that in the case of TFSA the ionic self-diffusion is coupled to conformational exchange. Although the +0.7 cm³/mol reaction volume for trans-to-cis TFSA conversion cited above is relatively small, the activation volume for conformational exchange could be much larger, and thus contribute to the larger activation volume for TFSA anion self-diffusion compared to the EMIM cation. Borodin and coworkers¹² did not note a difference in self-diffusion between the cations and the TFSA anion when they artificially increased the TFSA conformational exchange barrier in their simulations, however the difference is quite evident in our pressure data.

The conformation and shape of the cation and its alkyl chain have also been shown to affect the self-diffusion coefficients of the ions, which Tsuzuki et. al. demonstrated for EMIM cation TFSA and other ILs using molecular dynamics simulations.⁴⁹ Simulated D values of both the EMIM cation and TFSA anion were reduced by 39% and 34% respectively when the conformational flexibility of the alkyl chain was restricted along the C₂-N₁-C₇-C₈ torsional angle.

Consequently, molecular dynamics simulations predict that restriction of conformational exchange results in slowing self-diffusion for both the TFSA anion and the EMIM cation to similar degrees, regardless of whether the restriction is imposed on the anion or the cation, although the effects may be larger in the case of restricting the anion. This situation left open the question of whether the remarkable effect shown in Figure 7 could be due to pressure-induced conformational restriction of the anion, the cation or both ions. We therefore set out to measure activation volumes for the related ILs EMIM FSA and EMIM BF₄ and to compare our results with activation volumes for other ILs available in the literature. We selected EMIM FSA in order to test the predictions of Borodin et al.¹² in contrast to EMIM TFSA, and EMIM BF₄ was selected to provide a small anion with no conformational exchange and also because pressure-diffusion data for longer-chain imidazolium BF₄ ILs was available in the literature for comparison. The results are shown in Table 4 along with selected results derived from the literature. A much larger ΔV^‡ set for self-diffusion and fluidity (= 1/viscosity), calculated from literature data and covering 18 ILs, is presented in Supporting Information Section 2.)

Several trends are evident from the data in Table 4. First, the activation volumes for ionic self-diffusion in EMIM FSA and EMIM BF₄ are very similar for anions and cations in the same IL. The ΔV^‡ values for EMIM cation self-diffusion are slightly smaller for the FSA and BF₄ ILs than for the TFSA salt. Significantly, the activation volumes for FSA and BF₄ self-diffusion in the EMIM IL series are much smaller than that of TFSA, and ΔV^‡ is larger for BF₄ than for FSA despite the former anion having less than half the ionic volume of the latter one. These results comport with the predictions of Borodin et al.¹² that conformational restriction of the anion would have no effect on diffusion in EMIM FSA, whereas it would have a strong effect in EMIM TFSA. Comparison of EMIM FSA and EMIM BF₄ shows that the primary ΔV^‡ effect is not related simply to anion size, so the dynamics of the TFSA anion is the key factor.

However, the MD simulations summarized above predict that diffusion of both ions would be affected comparably but that is not observed in EMIM TFSA. In the case of BMIM TFSA, ΔV^‡ for cation diffusion is more than 4 cm³/mol larger than for EMIM, whereas ΔV^‡ for the TFSA anion is more than 6 cm³/mol larger than for EMIM than for BMIM, although the uncertainties for both are fairly large. As the alkyl chain on the cation grows longer, pressure effects on its conformational dynamics can also influence the activation volumes. Thus, the EMIM cation would appear to be particularly suited for exposing the role of conformational dynamics in the diffusion of TFSA anion.

The effects of increasing imidazolium alkyl chain length on ΔV^‡ for self-diffusion can be seen among the entries for the BF₄ salts in Table 4. Comparison of the results we obtained for EMIM BF₄ with those for BMIM BF₄ with OMIM BF₄ calculated from the literature show that the activation volumes for self-diffusion of the cation and anion in a given IL are the same within the error limits, and they increase significantly as the alkyl chain length increases. The increases with chain length have to be inspected carefully because of the temperature differences in the measurements. As seen in with ΔV^‡_BMIM for BMIM BF₄, in the fourth column of Table 4 and in many examples in Supporting Information Section 2 Table S22, the activation volumes decrease with increasing temperature, since the free volume increases as the density decreases.

The effects of alkyl chain length in the BMIM, HMIM and OMIM PF₆ series (see Table S22, Supporting Information Section 2) are harder to compare due to the scarcity of data sets at temperatures in common. Clear increases with chain length are seen in ΔV^‡_PF6 but the pattern in ΔV^‡_cation is less clear. Also, ΔV^‡_PF6 is clearly larger than ΔV^‡_HMIM at 50 °C and ΔV^‡_OMIM at 75 and 80 °C, but ΔV^‡_PF6 and ΔV^‡_cation are approximately the same for BMIM and for HMIM at higher temperatures. A differential effect on the PF₆ anion cannot arise from conformational exchange since it has none, however MD simulations have shown that there are profound changes in the structural organization of this family of ILs as the alkyl chains lengthen.^57,58 Longer alkyl chains lead to increasing degrees of polar-nonpolar domain segregation, and as the chains grow longer the polar domain where the PF₆ anions reside changes from an essentially isotropic 3-dimensional space to a network of ionic channels that confine diffusion of the anion (see the void spaces in Figure 6 of Reference 58), which may produce a relative increase in ΔV^‡_PF6 with chain length. The reason why the BF₄ and PF₆ IL families differ in their behavior (at least within the limited amount of available data) is beyond the scope of this discussion but it may involve differences in the interactions of the respective anions with the imidazolium cations.

N-butyl-N-methylpyrrolidimium TFSA (BMpyrr TFSA) is the only non-imidazolium IL for which pressure-dependent self-diffusion constants are available,⁵⁹ and it is distinguished from the imidazolium salts by the fact that the saturated pyrrolidine ring undergoes its own conformational exchange (pseudorotation)⁴⁷ while the planar aromatic imidazolium cations are rigid. (Calculated activation volumes for BMpyrr TFSA are presented in Supporting Information Section 2 Table S22.) Consequently, there are three types of conformational exchange occurring in BMpyrr TFSA, cation alkyl chain reorientation, cation ring pseudorotation and anion cis-trans isomerization. The activation volume for BMpyrr diffusion in BMpyrr TFSA (30.5 ± 0.3 cm³/mol at 30 °C) is significantly larger than the one we measured for BMIM in BMIM TFSA (19.2 ± 1.4 cm³/mol at 25 °C). Since BMpyrr and BMIM have the same number of non-hydrogen atoms, the large difference in activation volumes clearly exposes the dynamical consequences of the non-planarity and conformational lability of the BMpyrr cation on the transport properties of the IL.

The activation volume results for ionic self-diffusion thus serve as important experimental corroboration of the findings from molecular dynamics simulations described above that conformational exchange plays a major role in ion transport within ILs. With its small size and minimal configurational dynamics, the EMIM cation turns out to be very useful for exposing dynamical effects of its counterions. Effects that are observable in ILs containing small ions can get washed out as the ions increase in size, and they can also be overshadowed by the effects of structural inhomogeneity as the ions become elaborated enough to induce domain segregation or other types of specific interactions.

It is unfortunate that the number of results for pressure-dependent IL self-diffusion coefficients available in the literature is limited only to the examples discussed above (as far as we could find using resources including SciFinder, ILThermo⁶⁰ and Web of Science), but it is not surprising due to the specialized equipment and copious instrument time required for the measurements. To expand the range of activation volume data for transport phenomena in ILs we examined the reported pressure dependences of the viscosities of the ILs for which we had diffusion data and related ones sharing the same cations and/or anions. The results are presented in the right-hand columns of Supporting Information Section 2 Table S22 and the fits are individually presented in Section 2 as well. In order to keep the sign of the calculated activation volumes consistent with the diffusion results, the natural log of the fluidity, or inverse viscosity, was plotted versus pressure. In most cases the activation volume for viscous flow ΔV^‡_fluidity for a given IL is slightly larger than the self-diffusion activation volumes ΔV^‡_cation and ΔV^‡_anion at the same temperature. There is also more scatter in the ΔV^‡_fluidity results, owing to measurements by different methods and groups that sometimes disagree and in other instances concur. (Data with too few observations or with obvious problems such as inconsistency with the preponderance of published ambient-pressure data were not included in Table S22. In some cases data from multiple sources was analyzed and reported.)

Generally speaking, the ΔV^‡_fluidity results support the more limited self-diffusion results in terms of trends among families sharing common anions and differences between anion families. As expected, the trend of decreasing ΔV^‡_fluidity with higher temperature also occurs to a similar degree as with the self-diffusion results. Two points deserve specific mention. First, ΔV^‡_fluidity values for EMIM BF₄ at 20 and 30 °C (24.4 and 23.0 cm³/mol, respectively) are much larger than ΔV^‡_EMIM (14.0 cm³/mol) and ΔV^‡_BF4 (15.3 cm³/mol) at 22 °C. To our knowledge there is no pressure-dependent viscosity data available for EMIM FSA at present, so we cannot be sure whether the EMIM BF₄ results are unique or part of a trend. Second, our calculations revealed huge ΔV^‡_fluidity values for two salts of the tris(pentafluoroethyl)trifluorophosphate (FAP) anion, namely 1-butyl-2-methyl-3-methylimidazolium (BMMIM) FAP and N-butyl-N-methoxyethylpyrrolidinium ((EOM)Mpyrr) FAP, 45.4 and 41.8 cm³/mol respectively at 40 °C. The FAP anion is significantly larger than any of the other anions we studied however it is nominally matched in size by the OMIM and C₁₀MIM cations, but not by the ΔV^‡_fluidity values for their respective ILs in Table S22. Clearly the transport dynamics of FAP ILs will be a fruitful area for further studies.

Conclusion

Complete NMR T₁ and D measurements were performed on selectively-deuterated EMIM TFSA samples as a function of both temperature (20–100 °C) and pressure (0.1–250 MPa). Selective deuteration of the various sites (TD₃, MD₃ and D₂) allowed assessment of local short-range motions through determination of the ²H T₁s. The values ranked in the order MD₃ > TD₃ > D₂ at each temperature and the activation energies determined followed the same order. The differences in the T₁ activation energies are possibly due to variations in the strength of the hydrogen bonds at the deuterated sites in the network of cations and anions.

Several theoretical studies on the gas-phase interactions of the imidazolium cation and TFSA anion reveal an expanded network whereby anions and cations interact through hydrogen bonds, the strongest of which exist through the hydrogen at the C2 location on the imidazolium ring.^40–42 Central to formation of these bonds are the conformations of both the cation and anion and the sites of interactions. For the imidazolium-based cation, nine sites of interactions are favored by the anions.^40,41 However, due to several factors that include Coulombic repulsion and anion size, not all sites can be occupied simultaneously. The fewer sites occupied, the weaker and less ordered the network.^40,41 For TFSA, it takes only two anions to fully encapsulate the cation, which results in a weakly linked network of ions with a high degree of disorder due to its conformations.

It is expected that frequent fluctuations of these bonds can cause fluctuations in ionic positions and orientations, thereby affecting the transport of the ionic species. In addition to reducing bond distances as shown by Raman spectroscopy,^27–31 increasing pressure will also strengthen hydrogen bonds, thereby creating a more rigid network. We see this in the variable pressure ²H T₁ data, which shows two activation volumes for both D₂ and MD₃ in the pressure ranges 0.1–100 and 100–250 MPa. One could consider these two regions as having different local structures, with 100 MPa being the transition point. It is interesting that the TD₃ group does not show this type of behavior, which may be due to its distance from the electron-withdrawing cationic imidazolium ring.

The measurements of ionic self-diffusion constants as a function of pressure produced the provocative finding that the activation volume for TFSA diffusion in EMIM TFSA is approximately twice that of the EMIM cation. The difference in activation volumes is far smaller for BMIM TFSA and there are few examples in the literature data we analyzed (Table S22) where the difference between ions in the same IL is statistically significant, and none that are comparably dramatic. To probe the factors contributing to this remarkable difference, we determined activation volumes for self-diffusion in EMIM FSA and EMIM BF₄. In both ILs we found that the activation volumes of both ions were small (11–15 cm³/mol) and comparable to that of EMIM in EMIM TFSA. The apparently small inherent activation volume for EMIM thus provides contrast to observe the much larger ΔV_diff for TFSA, and provokes reflection about its origins.

As described above, MD simulations of Borodin¹² predicted that restriction of TFSA conformational exchange in EMIM TFSA would lead to reduced transport of both ions but that the same type of restriction on the FSA anion in EMIM FSA would have no effect. Canongia Lopes and coworkers also noted that the conformational change in FSA is subtle compared to TFSA.⁶¹ By probing the effect of increasing pressure on self-diffusion rates, we tested this hypothesis by using pressure to reduce the free volume available to accommodate interconversion between the cis and trans conformers of TFSA. Compared to EMIM FSA, we did indeed see a dramatic effect, but only in the ΔV_diff for TFSA anion and not for the EMIM cation. TFSA anion has trifluoromethyl groups that FSA anion lacks, and the displacement of the CF₃ groups during cis-trans interconversion consequently places greater steric demands on diffusion that show up in ΔV_diff. We believe this is solid evidence for the connection between TFSA conformational exchange and diffusion. Thus, the TFSA anion ambulates through an ionic liquid by twisting between its two conformers, similar to how a snake moves by slithering.

We suggest that our experimental activation volume results provide support for theoretical interpretations of how configurational interconversion is important for diffusion in ionic liquids, which are not easy to validate by other experimental approaches. Activation volume results have proven very valuable for detailed mechanistic studies in ionic liquids⁶² as well as many other areas of chemistry.^63,64 The results we have obtained so far suggest promising avenues for further investigations, which we hope will be enhanced by complementary molecular dynamics studies.