A biomechanical case study on the optimal orthodontic force on the maxillary canine tooth based on finite element analysis

Abstract

Excessive forces may cause root resorption and insufficient forces would introduce no effect in orthodontics. The objective of this study was to investigate the optimal orthodontic forces on a maxillary canine, using hydrostatic stress and logarithmic strain of the periodontal ligament (PDL) as indicators. Finite element models of a maxillary canine and surrounding tissues were developed. Distal translation/tipping forces, labial translation/tipping forces, and extrusion forces ranging from 0 to 300 g (100 g=0.98 N) were applied to the canine, as well as the force moment around the canine long axis ranging from 0 to 300 g·mm. The stress/strain of the PDL was quantified by nonlinear finite element analysis, and an absolute stress range between 0.47 kPa (capillary pressure) and 12.8 kPa (80% of human systolic blood pressure) was considered to be optimal, whereas an absolute strain exceeding 0.24% (80% of peak strain during canine maximal moving velocity) was considered optimal strain. The stress/strain distributions within the PDL were acquired for various canine movements, and the optimal orthodontic forces were calculated. As a result the optimal tipping forces (40–44 g for distal-direction and 28–32 g for labial-direction) were smaller than the translation forces (130–137 g for distal-direction and 110–124 g for labial-direction). In addition, the optimal forces for labial-direction motion (110–124 g for translation and 28–32 g for tipping) were smaller than those for distal-direction motion (130–137 g for translation and 40–44 g for tipping). Compared with previous results, the force interval was smaller than before and was therefore more conducive to the guidance of clinical treatment. The finite element analysis results provide new insights into orthodontic biomechanics and could help to optimize orthodontic treatment plans.

1. Introduction

Orthodontic forces represent a major inducing factor for tooth movement. Such forces are produced by orthodontic appliances and exert on the tooth crown, with the forces transferring to surrounding periodontal tissues through the tooth body, triggering tissue remodeling after cushioning and absorbtion by the periodontal ligament (PDL) (Kim et al., 2010; Lombardo et al., 2012). The magnitude of the forces is crucial (Hohmann et al., 2007; Rohan et al., 2015), where oversized forces may lead to root resorption, or even tooth exfoliation in the worst case scenario. In addition, orthodontic treatment is almost irreversible, and it is hard to repair failed cases. As a result, serious adverse effects can result from treatment failure. On the other hand, if the forces are too small, the tooth will not move or move at a speed that is too low, extending the treatment period. The willingness and enthusiasm of the patient would likely be reduced at the same time, complicating the effort to realize an ideal orthodontic treatment.

In the physiological process of tooth movement, the PDL plays a crucial role in regulating orthodontic movement (Liao et al., 2016). The strain of PDL is linearly related to the tooth movement rate—a tooth will not move with a PDL strain that is too low, and bone remodeling would be triggered until the strain reaches 0.03%. With the strain continually increasing to 0.3%, tooth movement rate would increase to a limit, with the maximum velocity of the canine moving at 0.0414 mm/d (Qian et al., 2008). Li (2014) regarded PDL strain as an indicator of tooth movement, and considered that the optimal PDL strain would range from 0.24% (80% of 0.3%) to 2.4% (8 times of 0.3%) during tooth movement. Yet they did not provide a conventional explanation for the upper limit of 2.4%, and so further analysis is required to determine if it is reasonable or not. On the other hand, a series of studies revealed that the hydrostatic stress of the PDL is related to PDL tissue necrosis and hyalinization, and it can be used as an indicator for predicting root resorption (Hohmann et al., 2007, 2009). Several clinical studies proposed that tooth movement is initiated when the hydrostatic stress reaches a capillary blood pressure of 4.7 kPa (Dorow and Sander, 2005; Field et al., 2009; Chen et al., 2014), and if the pressure increases to the human systolic blood pressure of 16 kPa (Rygh, 1973), then this excessive pressure would start to induce PDL occlusion and dysfunction (Choy et al., 2000; Hohmann et al., 2009), as well as root resorption. Undoubtedly, such excessive pressure is not appropriate for tooth movement. Liao et al. (2016) considered PDL hydrostatic stress to be an indicator of tooth movement, and the lower and upper limits of optimal stress to be 0.47 and 16 kPa, respectively. However, they had only considered root resorption, without studying tooth moving efficiency. When a stress of 0.47 kPa is reached, the tooth could move but only at a low rate, and so this could not be considered an optimal force. Actually, both the stress and the strain of PDL have a profound impact on tooth movement. In order to avoid root resorption and PDL occlusion, and to improve tooth moving efficiency at the same time, both the stress and strain of PDL must be fully considered. A more reliable and efficient orthodontic treatment process can thus be realized.

Based on the methods employed in studies of Li (2014) and Liao et al. (2016), accurate three-dimensional (3D) human maxillary canine models were constructed from clinical computed tomography (CT) images in the present study, including the canine, PDL, cortical bone, and cancellous bone. The optimum orthodontic forces for different tooth movements were investigated computationally using finite element analysis, by introducing an active spectrum of orthodontic forces in relation to hydrostatic stress and the logarithmic strain of the PDL. The movements analyzed included distal-direction translation/tipping, labial-direction translation/tipping, extrusion, and rotation around the canine long axis.

2. Materials and methods

2.1. Finite element models

Taking the maxillary canine as the subject of investigation, anatomically accurate 3D models (triangular meshes) of this tooth were constructed using Mimics 10.0 (Materialise NV, Leuven, Belgium), based on the CT images of an average subject, with a resolution of 0.5 mm/pixel. The procedure included three steps: thresholding, region growing, and 3D calculation. On the images, the canine, PDL, and alveolar bone were connected, with a manual operation for mask erase required to separate them from the whole tissues. Next, triangular mesh models were imported into Geomagic Studio 12.0 (3D System, Rock Hill, USA) for further processing, and the processed non-uniform rational basis spline (NURBS) models were exported as STP files for finite element analysis using Abaqus 6.13 (Dassault Simulia, Boston, USA). The resultant finite element models comprised one maxillary canine, the adjacent PDL with a thickness of 0.25 mm (Toms and Eberhardt, 2003), and surrounding cortical bone and cancellous bone. The models were meshed with 10-node tetrahedral elements, as displayed in Fig. 1. The numbers of elements of the canine, PDL, cortical bone, and cancellous bone were 1928, 1263, 17 898, and 13 234, respectively.

Fig. 1.

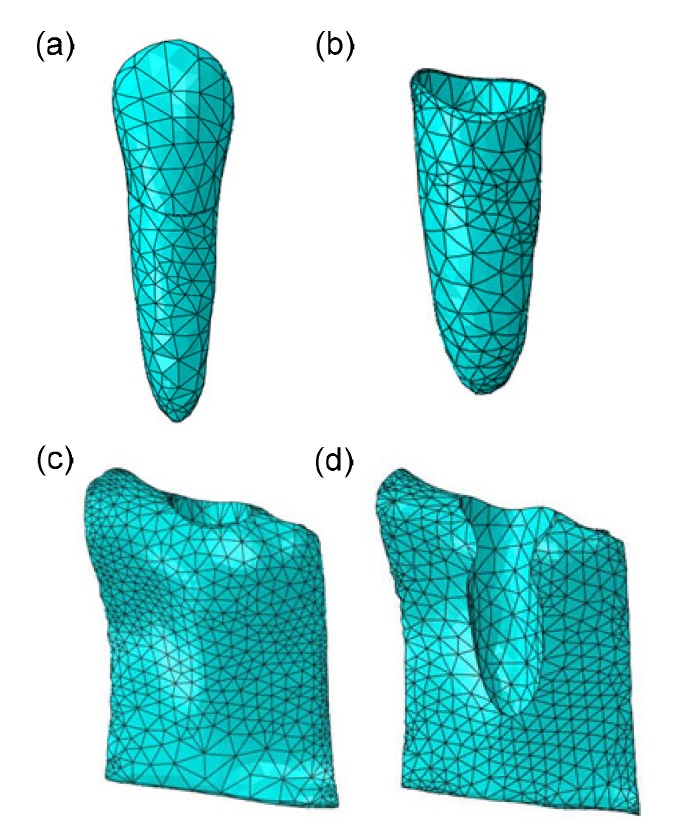
Meshed finite element models in Abaqus

(a) Canine; (b) PDL; (c) Cancellous bone; (d) Cortical bone

2.2. Material properties

The stress and strain of PDL were both chosen as indicators for tooth movements in this study. The PDL has been acknowledged as a hyperelastic-viscoelastic material in a series of studies (Natali et al., 2004; Oskui and Hashemi, 2016; Oskui et al., 2016), meaning that the PDL first shows a strong hyperelastic mechanical behavior at the beginning of loading, but then it shows a viscoelastic behavior as time goes on. The incorporation of nonlinearity of the PDL can significantly alter the finite element analysis results. A 2nd order Ogden model and normalized-based relaxation function were adopted in this analysis (Toms et al., 2002; Wei et al., 2014). The constitutive equations are shown in Eqs.(1) and (2).

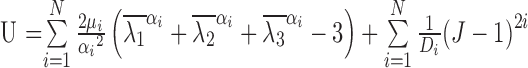, (1)

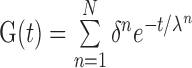, (1)

where U represents the strain energy density function, λ ₁, λ ₂, and λ ₃ are the three main percentages of the elongation of strain energy, =J^{− 1/13} λ_i and =1, J is the volume fraction, μ_i, α_i, and D_i are the material parameters, and parameter N is the order of the polynomial. G(t) represents the normalized-based relaxation function of time, δⁿ is a multiplier of energy function, λⁿ is a relaxation time constant, and t is time. The material parameters are listed in Tables 1 and 2. G(I), K(I) and TAU(I) are the parameters of PDL viscoelastic model in Prony form, with I being the order. To simplify the analysis and calculation, other than the PDL all parts were assumed to be homogeneous, isotropic, and linearly elastic materials in the simulation (Qian et al., 2008), as summarized in Table 3.

Table 1.

Parameters of normalized-based relaxation function

I	G(I)	K(I)	TAU(I)
1	0.027 696 8	0	0.139 27
2	0.097 696 7	0	10.419 00

Table 2.

Parameters of 2nd Ogden model

μ 1 (MPa)	μ 2 (MPa)	α 1	α 2	D 1 (MPa)	D 2 (MPa)
0.005 54	0.11	0.25	0.1153	0.1216	0.97

Table 3.

Material parameters of linearly elastic parts

Part	Young’s modulus (MPa)	Poisson’s ratio
Canine	20 000	0.30
Cortical bone	13 700	0.26
Cancellous bone	1370	0.38

2.3. Loading and boundary conditions

A local coordinate system was constructed for the description of force loading on the maxillary canine. The center of crown was set as the origin, and the lingual direction, root direction, and distal direction of the canine corresponded to the x-, y-, and z-axes (forward direction), respectively. As shown in Fig. 2, the local coordinate system conforms to the right-hand rule.

Fig. 2.

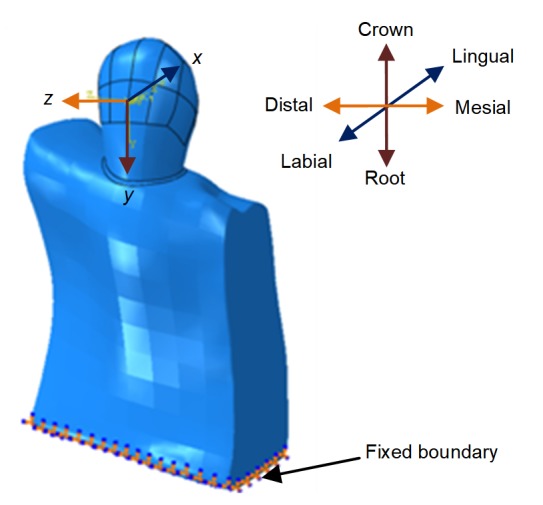
Loading and boundary conditions of finite element models

The bottom surface of the alveolarbone was fixed completely and orthodontic force was exerted on the origin of the local coordinate system. For tipping, the movement was uncontrolled pure tipping, and the rotating center was the center of the canine resistance. For translation, a moment with a specific moment to force ratio (M/F) was applied, coupled with the force, aiming to generate pure translation. The M/F ratios of different movements are listed in Table 4. Orthodontic forces ranging from 0 to 300 g were applied for distal, labial, and extrusion movements, and force moments ranging from 0 to 300 g·mm were used for canine rotation.

Table 4.

M/F ratios of canine in different movements

Movement	M/F (mm)
	x-axis	y-axis	z-axis
Distal translational	14.0	−3.5	0
Distal tipping	0	−3.5	0
Labil translational	0	1	14.0
Labial tipping	0	0	0
Extrusion	0	0	−2.8
Rotation around long axis	0	0	0

To reduce the computational effort, only the distal, labial, and extrusion movements of the canine were studied, while the mesio, lingual, and intrusion movements were omitted. This was mainly because the distribution of the PDL is almost uniform in the mesio-distal direction and labial-lingual direction, and even though the distribution of the alveolar bone might not be uniform in different directions, the amount of movement is too small in comparison with the bone thickness. At the same time, an alveolar bone with a Young’s modulus of 13 700 MPa is similar to a rigid body in contrast with a PDL with a Young’s modulus of 0.68 MPa (Qian et al., 2008). As a result, the optimal orthodontic forces with canine mesio-distal movements and labial-lingual movements are essentially the same. This hypothesis has been validated by previous studies (Liao et al., 2016). For intrusion-extrusion movements, bone remodeling was assumed to be equally sensitive to tensile and compressive stresses, and hence only extrusion movement was considered.

2.4. Optimal interval of PDL stress-strain

Liao et al. (2016) suggested that the applicable hydrostatic stress of the PDL should be higher than the capillary blood pressure of 4.7 kPa, but not exceed the human systolic pressure of 16.0 kPa. Actually, due to individual differences, bone category, teeth distribution, and other complex environmental factors, the upper and lower limits of optimal hydrostatic stress may be significantly different in clinical situations. In this paper, a conservative upper limit of 12.8 kPa (80% of the systolic pressure) was adopted, and the lower limit was set at 4.7 kPa (the capillary blood pressure). The areas where the absolute stress was lower than 4.7 kPa were named low stress areas, whereas the areas where the absolute stress was higher than 12.8 kPa were designated dangerous stress areas. Other areas were deemed good stress areas.

The tooth movement rate is related to the strain of the PDL. Qian et al. (2008) suggested that the tooth movement rate reached the upper limit when PDL strain increased to 0.3%. Based on their findings, Li (2014) believed that the optimal strain of the PDL should be higher than 0.24% (80% of 0.3%) in order to improve tooth moving efficiency. This suggestion was also adopted in the current study, i.e. the areas where the absolute strain was higher than 0.24% were named good strain areas, whereas other areas were low strain areas.

In order to improve tooth movement efficiency and to reduce the risk of root resorption at the same time, both the stress and the strain of the PDL must be within a reasonable range. The optimal orthodontic force can be interpreted as the force field that, when exerted on the tooth, causes the most areas of the PDL to be covered by both good stress and good strain.

3. Results

3.1. PDL stress distribution

Hydrostatic stress nephograms of the canine PDL are shown in Figs. S1–S6, exemplified with various movements. The red regions denote the areas under compression with a stress value between 4.7 and 12.8 kPa; the blue regions indicate the areas under tension with a stress value between −12.8 and −4.7 kPa. Both red and blue areas belong to the good stress areas. The areas where the stress either exceeded 12.8 kPa or was under −12.8 kPa are marked by grey and black, and both of them belong to dangerous stress areas with a possibility of root resorption. Regions indicated by other colors represent low stress areas, where the tooth would not move or move at only a low rate.

Based on the PDL stress nephogram with canine distal-direction translation as shown in Fig. S1), compression occurred on the distal surface and tension emerged on the mesial surface. Upon applying a force of 60 g, good stress was observed on the bottom of the canine PDL. Such good stress areas grew gradually with the rise of orthodontic force, and virtually covered most of the PDL when the force reached 95 g. A small region showing excessive stress appeared on the bottom of the distal surface with a force of 160 g, with a risk of local root resorption. Dangerous stress areas became more visible as force continued to increase.

Compared to translation, compression occurred on the upper region and tension occurred on the bottom in the distal surface of the PDL for distal-direction tipping movement (Fig. S2). A light tipping force was not enough to trigger tooth movement until a force of 20 g was applied, and it induced good stress areas appearing at both the cervical and root apical of the PDL. When force was increased to 45 g, dangerous stress areas appeared on the cervical of the PDL distal surface, and further expanded with increasing force.

As displayed in Fig. S3, the stress distribution of the labial-direction translation was similar to the distal-direction translation. Good stress areas began to emerge on both labial and lingual surfaces of the PDL when the force was increased to 45 g, and they covered most areas of the PDL as soon as force was increased to 60 g. However, along with the continual increase of force to 135 g, dangerous stress areas emerged on the root of the PDL with a risk of root resorption.

For labial-direction tipping motion of the canine as shown in Fig. S4, good stress areas covered most of the PDL when the tipping force was increased to 20 g, and dangerous stress areas began to emerge with a force of 30 g. With the continual increase of the orthodontic force, dangerous stress areas became predominant in the PDL.

The bottom of the PDL was the main bearing area in canine extrusion. Because the curvature radius of the root was small, stress concentration more likely occurred on the canine root. As shown in Fig. S5, when the force was increased to 10 g, good stress areas had already emerged on the bottom of the PDL. Dangerous stress areas started to emerge on the PDL root when force was increased to 45 g, but at the same time most of the PDL cervical areas were low stress areas, leading to the conclusion that resorption was more likely to occur in the canine root.

For rotation of the canine around the long axis as shown in Fig. S6, good stress areas emerged when the force moment reached 75 g·mm, and dangerous stress areas emerged when the force moment was increased to 210 g·mm.

3.2. PDL strain distribution

The strain nephograms of the PDL with different movements are shown in Figs. S7–S12. The red region denotes that the strain of the PDL was tensile (positive strain), with a strain value exceeding 0.24%. The blue region indicates that the strain was compressive (negative strain), with a value lower than −0.24%. The absolute strain of both the red and the blue areas exceeded 0.24%, and both are good strain areas. The areas of strain between −0.24% and 0.24% are low strain areas. Strain areas exceeding 2.4% and falling under −2.4% are marked by grey and black, respectively. The more good strain areas there are, the higher the tooth movement rate.

From the strain nephogram shown in Fig. S7, the distal surface was mainly filled with compressive strain, and the mesial surface was filled with tensile strain for canine distal-direction translation. Good strain areas occurred when the applied force reached 75 g, and the extent of good strain areas increased with the increase of the orthodontic force.

For distal-direction tipping movement, the strain distribution of the PDL is displayed in Fig. S8. Good strain areas first occurred on the cervical PDL when the applied force reached 20 g. The distribution of strain agreed with the stress of canine distal-direction tipping. With the development of red and blue areas, the extent of good strain areas increased.

Labial surface was filled with compressive strain and lingual surface was filled with tensile strain for canine labial-direction translation (Fig. S9). Some local areas were characterized by good strain with a force of 75 g.

For canine labial-direction tipping movement, the distribution of strain was similar to that for the distal-direction. As shown in Fig. S10, good strain areas emerged when the applied force reached 20 g.

The distribution of strain was similar to the distribution of stress for the extrusion of the canine (Fig. S11). Good strain areas initially occurred when the applied force reached 45 g, and PDL was gradually covered by good strain with increasing force. The distribution of strain was homogeneous, mainly because the PDL produced the same translational displacement driven by the canine root.

As shown in Fig. S12, good strain of the PDL first appeared when the force moment reached 60 g·mm for the canine rotation. During the rotation, if one side of the PDL was compressive, the adjacent side was tensile.

4. Discussion

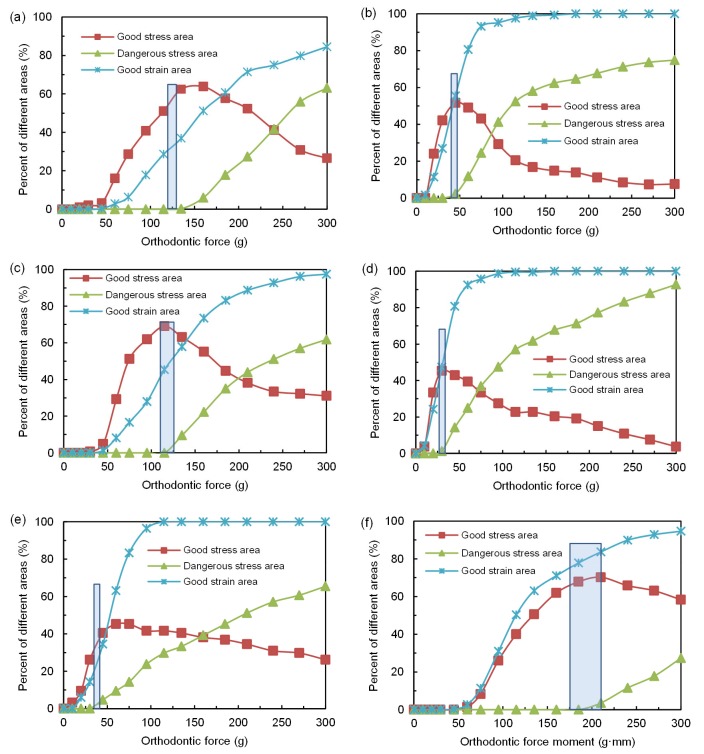
In order to better understand the relationship between PDL stress-strain behavior and the orthodontic force, the percentage extents of good stress areas, dangerous stress areas, and good strain areas were calculated as functions of orthodontic force changes under various canine movements (Fig. 3). Reducing the risk of root resorption and shortening the treatment period for a more reliable and efficient treatment require good stress areas of the PDL to be as large as possible, dangerous stress areas to be as small as possible, and good strain areas to be at least as large as the good stress areas. Therefore, the optimal orthodontic force was one that most closely meets these three requirements at the same time.

Fig. 3.

Percentages of good stress areas, dangerous stress areas, and good strain areas with the change of the orthodontic force or force moment

(a) Distal-direction translation; (b) Distal-direction tipping; (c) Labial-direction translation; (d) Labial-direction tipping; (e) Extrusion movement; (f) Rotation around canine long axis. The rectangular frames in figures are used to mark the optimal orthodontic force areas

The relationship between the different areas and the orthodontic force for canine distal-direction translation is shown in Fig. 3a, where the percentage of dangerous stress areas and good strain areas increased with force. When the applied force increased to 137 g, dangerous stress areas started to emerge. The percentage of good stress areas first increased, and then decreased. This showed that the magnitude of force increase to some extent was beneficial to canine movement, but it should not be increased too much, otherwise it can induce root resorption. The largest percentage of good stress areas was 65% with a translational force of 150 g. If the required percentage of dangerous stress area was 0, with good stress areas exceeding 60% and good strain areas exceeding 35%, the optimal force for canine distal-direction translation was 130–137 g.

In comparison, for the distal-direction tipping movement as displayed in Fig. 3b, the crest of the good stress curve was smaller than that for the translational movement. When the applied force was increased to 44 g, the percentage of good stress areas reached a maximum of 55%. If we require the percentage of dangerous stress areas to be under 2%, good stress areas to exceed 50%, and good strain areas to surpass 50% at the same time, the optimal force was 40–44 g.

The optimal orthodontic force of canine tipping was smaller than that for translation, chiefly because loading was exerted on the upper crown, but the PDL was rounded at the root of the canine, so a large torque would be generated at the PDL, with stress concentration easily occurring on the cervical and root apical of the PDL (Parker and Harris, 1998). As a result, dangerous stress areas would more likely emerge even with a small tipping force. We may draw the conclusion that a smaller orthodontic force was enough to induce canine tipping motion as compared to translation, and excessive force would cause root resorption.

For labial-direction translation, the trend of the curves was similar to that for distal-direction movement (Fig. 3c). The percentage of good stress areas reached a maximum of 68% when the applied force was increased to 116 g. If we require the percentage of dangerous stress areas to be under 2%, good stress areas to exceed 65%, and good strain areas to exceed 40%, the optimal force for labial-direction translation was 110–120 g.

The percentage of good stress areas reached a maximum of 45% when the applied force increased to 30 g for canine labial-direction tipping movement (Fig. 3d). If we require the percentage of dangerous stress areas to be under 2%, good stress areas to surpass 40%, and good strain areas to exceed 40%, the optimal force was 28–32 g.

In comparison, the optimal force for labial-direction translation was smaller than that for distal-direction. This was mainly because the canine was not an axisymmetric structure, with the width of the root in the mesio-distal direction smaller than that in the lingual-labial direction, and a smaller bearing area would produce a larger stress under the same magnitude of force. This point is important for clinical treatment, as the force needs to decrease appropriately if the bearing area in the tooth moving direction is small. A similar situation appeared on canine tipping movement, where good stress areas covered most of the PDL when the labial-direction tipping force was increased to 20 g, but only a small good stress area began to emerge at the cervical of the PDL labial surface even when the distal-direction tipping force was increased to 30 g. The optimal tipping force in the labial direction was smaller than that for the distal direction.

In terms of canine extrusion as revealed in Fig. 3e, the percentage of good stress areas reached a maximum of 45% when the applied force was increased to 60 g. If we require the percentage of dangerous stress areas to be under 2%, good stress areas to exceed 35%, and good strain areas to exceed 20%, the optimal force for extrusion was 38–40 g.

The downward trend was smoother than that for other movements after the good stress curve reached the peak for canine extrusion. This was mainly because the canine root had a taper in the direction of the force along the long axis of the canine, so loading was mainly exerted onto the root apex (Wilson et al., 1994; Rudolph et al., 2001) and the stress-strain of the PDL gradually diminished from the bottom to the cervical region. The original good stress areas were gradually transformed into dangerous stress areas with the increase of force, but at the same time, the low stress areas located in the upper part of the PDL were transformed into good stress areas, resulting in a gentle downward trend when the overall trend was downward.

The motion of the PDL was primarily shear in rotation as compared to others, and hydrostatic stress distribution of the PDL is related to canine root morphology. The hydrostatic stress is zero at the node when its moving direction is perpendicular to the external normal direction of the surface that the node exists. Hence, the more the cross section of the root became closer to circle, the lower overall hydrostatic stress of PDL, and the less likely root resorption was to occur. Greater stress and strain occurred on the areas with a low roundness. As shown in Fig. 3f, when the force moment was increased to 210 g·mm, the percentage of good stress areas reached a maximum of 70%. If we require the percentage of dangerous stress areas to be under 2%, good stress areas to exceed 65%, and good strain areas to exceed 75%, the optimal force moment for canine rotation was 170–210 g·mm.

To summarize the discussion and analysis above, the optimal orthodontic force of the canine for various movements is described in Table 5, where the range of the force was further narrowed, and it thus became more conducive to the guidance of clinical treatment as compared to other studies (Storey and Smith, 1952; Liao et al., 2016). The optimal force of translation was in good agreement with frequently used clinical orthodontic forces of 100 and 150 g, and consistent with the findings of Li (2014) (80–130 g for mesial-direction, and 90–140 g for lingual-direction movement). Besides, the optimal tipping force agreed with the results of Liao et al. (2016) (14–50 g using local hydrostatic stress). For extrusion, an experiment conducted by Proffit (Hemanth et al., 2015) concluded that the optimum force level for canine extrusion was 35–60 g, which was consistent with the results of this study. In terms of rotation around the long axis, Hemanth et al. (2015) found that one couple of force of 0.4 N produced a stress of 0.018 N/mm², which was well within the optimal range targeting the maxillary central incisor. Our findings were also consistent with the results of this previous study.

Table 5.

Optimal orthodontic force of the canine in different movements

Movement	Optimal force/moment
Distal-direction translational	130–137 g
Distal-direction tipping	40–44 g
Labial-direction translational	110–124 g
Labial-direction tipping	28–32 g
Extrusion	38–40 g
Rotation around long axis	170–210 g·mm

Li (2014) regarded PDL strain as an indicator of tooth movement and concluded that the reasonable force ranges for incisor mesio, lingual, and intrusion movements were 80–130, 90–140, and 35–50 g, respectively. In that paper, only the strain of the PDL was studied but the stress was not considered sufficiently. The upper strain of 2.4% was baseless, and whether the strain of 2.4% may be related to root resorption would require further studies, although it was related to the tooth movement rate. In addition, the PDL was assumed to be an inaccurate linear elastic material in their simulation, which also affected the accuracy of their results (Huang et al., 2016; Anneke et al., 2017). On the other hand, Liao et al. (2016) just considered the PDL stress but ignored the strain, and as a result, the optimal forces of the canine distal translation and tipping were 35–100 and 14–50 g, respectively, as defined by local hydrostatic pressure, and 76–266 and 37–135 g as defined by volume-averaged hydrostatic stress. In the situation of overlooked PDL strain, a token 0.47 kPa as the lower limit of optimal stress was improper, because the tooth movement rate was low with a hydrostatic stress of 0.47 kPa. Although the tooth may be able to move, the force could not be called “optimal force”. Also, the upper limit of 16 kPa was questionable. In their discussion, Liao et al. (2016) thought that the upper threshold of 16 kPa represented a more aggressive regime, with a rapid tooth movement featuring complete PDL occlusion, which could however increase the risk of excessive PDL necrosis and hence orthodontic root resorption and tooth movement deceleration. In order to improve the reliability of the treatment, a fairly conservative upper limit of 12.8 kPa (80% of 16 kPa) was employed in this study. Furthermore, only distal-direction translational/tipping movements of the canine were studied by Liao et al. (2016), resulting in incomplete statistical data on tooth movement. In comparison, various movements of the canine were more fully considered in the current study.

One limitation of the current study is that the upper limit of the optimal stress may not be constant because of the complex environmental factors, such as individual differences, bone category, and teeth distribution (Han et al., 2005). Except for the fluctuation of the upper limit, the lower limit may also vary from subject to subject, as it was reported that the capillary blood pressure can range between 2 and 4.7 kPa (Burstone and Pryputniewicz, 1980; Dorow and Sander, 2005). On the other hand, bone formation and resorption were assumed to be equally sensitive to hydrostatic tensile and compressive stress, with the thresholds on both tension and compression being the same, just as Liao et al. (2016) did. As these factors can all make an impact on the scope of the optimal force, it is therefore suggested that further studies should be conducted to investigate the relationships between biomechanical thresholds and cellular events in tooth movements.

In this study, a more appropriate property of hyperelastic-viscoelasticity was employed to describe the characteristics of PDL, but the material of PDL was still assumed homogeneous and isotropic. However, the responses of PDL in different directions are discrepant under an identical force, so the virtual PDL is anisotropic (Provatidis, 2000; Qian et al., 2001). Also, the thickness of PDL in different areas is not unified, while it was supposed to have a homogeneous thickness of 0.25 mm in this analysis. Besides, the percentages of different stress/strain areas were calculated by combined elements volume, and it is affected by the quality of grid partition. It means that a certain element either belongs to a dangerous area, or a good area, but it cannot belong to both areas. Therefore, a fine meshed grid is more favorable for the partition of different areas.

In addition, biomechanical investigation of the optimal orthodontic force was only carried out on the maxillary canine with a single root, and multiple root teeth were not studied. In future work, other teeth should be taken into account in order to obtain a more complete scientific picture, providing a stronger theoretical support for orthodontic treatment and scheme design.

5. Conclusions

A maxillary canine was chosen as the object of study, 3D finite element models of the canine and its surrounding periodontium were constructed based on CT images. Regarding the PDL as hyperelastic-viscoelastic material, finite element analysis was carried out with various movements of the canine, including distal-direction translation/tipping, labial-direction translation/tipping, extrusion, and rotation around canine long axis. The hydrostatic stress and logarithmic strain of the PDL were used as indicators of tooth movements, where if the absolute stress of the PDL ranged from 4.7 kPa (capillary blood pressure) to 12.8 kPa (80% of human systolic pressure), with the absolute strain of the PDL exceeding 0.24% at the same time, the orthodontic force would then be considered to be the optimal force. With an optimal force, root resorption caused by excessive orthodontic force can be avoided and a long treatment period caused by the use of too small forces can be shortened.

The percentages of different PDL areas resulting from changes in orthodontic force under various movements were calculated, including good stress areas, dangerous stress areas, and good strain areas. Based on the findings, the optimal orthodontic forces for canine distal-direction translational and tipping movements were 130–137 and 40–44 g, respectively, the optimal forces for labial-direction translation and tipping were 110–124 and 28–32 g, respectively, the optimal force for extrusion was 38–40 g, and the optimal force moment for canine rotation around the long axis was 170–210 g·mm. Compared to the previous results, the range of our optimal forces was further narrowed, facilitating the guidance of clinical treatment.

The optimal force for canine tipping was smaller than that for translation, and this was because the distribution of loading on the PDL was not uniform and stress concentration was obvious in the cervical and root apical of the PDL. In addition, because the bearing area in the labial surface was smaller than that in the distal surface, the optimal force for labial-direction movement was smaller than that for distal-direction movement. Hence, the orthodontic force should be adjusted appropriately depending on the bearing area of the PDL in the movement direction in clinical applications, i.e. the design of a personalized orthodontic plan according to the individual. The current study provided a strong biomechanical support for the clinical applications of orthodontic forces.

List of electronic supplementary materials

Fig. S1

Hydrostatic stress distribution of canine PDL with distal-direction translation under force

Fig. S2

Hydrostatic stress distribution of canine PDL with distal-direction tipping movement under force

Fig. S3

Hydrostatic stress distribution of canine PDL with labial-direction translation under force

Fig. S4

Hydrostatic stress distribution of canine PDL with labial-direction tipping movement under force

Fig. S5

Hydrostatic stress distribution of canine PDL with extrusion under force

Fig. S6

Hydrostatic stress distribution of canine PDL with rotation around long axis under force moment

Fig. S7

Logarithmic strain distribution of canine PDL with distal-direction translation under force

Fig. S8

Logarithmic strain distribution of canine PDL with distal-direction tipping movement under force

Fig. S9

Logarithmic strain distribution of canine PDL with labial-direction translation under force

Fig. S10

Logarithmic strain distribution of canine PDL with labial-direction tipping movement under force

Fig. S11

Logarithmic strain distribution of canine PDL with extrusion under force

Fig. S12

Logarithmic strain distribution of canine PDL with rotation around long axis under force moment