Cation-Dependent Conformations in 25-Hydroxyvitamin D3-Cation Adducts Measured by Ion Mobility-Mass Spectrometry and Theoretical Modeling

Abstract

Ion mobility-mass spectrometry is a useful tool in separation of biological isomers, including clinically relevant analytes such as 25-hydroxyvitamin D3 (25OHD3) and its epimer, 3-epi-25-hydroxyvitamin D3 (epi25OHD3). Previous research indicates that these epimers adopt different gas-phase sodiated monomer structures, either the “open” or “closed” conformer, which allow 25OHD3 to be readily resolved in mixtures. In the current work, alternative metal cation adducts are investigated for their relative effects on the ratio of “open” and “closed conformers. Alkali and alkaline earth metal adducts caused changes in the 25OHD3 conformer ratio, where the proportion of the “open” conformer generally increases with the size of the metal cation in a given group. As such, the ratio of the “open” conformer, which is unique to 25OHD3 and absent for its epimer, can be increased from approximately 1:1 for the sodiated monomer to greater than 8:1 for the barium adduct. Molecular modeling and energy calculations agree with the experimental results, indicating that the Gibbs free energy of conversion from the “closed” to the “open” conformation decreased with increasing cation size, correlating with the variation in ratio between the conformers. This work demonstrates the effect of cation adducts on gas-phase conformations of small, flexible molecules and offers an additional strategy for resolution of clinically relevant epimers.

Graphical abstract

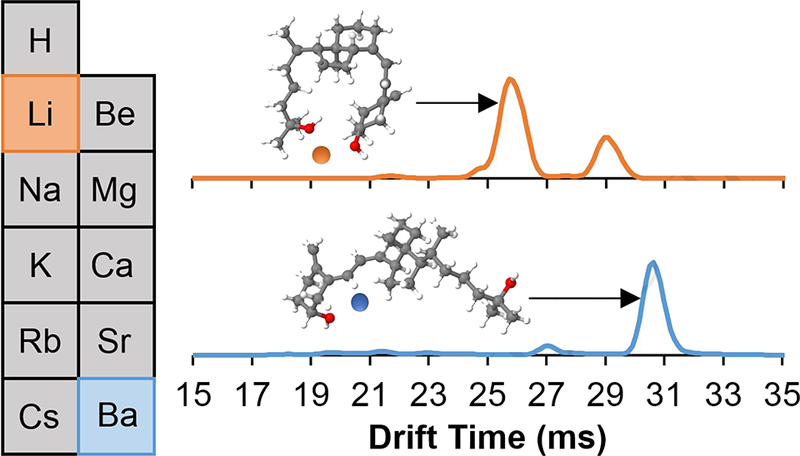
Introduction

Ion mobility spectrometry (IMS) is a widely recognized technique that has been used for decades both as a gas-phase separation method and for structural characterization [1, 2]. IMS allows determination of collision cross section (CCS) [1, 3, 4] and is often coupled with mass spectrometry (IM-MS) to provide identification by measurement of m/z. However, whereas mass spectrometry cannot differentiate isomers due to identical chemical composition, this technique is capable of resolving not only isomers with structural or stereochemical bond differences, but also of distinguishing unique gas-phase conformers of the same compound. To further improve these separation capabilities, especially for diastereomers, epimers, and enantiomers, many strategies have been implemented to augment structural differences [5–15]. Notably, complexation and adduct formation with various metal ions can affect the overall gas-phase structure of the target species. This provides improved separation, as well as a method for studying the structural effects of such interactions (i.e., conformational differences).

IM-MS has been implemented to characterize gas-phase structure across a wide range of molecular classes. This technique has proved to be especially informative in identifying structural differences for various ion-neutral complexes. One such example involves those complexes that include metal cations, such as alkali, alkaline earth, and transition metals. The Bowers group demonstrated various structural conformations of 18-crown-6 when complexed with alkali metals Li⁺, Na⁺, K⁺, and Cs⁺ [16], and additional polyether complexes including synthetic polymers polyethylene glycol (PEG) [17] and polyethylene terephthalate [18]. The available information from these experiments was soon after geared towards biological systems. Leavell et al. studied the conformations of Zn/hexose diastereomers using a combination of IMS and density functional theory calculations, further displaying the power of IMS when applied in conjunction with theoretical modeling [14]. The effect of various cations, including divalent metal ions, on peptide structure and unfolding was also studied, indicating that gas-phase structure was highly dependent on the binding properties of the metal ions [19]. Furthermore, formation of various cation adducts has been a widely employed strategy for improved separation of isomeric carbohydrates and glycans [14, 15, 20–25]. This has also been demonstrated extensively across a wide range of other compound classes, including proteins [26–28], peptides and peptide complexes [19, 29–35], flavonoids [6], amino acids [9, 36], steroids [37], and numerous other diastereomers [7, 13, 38–41].

Recently, our group used IM-MS and molecular modeling to investigate the gas- phase structure of 25-hydroxyvitamin D3 (25OHD3) [42], the most common target analyte in clinical tests for vitamin D deficiency [43, 44]. Assays for this analyte suffer from the presence of an isomeric interference due to its epimer 3-epi-25-hydroxyvitamin D3 (epi25OHD3), which is difficult to separate chromatographically and cannot be differentiated with single-stage mass spectrometry [45]; the structures of these epimers are shown in Figure S1. Our results indicated that 25OHD3 adopts two different gas- phase conformations of the sodiated monomer: (a) the “closed” conformer involves a bending of the two distal hydroxyl groups, such that both interact simultaneously with the sodium ion; and (b) the “open” conformer involves sodium interaction with only the C3 hydroxyl group, yielding a more elongated structure and larger collision cross section. The “open” conformation is energetically unique to 25OHD3, and not accessible to epi25OHD3 under standard experimental conditions. This allows rapid identification of 25OHD3 in mixtures with IM-MS. However, the “closed” conformer adopted by both species produces overlapping drift peaks that are not separated. Historically, clinical interest has been primarily in quantitation of 25OHD3, but recent studies have indicated that the biological activity of epi-1,25-dihydroxyvitamin D3 (which is formed from epi25OHD3) is reduced in comparison with its counterpart [44, 46–50]. As such, a rapid method capable of identifying and quantitating these compounds in a biological mixture is desired. Here, we demonstrate that formation of different metal cation adducts affects the ratio of 25OHD3 conformers, such that larger cations increase the “open”:”closed” ratio to >> 1:1. This effectively reduces the overlap and produces only two major drift peaks: the “closed” conformer of epi25OHD3 and the “open” conformer of 25OHD3. Molecular modeling confirms the trend of the energetically favorable “open” conformer with larger cation adducts.

Experimental Methods

Materials and Reagents

25-hydroxyvitamin D3, D₆-25-hydroxyvitamin D3, and 3-epi-25-hydroxyvitamin D3 standards (100 μg/mL in ethanol) were purchased from IsoSciences (King of Prussia, PA). These standards were diluted to a final concentration of 10 μg/mL in Fisher Optima LC-MS grade water, purchased from Fisher Scientific (Pittsburgh, PA), with no additives.

Lithium acetate, magnesium acetate tetrahydrate, and calcium acetate monohydrate were purchased from Acros Organics (Geel, Belgium). Potassium acetate was purchased from Alfa Aesar (Haverhill, MA). Rubidium acetate was purchased from Strem Chemicals (Newburyport, MA). Cesium acetate was purchased from MP Biomedicals (Santa Ana, CA). Strontium acetate was purchased from Sigma-Aldrich (St. Louis, MO). Barium acetate was purchased from Chem-Impex International, Inc. (Wood Dale, IL). These standards were combined with the aforementioned vitamin D standards and were diluted to a final concentration of 10 μg/mL in Fisher Optima LC-MS grade methanol or a 1:1 mixture of Fisher Optima LC-MS grade water and methanol, depending on their relative solubility. Flame emission testing was used to estimate the sodium concentration in the solvents as approximately 185 ppb (water) and 220 ppb (methanol).

IM-MS Analysis

All analyses were performed with an Agilent 6560 IM-QTOF instrument (Santa Clara, CA). Standard solutions were direct infused by syringe pump at a flow rate of 10 μL/min. All compounds were analyzed in positive mode using an Agilent Jet Stream electrospray ionization source, with conditions as follows: capillary voltage: +5000 V; nozzle voltage: +1000 V; drying gas: 325 °C at 5 L/min; sheath gas: 275 °C at 8 L/min. The fragmentor voltage was set to 400 V. The high pressure ion funnel delta was set to 170 V and the RF amplitude was set to 150 V_PP. The ion funnel trap parameters were as follows: delta: 165 V; RF: 150 V_PP; exit: 10 V; entrance grid low: 97.5 V; entrance grid delta: 14.5 V; entrance: 91 V; exit: 90 V; exit grid 1 low: 87.6 V; exit grid 1 delta: 7 V; exit grid 2 low: 86 V; exit grid 2 delta: 1.5 V. The IM-QTOF instrument includes a 78 cm uniform field drift tube maintained at approximately 4 Torr nitrogen drift gas and 32 °C. These constant drift tube conditions allow direct comparison of drift time spectra, which were acquired over a 60 ms window. A modified version of the Mason-Schamp equation [1, 3, 4] was used to calculate collision cross section (CCS) based on corrected drift time (t_d) measured with the step field method at eight different drift tube fields (ranging from 9.6–18.6 V/cm), as with previous work for these compounds [51]. CCS uncertainty displayed in tables is based on calculated CCS from each of the eight drift tube fields.All drift time spectra shown were acquired at a drift tube field of 18.6 V/cm, as optimal peak resolving power was achieved at this field strength. Time of flight mass spectra were acquired in full scan high resolution mode over a range from m/z 100–1700. All IM- MS data processing was performed using Agilent IM-MS Browser B.07.01.

Theoretical Modeling Methods

The most stable in-water structures of 25OHD3 and epi25OHD3 with the addition of a sodium ion were reported previously [42]. Due to the high flexibility of these molecules, obtaining the most stable structures is a challenging task. For this reason, a laborious protocol was used to perform conformational searches for these molecules.

Monomer structures were reoptimized in-water by replacing the sodium ion by other alkali metals (lithium, potassium, rubidium, and cesium). The resulting structures should provide a reasonable estimate of the most stable in-water structures of 25OHD3 and epi25OHD3 with each ion. The calculations were performed using the Gaussian 09 program [52] at the level B3LYP-D3/6–31G* for lithium and potassium and at the level B3LYP-D3/LANL2DZ for rubidium and cesium, where D3 means that the Grimme’s empirical dispersion correction [53] was added to the B3LYP functional, and the SMD implicit solvation model designed by Truhlar and coworkers [54] was used to account for solvent effects. The Gibbs free energy values at T = 300 K for all structures were also obtained by performing vibrational frequency calculations at the same level of theory.

These in-water structures were submitted to gas-phase geometry optimizations, and each resulting structure was submitted to a gas-phase collision cross section calculation using the trajectory method (TM) in a modified version of the MOBCAL software package [55] to perform calculations with N2 as the drift gas [56]. The atomic point charges necessary for CCS calculations with TM were obtained using CHelpG [57] calculations at the B3LYP-D3/6–31+G(d,p) level using the Gaussian 09 program [52]. Even though the CCS calculations were done for single structures, by the construction of the Trajectory Method it is possible to compute the standard deviation associated with a given CCS value. Previous works in the literature have shown that the addition of thermal effects by performing multiple CCS calculations for different structures corresponding to a given temperature further improves the agreement between theoretical and experimental CCS values. However, as in this work our intent is only to describe the trends observed experimentally, single structure CCS calculations are enough to achieve this goal.

The initial solution-phase calculations are necessary because previous research [51] involving similar ion mobility experiments has shown agreement between experimental results and theoretical modeling only if the theoretical prediction of the stability of conformers is made in solution-phase, rather than in the gas-phase. The hypothesis to support this is that the ions are being formed in solution and once they go to the gas-phase through the electrospray ionization process, the ions only have enough time to relax their solution-phase structures, and thus they do not necessarily assume their most favorable gas-phase conformations.

Results and Discussion

Alkali Metal Adducts

25OHD3 and epi25OHD3 were compared after addition of several alkali metals (lithium, potassium, rubidium, and cesium) to investigate differences in drift time/collision cross section and relative intensity of the “open” and “closed” conformers. For each individual alkali metal cation added (as acetate salt), the major ionization species identified included singly charged monomers [M+X]⁺ and dimers [2M+X]⁺; this pattern is similar to that observed previously for the sodiated ions [42]. Drift spectra were collected for each of the major species, and the spectra for 25OHD3 [M+X]⁺ are shown in Figure 1.

Figure 1.

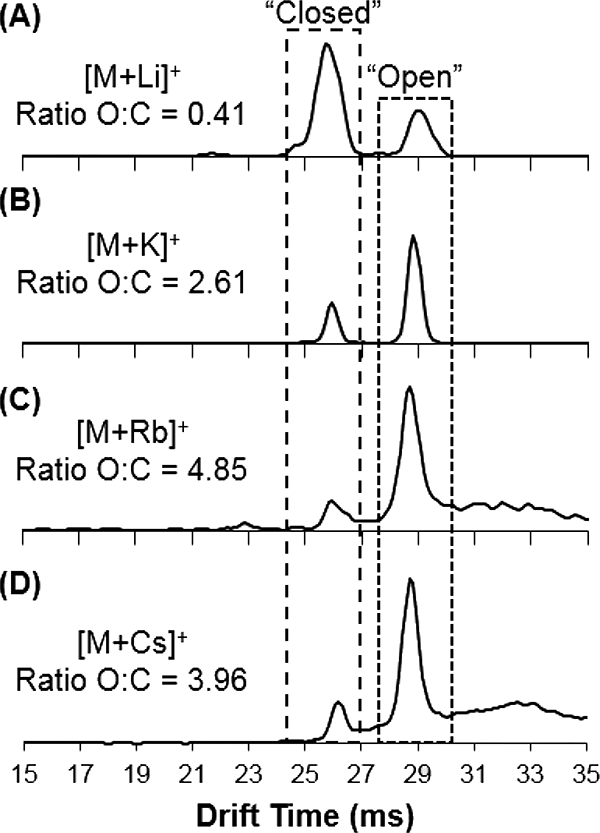
Drift time spectra collected for 25OHD3 monomer with addition of alkali metal adducts (a) lithium, (b) potassium, (c) rubidium, and (d) cesium. For each species, the ratio of the “open”:”closed” (O:C) conformers is listed.

Several observations were made for the alkali metal adducts, in comparison with their sodiated equivalents. First, the overall intensity for the cation adducts of lithium and potassium were only slightly higher than that of the sodiated adducts (without the addition of any sodium), while the adducts of rubidium and cesium were considerably lower than the sodiated species, indicating less efficient formation of these adducts; in addition, the sodiated species were still observed at a significant intensity in the spectrum for each cation adduct, indicating a relatively higher formation efficiency for the sodiated adducts. Figure S2 shows mass spectra collected for all alkali metal adducts, noting that [M+Na]⁺ at m/z 423 is present in all spectra. Theoretical binding free energies were calculated (Table 1) in solution for 25OHD3 cation adducts with each alkali metal, and show that the strongest binding free energy is obtained for lithium, followed by sodium and potassium adducts. For rubidium and cesium adducts, we see considerably lower values in comparison to the other adducts; these theoretical values agree with the overall trend observed experimentally in the mass spectra. Table 1 shows that the binding free energy is positive for some adducts X (i.e., Rb and Cs), indicating the formation of the complex [M+X] is unfavorable. However, given the initial concentrations of 25OHD3, X and sodium (see section Materials and Reagents), calculation of the equilibrium constant for each formation reaction indicates that the complex [M+X] will be formed in some amount.

Table 1.

Theoretical binding free energy in solution of 25OHD3 cation adducts for alkali metals.

	Binding Gibbs Free Energy (kcal/mol)
Process	“Open” conformation	“Closed” conformation
${[\text{M}]}_{\text{aq}}+{[\text{Li}]}_{\text{aq}}^{+}\to {[\text{M+Li}]}_{\text{aq}}^{+}$	-18.47	-25.12
${[\text{M}]}_{\text{aq}}+{[\text{Na}]}_{\text{aq}}^{+}\to {[\text{M+Na}]}_{\text{aq}}^{+}$	-17.05	-19.17
${[\text{M}]}_{\text{aq}}+{[\text{K}]}_{\text{aq}}^{+}\to {[\text{M+K}]}_{\text{aq}}^{+}$	-12.31	-10.86
${[\text{M}]}_{\text{aq}}+{[\text{Rb}]}_{\text{aq}}^{+}\to {[\text{M+Rb}]}_{\text{aq}}^{+}$	-0.49	3.72
${[\text{M}]}_{\text{aq}}+{[\text{Cs}]}_{\text{aq}}^{+}\to {[\text{M+Cs}]}_{\text{aq}}^{+}$	0.55	4.21

Second, the most interesting observation was the trend in ratio between “open” and “closed” conformers for 25OHD3, identified as separate drift species at ~29 and ~26 ms, respectively. Our previous work [42, 58] showed that the intensity for these conformers as sodiated adducts was roughly equivalent under current experimental conditions (Ratio, “Open:”Closed” = 0.88), but could be slightly altered by changing experimental parameters (i.e., ion source temperature) and thus the energy in the system; the full range of experimental variables capable of affecting the ratio of conformers (i.e., source parameters, high pressure and trap funnel conditions, etc.) was not further investigated in this work. Here, we observe that formation of different alkali metal adducts also has an effect on that ratio. Specifically, the “open”:”closed” ratio generally trends upward with increasing size of the alkali cation. This trend is due to the increased ionic radius of the alkali cation, which increases the relative distance between the C3 and C25 hydroxyl group oxygen atoms in interaction with the cation in the “closed” conformer. This is depicted by the most energetically stable structures for “open” and “closed” conformations of these adducts, which are shown in Figure 2. By causing the 25OHD3 molecule to open more, with less attraction between hydroxyl groups and the cation, the energy difference between the two conformations decreases, prompting an increase in the relative intensity of the “open” conformation. Figure 1 demonstrates this relative increase in intensity for the “open” conformer at approximately 29 ms, as Li < Na < K < Rb (the “open”:”closed” ratio for sodium is shown in previous work [42]); this correlates with an increase in the interatomic distance between -OH and X⁺ for these species (Figure 2). It should be noted that the ratios for rubidiated and cesiated adducts do not follow this trend, however the theoretical calculations show the interatomic distance between the two oxygens decrease from rubidium to cesium (indicating that the 25OHD3 is more closed for cesium), which supports this experimental observation. These results, in addition to providing information on the dependence of gas-phase conformation on adduct ions, are especially important in differentiating 25OHD3 from epi25OHD3, as the overlapping drift peak that results from the “closed” conformation of each has progressively less contribution from 25OHD3. For purposes of separation and quantitation of these species in a mixture (i.e., biological samples), altering the cation adduct can improve differentiation between the epimers by reducing overlap.

Figure 2.

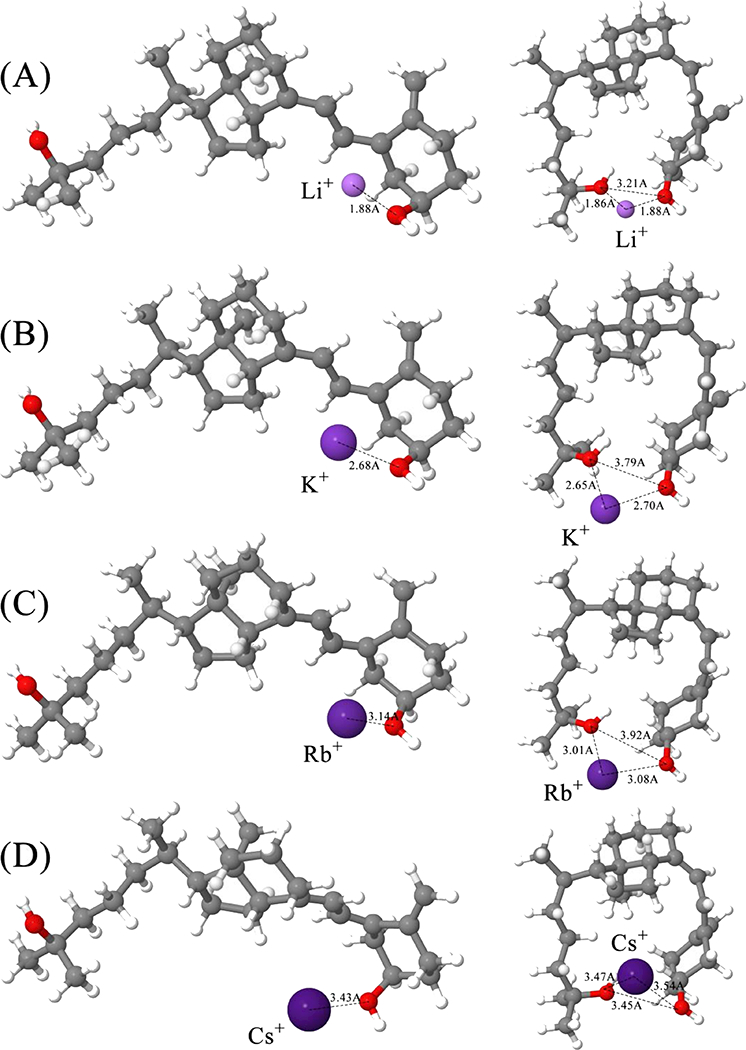
“Open” (left) and “closed” (right) in-water optimized structures of the 25OHD3 monomer with addition of alkali metal adducts: (a) lithium, (b) potassium, (c) rubidium, and (d) cesium.

Collision Cross Sections and Free Energy Calculations

To further investigate the observation of cation-dependent conformer ratios, collision cross section and Gibbs free energy calculations were performed on the monomer species for each of the alkali metals. Theoretical cross sections agree with those obtained experimentally (Table 2), but more importantly the Gibbs free energy for the “open” conformer of 25OHD3, previously demonstrated to be less energetically favorable than the “closed” conformer in sodiated adducts, becomes less positive (more favorable) with increasing cation size. These free energy calculations agree with the experimental results, showing that increasing size of the cation decreases the free energy barrier between conformations and allows the “open” conformer to be more populated. In fact, for [M+K]⁺, [M+Rb]⁺ and [M+Cs]⁺, the Gibbs free energy of conversion from “closed” to “open” is actually negative, indicating that the “open” conformation is the preferred state and correlating with the >> 1 “open”:”closed” ratio observed experimentally for these species. The trends in Gibbs free energy values also agree with the experimental ratios for cesium in rubidium, as ΔGc_s < ΔGRb.

Table 2.

Comparison of 25OHD3 cation adducts for alkali metals, demonstrating the ratio between “open” and “closed” conformers and theoretical Gibbs free energy difference between conformers in solution.

Ion	m/z	Ratio O:C	ΔG (C→0) (kcal/mol)
[M+Li]+	407.350	0.41	6.65
[M+Na]+	423.324	0.88	2.12
[M+K]+	439.298	2.61	−1.44
[M+Rb]+	485.246	4.85	−4.21
[M+Cs]+	533.240	3.96	−3.66

Experimental collision cross sections were measured for “open” and “closed” conformations of each adduct for comparison with theoretically calculated values. The experimental versus theoretical CCS difference for each adduct is at most 4.2%. While a 4.2% error is larger than the errors obtained in accurate trajectory method CCS predictions reported in other works, including our previous study for 25-hydroxyvitamin D3 sodiated epimers [42], we emphasize that in this work our focus is only on describing the trends observed experimentally, and not necessarily on an accurate quantitative description of the CCS values. Cross section values are displayed in Table 3. Experimental and theoretical cross sections were also obtained for epi25OHD3 and are shown in Table S1.

Table 3.

Experimentally obtained and theoretically calculated collision cross sections for the “open” and “closed” conformations of 25OHD3 adducts with alkali metals.Experimental uncertainly measured across eight different drift tube fields. Theoretical CCS standard deviations are shown.

	“Open” Conformation			Closed” Conformation
Ion	DTCCSN2 (Å2) Experimental	DTCCSN2 (Å2) Theoretical	ΔCCS	DTCCSN2 (Å2) Experimental	DTCCSN2 (Å2) Theoretical	ΔCCS
[M+Li]+	236.8 ± 0.2	228.7 ±2.0	3.4%	211.1 ±0.2	203.9 ± 1.9	3.4%
[M+Na]+	232.9 ±0.5	231.7 ±2.5	0.5%	207.1 ±0.3	206.2 ±2.8	0.4%
[M+K]+	232.3 ±0.3	232.7 ±2.2	0.2%	207.4 ±0.2	204.7 ±1.9	1.3%
[M+Rb]+	230.2 ±0.3	239.6 ±2.0	4.1%	207.8 ±0.3	210.9± 1.2	1.5%
[M+Cs]+	229.4 ±0.3	239.1 ±2.0	4.2%	209.4 ±0.3	208.4 ±1.4	0.5%

Alkaline Earth Metal Adducts

Similar experiments were then performed with alkaline earth metals (magnesium, calcium, strontium, and barium) dissolved as acetate salts. Under these experimental conditions, the major ionization species identified were those in the +1 charge state, such that the predominant ions were singly charged monomer [M+X+Acetate]⁺ and singly charged dimer [2M+X+Acetate]⁺, with acetate as a counter anion in each case. The doubly charged species, [M+X]²⁺ and [2M+X]²⁺ were not detected under these conditions. Drift spectra were collected for each species, and the spectra for [M+X+Acetate]⁺ are shown in Figure 3, with accompanying value for “open”:”closed” ratio.

Figure 3.

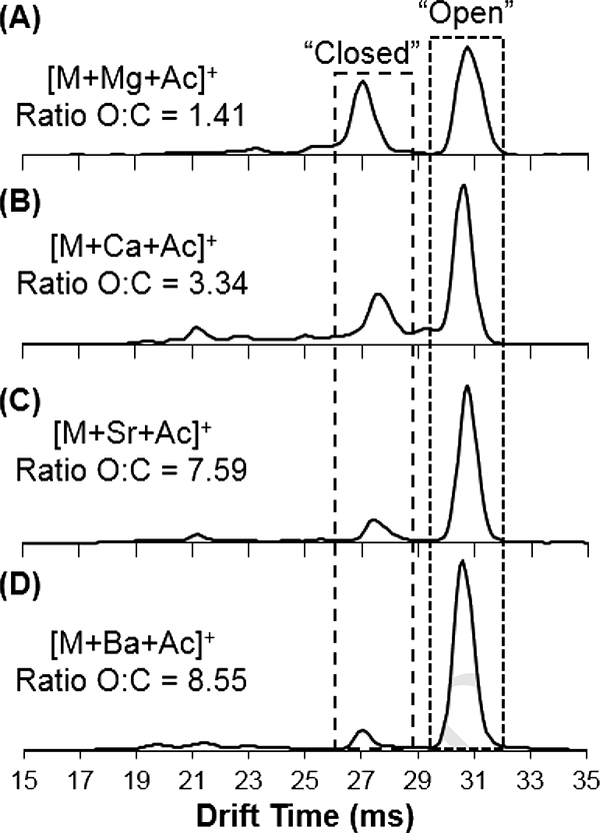
Drift time spectra collected for 25OHD3 monomer alkaline earth metal adducts (with acetate anion) with (a) magnesium, (b) calcium, (c) strontium, and (d) barium. For each species, the ratio of the “open”:”closed” (O:C) conformers is listed.

As with the alkali metal species, the overall intensities were lower in comparison with sodiated species, and again the sodiated species was still observed at a significant intensity in the spectrum for each cation adduct (Figure S3). However, the trend of increasing ratio of “open”:”closed” conformations with increasing size of the metal ion continued, and the ratios grew even higher than those for alkali metal adducts. Figure 3 demonstrates the relative increase in intensity for the “open” conformer at ~31 ms, as Mg < Ca < Sr <Ba. The values for “open”:”closed” ratio and experimentally obtained collision cross section are displayed in Table 4.

Table 4.

Comparison of 25OHD3 cation adducts for alkaline earth metals, demonstrating the ratio between “open” and “closed” conformers and experimentally obtained collision cross sections.

Ion	m/z	Ratio O:C	DTCCSN2 (Å2) “Open”	DTCCSN2 (Å2) “Closed”
[M+Mg+Ac]+	483.332	1.41	249.6 ± 0.3	218.2 ±0.3
[M+Ca+Ac]+	499.310	3.34	246.6 ± 0.3	223.8 ± 0.3
[M+Sr+Ac]+	547.235	7.59	246.6 ± 0.3	221.1 ±0.3
[M+Ba+Ac]+	597.253	8.55	245.1 ±0.3	215.3 ±0.3

The epimers were also run as a mixture, using a deuterium-labeled 25OHD3 (to distinguish compounds by mass) with each cation. The same pattern observed for the compounds run individually (two conformers for 25OHD3, one for epi25OHD3) was maintained, indicating that these conformers are not affected by the presence of the other epimer. Figure 4 shows the results from mixtures of epi25OHD3/D₆-25OHD3 with potassium and barium; these IM-MS spectra show the absence of the “open” conformation for epi25OHD3 and the relatively higher abundance of the “open” conformation for 25OHD3 in comparison with its “closed” conformer, which is nearly absent for the barium adduct species.

Figure 4.

IM-MS spectrum of a mixture of epimers (isotopically labeled 25OHD3), demonstrating the increased relative abundance of the “open” conformation of 25OHD3 for both (A) potassium adducts and (B) barium adducts.

The potential analytical benefit of these adducts is displayed in Figure 5, which shows overlays for 25OHD3 and epi25OHD3 as [M+Na]⁺, [M+K]⁺, [M+Sr+Acetate]⁺, and [M+Ba+Acetate]⁺ adducts to demonstrate the effective reduction of the overlap in “closed” conformer drift peaks, due to loss in intensity of the “closed” conformer of 25OHD3. Despite decreases in overall intensity for these cation adducts, this observation could offer potential for improved separation of 25OHD3 from its epimer. Further studies on the quantitative potential of this methodology (i.e., potential improvements in reproducibility for the individual epimers measured simultaneously in a mixture) will be the subject of future work.

Figure 5.

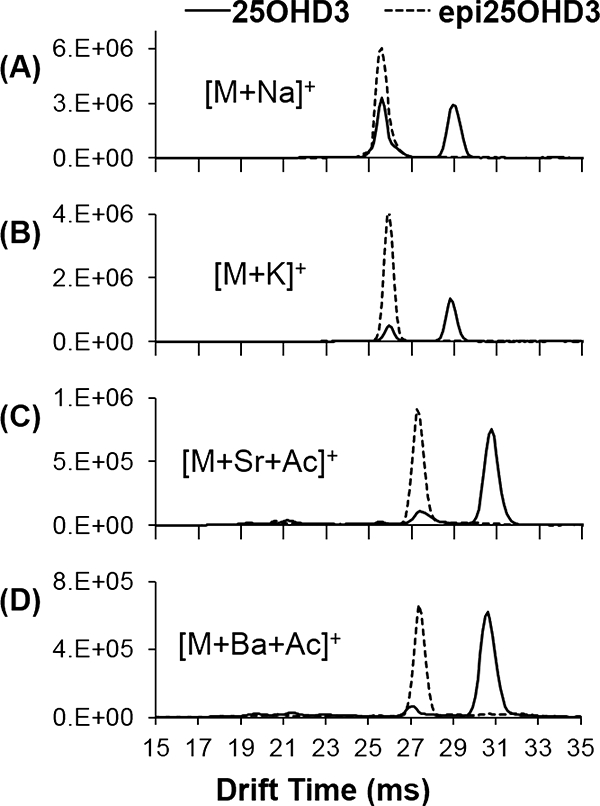
Drift time spectra overlays collected for 25OHD3 and epi25OHD3 monomers with (a) sodium, (b) potassium, (c) strontium, and (d) barium.

Conclusions

This work has demonstrated the use of IM-MS in the study of clinically relevant 25- hydroxyvitamin D3 and its epimer. Specifically, previous work demonstrating a unique “open” gas-phase conformation for the sodiated monomer of 25OHD3 was expanded upon to show that the relative abundance of this unique conformation is highly dependent on the specific cation adduct. In general, within a group of metals (e.g., alkali or alkaline earth), the ratio of “open”:”closed” conformers increases with increasing size of the cation adduct. Theoretical calculations were performed to determine the Gibbs free energy difference between conformers, and these results agree with the experimental trends. In addition, because these cation adducts do not affect the gas- phase structure of the epimer interference, epi25OHD3 (i.e., this compound remains in the “closed” conformation, regardless of cation addition), this method also serves as a useful tool for separation of these isomers in a mixture and has potential for application in targeted clinical analysis for Vitamin D deficiency. Studies are underway to explore the effectiveness of this strategy for the identification and quantitation of the individual epimers in biological samples.

Highlights.

• IM-MS analysis reveals two gas-phase conformations for sodiated 25- hydroxyvitamin D3, including the “closed” conformer and unique “open” conformer not observed for its epimer

• The experimental “open” to “closed” ratio is positively correlated with size of the cation adduct

• Molecular modeling calculations of Gibbs free energy for cation adducts agree with experimental results; the “open” conformer is more energetically favored for larger cation adducts

• Addition of specific cations can allow identification and separation of both 25- hydroxyvitamin D3 and its epimer in mixtures