Optimal Individualized Treatments in Resource-Limited Settings

Abstract

An individualized treatment rule (ITR) is a treatment rule which assigns treatments to individuals based on (a subset of) their measured covariates. An optimal ITR is the ITR which maximizes the population mean outcome. Previous works in this area have assumed that treatment is an unlimited resource so that the entire population can be treated if this strategy maximizes the population mean outcome. We consider optimal ITRs in settings where the treatment resource is limited so that there is a maximum proportion of the population which can be treated. We give a general closed-form expression for an optimal stochastic ITR in this resource-limited setting, and a closed-form expression for the optimal deterministic ITR under an additional assumption. We also present an estimator of the mean outcome under the optimal stochastic ITR in a large semiparametric model that at most places restrictions on the probability of treatment assignment given covariates. We give conditions under which our estimator is efficient among all regular and asymptotically linear estimators. All of our results are supported by simulations.

1. Introduction

Suppose one wishes to maximize the population mean of some outcome using some binary point treatment, where for each individual clinicians have access to (some subset of) measured baseline covariates. Such a treatment strategy is termed an individualized treatment regime (ITR), and the (counterfactual) population mean outcome under an ITR is referred to as the value of an ITR. The ITR which maximizes the value is referred to as the optimal ITR or the optimal rule. There has been much recent work on this problem in the case where treatment is an unlimited resource (see Murphy [1] and Robins [2] for early works on the topic, and Chakraborty and Moodie [3] for a recent overview). It has been shown that the optimal treatment in this context is given by checking the sign of the average treatment effect conditional on (some subset of) the baseline covariates, also known as the blip function [2].

The optimal ITR assigns treatment to people from a given strata of covariates for which treatment is on average beneficial, and does not assign treatment to this strata otherwise. If treatment is even slightly beneficial to all subsets of the population, then such a treatment strategy would suggest treating the entire population. There are many realistic situations in which such a treatment strategy, or any strategy that treats a large proportion of the population, is not feasible due to limitations on the total amount of the treatment resource. In a discussion of Murphy [1], Arjas observed that resource constraints may render optimal ITRs of little practical use when the treatment of interest is a social or educational program, though no solution to the constrained problem was given [4].

The mathematical modeling literature has considered the resource allocation problem to a greater extent. Lasry et al. [5] developed a model to allocate the annual CDC budget for HIV prevention programs to subpopulations which would benefit most from such an intervention. Tao et al. [6] consider a mathematical model to optimally allocate screening procedures for sexually tranmitted diseases subject to a cost constraint. Though Tao et al. do not frame the problem as a statistical estimation problem, they end up confronting similar optimization challenges to those that we will face. In particular, they confront the (weakly) NP-hard knapsack problem from the combinatorial optimization literature [7, 8]. We will end up avoiding most of the challenges associated with this problem by primarily focusing on stochastic treatment rules, which will reduce to the easier fractional knapsack problem [9, 8]. Stochastic ITRs allow the treatment to rely on some external stochastic mechanism for individuals in a particular strata of covariates.

We consider a resource constraint under which there is a maximum proportion of the population which can be treated. We primarily focus on evaluating the public health impact of an optimal resource-constrained (R-C) ITR via its value. The value function has been shown to be of interest in several previous works (see, e.g., Zhang et al. [10], van der Laan and Luedtke [11], Goldberg et al. [12]. Despite the general interest of this quantity, estimating this quantity is challenging for unconstrained deterministic regimes at so-called exceptional laws, i.e. probability distributions at which the blip function is zero in some positive probability strata of covariates [2]; a slightly more general assumption is given in Luedtke and van der Laan [13]. Chakraborty et al. [14] showed that one can develop confidence intervals for this parameter using m-out-of-n bootstrap, though these confidence intervals shrink at a slower than root-n rate. Luedtke and van der Laan [13] showed that root-n rate confidence intervals can be developed for this quantity under reasonable conditions in the large semiparametric model which at most places restrictions on the treatment mechanism.

We develop a root-n rate estimator for the optimal R-C value and corresponding confidence intervals in this same large semiparametric model. We show that our estimator is efficient among all regular and asymptotically linear estimators under conditions. When the baseline covariates are continuous and the resource constraint is active, i.e. when the optimal R-C value is less than the optimal unconstrained value, these conditions are far more reasonable than the non-exceptional law assumption needed for regular estimation of the optimal unconstrained value.

We now give a brief outline of the paper. Section 2 defines the statistical estimation problem of interest, gives an expression for the optimal deterministic rule under a condition, and gives a general expression for the optimal stochastic rule. Section 3 presents our estimator of the optimal R-C value. Section 4 presents conditions under which the optimal R-C value is pathwise differentiable, and gives an explicit expression for the canonical gradient under these conditions. Section 5 describes the properties of our estimator, including how to develop confidence intervals for the optimal R-C value. Section 6 presents our simulation methods. Section 7 presents our simulation results. Section 8 closes with a discussion and areas of future research. All proofs are given in the Appendix.

2. Optimal R-C rule and value

Suppose we observe n independent and identically distributed (i.i.d.) draws from a single time point data structure (W, A, Y)~P₀, here the vector of covariates W has support $\mathcal{W}$, the treatment A has support {0,1}, and the outcome Y has support in the closed unit interval. Our statistical model is nonparametric, beyond possible knowledge of the treatment mechanism, i.e. the probability of treatment given covariates. Little generality is lost with the bound on Y, given that any continuous outcome bounded in [b, c] can be rescaled to the unit interval with the linear transformation (y – b)/(c – b). Suppose that treatment are resources are limited so that at most a κ ϵ (0,1) proportion of the population can receive the treatment A = 1. Let V be some function ofW, and denote the support of V with $\mathcal{V}$. A deterministic treatment rule $\tilde{d}$ takes as input a function of the covariates $v\in \mathcal{V}$ and outputs a binary treatment decision $\tilde{d}\left(v\right)$. The stochastic treatment rules considered in this work are maps from $\mathcal{U}\in \mathcal{V}$ to {0,1}, where $\mathcal{U}$ is the support of some random variable U~P_U. If d is a stochastic rule and $u\in \mathcal{U}$ is fixed, then d(u,·) represents a deterministic treatment rule. Throughout this work we will let U be drawn independently of all draws from P₀.

For a distribution P, let ${\overline{Q}}_P(a,w)\triangleq E_P[Y|A=a,W=w]$. For notational convenience, we let ${\overline{Q}}_0\triangleq {\overline{Q}}_{P_0}$. Let $\tilde{d}$ be a deterministic treatment regime. For a distribution P, let ${\tilde{\mathrm{\Psi }}}_{\tilde{d}}\triangleq E_{P_0}[{\overline{Q}}_P(\tilde{d}(V),W)]$ represent the value of $\tilde{d}$. Under causal assumptions, this quantity is equal to the counterfactual mean outcome if, possibly contrary to fact, the rule d̃ were implemented in the population [15, 16]. The optimal R-C deterministic regime at P is defined as the deterministic regime d̃ which solves the optimization problem

$$\mathrm{Maximize}{\tilde{\mathrm{\Psi }}}_{\tilde{d}}(P)\mathrm{subject}\mathrm{to}{E}_{P_0}[\tilde{d}(V)]\le \kappa .$$ (1)

For a stochastic regime d, let ${\mathrm{\Psi }}_d(P)\triangleq E_{P_U}[{\tilde{\mathrm{\Psi }}}_d(U,.)(P)]$ represent the value of d. Under causal assumptions, this quantity is equal to the counterfactual mean outcome if, possibly contrary to fact, the stochastic rule d were implemented in the population (see Ref. [17] for a similar identification result). The optimal R-C stochastic regime at P is defined as the stochastic treatment regime dwhich solves the optimization problem

$$\mathrm{Maximize}{\mathrm{\Psi }}_d(P)\mathrm{subject}\mathrm{to}{E}_{P_U\times P}[d(U,V)]\le \kappa .$$ (2)

We call the optimal value under a R-C stochastic regime Ψ(P). Because any deterministic regime can be written as a stochastic regime which does not rely on the stochastic mechanism U, we have that $\mathrm{\Psi }(P)\ge \tilde{\mathrm{\Psi }}(P)$. The constraint $E_{P_U\times P}[d(U,V)]\le \kappa$ above is primarily meant to represent a clinical setting where each patient arrives at the clinic with covariate summary measure V, a value of U is drawn from P_Ufor this patient, and treatment is then assigned according to d(U, V). By Fubini’s theorem, this is like rewriting the above constraint as $E_P{E}_{P_U}[d(U,V)]\le \kappa$. Nonetheless, this constraint also represents the case where a single value of U = u is drawn for the entire population, and each individual is treated according to the deterministic regime d(u, ·), i.e. $E_{P_U}{E}_P[d(U,V)]\le \kappa$. This case appears less interesting because, for a fixed u, there is no guarantee that E_P[d(u, V)] ≤ κ.

For a distribution P, define the blip function as

$${\overline{Q}}_{b,P}(v)\triangleq E_P[{\overline{Q}}_P(1,W)-{\overline{Q}}_P(0,W)|V=v].$$

Let S_P represent the survival function of ${\overline{Q}}_{b,P}$, i.e. $\tau \mapsto P{r}_P({\overline{Q}}_{b,P}>\tau )$. Let

$${\eta }_P\triangleq \inf \{\tau :S_P(\tau )\le \kappa \}$$

$${\tau }_P\triangleq \max \{{\eta }_P,0\}.$$ (3)

For notational convenience we let ${\overline{Q}}_{b,0}\triangleq {\overline{Q}}_{b,P_0}$, $S_0\triangleq S_{P_0}$, ${\eta }_0\triangleq {\eta }_{P_0}$, and ${\tau }_0\triangleq {\tau }_{P_0}$.

Define the deterministic treatment rule ${\tilde{d}}_P$ as $v\mapsto I({\overline{Q}}_{b,P}(v)>{\tau }_P)$, and for notational convenience let ${\tilde{d}}_0\triangleq {\tilde{d}}_{P_0}$. We have the following result.

Theorem 1

If $P{r}_P({\overline{Q}}_{b,P}(V)={\tau }_P)=0$ , then the ${\tilde{d}}_P$ is an optimal deterministic rule satisfying the resource constraint, i.e. ${\tilde{\mathrm{\Psi }}}_{{\tilde{d}}_P}(P)$ attains the maximum described in eq. (1).

One can in fact show that ${\tilde{d}}_P$ is the P almost surely unique optimal deterministic regime under the stated condition. We do not treat the case where $P{r}_P({\overline{Q}}_{b,P}(V)={\tau }_P)>0$ for deterministic regimes, since in this case (1) is a more challenging problem: for discrete V with positive treatment effect in all strata, eq. (1) is a special case of the 0–1 knapsack problem, which is NP-hard, though is considered one of the easier problems in this class [7, 8]. In the knapsack problem, one has a collection of items, each with a value and a weight. Given a knapsack which can only carry a limited weight, the objective is to choose which items to bring so as to maximize the value of the items in the knapsack while respecting the weight restriction. Considering the optimization problem over stochastic rather than deterministic regimes yields a fractional knapsack problem, which is known to be solvable in polynomial time [9, 8]. The fractional knapsack problem differs from the 0–1 knapsack problem in that one can pack partial items, with the value of the partial items proportional to the fraction of the item packed.

Define the stochastic treatment rule d_P by its distribution with respect to a random variable drawn from P_U:

$$P{r}_{P_U}(d_P(U,v)=1)=\{\begin{array}{ll}\kappa -S_P({\tau }_P),& \mathrm{if}{\overline{Q}}_{b,P}(v)={\tau }_P\mathrm{and}{\tau }_P>0\\ I({\overline{Q}}_{b,P}(v)>{\tau }_P),& \mathrm{otherwise}.\end{array}$$

We will let $d_0\triangleq d_{P_0}$. Note that ${\tilde{d}}_P(V)$ and d_P(U, V) are P_U × P almost surely equal if $P{r}_P({\overline{Q}}_{b,P}(V)={\tau }_P)=0$ or if τ_P ≤ 0, and thus have the same value in these settings. It is easy to show that

$$E_{P_U\times P}[d_P(U,V)]=\kappa \mathrm{if}{\tau }_P>0.$$ (4)

The following theorem establishes the optimality of the stochastic rule d_P in a resource-limited setting.

Theorem 2

The maximum in eq. (2) is attained at d = d_P, i.e. d_P is an optimal stochastic rule.

Note that the above theorem does not claim that d_P is the unique optimal stochastic regime. For discrete V, the above theorem is an immediate consequence of the discussion of the knapsack problem in Dantzig [9].

In this paper we focus on the value of the optimal stochastic rule. Nonetheless, the techniques that we present in this paper will only yield valid inference in the case where the data are generated according to a distribution P₀ for which $P{r}_0({\overline{Q}}_{b,0}(V)={\tau }_0)=0$. This is analogous to assuming a non-exceptional law in settings where resources are not limited [13, 2], though we note that for continuous covariates V this assumption is much more likely if τ₀ > 0. It seems unlikely that the treatment effect in some positive probability strata of covariates will concentrate on some arbitrary (determined by the constraint κ) value τ₀. Nonetheless, one could deal with situations where $P{r}_0({\overline{Q}}_{b,0}(V)={\tau }_0)>0$ using similar martingale-based online estimation techniques to those presented in Luedtke and van der Laan [13].

3. Estimating the optimal optimal R-C value

We now present an estimation strategy for the optimal R-C rule. The upcoming sections justify this strategy and suggest that it will perform well for a wide variety of data generating distributions. The estimation strategy proceeds as follows:

1. Obtain estimates ${\overline{Q}}_n$ , ${\overline{Q}}_{b,n}$, and g_n of ${\overline{Q}}_0$, ${\overline{Q}}_{b,0}$, and g₀ using any desired estimation strategy which respects the fact that Y is bounded in the unit interval.

2. Estimate the marginal distributions of W and V with the corresponding empirical distributions.

3. Estimate S₀ with the plug-in estimator S_n given by $\tau \mapsto \frac{1}{n}{\sum }_{i=1}^{n}I({\overline{Q}}_{b,n}(v_i)>\tau )$.

4. Estimate η₀ with the plug-in estimator ${\eta }_n\triangleq \inf \{\tau :S_n(\tau )\le \kappa \}$.

5. Estimate τ₀ with the plug-in estimator given by ${\tau }_n\triangleq \max \{{\eta }_n,0\}$.

6. Estimate d₀ with the plug-in estimator d_n with distribution

   $$P{r}_{P_U}(d_n(U,v)=1)=\{\begin{array}{ll}\kappa -S_n({\tau }_n),& \mathrm{if}{\overline{Q}}_{b,n}(v)={\tau }_n\mathrm{and}{\tau }_n>0\\ I({\overline{Q}}_{b,n}(v)>{\tau }_n),& \mathrm{otherwise}.\end{array}$$
7. Run a TMLE for the parameter ${\mathrm{\Psi }}_{d_n}(P_0)$:

   • (a)
     For $\tilde{a}\in \{0,1\}$, define $H(a,w)\triangleq \frac{P{r}_{P_U}(d_n(U,v)=a)}{g_n(a|w)}$. Run a univariate logistic regression using:

     • Outcome : (y_i : i = 1,..., n)
     • Offset : $(\mathrm{logit}{\overline{Q}}_n(a_i,w_i):i=1,\dots ,n)$
     • Covariate : (H(a_i, w_i) : i = 1,..., n).

Let ε_n represent the estimate of the coefficient for the covariate, i.e.

$${\epsilon }_n\triangleq \underset{\epsilon \in ℝ}{\arg \max }\frac{1}{n}{\displaystyle \sum _{i=1}^n[{\overline{Q}}_n^{\epsilon }(a_i,w_i)\log y_i+(1-{\overline{Q}}_n^{\epsilon }(a_i,w_i))\log (1-y_i)]},$$

where ${\overline{Q}}_n^{\epsilon }(a,w)\triangleq \log {\mathrm{it}}^{-1}(\log \mathrm{it}{\overline{Q}}_n(a,w)+\epsilon H(a,w))$.

• (b)Define ${\overline{Q}}_n^{*}\triangleq {\overline{Q}}_n^{{\epsilon }_n}$.
• (c)
  Estimate ${\mathrm{\Psi }}_{d_n}(P_0)$ using the plug-in estimator given by

  $${\mathrm{\Psi }}_{d_n}(P_n^{*})\triangleq \frac{1}{n}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{a=0}^1{\overline{Q}}_n^{*}}}(a,w_i)P{r}_{P_U}(d_n(U,v_i)=a).$$

We use ${\mathrm{\Psi }}_{d_n}(P_n^{*})$ as our estimate of Ψ(Ρ₀). We will denote this estimator $\widehat{\mathrm{\Psi }}$, where we have defined $\widehat{\mathrm{\Psi }}$ so that $\widehat{\mathrm{\Psi }}(P_n)={\mathrm{\Psi }}_{d_n}(P_n^{*})$. Note that we have used a TMLE for the data dependent parameter ${\mathrm{\Psi }}_{d_n}(P_0)$, which represents the value under a stochastic intervention d_n. Nonetheless, we assume that $P{r}_{P_0}({\overline{Q}}_{b,0}(V)={\tau }_0)=0$ for many of the results pertaining to our estimator $\widehat{\mathrm{\Psi }}$, i.e. we assume that the optimal R-C rule is deterministic. We view estimating the value under a stochastic rather than deterministic intervention as worthwhile because one can give conditions under which the above estimator is (root-n) consistent for Ψ(P₀) at all laws P₀, even if non-negligible bias invalidates standard Wald-type confidence intervals for the parameter of interest at laws P₀ for which $P{r}_{P_0}({\overline{Q}}_{b,0}(V)={\tau }_0)>0$.

We will use $P_n^{*}$ to denote any distribution for which ${\overline{Q}}_{P_n^{*}}={\overline{Q}}_n^{*}$, $g_{P_n^{*}}=g_n$and $P_n^{*}$ has the marginal empirical distribution of W for the marginal distribution of W. We note that such a distribution $P_n^{*}$ exists provided that ${\overline{Q}}_n^{*}$ and g_n fall in the parameter spaces of $P\mapsto {\overline{Q}}_P(W)$ and P⟼g_P, respectively.

In practice we recommend estimating ${\overline{Q}}_0$ and ${\overline{Q}}_{b,0}$ using an ensemble method such as super-learning to make an optimal bias-variance trade-off (or, more generally, minimize cross-validated risk) between a mix of parametric models and data adaptive regression algorithms [18, 19]. If the treatment mechanism g₀ is unknown then we recommend using similar data adaptive approaches to obtain the estimate g_n. If g₀ is known (as in a randomized controlled trial without missingness), then one can either take g_n = g₀ or estimate g₀ using a correctly specified parametric model, which we expect to increase the efficiency of estimators when the ${\overline{Q}}_0$ part of the likelihood is misspecified [20, 21].

There is typically little downside to using data adaptive approaches to estimate the needed portions of the likelihood, though we do give a formal empirical process condition in Section 5.1 which describes exactly how data adaptive these estimators can be. If one is concerned about the data adaptivity of the estimators of the needed portions of the likelihood, then one can consider a cross-validated TMLE approach such as that presented in van der Laan and Luedtke [20] or an online one-step estimator as that presented in Luedtke and van der Laan [13]. These two approaches make no restrictions on the data adaptivity of the estimators of ${\overline{Q}}_0$, ${\overline{Q}}_{b,0}$, or g₀.

We now outline the main results of this paper, which hold under appropriate consistency and regularity conditions.

- Asymptotic linearity of $\widehat{\mathrm{\Psi }}$ :

$$\widehat{\mathrm{\Psi }}(P_n)-\mathrm{\Psi }(P_0)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{D}_0}(O_i)+o_{P_0}(n^{-1/2}),$$

with D₀ a known function of P₀.

- $\widehat{\mathrm{\Psi }}$ is an asymptotically efficient estimate of Ψ(P₀).

- One can obtain a consistent estimate ${\sigma }_n^2$ for the variance of D₀(O). An asymptotically valid 95% confidence intervals for Ψ(P₀) given by $\widehat{\mathrm{\Psi }}(P_n)\pm 1.96{\sigma }_n/\sqrt{n}$.

The upcoming sections give the consistency and regularity conditions which imply the above results.

4. Canonical gradient of the optimal R-C value

The pathwise derivative of Ψ will provide a key ingredient for analyzing the asymptotic properties of our estimator. We refer the reader to Pfanzagl [22] and Bickel et al. [23] for an overview of the crucial role that the pathwise derivative plays in semiparametric efficiency theory. We remind the reader that an estimator $\widehat{\mathrm{\Phi }}$ is an asyptotically linear estimator of a parameter Φ (P₀) with influence curve $I{C}_{P_0}$ provided that

$$\widehat{\mathrm{\Phi }}(P_n)-\mathrm{\Phi }(P_0)=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}I{C}_{P_0}(O_i)+o_{P_0}}(n^{-1/2}).$$

If Φ is pathwise differentiable with canonical gradient $I{C}_{P_0}$ then $\widehat{\mathrm{\Phi }}$ is RAL and asymptotically efficient (minimum variance) among all such RAL estimators of Φ(Ρ₀) [23, 22].

For $o\in \mathcal{O}$, a deterministic rule $\tilde{d}$, and a real number τ, define

$$D_1(\tilde{d},P)(o)\triangleq \frac{I(a=\tilde{d}(v))}{g_P(a|w)}(y-{\overline{Q}}_P(a,w))$$

$$D_2(\tilde{d},P)(o)\triangleq {\overline{Q}}_P(\tilde{d}(v),w)-E_P{\overline{Q}}_P(\tilde{d}(v),w),$$

where $g_P(a|W)\triangleq P{r}_P(A=a|W)$. We will let $g_0\triangleq g_{P_0}$. We note that $D_1(\tilde{d},P)+D_2(\tilde{d},P)$ is the efficient influence curve of the parameter ${\tilde{\mathrm{\Psi }}}_{\tilde{d}}(P)$.

Let d be some stochastic rule. The canonical gradient of Ψ_d is given by

$$I{C}_d(P)(o)\triangleq E_{P_U}[D_1(d(U,\cdot ),P)(o)+D_2(d(U,\cdot ),P)(o)].$$

Define

$$D(d,\tau ,P)(o)\triangleq I{C}_d(P)(o)-\tau (E_{P_U}[d(U,v)]-\kappa ).$$

For ease of reference, let $D_0\triangleq D(d_0,{\tau }_0,P_0)$. The upcoming theorem makes use of the following assumptions.

• C1. g₀ satisfies the positivity assumption: Pr₀(0 < g₀(1|W) < 1) = 1.

• C2. ${\overline{Q}}_{b,0}(W)$ has density f₀ at η₀, and 0 < f_ο(η₀) < ∞

• C3. S₀ is continuous in a neighborhood of η₀.

• C4. $P{r}_0({\overline{Q}}_{b,0}(V)=\tau )=0$ 0 for all τ in a neighborhood of τ₀.

We now present the canonical gradient of the optimal R-C value.

Theorem 3

Suppose C1 through C4. Then Ψ is pathwise differentiable at P₀ with canonical gradient D₀.

Note that C3) implies that $P{r}_0({\overline{Q}}_{b,0}(V)={\tau }_0)=0$. Thus d₀ is (almost surely) deterministic and the expectation over P_U in the definition of D₀ is superfluous. Nonetheless, this representation will prove useful when we seek to show that our estimator solves the empirical estimating equation defined by an estimate of D(d₀, τ₀, P₀).

When the resource constraint is active, i.e. τ₀ > 0, the above theorem shows that Ψ has an additional component over the optimal value parameter when no resource constraints are present [11]. The additional componentis ${\tau }_0\times (E_{P_U}\left[d_0\left(U,v\right)-\kappa \right)$, and is the portion ofthe derivative that relies on the fact that d₀ is estimated and falls on the edge of the parameter space. We note that it is possible that the variance of D₀ (O) is greater than the variance of $I{C}_{d_0}\left(P_0\right)\left(O\right)$.If τ₀ = 0 then these two variances are the same, so suppose τ₀ > 0. Then, provided that $P{r}_0({\overline{Q}}_{b,0}(V)={\tau }_0)=0$, we have that

$$Va{r}_{P_0}(D_0(O))-Va{r}_{P_0}(I{C}_{d_0}(P_0))={\tau }_0\kappa (1-\kappa )\left({\tau }_0-2E_{P_0}\left[{\overline{Q}}_0(1,W)|{\tilde{d}}_0(V)=1\right]+2E_{P_0}\left[{\overline{Q}}_0(0,W)|{\tilde{d}}_0(V)=0\right]\right).$$

For any κ ∈(0,1), it is possible to exhibit a distribution P₀ which satisfies the conditions of Theorem 3 and for which $Va{r}_{P_0}(D_0(O))>Va{r}_{P_0}(I{C}_{d_0}(P_0)(O))$. Perhaps more surprisingly, it is also possible to exhibit a distribution P0 which satisfies the conditions of Theorem 3 and for which $Va{r}_{P_0}(D_0(O))<Va{r}_{P_0}(I{C}_{d_0}(P_0)(O))$. We omit further the discussion here because the focus of this work is on considering the estimating the value from the optimization problem (2), rather than discussing how this procedure relates to the estimation of other parameters.

5. Results about the proposed estimator

We now show that $\widehat{\mathrm{\Psi }}$ is an asymptotically linear estimator for Ψ(Ρ₀) with influence curve D₀ provided our estimates of the needed parts of P₀ satisfy consistency and regularity conditions. Our theoretical results are presented in Section 5.1, and the conditions of our main theorem are discussed in Section 5.2.

5.1. Inference for Ψ(Ρ₀)

For any distributions P and P₀ satisfying positivity, stochastic intervention d, and real number τ, define the following second-order remainder terms:

$$R_{10}(d,P)\triangleq E_{P_U\times P_0}\left[\left(1-\frac{g_0(d|W)}{g(d|W)}\right)({\overline{Q}}_P(d,W)-{\overline{Q}}_0(d,W))\right]$$

$$R_{20}(d)\triangleq E_{P_U\times P_0}[(d-d_0)({\overline{Q}}_{b,0}(V)-{\tau }_0)].$$

Above the reliance of d and d₀ on (U, V) is omitted in the notation. Let $R_0(d,P)\triangleq R_{10}(d,P)+R_{20}(d)$. The upcoming theorem will make use of the following assumptions.

1. g₀ satisfies the strong positivity assumption: Pr₀(δ < g₀(1|W) < 1 — δ) — 1 for some δ > 0.

2. g_n satisfies the strong positivity assumption for a fixed δ > 0 with probability approaching 1: there exists some δ > 0 such that, with probability approaching 1, Pr₀(δ < g_n(1|W) < 1 — δ) — 1.

3. $R_0(d_n,P_n^{*})=o_{P_0}(n^{-1/2})$.

4. $E_{P_0}\left[{(D(d_n,{\tau }_0,P_n^{*})(O)-D_0(O))}^2\right]=o_{P_0}(1)$.

5. $D(d_n,{\tau }_0,P_n^{*})$ belongs to a P₀-Donsker class $\mathcal{D}$ with probability approaching 1.

6. $\frac{1}{n}{\sum }_{i=1}^{n}D(d_n,{\tau }_0,P_n^{*})(O_i)=o_{P_0}(n^{-1/2})$.

We note that the τ₀ in the final condition above only enters the expression in the sum as a multiplicative constant in front of $-E_{P_U}\left[d\left(U,v_i\right)\right]-\kappa$.

Theorem 4 ($\widehat{\mathbf{\Psi }}$ is asymptotically linear)

Suppose C2) through 6. Then $\widehat{\mathrm{\Psi }}$ is a RAL estimator of Ψ(Ρ₀) with influence curve D₀, i.e.

$$\widehat{\mathrm{\Psi }}(P_n)-\mathrm{\Psi }(P_0)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{D}_0(O_i)+o_{P_0}(n^{-1/2}}).$$

Further, $\widehat{\mathrm{\Psi }}$is efficient among all such RAL estimators of Ψ(Ρ₀).

Let ${\sigma }_0^2\triangleq Va{r}_{P_0}(D_0)$ By the central limit theorem, $\sqrt{n}\left(\widehat{\mathrm{\Psi }}(P_n)-\mathrm{\Psi }(P_0)\right)$ converges in distribution to a $N(0,{\sigma }_0^2)$ distribution. Let ${\sigma }_n^2\triangleq \frac{1}{n}{\sum }_{i=1}^{n}D(d_n,{\tau }_n,P_n^{*}){(O_i)}^2$ be an estimate of ${\sigma }_0^2$. We now give the following lemma, which gives sufficient conditions for the consistency of τ_n for τ₀.

Lemma 5(Consistency of τ_n)

Suppose C2) and C3). Also suppose ${\overline{Q}}_{b,n}$ is consistent for ${\overline{Q}}_{b,0}$ in L¹(P₀) and that the estimate ${\overline{Q}}_{b,n}$ belongs to a P₀ Glivenko Cantelli class with probability approaching 1. Then τn → τ₀ in probability.

It is easy to verify that conditions similar to those of Theorem 4, combined with the convergence of τ_n to τ₀ as considered in the above lemma, imply that σ_n → σ₀ in probability. Under these conditions, an asymptotically valid two-sided 1 — α confidence interval is given by

$$\widehat{\mathrm{\Psi }}(P_n)\pm z_{1-\alpha /2}\frac{{\sigma }_n}{\sqrt{n}},$$

where z_1—α/2 denotes the 1 — α/2 quantile of a N(0,1) random variable.

5.2. Discussion of conditions of Theorem 4

Conditions C2) and C3).

These are standard conditions used when attempting to estimate the κ-quantile η₀, defined in eq. (3). Provided good estimation of ${\overline{Q}}_{b,0}$, these conditions ensure that gathering a large amount of data will enable one to get a good estimate of the κ-quantile of the random variable ${\overline{Q}}_{b,0}$. See Lemma 5 for an indication of what is meant by “good estimation” of ${\overline{Q}}_{b,0}$. It seems reasonable to expect that these conditions will hold when V contains continuous random variables and η₀ ≠ 0, since we are essentially assuming that ${\overline{Q}}_{b,0}$ is not degenerate at the arbirtrary (determined by κ) point η₀.

Condition C4).

If τ₀ > 0, then C4) is implied by C3). If τ₀ = 0, then C4) is like assuming a non-exceptional law, i.e. that the probability of a there being no treatment effect in a strata of V is zero. Because τ0 is not known from the outset, we require something slightly stronger, namely that the probability of any specific small treatment effect is zero in a strata of V is zero. Note that this condition does not prohibit the treatment effect from being small, e.g. $P{r}_0(|{\overline{Q}}_{b,0}(V)|<\tau )>0$ for all τ>0, but rather it prohibits there existing a sequence τ_m ↓ 0 with the property that $P{r}_0({\overline{Q}}_{b,0}(V)={\tau }_m)>0$ infinitely often. Thus this condition does not really seem any stronger than assuming a non-exceptional law. If one is concerned about such exceptional laws then we suggest adapting the methods in [13] to the R-C setting.

Condition 1.

This condition assumes that people from each strata of covariates have a reasonable (at least a δ > 0) probability of treatment.

Condition 2.

This condition requires that our estimates of g0 respect the fact that each strata of covariates has a reasonable probability of treatment.

Condition 3.

This condition is satisfied if $R_{10}(d_n,P_n^{*})=o_{P_0}(n^{-1/2})$ and $R_{20}(d_n)=o_{P_0}(n^{-1/2})$. The term $R_{10}(d_n,P_n^{*})$ takes the form of a typical double robust term that is small if either or ${\overline{Q}}_0$ is estimated well, and is second-order, i.e. one might hope that $R_{10}(d_n,P_n^{*})=o_{P_0}(n^{-1/2})$, if both both g₀ and ${\overline{Q}}_0$ are estimated well. One can upper bound this remainder with a product of the L²(P₀) rates of convergence of these two quantities using the Cauchy-Schwarz inequality. If g₀ is known, then one can take g_n = g₀ and this term is zero.

Ensuring that $R_{20}(d_n)=o_{P_0}(n^{-1/2})$requires a little more work but will still prove to be a reasonable condition. We will use the following margin assumption for some α > 0:

$$P{r}_0(0<|{\overline{Q}}_{b,0}-{\tau }_0|\le t)\lesssim t^{\alpha }\mathrm{for}\mathrm{all}t>0,$$ (5)

where “≲” denotes less than or equal to up to a multiplicative constant. This margin assumption is analogous to that used in Audibert and Tsybakov [24]. The following result relates the rate of convergence of R₂₀(d_n) to the rate at which ${\overline{Q}}_{b,n}-{\tau }_n$ converges to ${\overline{Q}}_{b,0}-{\tau }_0$.

Theorem 6

If eq. (5) holds for some α > 0, then

1. $|R_{20}(d_n)|\lesssim \Vert ({\overline{Q}}_{b,n}-{\tau }_n)-({\overline{Q}}_{b,0}-{\tau }_0){\Vert }_{2,P_0}^{2(1+\alpha )/(2+\alpha )}$

2. $|R_{20}(d_n)|\lesssim \Vert ({\overline{Q}}_{b,n}-{\tau }_n)-({\overline{Q}}_{b,0}-{\tau }_0){\Vert }_{\infty ,P_0}^{1+\alpha }.$

The above is similar to Lemma 5.2 in Audibert and Tsybakov [24], and a similar result was proved in the context of optimal ITRs without resource constraints in Luedtke and van der Laan [13]. If S₀ has a finite derivative at τ₀, as is given by C2), then one can take α = 1. The above theorem then implies that $R_{20}(d_n)=o_{P_0}(n^{-1/2})$ if either $\Vert ({\overline{Q}}_{b,n}-{\tau }_n)-({\overline{Q}}_{b,0}-{\tau }_0){\Vert }_{2,P_0}$ is $o_{P_0}(n^{3/8})$ or $\Vert ({\overline{Q}}_{b,n}-{\tau }_n)-({\overline{Q}}_{b,0}-{\tau }_0){\Vert }_{\infty ,P_0}$ is $o_{P_0}(n^{1/4})$

Condition 4.

This is a mild consistency condition which is implied by the L²(P₀) consistency of d_n, g_n, and ${\overline{Q}}_n^{*}$ to d₀, g₀, and ${\overline{Q}}_0$. We note that the consistency of the intial (unfluctuated) estimate ${\overline{Q}}_n$ for ${\overline{Q}}_0$ will imply the consistency of ${\overline{Q}}_n^{*}$ to ${\overline{Q}}_0$ given 2, since in this case ε_n → 0 in probability, and thus $\Vert {\overline{Q}}_n^{*}-{\overline{Q}}_n{\Vert }_{2,P_0}\to 0$ in probability.

Condition 5.

This condition places restrictions on how data adaptive the estimators of d₀, g₀, and ${\overline{Q}}_0$ can be. We refer the reader to Section 2.10 of van der Vaart and Wellner [25] for conditions under which the estimates of d₀, g₀, and ${\overline{Q}}_0$ belonging to Donsker classes implies that $D(d_n,{\tau }_0,P_n^{*})$ belongs to a Donsker class. We note that this condition was avoided for estimating the value function using a cross-validated TMLE in van der Laan and Luedtke [20] and using an online estimator of the value function in Luedtke and van der Laan [13], and using either technique will allow one to avoid the condition here as well.

Condition 6.

Using the notation Pf=∫f(o)dP(o) for any distribution P and function f : $\mathcal{O}\to \mathbb{R}$, we have that

$$P_{n}D(d_n,{\tau }_0,P_n^{*})=P_n{D}_1(d_n,P_n^{*})+P_n{D}_2(d_n,P_n^{*})-{\tau }_0\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{E}_{P_U}[d_n(U,v_i)]-\kappa }\right).$$

The first term is zero by the fluctuation step of the TMLE algorithm and the second term on the right is zero because $P_n^{*}$ uses the empirical distribution of W for the marginal distribution of W. If τ₀ = 0 then clearly the third term is zero, so suppose τ₀ > 0. Combining eq. (4) and the fact that d_n is a substitution estimator shows that the third term is 0 with probability approaching 1 provided that τ_n > 0 with probability approaching 1. This will of course occur if τ_n → τ₀ > 0 in probability, for which Lemma 5 gives sufficient conditions.

6. Simulation methods

We simulated i.i.d. draws from two data generating distributions at sample sizes 100, 200, and 1,000. For each sample size and distribution we considered resource constraints κ = 0·1 and κ = 0·9. We ran 2,000 Monte Carlo draws of each simulation setting. All simulations were run in R [26].

We first present the two data generating distributions considered, and then present the estimation strategies used.

6.1. Data generating distributions

6.1.1. Simulation 1

Our first data generating distribution is identical to the single time point simulation considered in van der Laan and Luedtke [20] and Luedtke and van der Laan [18]. The outcome is binary and the baseline covariate vector W = (W₁, ..., W₄) is four dimensional for this distribution, with

$$W_1,W_2,W_3,W_4\stackrel{i.i.d.}{\sim }N(0,1)$$

$$A|W\sim \mathrm{Bernoulli}(1/2)$$

$$\log \mathrm{it}(E_{P_0}[Y|A,W,H=0])=1-W_1^2+3W_2+A(5W_3^2-4.45)$$

$$\log \mathrm{it}(E_{P_0}[Y|A,W,H=1])=-0.5-W_3+2W_1{W}_2+A(3\left|W_2\right|-1.5),$$

where H is an unobserved Bernoulli(1/2) variable independent of A, W. For this distribution $E_{P_0}[{\overline{Q}}_0(0,W)]\approx E_{P_0}[{\overline{Q}}_0(1,W)]\approx 0.464$.

We consider two choices for V, namely V = W₃, and V = W₁,..., W₄. We obtained estimates of the approximate optimal R-C optimal value for this data generating distribution using 10⁷ Monte Carlo draws. When κ = 0.1, Ψ(Ρ₀) ≈ 0.493 for V = W₃ and Ψ(Ρ₀) ≈ 0.511 for V = W₁,..., W₄. When κ = 0.9, Ψ(Ρ₀) ≈ 0.536 for V = W₃ and Ψ(Ρ₀) ≈ 0.563 for V = W₁,..., W₄. We note that the resource constraint is not active (τ₀ = 0) when κ = 0.9 for either choice of V.

6.1.2. Simulation 2

Our second data generating distribution is very similar to one of the distributions considered in Luedtke and van der Laan [13], though has been modified so that the treatment effect is positive for all values of the covariate. The data are generated as follows:

$$W\sim \mathrm{Uniform}\left(-1,1\right)$$

$$A|W\sim \mathrm{Bernoulli}\left(1/2\right)$$

$$Y|A,W\sim \mathrm{Bernoulli}\left({\mathrm{Q}}_0\left(A,W\right)\right),$$

where for $\tilde{W}\triangleq W+5/6$ we define

$${\overline{Q}}_0(A,W)-\frac{6}{10}\triangleq \{\begin{array}{ll}0,\hfill & \mathrm{if}A=1\mathrm{and}-1/2\le W\le 1/3\hfill \\ -{\tilde{W}}^3+{\tilde{W}}^2-\frac{1}{3}\tilde{W}+\frac{1}{27},\hfill & \mathrm{if}A=1\mathrm{and}W<-1/2\hfill \\ -{\tilde{W}}^3+W^2-\frac{1}{3}W+\frac{1}{27},\hfill & \mathrm{if}A=1\mathrm{and}W>1/3\hfill \\ -\frac{3}{10}\hfill & \mathrm{otherwise}.\hfill \end{array}$$

For this distribution $E_{P_0}[{\overline{Q}}_0(0,W)]=0.3$ and $E_{P_0}[{\overline{Q}}_0(1,W)]\approx 0.583$.

We use V = W. This simulation is an example of a case where ${\overline{Q}}_{b,0}(V)>0$ almost surely, so any constraint on resources will reduce the optimal value from its unconstrained value of 0.583. In particular, we have that Ψ(Ρ₀) ≈ 0.337 when κ = 0.1 and Ψ(Ρ₀) ≈ 0.572 when κ = 0.9.

6.2. Estimating nuisance functions

We treated g₀ as known in both simulations and let g_n = g₀. We estimated ${\overline{Q}}_0$ using the super-learner algorithm with the quasi-log-likelihood loss function (family = binomial) and a candidate library of data adaptive (SL.gam and SL.nnet) and parametric algorithms (SL.bayesglm, SL.glm, SL.glm. interaction, SL.mean, SL.step, SL.step.interaction, and SL.step.forward). We refer the reader to table 2 in the technical report Luedtke and van der Laan [18] for a brief description of these algorithms. We estimated ${\overline{Q}}_{b,0}$ by running a super-learner using the squared error loss function and the same candidate algorithms and used W to predict the outcome $\tilde{Y}\triangleq \frac{2A-1}{g_0(A|W)}(Y-{\overline{Y}}_n)+{\overline{Y}}_n$, where ${\overline{Y}}_n$ represents the sample mean of Y from the n observations. See Luedtke and van der Laan [18] for a justification of this estimation scheme.

Once we had our estimates ${\overline{Q}}_n$, ${\overline{Q}}_{b,n}$ and g_n we proceeded with the estimation strategy described in Section 3.

6.3. Evaluating performance

We used three methods to evaluate our proposed approach. First, we looked at the coverage of two-sided 95% confidence intervals for the optimal R-C value. Second, we report the average confidence interval widths. Finally, we looked at the power of the α = 0.025 level test H₀ : Ψ(Ρ₀) = μ₀ against H₁ : Ψ(Ρ₀) > μ₀, where ${\mu }_0\triangleq E_0[{\overline{Q}}_0(0,W)]$ is treated as a known quantity. Under causal assumptions, μ₀ can be identified with the counterfactual quantity representing the population mean outcome if, possibly contrary to fact, no one receives treatment. If treatment is not currently being given in the population, one could substitute the population mean outcome (if known) for μ₀. Our test of significance consisted of checking of the lower bound in the two-sided 95% confidence interval is greater than μ₀. If an estimator of Ψ(Ρ₀) is low-powered in testing H₀ against H₁ then clearly the estimator will have little practical value.

7. Simulation results

Coverage

The proposed estimation strategy performed well overall. Figure 1 demonstrates the coverage of 95% confidence intervals for the optimal R-C value. All methods performed well at all sample sizes for the highly constrained setting where κ = 0.1. The results were more mixed for the resource constraint κ = 0.9. All methods performed well at the largest sample size considered. This supports our theoretical results, which were all asymptotic in nature. For Simulation 1, in which the resource constraint was not active for either choice of V, the coverage dropped off at lower sample sizes. Coverage was approximately 90% in the two smaller sample sample sizes for V = W₃, which may be expected for such an asymptotic method. For the more complex problem of estimating the optimal value when V = W₁,..., W₄ the coverage was somewhat lower (80% when n = 100 and 84% when n = 200). In Simulation 2, the coverage was better ( > 91%) for the smaller sample sizes. We note that the resource constraint was still active (τ₀ > 0) when κ = 0.9 for this simulation, and also that the estimation problem is easier because the baseline covariate was univariate.

Figure 1:

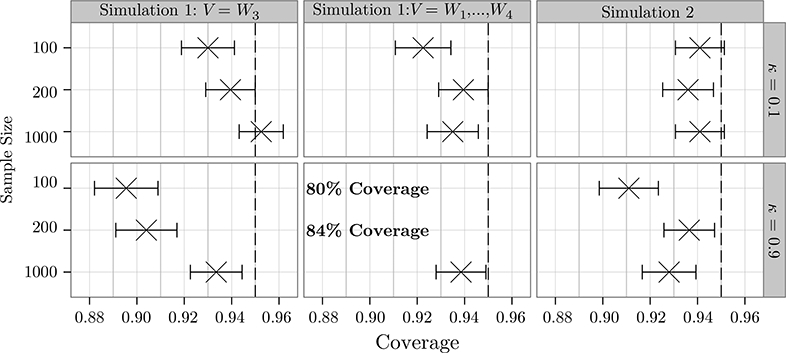
Coverage of two-sided 95% confidence intervals. As expected, coverage increases with sample size. The coverage tends to be better for κ = 0.1 than for κ = 0.9, though the estimator performed well at the largest sample size (1,000) for all simulations and choices of κ. Error bars indicate 95% confidence intervals to account for uncertainty from the finite number of Monte Carlo draws.

We report the average confidence interval widths across the 2,000 Monte Carlo draws. For n = 100, average confidence interval widths were between 0.25 and 0.26 across all simulations and choices of κ. For n = 200, all average confidence interval widths were between 0.17 and 0.18. For n = 1000, all average confidence interval widths were approximately 0.08. We note that the usefulness of such confidence intervals varies across simulations and choices of κ. When V = W₃ and κ = 0.1 in Simulation 1, the optimal R-C value is approximately 0.493, versus a baseline value ${\mu }_0=E_{P_0}[{\overline{Q}}_0(0,W)]$ of approximately 0.464. Thus here the confidence interval would give the investigator little information, even at a sample size of 1,000. In Simulation 2 with κ = 0.9, on the other hand, the optimal R-C value is approximately 0.572, versus a baseline value of μ₀ ≈ 0.3. Thus here all confidence intervals would likely be informative for investigators, even those made for data sets of size 100.

Figure 2 gives the power of the α = 0.025 level test H₀: Ψ(Ρ₀) = μ₀ against the alternative H₁: Ψ(Ρ₀) >μ₀. Overall our method appears to have reasonable power in this statistical test. We see that power increases with sample size, the key property of consistent statistical tests. We also see that power increases with κ, which is unsurprising given that Y is binary and g₀(a|w) is 1/2 for all a,w. We note that power will not always increase with κ, for example if P₀ is such that g₀(1|w) is very small for individuals with covariate w who are treated at κ = 0.9 but not at κ = 0.1. This observation is not meant as a criticism to the estimation scheme that we have presented because we assume that κ will be chosen to reflect real resource constraints, rather than to maximize the power for a test $H_0^{\prime }:\mathrm{\Psi }(P_0)=\mu \prime$ versus $H_1^{\prime }:\mathrm{\Psi }(P_0)>\mu \prime$ for some fixed μ’.

Figure 2:

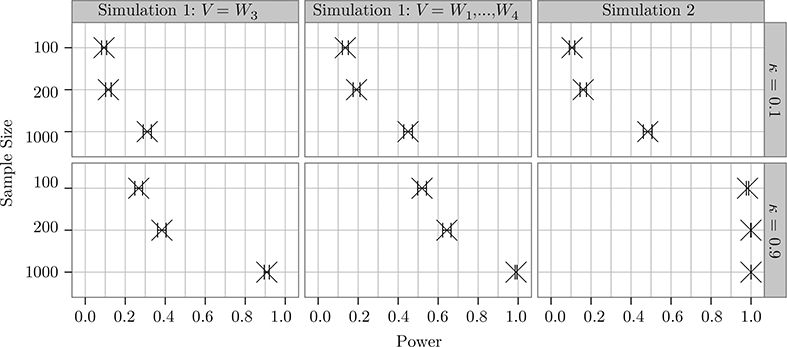
Power of the α = 0.025 level test of H₀ : Ψ(Ρ₀) = μ₀ against H₁ : Ψ(Ρ₀) >μ₀, where ${\mu }_0=E_{P_0}[{\overline{Q}}_0(0,W)]$ is treated as known. Power increases with sample size and κ. Error bars indicate 95% confidence intervals to account for uncertainty from the finite number of Monte Carlo draws.

We also implemented an estimating equation based estimator for the optimal R-C value and found the two methods performed similarly. We would recommend using the TMLE in practice because it has been shown to be robust to near positivity violations in a wide variety of settings [27]. We note that g₀(1|w) = 1/2 for all w in both of our simulations, so no near positivity violations occurred. We do not consider the estimation equation approach any further here because the focus of this work is on considering the optimization problem (2), rather than on comparing different estimation frameworks.

8. Discussion and future work

We have considered the problem of estimating the optimal resource-constrained value. Under causal assumptions, this parameter can be identified with the maximum attainable population mean outcome under individualized treatment rules which rely on some summary of measured covariates, subject to the constraint that a maximum proportion κ of the population can be treated. We also provided an explicit expression for an optimal stochastic rule under the resource constraint.

We derived the canonical gradient of the optimal R-C value under the key assumption that the treatment effect is not exactly equal to τ₀ in some strata of covariates which occurs with positive probability. The canonical gradient plays a key role in developing asymptotically linear estimators. We found that the canonical gradient of the optimal R-C value has an additional component when compared to the canonical gradient of the optimal unconstrained value when the resource constraint is active, i.e. when τ₀ > 0.

We presented a targeted minimum loss-based estimator for the optimal R-C value. This estimator was designed to solve the empirical mean of an estimate of the canonical gradient. This quickly yielded conditions under which our estimator is RAL, and efficient among all such RAL estimators. All of these results rely on the condition that the treatment effect is not exactly equal to τ₀ for positive probability strata of covariates. This assumption is more plausible than the typical non-exceptional law assumption when the covariates are continuous and the constraint is active because it may be unlikely that the treatment effect concentrates on an arbitrary (determined by κ) τ₀ > 0. We note that this pseudo-non-exceptional law assumption has implied that the optimal stochastic rule is almost surely equal to the optimal deterministic rule. Though we have not presented formal theorems here, it is not difficult to derive conditions under which our estimator of the optimal value under a R-C stochastic rule is (root-n) consistent even when the treatment effect is equal to τ₀ with positive probability, though the bias will be non-negligible (converge to zero at the same root-n rate as the variance). One could use an analogue of the variance-stabilized online estimator presented in Luedtke and van der Laan [13] to get inference for the optimal R-C value in this setting.

Our simulations confirmed our theoretical findings. We found that coverage improved with sample size, with near-nominal coverage at the largest sample size considered. This is not surprising given that most of our analytic results were asymptotic, though we note that the method also performed well at the smaller sample sizes considered. The confidence intervals were informatively tight when one considered the difference between the optimal R-C value and the value under no treatment. Further simulations are needed to fully understand the behavior of this method in practice.

Some resource constraints encountered in practice may not be of the form $E_{P_U\times P_0}[d(U,V)]\le \kappa$. For example, the cost of distributing the treatment to people may vary based on the values of the covariates. For simplicity assume V = W. If c : W → [0,∞)is a cost function, then this constraint may take the form $E_{P_U\times P_0}[c(W)d(U,W)]\le \kappa$. If τ₀ = 0, then an optimal stochastic rule under such a constraint takes the form $(u,w)\mapsto I({\overline{Q}}_{b,0}(w)>0)$. If τ₀ > 0, then an optimal stochastic rule under such a constraint takes the form $(u,w)\mapsto I({\overline{Q}}_{b,0}(w)>{\tau }_{0}c(w))$ for w for which ${\overline{Q}}_{b,0}(w)\ne {\tau }_{0}c(w)$ or c(w) = 0, and randomly distributes the remaining resources uniformly among all remaining w. We leave further consideration of this more general resource constraint problem to future work.

In this work our primary focus has been on estimating the optimal value under a resource constraint, rather than the optimal rule under a resource constraint. Nonetheless, our estimation procedure yields an estimate d_n of the optimal R-C rule. It would be interesting to further analyze d_n in future work to better understand how well this estimator will perform, or if there are better estimators which more directly frame the estimation challenge as a (weighted) classification problem [28, 29]. Note that we are not guaranteed that d_n satisfies the constraint, i.e. it is quite possible that $E_{P_U\times P_0}[d_n(U,W)]>\kappa$, though concentration inequalities suggest that one can give conditions under which $E_{P_U\times P_0}[d_n(U,W)]-\kappa$ is small with probability approaching 1. One could also seek an optimal rule estimate $d_n^{\prime }$ which satisfies that, with probability at least 1 — δ for some user-defined δ > 0, $E_{P_{U\times P_0}}[d_n^{\prime }(U,V)]\le \kappa$.

Further work is needed to generalize this work to the multiple time point setting. Before generalizing the procedure, one must know exactly what form the multiple time point constraint takes. For example, it may be the case that only a κ proportion of the population can be treated at each time point, or it may be the case that treatment can only be administered at a κ proportion of patient-time point pairs. Regardless of which constraint one chooses, it seems that the nice recursive structure encountered in Q-learning may not hold for multiple time point R-C problems. While useful for computational considerations, being able to express the optimal rule using approximate dynamic programming is not necessary for the existence of a good optimal rule estimator, especially when the number of time points is small. If the computational complexity of the procedure is a major concern, it may be beneficial to frame the multiple time point learning problem as a single optimization problem, using smooth surrogates for indicator functions as Zhao et al. [30] do when they introduce simultaneous outcome weighted learning (SOWL). One would then need to appropriately account for the fact that the empirical resource constraint may only be approximately satisfied.

We have not considered the ethical considerations associated with allocating limiting resources to a population. The debate over the appropriate means to distribute limited treatment resources to a population is ongoing (see, e.g., Brock and Wilder [31], Macklin and Cowan [32], Singh [33], for examples in the treatment of HIV/AIDS). Clearly any investigator needs to consider the ethical issues associated with certain resource allocation schemes. Our method is optimal in a particular utilitarian sense (maximizing the expected population mean outcome with respect to an outcome of interest) and yields a treatment strategy which treats individuals who are expected to benefit most from treatment in terms of our outcome of interest. One must be careful to ensure that the outcome of interest truly captures the most important public health implications. Unlike in unconstrained individualized medicine, inappropriately prescribing treatment to a stratum will also have implications for individuals outside of that strata, namely for the individuals who do not receive treatment due to its lack of availability. We leave further ethical considerations to experts on the matter. It will be interesting to see if there are settings in which it is possible to transform the outcome or add constraints to the optimization problem so that the statistical problem considered in this paper adheres to the ethical guidelines in those settings.

We have looked to generalize previous works in estimating the value of an optimal individualized treatment regime to the case where the treatment resource is a limited resource, i.e. where it is not possible to treat the entire population. This work should allow for the application of optimal personalized treatment strategies to many new problems of interest.

Appendix: Proofs

Proofs for Section 2

We first state a simple lemma.

Lemma 6

For a distribution P and a stochastic rule d, we have the following representation for Ψ_d:

$${\mathrm{\Psi }}_d(P)\triangleq E_{P_U\times P}[d(U,V){\overline{Q}}_{b,P}(V)]+E_P[{\overline{Q}}_P(0,W)].$$

Proof of Lemma 6. We have that

$$\begin{array}{lll}{\mathrm{\Psi }}_d(P)\hfill & =\hfill & E_{P_U\times P}[d(U,V){\overline{Q}}_P(1,W)]+E_{P_U\times P}[1-d(U,V){\overline{Q}}_P(0,W)]\hfill \\ \hfill & =\hfill & E_{P_U\times P}[d(U,V)({\overline{Q}}_P(1,W)-{\overline{Q}}_P(0,W))]+E_P[{\overline{Q}}_P(0,W)]\hfill \\ \hfill & =\hfill & E_{P_U\times P}[d(U,V)({\overline{Q}}_{b,P}(V)+E_P[{\overline{Q}}_P(0,W)],\hfill \end{array}$$

where the final equality holds by the law of total expectation

Proof of Theorem 1.

This result will be a consequence of Theorem 2. If $P{r}_P({\overline{Q}}_{b,0}(V)={\tau }_P)=0$, then d_P (U, V ) is P_U × P almost surely equal to ${\tilde{d}}_P(V)$, and thus ${\tilde{\mathrm{\Psi }}}_{{\tilde{d}}_P}(P)={\mathrm{\Psi }}_{d_P}(P)$. Thus $(u,v)\mapsto {\tilde{d}}_P(v)$ is an optimal stochastic regime. Because the class of deterministic regimes is a subset of the class of stochastic regimes, ${\tilde{d}}_P$is an optimal deterministic regime.

Proof of Theorem 2.

Let d be some stochastic treatment rule which satisfies the resource constraint. For (b, c) ∈ {0,1}², define $B_{bc}\triangleq \{(u,v):d_P(u,v)=b,d(u,v)=c\}$. Note that

$$\begin{array}{lll}{\mathrm{\Psi }}_{d_P}(P)-{\mathrm{\Psi }}_d(P)\hfill & =\hfill & E_{P_U\times P}[(d_P(U,V)-d(U,V)){\overline{Q}}_{b,0}(V)]\hfill \\ \hfill & =\hfill & E_{P_U\times P}[{\overline{Q}}_{b,0}(V)I((U,V)\in B_{10})]-E_{P_U\times P}[{\overline{Q}}_{b,0}(V)I((U,V)\in B_{01})]\hfill \end{array}$$ (6)

The ${\overline{Q}}_{b,0}(V)$ in the first term in 1 can be upper bounded by τ_Ρ, and in the second term can be lower bounded by τ_Ρ. Thus,

$$\begin{array}{l}{\mathrm{\Psi }}_{d_P}(P)-{\mathrm{\Psi }}_d(P)\ge {\tau }_P[P{r}_{P_U\times P}((U,V)\in B_{10})-P{r}_{P_U\times P}((U,V)\in B_{01})]\\ ={\tau }_P[P{r}_{P_U\times P}((U,V)\in B_{10}\cup B_{11})-P{r}_{P_U\times P}((U,V)\in B_{01}\cup B_{11})]\\ ={\tau }_P(E_{P_U\times P}[d_P(U,V)]-E_{P_U\times P}[d(U,V)]).\end{array}$$

If τ_Ρ = 0 then the final line is zero. Otherwise, $E_{P_U\times P}[d_P(U,V)]=\kappa$ by eq. (4). Because d satisfies the resource constraint, $E_{P_U\times P}[d(U,V)]\le \kappa$ and thus the final line above is at least zero. Thus ${\mathrm{\Psi }}_{d_P}(P)-{\mathrm{\Psi }}_d(P)\ge 0$ for all τ_Ρ. Because d was arbitrary, d_P is an optimal stochastic rule.

Proofs for Section 4

Proof of Theorem 3.

The pathwise derivative of Ψ(Q) is defined as $\frac{d}{d\epsilon }\mathrm{\Psi }(Q(\epsilon )){|}_{\epsilon =0}$ along paths $\{P_{\epsilon }:\epsilon \}\subset \mathcal{M}$. In particular, these paths are chosen so that

$$d{Q}_{W,\epsilon }=(1+\epsilon H_W\left(W\right))d{Q}_W,$$

$$\mathrm{where}E{H}_W\left(W\right)=0\mathrm{and}{C}_W\triangleq \underset{W}{\sup }|H_W(w)|<\infty$$

$$d{Q}_{Y,\epsilon }(Y|A,W)=(1+\epsilon H_Y(Y|A,W))d{Q}_Y(Y|A,W),$$

$$\mathrm{where}E\left(H_Y\right|A,W)=0\mathrm{and}\underset{w,a,y}{\sup }|H_Y(y|a,w)|<\infty$$

The parameter Ψ is not sensitive to fluctuations of g₀(a\w) = Pr₀(a\w), and thus we do not need to fluctuate this portion of the likelihood. Let ${\overline{Q}}_{b,\epsilon }\triangleq {\overline{Q}}_{b,P_{\epsilon }}$, ${\overline{Q}}_{\epsilon }\triangleq {\overline{Q}}_{P_{\epsilon }}$, $d_{\epsilon }\triangleq d_{P_{\epsilon }}$, ${\eta }_{\epsilon }\triangleq {\eta }_{P_{\epsilon }}$, ${\tau }_{\epsilon }\triangleq {\tau }_{P_{\epsilon }}$ and $S_{\epsilon }\triangleq S_{P_{\epsilon }}$. First note that

$${\overline{Q}}_{b,\epsilon }(v)={\overline{Q}}_{b,0}(v)+\epsilon h_{\epsilon }(v)$$ (7)

for an h_ε with

$$\underset{|\epsilon |<1}{\sup }\underset{v}{\sup }|h_{\epsilon }(v)|\triangleq C_1<\infty .$$ (8)

Note that C4) implies that d₀ is (almost surely) deterministic, i.e. d₀(U, ·) is almost surely a fixed function. Let $\tilde{d}$ represent the deterministic rule $v\mapsto I({\overline{Q}}_{b,0}(v)>0)$ to which d(u, ·) is (almost surely) equal for all u. By Lemma 1,

$$\begin{array}{lll}\mathrm{\Psi }(P_{\epsilon })-\mathrm{\Psi }(P_0)\hfill & =\hfill & {\displaystyle {\int }_w\left(E_{P_U}[d_{\epsilon }(U,V)]-{\tilde{d}}_0(V)\right)}{\overline{Q}}_{b,\epsilon }d{Q}_{W,\epsilon }\hfill \\ \hfill & \hfill & +{\displaystyle {\int }_w{\tilde{d}}_0(V)({\overline{Q}}_{b,\epsilon }d{Q}_{W,\epsilon }-{\overline{Q}}_{b,0}d{Q}_{W,0})}\hfill \\ \hfill & \hfill & +E_{P_{\epsilon }}{\overline{Q}}_{\epsilon }(0,W)-E_{P_0}{\overline{Q}}_0(0,W)\hfill \\ \hfill & =\hfill & {\displaystyle {\int }_w\left(E_{P_U}[d_{\epsilon }(U,V)]-{\tilde{d}}_0(V)\right)}({\overline{Q}}_{b,\epsilon }-{\tau }_0)d{Q}_{W,\epsilon }\hfill \\ \hfill & \hfill & +{\tau }_0{\displaystyle {\int }_w\left(E_{P_U}[d_{\epsilon }(U,V)]d{Q}_{W,\epsilon }-{\tilde{d}}_0(V)d{Q}_{W,0}\right)}\hfill \\ \hfill & \hfill & -{\tau }_0{\displaystyle {\int }_w{\tilde{d}}_0(V)(d{Q}_{W,\epsilon }-d{Q}_{W,0})}\hfill \\ \hfill & \hfill & +{\mathrm{\Psi }}_{d_0}(P_{\epsilon })-{\mathrm{\Psi }}_{d_0}(P_0).\hfill \end{array}$$ (9)

Dividing the fourth term by ε and taking the limit as ε → 0 gives the pathwise derivative of the mean outcome under the rule that treats d₀ as known. The third term can be written as $-\epsilon {\tau }_0{\displaystyle {\int }_w{\tilde{d}}_0(V)H_{W}d{Q}_{W,0}}$, and thus the pathwise derivative of this term is $-{\displaystyle {\int }_w{\tau }_0{\tilde{d}}_0(V)H_{W}d{Q}_{W,0}}$. If τ₀ > 0, then $E_{P_U}{{}_{\times }}_{P_0}[{\tilde{d}}_0(V)]=\kappa$. The pathwise derivative of this term is zero if τ₀ = 0. Thus, for all τ₀,

$$\underset{\epsilon \to 0}{\lim }-\frac{1}{\epsilon }{\tau }_0{\displaystyle {\int }_w{\tilde{d}}_0(V)(d{Q}_{W,\epsilon }-d{Q}_{W,0})}={\displaystyle {\int }_w\left(-{\tau }_0({\tilde{d}}_0(v)-\kappa )\right)}{H}_W(w)d{Q}_{W,0}(w).$$

Thus the third term in eq. (9) generates the $v\mapsto -{\tau }_0({\tilde{d}}_0(v)-\kappa )$ portion of the canonical gradient, or equivalently $v\mapsto -{\tau }_0(E_{P_U}[d_0(U,v)]-\kappa )$. The remainder of this proof is used to show that the first two terms in eq. (9) are _o(ε).

Step 1: η_ε→η₀.

We refer the reader to eq. (3) for a definition of the quantile P→n_P. This is a consequence of the continuity of S₀ in a neighborhood of n₀. For γ > 0,

$$|{\eta }_{\epsilon }-{\eta }_0|>\gamma \mathrm{implies}\mathrm{that}{S}_{\epsilon }({\eta }_0+\gamma )\le \kappa \mathrm{or}{S}_{\epsilon }({\eta }_0+\gamma )>\kappa .$$ (10)

For positive constants C₁ and C_w,

$$S_{\epsilon }({\eta }_0-\gamma )\ge (1-C_W|\epsilon |)P{r}_0({\overline{Q}}_{b,\epsilon }>{\eta }_0-\gamma )\ge (1-C_W|\epsilon |)S_0({\eta }_0-\gamma +C_1|\epsilon |).$$

Fix γ > 0 small enough so that S₀ is continuous at n₀ — γ. In this case we have that S₀(η₀ — γ + c₁|ε|) → S₀(η₀ — γ) as ε → 0. By the infimum in the definition of η₀, we know that S₀(η₀ — γ) >κ. Thus S_ε(η₀ — γ) >κ for all |ε| small enough.

Similarly, S_ε(η₀ + γ) ≤ (1 + C_w|ε|) S₀(η₀ + γ — C₁|ε|). Fix γ > 0 small enough so that S₀ is continuous at η₀ + γ. Then S₀(η₀ + γ — C₁|ε|) → S₀(η₀ + γ) as ε → 0. Condition C2) implies the uniqueness of the κ-quantile of ${\overline{Q}}_{b,0}$, and thus that S₀(η₀ + γ) < κ. It follows that S_ε(η₀ + γ) < κ for all |ε| small enough.

Combining S_ε(η₀ — γ) > κ and S_ε(η₀ + γ) < κ for all ε close to zero with eq. (10) shows that η_ε → η₀ as ε → 0.

Step 2: Second term of eq. (9) is 0 eventually.

If τ₀ = 0 then the result is immediate, so suppose τ₀ > 0. By the previous step, η_ε → η₀, which implies that τ_ε → τ₀ > 0 by the continuity of the max function. It follows that τ_ε > 0 for ε large enough. By eq. (4), $P{r}_{P_U\times P_{\epsilon }}\left(d_{\epsilon }\left(U,V\right)=1\right)=\kappa$ for all sufficiently small |ε| and $P{r}_0\left({\tilde{d}}_0\left(V\right)=1\right)=\kappa$ Thus the second term of eq. (9) is 0 for all |ε| small enough.

Step 3: τ_ε - τ₀ = 0(ε).

Note that κ< S_ε(η_ε — |ε|) ≤ (1 + C_w|ε|)S₀(η_ε — (1 + C₁)|ε|). A Taylor expansion of S₀ about η₀ shows that

$$\begin{array}{l}\kappa <(1+C_W|\epsilon |)(S_0({\eta }_0)+({\eta }_{\epsilon }-{\eta }_0-(1+C_1)\left|\epsilon \right|)(-f_0({\eta }_0)+o(1)))\\ \begin{array}{cc}& =\kappa +({\eta }_{\epsilon }-{\eta }_0-(1+C_1)|\epsilon |)(-f_0({\eta }_0)+o(1))\end{array}+O(\epsilon )\\ \begin{array}{cc}& =\kappa -({\eta }_{\epsilon }-{\eta }_0)f_0({\eta }_0)+o({\eta }_{\epsilon }-{\eta }_0)+O(\epsilon )\end{array}.\end{array}$$ (11)

The fact that f₀(η₀) ε (0, ∞) shows that η_ε — η₀ is bounded above by some 0(ε) sequence. Similarly, κ ≥ S(η_ε+|ε|) ≥ (1-C_W|ε|)S₀(η_ε+(1+C₁)|ε|)). Hence,

$$\begin{array}{l}\kappa \ge (1+C_W|\epsilon |)(S_0({\eta }_0)+({\eta }_{\epsilon }-{\eta }_0+(1+C_1)\left|\epsilon \right|)(-f_0({\eta }_0)+o(1)))\\ \begin{array}{cc}& =\kappa -({\eta }_{\epsilon }-{\eta }_0)f_0({\eta }_0)+o({\eta }_{\epsilon }-{\eta }_0)+O(\epsilon )\end{array}.\end{array}$$

It follows that η_ε — η₀ is bounded below by some 0(ε) sequence. Combining these two bounds shows that η_ε — η₀ = 0(ε), which immediately implies that τ_ε — τ₀ = max{0(ε), 0} = 0(ε).

Step 4: First term of eq. (9) is ο(ε).

We know that

$${\overline{Q}}_{b,0}(V)-{\tau }_0+O(\epsilon )\le {\overline{Q}}_{b,\epsilon }(V)-{\tau }_{\epsilon }\le {\overline{Q}}_{b,0}(V)-{\tau }_0+O(\epsilon ).$$

By C4), it follows that there exists some δ>0 such that ${\sup }_{\left|\epsilon \right|<\delta }P{r}_0({\overline{Q}}_{b,\epsilon }(V)={\tau }_{\epsilon })=0$. By the absolute continuity of Q_w,_ε with respect to Q_W,0, ${\sup }_{\left|\epsilon \right|<\delta }P{r}_{P_{\epsilon }}({\overline{Q}}_{b,\epsilon }(V)={\tau }_{\epsilon })=0$ It follows that, for all small enough |ε| and almost all $u,d_{\epsilon }(u,v)=I({\overline{Q}}_{b,\epsilon }(v)>{\tau }_{\epsilon })$ Hence,

$$\begin{array}{l}{\displaystyle {\int }_w\left(E_{P_U}[d_{\epsilon }(U,V)]-d_0(V)\right)}({\overline{Q}}_{b,\epsilon }-{\tau }_0)d{Q}_{W,\epsilon }\\ \begin{array}{cc}& =\left|{\displaystyle {\int }_w(I({\overline{Q}}_{b,\epsilon }>{\tau }_{\epsilon })-I({\overline{Q}}_{b,0}>{\tau }_0))({\overline{Q}}_{b,\epsilon }-{\tau }_0)d{Q}_{W,\epsilon }}\right|\end{array}\\ \begin{array}{cc}& \le {\displaystyle {\int }_w|I({\overline{Q}}_{b,\epsilon }>{\tau }_{\epsilon })-I({\overline{Q}}_{b,0}>{\tau }_0)|(|{\overline{Q}}_{b,0}-{\tau }_0|+C_1|\epsilon |)d{Q}_{W,\epsilon }}\end{array}\\ \begin{array}{cc}& \le {\displaystyle {\int }_{w}I(|{\overline{Q}}_{b,0}>{\tau }_0|\le |{\overline{Q}}_{b,0}-{\tau }_0-{\overline{Q}}_{b,\epsilon }+{\tau }_{\epsilon }|)|(|{\overline{Q}}_{b,0}-{\tau }_0|+C_1\left|\epsilon \right|)d{Q}_{W,\epsilon }}\end{array}\\ \begin{array}{cc}& ={\displaystyle {\int }_{w}I(0<|{\overline{Q}}_{b,0}-{\tau }_0|\le |{\overline{Q}}_{b,0}-{\tau }_0-{\overline{Q}}_{b,\epsilon }+{\tau }_{\epsilon }|)|(|{\overline{Q}}_{b,0}-{\tau }_0|+C_1\left|\epsilon \right|)d{Q}_{W,\epsilon }}\end{array}\\ \begin{array}{cc}& \le O(\epsilon ){\displaystyle {\int }_{w}I(0<|{\overline{Q}}_{b,0}-{\tau }_0|\le |O(\epsilon ))d{Q}_{W,\epsilon }}\end{array}\\ \begin{array}{cc}& \le O(\epsilon )(1+C_W|\epsilon |)\end{array}P{r}_0(0<|{\overline{Q}}_{b,0}-{\tau }_0|\le O(\epsilon )),\end{array}$$

where the penultimate inequality holds by Step 3 and eq. (7). The last line above is ο(ε) because Pr(0 < X ≤ ε) → 0 as ε → 0 for any random variable X. Thus dividing the left-hand side above byε and taking the limit as ε → 0 yields zero.

Proofs for Section 5

We give the following lemma before proving Theorem 4.

Lemma 7

Let P₀ and P be distributions which satisfy the positivity assumption and for which Y is bounded in probability. Let d be some stochastic treatment rule and τ be some real number. We have that Ψ_d(P) - Ψ(P₀)= -EP₀ [D(d, τ₀, P)(O)]+ R₀(d, P).

Proof of Lemma 12. Note that

$$\begin{array}{l}{\mathrm{\Psi }}_d(P)-\mathrm{\Psi }(P_0)+E_{P_0}[D(d,{\tau }_0,P)(O)]\\ \begin{array}{cc}& =\end{array}{\mathrm{\Psi }}_d(P)-{\mathrm{\Psi }}_d(P_0)+{\displaystyle \sum _{j=1}^2{E}_{P_U\times P_0}}[D_j(d(U,\cdot ),P)(O)]\\ \begin{array}{ccc}& & +\end{array}{\mathrm{\Psi }}_d(P_0)-{\mathrm{\Psi }}_{d_0}(P_0)-{\tau }_0{E}_{P_U\times P_0}[d(U,V)-\kappa ].\end{array}$$

Standard calculations show that the first term on the right is equal to R₁₀(d,P) [21]. If τ₀> 0, then eq. (4) shows that ${\tau }_0{E}_P{}_{{}_U\times P_0}\left[d-\kappa \right]={\tau }_0{E}_P{}_{{}_U\times P_0}[(d-d_0){\overline{Q}}_{b,0}]$. If τ₀ = 0, then obviously τEp_UxP0[d — κ] = τ₀E_pUxP0[d — d₀] Lemma 1 shows that ${\mathrm{\Psi }}_d(P_0)-{\mathrm{\Psi }}_{d_0}(P_0)=E_P{}_{{}_U\times P_0}[(d-d_0){\overline{Q}}_{b,0}]$. Thus the second line above is equal to ^R20^(d).

Proof of Theorem 4.

We make use of empirical process theory notation in this proof so that Pf = E_P [f (O)] for a distribution P and function f. We have that

$$\widehat{\mathrm{\Psi }}(P_n)-\mathrm{\Psi }(P_0)=-P_{0}D(d_n,{\tau }_0,P_n^{*})+R_0(d_n,P_n^{*})$$ (12)

$$=(P_n-P_0)D(d_n,{\tau }_0,P_n^{*})+R_0(d_n,P_n^{*})+o_{P_0}(n^{-1/2})$$

$$=(P_n-P_0)D_0+(P_n-P_0)(D(d_n,{\tau }_0,P_n^{*})-D_0)+R_0(d_n,P_n^{*}).$$ (13)

The middle term on the last line is $o_{P_0}(n^{-1/2})$ by 1, 2, 4, and 5 [25], and the third term is $o_{P_0}(n^{-1/2})$ by 3. This yields the asymptotic linearity result. Proposition 1 in Section 3.3 of Bickel et al. [23] yields the claim about regularity and asymptotic efficiency when conditions C2), C3), C4), and 1 hold (see Theorem 3).

Proof of Lemma 5.

We will show that η_η → η₀ in probability, and then the consistency of τ_n follows by the continuous mapping theorem. By C3), there exists an open interval N containing η₀ on which S₀ is continuous. Fix η ε N. Because ${\overline{Q}}_{b,n}$ belongs to a Glivenko-Cantelli class with probability approaching 1, we have that

$$\begin{array}{lll}|S_n(\eta )-S_0(\eta )|\hfill & =\hfill & |P_{n}I({\overline{Q}}_{b,n}>\eta )-P_{0}I({\overline{Q}}_{b,0}>\eta )|\hfill \\ \hfill & \le \hfill & |P_0(I({\overline{Q}}_{b,n}>\eta )-I({\overline{Q}}_{b,0}>\eta ))|+(P_n-P_0)I({\overline{Q}}_{b,n}>\eta )|\hfill \\ \hfill & \le \hfill & \underset{\triangleq T_n(\eta )}{\underbrace{|P_0(I({\overline{Q}}_{b,n}>\eta )-I({\overline{Q}}_{b,0}>\eta ))|}}+o_P{}_{{}_0}(1),\hfill \end{array}$$ (14)

where we use the notation Pf = E_P [f (O)] for any distribution P and function f. Let $Z_n(\eta )(w)\triangleq {(I({\overline{Q}}_{b,n}(w)>\eta )-I({\overline{Q}}_{b,0}(w)>\eta ))}^2$. The following display holds for all q> > 0:

$$\begin{array}{lll}{T}_n(\eta )\hfill & \le \hfill & P_0{Z}_n(\eta )\hfill \\ \hfill & =\hfill & P_0{Z}_n(\eta )I(|{\overline{Q}}_{b,0}-\eta |>q)+P_0{Z}_n(\eta )I(|{\overline{Q}}_{b,0}-\eta |\le q)\hfill \\ \hfill & =\hfill & P_0{Z}_n(\eta )I(|{\overline{Q}}_{b,0}-\eta |>q)+P_0{Z}_n(\eta )I(0<|{\overline{Q}}_{b,0}-\eta |\le q)\hfill \end{array}$$ (15)

$$\le P_0{Z}_n(\eta )I(|{\overline{Q}}_{b,0}-{\overline{Q}}_{b,0}|>q)+P_0{Z}_n(\eta )I(0<|{\overline{Q}}_{b,0}-\eta |\le q)$$ (16)

$$\le P{r}_0(|{\overline{Q}}_{b,n}-{\overline{Q}}_{b,0}|>q)+P{r}_0(0<|{\overline{Q}}_{b,0}-\eta |\le q)$$

$$\le \frac{P_0|{\overline{Q}}_{b,n}-{\overline{Q}}_{b,0}|}{q}+P{r}_0(0<|{\overline{Q}}_{b,0}-\eta |\le q).$$

Above eq. (15) holds because C3) implies that $P{r}_0({\overline{Q}}_{b,0}=\eta )=0$ eq. (16) holds because Ζ_η(η) = 1 implies that $|{\overline{Q}}_{b,n}-{\overline{Q}}_{b,0}|\ge |{\overline{Q}}_{b,0}-\eta |$ and the final inequality holds by Markov’s inequality. The lemma assumes that $E_{P_0}|{\overline{Q}}_{b,n}-{\overline{Q}}_{b,0}|=O_{P_0}(1)$, and thus we can choose a sequence q_n ↓ 0 such that

$$T_n(\eta )\le P{r}_0(0<|{\overline{Q}}_{b,0}-\eta |\le q_n)+o_P{}_{{}_0}(1).$$

To see that the first term on the right is o(1), note that $P{r}_0({\overline{Q}}_{b,0}=\eta )=0$ combined with the continuity of S₀ on N yield that, for n large enough,

$$P{r}_0(0<|{\overline{Q}}_{b,0}-\eta |\le q_n)=S_0(-q_n+\eta )-S_0(q_n+\eta ).$$

The right-hand side is 0(1), and thus $T_n(\eta )=o_{P_0}(1)$. Plugging this into eq. (14) shows that S_n(η) → S₀(η) in probability. Recall that η € N was arbitrary.

Fix γ > 0. For γ small enough, η₀ — γ and η₀ + γ are contained in N. Thus S_n(η₀ — γ) → S₀(η₀ + γ) and S_n(η₀ + γ) → S₀(η₀ - γ) in probability. Further, S₀(η₀ - γ) > k by the definition of η₀ and S₀(η₀ + γ) < κ by Condition C2). It follows that, with probability approaching 1, S_n(η₀ — γ) >κ and S_n(η₀ + γ) < κ. But |η_n — η₀| > γ implies that S₀(η₀ - γ)— γ) ≤ κ or S_n(η₀ + γ) > κ, and thus |η_n —η₀| γ with probability approaching 1. Thus η_n → η₀ in probability, and τ_n → τ₀ by the continuous mapping theorem.

Proof of Theorem 6.

This proof mirrors the proof of Lemma 5.2 in Audibert and Tsybakov [24]. It is also quite similar to the proof of Theorem 7 in Luedtke and van der Laan [13], though the proof given in that working technical report is for optimal rules without any resource constraints, and also contains several typographical errors which will be corrected in the final version.

Define B_n to be the function $v\mapsto {\overline{Q}}_{b,n}(v)-{\tau }_n$ and B₀ to be the function $v\mapsto {\overline{Q}}_{b,0}(v)-{\tau }_0$. Below we omit the dependence of B_n, B₀ on V in the notation and of d_n, d₀ on U and V. For any t> 0, we have that

$$\begin{array}{lll}|R_{20}(d_n)|\hfill & \le \hfill & E_{P_{U\times P_0}}[|(d_n-d_0)B_0|]\hfill \\ \hfill & =\hfill & E_{P_U\times P_0}[I(d_n\ne d_0)B_0]\hfill \\ \hfill & =\hfill & E_{P_U\times P_0}[I(d_n\ne d_0)|B_0|I(0<\left|B_0\right|\le t)]+E_{P_U\times P_0}[I(d_n\ne d_0)|B_0|I(\left|B_0\right|>t)]\hfill \\ \hfill & \le \hfill & E_{P_{{}_0}}[|B_n-B_0|I(0<\left|B_0\right|\le t)]+E_{P_{{}_0}}[|B_n-B_0|I(|B_n-B_0|\le t)]\hfill \\ \hfill & \le \hfill & \left|\right|B_n-B_0|{|}_{2,P_0}P{r}_0{(0<|B_0|\le t)}^{1/2}+\frac{\left|\right|B_n-B_0|{|}_{2,P_0}^2}{t}\hfill \\ \hfill & \le \hfill & \Vert B_n-B_0{\Vert }_{2,P_0}{C}_0^{1/2}{t}^{\alpha /2}+\frac{\Vert B_n-B_0{\Vert }_{2,P_0}^2}{t}\hfill \end{array}$$

where the second inequality holds because d_n ≠ d₀ implies that |B_n — B₀| > |B₀| when |B₀| > 0, the third inequality holds by the Cauchy-Schwarz and Markov inequalities, and the C0 on the final line is the constant implied by eq. (5). The first result follows by plugging $t=\Vert B_n-B_0{\Vert }_{2,P_0}^{2/(2+\alpha )}$ into the upper bound above. We also have that

$$\begin{array}{lll}|R_{20}(d_n)|\hfill & \le \hfill & E_{P_U\times P_0}[I(d_n\ne d_0)|B_0|]\hfill \\ \hfill & \le \hfill & E_{P_0}[I(0\left|B_0\right|\le |B_n-B_0|)|B_0|]\hfill \\ \hfill & \le \hfill & E_{P_0}[I(0<\left|B_0\right|\le \Vert B_n-B_0{\Vert }_{\infty ,P_0})|B_0|]\hfill \\ \hfill & \le \hfill & \Vert B_n-B_0{\Vert }_{\infty ,P_0}P{r}_0\left(0<\left|B_0\right|\le \Vert B_n-B_0{\Vert }_{\infty ,P_0}\right).\hfill \end{array}$$

By eq. (5), it follows that $|R_{20}(d_n)\lesssim \Vert B_n-B_0{\Vert }_{\infty ,P_0}^{1+\alpha }$