Error Variance Estimation in Ultrahigh-Dimensional Additive Models

Abstract

Error variance estimation plays an important role in statistical inference for high dimensional regression models. This paper concerns with error variance estimation in high dimensional sparse additive model. We study the asymptotic behavior of the traditional mean squared errors, the naive estimate of error variance, and show that it may significantly underestimate the error variance due to spurious correlations which are even higher in nonparametric models than linear models. We further propose an accurate estimate for error variance in ultrahigh dimensional sparse additive model by effectively integrating sure independence screening and refitted cross-validation techniques (Fan, Guo and Hao, 2012). The root n consistency and the asymptotic normality of the resulting estimate are established. We conduct Monte Carlo simulation study to examine the finite sample performance of the newly proposed estimate. A real data example is used to illustrate the proposed methodology.

1 Introduction

Statistical inference on regression models typically involves the estimation of the variance of its random error. Hypothesis testing on regression functions, confidence/prediction interval construction and variable selection all require an accurate estimate of the error variance. In the classical linear regression analysis, the adjusted mean squared error is an unbiased estimate of the error variance, and it performs well when the sample size is much larger than the number of predictors, or more accurately when the degree of freedom is large. It has been empirically observed that the mean squared error estimator leads to an underestimation of the error variance when model is significantly over-fitted. This has been further confirmed by the theoretical analysis of Fan, Guo and Hao (2012), in which the authors demonstrated the challenges of error variance estimation in the high-dimensional linear regression analysis, and further developed an accurate error variance estimator by introducing refitted cross-validation techniques.

Fueled by the demand in the analysis of genomic, financial, health, and image data, the analysis of high dimensional data has become one of the most important research topics during last two decades (Donoho, 2000; Fan and Li, 2006). There have been a huge number of research papers on high dimensional data analysis in the literature. It is impossible for us to give a comprehensive review here. Readers are referred to Fan and Lv (2010), Bühlmann and Van de Geer (2011) and references therein. Due to the complex structure of high dimensional data, the high dimensional linear regression analysis may be a good start, but it may not be powerful to explore nonlinear features inherent into data. Nonparametric regression modeling provides valuable analysis for high dimensional data (Ravikumar, et al. 2009; Hall and Miller, 2009; Fan, Feng and Song, 2011). This is particularly the case for error variance estimation, as nonparametric modeling reduces modeling biases in the estimate, but creates stronger spurious correlations. This paper aims to study issues of error variance estimation in ultrahigh dimensional nonparametric regression settings.

In this paper, we focus on sparse additive model. Our primary interest is to develop an accurate estimator for error variance in ultrahigh dimensional additive model. The techniques developed in this paper are applicable to other nonparametric regression models such as sparse varying coefficient models and some commonly-used semiparametric regression models such as sparse partial linear additive models and sparse semi-varying coefficient partial linear models. Since its introduction by Friedman and Stuetzle (1981), additive model has been popular, and many statistical procedures have been developed for sparse additive models in the recent literature. Lin and Zhang (2006) proposed COSSO method to identify significant variables in multivariate nonparametric models. Bach (2008) studied penalized least squares regression with group Lasso-type penalty for linear predictors and regularization on reproducing kernel Hilbert space norms, which is referred to as multiple kernel learning. Xue (2009) studied variable selection problem in additive models by integrating a group-SCAD penalized least squares method (Fan and Li, 2001) and the regression spline technique. Ravikumar, et. al. (2009) modified the backfitting algorithm for sparse additive models, and further established the model selection consistency of their procedure. Meier, Van de Geer and Bühlmann (2009) studied the model selection and estimation of additive models with a diverging number of significant predictors. They proposed a new sparsity and smoothness penalty and proved that their method can select all nonzero components with probability approaching to 1 as the sample size tends to infinity. With the ordinary group Lasso estimator as the initial estimator, Huang, Horowitz and Wei (2010) applied adaptive group Lasso to additive model under the setting in which there are only finite fixed number of significant predictors. Fan, Feng and Song (2011) proposed a nonparametric independent screening procedure for sparse ultrahigh dimensional data, and established its sure screening property in the terminology of Fan and Lv (2008).

In this paper, we propose an error variance estimate in ultrahigh dimensional additive models. It is typical to assume sparsity in ultrahigh dimensional data analysis. By sparsity, it means that the regression function depends only on a few significant predictors, and the number of significant predictors is assumed to be much smaller than the sample size. Because of the basis expansion in nonparametric fitting, the actual number of terms significantly increases in additive models. Therefore, the spurious correlation documented in Fan, Guo and Hao (2012) increases significantly. This is indeed demonstrated in Lemma 1, which shows that the spurious correlation with the response increases from $\sqrt{n^{-1}log(p)}$ using one most correlated predictor among p variables to $\sqrt{d_n{n}^{-1}log(p{d}_n)}$ by using one most correlated predictor with d_n basis functions. If s variables are used, the spurious correlation may increase to its upper bound at an exponential rate of s.

To quantify this increase and explain more clearly the concept and the problem, we simulate n = 50 data points from the independent normal covariates ${\{X_j\}}_{j=1}^p$ (with p = 1000) and also independently normal response Y . In this null model, all covariates ${\{X_j\}}_{j=1}^p$ and the response Y are independent and follow the standard normal distribution. As in Fan, Guo and Hao (2012), we compute the maximum “linear” spurious correlation ${\zeta }_n^L={max}_{1\le j\le p}\mid \widehat{\text{corr}}(X_j,Y)\mid$ and the maximum “nonparametric” spurious correlation ${\zeta }_n^N={max}_{1\le j\le p}\mid \widehat{\text{corr}}({\widehat{f}}_j(X_j),Y)\mid$, where f̂_j(X_j) is the best cubic spline fit of variable X_j to the response Y , using 3 equally spaced knots in the range of the variable X_j which create d_n = 6 B-spline bases for X_j . The concept of the maximum spurious “linear” and spurious “nonparametric” (additive) correlations can easily be extended to s variables, which are the correlation between the response and fitted values using the best subset of s-variables. Based on 500 simulated data sets, Figure 1 depicts the results, which show the big increase of spurious correlations from linear to nonparametric fit. As the result, the noise variance is significantly underestimated.

Figure 1.

Distributions of the maximum “linear” and “nonparametric” spurious correlations for s = 1 and s = 2 (left panel, n = 50 and p = 1000) and their consequences on the estimating of noise variances (right panel). The legend ‘LM’ stands for linear model, and ‘AM’ stands for additive model, i.e., nonparametric model.

The above reasoning and evidence show that the naive estimation of error variance is seriously biased. This is indeed shown in Theorem 1. This prompts us to propose a two-stage refitted cross-validation procedure to reduce spurious correlation. In the first stage, we apply a sure independence screening procedure to reduce the ultrahigh dimensionality to relative large dimensional regression problem. In the second stage, we apply refitted cross validation technique, which was proposed for linear regression model by Fan, Guo and Hao (2012), for the dimension-reduced additive models obtained from the first stage. The implementation of the newly proposed procedure is not difficult. However, it is challenging in establishing its sampling properties. This is because the dimensionality of ultrahigh dimensional sparse additive models becomes even higher.

We propose using B-splines to approximate the nonparametric functions, and first study the asymptotic properties of the traditional mean squared error, a naive estimator of the error variance. Under some mild conditions, we show that the mean squared error leads to a significant underestimate of the error variance. We then study the sampling properties of the proposed refitted cross-validation estimate, and establish its asymptotic normality. From our theoretical analysis, it can be found that the refitted cross-validation techniques can eliminate the side effects due to over-fitting. We also conduct Monte Carlo simulation studies to examine the finite sample performance of the proposed procedure. Our simulation results show that the newly proposed error variance estimate may perform significantly better than the mean squared error.

This paper makes the following major contributions. (a) We show the traditional mean squared errors as a naive estimation of error variance is seriously biased. Although this is expected, the rigorous theoretical development indeed is challenging rather than straightforward. (b) We propose a refitted cross-validation error variance estimation for ultrahigh dimensional nonparametric additive models, and further establish the asymptotic normality of the proposed estimator. The asymptotic normality implies that the proposed estimator is asymptotic unbiased and root n consistent. The extensions of refitted cross-validation error variance estimation from linear models to nonparametric models are interesting, and not straightforward in terms of theoretical development because the bias due to approximation error calls for new techniques to establish the theory. Furthermore, the related techniques developed in this paper may be further applied for refitted cross-validation error variance estimation in other ultrahigh-dimensional nonparametric regression models such as varying coefficient models and ultrahigh dimensional semiparametric regression models such as partially linear additive models and semiparametric partially linear varying coefficient models.

This paper is organized as follows. In Section 2, we propose a new error variance estimation procedure, and further study its sampling properties. In Section 3, we conduct Monte Carlo simulation studies to examine the finite sample performance of the proposed estimator, and demonstrate the new estimation procedure by a real data example. Some concluding remarks are given in Section 4. Technical conditions and proofs are given in the Appendix.

2 New procedures for error variance estimation

Let Y be a response variable, and x = (X₁; ⋯ , X_p)^T be a predictor vector. The additive model assumes that

$$Y=\mu +\sum _{j=1}^p{f}_j(X_j)+\epsilon ,$$ (2.1)

where μ is intercept term, {f_j(·), j = 1, ⋯ , p} are the unknown functions and ε is the random error with E(ε) = 0 and var(ε) = σ². Following the convention in the literature, it is assumed throughout this paper that Ef_j(X_j) = 0 for j = 1, ⋯ , p so that model (2.1) is identifiable. This assumption implies that μ = E(Y ). Thus, a natural estimator for μ is the sample average of Y’s. This estimator is root n consistent, and its rate of convergence is faster than that for the estimator of nonparametric function f_j’s. Without loss of generality, we further assume μ = 0 for ease of notation. The goal of this section is to develop an estimation procedure for σ² for additive models.

2.1 Refitted cross-validation

In this section, we propose a strategy to estimate the error variance when the predictor vector is ultrahigh dimensional. Since f_j’s are nonparametric smoothing functions, it is natural to use smoothing techniques to estimate f_j . In this paper, we employ B-spline method throughout this paper. Readers are referred to De Boor (1978) for detailed procedure of B-spline construction. Let {B_jk(x), k = 1, ⋯ , d_j , a ≤ x ≤ b} be B-spline basis of space ${\mathcal{S}}_j^l([a,b])$ with knots depending on j, the polynomial spline space defined on finite interval [a, b] with degree l ≥ 1. Approximate f_j by its spline expansion

$$f_j(x)\approx \sum _{k=1}^{d_j}{\gamma }_{jk}{B}_{jk}(x)$$ (2.2)

for some d_j ≥ 1. In practice, d_j is allowed to grow with the sample size n, and therefore denoted by d_jn to emphasize the dependence of n. With slightly abuse of notation, we use d_n stands for d_jn for ease of notation. Thus, model (2.1) can be written as

$$Y\approx \sum _{j=1}^p\sum _{k=1}^{d_n}{\gamma }_{jk}{B}_{jk}(X_j)+\epsilon ,$$ (2.3)

Suppose that {(x_i, Y_i)}, i = 1, ⋯ , n is a random sample from the additive model (2.1). Model (2.3) is not estimable when pd_n > n. It is common to assume sparsity in ultrahigh-dimensional data analysis. By sparsity in additive model, it means that only a few ${\Vert f_j\Vert }^2=E{f}_j^2(X_j)\ne 0$ and other ||f_j|| = 0. A general strategy to reduce ultrahigh dimensionality is sure independent feature screening, which enables one to reduce ultrahigh dimension to large or high dimension. Some existing feature screening procedures can be directly applied for ultrahigh dimensional sparse additive models. Fan, Feng and Song (2011) proposed nonparametric sure independent (NIS) screening method and further showed that the NIS screening method possesses sure screening property for ultrahigh dimensional additive models. That is, under some regularity conditions, with an overwhelming probability, the NIS is able to retain all active predictors after feature screening. Li, Zhong and Zhu (2012) proposed a model free feature screening procedure based on distance correlation sure independent screening (DC-SIS). The DC-SIS is also shown to have sure screening property. Both NIS and DC-SIS can be used for feature screening with ultrahigh dimensional sparse additive models, although we will use DC-SIS in our numerical implementation due to its intuitive and simple implementation.

Hereafter we always assume that all important variables have been selected by screening procedure. Under such assumption, we will overfit the response variable Y and underestimate the error variance σ². This is due to the fact that extra variables are actually selected to predict the realized noises (Fan, Guo and Hao, 2012). After feature screening, a direct estimate of σ² is the mean squared errors of the least squares approach. That is, we apply a feature screening procedure such as DC-SIS and NIS to screen x-variables and fit the data to the corresponding selected spline regression model. Denoted by 𝒟^* the indices of all true predictors and 𝒟̂^* the indices of the selected predictors respectively, satisfying the sure screening property 𝒟^* ⊂ 𝒟̂^*. Then, we minimize the following least squares function with respect to γ:

$$\sum _{i=1}^n{\left\{Y_i-\sum _{j\in {\widehat{\mathcal{D}}}^{\ast }}\sum _{k=1}^{d_n}{\gamma }_{jk}{B}_{jk}(X_{ij})\right\}}^2.$$ (2.4)

Denote by γ̂_jk the resulting least squares estimate. Then, the nonparametric residual variance estimator is

$${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2=\frac{1}{n-\mid {\widehat{\mathcal{D}}}^{\ast }\mid ·d_n}\sum _{i=1}^n{\left\{Y_i-\sum _{j\in {\widehat{\mathcal{D}}}^{\ast }}\sum _{k=1}^{d_n}{\widehat{\gamma }}_{jk}{B}_{jk}(X_{ij})\right\}}^2.$$

Hereafter |𝒟| stands for the cardinality of a set 𝒟 and we have implicitly assumed that the choice of 𝒟̂^* and d_n is such that n ≫ | 𝒟̂^*| · d_n. It will be shown in Theorem 1 below that ${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2$ significantly underestimates σ², due to spurious correlation between the realized but unobserved noises and the spline bases. Indeed we will show that ${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2$ is inconsistent estimate when | 𝒟̂^*| · d_n is large. Specifically, let P_𝒟̂^* be the corresponding projection matrix of model (2.4) with the entire samples. Denoted by ${\widehat{\gamma }}_n^2={\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}\mathit{\epsilon }/{\mathit{\epsilon }}^T\mathit{\epsilon }$, where ε = (ε₁, ⋯ , ε_n)^T . We will show that ${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2/(1-{\widehat{\gamma }}_n^2)$ converges to σ² with root n convergence rate, yet the spurious correlation ${\widehat{\gamma }}_n^2$ is of order

$${\widehat{\gamma }}_n^2=O\left({\left(\frac{2}{1-\delta }\right)}^{\mid {\widehat{\mathcal{D}}}^{\ast }\mid }\frac{d_{n}log(p{d}_n)}{n}\right),\text{for}\text{some}\delta \in (0,1).$$ (2.5)

See Lemma 1 and Theorem 1 in Section 2.2 for details. Our first aim is to propose a new estimation procedure of σ² by using refitted cross-validation technique (Fan, Guo and Hao, 2012).

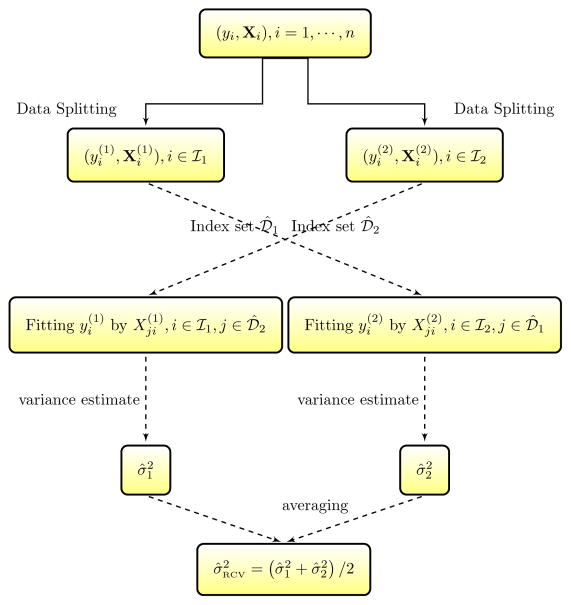
The refitted cross-validation procedure is to randomly split the random samples into two data sets denoted by ℐ₁ and ℐ₂ with approximately equal size. Without loss of generality, assume through this paper that ℐ₁ and ℐ₂ have the same sample size n/2. We apply a feature screening procedure (e.g., DC-SIS or NIS) for each set, and obtain two index sets of selected x-variables, denoted by 𝒟̂₁ and 𝒟̂₂. Both of them retain all important predictors. The refitted cross-validation procedure consists of three steps. In the first step, we fit data in ℐ_l to the selected additive model 𝒟̂_3−l for l = 1 and 2 by the least squares method. These results in two least squares estimate γ̂^(3−l) based on ℐ_l, respectively. In the second step, we calculate the mean squared errors for each fit:

$${\widehat{\sigma }}_l^2=\frac{1}{n/2-\mid {\widehat{\mathcal{D}}}_{3-l}\mid ·d_n}\sum _{i\in {\mathcal{I}}_l}{\left\{Y_i-\sum _{j\in {\widehat{\mathcal{D}}}_{3-l}}\sum _{k=1}^{d_n}{\widehat{\gamma }}_{jk}^{(3-l)}{B}_{jk}(X_{ij})\right\}}^2$$

for l = 1 and 2. Then the refitted cross-validation estimate of σ² is defined by

$${\widehat{\sigma }}_{\text{RCV}}^2=({\widehat{\sigma }}_1^2+{\widehat{\sigma }}_2^2)/2.$$

This estimator is adapted from the one proposed in Fan, Guo and Hao (2012) for linear regression models, however, it is much more challenge in establishing the asymptotic property of ${\widehat{\sigma }}_{\text{RCV}}^2$ for the large dimensional additive models than that for linear regression models. The major hurdle is to deal with the approximation error in nonparametric modeling as well as the correlation structure induced by the B-spline bases. The procedure of refitted cross validation is illustrated schematically in Figure 2.

Figure 2.

Refitted Cross Validation Procedure

2.2 Sampling properties

We next study the asymptotic properties of ${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2$ and ${\widehat{\sigma }}_{\text{RCV}}^2$. The following technical conditions are needed to facilitate the proofs, although they may not be the weakest.

• (C1)There exist two positive constants A₁ and A₂ such that E {exp(A₁ |ε|)|x}≤ A₂.
• (C2)
  For all j, f_j(·) ∈ 𝒞^d ([a, b]), which consists of functions whose r-th derivative $f_j^{(r)}$ exists and satisfies

  $$\left|f_j^{(r)}(s)-f_j^{(r)}(t)\right|\le L{\mid s-t\mid }^{\alpha },\text{for}s,t\in [a,b],j=1,\cdots ,p,$$ (2.6)

• for a given constant L > 0, where r ≤ l is the “integer part” of d and α ∈ (0, 1] such that d = r+α ≥ 2. Furthermore, it is assumed that d_n = O(n^1/(2d+1)), the optimal nonparametric rate (Stone, 1985).

• (C3)The joint distribution of predictors X is absolutely continuous and its density g is bounded by two positive numbers b and B satisfying that b ≤ g ≤ B. The predictor X_j , j = 1, ⋯ , p has a continuous density function g_j , which satisfies that for any x ∈ [a, b], 0 < A₃ ≤ g_j(x) ≤ A₄ < ∞ for two positive constants A₃ and A₄.

Condition (C1) is a tail condition on the random error. Condition (C2) is a typical smoothness condition in the literature of regression splines. Condition (C3) is a mild condition on the densities of the predictors, and this condition was imposed in Stone (1985) for low-dimensional additive models, and implies that there is no collinearity between the candidate predictors with probability one. The asymptotic properties of ${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2$ are given in the following theorem, in which we use p_n to stand for p to emphasize that the dimension p of the predictor vector may depend on n. Since the DC-SIS and the NIS possess sure screening property, the resulting subset of predictors selected by the utilized screening procedure contains all active predictors, with probability tending to one. Thus, we assume that all active predictors are retained in the stage of feature screening in the following two theorems. This can be achieved by imposing the conditions in Li, Zhong and Zhu (2012) for the DC-SIS and the conditions in Fan, Feng and Song (2011) for the NIS. We first derive the orders of ε^TP_𝒟̂^*ε and ${\widehat{\gamma }}_n^2$ in next lemma, which plays a critical role in the proofs of Theorems 1 and 2 below. The proofs of Lemma 1 and Theorems 1 and 2 will be given in the Appendix.

Lemma 1

Under Conditions (C1)—(C3), it follows that

$${\mathit{\epsilon }}^T{\mathbf{P}}_{\widehat{\mathcal{D}}\ast }\mathit{\epsilon }=O_p\left\{{\left(\frac{2}{1-\delta }\right)}^{\widehat{s}}{d}_{n}log(p{d}_n)\right\},\text{and}{\widehat{\gamma }}_n^2=\frac{{\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}\mathit{\epsilon }}{{\mathit{\epsilon }}^T\mathit{\epsilon }}=O_p\left\{{\left(\frac{2}{1-\delta }\right)}^{\widehat{s}}\frac{d_{n}log(p{d}_n)}{n}\right\},$$

where $\delta \in (\sqrt{1-b^2{\zeta }_0/B^2},1)$ for some constant ζ₀ ∈ (0, 1) with b and B being given in Condition (C3).

Lemma 1 clearly shows that the spurious correlation ${\widehat{\gamma }}_n^2$ increases to its upper bound at an exponential rate of ŝ since δ ∈ (0, 1) and 2/(1 − δ) > 2.

Theorem 1

Assume that $lim{sup}_{n\to \infty }{\widehat{\gamma }}_n^2<1$. Let ŝ = |𝒟̂^*| be the number of elements in the estimated active index set 𝒟̂^*. Assume that all active predictors are retained in the stage of feature screening. That is, 𝒟̂^* contains all active predictors. Under Conditions (C1)–(C3), the following statements hold:

1. If log(p_n) = O(n ^ζ), 0 ≤ ζ < 1 and ŝ = O_p(log(n)), then ${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2/(1-{\widehat{\gamma }}_n^2)$ converges to σ² in probability as n → ∞;

2. If log(p_n) = O(n ^ζ), 0 ≤ ζ < 3/(2d + 1) and ŝ = O_p(log(n)), then it follows that

   $$\sqrt{n}\left({\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2/(1-{\widehat{\gamma }}_n^2)-{\sigma }^2\right)\stackrel{\mathcal{L}}{\to }\mathcal{N}(0,\mathrm{E}{\epsilon }_1^4-{\sigma }^4),$$ (2.7)

   where $\stackrel{\mathcal{L}}{\to }$ stands for convergence in law.

Theorem 1 (i) clearly indicates that the naive error variance estimator ${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2$ underestimates σ² by a factor of ( $1-{\widehat{\gamma }}_n^2$), yet by Lemma 1, ${\widehat{\gamma }}_n^2$ is of order given in (2.5) and is not small. Since ${\widehat{\gamma }}_n^2$ can not be estimated directly from the data, it is challenging to derive an adjusted error variance by modifying the commonly-used mean squared errors. On the other hand, the refitted cross-validation method provides an automatic bias correction via refitting and hence a consistent estimator, as we now show.

Theorem 2

Assume that ${\widehat{\mathcal{D}}}_j^{\ast }$ contains all active predictors, for j = 1 and 2. Let ${\widehat{s}}_j=\mid {\widehat{\mathcal{D}}}_j^{\ast }\mid$ be the number of elements in ${\widehat{\mathcal{D}}}_j^{\ast }$. Under Conditions (C1)–(C3), if ŝ₁ = o(n^{(2d−1)/4(2d+1)}), and ŝ₂ = o(n^{(2d−1)/4(2d+1)}), then

$$\sqrt{n}({\widehat{\sigma }}_{\text{RCV}}^2-{\sigma }^2)\stackrel{\mathcal{L}}{\to }\mathcal{N}(0,\mathrm{E}{\epsilon }_1^4-{\sigma }^4)$$ (2.8)

Comparing with the result in the theorem 1, the refitted cross-validation method can eliminate the side-effect of the selected redundant variables to correct the bias of the naive variance estimator through the contributions of refitting. This bias factor can be non-trivial.

Remark 1

This remark provides some implications and limitations of Theorems 1 and 2 and some clarification of conditions implicitly required by Theorem 2.

1. From the proof of Theorems 1 and 2, it has been shown that ${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2/(1-{\widehat{\gamma }}_n^2)={\sigma }^2+O_p(1/\sqrt{n})$ and ${\widehat{\sigma }}_{\text{RCV}}^2={\sigma }^2+O_p(1/\sqrt{n})$. As a result, the ratio of RCV estimate to the naive estimator may be used to provide one an estimate of the shrinkage factor $1-{\widehat{\gamma }}_n^2$.

2. Theorem 2 is applicable provided that the active index sets ${\widehat{\mathcal{D}}}_j^{\ast }$, j = 1 and 2 include all active predictor variables. Here we emphasize that the RCV method can be integrated with any dimension reduction procedure to effectively correct the bias of naive error variance estimate, and do not directly impose condition on the dimension p_n. In practical implementation, the assumption that both two active index sets include all important variables implies further condition on p_n. In particular, the condition log(p_n) = o(n) is necessary for DC-SIS (Li, Zhong and Zhu, 2012) to achieve sure screening property. This condition is also necessary for other sure screening procedures such as the NIS (Fan, Feng and Song, 2011) to achieve sure screening property. In Theorems 1 and 2, we have imposed conditions on ŝ, ŝ₁ and ŝ₂. These conditions may implicitly require extra conditions on the DC-SIS to ensure that the size of the subset selected by DC-SIS is of order required by the conditions. For NIS, by Theorem 2 of Fan, Feng and Song (2011), we need to impose some explicit conditions on the signal strength as well as the growth of the operator norm of the covariance matrix of covariates.

3. The RCV method can be combined with any feature screening methods such as DC-SIS and NIS and variable selection methods such as grouped LASSO and grouped SCAD (Xue, 2009) for ultrahigh dimensional additive models. The NIS method needs to choose a smoothing parameter for each predictor. The grouped LASSO and the grouped SCAD methods are expensive in terms of computational cost. We focus only on DC-SIS in the numerical studies to save space.

4. For sure independent screening procedures such as the SIS and DC-SIS, the authors recommended to set ŝ = n/log(n). The diverging rate of ŝ, ŝ₁ and ŝ₂ required in Theorems 1 and 2 are slower than this due to the nonparametric nature. It seems that it is difficult to further relax the conditions in Theorems 1 and 2. This can be viewed as a limitation of our theoretical results. From our simulation studies and real data examples, the performance of the naive method certainly relies on the choice of ŝ, while the RCV method performs well for a wide range of ŝ₁ and ŝ₂. As shown in Tables 1 and 2, the resulting estimate of the RCV method is very close to the oracle estimate across all scenarios in the tables. Theoretical studies on how to determine ŝ₁ and ŝ₂ are more related to the topic of feature screening than the variance estimation and we do not intend to pursue further in this paper. In practical implementation, the choices of these parameters should take into account of the degree of freedoms in the refitting stage so that the residual variance can be estimated with a reasonable accuracy. We would recommend considering several possible choices of ŝ₁ and ŝ₂ to examine whether the resulting variance estimate is relatively stable to the choices of ŝ₁ and ŝ₂. This is implemented in the real data example in Section 3.2.

Table 1.

Simulation Results for different ŝ (σ² = 1)

	ŝ = 20	ŝ = 30	ŝ = 40	ŝ = 50
Method	a = 0
Oracle	1.0042 ( 0.0618 )*	1.0042 ( 0.0618 )	1.0042 ( 0.0618 )	1.0042 ( 0.0618 )
Naive	0.8048 ( 0.0558 )	0.7549 ( 0.0589 )	0.7138 ( 0.0584 )	0.6771 ( 0.0584 )
RCV	1.0022 ( 0.0656 )	0.9994 ( 0.0666 )	0.9990 ( 0.0698 )	0.9967 ( 0.0705 )
	$a=1/\sqrt{3}$
Oracle	1.0049 ( 0.0617 )	1.0049 ( 0.0617 )	1.0049 ( 0.0617 )	1.0049 ( 0.0617 )
Naive	0.9054 ( 0.0572 )	0.8683 ( 0.0592 )	0.8387 ( 0.0615 )	0.8143 ( 0.0644 )
RCV	1.0704 ( 0.1300 )	1.0493 ( 0.1187 )	1.0374 ( 0.1095 )	1.0273 ( 0.1106 )
	$a=2/\sqrt{3}$
Oracle	1.0072 ( 0.0618 )	1.0072 ( 0.0618 )	1.0072 ( 0.0618 )	1.0072 ( 0.0618 )
Naive	0.9618 ( 0.0647 )	0.9618 ( 0.0647 )	0.9306 ( 0.0687 )	0.9194 ( 0.0780 )
RCV	1.0026 ( 0.0657 )	1.0026 ( 0.0657 )	1.0020 ( 0.0735 )	1.0013 ( 0.0779 )

^*Values in parentheses are standard errors

Table 2.

Simulation results with different n (σ² = 1)

	n = 400	n = 600
Method	a = 0
Oracle	1.0044 ( 0.0646 )*	0.9924 ( 0.0575 )
Naive	0.6969 ( 0.0610 )	0.7340 ( 0.0542 )
RCV	0.9905 ( 0.0837 )	0.9845 ( 0.0729 )
	$a=1/\sqrt{3}$
Oracle	1.0047 ( 0.0737 )	0.9970 ( 0.0552 )
Naive	0.8390 ( 0.0815 )	0.8533 ( 0.0555 )
RCV	1.1273 ( 0.1528 )	1.0144 ( 0.0954 )
	$a=2/\sqrt{3}$
Oracle	0.9903 ( 0.0687 )	1.0075 ( 0.0643 )
Naive	0.9013 ( 0.0785 )	0.9340 ( 0.0691 )
RCV	1.0241 ( 0.1886 )	1.0031 ( 0.0780 )

^*Values in parentheses are standard errors

3 Numerical studies

In this section, we investigate the finite sample performances of the newly proposed procedures. We further illustrate the proposed procedure by an empirical analysis of a real data example. In our numerical studies, we report only results of the proposed RCV method with DC-SIS to save space, although the NIS method, the grouped LASSO and the grouped SCAD (Xue, 2009) can be used to screen or select variables. All numerical studies are conducted using Matlab code.

3.1 Monte Carlo simulation

Since there is little work to study the variance estimate for ultra-high dimensional nonparametric additive model, this simulation study is designed to compare the finite sample performances of two-stage naive variance estimate and refitted cross-validation variance estimate. In our simulation study, data were generated from the following sparse additive model

$$y=a\left(X_1+0.75X_2^2+2.25cos(X_5)\right)+\epsilon ,$$ (3.1)

where ε ~ N(0, 1), and {X₁, ⋯ , X_p} ~ N_p(0, Σ) with $\mathrm{\sum }={\{{\rho }_{ij}\}}_{i,j=1}^p$ where ρ_ii = 1 and ρ_ij = 0.2 for i ≠ j. We set p = 2000 and n = 600. We take a = 0, $1/\sqrt{3}$, and $2/\sqrt{3}$ in order to examine the impact of signal-to-noise ratio to error variance estimation. When a = 0, the DC-SIS always can pick up the active sets and the challenge is to reduce spurious correlation, while when $a=2/\sqrt{3}$, the signal is strong enough to pick up active sets so that DC-SIS performs very well. The case $a=1/\sqrt{3}$ corresponds to the signal-to-noise equalling to 1. This is a difficult case to distinguish signals and noises and is the most challenge one for DC-SIS among these three cases considered: the first and the third case are easy to achieve sure screening with relative fewer number of selected variables and this reduces the biases of the RCV method and leaves more degrees of freedoms for estimating the residual variance. We intended to design such a case to challenge our proposed procedure, as sure screening is harder to achieve.

As a benchmark, we include the oracle estimator in our simulation. Here the oracle estimator corresponds to the mean squared errors for the fitting of the oracle model that includes only X₁, X₂ and X₅ for a ≠ 0, and include none of predictors when a = 0. In our simulation, we employ the distance correlation to rank importance of predictors, and screen out p − ŝ predictors with low distance correlation. Thus, the resulting model includes ŝ predictors. We consider ŝ=20, 30, 40 and 50 in order to illustrate the impact of choices of ŝ on the performance of the naive estimator and the refitted cross validation estimator.

In our simulation, each function f_j(·) is approximated by a linear combination of an intercept and 5 cubic B-splines bases with 3 knots equally spaced between the minimum and maximum of the j^th variable. Thus, when ŝ = 50, the reduced model actually has 251 terms, which is near half of the sample size. Table 1 depicts the average and the standard error of 150 estimates over the 150 simulations. To get an overall picture how the error variance estimates change over ŝ, Figure 3 depicts the overall average of the 150 estimates. In Table 1 and Figure 3, ‘Oracle’ stands for the oracle estimate based on nonparametric additive models using only active variables, ‘Naive’ for the naive estimate, and ‘RCV’ for the refitted cross validation estimate.

Figure 3.

Variance estimators for different signal-to-noise ratios

Table 1 and Figure 3 clearly show that the naive two-stage estimator significantly underestimates the error variance in the presence of many redundant variables. The larger the value ŝ, the bigger the spurious correlation ${\gamma }_n^2$, and hence the larger the bias of the naive estimate. The performance of the naive estimate also depends on the signal to noise ratio. In general, it performs better when the signal to noise ratio is large. The RCV estimator performs much better than the naive estimator. Its performance is very close to that of the oracle estimator for all cases listed in Table 1.

In practice, we have to choose one ŝ in data analysis. Fan and Lv (2008) suggested ŝ = [n/log(n)] for their sure independence screening procedure based on Pearson correlation ranking. We modify their proposal and set ŝ = [n^4/5/log(n^4/5)] to take into account effective sample size in nonparametric regression. Table 2 depicts the average and the standard error of 150 estimates over the 150 simulations when the sample size n = 400 and 600. The caption of Table 2 is the same as that in Table 1. Results in Table 2 clearly show that the RCV performs as well as the oracle procedure, and outperforms the naive estimate.

We further studied the impact of randomly splitting data strategy on the resulting estimate. As an alterative, one may repeat the proposed procedure several times, each randomly splitting data into two parts, and then take the average as the estimate of σ². Our findings from our simulations study are consistent with the discussion in Fan, Guo and Hao (2012): (a) the estimates of σ² for different numbers of repetitions are almost the same; and (b) as the number of repetitions increases, the variation slightly reduces at the price of computational cost. This implies that it is unnecessary to repeat the proposed procedure several times. As another alternative, one may randomly split the sample data into k groups. Specifically, the case k = 2 is the proposed RCV methods in the paper. Similarly, we can use data in one group to select useful predictors, data in other groups to fit the additive model. We refer this splitting strategy to as multi-folder splitting. Our simulation results implies that the multi-folder splitting leads to (a) less accurate estimate for the coefficients and (b) increased variation of ${\widehat{\sigma }}_l^2$ used to construct the RCV estimate. This is because this strategy splits the data into many subsets with even smaller sample size. If the sample size n is large, as nowadays Big Data, it may be worth to try multiple random splits, otherwise we do not recommend it.

3.2 A real data example

In this section, we illustrate the proposed procedure by an empirical analysis of a supermarket data set (Wang, 2009). The data set contains a total of n = 464 daily records of the number of customers (Y_i) and the sale amounts of p = 6, 398 products, denoted as X_i1, ⋯ , X_ip, which will be used as predictors. Both the response and predictors are standardized so that they have zero sample mean and unit sample variance. We fit the following additive model in our illustration.

$$Y_i=\mu +f_1(X_1)+\cdots +f_p(X_p)+{\epsilon }_i,$$

where ε_i is a random error with E(ε_i) = 0 and var(ε_i|x_i) = σ².

Since the sample size n = 464, we set ŝ = [n^4/5/log(n^4/5)] = 28. The naive error variance estimate equals 0.0938, while the RCV error variance estimate equals 0.1340, an 43% increase of the estimated value when the spurious correlation is reduced. Table 3 depicts the resulting estimates of the error variance with different values of ŝ, and clearly shows that the RCV estimate of error variance is stable with different choices of ŝ, while the estimate of error variance by the naive method reduces as ŝ increases. This is consistent with our theoretical and simulation results.

Table 3.

Error Variance Estimate for Market Data

ŝ	40	35	30	28	25
Naive	0.0866	0.0872	0.0910	0.0938	0.0990
RCV	0.1245	0.1104	0.1277	0.1340	0.1271

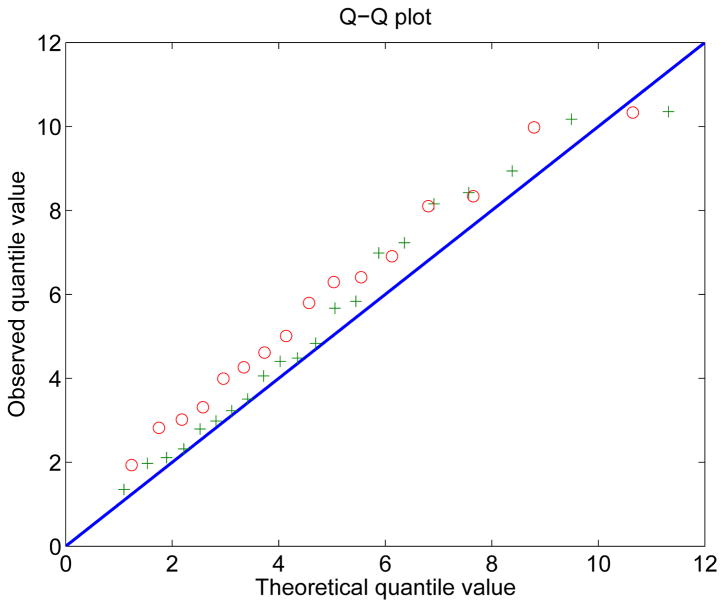
Regarding the selected models with ŝ predictors as a correct model and ignoring the approximation errors (if any) due to B-spline, we further employ the Wald’s χ²-test for hypothesis whether (γ_j1, ⋯ , γ_jdj)^T equals zero, namely whether the j^th variable is active in presence of the rest variables. Such Wald’s χ² statistics offer us a rough picture whether X_j is significant or not. The Wald’s χ²-test with the naive error variance estimate concludes 12 significant predictors at significant level 0.05, while the Wald’s χ²-test with the RCV error variance estimate concludes seven significant predictors at the same significant level. Figure 4 depicts the Q-Q plot of values of the χ²-test statistic of those insignificant predictors identified by the Wald’s test. Figure 4 clearly shows that the χ²-test values using naive error variance estimate systematically deviate from the 45-degree line. This implies that the naive method results in an underestimate of error variance, while the RCV method results in a good estimate of error variance.

Figure 4.

Quantile-quantile plot of χ²-test values. “o” stands for χ²-test using naive error variance estimate. “+” stands for χ²-test using RCV error variance estimate.

The Wald’s test at level 0.05 is in favor that seven predictors, X₁₁, X₁₃₉, X₃, X₃₉, X₆, X₆₂ and X₄₂, are significant. We refit the data with the additive model with these 7 predictors. The corresponding mean squared errors is 0.1207, which is close to the ${\widehat{\sigma }}_{\text{RCV}}^2=0.1340$. Note that σ² is the minimum possible prediction error. It provides a benchmark for other methods to compare with and is achievable when modeling bias and estimation errors are negligible.

To see how the above selected variables perform in terms of prediction, we further use the leave-one-out cross-validation (CV) and five-fold CV to estimate the mean squared prediction errors (MSPE). The leave-one-out CV yields MSPE=0.1414, and the average of the MSPE obtained from five-fold CV based on 400 randomly splitting data yields is 0.1488 with the 2.5th percentile and 97.5 percentile being 0.1411 and 0.1626, respectively. The MSPE is slightly greater than ${\widehat{\sigma }}_{\text{RCV}}^2$.

This is expected as the uncertainty of parameter estimation has not been accounted. This bias can be corrected from the theory of linear regression analysis.

Suppose that {x_i, Y_i}, i = 1, ⋯ , n is an independent and identically distributed random sample from a linear regression model Y = x^Tβ + ε, the linear predictor Ŷ = x^T β̂, where β̂ is the least squares estimate of β, has prediction error at a new observation $\{{\mathbf{x}}_{\ast },y_{\ast }\}:E\{{(y_{\ast }-{\mathbf{x}}_{\ast }^T\widehat{\mathit{\beta }})}^2\mid \mathbf{X}\}={\sigma }^2(1+{\mathbf{x}}_{\ast }^T{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{x}}_{\ast })$, where σ² is the error variance and X is the corresponding design matrix. This explains why the MSPE is slightly greater than ${\widehat{\sigma }}_{\text{RCV}}^2$. To further gauge the accuracy of the RCV estimate of σ², define weighted prediction error $\mid y_{\ast }-{\mathbf{x}}_{\ast }^T\widehat{\mathit{\beta }}\mid /\sqrt{1+{\mathbf{x}}_{\ast }^T{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{x}}_{\ast }}$. Then the leave-one-out method leads to the mean squared weighted predictor error (MSWPE) 0.1289 and the average of five-fold CV based on 400 randomly splitting data yields MSWPE 0.1305 with the 2.5th percentile and 97.5 percentile being 0.1254 and 0.1366, respectively. These results imply (a) the seven selected variables achieves the benchmark prediction; (b) the modeling biases using the additive models of these seven variables are negligible; (c) ${\widehat{\sigma }}_{\text{RCV}}^2$ provides a very good estimate for σ².

Their estimated functions f̂_j(x_j) are depicted in Figure 5, from which it seems that all predictors shown in Figure 5 are not significant since zero crosses the entire confidence interval. This can be due to the fact that we have used too many variables which increases the variance of the estimate.

Figure 5.

Estimated functions based on 7 variables selected from 28 variables that survive DC-SIS screening by the χ²-test with the RCV error variance estimator.

We further employ the Wald’s test with Bonferroni correction for 28 null hypotheses. This leads only two significant predictors, X₁₁ and X₆, at level 0.05. We refit the data with the two selected predictors. Figure 6 depicts the plot of f̂₁₁(x₁₁) and f̂₆(x₆).

Figure 6.

Estimated functions based on 2 variables selected from 28 variables that survive DC-SIS screening by the χ²-test with the RCV error variance estimator and the Bonferroni adjustment.

4 Discussions

In this paper, we proposed an error variance estimator in ultrahigh dimensional additive model by using refitted cross validation technique. This is particularly important given the high level of spurious correlation induced by the nonparametric models (See Figure 1 and Lemma 1). We established the root n consistency and asymptotic normality of the resulting estimator, and examined the empirical performance of the proposed estimator by Monte Carlo simulation. We further demonstrated the proposed methodology via an empirical analysis of supermarket data. The proposed estimator performs well with moderate sample size. However, when the sample size is very small, the refitted cross validation procedure may be unstable. How to construct an accurate error variance estimate with very small sample size is challenging and will be an interesting topic for future research.

Appendix: Proofs

A.1 Proofs of Lemma 1 and Theorem 1

Let Ψ be the corresponding design matrix of model (2.3). Specifically, Ψ is a n × (pd_n) matrix with ith row being (B₁₁(X_i1), ⋯ , B_1dn(X_i1), B₂₁(X_i2), ⋯ , B_pdn(X_ip)). Denote by Ψ^(𝒟̂*) the corresponding design matrix of model 𝒟̂^*, and P_𝒟̂^* the corresponding projection matrix. That is, P_𝒟̂^* = Ψ^(𝒟̂*)(Ψ^(𝒟̂*)T Ψ^(𝒟̂*))⁻¹Ψ^(𝒟̂*)T. Denote ${\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c=I_n-{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}$. Without loss of generality, assume that the first s non-parametric components are nonzero and others are all zero. By the assumption that all active predictors are retained by DC-SIS screening procedure. For ease of notation and without loss of generality, assume that 𝒟̂^* = {1, 2, ⋯ , ŝ}, where ŝ = |𝒟̂^*|.

Proof of Lemma 1

Note that

$${\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}\mathit{\epsilon }={\mathit{\epsilon }}^T{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}{({{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })})}^{-1}{{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T\mathit{\epsilon }\le {\lambda }_{min}^{-1}({{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}){\Vert {{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T\mathit{\epsilon }\Vert }_2^2,$$ (A.1)

where λ_min(A) stands for the minimal eigenvalue of matrix A. To show Lemma 1, we need to derive the bound of eigenvalue of matrix Ψ^(𝒟̂*)T Ψ^(𝒟̂*). Note that Ψ^(𝒟̂*) = (Ψ₁, ⋯ , Ψ_ŝ) with

$${\mathbf{\Psi }}_j=\left(\begin{array}{ccc}{B}_{j1}(X_{j1})& \cdots & B_{j{d}_n}(X_{j1})\\ \cdots & \cdots & \cdots \\ B_{j1}(X_{jn})& \cdots & B_{j{d}_n}(X_{jn})\end{array}\right),j=1,\cdots ,\widehat{s}.$$ (A.2)

Let $\mathbf{b}={({\mathbf{b}}_1^T,\cdots ,{\mathbf{b}}_{\widehat{s}}^T)}^T$ and ${\Vert \mathbf{b}\Vert }_2^2={\mathbf{b}}^T\mathbf{b}=1$. Then we have Ψ^(𝒟̂*)b = Ψ₁b₁ + ⋯ + Ψ_ŝb_ŝ. As shown in Lemma S.5 in the supplemental material of this paper, it follows that

$${(\frac{1-\delta }{2})}^{\widehat{s}-1}{({\Vert {\mathbf{\Psi }}_1{\mathbf{b}}_1\Vert }_2+\cdots +{\Vert {\mathbf{\Psi }}_{\widehat{s}}{\mathbf{b}}_{\widehat{s}}\Vert }_2)}^2\le {\Vert {\mathbf{\Psi }}_1{\mathbf{b}}_1+\cdots +{\mathbf{\Psi }}_{\widehat{s}}{\mathbf{b}}_{\widehat{s}}\Vert }_2^2={\mathbf{b}}^T{{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}\mathbf{b}.$$ (A.3)

This yields that

$${(\frac{1-\delta }{2})}^{\widehat{s}-1}\left(\sum _{i=1}^{\widehat{s}}{\mathbf{b}}_i{\mathbf{\Psi }}_i^T{\mathbf{\Psi }}_i{\mathbf{b}}_i\right)\le {\mathbf{b}}^T{{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}\mathbf{b},$$ (A.4)

since ||Ψ_ib_i||₂ ≥ 0. Furthermore,

$${(\frac{1-\delta }{2})}^{\widehat{s}-1}\left(\sum _{i=1}^{\widehat{s}}{\mathbf{b}}_i{\mathbf{\Psi }}_i^T{\mathbf{\Psi }}_i{\mathbf{b}}_i\right)\ge {(\frac{1-\delta }{2})}^{\widehat{s}-1}\left(\sum _{{\mathbf{b}}_i^T{\mathbf{b}}_i\ne 0}{\lambda }_{min}({\mathbf{\Psi }}_i^T{\mathbf{\Psi }}_i){\mathbf{b}}_i^T{\mathbf{b}}_i\right).$$

Recalling Lemma 6.2 of Zhou, Shen and Wolfe (1998), there exists two positive constants C₁ and C₂ such that, for any 1 ≤ i ≤ ŝ,

$$C_1{d}_n^{-1}n\le {\lambda }_{min}({\mathbf{\Psi }}_i^T{\mathbf{\Psi }}_i)\le {\lambda }_{max}({\mathbf{\Psi }}_i^T{\mathbf{\Psi }}_i)\le C_2{d}_n^{-1}n.$$ (A.5)

Thus,

$${(\frac{1-\delta }{2})}^{\widehat{s}-1}\left(\sum _{{\mathbf{b}}_i^T{\mathbf{b}}_i\ne 0}{\lambda }_{min}({\mathbf{\Psi }}_i^T{\mathbf{\Psi }}_i){\mathbf{b}}_i^T{\mathbf{b}}_i\right)\ge C_1{(\frac{1-\delta }{2})}^{\widehat{s}-1}{d}_n^{-1}n\sum _{{\mathbf{b}}_i^T{\mathbf{b}}_i\ne 0}{\mathbf{b}}_i^T{\mathbf{b}}_i=C_1{(\frac{1-\delta }{2})}^{\widehat{s}-1}{d}_n^{-1}n.$$ (A.6)

The last equation is valid due to ${\Vert \mathbf{b}\Vert }_2^2={\mathbf{b}}^T\mathbf{b}=1$. Combining the equation (A.4) and (A.6), we have

$${\lambda }_{min}({{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })})\ge C_1{(\frac{1-\delta }{2})}^{\widehat{s}-1}{d}_n^{-1}n.$$ (A.7)

Thus, it follows by using (A.1) that

$${\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}\mathit{\epsilon }\le C_1^{-1}{\left(\frac{2}{1-\delta }\right)}^{\widehat{s}-1}{d}_n{n}^{-1}{\Vert {{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T\mathit{\epsilon }\Vert }_2^2.$$ (A.8)

By the notation (A.2), we have

$${\mathbf{\Psi }}_i^T\mathit{\epsilon }=\left(\begin{array}{c}{\sum }_{k=1}^n{B}_{i1}(X_{ik}){\epsilon }_k\\ {\sum }_{k=1}^n{B}_{i2}(X_{ik}){\epsilon }_k\\ ⋮\\ {\sum }_{k=1}^n{B}_{i{d}_n}(X_{ik}){\epsilon }_k\end{array}\right).$$ (A.9)

Recalling that 0 ≤ B_ij(·) ≤ 1, for any i, j and $\mathrm{E}{\mid B_{ij}(X_{ik})\mid }^2\le C_4{d}_n^{-1}$ (Stone, 1985), we note the fact that for m ≥ 2, $\mathrm{E}{\mid B_{ij}(X_{ik})\mid }^m\le \mathrm{E}{\mid B_{ij}(X_{ik})\mid }^2\le C_4{d}_n^{-1}$. Observe that, using Condition (C1), for any integers i and j

$$\mathrm{E}{\mid B_{ij}(X_{ik}){\epsilon }_k\mid }^m=\mathrm{E}{\mid B_{ij}(X_{ik})\mid }^m·\mathrm{E}{\mid {\epsilon }_k\mid }^m\le \mathrm{E}{\mid B_{ij}(X_{ik})\mid }^m\mathrm{E}(m!a^{m}exp\{\mid {\epsilon }_1\mid /a\}).$$ (A.10)

Taking A₁ = 1/a and A₂ = b in Condition (C1), it follows that the right hand side of above inequality will not exceed

$$C_{4}m!a^m{d}_n^{-1}\mathrm{E}(exp\{\mid {\epsilon }_1\mid /a\})\le \frac{C_4}{2}m!(2d_n^{-1}b{a}^2)a^{m-2}.$$ (A.11)

Using Bernstein’s Inequality (see Lemma 2.2.11 of Van der Vaart and Wellner, 1996), we have

$$\begin{array}{l}\mathrm{P}\left(\underset{\begin{array}{c}1\le i\le p\\ 1\le j\le d_n\end{array}}{max}\left|\sum _{k=1}^n{B}_{ij}(X_{ik}){\epsilon }_k\right|\ge M\right)\le \sum _{i=1}^p\sum _{j=1}^{d_n}\mathrm{P}\left(\left|\sum _{k=1}^n{B}_{ij}(X_{ik}){\epsilon }_k\right|\ge M\right)\le 2p{d}_{n}exp\left\{-\frac{M^2}{2(2d_n^{-1}b{a}^{2}n+aM)}\right\}\\ =2exp\left\{log(p{d}_n)\left(1-\frac{1}{4log(p{d}_n)n{d}_n^{-1}b{a}^2{M}^{-2}+2log(p{d}_n)a{M}^{-1}}\right)\right\}.\end{array}$$

When we take $M=C_5\sqrt{nlog(p{d}_n)/d_n}$, with $\frac{d_{n}log(p{d}_n)}{n}\to 0$ and sufficiently large C₅, the power in the last equation goes to negative infinity. Thus, with probability approaching to one, we have $\underset{\begin{array}{c}1\le i\le p\\ 1\le j\le d_n\end{array}}{max}\mid {\sum }_{k=1}^n{B}_{ij}(X_{ik}){\epsilon }_k\mid \le C_5\sqrt{nlog(p{d}_n)/d_n}$ and

$${\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}\mathit{\epsilon }\le C_1^{-1}{\left(\frac{2}{1-\delta }\right)}^{\widehat{s}-1}{d}_n{n}^{-1}{\Vert {{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T\mathit{\epsilon }\Vert }_2^2\le C_5^2{C}_1^{-1}{\left(\frac{2}{1-\delta }\right)}^{\widehat{s}-1}{d}_{n}log(p{d}_n).$$ (A.12)

Due to the independent and identically distributed random errors with mean 0 and variance σ², by the Law of Large Number, we have

$$\frac{1}{n}\sum _{i=1}^n{\epsilon }_i\stackrel{\text{a.s.}}{\to }0,\frac{1}{n}\sum _{i=1}^n{\epsilon }_i^2\stackrel{\text{a.s.}}{\to }{\sigma }^2,$$ (A.13)

Thus, we obtain that

$${\widehat{\gamma }}_n^2=\frac{{\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}\mathit{\epsilon }}{{\mathit{\epsilon }}^T\mathit{\epsilon }}=O_p\left\{{\left(\frac{2}{1-\delta }\right)}^{\widehat{s}}\frac{d_{n}log(p{d}_n)}{n}\right\}.$$ (A.14)

Proof of Theorem 1

Note that

$${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2=\frac{1}{n-\widehat{s}{d}_n}\left[\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_j^T({\mathbf{X}}_j){\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)+2{\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)+{\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c\mathit{\epsilon }\right],$$

where f_j(X_j) = (f_j(X_j1), ⋯ , f_j(X_jn)^T , j = 1, ⋯ , p. To simplify the first term in ${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2$, let ${\mathrm{\Delta }}_1={\sum }_{j=1}^{\widehat{s}}{\mathbf{f}}_j^T({\mathbf{X}}_j){\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c{\sum }_{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)$. Then

$${\mathrm{\Delta }}_1={\{\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)-\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)+\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c\{\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)-\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)+\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\},$$

where f_nj(X_j) = (f_nj(X_j1), ⋯ , f_nj(X_jn))^T = (B_j(X_j1)^T Γ_j , ⋯ , B_j(X_jn)^T Γ_j)^T , j = 1, ⋯ , p. Define

$$\begin{array}{l}{\mathrm{\Delta }}_{11}={\{\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)-\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c\{\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)-\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\},\\ {\mathrm{\Delta }}_{12}={\{\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c\{\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\},\\ {\mathrm{\Delta }}_{13}=2{\{\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)-\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c\{\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\}.\end{array}$$

Then Δ₁ = Δ₁₁ + Δ₁₂ + Δ₁₃. Note that ${\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c$ is a projection matrix on the complement of the linear space of Ψ^(𝒟̂*), and therefore ${\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c\{{\sum }_{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\}=0$. Thus, both Δ₁₂ and Δ₁₃ equal 0. We next calculate the order of Δ₁₁. By the property of B-spline (Stone, 1985), there exists a constant c₁ > 0 such that ${\Vert f_j-f_{nj}\Vert }^2\le c_1{d}_n^{-2d}$. Since ${\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c$ is a projection matrix, its eigenvalues equal either 0 or 1. By the Cauchy-Schwarz inequality and some straightforward calculation, it follows that ${\mathrm{\Delta }}_{11}=O_p({\widehat{s}}^{2}n{d}_n^{-2d})$. Therefore ${\mathrm{\Delta }}_1=O_p({\widehat{s}}^{2}n{d}_n^{-2d})$. Under conditions in Theorem 1(i), $O_p({\widehat{s}}^2{d}_n^{-2d})=o_p(1)$. As a result, Δ₁ = o_p(n). Under conditions in Theorem 1(ii), ŝ = o(n^{(2d−1)/4(2d+1)}) and therefore ${\mathrm{\Delta }}_1=o_p(\sqrt{n})$.

Now we deal with the second term in ${\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2$. Denote ${\mathrm{\Delta }}_2=2{\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c{\sum }_{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)$. Since ${\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c\{{\sum }_{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\}=0$, it follows that

$${\mathrm{\Delta }}_2=2{\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}^c\left(\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)-\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\right).$$

Denote ${\mathrm{\Delta }}_{21}={\sum }_{j=1}^{\widehat{s}}{\sum }_{i=1}^n(f_j(X_{ji})-f_{nj}(X_{ji})){\epsilon }_i$ and ${\mathrm{\Delta }}_{22}=({\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }})\left({\sum }_{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)-{\sum }_{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\right)$. Thus, Δ₂ = 2(Δ₂₁ − Δ₂₂). To deal with Δ₂₁, we bound the tails of (f_j(X_ji) − f_nj(X_ji)) ε_i, i = 1, ⋯ , n j = 1, ⋯ , ŝ. For any m ≥ 2, because f_j ∈ 𝒞^d ([a, b]) and f_nj belongs to the spline space 𝒮^l ([a, b]), we have

$$\mathrm{E}{\mid (f_j(X_{ji})-f_{nj}(X_{ji})){\epsilon }_i\mid }^m=\mathrm{E}({\mid f_j(X_{ji})-f_{nj}(X_{ji})\mid }^m\mathrm{E}({\mid {\epsilon }_i\mid }^m\mid {\mathbf{x}}_i)),$$

which is bounded by $C_6^{m-2}\mathrm{E}\left({\mid f_j(X_{ji})-f_{nj}(X_{ji})\mid }^2\mathrm{E}({\mid {\epsilon }_i\mid }^m\mid {\mathbf{x}}_i)\right)$ for some constant C₆ by the property of B-spline approximation. There exists a constant c₁ > 0 such that ${\Vert f_j-f_{nj}\Vert }^2\le c_1{d}_n^{-2d}$ by the property of B-spline (Stone, 1985). Applying Condition (C1) for E{exp(A₁ |ε_i|)|x_i}, it follows that

$$\mathrm{E}{\mid (f_j(X_{ji})-f_{nj}(X_{ji})){\epsilon }_i\mid }^m\le m!{\left(\frac{C_6}{A_1}\right)}^{m-2}\frac{A_2}{A_1^2}{c}_1{d}_n^{-2d}.$$

Denote $C_7=c_1{A}_2/A_1^2$, and C₈ = C₆/A₁. Using the Bernstein’s inequality, for some M, we have

$$\mathrm{P}\left(\underset{1\le j\le p}{max}\left|\sum _{i=1}^n(f_j(X_{ji})-f_{nj}(X_{ji})){\epsilon }_i\right|>M\right)\le 2pexp\left\{-\frac{1}{2}\frac{M^2}{2C_{7}n{d}_n^{-2d}-C_{8}M}\right\}.$$ (A.15)

If we take $M=C_9\sqrt{log(p)n{d}_n^{-2d}}$, and for sufficiently large C₉, then the tail probability (A.15) goes to zero. Thus,

$${\mathrm{\Delta }}_{21}=O_p\left(\widehat{s}\sqrt{log(p)n{d}_n^{-2d}}\right).$$ (A.16)

Under condition of Theorem 1(i), ŝ = o(n^{(4d+1)/2(2d+1)}) with ζ < 1. Thus, $O_p(\widehat{s}{d}_n^{-d}\sqrt{log(p{d}_n)})=o_p(\sqrt{n})$. Following the similar arguments dealing with Δ₁₁, it follows that Δ₂₁ = o_p(n). Under condition of Theorem 1(ii), ŝ = o(n^{d/(2d+1)−ζ/2}) with ζ < 3/(2d+1). Thus, ${\mathrm{\Delta }}_{21}=o_p(\sqrt{n})$. By the Cauchy-Schwarz inequality, it follows by Lemma 1 that

$$\begin{array}{l}{\mathrm{\Delta }}_{22}\le {\Vert {\mathit{\epsilon }}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}\Vert }_2·{\Vert \sum _{j=1}^{\widehat{s}}{\mathbf{f}}_j({\mathbf{X}}_j)-\sum _{j=1}^{\widehat{s}}{\mathbf{f}}_{nj}({\mathbf{X}}_j)\Vert }_2\\ =O_p({(\frac{2}{1-\delta })}^{\widehat{s}}\sqrt{d_{n}log(p{d}_n)})·O_p(\widehat{s}{n}^{1/2}{d}_n^{-d})\\ =O_p({(\frac{2}{1-\delta })}^{\widehat{s}}\sqrt{log(p{d}_n)}{d}_n^{-d+1/2}).\end{array}$$

When ζ < 4d/(2d+1), and ŝ = O_p(log(n^α), α≤ 4d/(2d+1)− ζ, it follows that Δ₂₂ = o_p(n) under condition of Theorem 1(i). When ζ < (2d − 1)/(2(2d + 1)) and ŝ = log(n^α), α ≤ (2d − 1)/(2(2d + 1)) − ζ, ${(2/(1-\delta ))}^{\widehat{s}}{n}^{1/2}\sqrt{log(p{d}_n)}{d}_n^{-d+1/2}=o_p(\sqrt{n})$. Thus, ${\mathrm{\Delta }}_{22}=o_p(\sqrt{n})$ under condition of Theorem 1(ii). Comparing the order of Δ₁₁, Δ₂₁ and Δ₂₂, we obtain the order of ŝ in Theorem 1. Therefore, we have

$$\begin{array}{l}{\mathbf{Y}}^T\left(I_n-{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}{({{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })})}^{-1}{{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T\right)\mathbf{Y}={\mathit{\epsilon }}^T\left(I_n-{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}\right)\mathit{\epsilon }+{\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2\\ ={\mathit{\epsilon }}^T\left(I_n-{\mathbf{P}}_{{\widehat{\mathcal{D}}}^{\ast }}\right)\mathit{\epsilon }+O_p({\widehat{s}}^{2}n{d}_n^{-2d})+O_p\left(\widehat{s}\sqrt{log(p)n{d}_n^{-2d}}\right)+{\mathrm{\Delta }}_{22}.\end{array}$$

and it follows by the definition of ${\widehat{\gamma }}_n^2$ that

$$\begin{array}{l}{\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2=\frac{1}{n-\widehat{s}{d}_n}{\mathbf{Y}}^T\left(I_n-{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}{({{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })})}^{-1}{{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}^{\ast })}}^T\right)\mathbf{Y}\\ =\frac{1}{n-\widehat{s}{d}_n}{\mathit{\epsilon }}^T\mathit{\epsilon }(1-{\widehat{\gamma }}_n^2)+O_p(\frac{{\widehat{s}}^{2}n{d}_n^{-2d}}{n-\widehat{s}{d}_n})+O_p(\frac{\sqrt{log(p){\widehat{s}}^{2}n{d}_n^{-2d}}}{n-\widehat{s}{d}_n})+\frac{{\mathrm{\Delta }}_{22}}{n-\widehat{s}{d}_n}.\end{array}$$

Since ŝ d_n = o_p(n) and ${\widehat{\gamma }}_n^2<1$, we have

$$\frac{{\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2}{(1-{\widehat{\gamma }}_n^2)}=\frac{1}{n-\widehat{s}{d}_n}{\mathit{\epsilon }}^T\mathit{\epsilon }+O_p({\widehat{s}}^2{d}_n^{-2d})+O_p(\sqrt{log(p)}\widehat{s}{n}^{-1/2}{d}_n^{-d})+O_p(\frac{{\mathrm{\Delta }}_{22}}{n}).$$ (A.17)

Under conditions of Theorem 1(i), the small order term in (A.17) is bounded by o_p(1). We have

$$\frac{{\widehat{\sigma }}_{{\widehat{\mathcal{D}}}^{\ast }}^2}{1-{\widehat{\gamma }}_n^2}\stackrel{\mathrm{p}}{\to }{\sigma }^2.$$ (A.18)

To establish the asymptotic normality, we should study the asymptotic bias of the estimator. By the Central Limit Theorem, it follows that

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n({\epsilon }_i^2-{\sigma }^2)\stackrel{\mathcal{L}}{\to }\mathcal{N}(0,\mathrm{E}{\epsilon }_1^4-{\sigma }^4).$$ (A.19)

Note that under conditions of Theorem 1(ii), the small order term in (A.17) is bounded by o_p(n^−1/2). Therefore, the asymptotic normality holds.

A.2 Proof of Theorem 2

Define events ${\mathcal{A}}_{n1}=\{{\mathcal{D}}^{\ast }\subset {\widehat{\mathcal{D}}}_1^{\ast }\},{\mathcal{A}}_{n2}=\{{\mathcal{D}}^{\ast }\subset {\widehat{\mathcal{D}}}_2^{\ast }\}$ and 𝒜_n = 𝒜_n1 ∩ 𝒜_n2. Unless specifically mentioned, our analysis and calculation are based on the event 𝒜_n.

Let ${\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}_1^{\ast })}$ be the design matrix corresponding to ${\widehat{\mathcal{D}}}_1^{\ast },{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}={\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}_1^{\ast })}{({{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}_1^{\ast })}}^T{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}_1^{\ast })})}^{-1}{{\mathbf{\Psi }}^{({\widehat{\mathcal{D}}}_1^{\ast })}}^T$, and ${\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}^c=I-{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}$. Note that ${\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}^c\left({\sum }_{j=1}^{{\widehat{s}}_1}{\mathbf{f}}_{nj}({\mathbf{X}}_j^{(2)})\right)=0$. Thus,

$$(n/2-{\widehat{s}}_1{d}_n){\widehat{\sigma }}_{{\widehat{\mathcal{D}}}_1^{\ast }}^2={{\mathit{\epsilon }}^{(2)}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}^c{\mathit{\epsilon }}^{(2)}+{\left(\sum _{j=1}^{{\widehat{s}}_1}{\mathbf{f}}_j({\mathbf{X}}_j^{(2)})-\sum _{j=1}^{{\widehat{s}}_1}{\mathbf{f}}_{nj}({\mathbf{X}}_j^{(2)})\right)}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}^c\left(\sum _{j=1}^{{\widehat{s}}_1}{\mathbf{f}}_j({\mathbf{X}}_j^{(2)})-\sum _{j=1}^{{\widehat{s}}_1}{\mathbf{f}}_{nj}({\mathbf{X}}_j^{(2)})\right).$$

By the same argument as that in the proof of Theorem 1, the second term in the above equation is of the order $O_p({\widehat{s}}_1^{2}n{d}_n^{-2d})$. Thus,

$$(n/2-{\widehat{s}}_1{d}_n)({\widehat{\sigma }}_{{\widehat{\mathcal{D}}}_1^{\ast }}^2-{\sigma }^2)=\left({{\mathit{\epsilon }}^{(2)}}^T{\mathit{\epsilon }}^{(2)}-\frac{n}{2}{\sigma }^2\right)-\left({{\mathit{\epsilon }}^{(2)}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}{\mathit{\epsilon }}^{(2)}-{\widehat{s}}_1{d}_n{\sigma }^2\right)+O_p({\widehat{s}}_1^{2}n{d}_n^{-2d}).$$

We next calculate the order of $\left({{\mathit{\epsilon }}^{(2)}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}{\mathit{\epsilon }}^{(2)}-{\widehat{s}}_1{d}_n{\sigma }^2\right)$. Note that

$$\mathrm{E}\left({{\mathit{\epsilon }}^{(2)}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}{\mathit{\epsilon }}^{(2)}-{\sigma }^2\mathbf{tr}({\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }})|{\mathbf{X}}_{{\widehat{\mathcal{D}}}_1^{\ast }}^{(2)}\right)=0.$$

We now calculate its variance

$$\text{Var}\left({{\mathit{\epsilon }}^{(2)}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}{\mathit{\epsilon }}^{(2)}-{\sigma }^2\mathbf{tr}({\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }})|{\mathbf{X}}_{{\widehat{\mathcal{D}}}_1^{\ast }}^{(2)}\right)=\mathrm{E}\left({\left({{\mathit{\epsilon }}^{(2)}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}{\mathit{\epsilon }}^{(2)}\right)}^2|{\mathbf{X}}_{{\widehat{\mathcal{D}}}_1^{\ast }}^{(2)}\right)-{\sigma }^4{\mathbf{tr}}^2{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}.$$ (A.20)

Denote by P_ij the (i, j)th entry of matrix ${\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}$. The first term in the right-hand side of the last equation can be written as

$$\mathrm{E}\left(\sum _{i,j,k,l}{\epsilon }_i{\epsilon }_j{\epsilon }_k{\epsilon }_l{P}_{ij}{P}_{kl}|{\mathbf{X}}_{{\widehat{\mathcal{D}}}_1^{\ast }}^{(2)}\right).$$

It follows by the independence between X and ε that

$$\begin{array}{l}\mathrm{E}\left({{\mathit{\epsilon }}^{(2)}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}{\mathit{\epsilon }}^{(2)}|{\mathbf{X}}_{{\widehat{\mathcal{D}}}_1^{\ast }}^{(2)}\right)\\ =\mathrm{E}{\epsilon }_1^4\sum _{i=1}^{n/2}{P}_{ii}^2+{\sigma }^4\sum _{i\ne j}{P}_{ii}{P}_{jj}+2{\sigma }^4\sum _{i\ne j}{P}_{ij}^2.\end{array}$$

Therefore, it follows that the equation (A.20) equals to

$$\begin{array}{l}\mathrm{E}{\epsilon }_1^4\sum _{i=1}^{n/2}{P}_{ii}^2+{\sigma }^4\sum _{i\ne j}{P}_{ii}{P}_{jj}+2{\sigma }^4\sum _{i\ne j}{P}_{ij}^2-{\sigma }^4{\left(\sum _{i=1}^{n/2}{P}_{ii}\right)}^2\\ =\mathrm{E}{\epsilon }_1^4\sum _{i=1}^{n/2}{P}_{ii}^2+2{\sigma }^4\sum _{i\ne j}{P}_{ij}^2-{\sigma }^4\sum _{i=1}^{n/2}{P}_{ii}^2.\end{array}$$

Noting the fact that σ⁴ = (E ε²)² ≤ Eε⁴, the last equation is bounded by

$$\begin{array}{l}\mathrm{E}{\epsilon }_1^4\sum _{i=1}^{n/2}{P}_{ii}^2-{\sigma }^4\sum _{i=1}^{n/2}{P}_{ii}^2+{\sigma }^4\sum _{i\ne j}{P}_{ij}^2+\mathrm{E}{\epsilon }_1^4\sum _{i\ne j}{P}_{ij}^2\\ =(\mathrm{E}{\epsilon }_1^4+{\sigma }^4)\sum _{i=1}^{n/2}\sum _{j=1}^{n/2}{P}_{ij}^2-2{\sigma }^4\sum _{i=1}^{n/2}{P}_{ii}^2.\end{array}$$ (A.21)

Note that

$$\begin{array}{l}\text{tr}({{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}}^2)=\text{tr}({{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }})=\sum _{i=1}^{n/2}\sum _{j=1}^{n/2}{P}_{ij}^2,\\ \text{tr}({\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }})=\text{tr}({{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}}^2)=\sum _{i=1}^{n/2}{P}_{ii},\\ {\text{tr}}^2({\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }})={\left(\text{tr}({\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }})\right)}^2=\sum _{i=1}^{n/2}{P}_{ii}^2+\sum _{i\ne j}{P}_{ii}{P}_{jj}.\end{array}$$

and that ${\text{tr}}^2({\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }})={\left({\sum }_{i=1}^{n/2}{P}_{ii}\right)}^2\le n{\sum }_{i=1}^{n/2}{P}_{ii}^2$. It follows that

$$\begin{array}{l}\text{Var}\left({{\mathit{\epsilon }}^{(2)}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}{\mathit{\epsilon }}^{(2)}-{\sigma }^2\text{tr}({\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }})|{\mathbf{X}}_{{\widehat{\mathcal{D}}}_1^{\ast }}^{(2)}\right)\le (\mathrm{E}{\epsilon }_1^4+{\sigma }^4)\text{tr}({\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }})-\frac{2{\sigma }^4}{n}{\text{tr}}^2({\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }})\\ \le (\mathrm{E}{\epsilon }_1^4+{\sigma }^4){\widehat{s}}_1{d}_n.\end{array}$$

since for the projection matrix ${\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }},\text{tr}({\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }})={\widehat{s}}_1{d}_n$. Consequently, by Markov’s inequality, we obtain

$${{\mathit{\epsilon }}^{(2)}}^T{\mathbf{P}}_{{\widehat{\mathcal{D}}}_1^{\ast }}{\mathit{\epsilon }}^{(2)}-{\sigma }^2{\widehat{s}}_1{d}_n=O_p\left(\sqrt{{\widehat{s}}_1{d}_n}\right)$$ (A.22)

Therefore, we have that

$$(\frac{n}{2}-{\widehat{s}}_1{d}_n)({\widehat{\sigma }}_{{\widehat{\mathcal{D}}}_1^{\ast }}^2-{\sigma }^2)={{\mathit{\epsilon }}^{(2)}}^T{\mathit{\epsilon }}^{(2)}-\frac{n}{2}{\sigma }^2+O_p\left(\sqrt{{\widehat{s}}_1{d}_n}\right)+O_p({\widehat{s}}_1^{2}n{d}_n^{-2d}).$$

Similarly, it follows that

$$(\frac{n}{2}-{\widehat{s}}_2{d}_n)({\widehat{\sigma }}_{{\widehat{\mathcal{D}}}_2^{\ast }}^2-{\sigma }^2)={{\mathit{\epsilon }}^{(1)}}^T{\mathit{\epsilon }}^{(1)}-\frac{n}{2}{\sigma }^2+O_p\left(\sqrt{{\widehat{s}}_2{d}_n}\right)+O_p({\widehat{s}}_2^{2}n{d}_n^{-2d}).$$

Finally, we deal with $\sqrt{n}({\widehat{\sigma }}_{\text{RCV}}^2-{\sigma }^2)$. Take ŝ₁ = o(n^{(2d−1)/4(2d+1)}), and ŝ₂ = o(n^{(2d−1)/4(2d+1)}) so that n/(n − 2ŝ₁d_n) = 1 + o_p(1) and n/(n − 2ŝ₂d_n) = 1 + o_p(1). Then

$$\begin{array}{l}\sqrt{n}({\widehat{\sigma }}_{\text{RCV}}^2-{\sigma }^2)\\ =\frac{\sqrt{n}}{n-2{\widehat{s}}_1{d}_n}\left({{\mathit{\epsilon }}^{(2)}}^T{\mathit{\epsilon }}^{(2)}-\frac{n}{2}{\sigma }^2+O_p\left(\sqrt{{\widehat{s}}_1{d}_n}\right)+O_p({\widehat{s}}_1^{2}n{d}_n^{-2d})\right)\\ +\frac{\sqrt{n}}{n-2{\widehat{s}}_2{d}_n}\left({{\mathit{\epsilon }}^{(1)}}^T{\mathit{\epsilon }}^{(1)}-\frac{n}{2}{\sigma }^2+O_p\left(\sqrt{{\widehat{s}}_2{d}_n}\right)+O_p({\widehat{s}}_2^{2}n{d}_n^{-2d})\right)\\ =\left\{\frac{1}{\sqrt{n}}\sum _{i=1}^n({\epsilon }_i^2-{\sigma }^2)\right\}\{1+o_p(1)\}+o_p(1)\\ \stackrel{\mathcal{L}}{\to }\mathcal{N}(0,\mathrm{E}{\epsilon }_1^4-{\sigma }^4),\text{as}n\to \infty .\end{array}$$

This completes the proof of Theorem 2.