Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2018 May 11;177(3):896–910. doi: 10.1104/pp.17.01648

A New Phenotyping Pipeline Reveals Three Types of Lateral Roots and a Random Branching Pattern in Two Cereals1,[OPEN]

Sixtine Passot a,b,2,3, Beatriz Moreno-Ortega b,c,2, Daniel Moukouanga a, Crispulo Balsera c, Soazig Guyomarc’h d, Mikael Lucas a,e, Guillaume Lobet f,g, Laurent Laplaze a,e, Bertrand Muller c,4, Yann Guédon b,4
PMCID: PMC6053009  PMID: 29752308

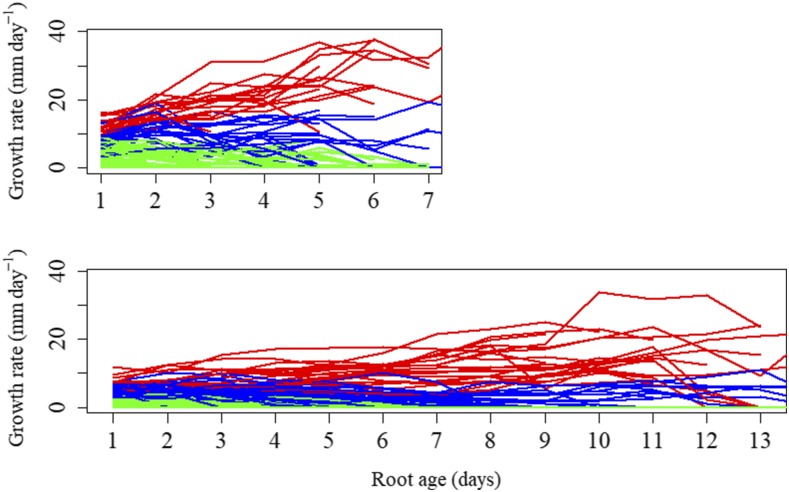
Lateral roots in both pearl millet and maize can be categorized into three types based on growth rate profiles.

Abstract

Recent progress in root phenotyping has focused mainly on increasing throughput for genetic studies, while identifying root developmental patterns has been comparatively underexplored. We introduce a new phenotyping pipeline for producing high-quality spatiotemporal root system development data and identifying developmental patterns within these data. The SmartRoot image-analysis system and temporal and spatial statistical models were applied to two cereals, pearl millet (Pennisetum glaucum) and maize (Zea mays). Semi-Markov switching linear models were used to cluster lateral roots based on their growth rate profiles. These models revealed three types of lateral roots with similar characteristics in both species. The first type corresponds to fast and accelerating roots, the second to rapidly arrested roots, and the third to an intermediate type where roots cease elongation after a few days. These types of lateral roots were retrieved in different proportions in a maize mutant affected in auxin signaling, while the first most vigorous type was absent in maize plants exposed to severe shading. Moreover, the classification of growth rate profiles was mirrored by a ranking of anatomical traits in pearl millet. Potential dependencies in the succession of lateral root types along the primary root were then analyzed using variable-order Markov chains. The lateral root type was not influenced by the shootward neighbor root type or by the distance from this root. This random branching pattern of primary roots was remarkably conserved, despite the high variability of root systems in both species. Our phenotyping pipeline opens the door to exploring the genetic variability of lateral root developmental patterns.

Plant breeding has long ignored the belowground part of the plant, but it is now acknowledged that the root system represents an opportunity for improving plant efficiency and tolerance to abiotic stresses (Bishopp and Lynch, 2015). A better knowledge of root system structure and function is thus needed for root system-oriented crop improvement. Phenotyping, as the evaluation of heritable plant traits in a given environment and in a reproducible manner, is one key approach to extend this knowledge. Recent progress in plant phenotyping platforms, including plant-handling automation and computer-assisted data acquisition, has allowed an increase in phenotyping throughput (i.e. the number of plants analyzed; Fahlgren et al., 2015b), which is critical for association studies and gene discovery. Besides increasing throughput, another strategy chosen in some phenotyping platforms is to improve data dimensionality and structure (Dhondt et al., 2013). In these platforms, the amount of data collected on a single plant is increased, either by measuring several traits that can be of different natures or by measuring the same trait at successive time points to focus on physiological processes (Fahlgren et al., 2015a).

The phenotyping of root systems presents specific challenges compared with the phenotyping of aerial parts of plants. The root system is by nature hidden, and root phenotyping platforms have to make a compromise between the relevance of growth conditions and trait measurement feasibility. Most root phenotyping platforms focus on measurements at high throughput of selected root traits on a large number of plants, with the objective of detecting quantitative trait loci usable in breeding (Kuijken et al., 2015). For example, Atkinson et al. (2015) reported a phenotyping platform where root systems grow in 2D on a filter paper for a few days. Platforms where root systems grow in 3D also have been developed (Iyer-Pascuzzi et al., 2010) and used for quantitative trait locus detection (Topp et al., 2013). Most of these platforms generate traits that give a global view of the root architecture. By contrast, the development of individual roots during long periods of time is rarely studied, whereas temporal analyses are more developed for the aerial parts (Lièvre et al., 2016). These studies have been hampered by the difficulty of collecting individual root growth data. In addition, the analysis of structured data, such as root growth rate profiles, is more challenging than the analysis of simple root traits.

The variability of lateral root length along a primary root is a widely observed feature of root systems (for review, see Forde, 2009), having been reported for annual dicots (e.g. sunflower [Helianthus annuus]; Aguirrezabal et al., 1994), annual monocots (e.g. maize [Zea mays]; Varney et al., 1991; Jordan et al., 1993; Wu et al., 2016), and perennials (oak [Quercus robur]; Pagès, 1995; rubber tree [Hevea brasiliensis]; Thaler and Pagès, 1996; and banana [Musa acuminata]; Lecompte et al., 2005). It also has been observed in the model species Arabidopsis (Arabidopsis thaliana; Freixes et al., 2002). Although variability in length likely originates from variability in growth rate, most of these descriptions do not consider growth dynamically. When they do (Pagès, 1995; Thaler and Pagès, 1996), they generally consider that the variability of growth rate profiles forms a continuum but do not investigate a possible structuring into distinct classes. Nevertheless, different lateral root types have been described, in particular in cereals, but these classifications are based on anatomical traits or diameter. Accordingly, three to four lateral root types have been reported in maize (Varney et al., 1991), three in pearl millet (Pennisetum glaucum; Passot et al., 2016) and rice (Oryza sativa; Gowda et al., 2011; Henry et al., 2016), and five in wheat (Triticum aestivum), barley (Hordeum vulgare), and triticale (Triticale hexaploide; Watt et al., 2008).

The variability of lateral root growth is likely an important lever of root system efficiency (Forde, 2009; Pagès, 2011). In order to provide an efficient frame to study this phenomenon and to characterize genetic and/or environmental impacts on that variability, we designed a phenotyping pipeline for producing high-quality spatiotemporal root system development data with a focus on lateral roots. This pipeline combines the SmartRoot image-analysis system (Lobet et al., 2011), which is able to reconstruct consistent spatiotemporal data on the basis of successive snapshots of root system architecture, with temporal and spatial statistical models. We used it to characterize the early developmental patterns of root systems in two cereals, pearl millet and maize. In a first step, lateral root growth rate profiles were analyzed using semi-Markov switching linear models (SMS-LMs; for another application of similar statistical models, see Lièvre et al., 2016). This model-based clustering of growth rate profiles led us to identify three types of lateral root. We also applied this clustering approach to the rootless concerning crown and seminal roots (rtcs) maize mutant affected in auxin signaling and to maize plants exposed to severe shading. We then investigated the relationships between lateral root types and morphological (apical diameter profile in maize) and anatomical (stele diameter and central xylem tracheary element diameter in pearl millet) traits. In a second step, potential dependencies in the succession of lateral root types along the primary root were analyzed using variable-order Markov chains, leading to a precise characterization of the primary root-branching pattern. Our phenotyping pipeline opens the door to a quantitative, model-assisted characterization of developmental patterns of lateral roots to support root system-oriented crop improvement.

RESULTS

Daily images of growing root systems were recorded for 15 and 21 d in a rhizotron system to analyze early root system development and architecture in pearl millet and maize, respectively. These temporal limits were imposed by the root systems reaching the bottom of the rhizotron. The difference between the two species was a consequence of a higher average elongation rate in pearl millet compared with maize. The ability of SmartRoot (Lobet et al., 2011) to cross-link information corresponding to different time points was then used to build consistent spatiotemporal data of root system development and architecture on the basis of the corresponding series of images. We chose to decompose the analysis of these spatiotemporal data into two steps. (1) Temporal analysis. We first analyzed growth rate profiles of lateral roots using SMS-LMs. Lateral roots were classified into types as a by-product of this longitudinal data analysis. (2) Spatial analysis. The intervals between consecutive lateral roots and the succession of lateral root types along the primary root were then analyzed.

A Model-Based Clustering of Lateral Root Growth Rate Profiles Reveals Three Classes of Lateral Root in Pearl Millet and Maize

The data set was composed of growth rate profiles of 1,254 lateral roots from eight plants in pearl millet and of 3,050 lateral roots from 13 plants in maize. The exploratory analysis of these growth rate profiles highlighted a strong longitudinal organization, with growth rates either increasing or decreasing with lateral root age (Fig. 1). The growth rate profiles are essentially divergent after root emergence, and the growth rate dispersion increases with the root age. Hence, lateral roots can be roughly ordered according to their growth rate profiles. This raised the question of a stronger structuring of these longitudinal data beyond a simple ordering of lateral root growth rate profiles. We thus chose to investigate a model-based clustering of these longitudinal data. This raised two types of difficulties: (1) the growth rate profiles were short and highly variable among lateral roots (one to 10 and one to 17 successive growth rates for pearl millet and maize, respectively); and (2) a high proportion of lateral roots were still growing on the last date of measurement. We thus designed a statistical model for clustering growth rate profiles, using only profiles lasting at least 5 d, based on the following assumptions: (1) a growth rate profile is modeled by a single growth phase either censored (to take into account lateral roots still growing on the last date of measurement) or followed by a growth arrest; and (2) changes in growth rate within a growth phase are modeled by a linear trend. This strong parametric assumption is a consequence of the short length of growth rate profiles. Hence, linear trend models should be viewed as instrumental models for clustering growth rate profiles and not as models for fitting each growth rate profile accurately.

Figure 1.

Figure 1.

Open in a new tab

Growth rate profiles of lateral roots. Lateral roots of one pearl millet (top) and one maize (bottom) plant were assigned to the lateral root types A, B, and C (in red, blue, and green, respectively) using the estimated SMS-LMs. Root age refers to the number of days following emergence.

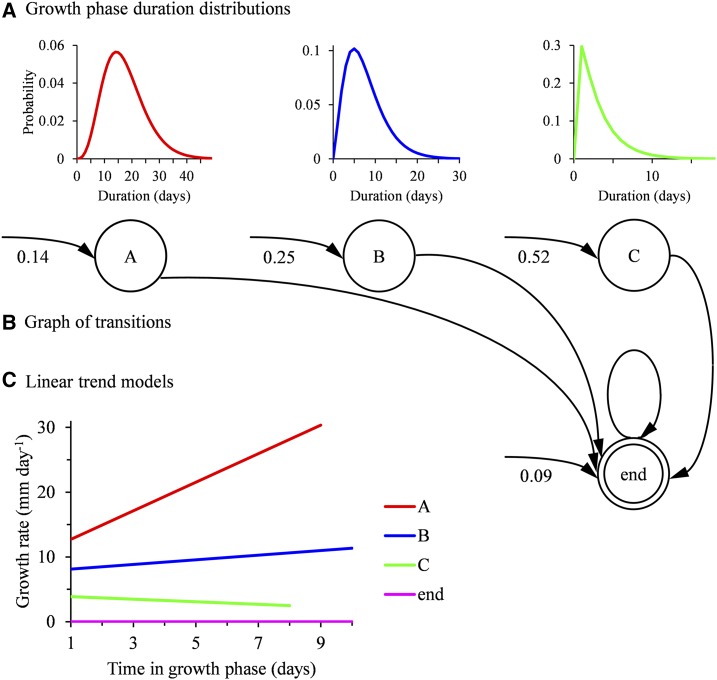
The proposed statistical model is composed of growth states, each corresponding to a lateral root growth rate profile type. A distribution representing the growth phase duration (in days) and a linear model representing changes in growth rate during the growth phase are associated with each of these growth states. Growth states are systematically followed by a growth arrest state. The overall model is referred to as an SMS-LM (for a formal definition, see “Materials and Methods” and Supplemental Methods S1). The number of states of a SMS-LM is thus the number of lateral root types plus one (the single growth arrest state). This kind of integrative statistical model makes it possible to estimate growth phase duration distributions combining complete and censored growth phases. The mechanism associated with an SMS-LM can be described as follows. A growth state is randomly selected according to an initial distribution. This initial distribution represents the lateral root type proportions. A growth phase duration is then randomly selected according to the corresponding distribution of the selected growth state. The growth rate then changes with time according to the linear trend model associated with the selected growth state until the end of the growth phase and the transition to the growth arrest state. In such SMS-LMs, the transitions from the growth arrest state to a growth state are not possible, and each state can be visited at most once (Fig. 2; Supplemental Fig. S1 for pearl millet and maize SMS-LM, respectively).

Figure 2.

Figure 2.

Open in a new tab

Four-state SMS-LM estimated on the basis of pearl millet lateral root growth rate profiles. The three growth states correspond to the lateral root types A, B, and C and the end state to growth arrest. A, Growth phase duration distributions. B, Graph of transitions. The possible transitions between states are represented by arcs (the attached probabilities are always equal to 1). The arcs entering in states indicate initial states, and the attached initial probabilities are noted nearby. C, Linear trend models estimated for each state.

We next had to select the number of growth states (i.e. the number of lateral root types). Because of the specific structure of the model where each state can be visited at most once, the usual model selection criteria such as the Bayesian information criterion do not apply. We thus designed an empirical model selection method for selecting the number of growth states, which is detailed in Supplemental Methods S2 and illustrated by Supplemental Tables S1 and S2 for pearl millet and maize, respectively. We selected for both species three lateral root types that correspond to the best compromise between (1) the proportion of unambiguously assigned lateral roots (between-cluster criterion) and (2) the relative dispersion of growth rate profiles, particularly for the most vigorous root type (within-cluster criterion). Having two classes only would dramatically increase the dispersion for the most vigorous root type (Supplemental Fig. S2 for pearl millet), whereas having four classes would increase the proportion of ambiguously assigned roots (Supplemental Fig. S3). Hence, clustering of lateral roots based on their growth rate profiles revealed three lateral root types in both pearl millet and maize. These three types, ordered in decreasing vigor, will be referred to as A, B, and C.

Growth Phases Are Similar in Both Species

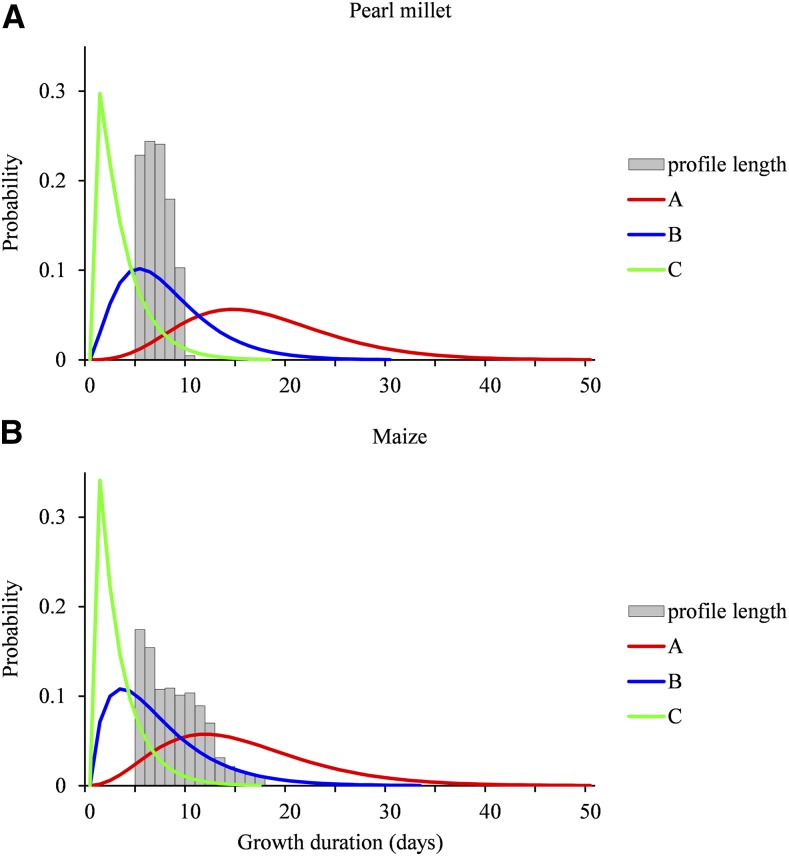
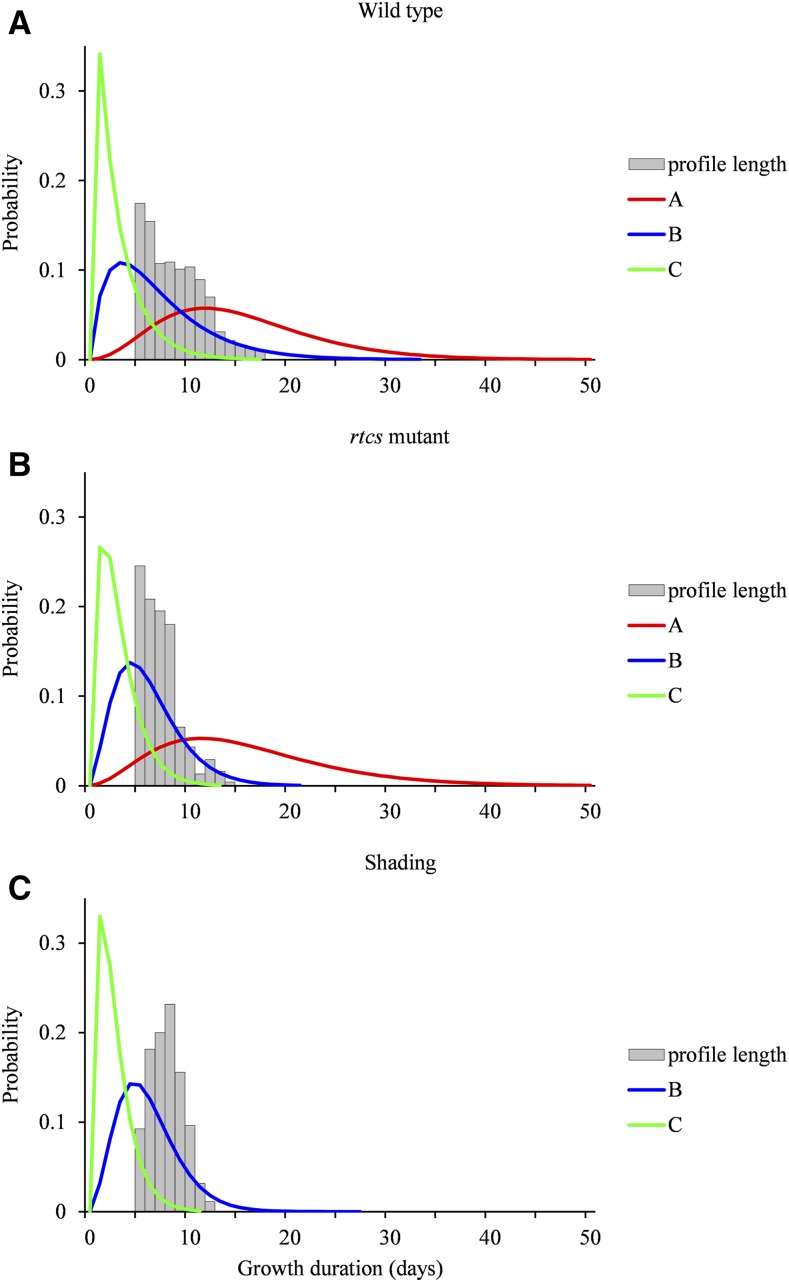
The estimated growth phase duration distributions are similar for each lateral root type between pearl millet and maize (Table I; Fig. 3). The censoring level is defined as the proportion of growth phase incompletely observed for a given lateral root type (the corresponding lateral roots were still growing on the last date of measurement). The censoring level is high for type A, intermediate for type B, and rather low for type C (Table I). The higher censoring level for pearl millet compared with maize is a direct consequence of the shorter average growth rate profiles for pearl millet (in relation to the faster root growth in this species), since the growth phase duration distributions are similar for the two species. It should be noted that the lengths of the growth rate profiles (i.e. the number of successive growth rates) are similar for the different lateral root types of a given species (Supplemental Fig. S4), suggesting no preferential location of the lateral roots of the different types along the primary root.

Table I. Characteristics (means and sd in d and censoring level [C.L.] in %) of growth phase duration distributions estimated for the three root types within the SMS-LMs for pearl millet and maize (wild-type plants, rtcs mutant, and wild-type plants exposed to shading).

Root Type Pearl Millet Maize
Wild Type rtcs Mutant Shading
Mean sd C.L. Mean sd C.L. Mean sd C.L. Mean sd C.L.
A 17.3 7.6 96.2 15.2 7.7 80.3 15.7 8.6 89.7
B 7.6 4.6 53.6 6.9 5 36.3 5.8 3.3 37 5.8 3 25.6
C 3.2 2.6 13.9 3 2.4 9.7 2.9 1.9 5.1 2.5 1.7 2.5
Open in a new tab

Figure 3.

Figure 3.

Open in a new tab

Growth phase duration distributions in pearl millet and maize. Distributions were estimated for lateral root types A, B, and C within the four-state SMS-LM for pearl millet (A) and maize (B). The relative frequency distributions of the lengths of growth rate profiles are drawn to illustrate the censoring level. Only lengths ≥ 5 corresponding to lateral roots used to build the SMS-LMs are shown.

Comparison of Growth Rate Profiles between the Two Species

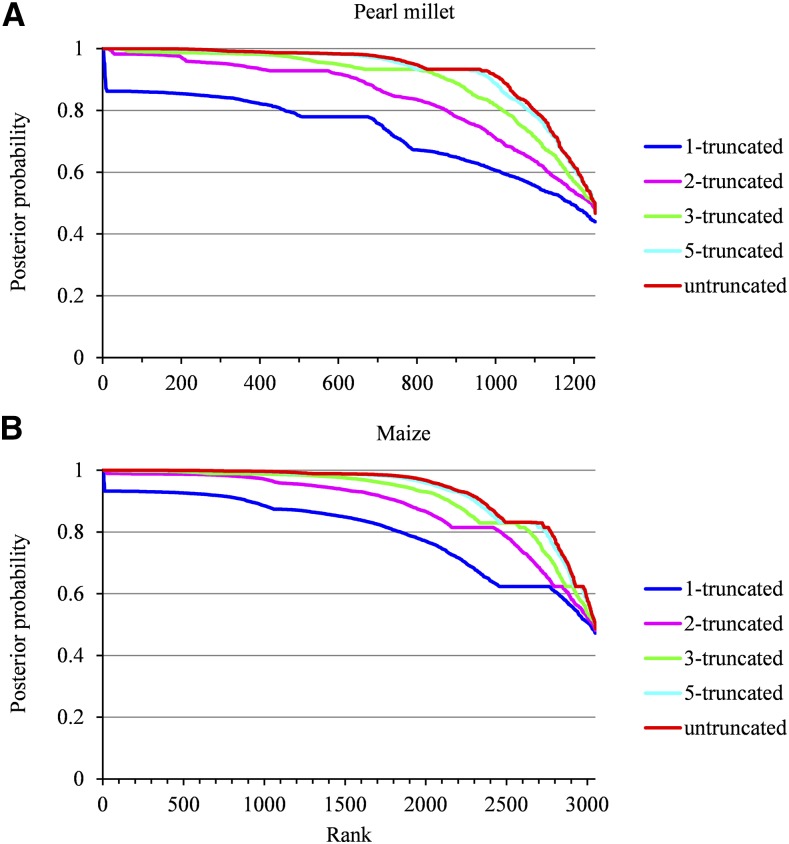
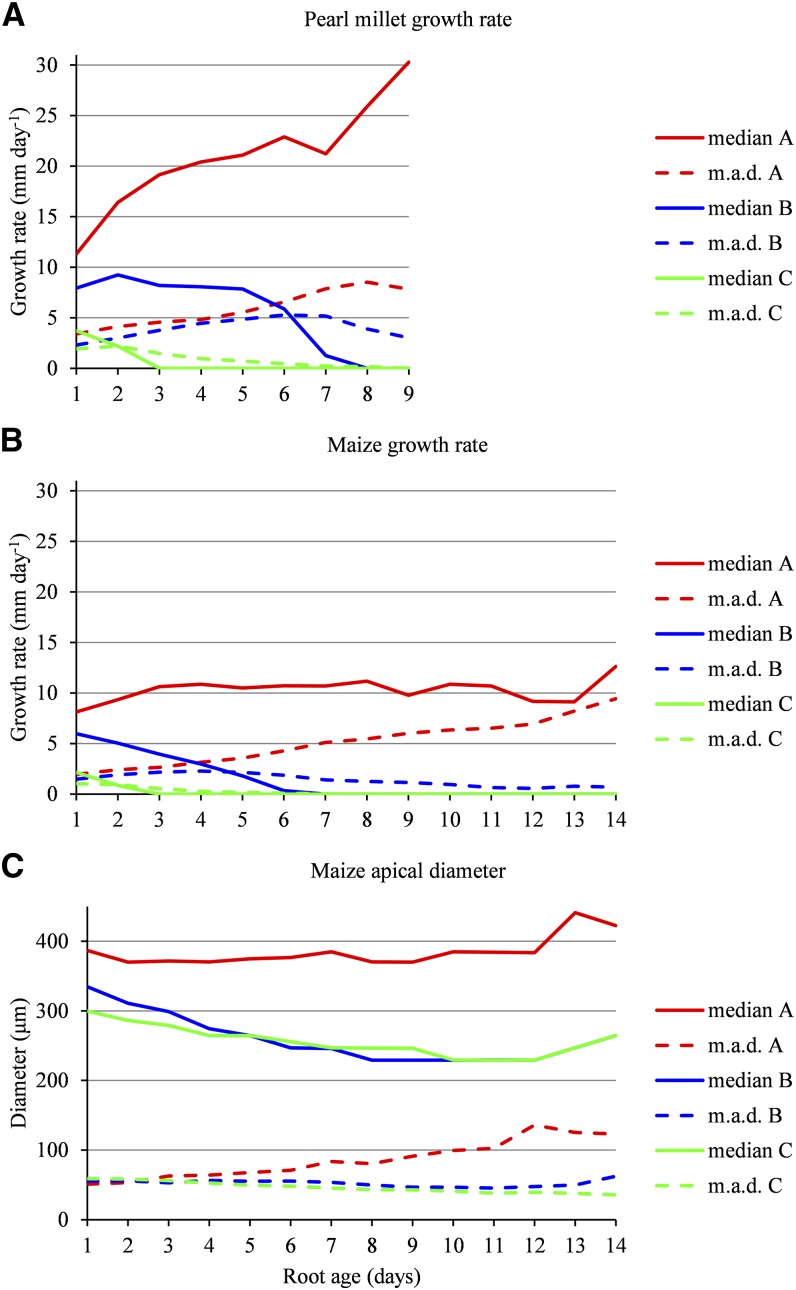
Only growth rate profiles of length ≥ 5 (corresponding to 652 lateral roots of cumulative length 4,367 for pearl millet and 2,029 lateral roots of cumulative length 17,257 for maize) were used for the building of SMS-LMs. Once an SMS-LM was built, the growth rate profiles belonging to the learning sample were assigned to lateral root types (see Fig. 1 for examples of clustering of lateral roots in pearl millet and maize). The posterior probabilities of the optimal assignment of growth rate profiles of length ≥ 5 to lateral root types (i.e. weights of the optimal assignment among all the possible assignments) were most often high: 92% above 0.8 and 88% above 0.9 for pearl millet (Supplemental Fig. S3A) and 94% above 0.8 and 81% above 0.8 for maize (Supplemental Fig. S3B), indicating a clear between-cluster separation (Supplemental Methods S2). Growth rate profiles of length < 5 (test sample corresponding to 602 lateral roots of cumulative length 1,945 for pearl millet and 1,021 lateral roots of cumulative length 2,958 for maize) also were assigned to lateral root types using the previously estimated SMS-LM. The posterior probabilities of the optimal assignment of these growth rate profiles to lateral root types were most often high despite the limited information conveyed by these profiles: 83% above 0.8 and 73% above 0.9 for pearl millet (Supplemental Fig. S5A) and 85% above 0.8 and 68% above 0.9 for maize (Supplemental Fig. S5B). These independent assignments constitute clear elements of validation of the clustering assumption. In order to assess the separation of lateral root types during growth, we compared the classification accuracy between growth rate profiles (whatever their length) truncated at successive lengths. Growth rate profiles truncated at length 1, 2, 3, and 5 and untruncated growth rate profiles were assigned to lateral root types (Fig. 4). The posterior probabilities of the optimal assignment of truncated growth rate profiles show that the classification accuracy improves rapidly on the very first days of growth before stabilizing around day 5, consistently with the divergence of growth rate profiles after root emergence (Fig. 1). In both species, daily median growth rates (computed from all the growth rate profiles whatever their length) are divergent between the three types of lateral roots (Fig. 5, A and B). Type A median growth rate stays positive at all ages in both species. Type B median growth rate reaches zero at day 8 in pearl millet and at day 6 in maize, while type C median growth rate reaches zero at day 3 in both species. The main differences between the two species, apart from differences in growth rates, concern (1) type A lateral roots, for which median growth rate continues to increase in pearl millet whereas it stays nearly constant after a few days in maize, and (2) type B lateral roots, for which median growth rate stays nearly constant up to day 5 in pearl millet whereas it starts to decrease immediately after emergence in maize. Dispersions in growth rate profiles are rather similar between the two species for types B and C (see the mean absolute deviation profiles in Fig. 5, A and B). A regular increase in mean absolute deviation with root age can be observed for type A lateral roots in maize. This may be due to the mixing at the later ages within this class of lateral roots whose growth rate started to decrease with lateral roots whose growth rate continued to increase.

Figure 4.

Figure 4.

Open in a new tab

Ranked posterior probabilities of the optimal assignment of each lateral root growth rate profile to a cluster. Growth rate profiles were truncated at length 1, 2, 3, and 5 or left untruncated for pearl millet (A) and maize (B).

Figure 5.

Figure 5.

Open in a new tab

Daily median growth rates and apical diameters of lateral roots in pearl millet and maize. A and B, Daily median growth rates and associated mean absolute deviations (m.a.d.) were computed for pearl millet (A) and maize (B) lateral root types A, B, and C. C, Daily median apical diameters and associated mean absolute deviations were computed for maize lateral root types A, B, and C.

The Apical Diameter Profiles Partially Match the Different Root Types Identified in Maize

The optimal assignment of lateral roots to types computed using the estimated SMS-LM was used to analyze the link between growth rate types and root apical diameter in maize (the lower apical diameter of lateral roots combined with the image resolution did not allow this analysis in pearl millet). Apical diameter profiles (Fig. 5C) clearly distinguish type A (higher diameters) from type B and C lateral roots but not type B from type C lateral roots (see the overlaps between apical diameter distributions for the successive ages in Supplemental Table S3). Apical diameter gradually decreases with root age for types B and C and converges toward median apical diameter around 230 μm. This corresponds to a high proportion of arrested roots and suggests the occurrence of a threshold value for the apical diameter, below which roots will ultimately stop growing.

Linking Lateral Root Growth Rate Profile with Anatomy in Pearl Millet

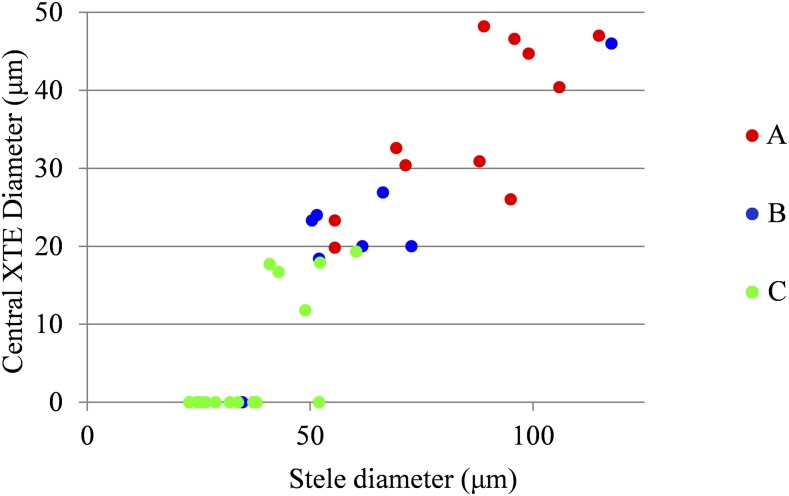
Previous studies have shown that different lateral root types can be defined based on their anatomy in pearl millet (Passot et al., 2016). To explore the links between root growth and root anatomy, we observed cross sections in 35 pearl millet lateral roots with contrasting growth rate profiles. Lateral roots were assigned to one of the three types defined previously, based on their growth rate profiles. Stele diameter and central xylem tracheary element (XTE) diameter, shown previously to be contrasting among individual roots in pearl millet (Passot et al., 2016), were measured. The classification of growth rate profiles in types A, B, and C is mirrored by a ranking of both stele diameter and central XTE diameter, although there is some overlap between types (Fig. 6). This is confirmed by the high Spearman’s rank correlation coefficients between anatomical traits and lateral root types for pearl millet (ρ = 0.81 between stele diameter and lateral root types and ρ = 0.91 between central XTE diameter and lateral root types).

Figure 6.

Figure 6.

Open in a new tab

Relationship between stele and central XTE diameter of lateral roots in pearl millet. Colors indicate the lateral root types determined on the basis of the assignment of growth rate profiles using SMS-LMs.

The Definition of Lateral Root Types Is Affected Neither by a Mutation Altering Auxin Signaling Nor by a Shading Treatment in Maize

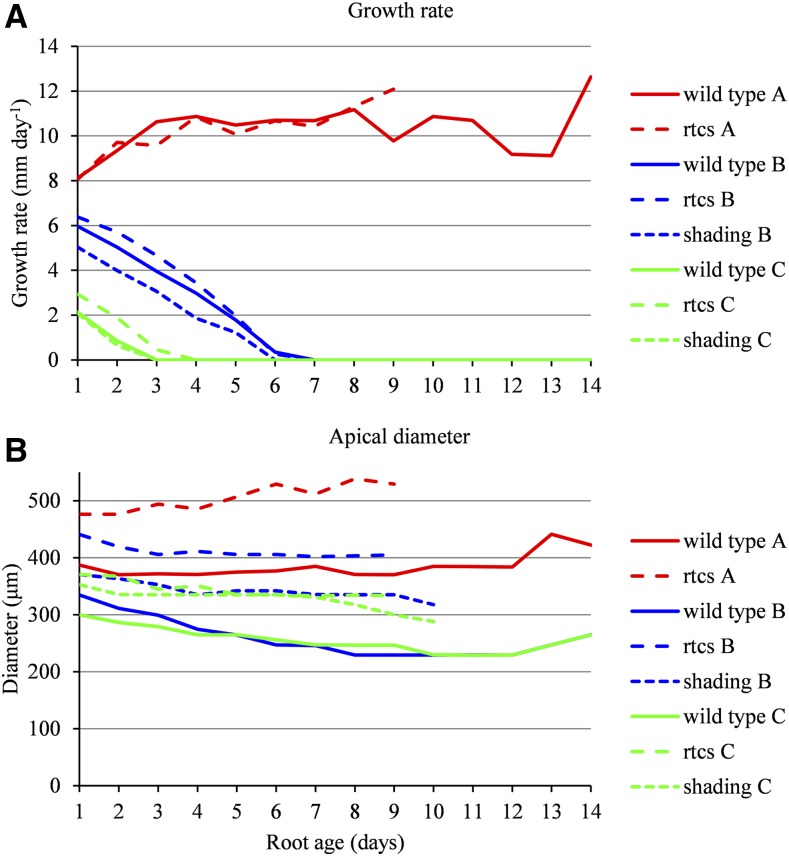
One of the aims of this study was to provide a pipeline of analysis able to account for genetic and environmental effects. We thus analyzed the growth rate profiles of lateral roots of a maize mutant with altered auxin signaling (rtcs mutant; RTCS encodes a LOB-domain transcription factor and carries auxin-responsive elements in its promoter; Taramino et al., 2007) and of wild-type maize plants exposed to severe shading. The data sets were composed of growth rate profiles of 1,597 lateral roots from nine rtcs mutant plants and of 572 lateral roots from six shaded plants. Growth rate profiles of 994 lateral roots of length ≥ 5 (length up to 14 and cumulative length of 7,022) were used for the building of SMS-LMs for the rtcs mutant. Growth rate profiles of 540 lateral roots of length ≥ 5 (length up to 12 and cumulative length of 4,129) were used for the building of SMS-LMs for shaded plants. Applying the empirical model selection procedure described previously, we obtained three lateral root types for the rtcs mutant and two for the shaded plants corresponding to types B and C identified in unshaded wild-type plants. The posterior probabilities of the optimal assignment of growth rate profiles of length ≥ 5 to lateral root types, using the SMS-LMs estimated previously on the basis of these learning samples, were most often high: 91% above 0.8 and 87% above 0.9 for the rtcs mutant and 93% above 0.8 and 80% above 0.9 for the shaded plants, indicating a clear between-cluster separation. Growth rate profiles of length < 5 (test sample corresponding to 603 lateral roots of cumulative length 1,499) also were assigned to lateral root types using the SMS-LM estimated previously for the rtcs mutant. The posterior probabilities of the optimal assignment of these growth rate profiles to lateral root types were most often high despite the limited information conveyed by these profiles: 85% above 0.8 and 50% above 0.9. These independent assignments constitute clear elements of validation of the clustering assumption for the rtcs mutant. The results of independent assignments are not reported for the shaded plants, since there were only 32 growth rate profiles of length < 5 in this case. For both the rtcs mutant and the shaded plants, the growth rate profiles were assigned to lateral root types using both the SMS-LM built on the basis of these lateral roots and the SMS-LM built on the basis of the unshaded wild-type plants. We obtained a match of 94% (938 lateral roots among 994) between the two independent assignments for the rtcs mutant and a match of 91% (492 lateral roots among 540) for the shaded plants, indicating that the lateral root types are robustly defined. The estimated growth phase duration distributions are similar for each lateral root type between the rtcs mutant and the wild-type SMS-LM as well as between the shaded and the unshaded SMS-LMs for types B and C (Fig. 7; Table I). The median growth rate profiles are affected only slightly by the mutation and shading treatment (Fig. 8A; Supplemental Figs. S6 and S7). In summary, the definition of lateral root types remains robust irrespective of the genotype or the environmental treatment. Differences from the control wild type concerned (1) the absence of type A lateral roots for the shaded plants and (2) the higher proportion of type B lateral roots compensated by a lower proportion of type C lateral roots for the rtcs mutant and a higher proportion of type C lateral roots for the shaded plants (Table II). Results concerning the shaded plants are consistent with the expectation of an inhibition of root growth in relation to a restriction in the supply of carbohydrates. Moreover, we could observe (3) larger diameters compared with the wild type for all root types in the rtcs mutant and for type C in the shaded plants (Fig. 8B) and (4) a hierarchy in apical diameter profiles between types B and C for the rtcs mutant, whereas type B and C apical diameter profiles are confounded in both wild-type and shaded plants (Fig. 8B; Supplemental Table S3).

Figure 7.

Figure 7.

Open in a new tab

Growth phase duration distributions in wild-type, rtcs mutant, and shaded maize. Distributions were estimated for lateral root types A, B, and C within the SMS-LM for wild-type (A), rtcs mutant (B), and shaded (C) maize. The relative frequency distributions of the lengths of growth rate profiles are drawn to illustrate the censoring level. Only lengths ≥ 5 corresponding to lateral roots used to build the SMS-LMs are shown.

Figure 8.

Figure 8.

Open in a new tab

Daily median growth rates and apical diameters of lateral roots in wild-type, rtcs mutant, and shaded maize. Daily median growth rates (A) and apical diameters (B) were computed for lateral root types A, B, and C of wild-type, rtcs mutant, and shaded maize.

Table II. Proportions (%) of lateral root types in pearl millet and maize (wild-type plants, rtcs mutant, and wild-type plants exposed to shading).

Root Type Pearl Millet Maize
Wild Type rtcs Mutant Shading
A 13.3 8.1 8
B 23.8 27.3 34.4 26
C 62.9 64.6 57.6 74
Open in a new tab

Identification of a Stationary Random Primary Root-Branching Pattern

In order to characterize the primary root-branching pattern in both pearl millet and maize, we first analyzed the length of the intervals between consecutive lateral roots and then the potential dependencies between successive lateral root types (A, B, and C) along the primary root. We first evaluated the impact of the root type on the length of the interval between a lateral root and its nearest neighbor in the rootward direction. No difference was found between the mean interval length for the three root types in both species (ANOVA, P = 0.83 and 0.33 for pearl millet and maize, respectively; Table III). The same type of analysis was conducted, splitting intervals into nine groups, depending on the types of the two lateral roots delimiting the interval (Supplemental Tables S4 and S5 for pearl millet and maize, respectively). No effect of the lateral root types was found on the interval lengths (ANOVA, P = 0.52 and 0.15 for pearl millet and maize, respectively). Hence, there is no influence of the root types on the length of the interval between two consecutive lateral roots.

Table III. Lengths of the intervals between successive lateral roots classified according to the type of lateral roots delimiting the interval in the shootward direction (sample size and mean and sd in mm for each type).

No significant differences between the means were found (ANOVA, P = 0.83 and P = 0.33 for pearl millet and maize, respectively).

Parameter Pearl Millet Maize
A B C A B C
Sample size 165 296 785 249 830 1,958
Mean 2.2 2.1 2.1 1.6 1.6 1.7
sd 2.7 2.7 1.9 1.6 1.5 1.5
Open in a new tab

We then analyzed the potential dependencies within lateral root type sequences, ignoring the length of the intervals between consecutive lateral roots (the branching sequences from the collar rootward were thus simply indexed by the rank of the successive lateral roots along the primary root). We first computed the Spearman’s rank autocorrelation function for these sequences (the lateral root type can be considered as a categorical ordinal variable with the three possible ordered categories A, B, and C). This autocorrelation function measures the correlation between ordinal variables at different distances apart. The autocorrelation function for positive lags is within the confidence interval corresponding to the randomness assumption for most of the plants (Supplemental Fig. S8, A–D), indicating that the distribution of the lateral root types along the primary root was stationary and suggesting no marked dependencies between successive lateral root types. This finding is consistent with the similar frequency distributions of the length of growth rate profiles for the three lateral root types (Supplemental Fig. S4). Since the length of a growth rate profile depends directly on the time of emergence of the lateral root and is thus related to its position along the primary root, this suggests that the proportions of the three lateral root types along the primary roots were roughly stationary. For some individuals (one for pearl millet and four for maize), the autocorrelation function fluctuates around the positive confidence limit (Supplemental Fig. S8, E and F), indicating a slight nonstationarity. We further investigated primary root-branching sequences applying a statistical modeling approach. To this end, we modeled potential dependencies between successive lateral root types along the primary roots. Three-state variable-order Markov chains, each state corresponding to a lateral root type, were built. The memories of variable-order Markov chains were selected (Csiszár and Talata, 2006) for each primary root-branching sequence and for samples of branching sequences corresponding to each species. For all plants and for both species, a zero-order Markov chain was selected. This confirmed that the type of a lateral root was independent of the type of the previous lateral roots. Hence, our results indicate that there is no influence of the lateral root growth pattern on the distance to or on the growth pattern of the next lateral root in pearl millet and maize.

Interindividual Variability of the Branching Pattern

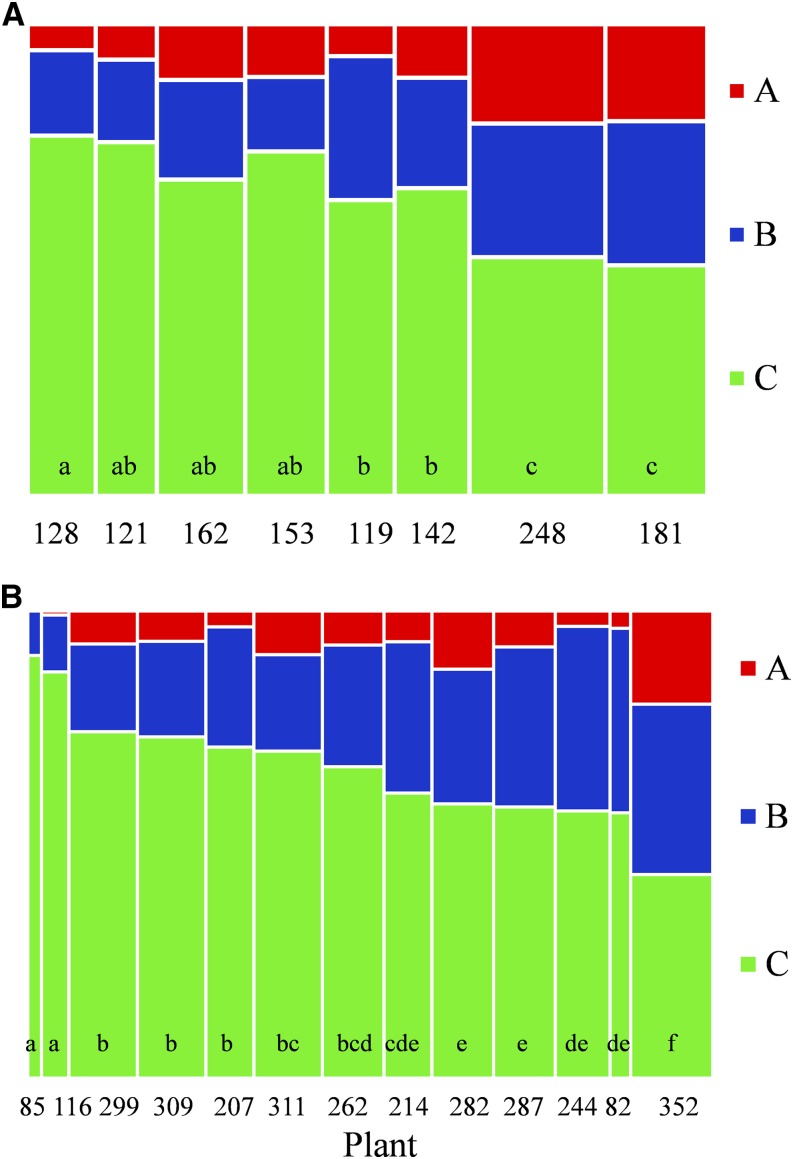
We evaluated the variability of the length of the interval between consecutive lateral roots and of the proportions of lateral root types among individual plants for each species. The mean interval lengths were not equal in all plants (ANOVA, P < 10−5 for pearl millet and P < 10−6 for maize). Plants were thus classified according to Tukey’s honest significant difference test. Two overlapping groups were found for both pearl millet and maize (Supplemental Fig. S9), with average interval length ranging from 0.21 to 0.31 cm in pearl millet and from 0.14 to 0.25 cm in maize. Significant differences among plants also were found for lateral root type proportions for both pearl millet and maize (Kruskal-Wallis test, P < 10−10 and P < 10−15 respectively; Fig. 9). For pearl millet, the eight plants were separated into three groups, with two groups overlapping and the type A lateral root proportion ranging from 0.06 to 0.21. The 13 maize plants were separated into six groups, with some overlaps between groups and the type A lateral root proportion ranging from 0 to 0.2. These results indicate that both species show significant between-individual differences in terms of length of intervals between consecutive lateral roots and lateral root type proportions. These differences were related neither to plant biomass, seed biomass, nor total root system length (data not shown). However, despite differences between plants in terms of lateral root type proportions, the stationary random branching pattern is markedly conserved in all plants.

Figure 9.

Figure 9.

Open in a new tab

Proportions of lateral root types. Proportions are shown for pearl millet (A) and maize (B) plants. Plants were assigned to groups (indicated by letters) using the Kruskal-Wallis test. Bin areas are proportional to the number of lateral roots of each type. Bin widths are proportional to the total number of lateral roots per plant (indicated below each bin).

DISCUSSION

A New Longitudinal Data Analysis Approach to Identify Lateral Root Types Based on Growth Rate Profiles

In this study, we designed a pipeline for analyzing lateral root growth rate profiles and primary root-branching pattern and applied it to explore the diversity of lateral roots in two cereals, pearl millet and maize. Previous efforts to classify lateral roots in cereal species have been reported (Varney et al., 1991; Watt et al., 2008; Rebouillat et al., 2009; Henry et al., 2016; Passot et al., 2016), but these classifications were often based on anatomical traits, mainly root diameter and vasculature. A first difficulty comes from the fact that some morphological traits change along lateral roots, typically root diameter (Wu et al., 2016), which was confirmed in our maize data. A different classification method, based on growth rates, was reported in rice (Rebouillat et al., 2009), for which growth rates were highly contrasting among lateral roots but assignment to classes was based on expert knowledge. In oak, lateral roots were classified based on empirical thresholds applied to individual growth rates (Pagès, 1995). Here, we assigned lateral roots to classes based on their growth rate profiles using dedicated statistical models. A strength of these statistical models is the capability to optimally combine complete and censored growth rate profiles, since some lateral roots were still growing at the end of the experiment. Our approach revealed three similar types of lateral roots in two different cereal species. In previous studies, three anatomical types of lateral roots were identified in maize (Varney et al., 1991; Moreno-Ortega et al., 2017) and pearl millet (Passot et al., 2016), and our results in pearl millet confirm that these types are well related to the types obtained from our model-based clustering of growth rate profiles. In maize, the root apical diameter profiles were at least partly linked to growth rate profiles, confirming a behavior already seen in other species, such as oak or rubber tree (Pagès, 1995; Thaler and Pagès, 1996), where diameter and growth rate change in parallel. Taken together, our results thus suggest that these changes observed at the macroscopic scale are at least partly linked to temporal changes in root anatomy and vasculature.

Variability between plants is known to be particularly high for root systems (Williamson et al., 2001; Aschehoug and Callaway, 2014), and this, in principle, hampers our capacity to identify patterns within a given architecture. Our classification was sufficiently robust to accommodate the high interindividual variability among replicate plants within the same experimental setup. We failed to identify the sources of such variability, since neither seed mass nor leaf area was able to account for differences among individuals, in line with the idea that interindividual variability could be an intrinsic property of root systems (Forde, 2009). Our classification also was sufficiently robust to accommodate genetic (mutation in auxin signaling) and environmental (severe shading) variations, showing that these sources of variation translate into altered proportions of lateral root types, not into a redefinition of each type. The strong reduction of mean lateral root length upon shading was expected (Muller et al., 1998; Freixes et al., 2002), but our analysis revealed that this effect was the result of the complete disappearance of vigorous, fast-growing lateral roots and a large increase in the proportion of lateral roots showing a rapid growth cessation. A mutation in auxin signaling, which controls the formation of nodal roots (Hetz et al., 1996), had only a limited impact on the proportion of the three lateral root types, whereas it had great impact on lateral root diameter. This suggests that our pipeline of analysis can be used to identify and characterize growth patterns within complex and variable architectures and to evaluate related functional hypotheses, such as the impact of hormone signaling (De Smet et al., 2003; Lavenus et al., 2013) or carbohydrate availability (Bingham and Stevenson, 1993).

Origin and Fate of the Three Lateral Root Types

The identification of three lateral root types raises questions about their origin during development. In rice, fast-growing lateral roots also are thicker, and additional periclinal cell divisions in the endodermal cell layer producing additional mesodermal cell layers during the process of primordia establishment have been reported in these large lateral roots (Rebouillat et al., 2009). Variability in the size of different lateral root primordia has been reported in maize (MacLeod, 1990) and could account for differences in apical diameter, at least at emergence. Accordingly, it has been proposed that lateral root variability would be determined early in development and would be tightly associated with morphology and anatomy (Thaler and Pagès, 1996). The relationship between root anatomy (stele and central XTE diameter) and types based on growth rate profile, evidenced in pearl millet, goes in this direction. In maize, lateral root types also could be well defined based on stele and vessel diameters (Varney et al., 1991), and it will be necessary to explore the match between anatomy and growth patterns in this species. Root diameters at emergence also are ranked according to growth rate profiles in maize, but this ranking is not strict, as shown by the large overlap of apical diameters between lateral root types. Another possibility is that growth rate variability would be determined after emergence in order to adapt in a more plastic manner to the local environmental conditions the roots encounter. Such plasticity is commonplace in root systems, and lateral roots are the most dynamic place for this plasticity (Drew, 1975; Farrar and Jones, 1986). The parallel between apical root diameter profiles and growth rate profiles in maize also is in favor of a progressive assignment of roots into one of the three types. These two hypotheses may not be exclusive, and growth patterns may result from a combination of these two influences that would occur preemergence and postemergence. Factors influencing initial growth rate, growth maintenance, and growth arrest also could be different, therefore rendering the picture more complex and leading to developmental patterns of lateral roots globally more plastic to face a variability of external and internal cues (Malamy, 2005). Interestingly, we showed recently in maize that the typology of growth patterns found in this study matches a typology of meristem length being far longer in type A lateral roots compared with type B lateral roots (means of 450 and 280 µm, respectively) and lacking in type C lateral roots (Moreno-Ortega et al., 2017). Moreover, meristem length variation was associated with a variation of the length of the elongation zone, suggesting that growth variation is the result of coordinated variations in both cell production and cell expansion (Moreno-Ortega et al., 2017).

Which Role for the Three Lateral Root Types?

The sharing of tasks between the three lateral root types could contribute to the overall root system efficiency in front of a changing and unpredictable environment. In maize, short roots (i.e. type C roots) with xylem differentiated down to the tip are suspected to facilitate water uptake (Varney and McCully, 1991; Wang et al., 1994). In rice, the presence of short, thin, and abundant lateral roots has been interpreted functionally as super root hairs (Nestler et al., 2016), increasing the root surface area and nutrient uptake, in particular for immobile ions such as phosphorus, while at the same time having a low carbon cost as compared with long lateral roots. By contrast, long lateral roots (i.e. type A roots) may contribute to widen the exploration in the horizontal dimension beyond the limited horizon explored by nodal roots, in opposition to exploration in depth covered by the primary root. They also contribute to the buildup of the overall root architecture, since only long lateral roots participate in higher levels of branching (Gowda et al., 2011). In perennials, only long lateral roots contribute to the perennial structure of the plant (Coutts, 1987). The functional efficiency of the root system also may be linked to the proportions of these different lateral root types. The production of too many long lateral roots is likely counterproductive because of their carbon cost as well as competition among individual roots for the capture of mobile soil resources such as water or nitrate (Lynch, 2018). Finally, the plasticity of the proportions of these different lateral root types also could contribute to the efficiency of the root system. In rice, the proportions of short and long lateral roots are highly plastic in response to low phosphorus, and there exists some genetic variability of this plasticity (Vejchasarn et al., 2016). The role of type B lateral roots is more speculative, but they could constitute a tradeoff between the two opposite strategies of type A and C lateral roots. They also could constitute a pool of potentially fast-growing roots if conditions are favorable. The added value of this overall variability and plasticity to enhance root-foraging capacity was already suggested (Forde, 2009), while its cost-benefit advantage compared with more homogenous lateral root patterns was demonstrated using simulated root systems (Pagès, 2011). In our case, the type A roots, the most expensive roots to construct (because of their length and diameter), represented only 13.3% and 8.1% of the lateral roots in pearl millet and maize, respectively. Thus, early growth cessation could well be an important strategy to avoid an excessive cost of the root system, therefore increasing the efficiency of each carbon molecule invested.

The Positioning of the Three Lateral Root Types Is Random along the Primary Root

One benefit of the proposed approach is that it enables a model-based architectural analysis. All lateral roots were assigned to types and precisely positioned along the primary root. We showed that, in both pearl millet and maize, the longitudinal spacing of lateral roots was highly variable, both within and between root systems. Our analyses showed that there was no relationship between the length of the interval between two successive lateral roots and the types of these lateral roots and that the succession of lateral root types was random along the primary root. If confirmed, this would tend to rule out the hypothesis of a negative signal emanating from, for example, a fast-growing root to prevent another fast-growing root to grow in its neighborhood. Moreover, the absence of relationship between lateral root spacing and growth rate suggests that lateral root initiation and later development are regulated independently. These various hypotheses could be challenged using mutants affected in some of the hormonal (e.g. auxin or cytokinin) checkpoints associated with initiation (Lavenus et al., 2013).

A New Experimental Design Is Required for Studying the Whole Growth Profile of Type A Lateral Roots

The experiment duration constrained by the rhizotron dimensions restricted observations to the beginning of type A lateral root growth. Hence, most of the growth rate profiles assigned to type A lateral roots were censored for both species. This makes a marked difference with type B and C lateral roots, for which the whole growth profile, up to growth arrest, was observed for a large proportion of individuals. Hence, it would be useful to design larger rhizotrons or to change the growth conditions in order to study the whole growth of type A lateral roots and, in particular, the transition from increasing or stationary growth rate to decreasing growth rate. In order to capture such behavior, the proposed modeling framework can be extended directly by adding states in series for modeling successive growth phases for type A lateral roots. Such an extension of semi-Markov switching models with states in series was developed recently for modeling successive developmental phase in Arabidopsis rosettes by Lièvre et al. (2016). We may expect a single state with decreasing growth rate following the current increasing growth rate state A or an intermediate roughly stationary growth state between the increasing and decreasing growth rate states. This would shed light on the future of indeterminate lateral roots, which, to date, is not documented, contrary to the mechanisms associated with growth arrest (Varney and McCully, 1991). In particular, it would be interesting to see if this future interferes with the decay of the primary root system reported in cereals, occurring, for example, within 2 months in pearl millet (Maiti and Bidinger, 1981).

An Avenue for Considering the Diversity of Lateral Roots in Future High-Throughput Phenotyping and Genetic Analyses

To date, genetic improvement based on structural features of the root system has essentially concentrated on its overall architecture, such as deep versus shallow rooting (Saengwilai et al., 2014), and on anatomy, such as the presence of aerenchyma in maize roots, which are suspected to decrease the carbon construction cost of roots without affecting their function (Zhu et al., 2010). Lateral roots have been comparatively overlooked, although they represent the best example of the overall structural plasticity of the root system to face the variable and unpredictable nature of the soil environment encountered (Drew, 1975). Therefore, there could exist a mine of genetic variation to exploit (and not only in cereals) if relevant phenotyping methods for characterizing the diversity of lateral roots were available. Depending on the environments for which genotypes are bred, it could be worth favoring or limiting the variability of lateral fates (Lynch, 2018). By combining image analysis and statistical modeling, our phenotyping pipeline is a step in this direction.

MATERIALS AND METHODS

Plant Growth

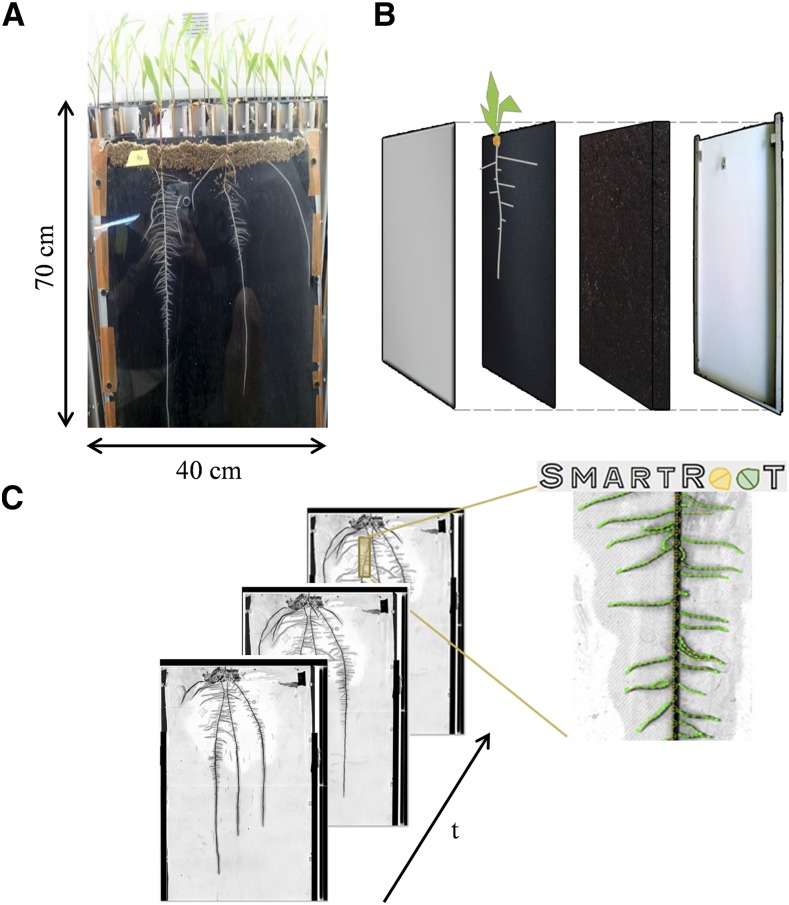
Pearl millet (Pennisetum glaucum) inbred line LCICMB1 (Passot et al., 2016) and maize (Zea mays) hybrid B73 × UH007 (referred to as the wild type) and rtcs mutants in the B73 background (Taramino et al., 2007; kindly provided by Frank Hochholdinger, University of Bonn) were used in this study. Root observation boxes (rhizotrons) were built according to Neufeld et al. (1989). The size of the frame was 40 cm × 70 cm, so that they could be imaged with two contiguous A3 images using a scanner (Fig. 10). The root system was sandwiched against a plexiglass surface by a layer of viscose that was impermeable to roots but permeable to water and nutrients. Rhizotrons were made of (back to front) a 5-mm-thick extruded polystyrene plate, a 2-cm layer of substrate, a layer of viscose, and a 5-mm-thick plexiglass plate, all joined together using aluminum U frames held by screws. The substrate used was composed of 30% (v/v) fine clay, 25% (v/v) peat fibers, 5% (v/v) blond peat, and 40% (v/v) frozen black peat (Klasmann-Deilmann). The substrate was sieved before using. The rhizotrons were weighed individually before and after filling to determine the weight of substrate contained in each one and later to manage daily irrigation.

Figure 10.

Figure 10.

Open in a new tab

Rhizotron development and root system measurement. Root observation boxes (rhizotrons) were built according to Neufeld et al. (1989). A and B, Rhizotrons were made of (back to front) an extruded polystyrene plate, a layer of substrate (sieved peat and compost), a layer of viscose (impermeable to roots but permeable to water and nutrients), and a plexiglass plate, all joined together using aluminum U frames held by screws. Germinated seedlings with similar primary root lengths were transferred individually. A layer of wet sphagnum on the top of the rhizotrons maintained the seedlings and prevented them from drying. Rhizotrons were placed in a growth room with climatic conditions adapted to each species. Rhizotrons were scanned daily with an A3 scanner. C, The SmartRoot software (Lobet et al., 2011) was used to extract root system architecture at successive dates and to compute root growth parameters.

Maize seeds were surface sterilized with 6% (v/v) hypochlorite for 5 min and rinsed in distilled water for 1 min. Seeds were then germinated on moistened filter paper in petri dishes (20 cm × 20 cm) and placed vertically in a growth chamber in the dark at 20°C. Pearl millet germination was performed with a similar protocol, except that seeds also were cleaned with ethanol solution (70% [v/v]) for 5 min after the first rinsing and germination temperature was set to 30°C. Germinated seedlings with similar primary root lengths were transferred individually in the rhizotrons. A layer of wet sphagnum on the top of the rhizotrons maintained the seedlings and prevented them from drying. Rhizotrons were placed in a growth room with climatic conditions adapted to each species: a temperature of 28°C during the day and 24°C during the night for pearl millet and a constant temperature of 20°C for maize, with a 14-h photoperiod for both species. Light was provided by six mercury lamps (HQI, 250 W; Osram) and measured by a light sensor (SKP215; Skye Instruments). In our conditions, photosynthetic photon flux density was 300 µmol m−2 s−1. Temperature and air humidity were recorded (HC2-SH; Rotronic) for each growth room. The sphagnum was watered twice per day at the beginning of the experiment and from 6 d after germination onward, and rhizotrons were watered daily using a one-tenth-strength Hoagland solution to maintain the humidity of the substrate. The amount of watering was monitored by a daily weighting of the rhizotron. In one experiment, plants were shaded by installing a net above the plants that reduced light intensity by 75%.

Imaging and Image Processing

From day 2 of growth, rhizotrons were scanned with an A3 scanner (Epson Expression 10000XL Pro) at 600 or 720 dots per inch. The histogram of the gray level intensities was adjusted to optimize the contrast on fine roots. As rhizotrons are twice the size of the scanner, two images (top part and bottom part of the rhizotron) were taken and aligned using Align_4 (http://www.mecourse.com/landinig/software/software.html) to recover an image of the entire root system, thanks to landmarks visible in both parts. These landmarks were either added intentionally on the rhizotron or were present naturally (water drops, the root system itself).

The SmartRoot software (Lobet et al., 2011) was used to extract root system architecture at successive dates as well as root growth parameters because it supports time-lapse images and focuses on the analysis of individual root behavior. SmartRoot needs images where roots appear darker than background. An ImageJ (National Institutes of Health) macro was developed to automatically invert and adjust the contrast of the rhizotron images by scaling the image intensity histogram on a fixed range. The optimal contrast (minimum and maximum values of the intensity range) was determined empirically to reduce the number of errors when using the algorithm for automatic lateral root tracing provided by SmartRoot using a subset of scan images and was applied to the whole set of images using the macro tool.

SmartRoot enables semiautomatic root tracing. The primary root was drawn on the first image. For the next days, the root system traced on the previous day was imported and aligned in such a way that the trace of the primary root elongated progressively, using automatic tracing. Crown and lateral roots were added as they appeared, either manually or using automatic detection. Their lengths increased progressively on the successive scans as for the primary root. When all roots were traced, the data were extracted with the batch export tool of SmartRoot. This tool provides several measurements, including the length, the insertion position, and the diameter for each root. The growth rates were extracted directly from successive length measurements. Because the resolution was not sufficient for pearl millet lateral roots, we only considered root diameter for maize. On average, it took about 2 d to process the data of one plant.

Correction of Growth Rate Profiles

In spite of manual supervision of root tracings, the exported data set contained some digitalization errors. Therefore, it was necessary to characterize the implausible data points resulting from such errors and to clean out the data set. We designed a data correction algorithm aimed at identifying implausible growth rate profiles that derive from errors in image analysis. The most typical errors were defaults in alignment, 1-d missing root length increments, or nonvisible root tips in the case of roots encountering an obstacle. This kind of error results in implausible trajectories for the root length at some time point, which can be better identified by examining growth rate profiles. Depending on the type of error, growth rate profiles were either corrected or truncated before the first implausible growth rate. The data correction algorithm is described in Supplemental Methods S3.

Statistical Models

Definition of SMS-LMs

SMS-LMs are two-scale models that generalize hidden semi-Markov chains by incorporating linear regression models as observation models. They are formally defined in Supplemental Methods S1. In our context, the succession and duration of growth phases (coarse scale) are represented by a nonobservable semi-Markov chain, while the growth rate trend within a growth phase (fine scale) is represented by observation linear models attached to each state of the semi-Markov chain. Hence, each state of the semi-Markov chain represents a growth phase. A J-state semi-Markov chain is defined by three subsets of parameters: (1) initial probabilities (πj; j = 0,…, J − 1) to model which is the first phase occurring in a growth rate profile; (2) transition probabilities (pij; i, j = 0,…, J − 1) to model the succession of growth phases; and (3) occupancy distributions attached to nonabsorbing states (a state is said to be absorbing if, after entering this state, it is impossible to leave it) to model the growth phase duration in number of days. We used, as possible parametric state occupancy distributions, binomial distributions B(d, n, p), Poisson distributions P(d, λ), and negative binomial distributions NB(d, r, p) with an additional shift parameter d ≥ 1.

An SMS-LM adds observation linear models to the nonobserveable semi-Markov chain. We chose to model growth rate trends within growth phases using simple linear regression models because of the short length of growth phases (up to 10 successive growth rates for pearl millet and up to 17 successive growth rates for maize).

An SMS-LM composed of parallel transient states followed by a final absorbing state was estimated on the basis of growth rate profiles corresponding to a given species. A state is said to be transient if, after leaving this state, it is impossible to return to it. The parallel transient states represent alternative growth phases. The final absorbing state represents the growth arrest, and a degenerate linear model corresponding to a constant null growth rate is associated with this state. The censoring level was computed for each growth state as a by-product of the estimation of the corresponding growth phase duration distribution within the SMS-LM. This censoring level takes into account all the possible assignments of growth rate profiles of length ≥ 5 incorporated in the learning sample. Each estimated model was used to compute the most probable state series for each observed growth rate profile (Guédon, 2003). This restored state series can be viewed as the optimal segmentation of the corresponding observed series into at most two subseries corresponding to a given growth phase either censored or followed by a growth arrest. Because of the transient growth states in parallel, this restoration can be interpreted as a classification of the lateral roots on the basis of their growth rate profiles. In the case of the maize rtcs mutant and the shading treatment, the growth rate profiles were segmented using both the model estimated on the corresponding growth rate profiles and the unshaded wild-type model.

Definition of Stationary Variable-Order Markov Chains

Most of the methods for analyzing local dependencies in discrete sequences rely on high-order Markov chains. However, the number of free parameters of a Markov chain increases exponentially with its order (i.e. with the memory length taken into account). For instance, in the case of three states (corresponding to three lateral root types), the number of free parameters is two for a zero-order Markov chain, six for a first-order Markov chain, 18 for a second-order Markov chain, etc. Since there are no models in between, this very discontinuous increase in the number of free parameters causes the estimated high-order Markov chains to be generally overparameterized. This drawback can be overcome by defining subclasses of parsimonious high-order Markov chains such as variable-order Markov chains (Ron et al., 1997; Bühlmann and Wyner, 1999), where the order is variable and depends on the context within the sequences instead of being fixed. Stationary variable-order Markov chains are formally defined in Supplemental Methods S4.

Pearl Millet Root Anatomy

Plants were grown in rhizotrons as described previously. Lateral root growth rate profiles were extracted before sampling to determine the type of each root. Sampling was performed around 15 d after germination. Selected roots were harvested and fixed overnight in an acetic acid:ethanol solution (1:9) and conserved in 70% (v/v) ethanol. Segments were taken around the middle of each lateral root. Root segments were gently dried on a filter paper and imbibed in warm (30°C–45°C) liquid 3% (w/v) agarose solution (SeaKem GTG Agarose; Lonza). Then, 55-µm-thick sections were obtained from solidified agarose blocks using a vibratome (speed 30, frequency 60; Microm HM 650V; Thermo Scientific). Individual root sections were then collected, transferred to microscope slides, and covered with a coverslip for direct observation.

Images were taken using a Leica DMRB microscope equipped with an epifluorescence filter (excitation range, UV; excitation filter, 460–480 nm). Two photographs were taken for each root section: one under visible light using Nomarsky optics and another using epifluorescence that takes advantage of the natural fluorescence of cell walls with secondary deposits. Images were taken using a Retiga SRV FAST 1394 camera and QCapture Pro-7 software. The RGB images were opened in ImageJ using the Bioformats importer plugin and transformed in gray level eight-bit images. A scale bar was added to the images according to their magnification. Measurements of the diameter, stele and metaxylem, and the number of xylem poles and vessels were recorded for each root section.

Supplemental Data

The following supplemental materials are available.

Dive Curated Terms

The following phenotypic, genotypic, and functional terms are of significance to the work described in this paper:

Acknowledgments

We thank Gaëlle Rolland for help during plant phenotyping using SmartRoot, Xavier Draye for fruitful discussions, and Frank Hochholdinger for providing the rtcs seeds.

Footnotes

1

This work was partly funded by the European Union EURoot project (FP7-KBBE-2011-5/289300) and the NewPearl project in the frame of the CERES initiative (Agropolis Fondation AF 1301-015 as part of the Investissement d’avenir ANR-l0-LABX-0001-0l and Fondazione Cariplo FC 2013-0891). S.P.’s PhD was funded by ENS Paris. B.M.-O.’s PhD was partly funded by INRA (Environment and Agronomy Division).

[OPEN]

Articles can be viewed without a subscription.

References

  1. Aguirrezabal LAN, Deleens E, Tardieu F (1994) Root elongation rate is accounted for by intercepted PPFD and source-sink relations in field and laboratory-grown sunflower. Plant Cell Environ 17: 443–450 [Google Scholar]
  2. Aschehoug ET, Callaway RM (2014) Morphological variability in tree root architecture indirectly affects coexistence among competitors in the understory. Ecology 95: 1731–1736 [DOI] [PubMed] [Google Scholar]
  3. Atkinson JA, Wingen LU, Griffiths M, Pound MP, Gaju O, Foulkes MJ, Le Gouis J, Griffiths S, Bennett MJ, King J, et al. (2015) Phenotyping pipeline reveals major seedling root growth QTL in hexaploid wheat. J Exp Bot 66: 2283–2292 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bingham IJ, Stevenson EA (1993) Control of root growth: effects of carbohydrates on the extension, branching and rate of respiration of different fractions of wheat roots. Physiol Plant 88: 149–158 [Google Scholar]
  5. Bishopp A, Lynch JP (2015) The hidden half of crop yields. Nat Plants 1: 15117. [DOI] [PubMed] [Google Scholar]
  6. Bühlmann P, Wyner AJ (1999) Variable length Markov chains. Ann Stat 27: 480–513 [Google Scholar]
  7. Coutts MP. (1987) Developmental processes in tree root systems. Can J For Res 17: 761–767 [Google Scholar]
  8. Csiszár I, Talata Z (2006) Context tree estimation for not necessarily finite memory processes, via BIC and MDL. IEEE Trans Inf Theory 52: 1007–1016 [Google Scholar]
  9. De Smet I, Signora L, Beeckman T, Inzé D, Foyer CH, Zhang H (2003) An abscisic acid-sensitive checkpoint in lateral root development of Arabidopsis. Plant J 33: 543–555 [DOI] [PubMed] [Google Scholar]
  10. Dhondt S, Wuyts N, Inzé D (2013) Cell to whole-plant phenotyping: the best is yet to come. Trends Plant Sci 18: 428–439 [DOI] [PubMed] [Google Scholar]
  11. Drew MC. (1975) Comparison of the effects of a localized supply of phosphate, nitrate, ammonium and potassium on the growth of the seminal root system, and the shoot, in barley. New Phytol 75: 479–490 [Google Scholar]
  12. Fahlgren N, Feldman M, Gehan MA, Wilson MS, Shyu C, Bryant DW, Hill ST, McEntee CJ, Warnasooriya SN, Kumar I, et al. (2015a) A versatile phenotyping system and analytics platform reveals diverse temporal responses to water availability in Setaria. Mol Plant 8: 1520–1535 [DOI] [PubMed] [Google Scholar]
  13. Fahlgren N, Gehan MA, Baxter I (2015b) Lights, camera, action: high-throughput plant phenotyping is ready for a close-up. Curr Opin Plant Biol 24: 93–99 [DOI] [PubMed] [Google Scholar]
  14. Farrar JF, Jones CL (1986) Modification of respiration and carbohydrate status of barley roots by selective pruning. New Phytol 102: 513–521 [Google Scholar]
  15. Forde BG. (2009) Is it good noise? The role of developmental instability in the shaping of a root system. J Exp Bot 60: 3989–4002 [DOI] [PubMed] [Google Scholar]
  16. Freixes S, Thibaud MC, Tardieu F, Muller B (2002) Root elongation and branching is related to local hexose concentration in Arabidopsis thaliana seedlings. Plant Cell Environ 25: 1357–1366 [Google Scholar]
  17. Gowda VRP, Henry A, Yamauchi A, Shashidhar HE, Serraj R (2011) Root biology and genetic improvement for drought avoidance in rice. Field Crops Res 122: 1–13 [Google Scholar]
  18. Guédon Y. (2003) Estimating hidden semi-Markov chains from discrete sequences. J Comput Graph Stat 12: 604–639 [Google Scholar]
  19. Henry S, Divol F, Bettembourg M, Bureau C, Guiderdoni E, Périn C, Diévart A (2016) Immunoprofiling of rice root cortex reveals two cortical subdomains. Front Plant Sci 6: 1139. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hetz W, Hochholdinger F, Schwall M, Feix G (1996) Isolation and characterization of rtcs, a maize mutant deficient in the formation of nodal roots. Plant J 10: 845–857 [Google Scholar]
  21. Iyer-Pascuzzi AS, Symonova O, Mileyko Y, Hao Y, Belcher H, Harer J, Weitz JS, Benfey PN (2010) Imaging and analysis platform for automatic phenotyping and trait ranking of plant root systems. Plant Physiol 152: 1148–1157 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Jordan MO, Harada J, Bruchou C, Yamazaki K (1993) Maize nodal root ramification: absence of dormant primordia, root classification using histological parameters and consequences on sap conduction. Plant Soil 153: 125–143 [Google Scholar]
  23. Kuijken RCP, van Eeuwijk FA, Marcelis LFM, Bouwmeester HJ (2015) Root phenotyping: from component trait in the lab to breeding. J Exp Bot 66: 5389–5401 [DOI] [PubMed] [Google Scholar]
  24. Lavenus J, Goh T, Roberts I, Guyomarc’h S, Lucas M, De Smet I, Fukaki H, Beeckman T, Bennett M, Laplaze L (2013) Lateral root development in Arabidopsis: fifty shades of auxin. Trends Plant Sci 18: 450–458 [DOI] [PubMed] [Google Scholar]
  25. Lecompte F, Pagès L, Ozier-Lafontaine H (2005) Patterns of variability in the diameter of lateral roots in the banana root system. New Phytol 167: 841–850 [DOI] [PubMed] [Google Scholar]
  26. Lièvre M, Granier C, Guédon Y (2016) Identifying developmental phases in the Arabidopsis thaliana rosette using integrative segmentation models. New Phytol 210: 1466–1478 [DOI] [PubMed] [Google Scholar]
  27. Lobet G, Pagès L, Draye X (2011) A novel image-analysis toolbox enabling quantitative analysis of root system architecture. Plant Physiol 157: 29–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lynch JP. (2018) Rightsizing root phenotypes for drought resistance. J Exp Bot (in press) [DOI] [PubMed] [Google Scholar]
  29. MacLeod RD. (1990) Lateral root primordium inception in Zea mays L. Environ Exp Bot 30: 225–234 [Google Scholar]
  30. Maiti RK, Bidinger FR (1981) Growth and Development of the Pearl Millet Plant. International Crops Research Institute for the Semi-Arid Tropics, Patancheru, India [Google Scholar]
  31. Malamy JE. (2005) Intrinsic and environmental response pathways that regulate root system architecture. Plant Cell Environ 28: 67–77 [DOI] [PubMed] [Google Scholar]
  32. Moreno-Ortega B, Fort G, Muller B, Guédon Y (2017) Identifying developmental zones in maize lateral root cell length profiles using multiple change-point models. Front Plant Sci 8: 1750. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Muller B, Stosser M, Tardieu F (1998) Spatial distributions of tissue expansion and cell division rates are related to irradiance and to sugar content in the growing zone of maize roots. Plant Cell Environ 21: 149–158 [Google Scholar]
  34. Nestler J, Keyes SD, Wissuwa M (2016) Root hair formation in rice (Oryza sativa L.) differs between root types and is altered in artificial growth conditions. J Exp Bot 67: 3699–3708 [DOI] [PubMed] [Google Scholar]
  35. Neufeld HS, Durall DM, Rich PM, Tingey DT (1989) A rootbox for quantitative observations on intact entire root systems. Plant Soil 117: 295–298 [Google Scholar]
  36. Pagès L. (1995) Growth patterns of the lateral roots of young oak (Quercus robur) tree seedlings: relationship with apical diameter. New Phytol 130: 503–509 [DOI] [PubMed] [Google Scholar]
  37. Pagès L. (2011) Links between root developmental traits and foraging performance. Plant Cell Environ 34: 1749–1760 [DOI] [PubMed] [Google Scholar]
  38. Passot S, Gnacko F, Moukouanga D, Lucas M, Guyomarc’h S, Ortega BM, Atkinson JA, Belko MN, Bennett MJ, Gantet P, et al. (2016) Characterization of pearl millet root architecture and anatomy reveals three types of lateral roots. Front Plant Sci 7: 829. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Rebouillat J, Dievart A, Verdeil JL, Escoute J, Giese G, Breitler JC, Gantet P, Espeout S, Guiderdoni E, Périn C (2009) Molecular genetics of rice root development. Rice (N Y) 2: 15–34 [Google Scholar]
  40. Ron D, Singer Y, Tishby N (1997) The power of amnesia: learning probabilistic automata with variable memory length. Mach Learn 25: 117–149 [Google Scholar]
  41. Saengwilai P, Tian X, Lynch JP (2014) Low crown root number enhances nitrogen acquisition from low-nitrogen soils in maize. Plant Physiol 166: 581–589 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Taramino G, Sauer M, Stauffer JL Jr, Multani D, Niu X, Sakai H, Hochholdinger F (2007) The maize (Zea mays L.) RTCS gene encodes a LOB domain protein that is a key regulator of embryonic seminal and post-embryonic shoot-borne root initiation. Plant J 50: 649–659 [DOI] [PubMed] [Google Scholar]
  43. Thaler P, Pagès L (1996) Root apical diameter and root elongation rate of rubber seedlings (Hevea brasiliensis) show parallel responses to photoassimilate availability. Physiol Plant 97: 365–371 [Google Scholar]
  44. Topp CN, Iyer-Pascuzzi AS, Anderson JT, Lee CR, Zurek PR, Symonova O, Zheng Y, Bucksch A, Mileyko Y, Galkovskyi T, et al. (2013) 3D phenotyping and quantitative trait locus mapping identify core regions of the rice genome controlling root architecture. Proc Natl Acad Sci USA 110: E1695–E1704 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Varney GT, McCully ME (1991) The branch roots of Zea. II. Developmental loss of the apical meristem in field-grown roots. New Phytol 118: 535–546 [Google Scholar]
  46. Varney GT, Canny MJ, Wang XL, McCully ME (1991) The branch roots of Zea. I. First order branches, their number, sizes and division into classes. Ann Bot 67: 357–364 [Google Scholar]
  47. Vejchasarn P, Lynch JP, Brown KM (2016) Genetic variability in phosphorus responses of rice root phenotypes. Rice (N Y) 9: 29. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Wang XL, McCully ME, Canny MJ (1994) The branch roots of Zea. IV. The maturation and openness of xylem conduits in first-order branches of soil-grown roots. New Phytol 126: 21–29 [Google Scholar]
  49. Watt M, Magee LJ, McCully ME (2008) Types, structure and potential for axial water flow in the deepest roots of field-grown cereals. New Phytol 178: 135–146 [DOI] [PubMed] [Google Scholar]
  50. Williamson LC, Ribrioux SPCP, Fitter AH, Leyser HMO (2001) Phosphate availability regulates root system architecture in Arabidopsis. Plant Physiol 126: 875–882 [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Wu Q, Pagès L, Wu J (2016) Relationships between root diameter, root length and root branching along lateral roots in adult, field-grown maize. Ann Bot 117: 379–390 [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Zhu J, Brown KM, Lynch JP (2010) Root cortical aerenchyma improves the drought tolerance of maize (Zea mays L.). Plant Cell Environ 33: 740–749 [DOI] [PubMed] [Google Scholar]

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES