Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 May 3;8(10):2285–2290. doi: 10.1021/acs.jpclett.7b00682

Two-Dimensional Electronic Spectroscopy Unravels sub-100 fs Electron and Hole Relaxation Dynamics in Cd-Chalcogenide Nanostructures

Tatjana Stoll †, Federico Branchi †, Julien Réhault †, Francesco Scotognella †,‡, Francesco Tassone ‡, Ilka Kriegel §,∥,*, Giulio Cerullo †,*
PMCID: PMC6053257  PMID: 28467717

Abstract

graphic file with name jz-2017-00682h_0005.jpg

We use two-dimensional electronic spectroscopy (2DES) to disentangle the separate electron and hole relaxation pathways and dynamics of CdTe nanorods on a sub-100 fs time scale. By simultaneously exciting and probing the first three excitonic transitions (S1, S2, and S3) and exploiting the unique combination of high temporal and spectral resolution of 2DES, we derive a complete picture for the state-selective carrier relaxation. We find that hot holes relax from the 1Σ3/2 to the 1Σ1/2 state (S2 → S1) with 30 ± 10 fs time constant, and the hot electrons relax from the Σ′ to the Σ state (S3 → S1) with 50 ± 10 fs time constant. This observation would not have been possible with conventional transient absorption spectroscopy due to the spectral congestion of the transitions and the very fast relaxation time scales.

The interest in semiconductor nanocrystals (NCs) has increased rapidly in the last three decades.1 In these types of materials, the quantum confinement effect leads to three peculiar physical phenomena: (i) the emergence of discrete electronic levels, (ii) a shift of the energy gap depending on the size of the NC, and (iii) the enhancement of the Coulomb interaction.2,3 For these reasons, quantum-confined semiconducting NCs can be considered as “artificial atoms”, which offer unique opportunities for controlling electromagnetic energy at the nanoscale. Because of their optical, electronic and transport properties, which can be finely tuned by advanced synthetic approaches,4 NCs have found application in a broad range of fields, including optics,5,6 photovoltaics,7 sensing,8 and electronics.9 Highly complex hybrid nanostructures have been synthesized for photovoltaic and photocatalytic applications,10 where electron and hole contribute separately to the photon-to-electron conversion efficiency. Understanding the carrier relaxation dynamics is of key importance for the design and optimization of such nanostructures.

Spherical NCs of radii of only a few nanometers have been extensively studied in the past, the most widely investigated material being CdSe.11−15 Femtosecond pump–probe spectroscopy is a powerful technique to visualize the electron/hole relaxation pathways and dynamics in real time. Investigations of the cooling dynamics of CdSe NCs as a function of their radius revealed an acceleration of the relaxation of the electron from the 1P to the 1S state with size reduction.11,12,16−19 This observation is in contrast with early theoretical work, predicting a slowdown of this decay process due to the “phonon bottleneck” phenomenon, claiming that for large electronic energy gaps relaxation occurs via interaction with several longitudinal optical phonons of the material.20−23 This discrepancy was resolved by the identification of an Auger relaxation pathway, in which the hot electrons relax by transferring their energy to the more closely spaced holes.24−29 Hole relaxation dynamics, on the contrary, are difficult to extract by conventional pump–probe spectroscopy: In fact, due to the energetic congestion of the states, broadband excitation leads to an overlap of their transient signals, while state-selective excitation with narrowband pulses does not provide sufficient temporal resolution to resolve the fast relaxation dynamics. To overcome this deficiency with classical spectroscopy, ingenious approaches in excitation and probing have been adopted. For instance, it was possible to extract the 2S3/2 to 1S3/2 hole relaxation dynamics in CdSe NCs only by modifying the crystal surface chemistry and thus allowing the hole to be scavenged.30 Pioneering studies have addressed the question of separate electron and hole pathways by employing an exciton selective approach to extract state-to-state exciton dynamics;12,16,18 however, they used indirect measurement techniques, such as subtractive methods.11,18

The emergence of two-dimensional electronic spectroscopy (2DES) techniques31 has pushed the investigation of the effects of quantum confinement on excitonic states even further. 2DES overcomes the limitations of pump–probe spectroscopy, providing simultaneously high temporal and spectral resolution; it can be seen as an extension of pump–probe with the extra capability of resolving the excitation energy dependence of the transient absorption signal. By spreading the information content along two frequency axes (excitation and detection), it allows visualizing couplings and relaxation processes between different transitions. 2DES has been employed to study the quantum coherence of exciton states in CdSe NCs,13−15 the electronic fine structure of PbS NCs,32,33 and the state dynamics of CdSe NCs.34

In this work we apply 2DES to the study of carrier dynamics of cadmium telluride (CdTe) nanorods (NRs), serving as model systems for more complex nanostructures. CdTe is an excellent material for photoenergy conversion, possessing a relatively low bandgap energy of 1.6 eV in bulk and a high absorption cross section. NRs are quasi-1D systems, with confined excitonic states and low degeneracy for hole and electron states close to the band edge.35 Furthermore, heterostructures of this material give the option to spatially separate electron and hole to enhance the exciton dissociation efficiency.1,7,10 Our 2DES setup has a spectral coverage sufficient to access the first three excitons of the NRs simultaneously in excitation and detection and to elucidate their relaxation dynamics and pathways. We show that 2DES provides the unique capability to disentangle the exciton states and to distinguish between electron and hole relaxation dynamics. Our results indicate extremely fast time constants for hot hole relaxation, on the order of 30 fs, and for hot electrons, on the order of ∼50 fs.

CdTe NRs were synthesized as reported elsewhere.36 Their transmission electron microscopy (TEM) image, shown in the inset of Figure 1a, reveals a length of ∼21 nm and a diameter of 5 nm. Figure 1a shows the steady-state absorption spectrum of a diluted colloidal solution of CdTe NRs in toluene (i.e., ∼0.5 mg/mL). Within the investigated spectral range three excitonic peaks are identified, around 1.8, 1.95, and 2.15 eV, indicated by the colored lines. Here the broad higher energetic peaks (1.95 and 2.15 eV) are composed of several transitions that do not necessarily have the same nature.35 However, for simplicity, we will refer in the following to three excitonic transitions S1, S2, and S3, respectively. The corresponding electron and hole energy levels have been determined using band-structure calculations within the effective mass approximation37 and are shown in Figure 1b. Electron states are characterized by the angular momentum of the envelope wave function m, with Σ and Π symmetry for m = 0 and 1, respectively. Holes are further characterized by their total angular momentum Jz, in addition to a numbering of states of the given symmetry.35 A detailed description of the electron and hole states and the assignment of the linear absorption spectra can be found in ref (35) and in the Supporting Information (SI).

Figure 1.

Figure 1

Open in a new tab

(a) Black solid line: steady-state absorption spectrum of CdTe NRs in toluene. The positions of the three lowest excitonic features are indicated by colored lines. Green dashed line: laser pump spectrum used for the 2DES experiments. A TEM image of the NRs, with average dimensions of 21 nm length and 5 nm width, is shown in the inset. (b) Energy level diagram for the CdTe NRs. Levels are detailed in the text; the first three excitons are labeled S1–S3 and have the same color code as in panel a.

Because of the high aspect ratio of the NRs (∼4), all transitions bear a 1D character peaking at the Γ point of the Brillouin zone (kz = 0). However, ab initio calculations by Lee and Wang38 in CdSe nanowires have shown that the S3 transition peaks away from the Γ point (kz ≠ 0) for both electrons and holes. Because of this peculiarity the S3 transition is indicated in Figure 1b as Σ′ → Σ′.

Our 2DES setup is described in detail elsewhere39 and in the SI. In brief, it works in the partially collinear pump–probe geometry, using the Translating-Wedge-Based Identical Pulses eNcoding System (TWINS) interferometer for the generation of the phase-locked excitation pulse pair.40 Two broadband noncollinear optical parametric amplifiers are used to generate the pump and probe pulses, with spectrum spanning the 1.7 to 2.3 eV range, allowing simultaneous coverage of the S1, S2, and S3 transitions. The instrumental response function (IRF) is well approximated by a Gaussian function with 15 fs full width at half-maximum.

Figure 2 shows a series of 2DES maps of CdTe NRs in toluene, as a function of excitation and detection energies, for different values of the waiting time t2 of 30, 60, 130, and 500 fs. In all maps the signal plotted is the differential transmission (ΔT/T). The positions of the S1, S2, and S3 excitons are indicated by dotted lines for both excitation and detection energies. They have been deduced experimentally from the diagonal peaks in the 2DES maps at short t2 delays. It should be noted that this method leads to slightly higher energetic positions of S2 and S3 than in previous works.35 In a 2DES map the peaks on the diagonal (solid line), corresponding to equal excitation and detection energies, probe the populations of the individual transitions, while the cross peaks, corresponding to different excitation and detection energies, probe couplings and relaxation dynamics between electronic states. In particular, peaks on the upper part of the diagonal, with excitation energy higher than detection energy, correspond to relaxation dynamics of higher energetic excitons to lower excitons or, in an electron/hole picture, to the relaxation of hot electrons and holes. Peaks below the diagonal correspond to coupling of excitonic states, for example, the excitation of a lower energy state, leading to absorption change when probing a higher energy state. The broad negative peaks (blue), in both the lower and upper triangle, are a consequence of excited-state energy level shifts, explained in detail in ref (35), largely related to the excitation-induced renormalization of the transition energy due to Stark17 or biexcitonic effects,12,16 leading to a derivative shape of the ΔT/T signal.

Figure 2.

Figure 2

Open in a new tab

2DES maps of CdTe NRs at waiting times t2 = 30, 60, 130, and 500 fs. Here red represents positive ΔT/T due to photobleaching and blue signifies negative (photoinduced absorption) signals induced by transition energy shifts.35 The excitation energy scale has been normalized by the pump laser spectrum, absolute color and contour scale is set to the minimum and maximum intensity, and the excitation pulse energy is 1.6 nJ corresponding to a fluence of 5 μJ/cm2. Dotted lines show the positions of the S1, S2, and S3 excitons at excitation and detection energies, while the solid black line shows the diagonal, where excitation and detection have equal energy.

At early waiting times t2 = 30 fs (upper left panel in Figure 2), both diagonal features and cross peaks are observed. Three distinct positive peaks are visible on the diagonal, corresponding to the photobleaching (PB) of the S1, S2, and S3 excitons. Already at t2 = 30 fs there are positive S2/S1 (excitation/detection) and S3/S1 cross peaks (red) along the vertical at 1.8 eV detection energy (dotted line S1). This implies that S3 and S2 have partially relaxed to S1 over such a short time. The positive signal at the S1/S2 cross peak is due to the shared electron level of the two excitons (see Figure 1b). At t2 = 60 and 130 fs (upper right and lower left panel in Figure 2) the amplitude of the S2/S1 and S3/S1 cross peaks grows, indicating further relaxation of S2 and S3 to S1. The S2/S2 diagonal peak is still discernible but much weaker with respect to shorter delays, while the S3/S3 diagonal peak, which is expected to vanish upon relaxation, does not decrease considerably in amplitude for t2 = 130 fs. For the much longer delay t2 = 500 fs (lower right panel), the 2DES maps appear to be quite similar to t2 = 130 fs, suggesting that most of the hot electron and hole dynamics occur on faster time scales. This is also confirmed by the negative signal observed around S3/S1, related to the excitation of higher excited states, and the thus induced energy level shifts, which vanishes within the first 130 fs until it is absent at a longer delay of t2 = 500 fs.35 The negative ΔT/T signal around detection energies of ∼2.05 eV (between S2 and S3 dotted vertical lines), together with the positive signal at slightly higher detection energies, expands over the entire excitation range and corresponds to the derivative shape of the excitonic peak centered on S3, which is interpreted as a red shift of the S3 energy level.35 The sign change over time from 30 to 500 fs of the ΔT/T signal in the upper triangle around S3/S3 is assigned to the overlap of the faster positive dynamics due to PB of S3 and the slower negative and positive dynamics induced by the energy level shift of S3 and will be discussed in detail later.

In the following we focus on the decay dynamics by monitoring different peaks in the 2DES maps, corresponding to specific excitation and detection energies. First we consider the dynamics involving the first and second excitonic levels, S1 and S2, respectively. Figure 3 displays the kinetic traces for the S1/S1 diagonal peak (a), the S2/S1 cross peak (b), the S1/S2 cross peak (c), and the S2/S2 diagonal peak (d), see the grid lines in excitation and detection axis of Figure 2 for the positions of the different excitons. To retrieve characteristic time constants, we fitted all dynamics by an exponential rise and a one- or two-component exponential decay, convoluted with the IRF. Following photoexcitation of the S1 state, in Figure 3a an instantaneous rise of the S1/S1 diagonal peak is observed within our time resolution due to occupation of the lowest electron and hole states. The shared electron state Σ of the two excitons S1 and S2 leads to the instantaneous rise also of the S1/S2 cross peak (Figure 3c). Because the S1 level is at the CdTe bandgap (1Σ1/2 → Σ), there is no thermalization of hot electrons or holes and the only observable dynamics for both detection energies corresponds to electron and hole recombination. The relatively fast picosecond dynamics observed are indicative of nonradiative recombination or surface trapping, for electrons in the case of Figure 3c (1Σ3/2→ Σ) and both electrons and holes in Figure 3a (1Σ1/2→ Σ), see insets, which have a comparable time constant of ∼1.5 ps, in agreement with previous results.35 Processes involving excitation of the S2 level show a more complex relaxation behavior (Figure 3b,d). For detection at S1 (S2/S1 cross peak, Figure 3b) we resolve a delayed rise of the PB signal, while detection of S2 (S2/S2 diagonal peak, Figure 3d) shows an instantaneous rise followed by an initial fast decay. We find matching time constants of 30 ± 10 fs for the rise in Figure 3b and the fast decay in Figure 3d, while the slower decay for both peaks has again a time constant of ∼1.5 ps. Excitation of S2 (1Σ3/2→ Σ, see inset in Figure 3) creates an electron state at the bandgap, while the hole is located at the first excited state 1Σ3/2. The hole thermalizes to the 1Σ1/2 level on a fast time scale, leading to additional Pauli blocking for the S1 transition and to the observed rise time of the S2/S1 cross peak (Figure 3c). The same thermalization leads to a decrease in Pauli blocking for the S2 transition and translates to the initial fast decay of the S2/S2 diagonal peak, observed in Figure 3d. Indeed, the PB of the S2 transition shows only about half the intensity after hole relaxation, indicative of the contribution of the electron only to the bleach signal. The excellent agreement between the time constants of the decay of the S2/S2 diagonal peak and the buildup of the S2/S1 cross peak indicates that they uniquely describe the relaxation of the hot hole from the 1Σ3/2 level to the 1Σ1/2 level. This process, which can be clearly resolved with 2DES, would be difficult to directly observe in a classical pump–probe experiment due to the proximity of the two states in energy and the very fast time scale. The second, slower decay then corresponds to the relaxation of the electron and the hole from the bandgap on the previously discussed slow (picosecond) time scale (extracted by excitation of S1, Figure 3a,c).

Figure 3.

Figure 3

Open in a new tab

Experimental data (black points) and fit (red line) of the ΔT/T signal obtained from the 2DES maps for selected excitation and detection energies, with S1 excitation and S1 detection (a), S2 excitation and S1 detection (b), S1 excitation and S2 detection (c), and S2 excitation and S2 detection (d). The fit functions are an exponential rise followed by a monoexponential decay (a–c) or a biexponential decay (d), all convoluted with the IRF. The signals have been normalized to the maximum of the 2DES maps of Figure 2. Energy schemes are shown in the insets.

We performed a similar analysis for S3 excitation (Σ′→ Σ′ transition, see insets in Figure 4). It is worth mentioning that there is no S1/S3 cross peak in the lower triangle of the 2DES maps, as the excitons share no common state. The S3/S1 cross peak (see Figure 4a), corresponding to excitation at S3 and detection at S1, shows a characteristic rise time of 49 ± 10 fs, followed by a slower decay (1.5 ps time scale). The S3/S3 diagonal peak (Figure 4c), on the contrary, has an instantaneous rise, followed by a first exponential decay with 49 ± 10 fs time constant and a second slower decay. Finally, by tuning the detection energy to S2 (S3/S2 cross peak, Figure 4b), we observe an almost instantaneous signal buildup followed by a slow decay. The fast initial decay of S3/S3 is in excellent agreement with the retarded buildup of the PB of S3/S1 cross peak (Figure 4a) and points to S3 → S1 relaxation. This process could occur through either the hot electron or the hot hole thermalization, that is, the energy relaxation of the excited electron Σ′→ Σ, or the excited hole, Σ′→ 1Σ1/2 (see insets in Figure 4a,c). (While we should strictly speak of relaxation of a correlated electron–hole pair to an electron–hole pair state of lower energy, here relaxation of just one excitonic component, either electron or hole, is certainly faster than a concerted, simultaneous electron and hole relaxation to the ground state. These concerted channels are dominant only when the ones considered here are energetically forbidden.)

Figure 4.

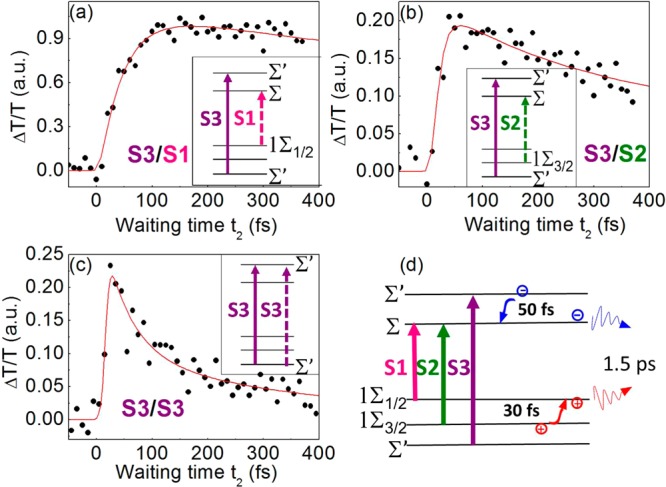
Figure 4

Open in a new tab

Experimental data (black points) and fits (red lines) of the ΔT/T signal obtained from the 2DES maps for selected excitation and detection energies, exciting the S3 exciton and detecting at S1 (a), S2 (b), and S3(c), together with the schemes for state relaxation in the insets. A summary of the identified relaxation pathways and respective time scales is shown in panel d.

For a better understanding of the carrier relaxation pathways, we have to consider that when exciting the S3 exciton the ΔT/T signal presents both positive and negative values (see 2DES maps in Figure 2). We assign these variations to the overlap of PB and a ΔT/T signal with derivative-shape of the excitonic absorption peaks as a result of excitation-induced renormalization of the transition energy due to Stark17 or biexcitonic effects,12,16 well established for semiconducting nanostructures. This effect, which complicates the extraction of the cross peak dynamics, is particularly strong when pumping higher excitons.35,41 To disentangle the contributions of PB and Stark shift from the ΔT/T spectra, we developed a model, described in detail in ref (35) and in the SI. This model fits the entire ΔT/T spectra at all time delays with two different spectral components: a series of Gaussian peaks having fixed centers and widths, accounting for the PBs of the S1–S3 excitonic transitions, and a series of derivatives of these Gaussians, accounting for their spectral shifts (details in the SI). Examples of fits for short and long times are given in Figures S2 and S3 in the SI. From this analysis we extracted dynamics that separately account for the PB and the peak shifts, allowing us to disentangle their contributions to the ΔT/T spectra (Figure S4 of the SI). We remark here that the fit parameters were restricted to the amplitudes and the shifts of the peaks, as energy values and the widths have been fixed to the values extracted from the steady-state absorption spectra (see the SI). This procedure uncovers the pure PB dynamics that are the result of the occupation of the respective electronic levels and gives direct information on the carrier relaxation dynamics. The early time dynamics of the PB for the S3 and S1 states are very similar to those extracted from the cross peaks of the 2DES maps and display a decay and a rise time, respectively, of 50 ± 10 fs. Remarkably, with this analysis a similar 50 fs rise time is extracted for the PB signal of S2, as opposed to the nearly instantaneous signal buildup directly observed in the S2/S3 cross peak of the 2DES maps. This immediate signal change is therefore assigned to an instantaneous shift of the S2 transition due to excitation of the S3 state. For both S1 and S2 PB, we fit a single exponential decay of 1.5 ps, in good agreement with the previously discussed relaxation of electron and hole from the bandgap. This analysis enables us to assign the charge relaxation pathways following S3 excitation: The initial fast decay of the S3 PB correlates well with the delayed rise of both S1 and S2 PB. Because S1 and S2 share the same electron state (the ground state Σ, see insets), this process corresponds to ultrafast relaxation of electrons from the Σ′ to the Σ level, leading to a decrease in the S3 PB because of reduced Pauli blocking and a corresponding increase in the S1/S2 PB. The hot electron relaxation process thus appears to be slightly slower than hot hole relaxation, although an improved signal-to-noise ratio of the measurements will be necessary to precisely determine and differentiate their dynamics.

Taken together, these data allow us to draw a detailed picture of the separate ultrafast electron and hole dynamics and relaxation pathways for the first three excitons of CdTe NRs (Figure 4d) and extract time constants in the sub-100 fs time range. In particular, we directly observe a hot hole thermalization from 1Σ3/2 to 1Σ1/2 in the range of 30 fs, while higher energetic electrons after S3 pumping relax from Σ′ to Σ with 50 fs time constant. Our results show that 2DES is an excellent tool for the direct observation of electron and hole relaxation pathways in excitonic systems occurring in the sub-100 fs time range due to the unique combination of high temporal and spectral resolution in excitation as well as in detection. We anticipate that 2DES, with its unique ability to follow the ultrafast relaxation processes of excitonic states, will be an important tool for the design of complex hybrid nanostructures that aim to separately control the electron and hole dynamics.

Acknowledgments

This project has received funding from the European Union’s Horizon 2020 research and innovation programme (MOPTOPus) under the Marie Skłodowska-Curie grant agreement No. [705444] as well as (SONAR) grant agreement no. [734690]. G.C. acknowledges financial support by the European Research Council (ERC-2011-AdG No. 291198). The authors acknowledge support from Laserlab-Europe (EU-H2020 654148).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.7b00682.

  • Experimental setup, spectral and temporal fitting models, spectral and temporal fit. (PDF)

Author Present Address

⊥ Institute of Applied Physics, University of Bern, Sidlerstrasse 5, 3012 Bern, Switzerland.

The authors declare no competing financial interest.

Supplementary Material

jz7b00682_si_001.pdf (896.6KB, pdf)

References

  1. Talapin D. V.; Lee J.-S.; Kovalenko M.-V.; Shevchenko E.-V. Prospects of Colloidal Nanocrystals for Electronic and Optoelectronic Applications. Chem. Rev. 2010, 110, 389–458. 10.1021/cr900137k. [DOI] [PubMed] [Google Scholar]
  2. Brus L. Electronic wave Functions in Semiconductor Clusters: Experiment and Theory. J. Phys. Chem. 1986, 90, 2555–2560. 10.1021/j100403a003. [DOI] [Google Scholar]
  3. Yoffe A. D. Semiconductor Quantum Dots and Related Systems: Electronic, Optical, Luminescence and Related properties ofD Low Dimensional Systems. Adv. Phys. 2001, 50, 1–208. 10.1080/00018730010006608. [DOI] [Google Scholar]
  4. Peng X.; Manna L.; Yang W.; Wickham J.; Scher E.; Kadavanich A.; Alivisatos A. P. Shape Control of CdSe Nanocrystals. Nature 2000, 404, 59–61. 10.1038/35003535. [DOI] [PubMed] [Google Scholar]
  5. Mauser C.; Limmer T.; Da Como E.; Becker K.; Rogach A. L.; Feldmann J.; Talapin D. V. Anisotropic Optical Emission of Single CdSe/CdS Tetrapod Heterostructures: Evidence for a Wavefunction Symmetry Breaking. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 153303. 10.1103/PhysRevB.77.153303. [DOI] [Google Scholar]
  6. Mauser C.; Da Como E.; Baldauf J.; Rogach A. L.; Huang J.; Talapin D. V.; Feldmann J. Spatio-Temporal Dynamics of Coupled Electrons and Holes in Nanosize CdSe-CdS Semiconductor Tetrapods. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 081306. 10.1103/PhysRevB.82.081306. [DOI] [Google Scholar]
  7. Zhou Y.; Li Y.; Zhong H. Z.; Hou J. H.; Ding Y. Q.; Yang C. H.; Li Y. Hybrid Nanocrystal/Polymer Solar Cells Based on Tetrapod-Shaped CdSexTe1–x Nanocrystals. Nanotechnology 2006, 17 (16), 4041–4047. 10.1088/0957-4484/17/16/008. [DOI] [PubMed] [Google Scholar]
  8. Gao T.; Wang T. H. Synthesis and Properties of Multipod-Shaped ZnO Nanorods for Gas-Sensor Applications. Appl. Phys. A: Mater. Sci. Process. 2005, 80 (7), 1451. 10.1007/s00339-004-3075-2. [DOI] [Google Scholar]
  9. Fang L.; Park J. Y.; Cui Y.; Alivisatos A. P.; Shcrier J.; Lee B.; Wang L. W.; Salmeron M. J. Mechanical and Electrical Properties of CdTe Tetrapods Studied by Atomic Force Microscopy. J. Chem. Phys. 2007, 127, 184704–1–184704–6. 10.1063/1.2786993. [DOI] [PubMed] [Google Scholar]
  10. Banin U.; Ben-Shahar Y.; Vinokurov K. Hybrid Semiconductor–Metal Nanoparticles: From Architecture to Function. Chem. Mater. 2014, 26, 97–110. 10.1021/cm402131n. [DOI] [Google Scholar]
  11. Sewall L.; Cooney R. R.; Anderson K. E. H.; Dias E. A.; Kambhampati P. State-to-State Exciton Dynamics in Semiconductor Quantum Dots. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 74, 235328. 10.1103/PhysRevB.74.235328. [DOI] [Google Scholar]
  12. Kambhampati P. Hot Exciton Relaxation Dynamics in Semiconductor Quantum Dots: Radiationless Transitions on the Nanoscale. J. Phys. Chem. C 2011, 115, 22089–22109. 10.1021/jp2058673. [DOI] [Google Scholar]
  13. Turner D. B.; Hassan Y.; Scholes G. D. Exciton Superposition States in CdSe Nanocrystals Measured using Broadband Two-Dimensional Electronic Spectroscopy. Nano Lett. 2012, 12, 880–6. 10.1021/nl2039502. [DOI] [PubMed] [Google Scholar]
  14. Caram J. R.; Zheng H.; Dahlberg P. D.; Rolczynski B. S.; Griffin G. B.; Fidler A. F.; Dolzhnikov D. S.; Talapin D. V.; Engel G. S. Persistent Inter-Excitonic Quantum Coherence in CdSe Quantum Dots. J. Phys. Chem. Lett. 2014, 5, 196–204. 10.1021/jz402336t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Cassette E.; Pensack R. D.; Mahler B.; Scholes G. D. Room-Temperature Exciton Coherence and Dephasing in Two-Dimensional Nanostructures. Nat. Commun. 2015, 6, 6086. 10.1038/ncomms7086. [DOI] [PubMed] [Google Scholar]
  16. Kambhampati P. Unraveling the Structure and Dynamics of Excitons in Semiconductor Quantum Dots. Acc. Chem. Res. 2011, 44, 1–13. 10.1021/ar1000428. [DOI] [PubMed] [Google Scholar]
  17. Klimov V. I. Optical Nonlinearities and Ultrafast Carrier Dynamics in Semiconductor Nanocrystals. J. Phys. Chem. B 2000, 104, 6112–6123. 10.1021/jp9944132. [DOI] [Google Scholar]
  18. Cooney R. R.; Sewall S. L.; Dias E. A.; Sagar D. M.; Anderson K. E. H.; Kambhampati P. Unified Picture of Electron and Hole Relaxation Pathways in Semiconductor Quantum Dots. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 75, 245311. 10.1103/PhysRevB.75.245311. [DOI] [Google Scholar]
  19. Klimov V. I.; McBranch D. W.; Leatherdale C. A.; Bawendi M. G. Electron and Hole Relaxation Pathways in Semiconductor Quantum Dots. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 60, 13740–13749. 10.1103/PhysRevB.60.13740. [DOI] [Google Scholar]
  20. Benisty H.; Sotomayer-Torrès C. M.; Weisbuch C. Intrinsic Mechanism for the Poor Luminescence Properties of Quantum-Box Systems. Phys. Rev. B: Condens. Matter Mater. Phys. 1991, 44, 10945. 10.1103/PhysRevB.44.10945. [DOI] [PubMed] [Google Scholar]
  21. Bockelmann U.; Bastard G. Phonon Scattering and Energy Relaxation in Two-, One-, and Zero-Dimensional Electron Gases. Phys. Rev. B: Condens. Matter Mater. Phys. 1990, 42, 8947. 10.1103/PhysRevB.42.8947. [DOI] [PubMed] [Google Scholar]
  22. Prabhu S. S.; Vengurlekar A. S.; Roy S. K.; Shah J. Nonequilibrium Dynamics of Hot Carriers and Hot Phonons in CdSe and GaAs. Phys. Rev. B: Condens. Matter Mater. Phys. 1995, 51, 14233–14246. 10.1103/PhysRevB.51.14233. [DOI] [PubMed] [Google Scholar]
  23. Inoshita T.; Sakaki H. Electron Relaxation in a Quantum Dot: Significance of Multiphonon Processes. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 46, 7260. 10.1103/PhysRevB.46.7260. [DOI] [PubMed] [Google Scholar]
  24. Califano M.; Bester G.; Zunger A. Prediction of a Shape-Induced Enhancement in the Hole Relaxation in Nanocrystals. Nano Lett. 2003, 3, 1197–1202. 10.1021/nl0343304. [DOI] [Google Scholar]
  25. Wang L. W.; Califano M.; Zunger A.; Franceschetti A. Pseudopotential Theory of Auger Processes in CdSe Quantum Dots. Phys. Rev. Lett. 2003, 91, 056404. 10.1103/PhysRevLett.91.056404. [DOI] [PubMed] [Google Scholar]
  26. Efros A. L.; Kharchenko V. A.; Rosen M. Breaking the Phonon Bottleneck in Nanometer Quantum Dots: Role of Auger-Like Processes. Solid State Commun. 1995, 93, 281–28. 10.1016/0038-1098(94)00760-8. [DOI] [Google Scholar]
  27. Guyot-Sionnest P.; Shim M.; Matranga C.; Hines M. Intraband Relaxation in CdSe Quantum Dots. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 60, R2181. 10.1103/PhysRevB.60.R2181. [DOI] [Google Scholar]
  28. Guyot-Sionnest P.; Wehrenberg B.; Yu D. Intraband Relaxation in CdSe Nanocrystals and the Strong Influence of the Surface Ligands. J. Chem. Phys. 2005, 123, 074709. 10.1063/1.2004818. [DOI] [PubMed] [Google Scholar]
  29. Cooney R. R.; Sewall S. L.; Anderson K. E. H.; Dias E. A.; Kambhampati P. Breaking the Phonon Bottleneck for Holes in Semiconductor Quantum Dots. Phys. Rev. Lett. 2007, 98, 177403. 10.1103/PhysRevLett.98.177403. [DOI] [Google Scholar]
  30. Liu C.; Peterson J. J.; Krauss T. D. Uncovering Hot Hole Dynamics in CdSe Nanocrystals. J. Phys. Chem. Lett. 2014, 5, 3032–3036. 10.1021/jz5015554. [DOI] [PubMed] [Google Scholar]
  31. Jonas D. M. Two-Dimensional Femtosecond Spectroscopy. Annu. Rev. Phys. Chem. 2003, 54, 425–63. 10.1146/annurev.physchem.54.011002.103907. [DOI] [PubMed] [Google Scholar]
  32. Harel E.; Rupich S. M.; Schaller R. D.; Talapin D. V.; Engel G. S. Measurement of Electronic Splitting in PbS Quantum Dots by Two-Dimensional Nonlinear Spectroscopy. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 86, 075412. 10.1103/PhysRevB.86.075412. [DOI] [Google Scholar]
  33. Park S. D.; Baranov D.; Ryu J.; Cho B.; Halder A.; Seifert S.; Vajda S.; Jonas D. M. Bandgap Inhomogeneity of a PbSe Quantum Dot Ensemble from Two-Dimensional Spectroscopy and Comparison to Size Inhomogeneity from Electron Microscopy. Nano Lett. 2017, 17 (2), 762–771. 10.1021/acs.nanolett.6b03874. [DOI] [PubMed] [Google Scholar]
  34. Griffin G. B.; Ithurria S.; Dolzhnikov D. S.; Linkin A.; Talapin D. V.; Engel G. S. Two-Dimensional Electronic Spectroscopy of CdSe Nanoparticles at Very Low Pulse Power. J. Chem. Phys. 2013, 138, 014705. 10.1063/1.4772465. [DOI] [PubMed] [Google Scholar]
  35. Kriegel I.; Scotognella F.; Soavi G.; Brescia R.; Rodríguez-Fernández J.; Feldmann J.; Lanzani G.; Tassone F. Delayed Electron Relaxation in CdTe Nanorods Studied by Spectral Analysis of the Ultrafast Transient Absorption. Chem. Phys. 2016, 471, 39–45. 10.1016/j.chemphys.2015.08.002. [DOI] [Google Scholar]
  36. Kriegel I.; Wisnet A.; Kandada A. R. S.; Scotognella F.; Tassone F.; Scheu C.; Zhang H.; Govorov A. O.; Rodríguez-Fernández J.; Feldmann J. Cation Exchange Synthesis and Optoelectronic Properties of Type II CdTe–Cu2–xTe Nano-Heterostructures. J. Mater. Chem. C 2014, 2 (17), 3189–3198. 10.1039/c3tc32049a. [DOI] [Google Scholar]
  37. Shabaev A.; Efros A. L.1D Exciton Spectroscopy of Semiconductor Nanorods. Nano Lett. 2004, 4, 1821–1825. 10.1021/nl049216f. [DOI] [Google Scholar]
  38. Li J.; Wang L.-W. High Energy Excitations in CdSe Quantum Rods. Nano Lett. 2003, 3, 101–105. 10.1021/nl020231z. [DOI] [Google Scholar]
  39. Réhault J.; Maiuri M.; Oriana A.; Cerullo G. Two-Dimensional Electronic Spectroscopy with Birefringent Wedges. Rev. Sci. Instrum. 2014, 85, 123107. 10.1063/1.4902938. [DOI] [PubMed] [Google Scholar]
  40. Brida D.; Manzoni C.; Cerullo G. Phase-Locked Pulses for Two-Dimensional Spectroscopy by a Birefringent Delay Line. Opt. Lett. 2012, 37, 3027–3029. 10.1364/OL.37.003027. [DOI] [PubMed] [Google Scholar]
  41. Soavi G.; Scotognella F.; Viola D.; Hefner T.; Hertel T.; Cerullo G.; Lanzani G. High Energetic Excitons in Carbon Nanotubes Directly Probe Charge-Carriers. Sci. Rep. 2015, 5, 9681. 10.1038/srep09681. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz7b00682_si_001.pdf (896.6KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES