Rapid Voltage Sensing with Single Nanorods via the Quantum Confined Stark Effect

Abstract

Properly designed colloidal semiconductor quantum dots (QDs) have already been shown to exhibit high sensitivity to external electric fields via the quantum confined Stark effect (QCSE). Yet, detection of the characteristic spectral shifts associated with the effect of the QCSE has traditionally been painstakingly slow, dramatically limiting the sensitivity of these QD sensors to fast transients. We experimentally demonstrate a new detection scheme designed to achieve shot-noise-limited sensitivity to emission wavelength shifts in QDs, showing feasibility for their use as local electric field sensors on the millisecond time scale. This regime of operation is already potentially suitable for detection of single action potentials in neurons at a high spatial resolution.

Fluorescent markers sensitive to the electric field in their local environment have found extensive use in biological studies.¹⁻³ This is particularly true for spatially mapping activity in neural networks, where classical electrophysiological approaches do not allow probing of the entire neural circuit. Most observations of neuronal activity are based on calcium imaging,⁴ an indirect proxy of membrane potential dynamics due to the slow kinetics of calcium transients. Lately, considerable efforts have been invested in development of voltage-sensitive organic dyes⁵ (VSDs) and genetically encoded voltage-sensitive proteins.⁶ Although these tools are likely to become essential for studying the brain, their performance is still lacking either the temporal or the spatial precision needed for simultaneous optical recording of action potentials (APs) from a large number of neurons inside the brain of a live, behaving animal. The current best performing VSDs are based on photoinduced electron transfer between an electron-rich quencher and an organic fluorophore.^2,5,7−9 This leads to a modulation of the fluorescence intensity as a function of the electric field. Yet, these markers still suffer from poor membrane retention, toxicity, membrane capacitance perturbation, and photobleaching and are incapable of resolving small features in neuronal membranes.^2,5,9

Highly fluorescent semiconductor nanoparticles, known as quantum dots (QDs), were recently suggested as an alternative to the classical VSDs¹⁰⁻¹⁴ for direct detection of electric fields via the use of the quantum confined Stark effect (QCSE). First observed in quantum wells,¹⁵ the QCSE leads to a shift in the luminescence center wavelength of the QD.^15,16 QCSE in QDs was first observed over two decades ago,^17,18 but was usually characterized in the ensemble.¹⁹ Additionally, QCSE from single QDs is easier to observe at low temperatures, where thermal broadening of the emission line width of QDs is negligible. Observation of QCSE-induced spectral shifts at room temperature was thought to be challenging due to the presence of stochastic meandering of the emission center wavelength known as spectral diffusion.¹⁷ Yet, emission wavelength shifts of several nanometers were recently reported at room temperature on single particles.¹⁶ The characteristic electric fields due to APs, on the order of hundreds of kV/cm, represent the perturbative limit of the QCSE described above. Thus, optical phenomena observed under much stronger fields are irrelevant.²⁰

QD markers exhibit several qualities that make them potentially favorable over their organic counterparts. Owing to their nanoscale volume, it is possible to embed QD-based sensors at different locations along cell membranes,¹⁴ opening the possibility for sensing and resolving the local electric field in a subdiffraction volume by using a single reporter QD. Importantly, functionalization of QDs with transmembrane α-helical peptides facilitates their spontaneous insertion into the membrane.¹⁴ Modification of functionalizing peptides with intracellular protein sequences that specifically recognize postsynaptic scaffolds, such as PSD95 and gephyrin,²¹⁻²⁵ could provide the possibility for QD targeting to synapses. Furthermore, fluorescence quantum yield and photostability of QDs are significantly higher,²⁶ qualities that can be preserved even in biological media,¹⁴ allowing for high photon flux from a single emitter over prolonged observation times. This is crucial for biological applications taking into account toxicity due to intense illumination for live samples.²⁷ In striking difference with standard VSDs and protein-based sensors, QD-based sensors can be used at very low concentrations without altering electrical properties of the membrane.^28,29 These unique advantages of QD-based sensors open up a new avenue for super-resolution voltage imaging in living cells. However, to be useful in realistic neuroscience applications, the QCSE has to be observed on the time scale of an AP, corresponding to a sub-millisecond time scale,³⁰ in stark contrast to the characteristic one-second time resolution of typical studies of either QCSE or spectral diffusion.³¹ The main goal of the following work is to examine whether detection of single-particle spectral shifts on a millisecond time scale is possible and whether these shifts can be measured down to the limit afforded by the shot noise, the noise limit in any classical physical system due to the probabilistic nature of the measurement process.

The response of QDs to an external electric field is usually described using perturbation theory.¹⁵ For a symmetric quantum well the first-order correction to the emission wavelength vanishes, and thus the spectral shift has a second-order dependence on the external field. As a result, in a spatially symmetric system an external electric field leads to a decrease in the band gap energy and a concomitant red shift of the emission spectrum, quadratic with the field amplitude. For an asymmetric well, in which the exciton has a permanent electric dipole, the energy shift is linear in the external field, resulting in either a blue-shift or a red-shift of the spectrum, depending on the relative orientation of the exciton dipole moment and the external field. Indeed, both blue-shifts and red-shifts were predicted^11,16 and observed for asymmetric type-II seeded nanorods.¹⁶ Neural membrane resting potential limits the application of symmetric wells for neuroimaging. While the potential difference between the resting potential (∼−70 mV) and the AP spike (∼+30 mV) is large,³⁰ a symmetric structure would exhibit only a small red-shift due to the difference of the absolute values (∼40 mV). In contrast, an asymmetric structure, responding in a linear fashion to voltage change, can exhibit a large spectral shift relating to the sum of absolute values (∼100 mV). In addition, since the electric field also modifies the spatial wave function of the electron and hole and influences their overlap, one expects the radiative lifetime to be affected. In general, an increase in the emission energy should be accompanied by an increased spatial hole and electron wave function overlap and a shortening of the radiative lifetime.¹¹

Several physical quantities can, in principle, be utilized for detecting changes in the local electric field. Most voltage sensors exhibit a change in the emission intensity due to the presence of the field. This is easily detected over a wide illumination area and is thus compatible with standard neuronal imaging setups. While this effect was measured in QDs,^12,16 it is expected to be rather small for high quantum efficiency QDs, where exciton recombination is dominated by radiative decay, as is necessary for fast detection.¹⁶ Perhaps the most intuitive signature that can be measured is the spectral shift, but lifetime imaging is also a possibility. Both of these approaches have been explored for VSDs³²⁻³⁴ and have generally been found to be inferior to imaging using intensity changes.^2,35 We present both of these voltage-dependent signals for QD-based sensors. A more detailed theoretical discussion of the various detection schemes can be found elsewhere.^10,11

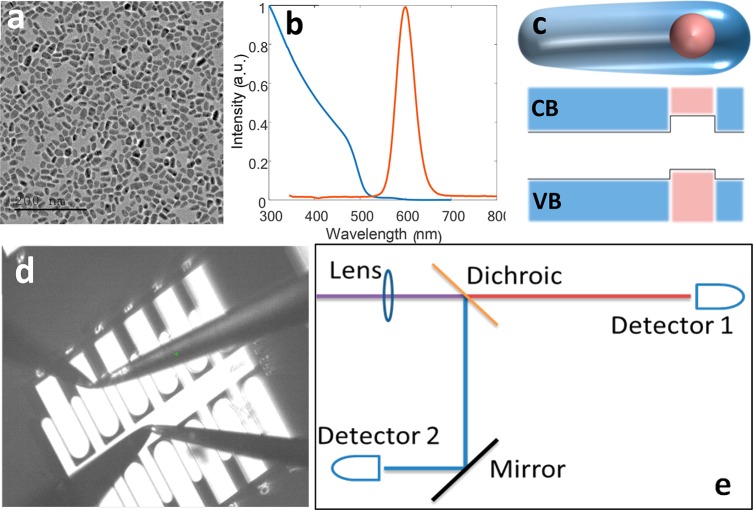
From the above considerations, it is clear that asymmetric QDs should be more sensitive to the effect of electric fields, as has recently been shown both theoretically¹¹ and experimentally.¹⁶ Here, we have chosen to work with type-II seeded nanorods (NRs) consisting of a spherical ZnSe core overcoated by a CdS rod, as seen in the transmission electron microscopy (TEM) image of Figure 1a and illustrated in Figure 1c.

Figure 1.

(a) TEM image of the type-II ZnSe/CdS NRs used in all experiments; scale bar is 200 nm. (b) Extinction (blue) and photoluminescence (red) spectra of the NRs. (c) Cartoon depicting the NRs’ shape. The rod-shaped shell is asymmetric, and the core is closer to the thicker edge. The corresponding energy level diagram of the NR is shown below. CB, conduction band; VB, valence band. (d) Overhead view of a coverslip fashioned with gold electrodes that were used to apply the electric field to the NRs. The probe needles are touching the ground (central) and one of the “live” electrodes. (e) Fluorescence detection scheme used whereby a dichroic mirror splits the PL peak into two channels.

In these particles, the core is not centered in the shell but rather close to the thicker edge of the rod.³⁶ Such particles have already been shown to exhibit a sizable QCSE due to the separation of the charge carriers’ wave functions and a close to linear dependence on the field.¹⁶ Synthesis of ZnSe/CdS nanorods was performed according to an adapted known procedure,³⁶ yielding particles of 14.4 ± 2.4 nm in width and 24.7 ± 3.7 nm in length (Figure S1); these have been shown to be an asymmetric type-II structure.³⁷ The extinction and photoluminescence (PL) of the ensemble suspended in solution are given in Figure 1b.

To characterize the ability to rapidly detect electric field changes, we deposit NRs on a horizontal electrode array. Figure 1d shows a top view of a coverslip patterned with gold electrodes. The large central electrode has six protruding fingers on each side, and the secondary electrodes are positioned between them. The gap between the electrodes is several micrometers, depending on the fabrication process. Voltage is applied using two metallic micromanipulator needles. The first, connected to the center electrode, is grounded, whereas the second is connected to an amplified voltage source, which is modulated at 1 kHz, and with a duty cycle of 50%. Voltages ranged between 50 and 100 V across a gap of several micrometers, yielding electric fields of comparable magnitude to membrane APs (see Methods section for more details).

Single NRs are identified within the gaps between the electrodes by observing blinking in a camera image taken through the microscope objective. Emission from the NRs is collected through an oil-immersion objective and then split using a dichroic mirror (Figure 1e), set to the center emission wavelength of the ensemble, onto two single-photon detectors. The detection time stamps are measured and logged using a time-correlated single photon counting module (see Methods).

The typical width of a single NR emission spectrum is on the order of tens of nanometers; thus detecting a shift of only a few nanometers may be challenging. The “balanced detector” depicted in Figure 1e is designed to provide maximal sensitivity to the emission spectral shifts. In addition, the use of high temporal resolution single-photon detectors enables monitoring changes in the decay rate of the emission. Thus, three independent measurements are performed simultaneously: intensity fluctuations known as ΔF, spectral shifts (Δλ), extracted from the intensity ratio of the two detectors, and lifetime variations (Δτ).

A typical time trace of a single NR emission is presented in Figure 2a, where the intensity recorded by each channel is approximately half of the total intensity. It is clear that the emitter fluctuates between a bright, a dark, and, in some cases, a “gray” intermediate state.^38,39 This phenomenon, known as blinking, is further illustrated by examining the histogram of the trace (Figure S2). Using the sum of the two channels a threshold is applied in order to eliminate dark “off”-state periods from the analysis (Figure S2).

Figure 2.

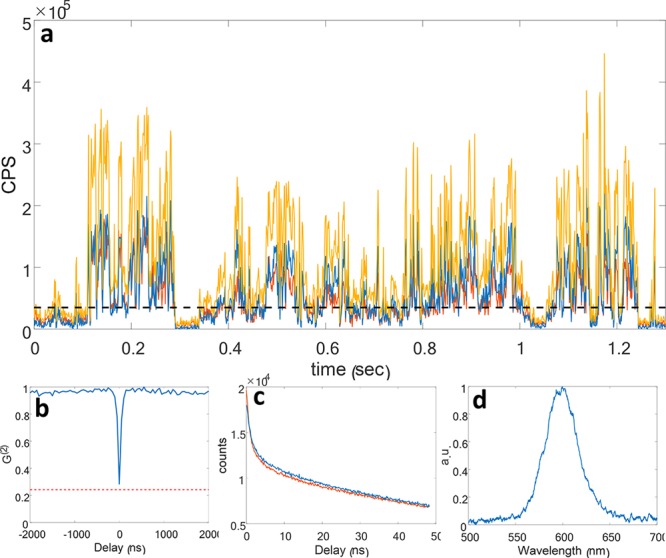
(a) Example of a blinking trace (bin size 1 ms) of a single NR when detected by the setup depicted in Figure 1e. The intensities recorded in the reflection (blue) and transmission (red) channels are almost identical, showing a 50:50 split of the emission peak by the dichroic. The sum of the signal from both channels (yellow) presents detection rates of up to 400 kHz. The threshold chosen for this measurement is shown with a black dashed line. (b) Photon detection coincidences as a function of delay between the two channels. A dip is evident at zero delay, where the correlation drops to 6% after correcting for the background, indicating that the fluorescence is collected from a single emitter. An estimated background level is plotted as a dashed red line. (c) Fluorescence decay in counts per second (CPS) as a function of time in the reflection (blue) and transmission (red) channels. (d) Example spectrum from a single NR (30 s exposure).

QDs are, to a large degree, single-photon emitters. After a single excitation cycle typically only a single photon is emitted even if multiple excitations occurred. This leads to an anticorrelation between detections in the two channels at times shorter than the radiative lifetime.^40,41 In Figure 2b such a correlation plot is given showing a significant antibunching dip at zero delay, 6% after correcting for correlations due to background. Note that for two uncorrelated emitters the antibunching at zero delay would be at least 50%, assuming similar intensities for both emitters. Using this method, we ensure further analysis is performed only on single NRs. Note that estimating the antibunching is not essential for imaging but is rather used here to separate clustering effects.

A typical fluorescence decay plot measured in the transmission and reflection channels is given in Figure 2c. The small difference in the decay constants between the channels arises from the slight difference in the overlap integral for different energy levels. A typical single NR spectrum is shown in Figure 2d; such measurements require long exposures (10s of seconds), making them unsuitable for detection of fast spectral shifts. Furthermore, to overcome the noise of the camera employed as the detector, spectra acquisition requires high excitation intensities that may bleach even the more stable NRs, rendering them nonfluorescent.

In order to extract the wavelength shift from the data collected in our setup, where the emission peak is split by wavelength into two channels, we used the following model, which is in line with previously discussed procedures.¹¹ The emission peak is modeled as a Gaussian function (Figure 3a), whose width is determined from the single-particle spectra that were collected and defined as σ = 25 nm for all calculations (see Supporting Information). A step function is used to simulate a dichroic mirror with zero loss and 50% transmission at a chosen wavelength (typically 600–605 nm). Next, a second, spectrally shifted, Gaussian is used to model a shift due to the QCSE. One needs to define a quantity that reliably relates the actual spectral shift in nanometers and the measured intensities. While one can propose different estimators such as the intensity ratio between the two detection channels,¹¹ it is advantageous to use an estimator that has the same properties as the estimated quantity, in this case linearity with the electric field, and we chose to use

1

where t and r are the transmission and reflection intensities recorded in the two channels, respectively, and the subscript indicates for which Gaussian they were calculated, 0 for the original Gaussian and V for the shifted one. This quantity is sensitive to wavelength shifts but not to intensity fluctuations since each part is normalized to the total intensity recorded in the same time period. Three examples of this estimator are given in Figure 3b, corresponding to three particles with a different center wavelength of emission. The sensitivity of the estimator and detection scheme, in general, is given by the slope of this curve. One can observe that while this sensitivity is reduced for a particle whose spectrum is not centered on the dichroic mirror’s transmission edge, it remains relatively high even for shifts as large as 20 nm. Clearly, maximal sensitivity is reached when the original spectrum is well centered on the dichroic or, alternatively, when the shift is in the direction of the dichroic cutoff wavelength.

Figure 3.

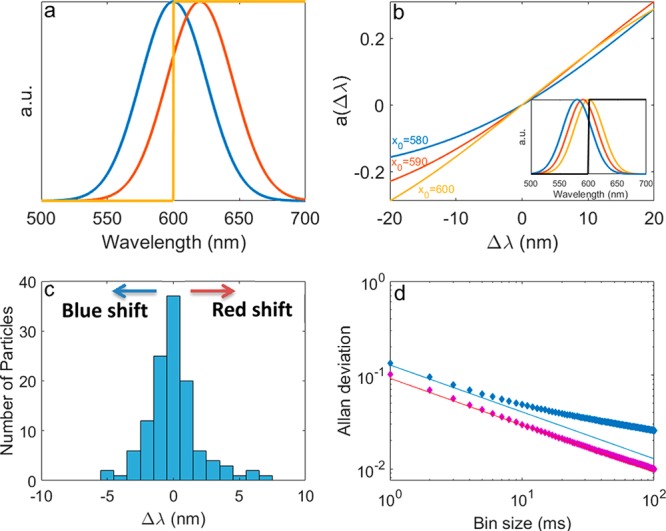
(a) Simulated emission spectrum centered at x₀ = 600 nm with σ = 25 nm (blue). The same spectrum shifted by Δλ = 10 nm while maintaining its width and area (red). A step function at 600 nm, simulating a dichroic mirror’s transmission coefficient (yellow). (b) Three examples of the QCSE estimator (a) plotted as a function of the wavelength shift (Δλ), where x₀ is the center of the original spectrum before voltage was applied; this is used to estimate Δλ from the data. The inset shows the three simulated spectra used and a step function. (c) Histogram of 120 QCSE spectral shifts measured from 82 NRs under various electric fields equivalent to those in neuronal membranes. (d) Allan deviation of the Δλ estimator of two different NRs as a function of bin size (diamonds), compared with theoretical curves of shot noise (lines) when accounting for the count rate.

Applying this model to experimental measurements is straightforward, as it is possible to numerically extract the spectral shift from the value of the estimator (see Supporting Information). It should be noted, however, that to determine whether or not an electric field was present does not require the aforementioned model. Rather, the model is used as a unit conversion method in order to present the results in units of wavelength. The results from 82 different NRs under various voltage modulation amplitudes (for details on the specific values used for each particle under study see Table S1) are presented as a histogram in Figure 3c, where it is evident that most NRs gave small, yet measurable, spectral shifts. This is mostly due to the shifts’ dependence on the orientation^11,16 between the electric field and the NR (as shown by the correlation with orientation presented in Figure S3) and to a lesser extent due to heterogeneity of structure and composition within the ensemble. QCSE-induced shifts are small when the electric field is perpendicular to the long dimension of the NR. The largest shifts measured are a red-shift of +7.1 nm and a blue-shift of −5.5 nm, which is comparable within the limited statistics of our measurements. Notably, the dependence of the spectral shift on the electric field amplitude is linear, as expected for a type-II system, and a transition from red-shift to blue-shift is observed upon inversion of the field direction (Figure S4).

To study the ability of this system to detect a transient applied voltage, we used a simple voltage scheme, where a 1 kHz, 50% duty cycle square wave was applied to the NRs (see Methods). Each time bin of 1 ms is divided into two halves, first when voltage is applied and second when no voltage is applied. The analysis is performed on each time bin separately such that the sensitivity and detection probability of a single short voltage pulse, similar in duration to an isolated AP, are extracted. The estimator is calculated only for time bins that cross the defined intensity threshold. An example of the estimator distribution for a single particle is given in Figure S5. The mean and standard deviation of the distribution are used to report the spectral shift and its error.

To show that this measurement is indeed shot noise limited, we calculate the error yielded by the model when only shot noise is considered (see Supporting Information). Taking care to average only consecutive “on-state” bins (see Supporting Information), we present the Allan deviation of two different NRs in Figure 3d. A shot-noise-limited process would show a decrease in the error of N^–0.5, where N is the number of photons or bins averaged over. Indeed, for short averaging time windows, the error in the estimator is only due to shot noise. At longer times, however, there is a decrease in the slope and the error does not improve as expected by shot noise. The averaging time for which the difference between the shot noise limit and the measured error varies among particles is between a few and tens of milliseconds, reaching more than 100 ms for some particles. This type of deviation is expected in the presence of a slow “red” noise, such as the one induced here by spectral diffusion. However, as we show here, it has little effect on the ability to sense fast, millisecond-scale, processes.

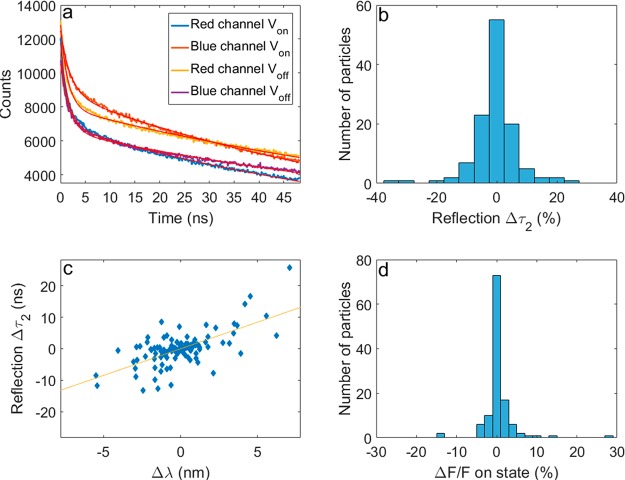
The use of avalanche photodiodes (APDs) affords high temporal resolution that enables an analysis of the fluorescence decay lifetime under an electric field at the single-particle level. The collected data contain information on the lifetime of both parts of the spectrum (reflected blue part and transmitted red part). Each of these can be separated into periods in which voltage is applied (V_on) and those in which it is not (V_off). As may be seen in the example in Figure 4a, all four curves were well fitted with a biexponential fit, yielding eight lifetime constants (τ). The lifetime variations are defined here as the difference in the decay lifetime within the same channel between V_on and V_off periods. Figure 4b shows all the measured lifetime changes of the long component due to QCSE in the reflected detection channel. Similar histograms are provided for the short component as well as for the transmission channel in Figure S6. As mentioned above, the spectral shift is to be accompanied by a change of the overlap between the wave functions of the hole and the electron changing according to the radiative lifetime decay. A positive correlation between the lifetime variation and the spectral shift is thus expected.¹¹ In Figure 4c this correlation is indeed visible: a blue-shift (negative Δλ) is accompanied by a shortening of the lifetime (negative Δτ). Similar plots for both lifetime components channel are given in Figure S7. While we measure a clear lifetime change by using data acquired over tens of seconds, performing an analysis of the lifetime variation on a millisecond time scale, similar to the one we present for the Δλ analysis, is difficult. Normally, determining the lifetime from a small number of photons is done by taking the mean of their time of arrival. This approach is limited when the excitation repetition period is comparable to the radiative lifetime, which is the case here. Lowering the repetition rate of excitation would decrease the photon flux but should enable detection of transient electric fields using the lifetime data. As an alternative, NRs with shorter lifetimes may be used.

Figure 4.

(a) Example of lifetime traces measured from a single particle in each channel while voltage was applied (V_on) and while it was not (V_off). A biexponential fit is plotted for each of the four curves, yielding eight lifetime constants per particle. (b) Histogram of the longer lifetime variation (Δτ₂) due to QCSE in the reflected channel. (c) Scatter plot depicting the correlation between spectral and lifetime shift. A trend line is shown as a guide for the eye. (d) Histogram of the intensity variations measured due to QCSE.

Determining the intensity fluctuation due to QCSE is done by examining the histogram of the blinking trace for periods of V_on and V_off separately (Figure S2). The intensity change shows only a weak correlation with the spectral shift (Figure S2 inset); this is due to the small magnitude of ΔF that is expected for high quantum yield QDs, making the measurement susceptible to the effects of the electric field on the blinking statistics, thus lowering the degree of correlation.

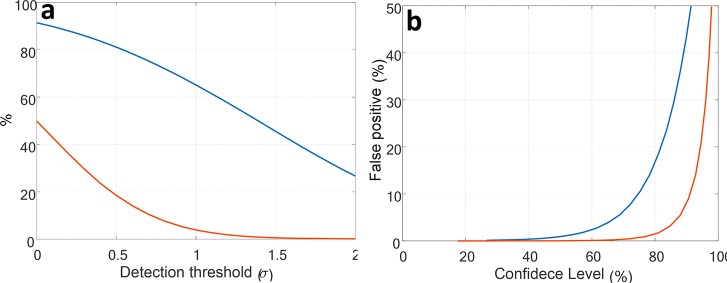
While the correlations between Δλ, Δτ, and ΔF are in agreement with the expected effect of QCSE, it is not possible to determine one by measuring the other as the degree of correlation is modest. Our data show, for example, that the particle exhibiting the largest Δλ (7.1 nm) also exhibits a negligible ΔF (0.2%). We present the detection and false positive probabilities of a 1.5 ms square voltage pulse (Figure 5) calculated from the data collected from the NR which exhibited the largest QCSE spectral shift (Δλ). A threshold is set in units of σ, the standard deviation of a(Δλ). We calculate a confidence level of 65% for detecting a 1.5 ms square voltage pulse with a false positive probability smaller than 4% or, alternatively, a 50% confidence level with less than 1% false positive probability (Figure 5). One should also consider that several NRs may be embedded in a single neuron to significantly increase the detection probability and nearly eliminate the false positive probability. For example, three well-oriented NRs would yield a false positive probability of 0.1% while maintaining a 61% detection probability, when considering a detection event when at least two of the three NRs crossed the detection threshold (Figure 5b, red).

Figure 5.

Numerical calculations for the detection of an action potential using the parameters extracted from the experimental data of the NR presenting the highest Δλ. (a) Detection confidence level (blue) and false positive probability (red) as a function of the threshold in units of σ. (b) False positive probability as a function of the detection confidence level for when a single (blue) or three (red) NRs are considered.

We experimentally demonstrate a detection scheme for spectral shifts due to the QCSE. We show that this scheme is sensitive to spectral shifts an order of magnitude smaller than the peak width. Moreover, we show our measurements are limited only by shot noise at short time scales. The detection scheme used enables simultaneous measurement of three effects that applied voltage has on QDs, Δλ, Δτ, and ΔF, allowing for thorough evaluation of the correlations between them.

We conclude that the use of a “balanced” detection scheme to observe spectral shifts yields superb sensitivity to voltage transients, enabling detection of a transient equivalent to a single AP with high levels of confidence especially when considering a realistic case of several NRs embedded in a single neuron membrane. Improving the detection capabilities further is possible with higher emission quantum efficiencies than the ones reported here. We find that measurement of spectral shifts yields better results even when compared to NRs with the strongest emission intensity modulation due to the QCSE (where the underlying microscopic process is likely stochastic charging). Overall, our results point at the feasibility of using NR voltage sensors for rapid, wide-field voltage sensing with a high spatial resolution. Moreover, the “balanced” detection scheme can be easily retrofitted to practically any commercial microscope using a standard low-noise camera and a commercial imaging dichroic splitter.

Methods

A 470 nm or a 510 nm pulsed laser diode with 20 MHz repetition rate (Edinburgh Instruments, EPL-470, EPL-510) was used for single-NR excitation. The excitation laser was coupled into a microscope (Zeiss, Axiovert 200 inverted microscope) and focused using a high-NA oil immersion objective (Zeiss, Plan Apochromat X63 NA 1.4). The epi-detected signal was filtered, using a dichroic mirror (Semrock, Di02-R488-25 × 36) and a long-pass filter (Semrock, 488LP edge basic), and directed to a home-built spectrally tunable balanced detection setup. A dichroic mirror (Semrock, Di02-R594) was used to split the emission peak from the NRs. Fine tuning of the dichroic cutoff wavelength to 600 nm was enabled by changing the angle of incidence. Each part of the spectrally split signal was coupled into a multimode fiber and detected by an avalanche photodiode (PerkinElmer SPCM-AQ4C) that was connected to a time-correlated single-photon counting (TCSPC) system (Picoquant, HydraHarp 400).

Single-particle spectra were measured using a fiber-coupled spectrometer (Princeton Instruments, Acton SP2300i) and a CCD camera (Princeton Instruments, Pixis256). A standard CCD camera (Thorlabs, DCC1645C) was used in top view imaging for positioning of the voltage probes.

Coverslips (#1.0, 25 mm diameter) were prepared with gold microelectrodes (Figure 1d; see Supporting Information for further details on the preparation of electrodes) using standard clean room photolithography procedures. NR samples were diluted in 4% poly(methyl methacrylate) (PMMA) (Sigma-Aldrich) in toluene and spin coated at 3000 rpm, and individual NRs were fixed in the PMMA layer. Probe positioners (Cascade Microtech, DPP-105-M–Al-S) were used to apply voltage to a chosen electrode pair, and a multimeter was used to measure the resistance between the electrodes to ensure there was indeed no short. Voltage was supplied from an amplifier (TREK, 2205) fed by a delay generator (Stanford Research Systems, DG645). A synchronized trigger was directed from the delay generator to the TCSPC to mark the beginning of each voltage cycle. In all experiments, the voltage applied was a 1 kHz 50% duty cycle square wave of amplitude 50–100 V after amplification, producing voltage pulses of 0.5 ms. Considering an ideal plate capacitor approximation, the electric field would be 125–400 kV/cm depending on the interelectrode gap. In practice, fields are expected to be lower, as this is far from an ideal plate capacitor. This field amplitude is comparable to the fields that exist in neuronal membranes. The voltage was applied to the central electrode (typically the ground) and an adjacent “finger” electrode. To reverse the voltage in the same measurement, the connections to the probes were switched.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsphotonics.8b00206.

• Details of the collection setup, nanorod synthesis, QCSE analysis, and microelectrode fabrication (PDF)

Author Contributions

O.B.E., D.S., and G.Y. conducted the experiments and performed data analysis. R.T., Y.K., and A.L. participated in data analysis and in experiment design. A.T., S.W., and D.O. conceived the project. The manuscript was written by O.B.E. and D.O. with significant contributions from all authors.

The authors declare no competing financial interest.