Optimization and prediction of the electron–nuclear dipolar and scalar interaction in ¹H and ¹³C liquid state dynamic nuclear polarization

Solution-state dynamic nuclear polarization (DNP) is a powerful tool for hyperpolarization and the study of intermolecular interactions in solution.

Abstract

During the last 10–15 years, dynamic nuclear polarization (DNP) has evolved as a powerful tool for hyperpolarization of NMR and MRI nuclides. However, it is not as well appreciated that solution-state dynamic nuclear polarization is a powerful approach to study intermolecular interactions in solution. For solutions and fluids, the ¹H nuclide is usually dominated by an Overhauser dipolar enhancement and can be significantly increased by decreasing the correlation time (τ_c) of the substrate/nitroxide interaction by utilizing supercritical fluids (SF CO₂). For molecules containing the ubiquitous ¹³C nuclide, the Overhauser enhancement is usually a profile of both scalar and dipolar interactions. For carbon atoms without an attached hydrogen, a dipolar enhancement usually dominates as we illustrate for sp² hybridized carbons in the fullerenes, C₆₀ and C₇₀. However, the scalar interaction is dependent on a Fermi contact interaction which does not have the magnetic field dependence inherent in the dipolar interaction. For a comprehensive range of molecular systems we show that molecules that exhibit weakly acidic complexation interaction(s) with nitroxides provide corresponding large scalar enhancements. For the first time, we report that sp hybridized (H–C) alkyne systems, for example, the phenylacetylene–nitroxide system exhibit very large scalar dominated enhancements. Finally, we demonstrate for a wide range of molecular systems that the Fermi contact interaction can be computationally predicted via electron–nuclear hyperfine coupling and correlated with experimental ¹³C DNP enhancements.

Introduction

In dynamic nuclear polarization, the electron–nucleus dipolar and scalar couplings can be described by the Hamiltonian,

Ĥ = hŝDÎ + hÎAŝ 1

where h is the Planck constant, Î is the nuclear spin angular momentum operator, ŝ is the electronic spin angular momentum operator, D is the dipolar coupling tensor, and A is the hyperfine coupling tensor (typically in units of MHz). One can compute the dipolar coupling tensor D; however, knowledge of the electron–nucleus dipole–dipole correlation function is required to determine the enhancement factor.1 Computation of this dipole–dipole correlation function can be achieved with a molecular dynamics simulation. However, such simulations are typically limited to select parameterized systems, and are very computationally intensive.1–3

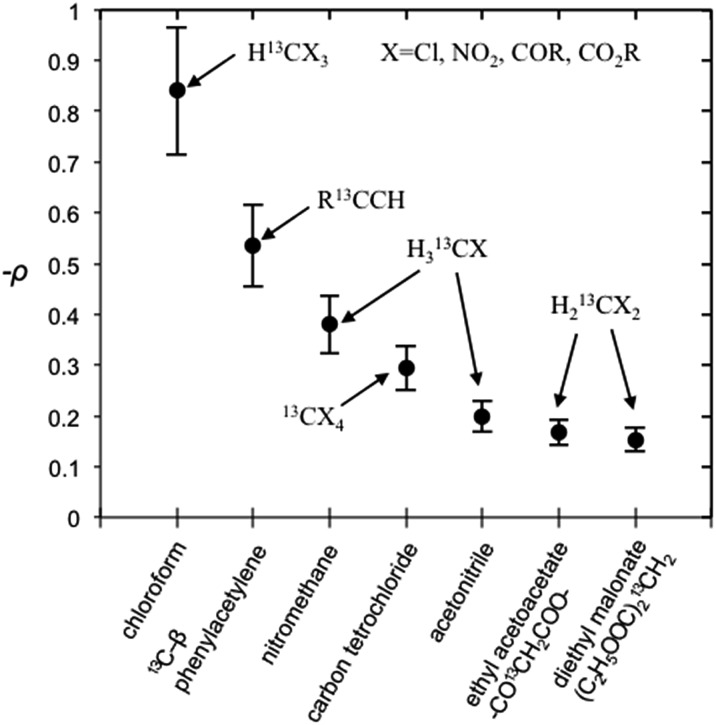
During the last two decades, significant advances have been made in the field of dynamic nuclear polarization (DNP).4,5 For liquid-state DNP, there has been a resurgence of interest in ameliorating liquid-state high magnetic field DNP enhancements.6–10 Liquid state Overhauser effect DNP has been applied for signal enhancement of flow imaging11–14 as well as the characterization of local water dynamics in biological systems.15–21 More recently, ¹H liquid state DNP measurements of water22–26 and small organic molecules27–29 at higher magnetic fields have been reported. However, liquid state DNP experiments also provide an excellent approach for understanding and predicting intermolecular solution interactions. The drawbacks for obtaining significant DNP enhancements (A) in the liquid state are well recognized, since the time-dependent electron–nuclear interaction dominates the Overhauser effect (Oe).30–35 This can be derived from eqn (2)–(4), where γ_S and γ_I are the magnetogyric ratios for the electron and nuclear spins, respectively, and the coupling (ρ) and leakage (f) factors are defined in terms of the nuclear transition probabilities in the presence of a free radical, WD2, WD0, WD1, which represent dipolar relaxation, and WSc0 due to scalar relaxation, as well as the transition probability in the absence of a free radical W₁₀ (Fig. 1).35 For molecular liquid systems, the time-dependent dipolar interaction dominates at low magnetic fields and/or short correlation times (τ_c) in the extreme narrowing limit ω_S²τ_c² ≪ 1 (ω_S electron Larmor frequency). Unfortunately, at the high magnetic fields (3–12 T) commonly employed in NMR, the coupling factor approaches zero (shown in Fig. 2).

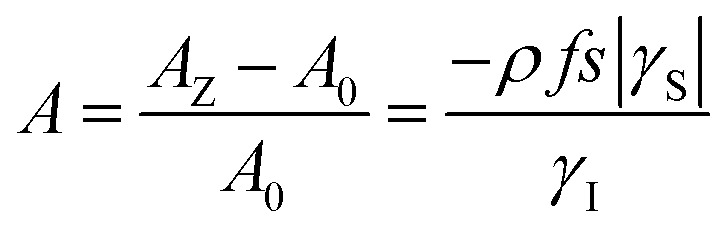2

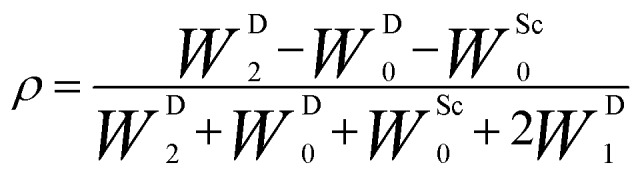3

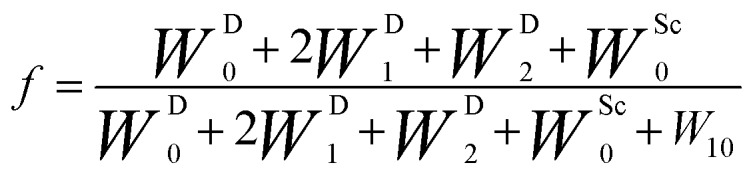4

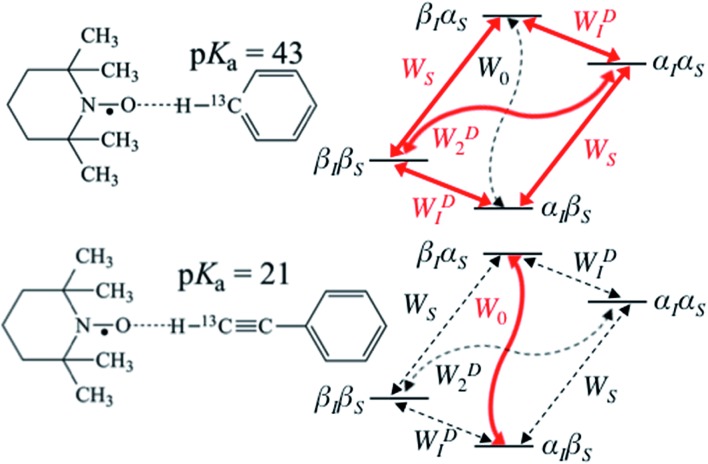
Fig. 1. Schematic diagram of energy level and transition probabilities for electron–nuclear (¹³C) spin systems for benzene/TEMPO (above) and phenylacetylene/TEMPO (below). α_S and β_S are the spin states of the unpaired nitroxide electron spin, and α_I and β_I are for nuclear spins. W_S represents the electron relaxation; W₀, WD1 and WD2 are zero, single and double quantum transitions, respectively. W₀ is equal to the sum of WSc0 and WD0 in eqn (3) and (4), which are transition rates of scalar and dipolar relaxation, respectively. ¹³C DNP enhancement of benzene is mainly due to dipolar relaxation, while scalar relaxation is the dominant mechanism for the β carbon of phenylacetylene.

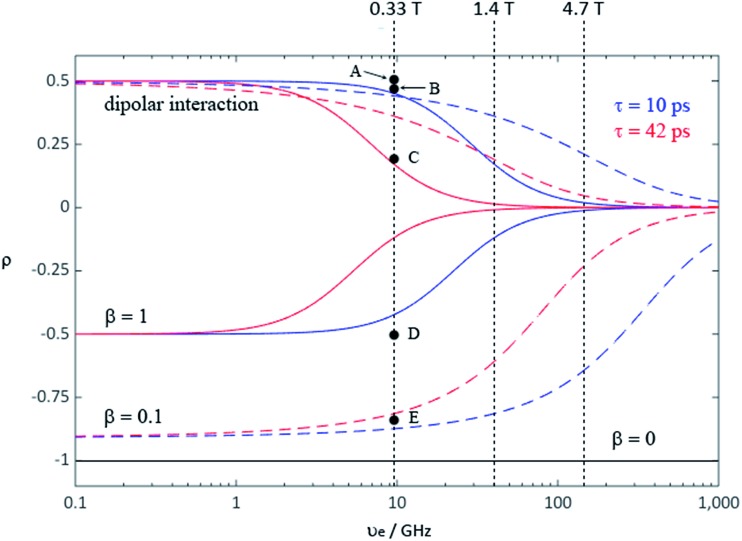
Fig. 2. Coupling factor (ρ) of the Overhauser effect enhancement depends on the electron Larmor frequency for rotational (solid line) and translational (dash line) motion with correlation time 10 ps (blue) and 42 ps (red); mixed with scalar enhancement of β = 1 (blue solid for τ_c = 10 ps and red solid for τ_c = 42 ps), and β = 0.1 (blue dash for τ_c = 10 ps and red dash for τ_c = 42 ps), where β values define different contributions from dipolar relaxation competing with pure scalar relaxation.34 Pure scalar enhancement (black solid line) is independent of magnetic field strength. Points A–E represent coupling factor values calculated from extrapolated experimental LLIT DNP enhancements polarized at 0.33 T: (A) ¹H of 9% benzene/0.001 M TEMPO/SF CO₂,43 (B) ¹H of chloroform/0.0015 M TEMPO44, (C) ¹H of 9% benzene/0.01 M TEMPO/C₆D₆,43 (D) ¹³C-β of phenylacetylene/0.01 M TEMPO45, and (E) ¹³C of chloroform/0.0052 M TEMPO.44 The relative standard deviation for ρ is about 15%. The two correlation times were estimated from ¹H DNP coupling factors of benzene in SF CO₂ and normal solvent by a rotational diffusion modulated dipolar interaction mechanism (see ESI† for derivation).

Scalar relaxation originates from the coupling of the magnetic moments of electrons and nuclei via the hyperfine coupling interaction.36 Although A in eqn (1) is the isotropic Fermi contact hyperfine coupling tensor, henceforth it is labelled as a_FC, in order to avoid confusion with the DNP enhancement, A vide infra.

For hydrogen containing molecules, ¹H DNP enhancements are usually dominated by the dipolar relaxation mechanism. If one assumes a rotationally modulated mechanism dominates the electron–nuclear dipolar interaction, the corresponding rotational correlation time (τ_r) can be estimated34,35,37 (see ESI† for detailed derivation). The corresponding DNP coupling factor modulated by exclusive rotational diffusion gives the magnetic field dependence shown in Fig. 2. More recently, it has been reported that translational diffusion predominantly modulates the dipolar interaction for water6,38,39 and some small organic molecular systems29,40 with organic radicals. Using the same correlation times, the field dependence of the DNP coupling factor modulated by translational diffusion33,35,41 is also represented by coloured dashed lines in Fig. 2. One notable exception for the ¹H nuclide is a nitroxide–trifluoroacetic acid system reported by Bates where the scalar interaction dominates the ¹H DNP enhancement.42

On the other hand, for the ¹³C nuclide, the coupling interaction can be dominated by a strong scalar interaction (WSc0 ≫ WD2, WD1, WD0) or a modest dipolar interaction (WSc0 ≪ WD2, WD1, WD0), or by a mixture of scalar and dipolar interactions. As illustrated in Fig. 1, it is well recognized that molecules with a (C–H) group can exhibit weak hydrogen bonding with nitroxides and show modest to large scalar enhancements.35,44,46–49 Griffin and coworkers have pointed out the importance of the scalar interaction for certain other nuclides (¹⁹F, ¹⁵N, ³¹P) besides ¹³C for high-field liquid-state DNP studies.50 Unfortunately, it is difficult to estimate the corresponding scalar correlation time τ_sc. For the case of acetonitrile/TEMPO, we previously reported ¹³C DNP τ_sc values 2–3 times longer than the dipolar correlation time (τ_r).49

As first reported by our laboratory, the solid–liquid intermolecular transfer (SLIT) DNP experiment has certain advantages when the radical is not present in the solution.51,52 In the SLIT DNP experiment, ¹³C contact shifts and spectral line broadening are avoided in the high field NMR detection magnet. The SLIT approach also has the advantage of improved low to high magnetic field transfer efficiencies allowing the transfer of radical free hyperpolarized metabolites for biological uses.53,54 The use of immobilized radicals for DNP approaches has recently been reconsidered and utilized to generate hyperpolarized water for clinical MRI applications.11–13,55,56 The efficiency of interactions between the radical and nuclei in immobilized radical flow methods can be in fact improved through better design of immobilizing methods,11,57 as well as the optimum synthesis of new radicals.58–60

In the current study, we demonstrate that ¹H LLIT (liquid–liquid intermolecular transfer) and ¹H SLIT DNP with solutes dissolved in supercritical fluid (SF) CO₂ result in enhanced electron–nuclear dipolar interactions and exhibit significant Oe DNP enhancements as a result of reduced correlation times. This is the first report of SF DNP with supercritical CO₂ except for the earlier ¹H DNP enhancement of supercritical ethylene by Wind and coworkers.61 It is well recognized that solutes dissolved in supercritical fluids exhibit significantly shorter molecular correlation times.62

For the case of the ¹³C nuclide, we present dipolar dominated ¹³C DNP enhancements for the fullerene C₇₀, with a trend attributable to the difference in the intermolecular distance for electron–nuclear interaction. In a large number of molecules with acidic C–H groups, significant scalar interactions and corresponding large positive enhancements are observed in the nitroxide–substrate complex. For example, we show that sp hybridized (H–C) alkyne systems, such as, the phenylacetylene–nitroxide system exhibit very large scalar dominated enhancements. It is also possible to directly compare liquid–liquid intermolecular scalar (Fermi contact) hyperfine couplings (a_FC) with experimental scalar DNP data utilizing density functional theory (DFT) modeling.49 We will subsequently demonstrate that computational predictions of the scalar hyperfine coupling constants (HFCs) across a wide set of nitroxide–substrate systems correlate strongly with the DNP enhancements for systems dominated by the scalar interaction.

Experimental

Samples

The production method used to obtain the C₆₀ and C₇₀ fullerenes utilized an apparatus similar to the original Krätschmer–Huffman63 arc-burning method. Cored rods (6 mm diameter) packed with a mixture of graphite and amorphous carbon (¹³C labelled) were arc-burned in a fullerene generator under a dynamic He atmosphere. Typical electric-arc operating production parameters consist of 20–25 V, 95–115 A, and 180–220 Torr of helium. The fullerenes were extracted by dissolution in CS₂ immediately after collection of the soot. Following this extraction protocol, the raw extract was filtered over a plug of glass wool. The C₆₀ and C₇₀ samples were separated chromatographically utilizing a pentabromobenzyl column, (PBB, 25 cm × 10 mm i.d., Phenomenex Co., Torrance, California) with CS₂ as the mobile phase. A mass spectrometer for the sample confirmed that the sample was ¹³C labelled at a level of approximately 12%. All other reagents and solvents for the LLIT DNP experiments were obtained commercially. C₆D₆ was purchased from the Isotic Inc, and other chemicals were purchased from Aldrich Chemical Co. and used without further purification. Sample solutions for the LLIT DNP experiments were prepared with TEMPO of varied concentrations from 0.001 to 0.14 M. The immobilized nitroxide materials used for the SLIT DNP experiments were synthesized in our lab by Rossi Gitti.53 The sample solutions were degassed by bubbling N₂ gas through during DNP experiments.

Dynamic nuclear polarization instrument

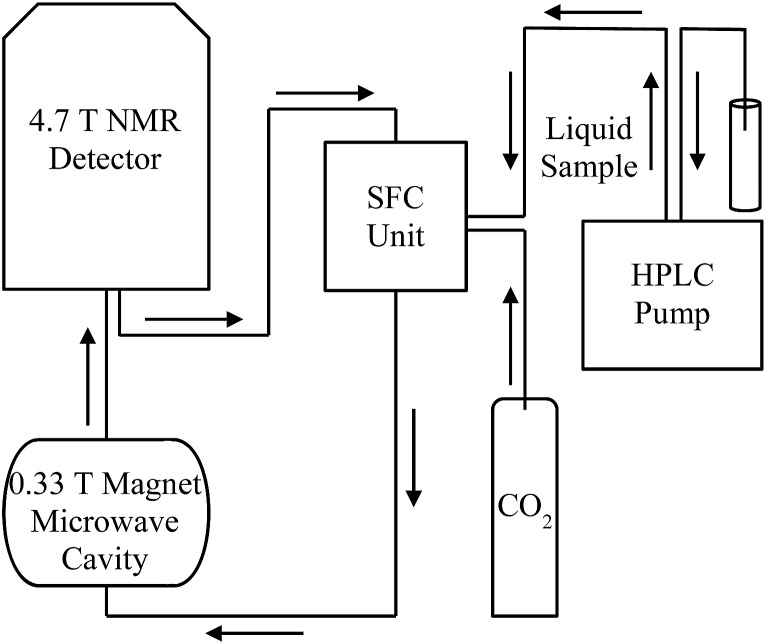
The instrument used for the LLIT DNP experiments was described previously.44 The flow transfer DNP apparatus for normal liquids and supercritical fluid CO₂ is shown in Fig. 4, where SF CO₂ can be used as the flowing solvent. For flow ¹H DNP performed under supercritical fluid conditions, N₂ degassed neat liquid benzene containing free radical TEMPO (0.1 M–0.01 M) originates at the HPLC pump and flows at a rate of 0.1 mL min^–1. The typical sample volumes inside the low field microwave cavity and high field NMR detector are 160 and 60 μL, respectively, and the volume of the transfer region is 80 μL. CO₂ is pumped from a syringe pump of a Suprex SFC/200A Multipurpose Unit and equilibrated to a flow rate of 1.01 mL min^–1 and 165 atm. The liquid sample is introduced into the CO₂ flow, and at a total flow rate of 1.11 mL min^–1 the sample solution enters the SFC oven where it is heated to 40 °C. The flow rate maintains the liquid sample concentration ensuring the liquid solutes solubility and also keeps optimum condition based on transfer and residence times for the flow ¹H DNP apparatus.

Fig. 4. Schematic drawing of apparatus for continuous-flow HPLC-DNP-NMR coupled with SF CO₂ (adapted from ref. 43, with the original figure shown in ESI†).

The instruments for the SLIT DNP performed in normal liquids and SF CO₂ were reported in our previous studies.51–54 The immobilized nitroxide radical is contained in a flow cell and located in the 0.33 T low field cavity, where electron spins are polarized. The experimental procedure of SLIT ¹H DNP is similar to that of LLIT ¹H DNP. The rate of liquid flow containing the sample was adjusted accordingly to obtain preferred concentrations in normal liquids or SF CO₂ as the flowing solvent.

Determination of experimental parameters

The determination of the leakage factor f and the electron spin saturation factor s is described previously for the DNP flowing system.44 In ref. 44, we reported a theoretical model for determining the absolute enhancement for the low to high magnetic field transfer experiments, which is scaled according to the observed enhancement considering relaxation losses during the transfer. This model is restated in ESI.† For most systems reported in this study, the DNP data were processed based on this model, and the absolute DNP enhancements were calculated using the method we applied previously.53,64,65 For benzaldehyde, nitrobenzene, toluene, diphenylmethane, triphenylmethane, benzonitrile, anisole, phenylamine and acetone systems, the absolute enhancements of ¹³C LLIT DNP were obtained utilizing a ratio method66–68 using the ¹³C enhancement of cyclohexane as the reference compound, with detailed procedures illustrated in the ESI.† Enhancements of ethyl acetoacetate and diethyl malonate were determined by the ratio method using ¹³C of benzene as the reference. The DNP enhancements of C₇₀ were also determined using the ratio method using C₆₀ as the reference. Compared to the former model, the ratio method does not require extrapolation from observed enhancements at varied liquid flow rates and microwave powers. The applicability of the ratio method was carefully evaluated utilizing the adamantane/TEMPO system, where the DNP enhancement was validated by this method using different microwave power levels (Table S1†). A detailed discussion is included in the ESI.† However, the ratio method does lead to low-to-high magnetic field transfer efficiency errors when the substrate molecules of interest contain quaternary carbons with significantly longer T₁ relaxation times. For the electron spin saturation parameter s, we employed relatively high radical concentrations (0.1 M and higher) for DNP experiments in normal solvents in this work, in order to saturate a single EPR line and also have leakage factors approaching unity. For the benzene/SF CO₂ studies a low nitroxide radical concentration (0.001 M) was employed since fast Heisenberg electron–electron exchange led to a single broad EPR line for this system.

Theory: geometry optimization, solvation, and thermochemistry

Geometry optimizations were performed for all species at the unrestricted M06-L69 level of density functional theory. The def2-SVP basis set70 was used for all atoms during optimization. The nature of stationary points was assessed in all cases by computation of analytic vibrational frequencies, which were also used to compute the molecular partition functions necessary to predict 298.15 K thermochemical quantities using the conventional ideal-gas, rigid-rotator, quantum-mechanical quasi-harmonic-oscillator71 approximation.72 Improved electronic energies were computed with the M06-2X density functional73 and the SMD continuum solvation model74 to account for the effects of the solvation environment, as single-point calculations, using the def2-TZVPP basis set70 on all atoms. Benzene was used for SMD solvent parameters on nitroxide/benzene and nitroxide/phenylacetylene systems; whereas cyclohexane SMD solvent parameters were specified for nitroxide/benzaldehyde and nitroxide/nitrobenzene systems.

Theory: isotropic hyperfine coupling

The ¹³C hyperfine coupling constants were computed in the gas phase at the unrestricted B3LYP level of DFT employing the EPR-III basis75 for C, N, H, O. We chose to use the B3LYP functional76 based on previously demonstrated good EPR performance for a nitroxide in aqueous solution.1 Hyperfine coupling constants were computed using the spin-orbit mean-field approximation SOMF(1X).77 For all substrate/TEMPO systems, Boltzmann weighted isotropic HFCs for nucleus j, a_iso^j, are determined from low-energy intermolecular configurations, c_i, as computed from eqn (5). a_iso^j,c_i is the isotropic HFC for nucleus j in geometrical configuration c_i, ΔG^c_i is the relative free energy of geometrical configuration c_i, R is the universal gas constant, and T is the temperature (taken to be 298.15 K). Symmetry equivalent atoms are averaged together.

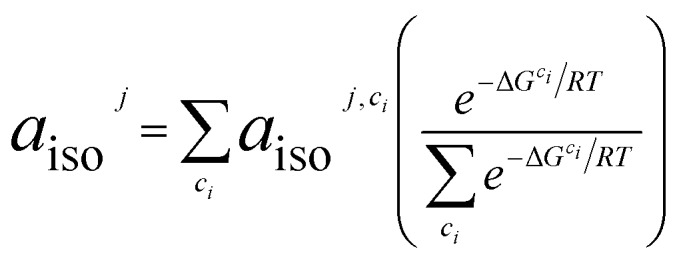5

Software

All optimization, thermochemistry, and solvation computations were accomplished using the Gaussian09 Rev D.01 suite of electronic structure programs.78 All EPR computations were accomplished in the gas phase using the ORCA 3.0.2 suite79 of electronic structure programs.

Results and discussion

LLIT ¹H DNP experiments in supercritical fluid (SF) CO₂

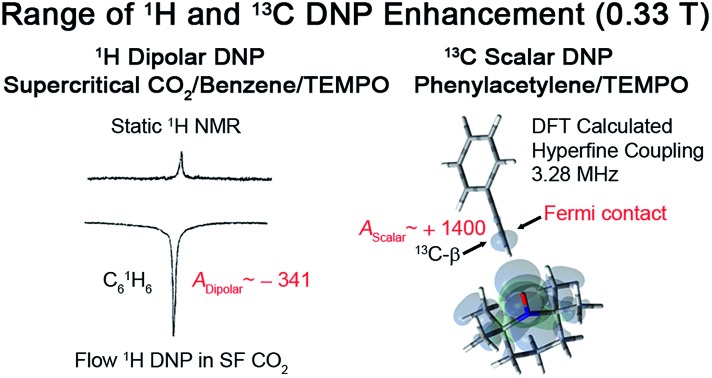
As previously indicated, solutes dissolved in supercritical fluid (SF) CO₂ should exhibit significant Oe DNP enhancements as a result of reduced correlation times. The static and flow ¹H NMR, and flow ¹H DNP spectra for 9% benzene/0.001 M TEMPO dissolved in SF CO₂ are illustrated in Fig. 5 and the LLIT ¹H DNP absolute enhancements of benzene dissolved in deuterated benzene and SF CO₂ are presented in Table 1.43 Benzene and chloroform have been extensively used as model systems in DNP studies: both molecules present negative ¹H DNP enhancements due to a dipolar-dominated Overhauser effect.40,47,80–88 The ¹H DNP absolute enhancement of chloroform gives a coupling factor approaching the dipolar enhancement limit (point B in Fig. 2). An important difference of nitroxides dissolved in normal liquids versus supercritical fluids is the higher Heisenberg exchange rates in the latter case. Batchelor,89 as well as Randolph and Carlier90 suggest a large increase in Heisenberg electron–electron exchange rates and hence the increased line widths of nitroxides in SF's may be due to critical clustering between solute and solvent molecules. Thus, the EPR signal for TEMPO collapses to a single broad line in SF CO₂ (see Fig. S2†). Also, the values of the saturation factor s are smaller in SF CO₂ compared with normal liquids (see Table S2† and saturation curves Fig. S3 and S4†). Han et al.91 and Bennati et al.6 have presented new models and alternative methods for quantifying the Overhauser DNP saturation factor especially for the case of low radical concentrations (∼0.001 M). However, their results suggest that at nitroxide concentrations of 0.01–0.02 M the errors in determining the saturation factor are not as significant. Thus, we have presented data in liquid C₆D₆ determined at both 0.001 M and 0.01 M of TEMPO concentrations as illustrated in Table 1 for comparison with the SF CO₂ data.

Fig. 5. ¹H spectra of 9% benzene/0.001 M TEMPO dissolved in SF CO₂ at 4.7 T. (a) Static ¹H NMR (S/N = 20), (b) flow ¹H NMR (S/N = 17) and (c) flow ¹H DNP (S/N = 124). Total flow of SF CO₂ was 1.1 mL min^–1. SF CO₂ conditions: d = 0.805 g mL^–1, SFC oven temperature 40 °C, P = 165 atm. All spectra were collected at 32 scans.

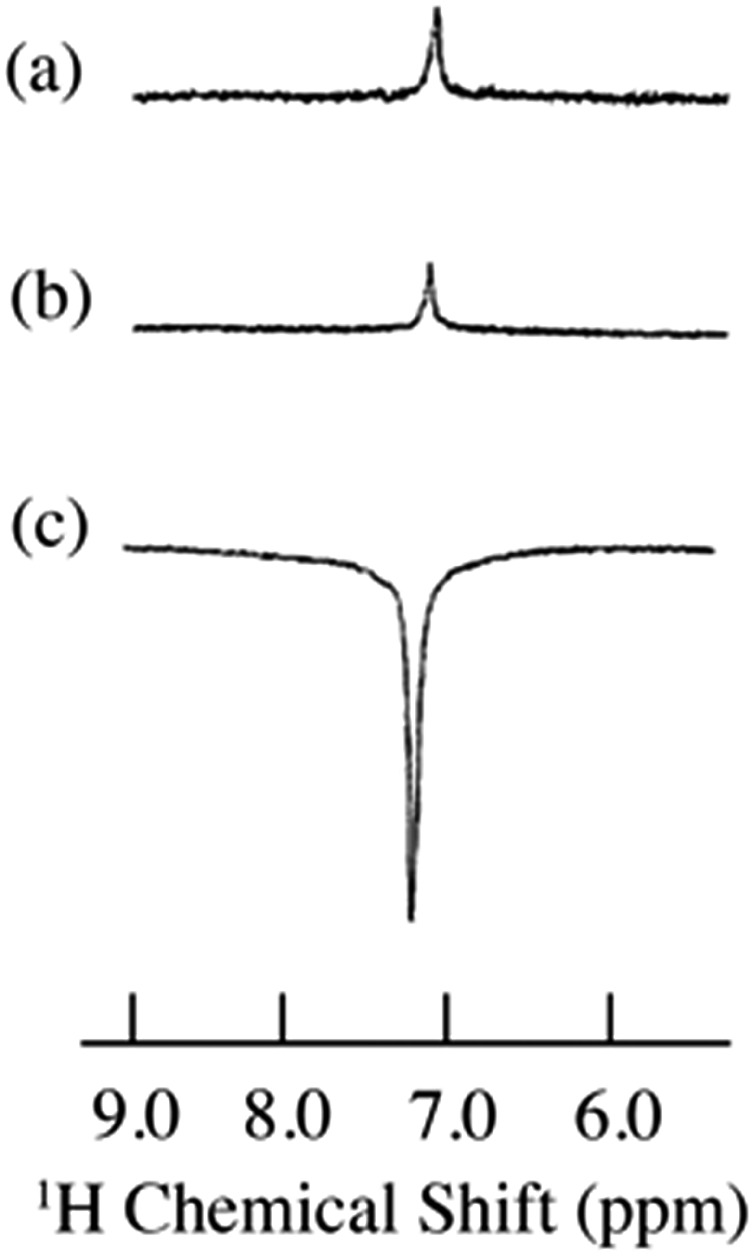
Table 1. LLIT ¹H DNP enhancements polarized at 0.33 T for benzene/TEMPO in C₆D₆ and SF CO₂.

System	Absolute enhancement
9% benzene/C6D6/0.001 M TEMPO	–120 ± 18
9% benzene/SF CO2/0.001 M TEMPO	–341 ± 36
9% benzene/C6D6/0.01 M TEMPO	–146 ± 20
9% benzene/SF CO2/0.01 M TEMPO	–293 ± 44

The increased ¹H DNP enhancement of benzene in SF CO₂ in comparison with benzene in liquid C₆D₆ is attributed to increased mobility of benzene provided by the supercritical fluid. There is an approximately 2–3 fold increase in the DNP enhancement of SF CO₂ compared with liquid C₆D₆, which is in agreement with the decreased factor of molecular correlation times of small molecules in SF CO₂.62,92,93 Assuming a rotationally dominated mechanism, predicts correlation times of 10 and 42 ps, respectively for SF CO₂ and liquid C₆D₆.43 Furthermore, within experimental error the absolute enhancement of 9% benzene in SF CO₂ with 0.001 M TEMPO approaches the dipolar limiting value of –330 corresponding to a coupling factor ρ = 0.5, leading to nearly the highest possible dipolar-dominant enhancement in the ¹H DNP experiment (point A in Fig. 2). This indicates that fast molecular motion of benzene in SF CO₂ satisfies the extreme narrowing limit ω_S²τ_c² ≪ 1 shown as the flat region at the low magnetic field strength in Fig. 2, for the pure dipolar relaxation models at 0.33 T. Based on discussion in the introduction for cases where the enhancement is induced by mixed scalar and dipolar relaxation, it is clear that by conducting flow transfer ¹H DNP using SF CO₂, both dipolar and scalar relaxation can result in substantial DNP Oe enhancements.

SLIT ¹H DNP experiments in supercritical fluid (SF) CO₂

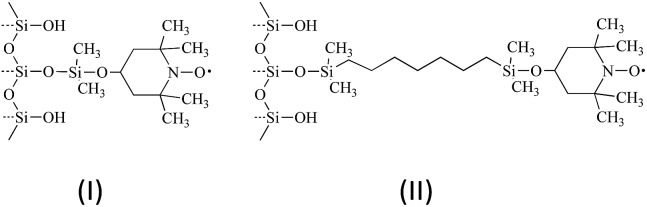
The solid–liquid intermolecular transfer (SLIT) ¹H DNP experiment has the advantage of the radical not being present in the liquid or fluid. We have obtained SLIT ¹H DNP results for benzene in supercritical CO₂ with two immobilized radicals that have been previously reported.53Table 2 presents the SLIT ¹H DNP absolute enhancements of benzene dissolved in deuterated benzene and SF CO₂ using the immobilized nitroxides43 (I) and (II) as illustrated in Fig. 3. The absolute enhancements were obtained by estimating a transfer efficiency of ∼80% (the efficiency with which the polarized sample bolus is transferred from the low to high field strength magnet).43 For I and II, a 3 to 4 fold increase is observed for the ¹H SLIT DNP enhancement for SF CO₂, in comparison with liquid C₆D₆, which is due to an increase in molecular motion of the immobilized nitroxide/benzene complex in SF CO₂. The absolute DNP enhancement from nitroxide II is slightly higher (A = –246) in comparison with radical I (A = –205) presumably due to the increased mobility (shorter correlation time τ_c) of the radical attached to a longer flexible chain off the surface of the silica gel for nitroxide II.

Table 2. SLIT ¹H DNP enhancements polarized at 0.33 T for benzene/nitroxide in C₆D₆ and SF CO₂.

System	Absolute enhancement
9% benzene/C6D6/nitroxide (I)	–67 ± 15
9% benzene/SF CO2/nitroxide (I)	–205 ± 24
9% benzene/C6D6/nitroxide (II)	–61 ± 17
9% benzene/SF CO2/nitroxide (II)	–246 ± 36

Fig. 3. Immobilized nitroxide material I (left) and II (right) used in SLIT ¹H DNP in normal liquids and SF CO₂.

LLIT ¹³C DNP experiments for molecular fullerene–nitroxide systems

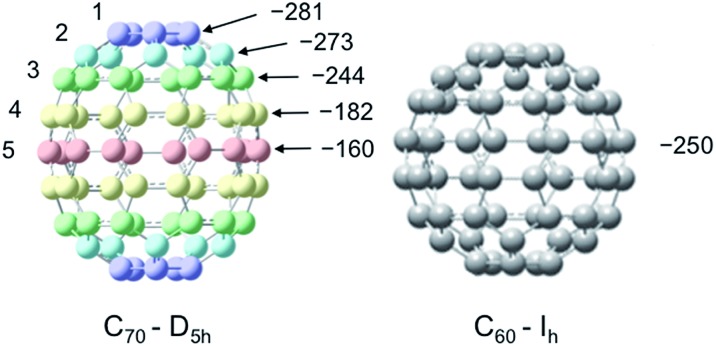
For the case of molecules containing the ¹³C nuclide, the Overhauser enhancement is usually a profile of both scalar and dipolar interactions. However, for molecules with quaternary sp² hybridized carbon atoms, a dipolar enhancement usually dominates. Our laboratory previously reported LLIT and SLIT ¹³C DNP results for the fullerene C₆₀/TEMPO system and observed dipolar dominated enhancements in both experiments.65 In contrast, the fullerene C₇₀ with ellipsoidal D_5h symmetry is very different in comparison with C₆₀, with 5 different non-equivalent carbon sites on the fullerene cage surface with significant differences in surface curvature as illustrated in Fig. 6. Johnson and coworkers have previously unambiguously assigned the five different carbons by 2D ¹³C NMR techniques.94

Fig. 6. Structures of C₇₀–D_5h and C₆₀–I_h and LLIT ¹³C DNP enhancements polarized at 0.33 T for different carbons of C₇₀/C₆D₆/0.1 M TEMPO system and the carbon of C₆₀/C₆D₆/0.1 M TEMPO system. Carbon atoms of C₇₀ are numbered from the apical to the equatorial positions. The relative standard deviation for A is about 15% (see Table S3†).

A surprising feature of the ¹³C DNP enhancements for the C₇₀/TEMPO system is the significantly higher dipolar enhancements (A = –281) observed at the polar cap carbons C₁ in comparison with the equatorial belt carbons C₅, A = –160. Moreover, there is a trend of decreasing enhancement values from the polar carbons (C₁) to the carbons at the equatorial position (C₅). The dipolar dominated ¹³C DNP enhancement value A = –250 for C₆₀ as well as the values for C₇₀ are remarkably large when compared with small aromatic molecules (e.g. benzene, A = –220, discussed in the next section). The relatively large dipolar ¹³C DNP enhancements can be partially attributed to the high I_h and D_5h symmetry of C₆₀ and C₇₀ with corresponding relatively short rotational correlation times. However, a model of mixed rotational and translational diffusion cannot be excluded for the electron–nuclear interaction of both systems. It is well recognized that ¹³C paramagnetic NMR shifts are a sensitive probe for the electron–nuclear hyperfine (scalar) interaction without the time-dependence noted above for dipolar interaction. The contact shifts of both fullerenes (Table S4†) indicate a very minor scalar contribution. Moreover, the T₁ relaxation times and corresponding similar f factors for these carbon sites exclude the influence of leakage factor f on the determination of absolute enhancements in the C₇₀ carbon sites (see Table S3† for relaxation data and leakage factor).

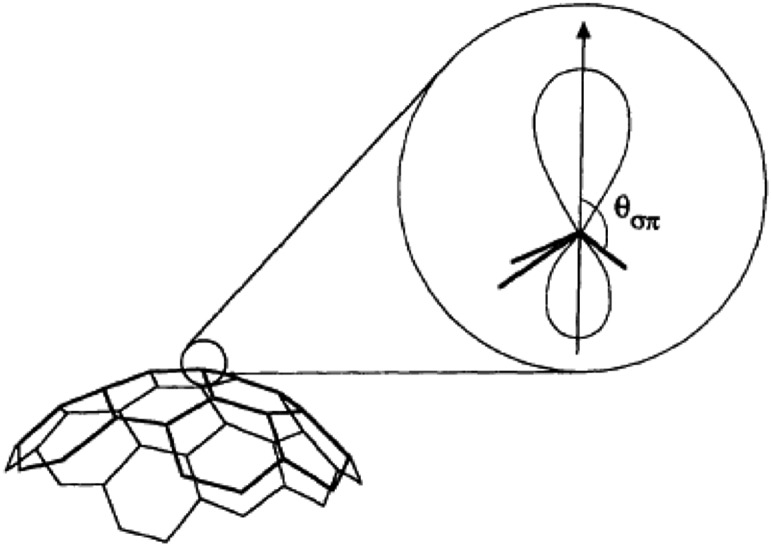
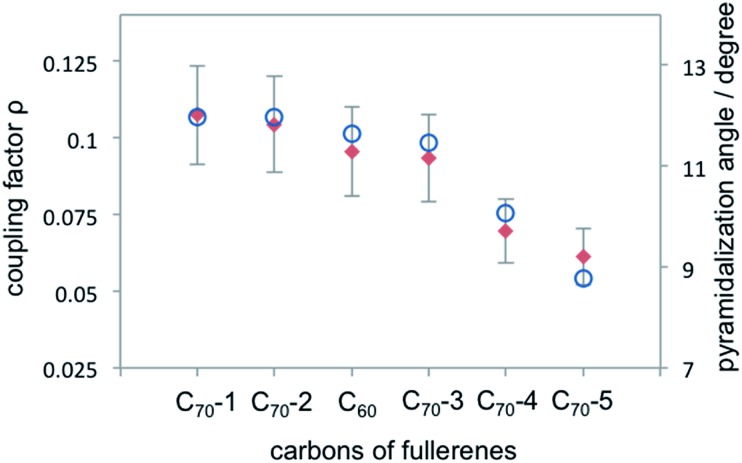
One possible origin of the enhancement differences of C₇₀ carbons is the variation of intermolecular distance between TEMPO and C₇₀ carbon from the polar to equatorial sites. Haddon has demonstrated the importance of expressing the curvature of a surface of sp² carbon atoms in terms of the π-orbital axis vector (POAV) to analyse local strain of fullerenes.95 The local curvature of the C₇₀ carbons is assessed with the pyramidalization angle (θ_σπ – 90), where θ_σπ is the angle between the carbon σ orbital and the π orbital as shown in Fig. 7.95 The curvature/POAV angle is related to the interaction distance between nitroxide radicals and the carbons of C₆₀ and C₇₀. The C₇₀ carbons with a larger pyramidalization angle are more accessible to the nitroxide radical in the weak intermolecular collisional complex, therefore resulting in a larger dipolar interaction. The correlation between the coupling factor ρ and the pyramidalization angle shown in Fig. 8 provides evidence for the dependence of the dipolar interaction on local curvature of the C₇₀ carbons.

Fig. 7. The π-orbital axis vector (POAV) is the vector of the π hybrid orbital with equal angles to the three σ bonds at a conjugated carbon atom. The average angle is denoted θ_σπ. Figure reproduced from ref. 95.

Fig. 8. Coupling factor derived from ¹³C LLIT DNP absolute enhancements of the indicated carbons for C₇₀–D_5h and C₆₀ are represented by red diamond; the pyramidalization angle of fullerene carbons for C₇₀ and C₆₀ (ref. 95) are represented by blue circle.

LLIT ¹³C DNP experiments of other molecular substrate–nitroxide systems and density functional theory computations: background

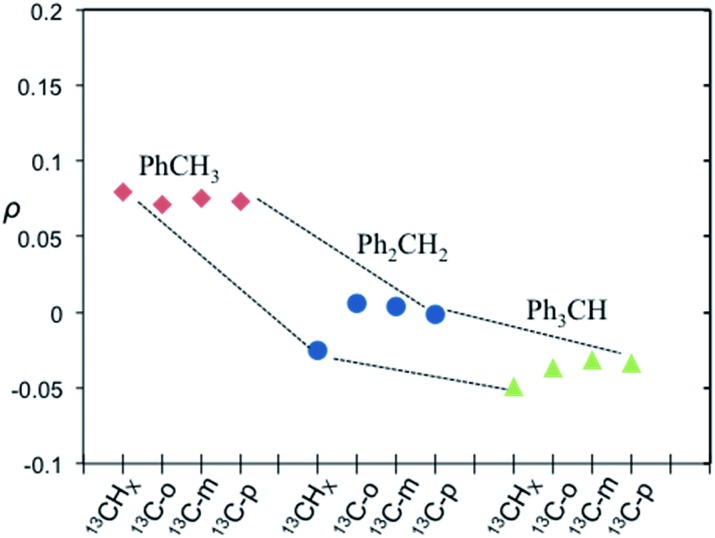
It is well recognized that molecules with C–H groups readily form weak complexes with nitroxides provide ¹³C DNP interactions ranging from modest dipolar to strong scalar interaction(s) dependent on the hydrocarbon acidity.44,46,50 For the case of molecules with sp³ hybridized carbons (C–H) that are not bound to electronegative elements, the ¹³C DNP presents modest dipolar enhancements as illustrated for the case of cyclohexane (A = –270) and adamantane (A = –254 and –209) (Table 6). It is well recognized that there is increasing acidity for the sp³ hybridized carbon (–C–H_X) group in progressing from toluene (pK_a = 41.2) to diphenylmethane (pK_a = 33.4), and triphenylmethane (pK_a = 31.4). This trend results in a significant change in the DNP enhancement originating from a modest dipolar (A = –209) to scalar interaction (A = +129) for ¹³CH_X (X = 1–3) (Fig. 9). The aromatic ortho, meta and para carbons reflect nearly the same dipolar to scalar trend as the sp³ hybridized (–C–H_X) group. This trend is especially relevant in view of the change in the molecular size (and corresponding correlation time) in progressing from toluene to triphenylmethane. Clearly, spin delocalization from the sp³ hybridized (–C–H_X) group to the aromatic pi system is an important factor dictating this trend. A second factor is the expected longer scalar correlation time for the nitroxide/triphenylmethane complex in comparison with the toluene complex, which results in a larger scalar component in the overall coupling factor. However, the sp² aromatic ipso carbons exhibit dipolar enhancements (see Fig. S7†). The absolute enhancement trend in these cases could have a larger error because of significantly longer T₁ relaxation times than the corresponding molecules with attached hydrogens (–C–H_X groups). On the other hand, for the case of sp³ hybridized carbons attached to electron withdrawing groups (X–C–H_X), these weakly acidic hydrocarbons lead to very significant scalar enhancements as represented by chloroform (HCCl₃) example with A = +2200, which is close to the scalar limit. In addition, there are numerous other examples of large scalar enhancements for electron withdrawing sp³ hybridized carbon (X–C–H_X) groups including nitromethane, diethyl malonate, ethylacetoacetate, and acetonitrile as illustrated in Fig. 10 and Table 6. All of these examples have acidic (C–H) groups with pK_a acidities ranging from 10 to 25. Thus, sp³ hybridized carbon hydrocarbons exhibit a wide range of DNP enhancements ranging from those with pK_as 40–50 (e.g., toluene, cyclohexane) that exhibit modest dipolar interactions, to hydrocarbons with C–H groups exhibiting pK_a acidities between 10 and 30 with large scalar enhancements (A = +400 to +2200). Even molecules with weakly acidic (C–H) sites exhibit significant scalar enhancements, for example, the C₁ carbon in 1-chlorobutane (A = +460), when the remaining non-acidic (C–H) sites (C₂–C₄) exhibit dipolar enhancements (Table 6). The ability of nitroxide radicals to probe the weak acidity of C–H groups in more complex molecular systems is a unique application of solution state DNP.

Table 6. LLIT ¹³C DNP enhancements polarized at 0.33 T for substrate/TEMPO systems and acid dissociation constants (pK_a)101,102 at 25 °C of ¹³C–H protons.

System (solute/solvent/TEMPO conc.)	Nucleus	Absolute enhancement	pKa	Type of carbon hybridization
Phenylacetylene/NA/0.01 M (ref. 45)	13C-β	+1400 ± 210	21	sp
Phenylacetylene/NA/0.14 M (ref. 45)	13C-α	+290 ± 44	—
Benzaldehyde/cyclohexane/0.1 M (ref. 67)	13CHO–	+373 ± 56	14.9	sp2
	13C-ortho	+131 ± 20	—
Nitrobenzene/cyclohexane/0.1 M (ref. 66)	13C-ortho	+587 ± 88	—
	13C-meta	+198 ± 30	—
	13C-para	+366 ± 55	—
Chloroform/0.0052 M (ref. 44)	13CHCl3	+2200 ± 330	15.5	sp3
Nitromethane/benzene/0.1 M (ref. 66)	13CH3NO2	+996 ± 149	10
Carbon tetracholoride/1-chlorobutane/0.08M (ref. 44)	13CCl4	+770 ± 115	—
Acetonitrile/carbon tetrachloride/0.1 M (ref. 103)	13CH3CN	+520 ± 100	25
1-Chlorobutane/carbon tetrachloride/0.08 M (ref. 44)	Cl13CH2CH2CH2CH3	+460 ± 70	—
Ethyl acetoacetate/benzene/cyclohexane/0.1 M (ref. 66)	CH3CO13CH2COOCH2CH3	+440 ± 66	11
Diethyl malonate/benzene/cyclohexane/0.1 M (ref. 66)	(CH3CH2OOC)213CH2	+401 ± 60	13
Triphenylmethane/cyclohexane/0.1 M (ref. 66)	13CH(Ph)3	+129 ± 19	31.4
Diphenylmethane/cyclohexane/0.1 M (ref. 66)	13CH2(Ph)2	+67 ± 10	33.4
Benzene/0.1 M (ref. 66)	13C6H6	–200 ± 30	43	sp2
C60/C6D6/0.1 M (ref. 65)	13C60	–250 ± 20	—
Benzonitrile/cyclohexane/0.1 M (ref. 67)	13C-ipso	–281 ± 42	—
Phenylamine/cyclohexane/0.1 M (ref. 67)	13C-ipso	–318 ± 48	—
Toluene/cyclohexane/0.1 M (ref. 66)	13C-ipso	–423 ± 63
Benzaldehyde/cyclohexane/0.1 M (ref. 67)	13C-ipso	–456 ± 20	—
Anisole/cyclohexane/0.1 M (ref. 67)	13C-ipso	–457 ± 69	—
Nitrobenzene/cyclohexane/0.1 M (ref. 66)	13C-ipso	–572 ± 86	—
Diethyl malonate/benzene/cyclohexane/0.1 M (ref. 66)	(CH3CH2OO13C)2CH2	–642 ± 96	—
Ethyl acetoacetate/benzene/cyclohexane/0.1 M (ref. 66)	CH3COCH213COOCH2CH3	–711 ± 107	—
	CH313COCH2COOCH2CH3	–720 ± 108	—
Acetone/carbon tetrachloride/cyclohexane/0.1 M (ref. 66)	(CH3)213CO	–744 ± 112	—
Toluene/cyclohexane/0.1 M (ref. 66)	13CH3Ph	–209 ± 31	41.2	sp3
Adamantane/benzene/0.1 M (ref. 66)	–13CH2–	–209 ± 13	—
	–13CH–	–254 ± 14	—
Cyclohexane/NA/0.1 M (ref. 45)	13C6H12	–270 ± 40	45
1-Chlorobutane/carbon tetrachloride/0.08 M (ref. 44)	ClCH213CH2CH2CH3	–200 ± 30	—
	ClCH2CH213CH2CH3	–400 ± 60	—
	ClCH2CH2CH213CH3	–290 ± 44	—

Fig. 9. Coupling factor derived from ¹³C LLIT DNP absolute enhancements of the indicated carbon (i.e.¹³CH_X, X = 1–3, ¹³C-ortho, ¹³C-meta, and ¹³C-para) for the series of toluene (red diamond), diphenylmethane (blue circle), and triphenylmethane (green triangle) (Ph_YCH_X, X = 1–3, Y = 4–X).66 Dashed lines illustrate motif trends for different molecules. The relative standard deviation for ρ is about 15%.

Fig. 10. Coupling factor (negative) derived from scalar dominant ¹³C LLIT DNP absolute enhancements of small molecules. The relative standard deviation for ρ is about 15%.

Benzene/TEMPO

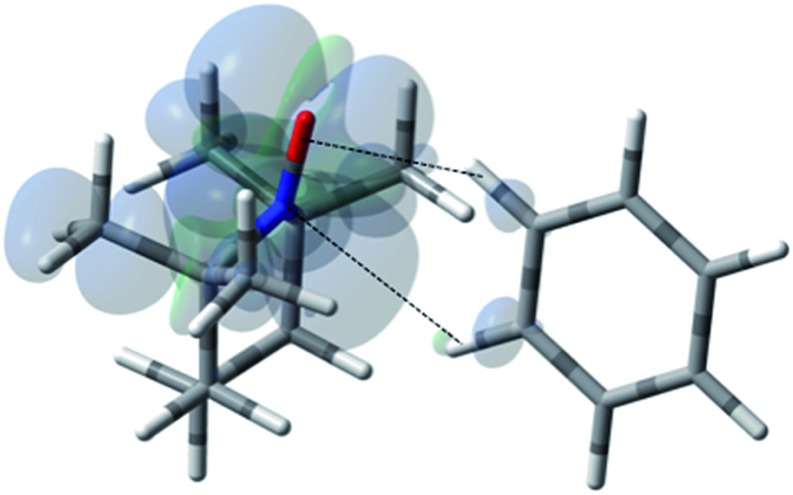
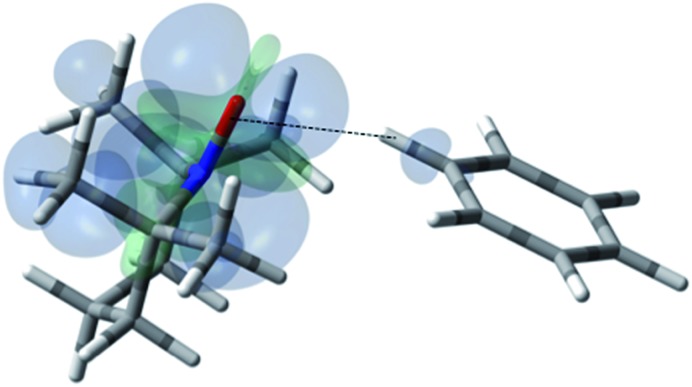
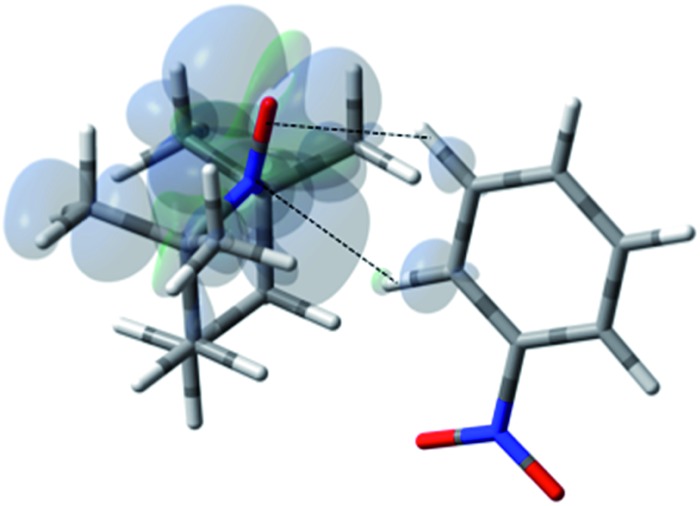
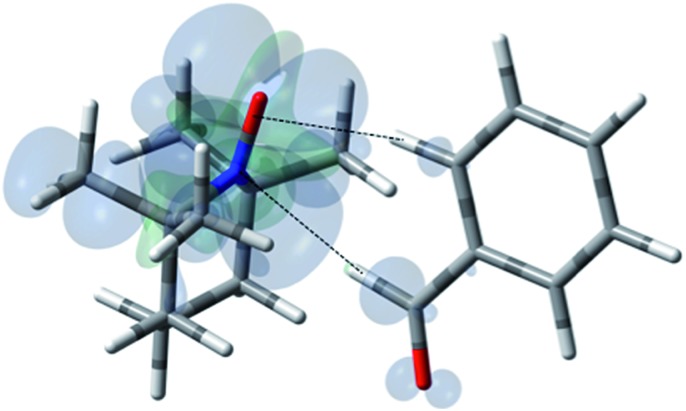
For the case of hydrocarbons with sp² hybridization, benzene has been an archetypal system for many previous solution state DNP studies. In addition, earlier NMR contact shift studies have clearly established a small scalar contribution to the dipolar dominated DNP enhancement for the benzene/TEMPO system, A = –220.44,68,96,97 Electron withdrawing groups attached to sp² hybridized quaternary carbons dramatically increase this dipolar interaction. For example, the aromatic ipso (quaternary) sp² carbons (¹³C–X) of monosubstituted benzenes such as benzonitrile, phenylamine, benzaldehyde, anisole, and nitrobenzene exhibit dipolar enhancements with both electron donating and electron withdrawing substitutents (X) (see Fig. S5†). A similar trend is observed for sp² hybridized carbonyl carbons with electronegative oxygens directly attached (Fig. S5†). The highest dipolar enhancement in this trend is for the carbonyl carbon of acetone with a dipolar enhancement of A = –744 representing a coupling factor of ∼55% of the dipolar limit at 0.33 T for this small molecule. For comparison, the significantly larger fullerene C₆₀ molecule with sp² hybridized quaternary carbons exhibits a solution state enhancement of A = –250 and does not have a significant scalar component vide supra.65 These results suggest that substrate molecules (100–700 Daltons) with sp² hybridized carbons that do not have a significant scalar contribution exhibit dipolar enhancements with TEMPO ranging from 25 to 50% of the dipolar limit at 0.33 T. As previously noted, at the lower end of this range, the benzene/TEMPO system represents a small molecule with both dipolar and scalar ¹³C interactions. We have previously reported based on DFT calculations that the formation of weak hydrogen bonding between C–H bond of substrate molecules and nitroxides results in unpaired spin density at the substrate carbon nuclei and results in non-trivial scalar contributions to the ¹³C DNP enhancements for acetonitrile/TEMPO and acetamide/TEMPO.49 It is of considerable interest to establish the important orientation and interaction site(s) for the electron–nuclear interaction for the case of the benzene/TEMPO system. We have obtained the Boltzmann weighted ¹³C a_FC = 0.80 MHz via DFT computations using eqn (5) by considering the four lowest-energy molecular configurations (see S6–S9 and Table S5† for optimized orientations and their parameters). The two important conformations with the largest contributions to the hyperfine coupling are shown in Fig. 11 and 12. It is important to note that in both conformations the nitroxide N–O bond vector is either orthogonal to one C–H bond vector or orthogonal between (T shape) two C–H bond vectors with interaction distances of 0.230 and 0.239 nm, respectively. This orthogonal approach of the N–O and C–H bond is also consistent for the lowest energy conformations found below for other monosubstituted benzene/TEMPO complexes vide infra. The computational average a_FC value (a_FC = 0.80 MHz) indicates a non-trivial scalar contribution to the ¹³C DNP NMR signal of benzene. For the comparison of benzene and monosubstituted benzenes, their comparable molecular size and lack of significant conformational differences allow the assumption of relatively small changes in the correlation times.

Fig. 11. The electronic spin density distribution of the largest ¹³C–H HFC contributing orientation between benzene and TEMPO where two C–H moieties bite the TEMPO N–O group. Dashed lines are given as guides for intermolecular distances, which are 2.39 Å for O···H (of C–H moiety with closest approach to TEMPO oxygen) and 2.86 Å for N···H (of C–H with closest approach to TEMPO nitrogen).

Fig. 12. The electronic spin density distribution of the second largest ¹³C–H HFC contributing orientation between benzene and TEMPO where one C–H moiety points at N–O group. Dashed line is given as a guide for intermolecular distance, which is 2.30 Å between the oxygen atom of TEMPO and the hydrogen atom of benzene C–H moiety.

Nitrobenzene/TEMPO

For the case of nitrobenzene/TEMPO (NMR and DNP spectra shown by Fig. 14), the introduction of the strong electron withdrawing nitro group on the aromatic ring leads to a lowest energy conformation with an orthogonal approach of the N–O and C–H bond vectors between the ortho and meta carbons (Fig. 13). The weighted Boltzmann averaging of HFC for the ortho carbon (a_FC = 1.424) is in strong agreement with the large scalar enhancement, A = +587 observed for this site (Table 3). The large ¹³C-para and ¹³C-meta contribution appears to originate from a slightly higher energy configuration (Fig. S23†) where the para C–H bond vector is orthogonal to the nitroxide, N–O bond vector. However, delocalization of polarized spin from the dominant ortho conformation to the meta and para sites can not be excluded. It is interesting to note in this regard that the strong electron withdrawing nitro group leads to scalar enhancements, whereas, electron donating groups such as the amino group of phenylamine leads to dipolar enhancements at all ortho, meta, and para carbon positions (Table S10†).

Fig. 14. ¹³C spectra of benzaldehyde/TEMPO in cyclohexane at 4.7 T (a) 0.1 M TEMPO without flow DNP, (b) 0.1 M TEMPO with flow DNP. (a) 3000 scans; (b) 735 scans.67.

Fig. 13. The electronic spin density distribution for the lowest energy orientation between nitrobenzene and TEMPO where ortho and meta C–H moieties complex with the TEMPO N–O group. Dashed lines are given as guides for intermolecular distances, which are 2.45 Å for O···H (of ortho C–H) and 2.53 Å for N···H (of para C–H).

Table 3. LLIT ¹³C DNP enhancements polarized at 0.33 T for nitrobenzene/cyclohexane/0.1 M TEMPO66 and a_FCvia DFT modeling.

System	Nucleus	Absolute enhancement	a FC a
Nitrobenzene	13C-ipso	–572 ± 86	0.399
	13C-ortho	+587 ± 88	1.424
	13C-meta	+198 ± 30	0.329
	13C-para	+366 ± 55	0.418

^a a _FC is the Fermi contact HFC in units of MHz computed as described.

Benzaldehyde/TEMPO

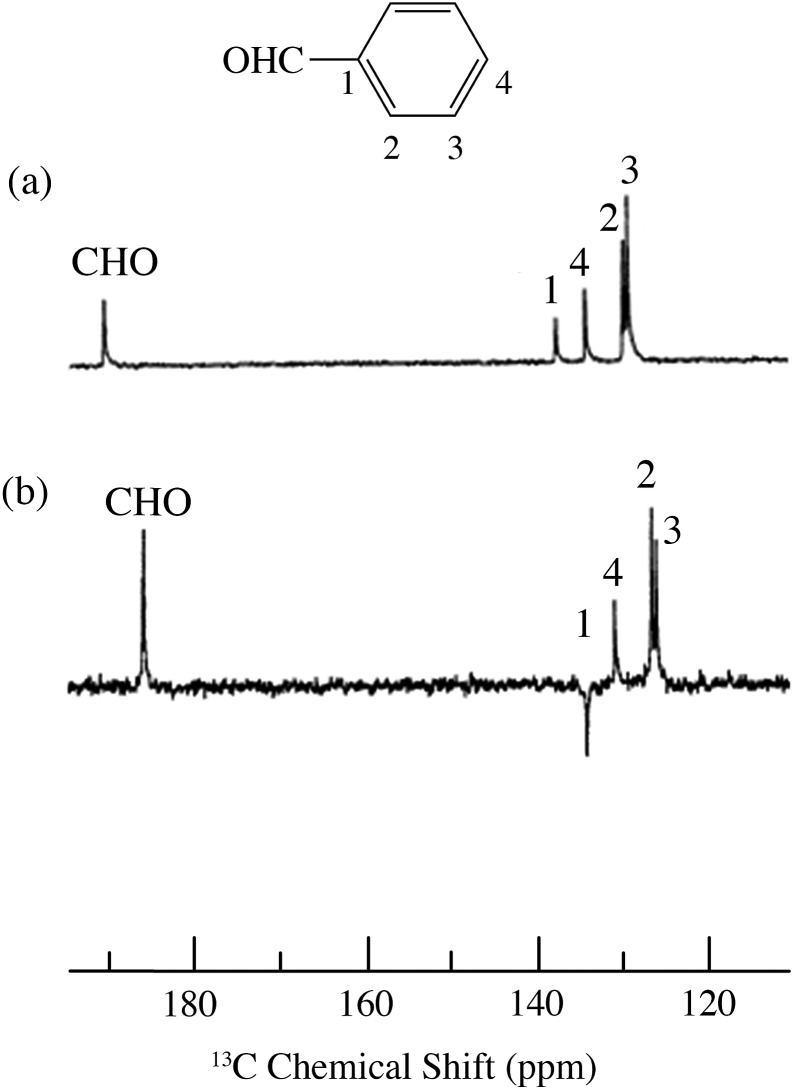
In contrast with benzene and nitrobenzene, the benzaldehyde/TEMPO system provides a system where two different weak sp² hybridized C–H bonds can complex with TEMPO (Fig. 15 and Table 4). The weighted Boltzmann averaging of hyperfine couplings continues to show strong agreement with the scalar enhancements measured by DNP (see Table S7† for details). In this case the ortho aromatic C–H bond and the aldehyde, O C–H bonds both contribute as a “dual complexation site” with TEMPO for the lowest energy conformation. In addition, this conformation is similar to the orthogonal bond vector conformations found for benzene and nitrobenzene. However, the more acidic aldehyde O C–H site exhibits a larger hyperfine coupling (a_FC = 1.155) and corresponding larger scalar enhancement (A = +373) in comparison with the modest hyperfine coupling and DNP enhancement found for ortho C–H site, a_FC = 0.442 and A = +131, respectively. It is also interesting to note that the modest electron withdrawing aldehyde group leads to modest scalar enhancements at all ortho, meta, and para carbon positions (Table 4).

Fig. 15. The electronic spin density distribution for the largest ¹³CHO– and ¹³C-ortho HFC contributing orientation between benzaldehyde and TEMPO where the aldehyde and ortho C–H moieties bite the N–O group. Dashed lines are given as guides for intermolecular distances, which are 2.39 Å for O···H (of ortho C–H) and 2.46 Å for N···H (of aldehyde C–H).

Table 4. LLIT ¹³C DNP enhancements polarized at 0.33 T for benzaldehyde/cyclohexane/0.1 M TEMPO67 and a_FCvia DFT modeling.

System	Nucleus	Absolute enhancement	a FC a
Benzaldehyde	13CHO–	+373 ± 56	1.155
	13C-ipso	–456 ± 20	0.284
	13C-ortho	+131 ± 20	0.442
	13C-meta	+93 ± 14	0.063
	13C-para	+78 ± 12	0.099

^a a _FC is the Fermi contact HFC in units of MHz computed as described.

Phenylacetylene/TEMPO

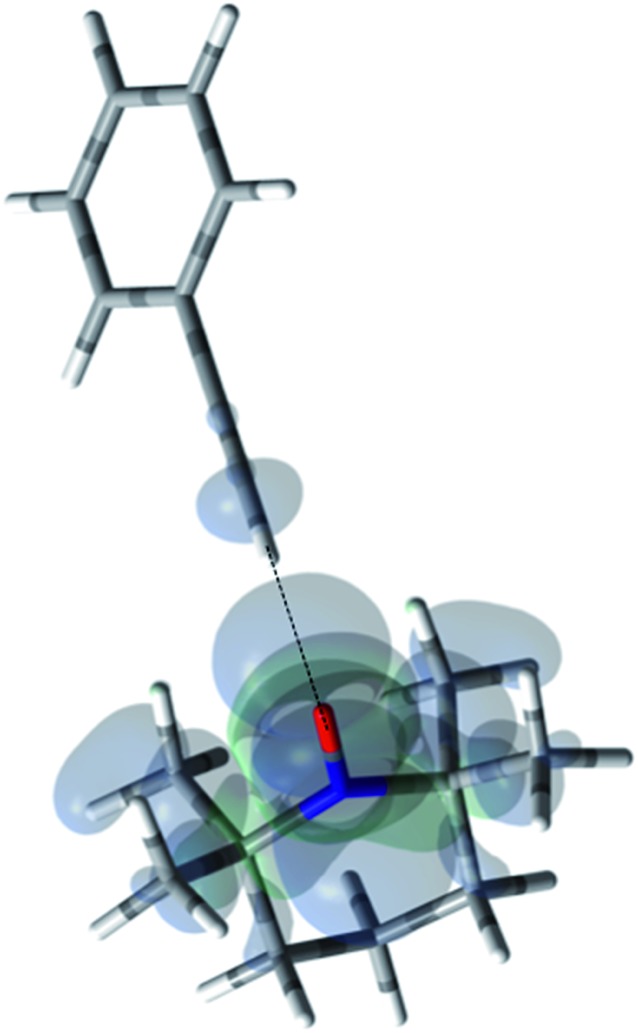
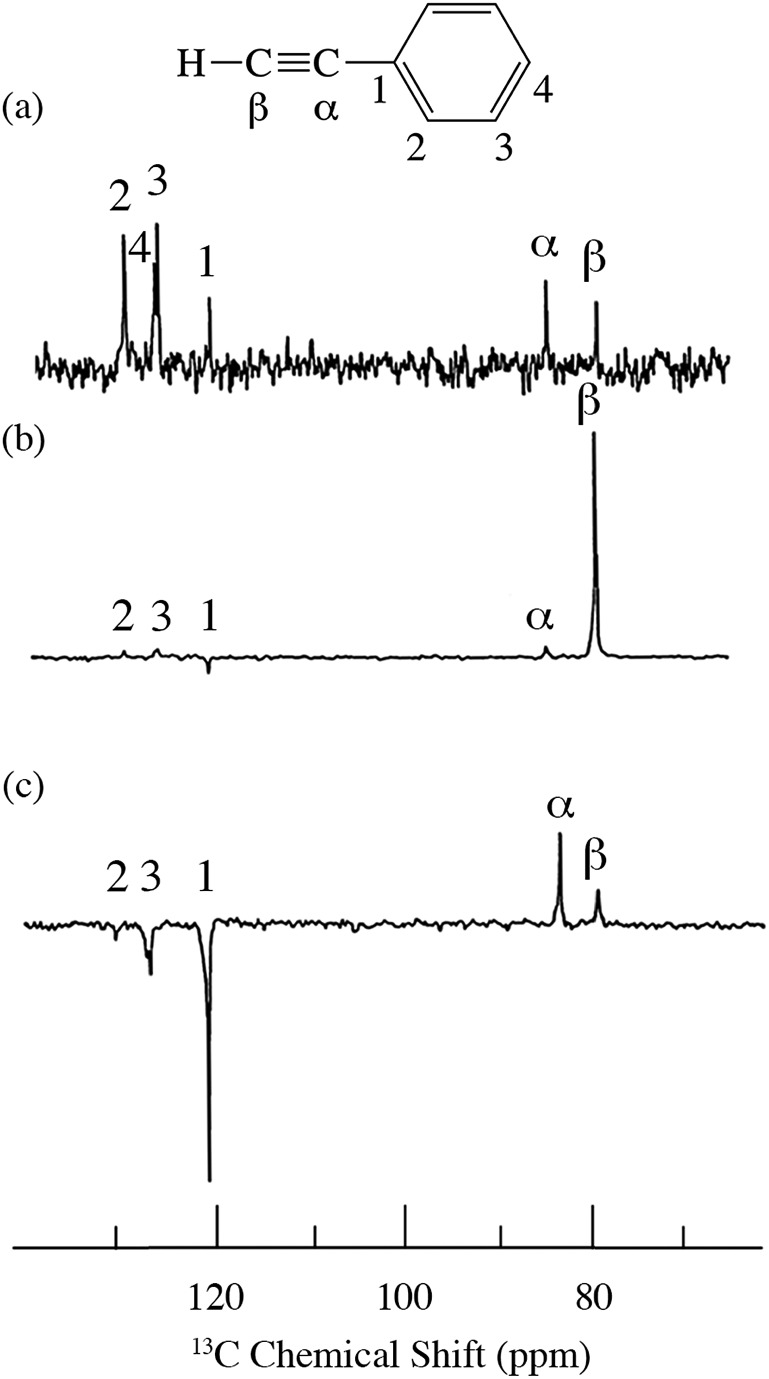
For the case of sp hybridized carbons there is a paucity of data for the complexation of alkynes with nitroxides. For cyano sp hybridized carbons modest ¹³C dipolar DNP enhancements have been reported for benzonitrile and acetonitrile (Table 6 and Table S16†). However, for the acidic sp hybridized C–H carbons there is a paucity of examples reported. In one notable early NMR shift study, a transient hydrogen bonding between phenylacetylene and di-tert-butyl nitroxide was proposed,68 since the former is a good proton donor with a pK_a of 21 (Fig. 1). It should be noted that alkynes are key components in the widely employed “click” reaction extensively employed in organic, polymer, and biomedical functionalization studies.98 Phenylacetylene has an acetylenic proton of relatively high acidity (pK_a of 21)99 compared with benzene as shown in Fig. 1. The DFT and DNP results for phenylacetylene/TEMPO are shown in Fig. 17 and Table 5. As predicted, the phenylacetylene/TEMPO exhibits a large hyperfine coupling, a_FC = 3.28 and corresponding large scalar dominated enhancement (A = +1400) for the sp hybridized C–H β carbon (shown in Table 5). Moreover, the β carbon exhibits the largest scalar-dominant DNP enhancement observed to date for a molecule not containing halogens, corresponding to a DNP coupling factor of –0.53 (point D in Fig. 2). In analogous fashion to the previous examples above, the lowest energy conformation has the N–O bond vector orthogonal to the sp hybridized C–H bond vector (Fig. 17), but the interaction distance is considerably shorter (0.203 nm) than the previous examples, vide supra. It is also interesting to note that the α sp hybridized carbon exhibits a notable scalar enhancement (A = +290) as well, also consistent with the relatively large computationally derived hyperfine coupling (a_FC = 0.871). The ortho, meta, and para carbons on the benzene ring of phenylacetylene show very small dipolar-dominated (negative) enhancements that are nearly zero. Clearly there is a large difference in the spin–lattice T₁ relaxation time of the scalar dominated β carbon relative to the o, m, and p carbons of the aromatic ring. At low radical (TEMPO) concentrations (0.01 M), the β carbon polarization is notably enhanced, but the other carbon atoms are barely observable. For the ring carbons having dipolar-dominated interactions, whereas, at higher radical concentrations (0.14 M) dipolar enhancements become observable, but the β carbon is barely observed because of the very short nuclear relaxation times at this concentration which limits the transfer efficiency from the low (0.33 T) to the high observable magnetic field (4.7 T). However, the lower radical concentration used (0.01 M) may diminish the observed DNP enhancements for the β carbon and other carbons because of a lower leakage factor and three-spin effects100 (Fig. 16b). These results suggest that for molecules having specific strong scalar complexation sites, it is possible to independently detect enhancements contributed by the scalar and dipolar interactions by varying the radical concentration.

Fig. 17. The electronic spin density distribution of the largest ¹³C-β HFC contributing orientation between phenylacetylene and TEMPO where the alkyne points at N–O group. Dashed line is given as guide for intermolecular distance, which is 2.03 Å between oxygen atom of TEMPO and the hydrogen atom of acetylene group of phenylacetylene.

Table 5. LLIT ¹³C DNP enhancements polarized at 0.33 T for phenylacetylene/0.001 M and 0.14 M TEMPO45 and a_FCvia DFT modeling.

System	Nucleus	Absolute enhancement	a FC a
Phenylacetylene b	13C-β c	+1400 ± 210	3.281
	13C-α	+290 ± 44	0.871
	13C-ipso	–280 ± 42	0.277
	13C-ortho	–36 ± 5	0.579
	13C-meta	–32 ± 5	0.117
	13C-para	N/A d	0.181

^a a _FC is the Fermi contact HFC in units of MHz computed as described.

^bInverse gated ¹H decoupling was employed.

^cC-β results are based on measurements of 0.01 M TEMPO solution, while C-α and C-1–3 results are from 0.14 M TEMPO solution.

^dC-4 signal is close to zero.

Fig. 16. ¹³C spectra of phenylacetylene/TEMPO at 4.7 T (a) 0.01 M TEMPO without flow DNP, (b) 0.01 M TEMPO with flow DNP and (c) 0.14 M TEMPO. (a) 16 scans; (b) 16 scans; (c) 64 scans.45.

Conclusions

In summary, we have found that for ¹H DNP, supercritical fluids provide a convenient approach for decreasing the correlation time for solutes and provide an alternative approach for improving dipolar enhancements at high magnetic fields without the need for polarization at low temperatures (∼4 K). For the system SF CO₂/benzene/TEMPO, the DNP enhancement approaches the dipolar limiting value of –330 (ρ = 0.5) at 0.33 T. For biomedical applications, there has been considerable interest in the DNP enhancement of water as reviewed by Günther.8 For example, Bennati and coworkers have experimentally reported an Oe dipolar DNP enhancement A = –170 for the water/TEMPONE-D-¹⁵N system at 9.7 GHz (0.33 T).22

For ¹³C DNP at 0.33 T, we have found that molecules (100–700 Daltons) dissolved in liquids containing carbon sites without a significant scalar contribution (e.g., carbonyls) exhibit dipolar enhancements ranging from, A = –250 to –740 with TEMPO vide supra. It is easy to predict that ¹³C DNP for these carbon sites could also exhibit ¹³C DNP enhancements 2 to 3 times greater if conducted in SF CO₂. For the biomedical metabolites, the enhancement in SF CO₂ followed by rapid dissolution in water or saline solutions and transfer to high magnetic fields could be a viable approach for NMR nuclides with long T₁ relaxation times for both NMR and MRI applications. Furthermore, other SF fluids, such as, supercritical water and nitrous oxide represent alternative fluids for decreasing correlation times at higher magnetic fields for DNP at high fields. For the case the C₇₀/TEMPO system, we have reported significantly higher dipolar enhancements at the polar cap carbons with greater sp² curvature in comparison with the equatorial belt carbons. For the case of ¹³C DNP where both dipolar and scalar interactions are important, the correlation between experimental scalar DNP enhancements (A) and the Boltzmann weighted hyperfine coupling constants (a_FC) calculated using the DFT methods provides a predictive tool for any substrate systems exhibiting a non-trivial scalar interaction as illustrated in Fig. 18. A cautionary note of these predictions is the importance of the scalar and/or dipolar correlation time(s) that is not included in the current computational approach. For this work, we assume similar correlation times for the monosubstituted benzenes employed in this study. Finally, of critical importance, molecules with sp hybridized C–H groups, such as, the β carbon of phenylacetylene deserve further study because of the large scalar enhancements observed for this system. The short intermolecular distance between the hydrogen attached to the β C–H group and the orthogonal O–N bond of the nitroxide in TEMPO is about 2.0 Å (see Fig. 17). The shorter intermolecular distance is an indication of stronger hydrogen bonding between the acetylene group and the radical, and hence has a greater effect on the scalar interaction, compared with other sp³ and sp² hybridized carbon systems. Furthermore, compared with sp² carbons such as the aldehyde carbon of benzaldehyde, the phenylacetylene β carbon has a greater s character of the bonding carbon hybrid orbital caused by sp hybridization. The hyperfine coupling constant (a_FC) is directly proportional to the unpaired electron spin density at the investigating carbon nucleus, hence the increased HFC value of phenylacetylene β carbon indicates the contribution of increased s character and corresponding greater spin density transfer from the radical to the sp carbon nucleus, |ψ(0)|². This conclusion is consistent with the observation of experimental and computed increasing s character for ¹³C–¹H coupling constants (J_CH) which increases markedly as a result of Fermi contact contributions104 with the trend, 159 Hz for benzene,105 173.7 Hz for the carbonyl group in benzaldehyde,106 (C₆H₅¹³C¹HO) and 251 Hz for the sp β carbon in phenylacetylene107 (C₆H₅C¹³C¹H). In conclusion, solution state DNP provides a unique approach for studying intermolecular weak bonding interactions of solutes in normal liquids and SF fluids.

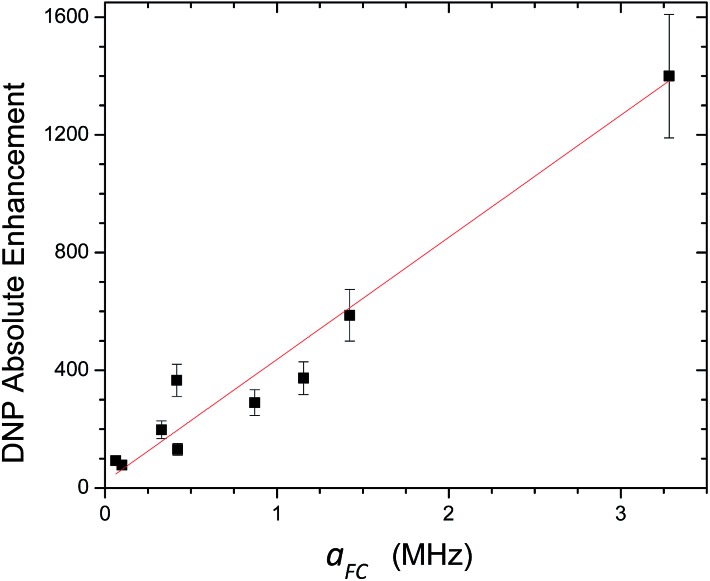
Fig. 18. Correlation between experimentally determined ¹³C LLIT DNP scalar dominated enhancements and their calculated AFC (Boltzmann weighted DFT computed Fermi contact hyperfine coupling constant) for the phenylacetylene/TEMPO, benzaldehyde/TEMPO, and nitrobenzene/TEMPO systems. After performing a linear regression with direct weighting of the DNP enhancement error, a line of best fit (y = mx + b) was determined having parameters m = 415 ± 23, b = 21 ± 52, and the goodness of the fit is computed as having an adjusted R² = 0.97.