Encoding of error and learning to correct that error by the Purkinje cells of the cerebellum

Summary

The primary output cells of the cerebellar cortex, Purkinje cells (P-cells), make kinematic predictions about ongoing movements via high-frequency simple spikes (SS), but receive sensory error information about that movement via low-frequency complex spikes (CS). How is the vector space of sensory errors encoded by this low-frequency signal? Here, we measured P-cell activity in the oculomotor vermis during saccades, then followed the chain of events from experience of visual error, generation of CS, modulation of SS, and ultimately change in motor-output. We found that while error direction affected probability of CS, error magnitude altered its temporal distribution. Production of CS changed the SS on the next trial, but regardless of the actual visual error, this change biased the movement only along a vector that was parallel to the P-cell’s preferred error. From these results, we inferred the anatomy of a sensory-to-motor adaptive controller that transformed visual error vectors into motor-corrections.

Introduction

Cerebellar Purkinje cells, P-cells, produce high frequency simple spikes to predict kinematics of the ongoing movement^1–6. These simple spikes are adaptable, changing following experience of a sensory error^7–9, which are transmitted to P-cells from the inferior olive¹⁰, resulting in complex spikes (CS)^11–13. However, CSs are rare events that occur approximately once per second¹⁴, producing a disparity between richness of information regarding predictions via the simple spikes, and the poverty of sensory error information in the CSs. Indeed, errors can double^15,16 or halve in size¹⁷ without significant changes in CS rates. How can P-cells accurately produce simple spikes when their teacher is seemingly so impoverished in its encoding of sensory errors?

One possibility is that error magnitude modulates the shape of CS waveforms. Properties of a sensory stimulus can affect the number of spikes in the climbing fiber¹⁸, thereby altering the duration of the resulting CS waveform^19,20. A longer CS waveform has been shown to induce a larger change in the simple spikes, producing a larger change in behavior^21,22.

Another possibility is that error magnitude may affect CS timing. The latency of the CS with respect to simple spikes in the flocculus has been shown to modulate plasticity at the parallel fiber to P-cell synapse²³. That is, CSs that arrive during a precise temporal window may have a larger effect on the simple spikes by maximizing the change in the strength of the recently active P-cell synapses.

Here, we considered saccadic eye movements to visual targets. At saccade end, sometimes the eyes missed the target, resulting in an error. We quantified how CSs encoded the vector space of visual errors, how this encoding changed the simple spikes that were produced in the subsequent saccade, and how the motor output in this subsequent saccade differed from those that the animal had produced before the experience of error.

We found that in the oculomotor vermis, each P-cell had a preference for a specific direction of visual error^16,24, with the error direction encoded in the probability of generating a CS. However, the magnitude of that error vector affected the CS timing. As the error became larger, CS timing became less variable and more likely to occur during a specific temporal window: the window that was most effective in inducing plasticity. Intriguingly, CSs that occurred in this temporal window were of longer duration. Using trial-by-trial analysis^7,9,21, we observed a chain of events that tied the P-cell’s preferred direction of error in visual-space to a vector of force production in motor-space.

From these functional results we made an anatomical inference. The error preference in a region of sensory-space, as signaled by the CSs, organized the P-cells into a computational unit that collectively predicted movement kinematics⁴. That preference for error also organized the downstream projections of the computational unit so that, through learning, the P-cells altered the motor output only along a vector that was parallel to their preferred error.

Results

We analyzed simple and CSs of n=67 well-isolated P-cells from the oculomotor vermis of 7 monkeys in 187,008 trials. Each trial began with fixation on a visual target. After a random interval the target was moved to a new location 10–25° away, resulting in a saccadic eye movement^16,24,25. In most trials (~65%) the target was displaced during the saccade (Fig. 1A). In the remaining trials the target was not displaced, but the inherent saccadic variability typically placed the eyes at a location other than the center of the target, resulting in a foveal error. In each trial we quantified the post-saccadic visual error as a vector that pointed from the eye location at saccade termination to the current target location.

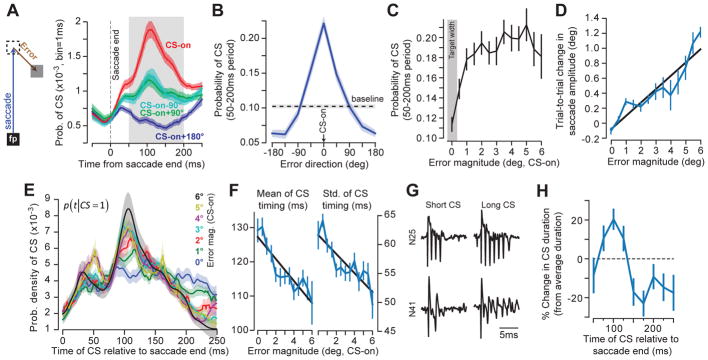
Figure 1. Error direction is encoded in the probability of the CS, whereas error magnitude modulates the distribution of CS timing.

A. While the eyes are gazing at a fixation point (FP), a target is presented (dashed square), and the animal makes a saccade toward it. During the saccade, in some trials the target is displaced to another location (gray square), resulting in a visual error (the vector between eye position at saccade end and the target). Probability of CS across trials was computed for each millisecond of time for each P-cell and for various error directions. CS-on refers to direction of error vector that produced the highest probability of CS. B. Probability of CS in the 50–200ms period following saccade end as a function of error direction. C. Probability of CS in the preferred error direction in the 50–200ms period following saccade end as a function of error magnitude (error direction is CS-on). D. The amount of trial-to-trial behavioral learning as a function of error magnitude. E. Probability density of CS timing for a range of error magnitudes. Bin size is 1ms. Error magnitude modulated the timing distribution, transforming it from a uniform to a unimodal pattern. F. For each P-cell, we computed the probability density of CS timing (over the range 0–250ms following saccade termination) for each error size, and then measured the mean and standard deviation of each distribution. As error magnitude increased, both the mean and standard deviation declined. G. CS waveforms for two representative P-cells. The duration of the CS waveform varied within each P-cell. H. Duration of the CS waveform as a function of when that CS was generated relative to saccade termination. Duration is expressed relative to each P-cell’s mean CS duration. In all cases, error bars indicate between-cell variability via standard error of the mean (SEM) across all cells (n=67).

Encoding of an error vector by the complex spikes

When the saccade completed but the eyes did not land on target, in the post-saccadic period, the P-cells produced a single CS with a probability that depended on the error direction (Figs. 1A and S1). (Presence of two CSs in the 250ms post-saccadic period was extremely rare, occurring in 0.33% of the CS present trials. In these cases we only considered the first CS.) For each P-cell, we labeled the error direction that produced the largest probability of CS as ‘CS-on’¹⁶. Across the population, probability of CS was modulated by error direction (Fig. 1B). Errors in direction CS-on increased CS probability by 120.9±10.1% with respect to baseline (the final 150ms of the fixation period, prior to target motion, paired t-test, t(66)=12.17; p<10⁻¹⁷), and errors in direction CS-on+180° reduced this probability by 36.6±5.2% (paired t-test, t(66)=−7.32; p<10⁻⁹). Therefore, the direction of the visual error was encoded in the probability of generating a CS, with each P-cell tuned to a preferred error direction.

In contrast, error magnitude did not modulate the probability of generating a CS (Fig. 1C), remaining invariant beyond 0.5° (RM-ANOVA, main effect of error magnitude F(10,530)=1.49; p=0.14). However, error magnitude clearly affected trial-to-trial change in behavior: on each trial we measured the component of the error vector along the direction of the primary target and then computed the trial-to-trial change in the amplitude of the saccade along that same direction. Larger errors produced larger trial-to-trial change in behavior (Fig. 1D, RM-ANOVA main effect of error magnitude F(6,172)=15.6; p<0.001). How could learning exhibit sensitivity to error magnitude when the signal that encoded that error in individual P-cells appeared to lack magnitude information?

We focused on trials in which an error occurred in direction CS-on and for each P-cell selected the subset of trials where a CS occurred in the 250ms post-saccadic period. We found that when the error was small, CS timing was distributed uniformly throughout the post-saccadic period (Fig. 1E). However, as error magnitude increased, CS timing transformed from a uniform to a unimodal distribution with a peak at ~110ms. As a result, increased error magnitude coincided with a reduction in the standard deviation (Fig. 1F, RM-ANOVA main effect of error magnitude, F(12,489)=5.74; p<0.001) and jitter of the CS timing distribution (Fig. S2, median absolute distance from the median, RM-ANOVA, F(12,515)=4.39; p<0.001).

Importantly, as CS timing changed, so did its waveform. In some instances, the duration of the CS waveform was short, whereas in other instances the same P-cell generated a longer duration CS (Fig. 1G). We measured the duration of each CS and then computed how this duration varied within each P-cell as a function of CS timing (Fig. 1H). We found that CS timing predicted CS duration (Fig. 1H): a CS that occurred at 100ms after saccade termination was about 20% longer in duration than average for that P-cell, whereas a CS that occurred at 200ms after saccade termination was about 10% shorter in duration than average (Fig. 1H, one-sample t-test comparing CS duration at 100ms, t(66)=3.7; p<0.001).

In summary, direction of error modulated the probability of producing a CS in the post-saccadic period, whereas magnitude of that error modulated the distribution of CS timing. As error magnitude increased, the temporal precision of CS production increased, focusing them in the 75–150ms period. A CS that occurred during this window of time was different than CSs that occurred earlier or later: its waveform was longer in duration.

Behavioral change following occurrence of a complex spike

Even when the error was in direction CS-on, a P-cell produced a CS in only 1/4^th of the trials (Fig. 1B). We sorted the data in a 2×2 design in which, after saccade completion, either an error was present or absent, and either the P-cell had produced a CS or not. We measured change in behavior via the difference in motor output (time series of eye velocity vectors) from the trial in which the error was experienced to the subsequent trial in which the same target was presented.

We began with trials in which the animal experienced an error in the CS-on direction of the P-cell (Fig. 2A). The probabilistic nature of CS produced a subset of trials in which the P-cell did not produce a CS in the post-saccadic period, and another subset of trials in which the P-cell did produce a CS. As expected for both cases, in the subsequent trial the motor commands pulled the eyes more in the direction of error, coinciding with CS-on of the P-cell under study (Fig. 2A, left panel). The errors were similar in trials that CS had or had not occurred (paired t-test, t(66)=1.25; p=0.21). Yet, the change in the motor output was significantly larger, i.e., the pull was stronger, following production of a CS (Fig. 2A, left panel, difference curve). A similar observation has been made in a different task (pursuit) when visual error was in direction CS-on of P-cells in the flocculus region of the cerebellum²¹.

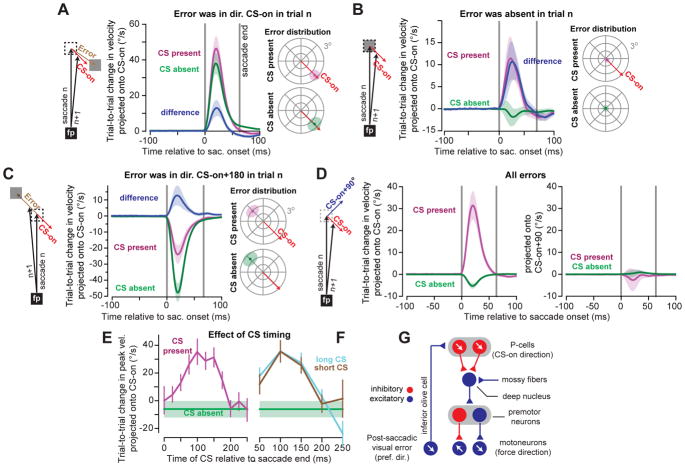
Figure 2. The influence of P-cells on motor output.

A. Analysis of trials in which the error was in the CS-on direction of the P-cell. We measured eye trajectory (velocity vectors as a function of time) during the saccade in the trial in which the error was experienced, as well as the trajectory in the subsequent trial in which saccade was made to the same target. To measure change in behavior, we projected the difference in the 2D sequence of velocity vectors onto the CS-on direction of the P-cell. Following experience of an error, the next trial exhibited an increase in the velocity vector along the direction of error. However, if the P-cell produced a CS, velocity on the next trial was larger in direction CS-on compared to when a CS was absent (mean+SEM across neurons). Distribution of errors for CS present and CS absent trials were comparable (right, shaded region denotes average SD of error distribution across neurons). B. Same as (A) except for trials in which there was no post-saccadic error (|error| < 0.25°). Even without an error, presence of a CS led to increased motor output along direction CS-on of the P-cell that had produced the CS. C. Same as (A), except for trials in which errors were in CS-on+180° of the P-cell under study. Even when the error was opposite the preferred direction, presence of a CS biased behavior in CS-on direction of that cell. D. Trial-to-trial change following any error. We projected the trial-to-trial change in velocity onto direction CS-on (left) and CS-on+90° (right) of the P-cell. When a CS was present, change in motor output was only in direction CS-on. E. A CS during a specific post-saccadic period (~75–150ms) resulted in more learning than earlier or later CS. F. Effect of CS waveform duration. For each P-cell, we split each CS into ‘long’ and ‘short’ with respect to median duration within each cell. At a given CS timing, CS waveform duration did not have a discernable effect on behavior. G. Hypothesized anatomy of the oculomotor vermis P-cells and cerebellar output. Red circles refer to inhibitory neurons; blue circles refer to excitatory neurons. Arrows indicate preferred error vector in sensory space for the inferior olive and P-cells, and direction of force for the motoneurons. The vectors are parallel in the sensory and motor spaces. All error bars are standard error of the mean (SEM)across all neurons (n=67) unless noted.

In some trials, the target was not moved and the saccade terminated with the eyes on target, completing the movement without an error (|error|<0.25°, Fig. 2B). Despite this paucity of error, the probabilistic nature of CS produced trials in which the P-cell nevertheless generated a CS in the post-saccadic period. Remarkably, in the subsequent trial the eyes were again pulled in the CS-on direction of that P-cell (Fig. 2B, CS present). This biasing of behavior was missing if the P-cell did not produce a post-saccadic CS (Fig. 2B, CS absent). Therefore, even without an error, the presence of a post-saccadic CS in a single P-cell was followed in the subsequent trial by a change in behavior: the eyes were pulled in the CS-on direction of that P-cell.

These results hinted that if a P-cell produced a post-saccadic CS, in the subsequent trial that P-cell (indirectly) influenced a specific group of motoneurons, those that produced force along the P-cell’s CS-on direction. To test this hypothesis, we focused on trials in which error was in direction CS-on+180° (i.e., error was opposite the preferred error direction of the P-cell). Following experience of this error, the behavior in the subsequent trial changed in the direction of that error (Fig. 2C, left panel). Remarkably, this learning was significantly smaller if the P-cell had produced a CS. A similar pattern emerged when we considered trials in which error was in direction CS-on+90° (Fig. S3): trial-to-trial change in behavior was in direction of error, but presence of a CS biased the motor commands in the CS-on direction. As a result, the difference between the trial-to-trial change in the motor commands that took place with and without a CS was always in direction CS-on, regardless of whether error was in direction CS-on (Fig. 2A), CS-on+90° (Fig. S3), CS-on+180° (Fig. 2C), or absent altogether (Fig. 2B).

We therefore made our analysis blind to the error that the animal had actually experienced and instead labeled each trial based on whether the P-cell had or had not produced a post-saccadic CS. If the P-cell produced a CS, then the trial-to-trial change in saccade velocity vector was entirely in the CS-on direction of that P-cell (CS present, Fig. 2D), with no component along CS-on+90°. In contrast, if the P-cell did not produce a CS, the trial-to-trial change was in direction CS-on+180° of that P-cell (CS absent, Fig. 2D). Therefore, following production of a post-saccadic CS in a given P-cell, in the subsequent trial the eyes were pulled along a vector that was parallel to the CS-on direction of that P-cell. Without a CS, in the subsequent trial the eyes were pushed away along that same vector.

How did timing and/or shape of the CS affect these behaviors? If the CS was early (0–50ms) or late (200–250ms) with respect to saccade termination, in the subsequent trial there was little or no change in behavior (Fig. 2E). However, if the CS was produced in the 75–150ms post-saccadic period, then the subsequent trial exhibited substantial changes (paired t-test relative to no CS, t(66)=4.9; p<0.001). Therefore, error magnitude affected CS timing (larger error made it more likely that a CS would occur at 75–150ms post saccade, Fig. 1E), and CS timing affected trial-to-trial change in behavior.

However, CS timing also affected the duration of the CS waveform (Fig. 1H). We classified each CS as either ‘long’ or ‘short’ (a with-in cell measure with respect to that cell’s median CS waveform duration), and then quantified the effect of CS waveform duration as a function of CS timing. Once CS timing was accounted for, changes in CS duration produced no additional modulation of learning (Fig. 2F). This implied that the critical factor that modulated learning from error was CS timing.

Our trial-by-trial analysis imposed a specific coordinate system on the P-cells: their preferred direction of error, i.e., CS-on. What if we considered a different coordinate system, the preferred direction of simple spikes (SS-on)? For each P-cell we found the direction of saccade that produced the largest modulation in the SS response from baseline (see methods), and then labeled all trials in which a CS had occurred during the post-saccadic period. We measured the trial-to-trial change in velocity and projected that change onto direction SS-on. Using this coordinate system, we observed no meaningful change in behavior (Fig. S4). Therefore, despite the fact that a P-cell influenced behavior via its simple spikes, it was the coordinate system with which that P-cell encoded error via its CS that revealed its role in influencing behavior.

These results allow us to conjecture about the anatomical organization of the P-cells in the oculomotor vermis and their downstream projections. About 50 P-cells project onto a single nucleus neuron²⁶, forming a micro-cluster. Functional⁴ and anatomical^10,27–29 evidence suggest that P-cells of a micro-cluster share a common preference for error. When a saccade ends and a visual error is detected, there is increased probability of a post-saccadic CS in the micro-cluster that prefers that error direction. If the P-cells in that cluster produce a CS in the post-saccadic period, in the subsequent trial the motor output is biased via an increased pull in the CS-on direction of those P-cells. Following a trial without a post-saccadic CS, the bias is in the opposite direction. Therefore, it appears that a P-cell’s simple spikes (indirectly) influence a population of motoneurons that produce a force parallel to that P-cell’s direction of preferred visual error. That is, the direction of force in the motor-space lies parallel to the direction of preferred error in the sensory-space (Fig. 2G).

Simple spike change following experience of a complex spike

During a saccade, some P-cells exhibited a burst of simple spikes while others exhibited a pause (Fig. S5), with activity modulation that outlasted saccade duration (Fig. 3A, upper plot). This diversity of activations is common for P-cells of the oculomotor vermis during saccadic movements^4,24,30,31, and for P-cells of the lateral cerebellum during wrist movements^32,33. However, when we randomly sampled our cells into groups of 50 that shared the same preference for error and counted the simple spikes produced by the population, the population produced a response that predicted saccade velocity in real-time⁴ (Fig. 3A, lower plot).

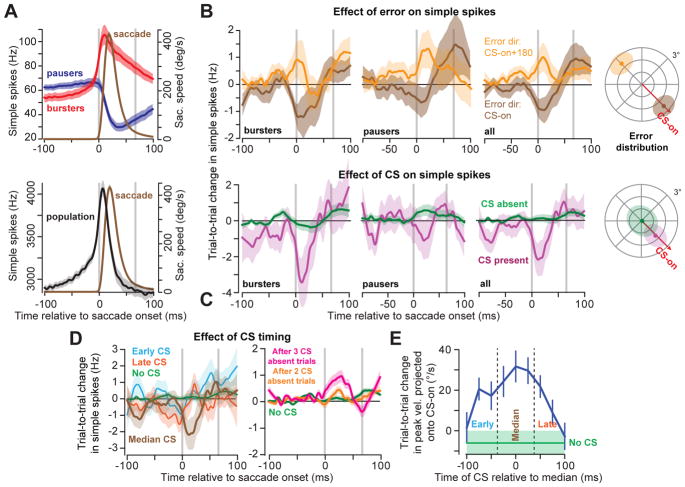
Figure 3. Complex spikes cause trial-to-trial depression in simple spike responses.

A. Average activity for all bursting (red) and pausing (blue) cells (top). Vertical gray lines indicate saccade onset and end. While neither of these subpopulations predict eye speed in real-time, their combined activity (bottom) into a population predicts the real-time speed of the eye⁴. B. Effect of error on simple spikes. Following an error in CS-on (high probability of CS), both burst and pause cells reduced their activity (top) whereas when the probability of CS was low (CS-on+180°), these cells increased their activity. The mean response across P-cells showed trial-to-trial changes which paralleled the responses of burst and pause cells. C. Effect of CS on simple spikes. When a CS was present within 25ms of the median CS response time in the post-saccadic period, simple spikes changed in the next trial for bursters, pausers, and across all cells (magenta), whereas when a CS was absent (green), there was little/no change in simple spike response on the next trial. D. CS timing played a critical role in changing the simple spikes. If the CS occurred during a temporal window of 50ms centered on the median CS time, it produced larger trial-to-trial change in simple spikes (brown) than if the CS occurred earlier (cyan) or later (red) than this time period. Lack of a CS (green) in a single trial was followed by little or no change in the simple spikes. Persistent lack of a CS in two (green) or three (red) trials resulted in increased simple spikes. E. A CS that occurred around the median period was most effective in producing trial-to-trial change in behavior. In all cases, median timing refers to a within-cell measure of post-saccadic distribution of CS timing. All error bars are standard error of the mean (SEM)across n=67 P-cells, except for part (A), where it reflects 95% confidence interval about the mean of bootstrap population of 50 randomly selected P-cells. Simple spike data were smoothed with a Savitzky-Golay filter with a width of 25ms.

Following an error in direction CS-on, in the subsequent trial around saccade onset there was a reduction in the simple spike discharge of both bursters and pausers (Fig. 3B, top row). In contrast, following experience of an error in direction CS-on+180°, there was an increase in the simple spike discharge of these cells. As a result, following experience of a CS-on error the average change across all cells was a trial-to-trial decrease in the number of simple spikes (Fig. 3B, bottom row), whereas following experience of a CS-on+180° error, the average change was an increase.

Importantly, these changes in simple spikes were almost entirely dependent on whether the P-cell had produced a CS during the 50ms window centered on the P-cell’s median CS time (113.1±14.6ms, mean±STD). For bursters and pauses, as well as all cells together, a CS in this temporal window was followed in the subsequent trial by a reduction in the simple spikes (Fig. 3C). However, despite experience of error, if no CS occurred in this temporal window, in the subsequent trial there was little or no change in the simple spikes. These results are consistent with observations made in the flocculus during visual pursuit^7,8 and vestibulo-ocular adaptation⁹, demonstrating that in different regions of the cerebellum, presence of a CS leads to trial-to-trial suppression in the number of simple spikes produced by the P-cells.

We next quantified the trial-to-trial change in simple spikes (Fig. 3D) and behavior (Fig. 3E) as a function of the timing of the post-saccadic CS. For each P-cell we computed the median of its CS timing distribution in the post-saccadic period (113.1±14.6ms, mean of the median±STD) and then measured the trial-to-trial change in the simple spikes with respect to this median. If the CS occurred early (<25ms before the median CS time for that P-cell) or late (>25ms after the median), in the following trial there was little or no change in the simple spikes of the population. However, if the CS occurred in the median period (median±25ms), there was a significant reduction in the simple spikes. Furthermore, this median period was critical for inducing a change in behavior: trial-to-trial changes in saccade velocity were largest following a CS that occurred at the median post-saccadic period (Fig. 3D). Absence of a CS also influenced the simple spikes. After consecutive no-CS trials, there was an increase in the simple spikes (Fig. 3D, right).

In summary, during a saccade some P-cells modulated their simple spike response via a burst, while others modulated their response via a pause. In both groups, as well as the population, the experience of a CS was followed on the subsequent trial by a reduction in the rate of simple spikes. In contrast, lack of a CS was followed by an increase in the simple spikes. The effect of a CS on the simple spikes, as well as on behavior, depended on timing: a CS that was generated in the post-saccadic period had its largest influence when it occurred at the median of the timing distribution, at around 110ms.

Bi-directional change in P-cell simple spikes during learning

In theory, with repetition, the trial-by-trial changes in the simple spikes should accumulate to produce large scale changes in behavior. However, previous studies have provided conflicting evidence of simple spike changes during blocks of adaptation. While one study reported that the changes in peak discharge appeared unrelated to changes in behavior during bouts of adaptation³⁴, a second study suggested that there are coherent simple spike changes²⁴. To shed light on this puzzle, we trained the monkeys in a “gain-down” protocol: on every trial, following saccade onset, the target was moved inward. By necessity, in some trials the primary saccade was in direction CS-on of the P-cell under study, while in other trials the primary saccade was in direction CS-on+180° of the same cell (total of 1,069±89 trials/neuron, mean±SEM). This training produced consistent reductions in saccade velocity and amplitude for both directions of movement (Fig. 4A, velocity: RM-ANOVA, main effect of adaptation trials F(9,1098)=13.5; p<0.001).

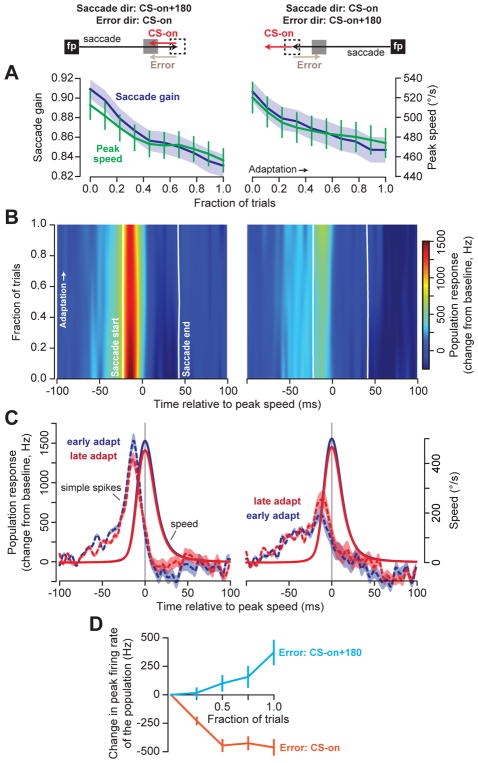
Figure 4. Persistent errors in a saccadic gain-down paradigm produce bidirectional changes in simple spikes.

A. Adaptation protocol. Saccades occurred in two directions. For both directions, upon saccade initiation the target was moved inward. As a result, in some trials the post-saccadic error was in direction CS-on (left), while in other trials the error was in CS-on+180° (right). Regardless of saccade/error direction, saccade gain (saccade amplitude divided by target amplitude) and saccade peak velocity declined with training. On average, the number of trials for each direction was 535±45 (mean±SEM). Error bars show standard error of the mean (SEM) across adaptation sessions for all cells (n=67). B. We organized the cells based on their CS-on direction. The plots show change in population response with respect to baseline during adaptation. Data in the amplitude axis were smoothed by a first-order Savitzky-Golay filter with a width of 3 bins. C. When errors were in direction CS-on, the population response decreased during adaptation. When errors were in direction CS-on+180°, the population response in the same cells increased. Error bars are 95% confidence intervals about the mean for bootstrap population of 50 cells. D. Change in peak response of the population relative to baseline from beginning to end of adaptation. Error bars are 95% confidence about the mean interval for bootstrap population of 50 cells.

The two directions of primary saccade implied that in some trials the post-saccadic error was in CS-on direction of the P-cell (Fig. 4A, left column), whereas in other trials the error was in CS-on+180° (Fig. 4A, right column). We therefore organized the P-cells into populations of 50 based on their preferred error direction. In early trials, the simple spike response of the population was strong when the primary saccade was in direction CS-on+180° (Fig. 4C, left subfigure, blue dashed line), and weak when that saccade was in direction CS-on (Fig. 4C, right subfigure, blue dashed line). This is consistent with the idea that the simple spikes of the population encode motion of the eyes during a saccade via a gain-field⁴, wherein the gain of simple spikes generated by the population is largest for saccades in direction CS-on+180°.

Despite the fact that velocity and amplitude decreased for both directions of the primary saccades, the population response changed in a way that depended on whether the post-saccadic errors were in direction CS-on, or CS-on+180°. When the saccade was in direction CS-on+180°, the post-saccadic error vector was in direction CS-on (increased probability of CS). For this movement direction the simple spike response of the population declined with adaptation (Fig. 4B–C, left). However, when the saccade was in direction CS-on, the post-saccadic error vector was in direction CS-on+180° (decreased probability of CS). For this movement direction, the simple spike response of the same P-cells increased (Fig. 4B–C, right). That is, change in the simple spike response was modulated by the direction of the experienced error (RM-ANOVA with main effect of error direction F(1, 98)=111.9; p<10⁻¹⁵, main effect of trial F(4, 392)=21.0; p<10⁻¹⁵, and a direction-by-trial interaction F(4, 392)=134.3, p<10⁻¹⁵). Therefore, when P-cells were organized based on their preference for error, the population simple spike response encoded the motion of the eyes during a saccade via a gain-field⁴. With training, the gain of this encoding simultaneously changed in two different directions: increasing for saccades in direction CS-on (because the post-saccadic error was in direction CS-on+180°), and decreasing for saccades in direction CS-on+180 (because the post-saccadic error was in direction CS-on, Fig. 4D).

The simultaneous, bi-directional changes we observed in P-cells during a single training session provide a rationale for why, in a previous saccade gain-down adaptation study, little or no changes were observed in simple spike rates³⁴: if we did not organize the P-cells based on their preference for error, the change in the population response for the two opposing directions canceled, producing no obvious changes in simple spike rates despite changes in behavior (Fig. S6). However, when the directionality of the error preference is taken into account²⁴, clear changes in the simple spike response can be uncovered.

Discussion

There is disparity between the simple spikes’ rich representation of predictions about the ongoing movement, and the CS’ sparse representation of error in those predictions. How can P-cells learn control of behavior from the infrequent occurrence of a CS?

We found that in the oculomotor vermis, after a saccadic eye movement, the direction of the visual error vector affected the probability of the post-saccadic CS (with each P-cell having a preference for an error direction¹⁶). In contrast, error magnitude affected CS timing, making it less variable, clustering the CSs around 110ms post saccade termination as the error magnitude grew larger. The CSs that occurred around this time had waveforms that were longer in duration. They induced greater plasticity in the simple spikes. And they produced greater trial-to-trial change in behavior. The chain of events that began with production of a CS in a single P-cell culminated in a specific change in behavior on the subsequent trial: the movement was biased along a force vector that was parallel to the preferred visual error vector of the parent P-cell.

If during the post-saccadic period the P-cell did not produce a CS, in the subsequent trial the eyes were pushed away along a vector that was also parallel to the CS-on direction of that cell. These results explain why, during the progression of gain-down adaptation, wherein the saccade velocity and amplitude decreased for all directions of movement, for some directions the simple spike response increased, while for other directions the response of the same P-cells decreased: the bi-directional changes in simple spikes were driven by post-saccadic errors that changed direction with respect to the P-cell’s preferred error.

In current models employed for decoding neuronal activity in the motor system, cells are placed into populations based on their patterns of spikes, for example, via tuning with respect to direction of movement³⁵, or covariance of their activity with respect to a behavioral variable³⁶. In contrast, our results suggest that in the cerebellum, P-cells form populations that may be difficult to infer based on their patterns of activity (simple spikes), but easy to organize based on their preference for error.

In the oculomotor vermis, P-cells may be organized into populations that share the same preference for error^4,10,27–29. Here, our results suggest that this preference for error also organizes the projections of each population onto the motor-space: the vector of preferred error in visual-space predicts the influence of those P-cells in movement-space (Fig. 5). To explain this idea, consider that in the oculomotor vermis, P-cells project onto cells in the caudal fastigial nucleus (cFN). cFN cells project to interneurons in the brainstem (burst generators)^37,38, which in turn project to motoneurons. Our results imply that a cFN neuron does not project to random premotor neurons, but only those that activate motoneurons that pull the eyes in the CS-on direction of the parent P-cells.

Figure 5. Transformation of a sensory error into a subsequent change in behavior in the oculomotor vermis.

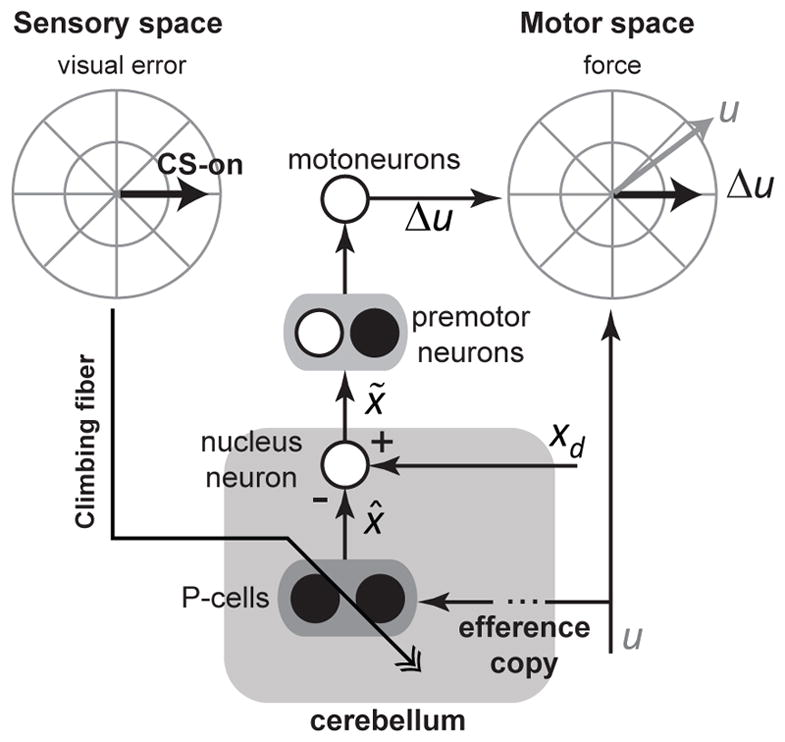
Experience of a visual error in the post-saccadic period increases the probability of generating a CS in a population of P-cells that prefer that error direction. If a CS is generated, it causes plasticity in the P-cells, modifying the simple spikes that are produced collectively by the population, altering their prediction of state x̂. At the deep cerebellar nucleus cell, the predicted state is an inhibitory signal that is compared with an excitatory signal from the mossy fibers, which possibly carry information about the desired state x_d. The output of the nucleus neuron is the difference between these two variables, reflecting a state correction xtilde; associated with the ongoing motor command u. This correction affects motor behavior in a specific direction: the direction of force specified by vector Δu. The preferred direction of visual error that produced a CS in the P-cells (i.e., CS-on) is parallel to the direction of force Δu in the effectors that the P-cells project to. Black filled circles are inhibitory neurons, and white filled circles are excitatory neurons.

The resulting circuit (Fig. 5) functions as an adaptive controller: experience of an error is encoded as a sensory event that affects CS probability and timing. The purpose of the controller is to nullify the error, returning the CS probability back to baseline. It accomplishes this by relying on the wiring of the P-cells: their discharge (indirectly) influences activity of effectors whose direction of action in motor-space is parallel to the direction of preferred error in sensory-space.

When an error occurs, for some P-cells this error will be in direction CS-on, while for others this error will be in direction CS-on+180°. Therefore, on the subsequent trial some clusters of P-cells will increase their simple spikes, while others will decrease their response. At the level of cerebellar output, do these changes counteract or cooperate with each other?

Our anatomical inference in Fig. 2G, coupled with functional changes reported in Figs. 3 and 4, and the known anatomy of cerebellar³⁹ and inferior olive projections⁴⁰, present a solution. If a saccade takes place and the error is to the left (Fig. S7). Following saccade completion, the leftward visual error vector engages the right superior colliculus, which in turn engages the left inferior olive. This up-regulates CS production in P-cells on the right side of the vermis, and down-regulates CS production in P-cells on the left side of the vermis. On the subsequent trial, P-cells with leftward CS-on will decrease their simple spike response, indirectly increasing the discharge in the motoneurons that pull to the left⁴¹. However, P-cells that have rightward CS-on preference will increase their simple spike response, resulting in a reduced drive to the motoneurons that pull to the right. That is, despite their opposite preferences for error, and opposite changes in their simple spikes, the two clusters of P-cells will cooperate to alter the drive to the agonist and antagonist motoneurons, reducing the error.

A cerebellar microcircuit is thought to be a group of P-cells that receive climbing fiber inputs that share the same preference for sensory input, and innervate a specific subset of cells in the deep nucleus that may have a similar output function^42,43. Our results provide functional evidence that P-cells likely organize into computational units that not only share the same preference for error, but also influence behavior through their projections by acting on effectors that specifically reduce that error. While individual P-cells produce disparate patterns of simple spikes during a given movement^24,30,44, those that prefer the same error may collectively form a single computational unit, influencing effectors that can contribute to homeostatic regulation of the unit’s complex spikes⁴⁵.

Methods

We analyzed saccade data from n=67 well-isolated P-cells from the oculomotor vermis of the cerebellum in 7 monkeys. No statistical methods were used to pre-determine sample sizes. Animals were not randomized into separate groups. All experiments were performed in accordance with the Guide for the Care and Use of Laboratory Animals (1997) and exceeded the minimal requirements recommended by the Institute of Laboratory Animal Resources and the Association for Assessment and Accreditation of Laboratory Animal Care International. All animal procedures were approved by the local Animal Care and Use Committee at the University of Washington.

General procedures

The experimental data set and methodology have been published previously^16,24,25. Briefly, the right eye of 7 rhesus monkeys (macaca mulatta, all males 5.0–7.4 kg: B, F, W, K, KO, P, and O) were surgically implanted with a scleral search coil and a restraint lug under aseptic conditions. Following recovery from the procedure, the monkeys were placed in a magnetic field, allowing measurement of eye kinematics (e.g., position and velocity) at 1kHz while the head was held stationary⁴⁶. Monkeys were trained to make visually guided saccades to a target dot (< 0.4° in diameter) in a dimly lit room. The target spot moved to a new location at a rate of approximately 1Hz. Targets were either presented via light emitting diodes (LEDs) which were placed at 1° eccentricities from center in 8 directions (45° spacing) or via a red laser beam whose position was controlled by two mirror galvanometers. All targets appeared within ±30° of straight ahead. Monkeys were continuously rewarded with applesauce for keeping their eyes within a virtual bounding box which extended ±3° in both the horizontal and vertical directions.

Once the monkey demonstrated proficiency tracking targets of various amplitudes and directions for an extended period of time (> 2hrs), each monkey underwent a second aseptic surgical procedure to implant a recording chamber which provided access to the oculomotor vermis (lobules VI and VII) of the cerebellum. The chamber was located on the midline, 14.5mm posterior to the intraoral axis, and directed straight down. Following recovery from surgery, we inserted single custom tungsten micro-electrodes into OMV. The electrodes were coated with iron particles to reduce their impedance to approximately 100kΩ at 1kHz. We recognized penetration of OMV by the characteristic saccade-related ‘swooshing’ in background activity. We identified single P-cells using three criteria: 1) the presence of high frequency saccade-related simple spike activity, 2) the presence of multi-peaked complex spikes, and 3) the presence of a complex spike linked pause in the simple spikes. We simultaneously recorded neurophysiology (50kHz sampling rate) and eye kinematics (1kHz sampling rate) via a Cambridge Electronic Design Power 1401. Data was displayed in real-time to the experimenter on a computer monitor running Spike2 as well as saved for offline analysis.

Complex spike identification and processing

Neurophysiology data were band-pass filtered between 30Hz and 10kHz prior to analysis. We used a semi-automated procedure to identify complex spikes from the recorded data. Briefly, the experimenter, blind to the animal’s behavior, manually identified a subset of complex spikes for each recording. We then used a template matching algorithm to identify onset of the complex spike waveform throughout the experimental session. Our template matching algorithm was intentionally strict, attempting to minimize the number of false positive identifications (i.e., simple spikes categorized as complex spikes). However, this procedure has the necessary consequence of potentially missing a small fraction of complex spikes (false negatives). Blind to the animal’s behavior, we intentionally excluded P-cells which did not consistently produce complex spikes throughout the entire recording period, indicating that the P-cell recording was not stable.

After the algorithm identified the onset of each complex spike, we also sought to identify the duration of that spike. For each complex spike identified in the 50–250ms period following saccade termination, a single experimenter (DJH) determined the duration of the complex spike waveform by manually marking termination of each waveform. The experimenter was blind to the animal’s behavior and the time of the complex spike within this 200ms post-saccadic period. The times of all identified complex spikes were down-sampled to 1kHz, corresponding to the sampling rate of the behavioral data.

After complex spike identification, we performed sorting on the Purkinje cell simple spikes and subsequently down-sampled the simple spike times to 1kHz. To convert simple spikes to instantaneous firing rates, we non-casually convolved each spike train with a normalized Gaussian kernel with a 2.5ms standard deviation (area of the kernel was normalized to 1.0). We included n=67 P-cells in our final dataset which had both well-isolated simple and complex spike responses for the duration of the recording session. No P-cells were excluded based on the animal’s behavior.

Behavioral data processing

We identified potential saccadic events via an absolute speed threshold of 100°/s. The onset of these potential saccades was determined by finding the time at which the eye speed exceeded 20°/s for more than 3ms. Similarly, the end of the saccade was defined as the time when eye speed fell below 20°/s for more than 3ms. For each saccade, we identified the maximum absolute speed during the saccadic period. Trials in which the monkey moved its eyes in the wrong direction relative to the target (> 90°) or trials in which the endpoint of the saccade landed more than 10° from the presented target location were excluded from further analysis (less than 5% of all trials).

In some cases, we induced a 3–5° post-saccadic visual error by displacing the target during the animal’s saccade. However, even in cases where we did not jump the target, the natural variability of eye movements resulted in post-saccadic errors. For each saccade, regardless of whether the target was intentionally jumped or not, we determined a post-saccdic foveal error vector from the monkey’s eye position at saccade termination to the center of the current target position. When the target was not displaced during the saccade, the average error magnitude was 2.0+0.1° (mean+SEM), indicating that the monkey made errors even without intra-saccadic perturbation of the target.

Determination of CS and SS preferred directions

After identification of post-saccadic errors and complex spike timing for each P-cell, we determined the preferred direction of complex spikes (CS-on) for each P-cell. For each trial, we labeled the presence or absence of a complex spike in a 50–200ms window following saccade termination^4,16. However, if a corrective saccade occurred during the 50–200ms window, we used the onset of the corrective saccade as the end of the CS window.

To determine CS-on, we divided post-saccadic errors across the experiment into 8 directions, spaced at 45° intervals. For each direction of error, we determined the probability of a CS during the post-saccadic period (number of trials with a given error direction and a CS, divided by the total number of trials with that error direction). The error direction with the highest probability of CS was labeled as CS-on. An example of this CS tuning profile for an individual neuron is shown in Fig. S1. We have previously shown that the probability of CS during the post-saccadic period depends on direction of the post-saccadic error and not the direction of the preceding saccade⁴.

For each cell we also determined the simple spike preferred direction. Here, we divided trials into 8 directions based on the direction of the animal’s saccade towards the presented target. For each trial, we determined the average instantaneous firing rate during the saccadic period (from saccade onset to saccade offset). In addition, we determined the average simple spike firing rate during a baseline period 200 to 50ms prior to saccade onset. We labeled the preferred simple spike direction (SS-on) as the saccade direction which elicited the largest absolute firing rate change from baseline, i.e., the direction with the largest modulation from baseline activity. In other regions of the cerebellum (e.g., the flocculus), there is an inverse relationship between the preferred direction of simple spikes and the preferred direction of CS⁴⁷. However, similar to previous studies in OMV, we found no evidence for such a link between these two preferred directions³¹. Rather, the distribution of angular difference between SS and CS preferred directions were not significantly different than an expected uniform distribution (χ²(7, n=67) = 2.37; p = 0.94).

Lack of encoding of error magnitude in probability of CS

In Fig. 1C, we asked whether foveal error magnitude was encoded in the probability of CS during the 50–200ms following saccade termination. We quantified the encoding of error magnitude along a single axis: each P-cell’s CS-on direction. Here, positive errors occurred in CS-on and negative errors occurred in the opposite direction, CS-on+180°. By necessity, the probability of complex spikes must pass through the P-cell’s baseline probability of CS when the error magnitude is 0°. To address whether there was a significant encoding of error magnitude in CS probability, we binned error magnitudes along the CS-on axis from 0° to 6° into 0.5° discrete bins. For each bin, we computed the probability of a CS occurring in the post-saccadic period across trials. Using repeated measures ANOVA, we asked if there was a significant main effect of error magnitude for errors in the CS-on direction (positive errors) for all errors larger than 0.5° (noting that as error magnitudes approach 0°, their direction is undefined). Our analysis suggested that there was not a significant relationship between probability of CS and error magnitude in the CS-on direction (F(10, 530) = 1.42; p = 0.17). Thus, once error direction was accounted for, we found no evidence for the hypothesis that error magnitude modulated probability of CS.

Quantifying trial-to-trial changes in behavior and simple spikes

In Fig. 2A we quantified how the presence of a CS in the post-saccadic period on trial n affected the next saccade in the same direction (n+m). To answer this question, we identified all trials in which the error was within 45° of the P-cell’s preferred error direction (CS-on). For each trial, we then found the next trial in the same direction with the same target amplitude. We ensured that there were no more than one intervening trial between the first identified trial (with an error in CS-on) and the next trial with the same direction/target amplitude. In our experiment, the direction of the target on each trial was chosen pseudo-randomly, with the caveat that the target eccentricity was never greater than ±30° from straight ahead. Therefore, by allowing an intervening trial in the opposite direction, we dramatically increased the amount of data available to determine trial-to-trial changes. After identifying pairs of trials in the same direction, we divided the pairs into two groups: those that had a complex spike during the post-saccadic period on trial n (CS present) and those that lacked a complex spike during this period (CS absent). For these two groups of trials, we found the trial-to-trial change in the saccade velocity profile from the first to the second trial, and then projected this change onto the CS-on direction for the neuron. That is, imagine that ẋ⁽ⁿ⁾(t) is the two dimensional saccade velocity profile in trial n, and ẋ^(n+m)(t) is the velocity profile of the next saccade in the same direction as trial n, (where m={1 or 2}). We found the trial-to-trial change in the velocity profile as ${\mathbf{b}}_i^T\left({{\stackrel{.}{\mathbf{x}}}_i}^{(n+m)}(t)-{{\stackrel{.}{\mathbf{x}}}_i}^{(n)}(t)\right)$, where b_i is a unit vector in the direction of CS-on for the i-th neuron (i.e., ${\left[\begin{array}{ll}cos({\theta }_i^{(CS-\text{on})})\hfill & sin({\theta }_i^{(CS-\text{on})})\hfill \end{array}\right]}^T$) and the superscript T indicates the transpose operator. Our results indicated that the presence of a CS in trial n biased the next movement in the CS-on direction of the P-cell that expressed that CS (Fig. 2D).

In Fig. S3, we project the trial to trial change onto CS+90°, such that ${\mathbf{b}}_i={\left[\begin{array}{ll}cos({\theta }_i^{(CS-on)}+\pi /2)\hfill & sin({\theta }_i^{(CS-on)}+\pi /2)\hfill \end{array}\right]}^T$, whereas in Fig. S4 we define ${\mathbf{b}}_i={\left[\begin{array}{ll}cos({\theta }_i^{(SS-on)})\hfill & sin({\theta }_i^{(SS-on)})\hfill \end{array}\right]}^T$ and ${\mathbf{b}}_i={\left[\begin{array}{ll}cos({\theta }_i^{(SS-on)}+\pi /2)\hfill & sin({\theta }_i^{(SS-on)}+\pi /2)\hfill \end{array}\right]}^T$.

Identification of burst and pause cells

P-cells in the oculomotor vermis display heterogeneity in their responses during saccades (Fig. S5). Some P-cells increase their activity (burst), while others decrease their activity (pause), or show combinations of these responses. To demonstrate this diversity, we artificially divided our population of cells into two speculative classes: bursters and pausers. For each cell, we measured the average firing rate over the duration of each saccade to a target regardless of amplitude or direction. Cells that, on average, increased their activity relative to a baseline period (baseline defined as 200 - 50ms prior to saccade onset) were classified as putative bursters, and all other cells were classified as pausers⁴. In our dataset, we identified n=35 bursting cells and n=32 pausing cells. The average responses of each of these two cell groups are shown in Fig. 3A. Both the burst and pause sub-populations showed saccade related activity, but this activity was not directly related to real-time motion of the eye⁴.

Population response

Approximately 50 P-cells in the cerebellar cortex project to a single neuron in the deep cerebellar nucleus (DCN)²⁶. To estimate the population response in Fig. 3A and Fig. 4, we randomly sampled populations of 50 P-cells with replacement. The population response for this subset of neurons was the sum of instantaneous firing rates, corresponding to the number of pre-synaptic spikes that would be observed by the post-synaptic neuron in the caudal fastigial nucleus (cFN), the most medial of the deep cerebellar nuclei. Since individual P-cell simple spike responses in OMV are heterogeneous^24,31 (e.g., bursting or pausing), simply estimating the standard error of the mean across individual neuron responses would significantly over-estimate the variance of the response observed by a cFN neuron. Therefore, we estimated confidence intervals on the population response by performing this same analysis 50 times, and showing the mean population response with 95% confidence intervals across these 50 bootstrapped samples. Therefore, the error bars in the population response in Fig. 3A and Fig. 4B are 95% confidence intervals across the bootstrapped samples.

Saccade adaptation

For the vast majority of cells (n=56), we were able to estimate the P-cell’s CS-on direction online^16,24. We then performed blocks of trials in which the targets were presented along the CS-on axis. During saccades to targets in either the CS-on or CS-on+180° directions, the target was displaced inwards, eliciting gain-down adaptation (Fig. 4A). For the remainder of the cells (n=11)²⁵, we performed gain-down adaptation strictly in the horizontal axis. Even for this paradigm, we were able to determine the P-cell’s CS-on direction offline, and assign the closest horizontal direction as CS-on. We were able to stably record the P-cells for an average of 1,069±89 (mean±sem) trials during the adaptation period. To collapse across sessions with different numbers of adaptation trials, we normalized the adaptation period for each P-cell between [0, 1]. Here, zero corresponds to the beginning of adaptation and one corresponds to the end of adaptation.

Statistical analysis

Statistical analysis was completed using R. We used two tailed t-tests to compare means without a repeated measures component. Remaining tests were performed using repeated measures analysis of variance (RM-ANOVA). Data distributions were assumed to be normal and not formally tested unless otherwise stated.

Data and Code availability

The data and analysis code of the current study are available from the corresponding author upon reasonable request.

Reporting summary

A Life Sciences Reporting Summary is attached to this manuscript.