A multi-institutional study of independent calculation verification in inhomogeneous media using a simple and effective method of heterogeneity correction integrated with the Clarkson method

Abstract

In inhomogeneous media, there is often a large systematic difference in the dose between the conventional Clarkson algorithm (C-Clarkson) for independent calculation verification and the superposition-based algorithms of treatment planning systems (TPSs). These treatment site–dependent differences increase the complexity of the radiotherapy planning secondary check. We developed a simple and effective method of heterogeneity correction integrated with the Clarkson algorithm (L-Clarkson) to account for the effects of heterogeneity in the lateral dimension, and performed a multi-institutional study to evaluate the effectiveness of the method. In the method, a 2D image reconstructed from computed tomography (CT) images is divided according to lines extending from the reference point to the edge of the multileaf collimator (MLC) or jaw collimator for each pie sector, and the radiological path length (RPL) of each line is calculated on the 2D image to obtain a tissue maximum ratio and phantom scatter factor, allowing the dose to be calculated. A total of 261 plans (1237 beams) for conventional breast and lung treatments and lung stereotactic body radiotherapy were collected from four institutions. Disagreements in dose between the on-site TPSs and a verification program using the C-Clarkson and L-Clarkson algorithms were compared. Systematic differences with the L-Clarkson method were within 1% for all sites, while the C-Clarkson method resulted in systematic differences of 1–5%. The L-Clarkson method showed smaller variations. This heterogeneity correction integrated with the Clarkson algorithm would provide a simple evaluation within the range of −5% to +5% for a radiotherapy plan secondary check.

INTRODUCTION

A 5% action level has been proposed by the American Association of Physics in Medicine (AAPM) task group 114 (TG-114) for different calculation algorithms [1], for example, a 5% disagreement between a TPS using a superposition algorithm and calculation verification using a conventional Clarkson method [2] (C-Clarkson). These tolerance levels were arrived at by consensus, and were not defined by quantitative data, which is one reason there have been few reports on the quantitative analysis of inter-institutional verification results [1]. Thus, a multi-institutional study on calculation verification was performed in Japan [3–5]. Takahashi et al. showed that the 5% action level may be feasible for verification using the C-Clarkson method; however, an understanding of how larger differences occur in breast and lung plans is important in clinical practice because inhomogeneity corrections in the dose calculation algorithm for the TPS and verification software can affect the dose difference in inhomogeneous media and ‘missing tissue’ [3]. Kawai et al. showed systematic differences of >4% between pencil-beam convolution, adaptive convolve, an analytical anisotropic algorithm (AAA), and C-Clarkson methods for lung stereotactic body radiotherapy (SBRT) [5], with the AAA showing a particularly large systematic difference of 8.7% [5]. Recently, Varian Medical Systems (Palo Alto, CA, USA) released the advanced photon dose calculation algorithm Acuros XB (AXB) [6–10]. In a phantom study, Tsuruta et al. showed that AXB and an X-ray voxel Monte Carlo method (XVMC) had better agreement with measurements using an ionization chamber and film than the AAA, while a patient study involving a comparative analysis of dose–volumetric data and dose distributions with XVMC demonstrated that the AXB provided better agreement with XVMC than AAA. In the C-Clarkson calculation, correction for inhomogeneity in the depth direction is computed using the radiological path length (RPL); however, lateral scattering in the other directions is not considered. Thus, there may be systematic differences between the TPS and the monitor units (MU) calculation verification in a plan with treatment fields including ‘missing tissue’ in breast and inhomogeneous media in the lung.

To consider the dose contribution from the ‘missing tissue’ in a breast plan, a ‘virtual’ treatment field was created using manual contours of the breast from a beam’s eye view [1]. This method does have disadvantages, which include the fact that it can only be used for the breast where the border between breast and air is clear. In the lung, a tumor is surrounded by inhomogeneous media, including arteries with water-equivalent Hounsfield Units (HU) and air spaces with air-equivalent HU. Manual contouring to exclude the inhomogeneous areas would result in underestimation of the scattering. Another problem with the method is the user’s visual bias in creating the contour, which can affect the result of the secondary check. The use of the method is therefore limited.

To solve the above problems while using a tolerance level of 5% for the current radiotherapy secondary check, we designed and developed a simple and effective method of heterogeneity correction integrated with the Clarkson method (lateral-scattering considered Clarkson method, L-Clarkson), to account for the effects of the lateral dimension of heterogeneity. We then performed a multi-institutional study across four institutions to evaluate the effectiveness of the L-Clarkson method for conventional breast and lung treatments and lung SBRT.

MATERIALS AND METHODS

Ethical standards

This study was conducted in accordance with the ethical standards laid down in the Declaration of Helsinki by the World Medical Association, as well as with the ‘Ethical guidelines for epidemiological research’ presented by the Ministry of Health, Labour and Welfare in Japan. Formal consent was not required in our institution for this type of study, using previously acquired anonymous data.

Radiotherapy secondary check

The dose calculated by the treatment planning system was compared with the dose calculated by a different dose calculation system, and the plan generated by the treatment planning system was verified to check that the difference between the systems was within a tolerance [1, 11-16]. The C-Clarkson method is commonly used as the dose calculation algorithm for the secondary check [1, 17-20]. A survey of independent calculation verification in Japan shows 30.4% of sites use direct measurements, 18.6% use spreadsheet verification, and 16.7% use commercial software [21]. The spreadsheet and commercial software use an implementation of the C-Clarkson method. In the USA, 94% of sites use commercial software to perform independent MU verification for non-intensity-modulated radiation therapy (IMRT) [22].

The Clarkson method with consideration of lateral-scattering

To account for lateral scattering from inhomogeneous media when using the Clarkson method, the dose was calculated using the following three steps.

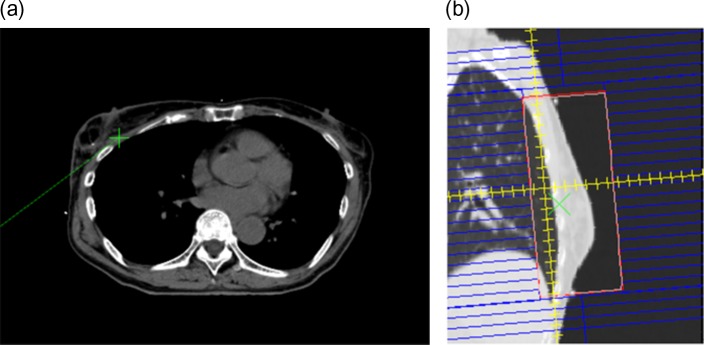
1. A 2D image perpendicular to the beam axis was reconstructed from computed tomography (CT) at the location of the reference point. An example of such a reconstructed image with a 0° gantry angle, 0° collimator angle and 0° couch angle is shown in Figure 1.

2. Each RPL from the reference point to the edge of the multileaf collimator (MLC) or jaw collimator was calculated using each pie sector of the reconstructed image according to Eq. 1:

   $$\mathrm{R}\mathrm{P}\mathrm{L}=\sum _{i=1}^N\left(\mathrm{P}{\mathrm{L}}_i\times \mathrm{E}{\mathrm{D}}_i\right)$$ (1)

   where PL_i is the physical length passing through the i-th voxel, ED_i is the relative electron density of i-th voxel, and N is the number of the voxels in each pie sector. Figure 2 shows examples of the physical length and RPL calculations for each pie sector using both the C-Clarkson and L-Clarkson methods on a reconstructed image. Subsequently, the tissue maximum ratio (TMR) and phantom scatter factor (S_p) were computed using the RPLs for the L-Clarkson method, while physical lengths were used for the TMR and S_p for the C-Clarkson method.

3. The dose was then computed using Eq 2:

$$D=MU\cdot D_0^{\text{'}}\cdot TMR\left(d,S_{\mathrm{e}\mathrm{f}\mathrm{f}}\right)\cdot Sc\left(C_{\mathrm{e}\mathrm{f}\mathrm{f}}\right)\cdot S_{\mathrm{p}}\left(S_{\mathrm{e}\mathrm{f}\mathrm{f}}\right)\cdot A_0\left(r\right)\cdot G\cdot Others,$$ (2)

where $\mathit{MU}$ is the monitor units, $D_0^{\prime }$ is the dose at reference depth, $\mathit{TMR}\left(d,S_{\mathrm{eff}}\right)$ is the tissue maximum ratio for an MLC aperture defined as the equivalent square field size of S_eff at a depth of d, $\mathit{Sc}\left(C_{\mathrm{eff}}\right)$ is the collimator scatter factor for a jaw collimator field size of C_eff, $S_{\mathrm{p}}\left(S_{\mathrm{eff}}\right)$ is the phantom scatter factor for an MLC aperture-defined field size of S_eff, $A_0\left(r\right)$ is the air off-axis ratio for distance from the central axis of r, $G$ is the inverse square law factor, and $\mathit{Others}$ includes the wedge factor or the non-wedge factor.

Fig. 1.

Beam eye’s view of the reconstructed image with 0° gantry angle, 0° collimator angle and 0° couch angle (a) from CT images (b). The reference point was located on the reconstructed image. The isocenter is shown by a yellow cross and the reference point by a green cross.

Fig. 2.

Examples of physical length and radiological path length calculations for each pie sector using the C-Clarkson and L-Clarkson methods, respectively, on a reconstructed image (a), physical length calculation in the C-Clarkson method (b) and radiological path length calculation in the L-Clarkson method (c).

Independent calculation verification software program

The calculation verification software program Simple MU Analysis (SMU; ver.1.4.9.8, Triangle Products, Chiba, Japan) was used at each institution as an independent calculation algorithm. Using the C-Clarkson and L-Clarkson algorithms, SMU calculates the physical length and RPL from the body surface to the dose reference (prescription) point using the CT images of the patient, and then uses this information to calculate the dose. SMU requires the TMR, off-axis ratio in air (OAR), collimator scatter factor (Sc), phantom scatter factor (S_p), physical wedge factor (PWF), non-physical wedge factor (NWF), off-axis factor in air for the physical wedge (OAR-PWF), MLC transmission factor (MLC-TF), and dosimetric leaf gap (DLG) as beam data parameters for each energy.

Multi-institutional study

A commissioning test was performed at all of the institutions to ensure the quality of the verification software program before the multi-institutional study. First, commissioning tests were performed using a 20-cm water-equivalent phantom. Treatment plans were generated using all of the TPSs installed in each institution. A 0.6-cm³ Farmer-type ionization chamber was placed at a 10-cm depth in the water-equivalent phantom. Second, inhomogeneous media were created using water-equivalent and lung-equivalent phantoms, and the same ionization chamber was placed at a 4-cm depth in the lung-equivalent phantom, as shown in Figure 3.

Fig. 3.

Phantom setting for inhomogeneous media.

To perform a multi-institutional retrospective analysis of disagreement between on-site TPSs and the verification software in the inhomogeneous media of the breast and lung, 261 non-IMRT plans including 1237 treatment fields were collected from four institutions. All institutions used a field-in-field technique for breast treatments and no wedge filter was used. Reference point locations were in the central axis and the off-axis. Table 1 lists the plan details from each of the institutions. No 2D treatment plans were included in this study. All of the plans were generated using the TPSs and CT images.

Table 1.

Details of the plans collected from the four institutions

Institution	A	B	C	D
Conventional breast treatment
Number of plans	20 (42)	20 (62)	20 (40)	20 (46)
Treatment planning system	Xio	Eclipse	Pinnacle3	Pinnacle3
Dose calculation algorithm	SP	AAA	AC	AC
Field size (mm)	114.33 ± 21.97	109.57 ± 8.95	89.79 ± 7.97	99.92 ± 16.88
No. of fields in field	6	48	0	20
Conventional lung treatment
Number of plans	20 (47)	20 (59)	20 (50)	20 (57)
Treatment planning system	Xio	Eclipse	Pinnacle3	Pinnacle3
Dose calculation algorithm	SP	AAA	AC	AC
Field size	92.03 ± 29.08	80.34 ± 18.63	74.70 ± 18.67	74.15 ± 16.71
Lung SBRT
Number of plans	20 (133)	30 (204)	20 (158)	31 (237)
Treatment planning system	Eclipse	Eclipse	Eclipse	Pinnacle3
Dose calculation algorithm	AXB	PBC	PBC	AC
Field size	55.03 ± 15.49	36.62 ± 5.02	36.96 ± 7.71	43.32 ± 4.68

Brackets show the number of treatment fields. SP = superposition, AXB = Acuros XB, AAA = analytical anisotropic algorithm, PBC = pencil-beam convolution with Batho power law, AC = adaptive convolve.

Comparisons between the TPS and the verification software were performed at the reference points corresponding to the reference (prescription) dose points of the TPS. When dose calculation was performed in the verification software, all institutions used 120 pie sectors for the C-Clarkson and the L-Clarkson methods. The dose difference between the TPS and the verification software was calculated for each treatment field using Eq. 3:

$$\delta =\frac{\left(D_{\mathrm{S}\mathrm{M}\mathrm{U}}-D_{\mathrm{T}\mathrm{P}\mathrm{S}}\right)}{D_{\mathrm{T}\mathrm{P}\mathrm{S}}}\cdot 100(\%),$$ (3)

where D_SMU is the dose calculated by the C-Clarkson or L-Clarkson methods, and D_TPS is the dose calculated by the on-site TPSs.

For the verification software, the C-Clarkson and L-Clarkson methods were used to calculate the doses. Subsequently, the dose differences for all treatment fields and composite fields were collected, and the means (${\delta }_{\text{mean}}$) and standard deviations (SD) of these dose differences were computed. The confidence limit for each treatment site was then calculated from ${\delta }_{\text{mean}}$ and the SD of the dose difference using Eq. 4:

$$ConfidenceLimit={\delta }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}\pm 2\mathrm{SD}$$ (4)

The variable ${\delta }_{\text{mean}}$ is the systematic overall dose difference between the TPS and the verification software for all plans from a particular treatment site. The variable 2SD expresses the variation in the dose difference, and was used to describe how closely the results of the verification software agreed with the TPSs’ values, following the methods of previous studies [23–25]. A total of 102 treatment fields with 10 cGy at the reference point were excluded from the analyses of each beam.

Statistical analyses

Statistical analyses were performed to examine inter-institutional differences for conventional breast and lung treatments and lung SBRT. Comparisons between two groups were performed using t-tests. A value of P < 0.05 was considered statistically significant.

RESULTS AND DISCUSSION

Commissioning test

The dose differences between the SMU and the measurements obtained with the solid water-equivalent phantom showed good agreement, being within 2% in the C-Clarkson and L-Clarkson methods. The measured dose differences obtained with the solid inhomogeneous phantom showed better agreement with the L-Clarkson method (−3.7 ± 1.1%) than with the C-Clarkson method (6.7 ± 2.6%).

Conventional breast treatment

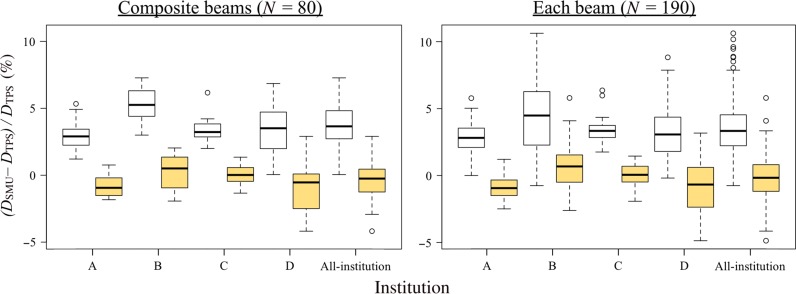
Figure 4 shows box-and-whisker plots for the breast plans. The L-Clarkson method showed closer agreement with the TPSs, with smaller systematic differences than the C-Clarkson method. Variations for the L-Clarkson method were similar or better than with the C-Clarkson method. The L-Clarkson method also resulted in less outlier values than the C-Clarkson method. These confidence limits, which include the systematic differences for the L-Clarkson method, were within the range −5% to +5% for both the composite fields and each individual field. Table 2 shows the distances of the reference points from the central axis for the breast plans. Tables 1 and 2 indicate that institution B had more plans with large treatment fields and off-axis reference points. Figure 5 shows an example of a breast plan. The breast is surrounded by air and lung tissue, with the reference point also being close to the lung. Therefore, in this case, the C-Clarkson method overestimated the dose because it did not take into account reduced lateral scattering from the inhomogeneous media of air and lung. However, the L-Clarkson method did consider the reduced lateral scattering from the inhomogeneous media, resulting in a difference that was close to 0%. Table 3 show the results of t-tests comparing the different institutions in regard to the dose differences between the TPS and verification software, which used the C-Clarkson and L-Clarkson methods, respectively. Institution B showed statistically significant differences from the other institutions, with a 5% systematic difference for the breast. This systematic difference was the greatest of the four institutions. When using the L-Clarkson method, institution C showed the smallest systematic differences and variations because the reference points were located at the isocenter in all plans.

Fig. 4.

Box-and-whisker plots for breast plans (C-Clarkson: white box plots; L-Clarkson: yellow box plots). Left: composite fields; right: each field.

Table 2.

Distances of the reference points from the central axis in breast plans

Institution	A	B	C	D
Distance from the central axis (mm)
Mean	20.37	60.05	0.00	18.97
SD	27.65	9.07	0.00	20.76

Fig. 5.

Example of a breast plan (C-Clarkson: 5.0%; L-Clarkson: 0.3%). The reference point on the CT image (a) and beam’s eye view with the reconstructed image (b).

Table 3.

P-values of t-tests comparing the different institutions in regard to the dose differences between the TPS and verification software using the L-Clarkson method

	A–B	A–C	A–D	B–C	B–D	C–D
Conventional breast treatment
Composite	<0.01	<0.01	0.989	0.427	0.041	0.082
Each	<0.01	<0.01	0.536	0.049	<0.01	0.037
Conventional lung treatment
Composite	0.567	0.402	0.946	0.707	0.516	0.363
Each	0.924	0.180	0.672	0.072	0.517	0.287
Lung SBRT
Composite	<0.01	<0.01	0.629	<0.01	<0.01	<0.01
Each	<0.01	<0.01	0.017	<0.01	<0.01	<0.01

Detailed comparisons of the results from the different institutions showed the greatest systematic difference for institution B when using the C-Clarkson method for the breast. This was because the irradiation field size used at institution B was relatively large, and the reference points were often located at a point that was 5-cm away from the central axis. In the breast protocol plans of institution B, the reference point should be located at a 3-cm distance away from the edge of the irradiation field. The other institutions used reference point locations that were within 5 cm of the central axis. It is evident that in the data from institution B, there were more uncertainties in the dose calculations at off-axis points of both the TPSs and the independent verification calculation software. In other words, the greater the distance from the central axis, the greater were the uncertainties.

Conventional lung treatment

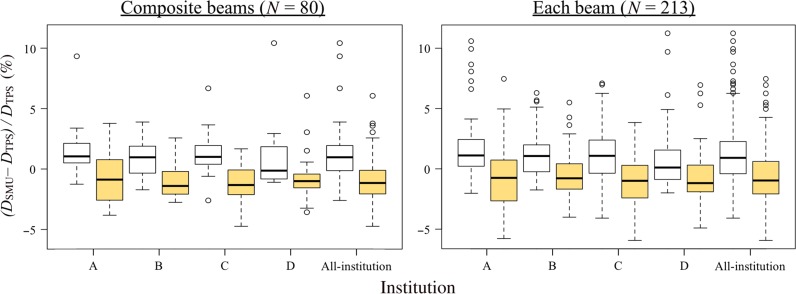
Figure 6 shows box-and-whisker plots for lung plans. Compared with the C-Clarkson method, the systematic differences for the L-Clarkson method were shifted towards negative values; however, the values were close to 0%. Variations with the L-Clarkson method were similar to those with the C-Clarkson method, although the number of outlier values for each field was reduced. Figures 7 and 8 show examples of lung plans where the L-Clarkson method produced better and worse agreement, respectively, than the C-Clarkson method. The tumor shown in Figure 7 was located near the mediastinum and was surrounded by the lung. The C-Clarkson method overestimated the dose because it did not take into account low-density materials. However, the L-Clarkson method calculated the dose with consideration of low-density materials, and the agreement in dose between the TPS and the verification software was closer. Furthermore, there were no significant changes in the ratio of the volumes of lung and water-equivalent materials inside the treatment field in the planes perpendicular to the beam axis. Thus, the L-Clarkson method showed better agreement with the TPS than the C-Clarkson method. Conversely,as seen in Figure 8, the L-Clarkson method showed a greater negative difference than the C-Clarkson method. In this example, there were changes in the ratio of the volumes of lung and water-equivalent materials inside the treatment field in the planes perpendicular to the beam axis. For example, one of the planes showed a similar volume of lung in relation to the mediastinum volume within the treatment field, while another of the planes showed a greater volume of mediastinum in relation to the lung volume within the treatment field. When using the L-Clarkson method, the reconstructed image shown in Figure 8b demonstrated similar ratios for the volumes of lung and mediastinum. The L-Clarkson method, therefore, underestimated the dose from the mediastinum.

Fig. 6.

Box-and-whisker plots for lung plans (C-Clarkson: white box plots; L-Clarkson: yellow box plots). Left: composite fields; right: each field.

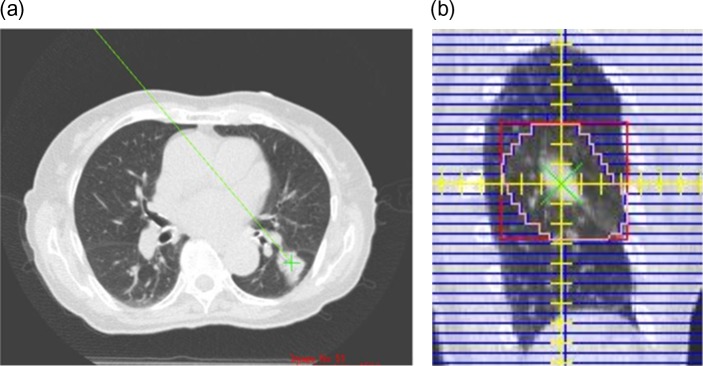
Fig. 7.

Example of a lung plan with better agreement when using the L-Clarkson method (C-Clarkson: 7.1%; L-Clarkson: 2.0%). The reference point on the CT image (a) and beam’s eye view with the reconstructed image (b).

Fig. 8.

Example of a lung with worse agreement when using the L-Clarkson method (C-Clarkson: −1.9%; L-Clarkson: −5.8%). (a) CT image and reference point (green cross); (b) beam’s eye view.

Lung SBRT

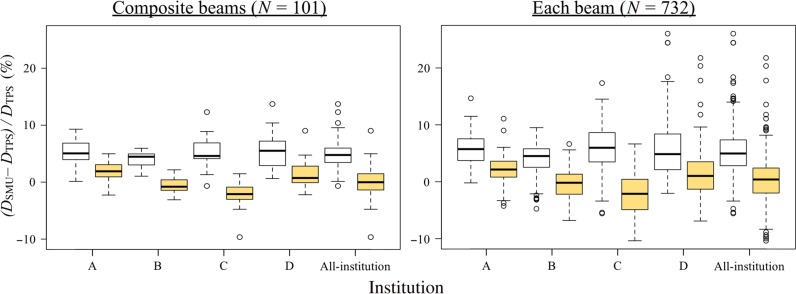
Figure 9 shows box-and-whisker plots for lung SBRT plans. Dose differences for the composite fields were within 5% for all plans, with the exclusion of plans with outlier values. The comparisons of the L-Clarkson and the C-Clarkson methods for the composite fields and each treatment field of the lung SBRT plans show better agreement between the TPSs and the verification software than was found for the breast plans. Compared with breast and conventional lung plans, a greater improvement was apparent, with the mean differences for all institutions being close to 0%. From Table 1 it can be seen that the treatment fields were generally small, ranging in size from 3 × 3 cm to 8 × 8 cm. The field sizes were similar between institutions B and C. Figures 10 and 11 show examples of lung SBRT plans with, respectively, better and worse agreement when using the L-Clarkson method as opposed to the C-Clarkson method. Figure 10 shows a case with an isolated tumor in the lung. The L-Clarkson method calculated the dose for low-density materials, where lateral scattering would be reduced, and the agreement between the TPS and the verification software was improved. Additionally, there were no significant changes in the ratio of the volumes of lung and water-equivalent materials inside the treatment field in the planes perpendicular to the beam axis. Conversely, the L-Clarkson method showed a greater negative difference in the example shown in Fig. 11. In this example, there were changes in the ratio of the volumes of lung and water-equivalent materials inside the treatment field in the planes perpendicular to the beam axis. For example, one of the planes showed larger areas for the lung and a smaller area for the tumor, as shown in Fig. 8b. However, when the beam passed through the mediastinum before the tumor, the volume of mediastinum was greater than the volume of lung in the other planes inside the treatment field. In such cases, the L-Clarkson method underestimated the dose from the mediastinum. Table 4 shows the results of t-tests comparing the different institutions in regard to the dose differences between the TPS and verification software using the C-Clarkson and L-Clarkson methods, respectively. There were larger variations in the systematic differences between the institutions, with the systematic deviation difference between institutions A and C being the greatest. The treatment field sizes of institution A were larger than those of institution C.

Fig. 9.

Box-and-whisker plots for lung SBRT plans (C-Clarkson: white box plots; L-Clarkson: yellow box plots). Left: composite fields; right: each field.

Fig. 10.

Example of a lung SBRT plan with better agreement when using the L-Clarkson method (C-Clarkson: 9.6%; L-Clarkson: 0.8%). Left: CT image and reference point (green cross); rRight: beam’s eye view.

Fig. 11.

Example of a lung SBRT plan with worse agreement when using the L-Clarkson method (C-Clarkson: 1.8%; L-Clarkson: −10.0%). Left: CT image and reference point (green cross); right: beam’s eye view.

Table 4.

P-values of t-tests comparing the different institutions in regard to the dose differences between the TPS and verification software using the C-Clarkson method

	A–B	A–C	A–D	B–C	B–D	C–D
Conventional breast treatment
Composite	<0.01	0.162	0.221	<0.01	<0.01	0.745
Each	<0.01	0.026	0.125	<0.01	<0.01	0.935
Conventional lung treatment
Composite	0.239	0.798	0.350	0.316	0.985	0.444
Each	0.172	0.147	0.056	0.807	0.369	0.546
Lung SBRT
Composite	0.028	0.794	0.637	0.038	0.011	0.870
Each	<0.01	0.744	0.446	<0.01	<0.01	0.732

Lung SBRT showed larger variations in the systematic differences between the institutions than did conventional breast treatments. This was due to treatment field size dependence; smaller treatment fields (such as 4 × 4 cm to 8 × 8 cm) are used for lung SBRT than are used in conventional breast and lung treatments. The accuracy of the dose calculation is susceptible to the smaller treatment fields. When the treatment field is small and the volume of the low-density tissue within the treatment field is high, the effects of the inhomogeneity correction are stronger. Thus, the TPSs algorithm and the Clarkson algorithm with heterogeneity correction in the verification software would show greater disagreement, even though the Clarkson algorithm with heterogeneity correction considered inhomogeneity in the lateral dimension.

Overall

The L-Clarkson method showed better agreement with the TPS than the C-Clarkson method, with the systematic difference being close to zero for all treatment sites with inhomogeneous media. The L-Clarkson method combined the C-Clarkson method with a reconstructed 2D CT image of the reference point to perform the heterogeneity correction. The C-Clarkson method is still broadly used for the secondary check in radiotherapy planning [21, 22], and the new L-Clarkson method could easily be installed in current clinical practice. Furthermore, the AAPM TG-114 noted that the effect of ‘missing tissue’ from tangential fields is estimated by contouring the surface of the breast to create a ‘virtual’ block, thereby reducing the volume of irradiated tissue [1]. In clinical practice, this method often seems to be used to remove potential systematic differences between different dose calculation algorithms. In this method, a manual contour of the breast tissue is visually defined by the user, and it should be clearly understood that the method relies on the user’s intervention and their intentional adjustment of the contour to adjust the disagreement between the TPS and the verification software to within the tolerance level. This method is used for the breast as it is easy to identify the border between the breast and air and thereby exclude the effect of missing tissue. However, it is difficult to use this method for the lung because there are contributions of dose from the low-density tissue in the lung, whereas there is almost no dose contribution from the air beside the breast. We therefore cannot use the ‘virtual’ block to exclude inhomogeneous media in the lung. This demonstrates the benefit of the simple and effective L-Clarkson method, which quantitatively corrects for the effect of heterogeneity without the user’s intervention.

However, variations between the C-Clarkson and L-Clarkson methods were similar. The L-Clarkson method still used Clarkson integration for the patient’s image slice reconstructed at the reference point, and thus no inhomogeneity corrections were applied for other layers, and variations still existed. Inhomogeneity corrections for multiple layers along the beam axis may be useful for reducing such variations.

CONCLUSION

We have designed and developed a simple and effective method of heterogeneity correction for the C-Clarkson algorithm, to take into account lateral scattering in inhomogeneous media. It should be easy to integrate the correction method with the C-Clarkson method commonly used in radiotherapy plan secondary checks. In a multi-institutional study, the heterogeneity correction method showed better agreement with the TPS than the C-Clarkson method. Use of the heterogeneity correction method will provide a simple action level within the range of −5% to 5% for the secondary check, without the need to consider systematic treatment-site differences for inhomogeneous media.

CONFLICT OF INTEREST

The authors have no conflicts of interest to declare.

FUNDING

This work was supported by the Japan Agency for Medical Research and Development (AMED) Grant Number 15ck0106185h0001.