Abstract
Pseudogenes are a paradigm of neutral evolution and their study has the potential to reveal intrinsic mutational biases. However, this potential is mitigated by the fact that pseudogenes are quickly purged from bacterial genomes. Here, we assembled a large set of pseudogenes from genomes experiencing reductive evolution as well as functional references for which we could establish reliable phylogenetic relationships. Using this unique dataset, we identified 857 independent insertion and deletion mutations and discover a pervasive bias towards deletions, but not insertions, with sizes multiples of 3 nt. We further show that selective constraints for the preservation of gene frame are unlikely to account for the observed mutational bias and propose that a mechanistic bias in alternative end-joining repair, a recombination-independent double strand break DNA repair mechanism, is responsible for the accumulation of 3n deletions.
Keywords: insertion–deletion, pseudogenes, mutations, indel
Introduction
Pseudogenes are commonly viewed as the paradigm of neutral evolution (Li et al. 1981) and they have been used extensively to infer intrinsic mutational bias in various eukaryotic and prokaryotic organisms (Li et al. 1981; Andersson and Andersson 2001; Zhang and Gerstein 2003; Lerat and Ochman 2004; Williams and Wernegreen 2013). However, pseudogenes are quickly purged in the genomes of free-living bacteria, making them scarce in high-coding density genomes (Kuo and Ochman 2010). Despite their value as neutral ground for the accumulation of mutations and their potential for revealing background mutation rates in organisms, their short retention time makes the use of pseudogenes generally impractical for the survey of background mutation processes. Highly accurate measures of mutation rates and spectra may instead be obtained through mutation accumulation experiments, where repeated single-cell bottlenecks ensure the fixation of all but the most deleterious mutations (Lynch 2008; Lee et al. 2012; Dillon et al. 2015). Possibly because insertion–deletion mutations (indels) have the highest potential to disrupt the production of proteins by introducing frameshift mutations in protein-coding genes, observed rates of indels per generation are generally an order of magnitude lower than base-substitution rates (Sung et al. 2016; Senra et al. 2018), hindering statistically robust inference of indel mutation spectra.
In the course of our studies of reductive genome evolution of Candidatus Burkholderia (Ca. Burkholderia) symbionts of Rubiaceae and Primulaceae plants, we noticed that the genomes of these obligate symbionts contained an inordinate amount of pseudogenes (Carlier and Eberl 2012; Carlier et al. 2015; Pinto-Carbó et al. 2016), and as a direct consequence some of the genomes studied have the smallest estimated coding capacity (i.e., cumulative size of functional ORFs to total genome size) of known prokaryotic genomes, ranging from 41.7% to 67.3% (Pinto-Carbó et al. 2016). Leaf nodule Ca. Burkholderia symbionts are uncultured, obligate for host development and are vertically transmitted through seeds. We have previously shown that the genomes of these symbionts are reduced compared with free-living Burkholderia and that deleterious mutations such as frameshift or null mutations have accumulated in all functional gene categories indiscriminately with the exception of housekeeping genes and genes related to the production of host-protective secondary metabolites (Carlier and Eberl 2012; Carlier et al. 2015; Pinto-Carbó et al. 2016).
Relaxation of purifying selection, a consequence of a small effective population size, may be the main driving force behind the slow purging of deleterious mutations in reduced genomes (Kuo et al. 2009). Accordingly, a vast majority of pseudogenes are not translated in these symbionts, making these an ideal test bed to study background mutation rates and profiles in prokaryotes (Carlier et al. 2013). Rather unusually, genome reduction is not a monophyletic trait in Burkholderia (Pinto-Carbó et al. 2018). A consequence of this is that many pseudogenes have functional orthologs in closely related free-living Burkholderia species. The relative long-term maintenance of pseudogenes in leaf nodule Burkholderia sp. and the sequence availability of homologs from closely related genomes affords the assembly of a unique dataset to analyze background indel mutation bias.
In this study, we take advantage of the abundance of pseudogenes in Ca. Burkholderia leaf nodule symbionts to assemble a large collection of pseudogenes with functional orthologs in related species. Using this dataset, we investigate the nature and frequency of insertions and deletions in genomic regions evolving neutrally. We observe an overrepresentation of small deletions of sizes multiples of 3 nt in pseudogenes, and show that this pattern is not due to selective constraints for the preservation of gene reading frame. We further demonstrate a 3n nt size bias in unrelated bacterial taxa, suggesting that the underlying mechanism may be universal in prokaryotes.
Materials and Methods
Data Collection and Pseudogene Prediction
All genomes used for this study were downloaded from NCBI Genbank, with the accession numbers listed in supplementary table S1, Supplementary Material online. Ortholog computations were done with the Orthomcl v1.4 software (Li et al. 2003), using Blastp cut-off values of 1.0 × 10−6 (e-value), 50% identity over 50% of query length. Pseudogene prediction was done previously for Burkholderia leaf nodule symbionts (Carlier and Eberl 2012; Carlier et al. 2013; Carlier et al. 2015; Pinto-Carbó et al. 2016). To avoid confusion in indel calling caused by multiple copies of IS elements, repeats were masked in the genomes of leaf nodule symbiotic Burkholderia species using the RepeatScout and RepeatMasker software (Price et al. 2005). In order to verify that repeat masking did not negatively impact the detection or introduced biases in downstream analyses, we performed pseudogene prediction on unmasked Ca. B. umbellata genome data. Of the candidate pseudogenes predicted only on unmasked data, none passed the criteria for downstream analysis as outlined below. For other genomes, intergenic regions (including flanking 100 bp) between functional CDS features were searched for homology with predicted functional proteins in ad-hoc databases consisting of predicted proteins of free-living relatives using the NCBI blastx program (Altschul et al. 1990). Only blastx hits with e-value < 10−6 and average identity > 50% were considered. Finally, candidate pseudogenes were aligned to the top blastx hit using the tfasty program of the FASTA software suite (Pearson 2000), and bona fide pseudogenes identified when they contained frameshifts or premature stop codons that affected >20% of gene length. Finally, in order to exclude candidate pseudogenes corresponding to spurious hypothetical genes, pseudogene sequences were searched against the Conserved Domain Database (Marchler-Bauer et al. 2015). Pseudogene sequences without CDD Hit were subsequently searched with Blastx against the NCBI Swissprot database and retained if they had at least one match with e-value <0.001 outside of the Burkholderia genus. The results of the CDD search are gathered in supplementary table S3, Supplementary Material online.
Pseudogene Data Set Selection
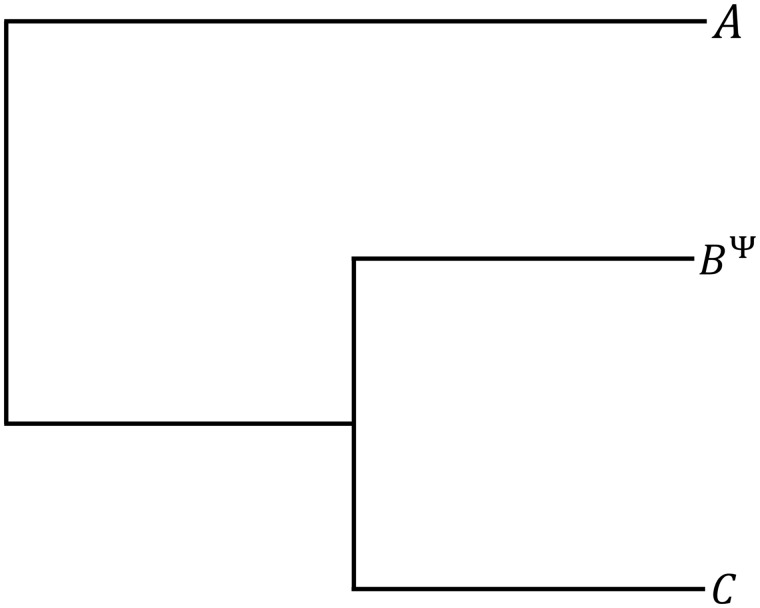
In order to select pseudogenes and unambiguously infer the direction of mutations (deletion or insertion) in a target genome, we identified two suitable reference genomes which were: 1) closely related (Average Nucleotide Identity (ANI) values > 85%), and 2) for which whole genome phylogeny indicated that one reference genome could act as an outgroup in phylogenetic analysis, that is, the rooted phylogenetic tree followed the pattern (A,(B, C)); where A and C are reference genomes and B is the target genome (fig. 1). The ANI value threshold was empirically chosen to maximize the number of indels while still allowing accurate alignment. Next, to ensure strict orthology between reference and target genes, we included only pseudogenes which were flanked by two genes with predicted orthologs in both reference genomes, with conserved synteny in all three genomes.
Fig. 1.
—Expected gene phylogeny guiding the selection of pseudogenes. Pseudogenes (BΨ) were chosen so that the ancestral state of indel mutations could be unambiguously inferred from an alignment with functional orthologs in related species (sequences A and C). In this configuration, A and C must be orthologs predicted to be functional.
Alignment of Pseudogenes to Reference Genes
The sequences of regions containing the target pseudogenes were extracted from unmasked genomes and flanking upstream and downstream genes were extracted using ad-hoc Python scripts. Corresponding syntenic regions were similarly extracted from the two reference genomes. The flanking genes were included in order to anchor the alignment. Sequences were aligned using the E-INS-i algorithm of the MAFFT v7 program with default parameters (Katoh and Standley 2013). All alignments were visually inspected in CLC Main Workbench v7.0 (Qiagen, Aarhus, Denmark) and alignments containing poorly aligned regions were discarded altogether. Indels for which we could not reliably infer the ancestral state were also discarded from our analysis. Alignments were then truncated to exclude regions flanking the reference genes and pseudogene, using the shortest functional ORF as a reference to avoid including mis-annotated start codons, and thus 5′UTR, in the alignments. Finally, to avoid including predicted pseudogenes resulting from sequencing errors, and because the first inactivating indel in a pseudogene may be subject to selection, we only included alignments with pseudogenes with at least three separate indels in our final dataset.
Alignments were analyzed using ad-hoc Python scripts. Deletions and insertions in pseudogenes were only counted if they were absent from both reference sequences. Directionality of the indel (i.e., deletion or insertion) was also inferred in relation to the consensus of the reference sequences. As a further control, and because individual genes may not follow species phylogeny, distance matrices were calculated for each alignment using the distmat tool of the EMBOSS package (Rice et al. 2000) with the Kimura two-parameter multiple substitution correction algorithm and gaps ignored. Alignments for which the computed minimal pairwise distance between the pseudogene sequence and either of the references was larger than the pairwise distance between the two reference genes may be due confounding factors such as horizontal acquisition or gene conversion. Alternatively, some pseudogene sequences may experience accelerated substitution rates and should still be included in our analyses. To distinguish between these possibilities, we constructed rooted phylogenies for 40 suspicious alignments using appropriate outgroup sequences selected as best nonself blastx hit in the NCBI refseq database (accessed January 2018). Our final dataset contained 151 curated alignments.
Dating of Pseudogenes
To estimate the age of the pseudogenes, we applied a method based on the calculation of the number of substitutions per site accumulated from the ancestor’s functional gene to the present pseudogene (Gomez-Valero et al. 2007). The rationale behind the method is that the number of substitutions per site for a pseudogene is the sum of the substitutions which occurred since the last common ancestor when the gene was still functional, plus those that occurred when the gene was evolving as a pseudogene. Nonsynonymous substitutions would tend to accumulate comparatively faster in pseudogenes than in functional counterparts and this property can be used to infer the age of a pseudogene, given appropriate calibration. Details of the method are given in supplementary information, Supplementary Material online.
Detection of Insertions Caused by Direct and Tandem Repeats
Direct repeat insertions in pseudogenes were detected using ad-hoc Python scripts. Upstream and downstream flanking regions surrounding insertion sites, of the exact size of the insertion, were extracted, allowing for 1 nt shift in either direction. The Hamming distance between the flanking strings and the string corresponding to the insertion was calculated. Direct repeats were called when the distance between at least one flanking string and the insertion string was 0 for insertions of sizes 2 or 3 bp, and ≤ 1 for insertions larger than 3 bp. The software Tandem Repeats Finder (Benson 1999) was used to detect tandem repeats in pseudogene sequences and aligned functional homologs with the following parameters: Weights for match, mismatch and indels = 2, 2, 7, respectively; Minimum alignment score = 25; Detection parameters Pm = 0.80 and Pi = 0.10; Maximum TR array size = 500.
Detection of Motifs around Deletion Sites
Deletion sites were analyzed for the presence of sequence motifs using ad-hoc Python scripts. The upstream flanking sequence of the deletion site was compared with the end of the deleted sequence and similarly the downstream flanking sequence was compared with the beginning of the deleted sequence. A motif was valid if: 1) the deleted sequence was ≤3 nt and had an identical match to either the up- or downstream flanking sequence, 2) the deleted sequence was >3 nt and had a near identical match (max. Hamming distance of 1) to either the up- or downstream flanking sequence, 3) the first/last n nucleotides of the deleted sequence were identical (n ≤ 3 nt) or near identical (n > 3 nt, max. Hamming distance of 1) to the first n nucleotides down-/upstream of the deletion site.
Annotation of Proteins Related to DNA Replication and Repair
Predicted protein sets were downloaded from NCBI Genbank and annotated using the eggNOG-mapper 1.0.3 software and the EggNOG database v 4.5 (Huerta-Cepas et al. 2016, 2017). HMM searches were limited to the bactNOG database of prokaryotic HMM profiles. Annotations were filtered according to COG category L (“Replication, recombination and repair”) and collated into supplementary table S2, Supplementary Material online.
Statistical Analyses
The size distribution of indels was investigated using two methods. Only indels with length ≤ 15 nt were used in the analysis. For non-Burkhorderia species, only indels ≤ 9 nt were used, as indels of size ≥ 10 nt were very rare in the dataset. Because indel size distribution has been shown to follow a power law in eukaryotic as well as prokaryotic genomes (Zhang and Gerstein 2003; Cartwright 2009), we fitted a linear model to the counts of indels according to their size using log-log-transformed data. In order to test whether indels of size 3n were enriched in our data, we added a categorical variable which takes the value of 1 if indel size is a multiple of 3 and 0 otherwise. Model fitting and statistical tests were performed in R, using the standard lm function.
The second method used nonparametric bootstrapping on the nontransformed data. Briefly, 10,000 bootstrap replications were performed, where each replication consists of creating a new indel population by sampling with replacement from the original population. For each indel length, a 95% confidence interval was estimated from the bootstrap distribution. Regression curves were calculated by fitting a power law function to the counts of non-3n indels and these were used to estimate expected counts for each indel size. Observed values were considered significantly different if the expected values fell outside of the 95% confidence interval estimated from the bootstrapped data. The bootstrapping analysis was performed in Python, using ad-hoc scripts and the “random” module for random sampling. The power-law was fitted to the data using the curve-fit function (using the trf method for least-squares), implemented in SciPy. To assess the correlation between pseudogene age and number of 3n-deletions the ratio of 3n to total deletions was calculated for each pseudogene. Pearson’s correlation coefficient and associated P-value were calculated as implemented in the SciPy package (http://www.scipy.org; accessed January 2018).
Genome-Wide Microhomology Distribution
The distribution of interval lengths of k-mers was assessed using ad-hoc Python scripts. For every k-mer length (2 ≤ k ≤ 6), the start positions of all possible k-mers (e.g., AA, AT, AC, … for 2-mers) were calculated from the genomes of two Ca. Burkholderia species (Ca. B. kirkii and Ca. B. brachyanthoides) and Lactobacillus johnsonii. The interval between two consecutive exact matches of that k-mer were computed. Frequency of intervals were pooled per k-mer length. Statistical overrepresentation of 3n interval lengths (up to 20 nt) was assessed by modelling the counts and the interval length and a factor considering if the interval length was a multiple of three or not. Negative binomial generalized linear models were found to best fit the data (lowest Akaike information criteria) and fitted using the MASS library in R.
Simulation of Deletion Frequencies
The method was adapted from Zhang and Gerstein (2003). Briefly, we created a random nucleotide string with the same length as the total length of pseudogenes in our dataset and simulated deletions events over different generations. Every mk generations, we introduced a deletion of length k (with k ranging from 1 up to 3) into the string. By fixing m1 and varying m2 and m3, we can estimate which ratio of deletion frequencies best fits with our observed data. Simulations were stopped when the number of deletions of size 1 reached the observed number. From every combination of 27 ≤ m2 ≤ 33 and 27 ≤ m3 ≤ 33 we found that m2 = 29 and m3 = 29 yielded a deletion distribution closest to our observed data (results for every combination were averaged over 100 runs).
Data and Computer Code Availability
The datasets used in this study as well as the computer scripts used for the analyses can be downloaded from https://github.com/ACarlierLab/indels-in-pseudogenes.
Results
Abundance of Pseudogenes in Symbiotic Burkholderia Genomes Is Not Due to an Altered Insertion/Deletion Bias
Bacterial genomes experience an extensive bias towards deletions (Mira et al. 2001; Kuo and Ochman, 2009; Moran et al. 2009; Sung et al. 2016), and we first asked whether the abundance of pseudogenes in relatively recently evolved leaf nodule symbionts was due to an altered insertion/deletion ratio or to relaxed selection constraints leading to the elimination of pseudogenes. To test this, we assembled a highly curated set of pseudogenes (table 1), where mutations are expected to accumulate in a neutral fashion (Li et al. 1981). Briefly, we chose sets of three genomes which included a target genome for pseudogene prediction and two reference genomes with no <85% pairwise average nucleotide identity as described in “Materials and Methods” section. Pseudogenes were predicted based on the presence of nonsense or frameshift mutations affecting at least 20% of the protein length. Pseudogenes, together with upstream and downstream flanking genes were then extracted and aligned to syntenic regions containing functional orthologs in the reference genomes. Pseudogenes and functional orthologs were further screened based on gene phylogeny so that the ancestral state of the pseudogene could be unambiguously determined (fig. 1). Because the first indel (possibly leading to inactivation of a gene) could have been selected for, we added the criterion that pseudogenes should have at least three independent indels separated by at least 10 bp to be included in the dataset. The final set contained 151 unique pseudogenes, originating from eight genomes and containing a total of 696 indels. We counted 396 deletions, for a total size of 7,421 nt and 300 insertions which summed up to 1,340 nt. This results in an insertion to deletion ratio of 0.758, corresponding to a size ratio of 0.181. Indels are thus strongly biased towards deletions in the genomes of leaf nodule symbionts, even taking into account that our data likely underestimates the total number of deletions since the requirement for the framing of pseudogenes by functional genes excluded large deletions spanning multiple genes. For comparison, we also extracted a set of 24 pseudogenes from various free-living Burkholderia species using the same methods and criteria. From these, we identified 42 deletions (1,662 bp in total) and 33 insertions (398 bp). The insertion to deletion rate in free living Burkholderia is 0.786, for a size ratio of 0.239, comparable to what we observed in leaf nodule symbiont genomes. These values are also consistent with the experimental values 16 insertions for 17 deletions (ratio = 0.941, size ratio = 0.321) reported for a mutation accumulation experiment in B. cenocepacia by Dillon et al. (Dillon et al. 2015).
Table 1.
Summary Table of Number of Pseudogenes and Indels of Different Candidatus Burkholderia Species
| Species | Pseudogenes | Indels | Deletions | Insertions |
|---|---|---|---|---|
| Ca. B. brachyanthoides | 39 | 191 | 96 | 95 |
| Ca. B. humilis | 5 | 17 | 11 | 6 |
| Ca. B. kirkii | 13 | 52 | 30 | 22 |
| Ca. B. pumila | 36 | 191 | 108 | 83 |
| Ca. B. punctata | 5 | 19 | 9 | 10 |
| Ca. B. schumanniana | 5 | 15 | 9 | 6 |
| Ca. B. umbellata | 45 | 203 | 129 | 74 |
| Ca. B. verschuerenii | 3 | 8 | 4 | 4 |
| Total | 151 | 696 | 396 | 300 |
Size of Small Deletions, but Not Insertions, Show a Distinct Bias towards Multiples of 3
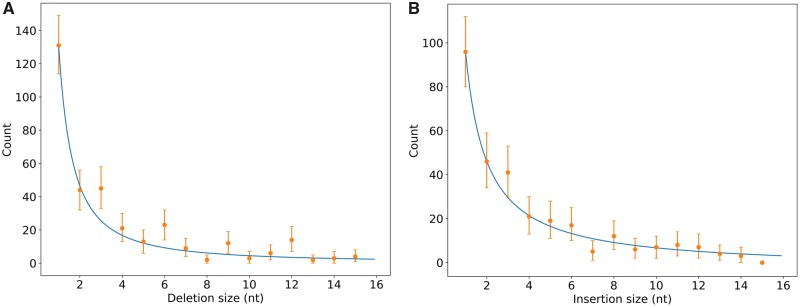
We next exploited our high quality dataset to ask whether the indel mutation rate is affected by local %G + C. We measured indel rate as the frequency of indels per kb. We estimated the ancestral length of pseudogenes by calculating the length of the alignment of the two functional orthologs. We did not observe any significant correlation between the rate of indels and the %G + C of the pseudogene (Pearson correlation coefficient = 0.0265, P-value = 0.74). During our analyses, however, we noticed that many of the pseudogenes in our dataset seemed to accumulate indels with sizes multiple of 3 nt (heretofore referred to as 3n indels). Because pseudogenes are not assumed to be translated into functional proteins, selective constraints resulting in the preservation of the reading frame are not expected. To investigate whether 3n indels are indeed overrepresented in our dataset, we analyzed further the distribution of indel sizes in our data. The size distribution of deletions or insertions follows a power law, as established previously for prokaryotic and eukaryotic genomes (Cartwright 2009; Sung et al. 2016). The tail of the distribution is very long, with few insertions or deletions exceeding a size of 15 nt. We therefore focused on indels of sizes ≤ 15 nt in order to simplify the statistical analyses. Because the mutational causes of insertions and deletions may differ mechanistically, we treated insertions and deletions separately (fig. 2). Linear regression analysis of log-transformed count and size data first revealed that deletions of size 3n are significantly overrepresented (P-value = 0.002). Bootstrap analysis further confirmed that deletions of sizes 3, 6, 9, and 12 are significantly more abundant than expected from a model built on deletion counts of sizes other than 3n (fig. 2A). Overrepresentation of deletions of sizes 3n was also significant in subsets of alignments of pseudogenes originating from individual species of leaf nodule symbionts, confirming that the pattern is not due to species-specific bias or outliers (supplementary fig. S2, Supplementary Material online). Lastly, we ruled out that 3n deletions could be on average overrepresented because of few pseudogenes with a high number of 3n deletions by calculating the ratio of 3n deletions to the number of pseudogenes (supplementary fig. S1, Supplementary Material online).
Fig. 2.
—Length distribution of deletions (A) and insertions (B) in 151 pseudogenes of Ca. Burkholderia species. Only indels ≤15 nt are shown. 95% confidence intervals are shown as error bars and a power law regression fitted on counts of non-3n indels is shown in blue.
We did not observe a similar bias towards insertions of size 3n (P-value = 0.898), with the exception of insertions of size 3 which are significantly overrepresented in our data (fig. 2B). Detailed analysis of pseudogene sets grouped by species revealed that overrepresentation of insertions of size 3 nt is significant only in the Ca. B. pumila data (supplementary fig. S2, Supplementary Material online). Closer inspection of the sequence alignments revealed that 13/28 insertions of sizes 3 nt or 6 nt in the Ca. B. pumila data resulted in the formation of direct repeats (DR). Further, 28/83 insertions in the Ca. B. pumila dataset also resulted in the formation of DR. A total of 46.4% of insertions involving DR are thus biased towards sizes of 3 or 6 nt. A similar proportion of insertions in other Ca. Burkholderia species involved DR (110/217 or 50.7%) but of these, only 19 were of size 3 or 6 bp (17.2% of 110). The overrepresentation of 3 or 6 nt insertions in the Ca. B. pumila data may thus reflect mutation dynamics that are specific to that genome. Overall, the size of deletions, but not insertions, are systematically biased towards multiples of 3 in neutrally evolving pseudogenes of Ca. Burkholderia leaf nodule symbionts.
Deletions of size 3n could also result from combinations of deletions of smaller sizes. For example, a deletion of 3 nt may result from adjacent independent deletions of size 1 and 2 nt. In order to rule this out, we estimated how likely deletions of size 3 formed by combinations of deletions of sizes 1 and 2 could occur by performing a computer simulation similar to previously reported (Zhang and Gerstein 2003). The results of our simulations show that in order to reach the observed deletion distribution, single deletions of size 2 and 3 should each occur 0.34 (10/29) times as often as deletions of size 1. These ratios are very similar to the observed ratios of deletions in our dataset (44/131 or 0.336 and 45/131 or 0.344 for sizes 1/2 and 1/3, respectively), indicating that almost all of the observed deletions of sizes 2 and 3 are derived from single deletion events, rather than combinations of smaller deletions.
Size Bias of Small Deletions Is Not Dependent on the Age of the Pseudogene
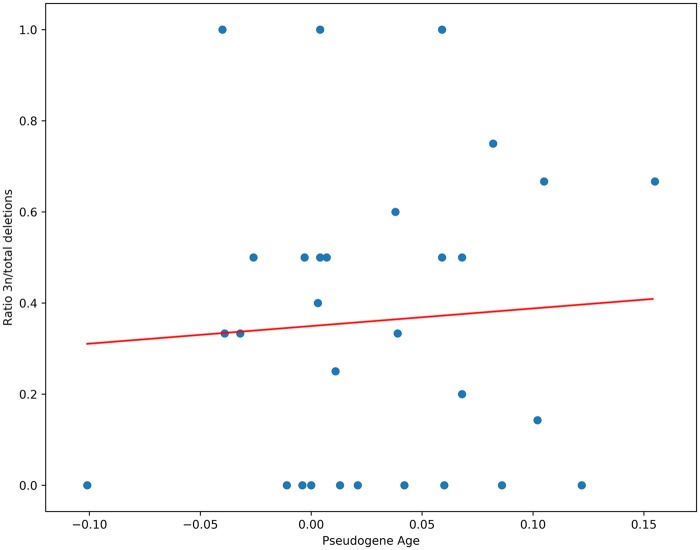
Because insertion sizes do not show a systematic bias towards sizes 3n, and deleterious mutations are presumed to accumulate neutrally in pseudogenes, we hypothesized that the observed bias towards 3n deletions is not due to selective constraints to preserve the reading frame. This may instead reflect an intrinsic or mechanistic bias in mutation profiles. We reasoned that if selective constraints for the preservation of a gene reading frame are responsible for the bias towards deletions of size 3n, the strength of these constraints should be higher for indel mutations which accumulated early in the gene’s history, i.e., whereas the gene was functional and translated, and more relaxed after the first inactivating mutation. Under this hypothesis, older pseudogenes, which have been evolving under a neutral model for a longer time, should have accumulated more deletions which do not show a particular bias towards sizes 3n. In other words, the relative age of pseudogene (i.e., the time elapsed since the first inactivating mutation occurred in the evolutionary history of the gene) should be inversely correlated with the proportion of 3n deletions. To test this hypothesis, we calculated the relative age of the pseudogenes by adapting a method first described by Gomez-Valero et al. (2007). Briefly, we calculated the number of substitutions per site accumulated from the ancestor’s functional gene to the present pseudogene, the rationale being that the number of substitutions per site for a pseudogene is the sum of the substitutions which occurred since the last common ancestor when the gene was still functional, plus those that occurred when the gene was evolving as a pseudogene. Nonsynonymous substitutions would tend to accumulate comparatively faster in pseudogenes than in functional counterparts and this property can be used to infer the age of a pseudogene. We applied this method to 30 pseudogenes of Ca. B. pumila, containing a total of 84 deletions ≤ 15 nt. We did not observe any correlation between the calculated age of pseudogenes and the ratio of 3n deletions (fig. 3). Similarly, no significant correlation between pseudogene age and ratio of 3n deletions was observed for the datasets of Ca. B. umbellata and Ca. B. brachyanthoides (supplementary fig. S3, Supplementary Material online). As further confirmation, the total number of indels, which can be seen as a proxy for the age of a pseudogene, did not correlate with the proportion of 3n deletions on our entire dataset (supplementary fig. S4, Supplementary Material online). Together with the fact that insertion sizes do not show a significant bias towards multiples of 3 nt, our data show that selective constraints for the preservation of the reading frame early in the evolutionary history of pseudogenes are not responsible for the observed bias towards 3n deletions.
Fig. 3.
—Ratio of 3n deletions to total deletions as a function of estimated pseudogene age in Ca. B. pumila. Pseudogene age is the time elapsed since the first inactivating mutation, giving rise to the pseudogene. The trend line shown was fitted using linear regression analysis (Pearson correlation coefficient and P-value were 0.065 and 0.73, respectively) on 30 pseudogenes. The total number of deletions per pseudogene ranges from 3 to 10. Details of the pseudogene age calculation are given in supplementary information, Supplementary Material online.
Sequence Motifs Associated with Small Deletions Hint at Molecular Mechanism
The sequence context surrounding indels may provide clues about the mechanisms causing small indels, in particular deletions. Short deletions generally arise from slipped strand mispairing (SSM) or error-prone repair of double strand breaks (DSB) (Garcia-Diaz and Kunkel 2006). SSM usually occurs in homopolymer runs, or in short direct repeats and results in short deletions or insertions (Levinson and Gutman 1987). To investigate whether SSM is a significant contributor to the formation of small deletions in our pseudogene dataset, we analyzed indels for the presence of homopolymeric runs and tandem repeats (TR). We did not find any instances of indels occurring in homopolymeric runs of size > 6 nt and only found 2/396 instances where deletions overlapped short tandem repeats and the deletion corresponded to a discrete number of TR repeats. SSM is therefore an unlikely contributor to deletion formation in pseudogenes, and by extension it is unlikely to contribute to the observed bias towards 3n deletions. Error-prone DSB repair is thus the most likely cause of the majority of the deletions observed in the pseudogenes of Ca. Burkholderia genomes. As opposed to homologous recombination, DSB repair by non-homologous end-joining (NHEJ) is often mutagenic and results in the formation of indels (Gong et al. 2005). Canonical bacterial NHEJ relies on the Ku-LigD system, a rudimentary version of the NHEJ system prevalent in eukaryotes (Della et al. 2004). However, homologs of Ku and LigD are absent from 6/8 genomes of leaf nodule Ca. Burkholderia (supplementary table S2, Supplementary Material online), ruling out canonical NHEJ as the likely source of errors in DSB repair. Intriguingly, we could detect microhomologies (1–12 nt) flanking deletion sites in 171/396 deletions (fig. 4). The size distribution of indels size flanked by microhomologies is similar to the rest of the deletion sites, also with a significant overrepresentation of 3n deletions (P-value = 0.000299).
Fig. 4.
—Examples of deletion sites involving microhomologies in Ca. Burkholderia pseudogenes. Sequence titles are species name abbreviations, with B. sp. YI23 = Burkholderia sp. YI23, Ca. B. ver. = Ca. B. verschuerenii and Ca. B. pum. = Ca. B. pumila. Microhomologies are shown in bold, deletions are represented by the gap character “–.”
Conservation of Bias in Other Taxa
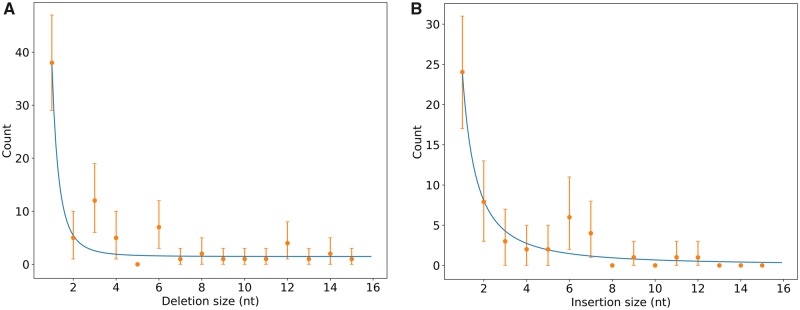
In order to determine if the bias towards 3n deletions is limited to Ca. Burkholderia genomes or affects other taxa as well, we applied our method for pseudogene detection to the genomes of bacteria from diverse Gram-negative and Gram-positive taxa. Pseudogenes fulfilling our stringent criteria of synteny, sequence conservation and containing a minimum number of 3 indels are rare, and we could only generate unambiguous alignments for 53 pseudogenes, corresponding to 17 species belonging to three phyla (Proteobacteria, Firmicutes, and Actinobacteria). The identified pseudogenes contained 104 deletions (including 81 with size ≤ 15 nt) and 57 insertions (including 52 ≤ 15 nt). Linear regression analysis of log-transformed count and size data did not reveal a significant contribution of size 3n over the whole range of size values (P-value = 0.119), possibly because of a lack of statistical power and because deletions larger than 8 nt are sparse in this dataset. Bootstrap analysis however showed a significant overrepresentation of deletions of 3 and 6 nt (fig. 5A). Insertions of size 3 nt are no more abundant than expected, however insertions of 6 nt seem to be overrepresented (fig. 5B). Data for insertions >8 nt are too sparse to infer more general trends. Insertions of 6 nt seem to be evenly distributed across taxa and we could not observe any particular motif explaining their overrepresentation. However, and because other insertions of size 3 nt are not overrepresented, this is unlikely to be due to selective constraints for preservation of gene reading frame. Together, these data suggest that background mutations are biased towards 3n deletions in a wide array of bacteria. We could not rule out confidently that the ratio of 3n deletions does not correlate with pseudogene age because individual data sets were too small for robust statistical analysis. In order to establish what mechanisms caused the short deletions in this dataset, we searched the deletion sites for motifs. Similar to what we observed for Ca. Burkholderia pseudogenes, slightly over 39% of the deletion sites (41 out of 104) contained microhomologies (1–11 nt).
Fig. 5.
—Length distribution of deletions (A) and insertions (B) in 53 pseudogenes of various bacterial species. Only indels ≤ 15 nt are shown. 95% confidence intervals are shown as error bars and a power law regression fitted on counts of non-3n indels is shown in blue. Pseudogenes were extracted from the 12 sets of 3 genomes listed in supplementary table S1, Supplementary Material online.
Genome-Wide Microhomology Interval Lengths Also Show a Bias towards Multiples of Three
Microhomologies flanking deletion sites resemble the signature of alternative end-joining (A-EJ), a form of NHEJ recently characterized in E. coli (Chayot et al. 2010). A-EJ makes use of microhomologies and RecBCD-mediated end resection-ligation to repair double stranded breaks. The overrepresentation of 3n deletions in pseudogenes could either be the result of a mechanistic bias of double-stranded break repair or may be due to underlying patterns in the genome-wide distribution of microhomologies serving as template for DNA repair. To test the latter hypothesis, we calculated the distribution of intervals between identical k-mers of lengths 2–6 nt in the genome of Ca. B. brachyanthoides (supplementary fig. S5, Supplementary Material online), as well as Ca. B. kirkii and Lactobacillus johnsonii (data not shown). In all genomes investigated, identical k-mers of lengths 2–6 are significantly more likely to occur at intervals of 3n nt (P-value < 0.0001). The size distribution of deletions in pseudogenes, and its bias towards 3n nt, may thus reflect the underlying distribution of microhomologies in bacterial genomes.
Discussion
Although the neutrally evolving properties of pseudogenes make them valuable to the investigation of intrinsic mutation profiles and biases, their short evolutionary retention time usually limits their usefulness. Here, we identified a large set of pseudogenes having accumulated multiple indel mutations which have unusually retained closely related functional homologs in free-living bacteria. Two factors probably contribute to the higher retention rate of pseudogenes and the large size of this dataset: 1) leaf nodule symbiosis is polyphyletic and has evolved several times in Burkholderia (now Caballeronia) over the past 10–15 Ma (Lemaire et al. 2011; Pinto-Carbó et al. 2016), resulting in multiple free-living and host captive lineages evolving in parallel; 2) vertical transmission and repeated transmission bottlenecks result in relaxed genome-wide purifying selection on the genomes of the Ca. Burkholderia symbionts, possibly significantly slowing down the purging of pseudogenes (Pinto-Carbó et al. 2016). The large number of pseudogenes in the genomes of these Ca. Burkholderia leaf nodule symbionts and the availability of reference functional genes with relatively low sequence divergence from free-living species therefore allowed us to explore mutational patterns and biases affecting rare mutations. Indels in particular are of high interest because of their potential to be more disruptive to gene function than substitutions, but accumulate too slowly to be effectively sampled by mutation accumulation (MA) experiments running over hundreds or thousands of generations. Studies combining data from multiple MA experiments have the potential to overcome these limitations, with the caveat that indels have a tendency to accumulate in genomic “hot-spots”, for example at sites rich in short tandem repeats (Dillon et al. 2017) resulting in possible sampling biases.
We first analyzed our data to investigate whether insertion/deletion ratios were skewed towards insertions in the genomes of obligate leaf nodule symbionts in order to explain the large proportion of noncoding sequence and the relatively large size of leaf nodule symbiont genomes. We found that indel ratios are comparable to those of free-living Burkholderia species, both inferred from MA experiments or from pseudogenes. Skewed indel rates are therefore unlikely to account for the relatively slow DNA loss and the accumulation of noncoding DNA in the genomes of Ca. Burkholderia leaf nodule symbionts. Relaxed purifying selection on neutral or deleterious “junk” DNA, combined with the relatively young age of leaf nodule symbiosis, estimated previously at 10–15 Ma (Pinto-Carbó et al. 2016), may instead account for the idiosyncratic features of genome reductive evolution in these organisms.
Consistent with previous reports on eukaryotic and prokaryotic indel profiles, the distribution of indel sizes in the pseudogenes of Ca. Burkholderia leaf nodule symbionts follows a power law (Zhang and Gerstein 2003; Cartwright 2009). However, we observed that the size distribution of deletions is skewed towards multiples of 3 and in particular for k = 3, 6, 9, and 12. As indels of size 3n are expected to be less deleterious because they preserve the gene reading frame, their negative effects on gene expression and protein function is lower than for indels of other sizes. Therefore, selective constraints for the preservation of gene frame could account for the overrepresentation of 3n deletions in our data. Both insertions and deletions have an equal potential to disrupt gene function, and if selective pressure to preserve reading frame accounts for the overrepresentation of 3n deletions in our data, the same should be true about insertions. However, insertions of sizes 3n were not enriched in our data, with the exception of insertions of 3 nt. This overrepresentation of 3 nt insertions was only observed in pseudogenes from Ca. B. pumila and may thus reflect mutation dynamics specific to this genome. In support of this interpretation, we found that almost half of all 3 nt and 6 nt insertions in pseudogenes of Ca. B. pumila resulted in direct repeats. In contrast, the proportion of 3 or 6 nt insertions in pseudogenes of other genomes is only 17.2%. We previously observed that IS30 family insertion elements were particularly abundant in the Ca. B. pumila genome (Pinto-Carbó et al. 2016). Insertion of IS30 elements generally results in direct repeats (DR) of 2–3 bp (Siguier et al. 2006), and multiple insertion–excision events of IS30 elements may explain the overrepresentation of DR of size 3 nt in Ca. B. pumila pseudogenes. Distinct constraints acting on insertions and deletions may thus explain the overrepresentation of 3n deletions in pseudogenes of Ca. Burkholderia species. The fact that pseudogene age does not correlate with the proportion of 3n deletions further demonstrates that selection for the preservation of gene frame does not account for the overrepresentation of 3n deletions. Mechanistic biases or constraints in DNA repair may instead explain this phenomenon.
Small deletions may result from error-prone DNA repair or slipped strand mispairing (Garcia-Diaz and Kunkel 2006). We could identify slipped strand mispairing as a possible reason for only 2/396 deletions, which occurred near or within short tandem repeats. Instead, 43% of all small deletions sampled occurred between microhomologies of 2–11 nt. This is reminiscent of the resection-dependent alternative end-joining (alt-EJ) mechanism involved in DSB repair in eukaryotes, which operates through recruitment of PARP1 and associated repair factors to microhomologies flanking DSBs (Ceccaldi et al. 2016). Recently, a homologous form of alt-EJ, termed A-EJ has been proposed to mediate DSB repair in E. coli in a Ku-LigD and RecA-independent fashion (Chayot et al. 2010). The molecular components of A-EJ are unknown, but are thought to include proteins involved in DNA replication and recombination, such as RecBCD and LigA. In contrast to Ku-LigD-dependent NHEJ, A-EJ repairs DSBs by degrading unprotected ends and largely relies on microhomologies to ligate compatible ends (Chayot et al. 2010). Interestingly, most leaf nodule Ca. Burkholderia lack a homolog of Ku, suggesting that nonhomologous repair of DSBs in these organisms relies exclusively on A-EJ.
Nonhomologous DSB repair may be particularly crucial for the biology of leaf nodule symbionts, and more generally bacteria which experience extended periods of slow or no growth and relatively small population sizes, for example obligate symbionts or pathogens. Under conditions of slow growth, gene conversion donors for homology-directed repair, for example multiple copies of actively replicating chromosomes, are absent. Error-prone end-joining repair via NHEJ or A-EJ is then a last resort mechanism to repair and ligate broken DNA ends when homology-directed repair is not available (Moeller et al. 2007; Pitcher et al. 2007). Leaf nodule bacteria encounter frequent periods of slow growth and environmental injury and may especially depend on these repair mechanisms for survival. For example, vertical transmission of the symbionts from one plant generation to the next entails transmission though the seeds. The development of the seeds of flowering plants concludes by a desiccation phase, followed by a period of dormancy (Angelovici et al. 2010). In the case of Psychotria species, seed dormancy lasts between 3 and 6 months (own observations) and it is unclear if or how the extracellular bacterial symbionts are protected from the environment during this critical phase. Indeed, aposymbiotic seedlings frequently and spontaneously arise, indicating that many symbionts do not survive seed transmission (Pinto-Carbó et al. 2018). In addition, the extremely small size of the transmitted symbiotic population, which we estimate in only a few hundred bacterial cells per seed on average (Pinto-Carbó, unpublished), makes the seed dormancy period a highly vulnerable stage for the symbiotic bacteria. Because of the small number of bacteria transmitted, mutations have a high probability of becoming fixed in this population and in particular frame-disruptive indels could cause population fitness to rapidly decline. Under circumstances where deleterious mutations cannot be efficiently purged by purifying selection, mitigating errors introduced by DSB repair seems particularly advantageous. It is tempting to speculate that NHEJ repair mechanisms, and perhaps A-EJ specifically, have evolved to minimize the most deleterious frameshifting errors of DSB repair by favoring deletions with sizes multiples of 3 nt. Alternatively, we found that microhomologies are more likely to occur at intervals of 3n nt, possibly as a consequence of the uneven distribution of codons in coding sequences. The reliance on microhomologies by A-EJ for DSB repair may thus intrinsically result in deletions that tend to minimize frameshifting errors. Furthermore, our analysis of pseudogene-rich genomes from other bacterial species and phyla suggests that 3n deletion bias may be universal in prokaryotes. Consistent with this pattern, a recent analysis of pooled data from mutation accumulation experiments across several unicellular prokaryotic and eukaryotic species uncovered more deletions of 3 nt (15 in total) than deletions of 2 nt (13 in total; Sung et al. 2016). Intriguingly, Zhang and Gerstein also previously reported that deletions of 3 nt were also overrepresented in human pseudogenes (Zhang and Gerstein 2003). These analyses and ours thus indicate that biases towards tri-nucleotides by DNA repair or replication mechanisms may be a universal phenomenon. More information about the molecular pathways underlying these mechanisms is necessary to take these conclusions outside of the realm of speculation.
Supplementary Material
Supplementary data are available at Genome Biology and Evolution online.
Supplementary Material
Acknowledgments
This work was supported by the Research Foundation—Flanders under grant G017717N and the Special Research fund of Ghent University under grant BOF17/STA/024. MPC acknowledges support from the University of Zurich URPP Evolution in Action. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Author Contributions
A.C. designed the research, B.D., M.P., and A.C. performed the research and analyzed the data; B.D. and A.C. wrote the manuscript.
Literature Cited
- Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ.. 1990. Basic local alignment search tool. J Mol Biol. 2153:403–410. [DOI] [PubMed] [Google Scholar]
- Andersson JO, Andersson SG.. 2001. Pseudogenes, junk DNA, and the dynamics of Rickettsia genomes. Mol Biol Evol. 185:829–839. [cited 2015 Feb 5]. Available from: http://www.ncbi.nlm.nih.gov/pubmed/11319266. [DOI] [PubMed] [Google Scholar]
- Angelovici R, Galili G, Fernie AR, Fait A.. 2010. Seed desiccation: a bridge between maturation and germination. Trends Plant Sci. 154:211–218. [DOI] [PubMed] [Google Scholar]
- Benson G. 1999. Tandem repeats finder: a program to analyze DNA sequences. Nucleic Acids Res. 272:573–580. [cited 2018 Mar 20]. Available from: http://www.ncbi.nlm.nih.gov/pubmed/9862982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlier A, et al. , . 2015. The genome analysis of Candidatus Burkholderia crenata reveals that secondary metabolism may be a key function of the Ardisia crenata leaf nodule symbiosis. Environ Microbiol. 18:2507–2522. [DOI] [PubMed] [Google Scholar]
- Carlier AL, Eberl L.. 2012. The eroded genome of a Psychotria leaf symbiont: hypotheses about lifestyle and interactions with its plant host. Environ Microbiol. 1410:2757–2769. [DOI] [PubMed] [Google Scholar]
- Carlier AL, Omasits U, Ahrens CH, Eberl L.. 2013. Proteomics analysis of Psychotria leaf nodule symbiosis: improved genome annotation and metabolic predictions. Mol Plant Microbe Interact. 2611:1325–1333. [DOI] [PubMed] [Google Scholar]
- Cartwright RA. 2009. Problems and solutions for estimating indel rates and length distributions. Mol Biol Evol. 262:473–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceccaldi R, Rondinelli B, D’Andrea AD.. 2016. Repair pathway choices and consequences at the double-strand break. Trends Cell Biol. 261:52–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chayot R, Montagne B, Mazel D, Ricchetti M.. 2010. An end-joining repair mechanism in Escherichia coli. Proc Natl Acad Sci USA. 1075:2141–2146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Della M, et al. 2004. Mycobacterial Ku and ligase proteins constitute a two-component NHEJ repair machine. Science 3065696:683–685. [DOI] [PubMed] [Google Scholar]
- Dillon MM, Sung W, Lynch M, Cooper VS.. 2015. The rate and molecular spectrum of spontaneous mutations in the GC-rich multichromosome genome of Burkholderia cenocepacia. Genetics 2003:935–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dillon MM, Sung W, Sebra R, Lynch M, Cooper VS.. 2017. Genome-wide biases in the rate and molecular spectrum of spontaneous mutations in Vibrio cholerae and Vibrio fischeri. Mol Biol Evol. 341:93–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia-Diaz M, Kunkel TA.. 2006. Mechanism of a genetic glissando: structural biology of indel mutations. Trends Biochem Sci. 314:206–214. [DOI] [PubMed] [Google Scholar]
- Gomez-Valero L, Rocha EPC, Latorre A, Silva FJ.. 2007. Reconstructing the ancestor of Mycobacterium leprae: the dynamics of gene loss and genome reduction. Genome Res. 178:1178–1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong C, et al. , . 2005. Mechanism of nonhomologous end-joining in mycobacteria: a low-fidelity repair system driven by Ku, ligase D and ligase C. Nat Struct Mol Biol. 124:304–312. [DOI] [PubMed] [Google Scholar]
- Huerta-Cepas J, et al. , . 2016. eggNOG 4.5: a hierarchical orthology framework with improved functional annotations for eukaryotic, prokaryotic and viral sequences. Nucleic Acids Res. 44(D1):D286–D293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huerta-Cepas J, et al. , . 2017. Fast genome-wide functional annotation through orthology assignment by eggNOG-mapper. Mol Biol Evol. 348:2115–2122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katoh K, Standley DM.. 2013. MAFFT multiple sequence alignment software version 7: improvements in performance and usability. Mol Biol Evol. 304:772–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo C-H, Ochman H.. 2009. Deletional Bias across the Three Domains of Life. Genome Biol. Evol. 1:145–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo C-H, Moran NA, Ochman H.. 2009. The consequences of genetic drift for bacterial genome complexity. Genome Res. 198:1450–1454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo C-H, Ochman H.. 2010. The extinction dynamics of bacterial pseudogenes. PLoS Genet. 68:e1001050.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee H, Popodi E, Tang H, Foster PL.. 2012. Rate and molecular spectrum of spontaneous mutations in the bacterium Escherichia coli as determined by whole-genome sequencing. Proc Natl Acad Sci USA. 10941:E2774–E2783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemaire B, Vandamme P, Merckx V, Smets E, Dessein S.. 2011. Bacterial leaf symbiosis in angiosperms: host specificity without co-speciation. PLoS One 69:e24430.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerat E, Ochman H.. 2004. Psi-Phi: exploring the outer limits of bacterial pseudogenes. Genome Res. 1411:2273–2278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levinson G, Gutman GA.. 1987. Slipped-strand mispairing: a major mechanism for DNA sequence evolution. Mol Biol Evol. 4:203–221. [DOI] [PubMed] [Google Scholar]
- Li L, Stoeckert CJ, Roos DSC-P.. 2003. OrthoMCL: identification of ortholog groups for eukaryotic genomes. Genome Res. 139:2178–2189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W-H, Gojobori T, Nei M.. 1981. Pseudogenes as a paradigm of neutral evolution. Nature 2925820:237–239. [DOI] [PubMed] [Google Scholar]
- Lynch M. 2008. The cellular, developmental and population-genetic determinants of mutation-rate evolution. Genetics 1802:933–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchler-Bauer A, et al. , . 2015. CDD: NCBI’s conserved domain database. Nucleic Acids Res. 43(D1):D222–D226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mira A, Ochman H, Moran NA.. 2001. Deletional bias and the evolution of bacterial genomes. Trends Genet. 1710:589–596. [cited 2013 Jan 31]. Available from: http://www.ncbi.nlm.nih.gov/pubmed/11585665. [DOI] [PubMed] [Google Scholar]
- Moeller R, et al. , . 2007. Role of DNA repair by nonhomologous-end joining in Bacillus subtilis spore resistance to extreme dryness, mono- and polychromatic UV, and ionizing radiation. J Bacteriol. 1898:3306–3311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran NA, McLaughlin HJ, Sorek R.. 2009. The dynamics and time scale of ongoing genomic erosion in symbiotic bacteria. Science 3235912:379–382. [DOI] [PubMed] [Google Scholar]
- Pearson WR. 2000. Flexible sequence similarity searching with the FASTA3 program package. Methods Mol Biol. 132:185–219. [cited 2012 Nov 26]. Available from: http://www.ncbi.nlm.nih.gov/pubmed/10547837. [DOI] [PubMed] [Google Scholar]
- Pinto-Carbó M, et al. , . 2016. Evidence of horizontal gene transfer between obligate leaf nodule symbionts. ISME J. 109:2092–2105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinto-Carbó M, et al. , . 2018. Leaf nodule symbiosis: function and transmission of obligate bacterial endophytes. Curr Opin Plant Biol. 44:23–31. [DOI] [PubMed] [Google Scholar]
- Pitcher RS, et al. , . 2007. NHEJ protects mycobacteria in stationary phase against the harmful effects of desiccation. DNA Repair (Amst) 69:1271–1276. [DOI] [PubMed] [Google Scholar]
- Price AL, Jones NC, Pevzner PA.. 2005. De novo identification of repeat families in large genomes. Bioinformatics 21(Suppl 1):i351–i358. [DOI] [PubMed] [Google Scholar]
- Rice P, Longden I, Bleasby A.. 2000. EMBOSS: the European molecular biology open software suite. Trends Genet. 166:276–277. [cited 2014 Jun 24]. Available from: http://www.ncbi.nlm.nih.gov/pubmed/10827456. [DOI] [PubMed] [Google Scholar]
- Senra MVX, et al. , . 2018. An unbiased genome-wide view of the mutation rate and spectrum of the endosymbiotic bacterium Teredinibacter turnerae. Genome Biol Evol. 103:723–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siguier P, Perochon J, Lestrade L, Mahillon J, Chandler MC-P.. 2006. ISfinder: the reference centre for bacterial insertion sequences. Nucleic Acids Res. 3490001:D32–D36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sung W, et al. , . 2016. Evolution of the insertion-deletion mutation rate across the tree of life. G3 (Bethesda) 6:2583–2591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams LE, Wernegreen JJ.. 2013. Sequence context of indel mutations and their effect on protein evolution in a bacterial endosymbiont. Genome Biol Evol. 53:599–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z, Gerstein M.. 2003. Patterns of nucleotide substitution, insertion and deletion in the human genome inferred from pseudogenes. Nucleic Acids Res. 3118:5338–5348. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.