Methodological implementation of mixed linear models in multi-locus genome-wide association studies

Abstract

The mixed linear model has been widely used in genome-wide association studies (GWAS), but its application to multi-locus GWAS analysis has not been explored and assessed. Here, we implemented a fast multi-locus random-SNP-effect EMMA (FASTmrEMMA) model for GWAS. The model is built on random single nucleotide polymorphism (SNP) effects and a new algorithm. This algorithm whitens the covariance matrix of the polygenic matrix K and environmental noise, and specifies the number of nonzero eigenvalues as one. The model first chooses all putative quantitative trait nucleotides (QTNs) with ≤ 0.005 P-values and then includes them in a multi-locus model for true QTN detection. Owing to the multi-locus feature, the Bonferroni correction is replaced by a less stringent selection criterion. Results from analyses of both simulated and real data showed that FASTmrEMMA is more powerful in QTN detection and model fit, has less bias in QTN effect estimation and requires a less running time than existing single- and multi-locus methods, such as empirical Bayes, settlement of mixed linear model under progressively exclusive relationship (SUPER), efficient mixed model association (EMMA), compressed MLM (CMLM) and enriched CMLM (ECMLM). FASTmrEMMA provides an alternative for multi-locus GWAS.

Introduction

Genome-wide association studies (GWAS) have been widely used in the genetic dissection of quantitative traits in human, animal and plant genetics, especially in combination with the output of genomic sequencing technologies. The most popular method for GWAS is the mixed linear model (MLM) method [1, 2] because of its demonstrated effectiveness in correcting the inflation from many small genetic effects (polygenic background) and controlling the bias of population stratification [3–7]. Since the MLM of Yu et al. [2] was published, many MLM-based methods have been proposed. However, most of them comprise a one-dimensional genome scan by testing one marker at a time, which is involved in multiple test correction for the threshold value of significance test. The widely used Bonferroni correction is often too conservative to detect many important loci for quantitative traits.

Most quantitative traits are controlled by a few genes with large effects and numerous polygenes with minor effects. However, the current one-dimensional genome scan approaches for GWAS do not match the true genetic model for these traits. To overcome this issue, multi-locus methodologies have been developed; for example, Bayesian least absolute shrinkage and selection operator (LASSO) [8], adaptive mixed LASSO [9], penalized Logistic regression [10–11], Elastic-Net [12], empirical Bayes (E-BAYES) [13] and E-BAYES LASSO [14]. If the number of markers is several times larger than sample size, all marker effects can be included in one single model and estimated in an unbiased way. If the number of markers is many times larger than sample size, however, these shrinkage approaches will fail. In this situation, we should consider how to reduce the number of marker effects in the multi-locus genetic model. For example, Zhou et al. [15] developed a Bayesian sparse linear mixed model, and Moser et al. [16] proposed a Bayesian mixture model. Under these models, two to four common components in the mixture distribution were considered and only a few variance components were estimated. Although about 500 effects in the genetic model are finally considered after several rounds of Gibbs sampling, the computing time becomes a major concern for these Bayesian approaches. Recently, Segura et al. [17] and Wang et al. [7] have proposed multi-locus MLM approaches. However, further refinement for fast algorithm is needed.

Zhang et al.’s [1] MLM method treated the quantitative trait nucleotide (QTN) effect as being random, in which three component variances owing to QTNs, polygenes and residual errors need to be estimated. If the number of effects is large, this calculation takes a long time. To reduce computing time and increase power in QTN detection, a compressed MLM (CMLM) with a population parameters previously determined (P3D) algorithm [18] and an enriched CMLM (ECMLM) [19] have been proposed. On the other hand, Kang et al. [3] proposed an efficient mixed model association (EMMA), and other authors suggested alternatives, such as EMMA eXpedited (EMMAX) [20], FaST-LMM [21], FaST-LMM-Select [22], genome-wide EMMA [4] and genome-wide rapid association using mixed model and regression-Gamma (GRAMMAR-Gamma) [23]. Recently, settlement of mixed linear model under progressively exclusive relationship (SUPER) [24] has been developed based on FaST-LMM. Among the above fast methods, the SNP effect was treated as being fixed. Goddard et al. [25] noted that a random-marker model has several advantages, compared with the fixed model [7, 26, 27]. For example, the random model approach will shrink the estimated SNP effects toward zero. However, Goddard et al. [25] did not provide an efficient computational algorithm to estimate marker effects.

In this article, we describe a new method that can quickly scan each random-effect marker throughout the genome by constructing a fast and new matrix transformation for the three component variances. Then, all the putative QTNs with ≤ 0.005 P-values were placed into one multi-locus genetic model and these QTN effects were estimated by EM empirical Bayes (EMEB) [28] for true QTN identification. This new method, called fast multi-locus random-SNP-effect EMMA (FASTmrEMMA), was validated by analysis of real data from Arabidopsis [29] and by a series of simulation studies and compared with the other methods, such as E-BAYES (multi-locus model) [30], SUPER, EMMA, ECMLM and CMLM (single-locus model).

Statistical approaches for GWAS

Fast multi-locus random-SNP-effect EMMA

FASTmrEMMA (Appendix A) is a multi-locus two-stage GWAS approach. In the first stage, SNP effect was treated as random and minor part of SNPs were picked up based on the prior premise that most SNPs should have no effect on the quantitative traits. Meanwhile, three techniques were implemented to save running time. First, a new matrix transformation was used to multiply original MLM and its purpose is to whiten the covariance matrix of the polygenic matrix K and environmental noise. Then, a polygenic-to-residual variance ratio under the null hypothesis was fixed in all the single marker genome tests. Finally, the number of nonzero eigenvalues was specified as one. In the second stage, all the selected SNP effects in the first stage were placed into one multi-locus model and then estimated by expectation and maximization empirical Bayes (EMEB) [28] for true QTN identification. The new method has been implemented in R and its software can be downloaded from https://cran.r-project.org/web/packages/mrMLM/index.html.

E-BAYES

E-BAYES is an existing multi-locus Bayesian approach implemented by the SAS program [30], and was used as a gold standard for multi-locus model comparison. In this method, all the SNP-effect variances are simultaneously estimated. Owing to the multi-locus nature, Bonferroni correction is replaced by a less stringent selection criterion. The critical value of P-value in the significance test is set at 0.05 in three simulation experiments.

EMMA

EMMA is an existing single-locus genome scan method for GWAS [3], and a fixed model version of the original MLM, in which QTN effect is treated as a fixed effect with no prior distribution assigned. The method was implemented by the R software package EMMA (http://mouse.cs.ucla.edu/emma/).

CMLM and ECMLM

CMLM [18] and ECMLM [19] are existing single-locus genome scan methods for GWAS. CMLM decreases the effective sample size by clustering individuals into groups and eliminates the need to re-compute variance components. ECMLM chooses the best combination of three kinship algorithms and eight grouping algorithms to increases statistical power. The two methods are also the fixed model version of the original MLM and approximation algorithm for SNP effect estimation.

SUPER

FaST-LMM [21] is a newly developed algorithm in GWAS that can solve the computational problem, but requires that the number of SNPs be less than the number of individuals. To overcome this shortcoming, SUPER [24] extracts a small subset of SNPs and uses them in the FaST-LMM. This SUPER not only retains the computational advantage of the FaST-LMM but also remarkably increases statistical power.

All ECMLM, CMLM and SUPER were implemented in the R software package GAPIT (http://zzlab.net/GAPIT).

The methodological comparison for the above approaches is listed in Table 1.

Table 1.

Comparison of six methods and their softwares for GWAS

Case	FASTmrEMMA	E-BAYES	EMMA	CMLM	ECMLM	SUPER
Model	Multi-locus model	Multi-locus model	Single-locus model	Single-locus model	Single-locus model	Single-locus model
QTN effect	Random	Random	Fixed	Fixed	Fixed	Fixed
Polygenic background control	Yes	No	Yes	Yes	Yes	Yes
Population structure control	Yes	No	Yes	Yes	Yes	Yes
Number of variance components	Three	No. of effects	Two	Two	Two	Two
Polygenic-to-residual variance ratio	Fixed	NA	NA	Fixed	Fixed	NA
Significant critical value	LOD (logarithm of odds)=3	P-value=0.05	P-value=0.05/p, where p is no. of markers	P-value=0.05/p	P-value=0.05/p	P-value=0.05/p
Transformation matrix and performances	${\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{-\frac{1}{2}}{\mathbf{Q}}_1^T$ where $\left({\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{\frac{1}{2}}{\mathbf{Q}}_1^T\right)\left({\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{\frac{1}{2}}{\mathbf{Q}}_1^T\right)={\widehat{\lambda }}_g\mathbf{Z}\mathbf{K}{\mathbf{Z}}^T+{\mathbf{I}}_n$ Covariance matrix of the polygenic matrix K and environmental noise are whitened.Number of nonzero eigenvalues is specified as one.	Shrinkage is selective. Large effects subject to virtually no shrinkage while small effects are shrunken to zero.	$\begin{array}{l}{\mathbf{U}}_R^T\text{ where }\\ \mathbf{SHS}={\mathbf{U}}_R\text{diag}\left({\xi }_1+\delta ,\cdots ,{\xi }_n+\delta \right){\mathbf{U}}_R^T\\ \mathbf{H}=\mathbf{ZK}{\mathbf{Z}}^T+\delta \mathbf{I}\text{ and }\mathbf{S}=\mathbf{I}-\mathbf{X}{\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}^T\end{array}$ One-dimensional optimization by deriving the likelihood as a function of QTN-to-residual variance ratio.	Kinship among individuals is replaced by the kinship among groups.Fit the groups as the random effect, and estimates population parameters only once and then fixes them to test genetic markers.	Kinship among individuals is replaced by the kinship among groups.Chooses the best combination between kinship algorithms and grouping algorithms.	Dramatically reduces the number of markers used to define individual relationships, and uses them in FaST-LMM.
Running time	Fast	Depend on the number of effects.	Slow	Fast	Fast	Moderate
Software Web site	https://cran.r-project.org/web/packages/mrMLM/index.html	http://statgen.ucr.edu/software.html	http://mouse.cs.ucla.edu/emma/	http://zzlab.net/GAPIT	http://zzlab.net/GAPIT	http://zzlab.net/GAPIT

Results

Fast multi-locus random-SNP-effect EMMA

Estimation of the QTN variance

FASTmrEMMA (Appendix A) is a new algorithm that can approximate the estimation of QTN variance. Thus, we need to know whether this approximation has a significant effect on the estimate of QTN variance. To answer this question, four flowering time traits in Arabidopsis [29] (Appendix B) were re-analyzed by FASTmrEMMA and an exact method implemented by PROC MIXED in SAS. The estimates for QTN variance are listed in Figure 1 and Supplementary Table S1. As a result, the relative error between the two methods ranged from 0.0% to 24.09%, and the average was 1.60%, indicating no effect on the QTN variance estimate using FASTmrEMMA under the conditions of this simulation.

Figure 1.

Comparison of the QTN-variance estimates between fast multi-locus random-SNP-effect EMMA (FASTmrEMMA) and one exact algorithm implemented by PROC MIXED in SAS. LD: days to flowering under long days; SDV: days to flowering under short days with vernalization; 8W GH LN: leaf number at flowering with 8 weeks vernalization, greenhouse; and 8W GH FT: days to flowering, 8 weeks vernalization, greenhouse.

To confirm the effectiveness of FASTmrEMMA, three Monte Carlo simulation experiments (Appendix C) were carried out and the simulation procedures were almost same as those in Wang et al. [7]. In the three experiments, various backgrounds (no, polygenes and epistasis) were simulated to conduct sensitivity analysis. Each sample in these simulation experiments was analyzed by six methods. In the six methods, FASTmrEMMA is also a new multi-locus algorithm within the framework of MLM, E-BAYES [30] is an existing multi-locus approach under the framework of Bayesian statistics and SUPER, EMMA, ECMLM and CMLM are the existing single-locus GWAS methods.

Statistical power for QTN detection

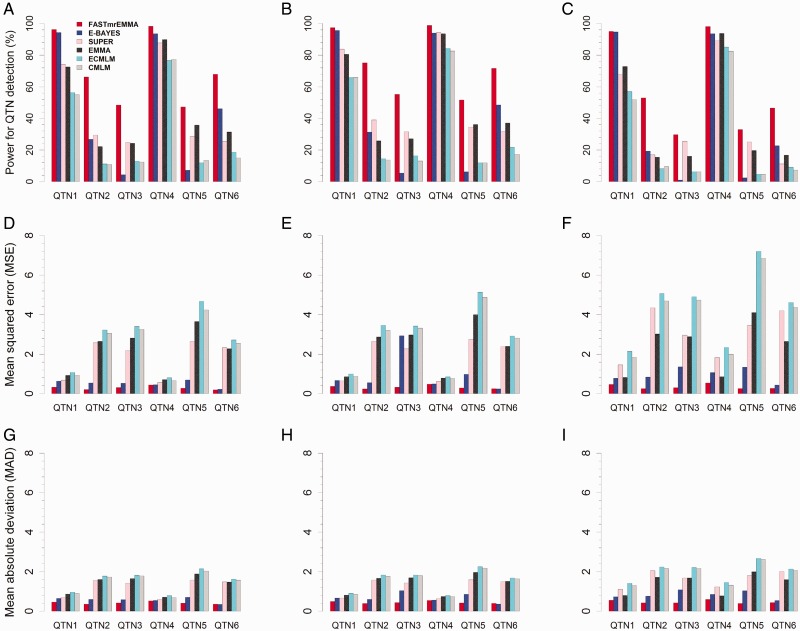
In the above three simulation experiments, the power for each QTN was defined as the proportion of samples where the QTN was detected (the P-value is smaller than the designated threshold). When only six QTNs were simulated in the first experiment, the power in the detection of each QTN was higher for FASTmrEMMA than for the others (Figure 2A;Supplementary Table S2). When a polygenic background ($h_{pg}^2=0.092$) was added to the first experiment, a similar trend was observed (Figure 2B;Supplementary Table S2). When the polygenic background was changed into an epistatic background ($h_{epi}^2=0.15$), the results were also similar to those in the first experiment (Figure 2C;Supplementary Table S2). These results demonstrate the highest power of FASTmrEMMA across all the approaches under various genetic backgrounds, although the other methods are also robust under these backgrounds.

Figure 2.

Comparison of FASTmrEMMA with the single- and multi-locus approaches under various genetic backgrounds. The single-locus model approaches include SUPER, EMMA, ECMLM and CMLM, and the multi-locus approach has E-BAYES. The powers are presented in A–C, MSEs are showed in D–F and MADs are listed in G–I. Six QTNs (A, D and G), six QTNs plus polygenes (B, E and H) and six QTNs plus three epistasis (C, F and I) were simulated, respectively, in the first to third simulation experiments.

Accuracy for estimated QTN effects

We used the average, mean squared error (MSE) and mean absolute deviation (MAD) to measure the accuracy of an estimated QTN effect. We evaluated the accuracies for the estimates of all the six simulated QTNs across all the six methods. As a result, the estimate of each QTN effect from FASTmrEMMA was much closer to the true value than the estimates obtained from the other methods. On these occasions (QTN numbers 1 and 4), the averages from E-BAYES were closer to the true value than those from FASTmrEMMA in three simulation experiments (Supplementary Table S2). The MSE and MAD for each QTN effect were significantly less from FASTmrEMMA than from the others with two exceptions for QTN number 6, E-BAYES method had slightly higher accuracy than FASTmrEMMA method in the first and second simulation experiments (Figure 2D–I; Supplementary Table S2). These results indicate that a higher accuracy for the estimate of QTN effect can be achieved using FASTmrEMMA than using the other methods.

False-positive rate and receiver operating characteristic curve

All the false QTNs, detected by the six methods, in three simulation experiments were used to calculate the empirical false-positive rates of the six methods. These results are listed in Supplementary Table S3. In these three simulation experiments, the empirical false-positive rates of the six methods were between 0.357 and 7.785 ($\times$1E-4), and had the same order of magnitude. ECMLM has the lowest false-positive rate followed by CMLM, FASTmrEMMA and EMMA methods, and SUPER has the maximum false-positive rate followed by E-BAYES method.

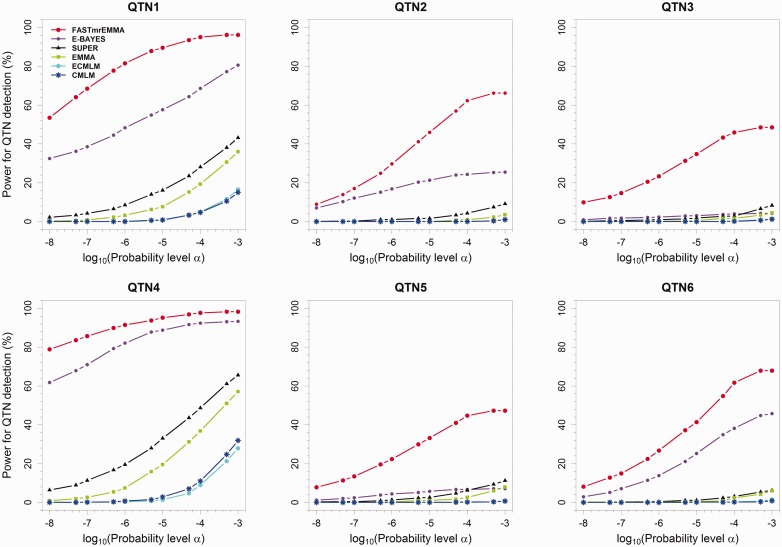
A receiver operating characteristic curve is a plot of the statistical power against the controlled type I error. This curve is frequently used to compare different methods for their efficiencies in the detection of significant effects; the higher the curve, the better is the method. When 11 probability levels for significance, between 1E-8 to 1E-3, were inserted, the corresponding powers were calculated in the first simulation experiment. The results are shown in Figure 3. Among the six approaches, clearly, FASTmrEMMA method is the best one and the next one is E-BAYES.

Figure 3.

Statistical powers for six simulated QTNs in the first simulation experiment plotted against type I error (in a log₁₀ scale) for the six GWAS methods (FASTmrEMMA, E-BAYES, SUPER, EMMA, ECMLM and CMLM).

Computing time

In each of the three simulation experiments, computing times for the six methods were recorded and are listed in Supplementary Table S4. In summary, FASTmrEMMA has the least computing time followed by ECMLM, E-BAYES, CMLM and SUPER methods, and EMMA has the maximum computing time.

Real data analysis in Arabidopsis

To validate FASTmrEMMA, this new method along with E-BAYES, SUPER, EMMA, ECMLM and CMLM was used to re-analyze the Arabidopsis data [29] for days to flowering under long days (LD), days to flowering under short days with vernalization (SDV), leaf number at flowering with 8 weeks vernalization, greenhouse (8W GH LN), and days to flowering, 8 weeks vernalization, greenhouse (8W GH FT) and the results are listed in Supplementary Table S5.

The numbers of SNPs significantly associated with the above four traits were 20, 17, 14 and 17, respectively, for traits LD, SDV, 8W GH LN and 8W GH FT, from FASTmrEMMA method. The corresponding numbers of the associated SNPs were 2, 6, 1 and 5 from E-BAYES; 21, 0, 0 and 0 from SUPER; 1, 5, 0 and 2 from EMMA; and 0, 1, 0 and 0 from both ECMLM and CMLM. Clearly, the number of significantly associated SNPs was much larger from FASTmrEMMA than from the other methods. These significantly associated SNPs for each trait were used to conduct a multiple linear regression analysis, and the corresponding Bayesian information criteria (BIC) were calculated. For example, the BIC value for the model of 8W GH LN was −103.47 for FASTmrEMMA, 77.76 for E-BAYES and 117.50 for the others. FASTmrEMMA method shows the lowest BIC values for all the four traits (Table 2), indicating the best model fit among the six approaches.

Table 2.

Bayesian information criterion values for four flowering time traits in Arabidopsis using six genome-wide association study approaches

Trait	FASTmr EMMA	E-BAYES	SUPER	EMMA	ECMLM	CMLM
LD	39.54	287.00	396.65	299.97	382.07	382.07
SDV	−88.09	43.20	179.54	100.69	169.87	169.87
8W GH LN	−103.47	77.76	117.50	117.50	117.50	117.50
8W GH FT	−321.72	−155.55	−82.41	−101.83	−82.41	−82.41

LD: days to flowering under long days; SDV: days to flowering under short days with vernalization; 8W GH LN: leaf number at flowering with 8 weeks vernalization, greenhouse; 8W GH FT: days to flowering, 8 weeks vernalization, greenhouse.

Based on the SNPs detected by FASTmrEMMA, 6, 11, 5 and 7 genes were previously reported to be associated with the above four traits [31–33]. In the vicinity of the SNPs detected by E-BAYES, the corresponding numbers of the known genes are 2, 1, 0 and 1, respectively, for the above four traits [31]. Only four known genes for LD (SUPER), two known genes for LD (EMMA) and three known genes for SDV (EMMA) are in the neighborhood of the detected SNPs [31, 33] (Table 3). Clearly, FASTmrEMMA method detected more known genes than did the other methods.

Table 3.

GWAS for four flowering time traits in Arabidopsis using six GWAS methods

Trait	Gene	Chr	SNP (bp)	FASTmrEMMA				E-BAYES				SUPER				EMMA				References
				LOD	Effect	MAF	r2 (%)	LOD	Effect	MAF	r2 (%)	P-value	Effect	MAF	r2 (%)	P-value	Effect	MAF	r2 (%)
LD	At1g22770	1	8045438	4.872	−0.112	0.395	0.549													[31]
	At1g23000	1	8128350	9.006	−0.197	0.461	1.767													[31]
	At2g22540	2	9588685	10.338	−0.330	0.281	4.034	10.753	−0.611	0.281	13.817					2.78E-09	−0.815	0.281	24.607	[31]
	At2g22610	2	9588685	10.338	−0.330	0.281	4.034	10.753	−0.611	0.281	13.817					2.78E-09	−0.815	0.281	24.607	[31]
	At3g61970	3	22949227	5.919	0.149	0.413	0.986													[31]
	At5g10140	5	3188328	12.759	−0.272	0.263	2.630													[31]
	At4g00310	4	153459									8.39E-08	−0.363	0.168	3.374					[31]
	At4g00335	4	167142									6.75E-08	−0.538	0.138	6.307					[31]
	At4g00450	4	196614									2.88E-08	−0.227	0.389	2.243					[31]
	At4g01280	4	516758									8.15E-08	−0.504	0.108	4.483					[31]
SDV	At1g05440	1	1595585	4.298	0.117	0.214	1.346													[31]
	At1g05470	1	1595585	4.298	0.117	0.214	1.346													[31]
	At1g77080	1	28965510	10.817	−0.177	0.484	4.576	4.020	−0.170	0.484	4.221									[31]
	At2g41890	2	17488070	4.339	0.099	0.302	1.208													[31]
	At3g20260	3	7084425	3.309	0.068	0.302	0.570													[31]
	At3g49600	3	18385143	4.529	0.118	0.321	1.774													[31]
	At4g05420	4	2748735	4.286	−0.091	0.459	1.203													[31]
	At5g04240	5	1164843	4.479	−0.137	0.220	1.884													[31]
	At5g09805	5	3055565	4.763	−0.105	0.233	1.151													[32]
	At5g57360	5	23249199	5.419	−0.141	0.321	2.533													[31]
	At5g57390	5	23249199	5.419	−0.141	0.321	2.533													[31]
	At5g46880	5	19044037													3.55E-08	0.408	0.107	9.296	[31]
	At5g67100	5	26794176													1.79E-07	−0.292	0.321	10.864	[31]
	At5g67200	5	26794176													1.79E-07	−0.292	0.321	10.864	[33]
8W GH LN	At1g77080	1	28965510	3.857	−0.109	0.497	2.610													[31]
	At2g27380	2	11703876	9.631	−0.153	0.325	4.514													[33]
	At4g32980	4	15918498	4.651	−0.147	0.147	2.384													[31]
	At5g15850	5	5196549	5.923	−0.106	0.319	2.145													[31]
	At5g45890	5	18600041	4.608	−0.107	0.423	2.456													[31]
8W GH FT	At1g03457	1	863771	5.055	0.040	0.460	1.199													[31]
	At2g27380	2	11703876	4.744	−0.043	0.323	1.122													[33]
	At2g47230	2	19396129	4.208	−0.038	0.298	0.911													[31]
	At3g56900	3	21079518	3.081	−0.032	0.311	0.661													[31]
	At3g57000	3	21079518	3.081	−0.032	0.311	0.661													[31]
	At5g06550	5	2002341	3.169	−0.070	0.186	2.241													[31]
	At5g06590	5	2002341	3.169	−0.070	0.186	2.241													[33]
	at5g67100	5	26781546					4.302	0.076	0.317	3.772									[31]

MAF: minor allele frequency. The individuals with missing phenotypes and the SNPs with MAF $\le 10\%$ were excluded. The critical value for significance was $\mathrm{LOD}\ge 3.0$ for FASTmrEMMA and E-BAYES, and approximately 2.8E-07 P-value for SUPER, EMMA, CMLM and ECMLM. The results from CMLM and ECMLM were not listed in this table because no genes were detected. The data set was derived from Atwell et al. (2010).

We also compared all the known genes detected in this study with all the candidate genes in Atwell et al. [29]. For example, among seven known genes (At1g03457, At2g27380, At2g47230, At3g56900, At3g57000, At5g06550 and At5g06590) for 8W GH FT in this study, no genes were within the 133 candidate genes in Atwell et al. [29]. Among 11 known genes for SDV in this study, only three genes (At5g04240, At5g57360 and At5g57390) were within the 153 candidate genes in Atwell et al. [29]. Clearly, FASTmrEMMA method detected new genes.

Discussion

When SNP effects are viewed as random, three variance components will be estimated. Generally, polygenic variance is larger than zero while variance components for most SNPs are zero because these markers are not associated with the trait of interest. In other words, as in most mixed model approaches, variance components in FASTmrEMMA are also estimated under the assumption that one variance component is zero.

FASTmrEMMA is a new algorithm, different from widely used one-dimensional genome scan approaches, such as SUPER, EMMA, ECMLM and CMLM. First, the SNP effects are viewed as being random in FASTmrEMMA while they are viewed as fixed in SUPER, EMMA, ECMLM and CMLM because the random model approach will shrink the estimated SNP effects toward zero when the simulated QTN effects are small, leading to maximum correlations between observed and predicted phenotypic values [25, 34]. Meanwhile, the power of detecting QTNs with random effects is higher than that with fixed effects [35].

Then, a quick single marker genome scan method was proposed to estimate the three variance components in the above mixed model. Here several techniques have been incorporated into the algorithm. The first technique is to fix the polygenic-to-residual variance ratio, which was adopted in CMLM/P3D [18] and EMMAX [20]. Although this algorithm is approximate, it has almost no effect on the estimate of SNP-effect variance, even if there is a large difference in the above ratios between the approximate and exact algorithms (Supplementary Table S1). Clearly, this provides evidence for fixing the ratio in FASTmrEMMA. The second technique is to use a quick matrix calculation algorithm, such as the eigen decomposition of matrix $X_c{X}_c^T$ is the same as that of ${\mathbf{X}}_c^T{\mathbf{X}}_c$ (a positive number). Thus, eigen decomposition, determinant and derivatives in the estimation of ${\lambda }_{\beta }$ can be quickly calculated. The final technique is to estimate residual variance along with the estimation of fixed effects. In the single marker genome scan, therefore, only one parameter ${\lambda }_{\beta }$ needs to be estimated so that running time is obviously decreased. Although GCTA algorithm [36] may be used to estimate the above three variance components, running time is a major concern. A similar situation is also apparent when using PROC MIXED in SAS in Zhang et al. (2005) [1].

Finally, our matrix transformation algorithm in FASTmrEMMA is different from those in SUPER, EMMA, ECMLM, CMLM and multi-locus random-SNP-effect mixed linear model (mrMLM) [7]. For example, when many random effects are included simultaneously in one genetic model and polygenic background also needs to be controlled, at present there are no methods available. However, the new matrix transformation algorithm can transfer polygenic background plus residual error into a normal residual error. This new model can be easily treated by a Bayesian method. The applied study will be reported in the near future.

The multi-variance-component algorithm, E-BAYES [30], was also used to conduct multi-locus GWAS, especially for the situation where the number of markers is several times larger than sample size. However, results from simulation experiments showed that FASTmrEMMA is more powerful in QTN detection and higher accurate in QTN effect estimation than is E-BAYES (Supplementary Table S2). FASTmrEMMA is different from the adaptive mixed LASSO [9]. If the number of markers is many times larger than sample size, the adaptive mixed LASSO does not work. FASTmrEMMA is also different from both the Bayesian sparse linear mixed model [15] and the Bayesian mixture model [16]. The latter two operate under the framework of Bayesian statistics, and the computing time becomes a major concern.

FASTmrEMMA is different from multi-locus mixed-model (MLMM) of Segura et al. [17] in two aspects. First, MLMM is a simple, stepwise mixed-model regression with forward inclusion and backward elimination and FASTmrEMMA is a two-step combined method. In MLMM, the computationally intensive forward-backward inclusion of SNPs is clearly a limiting factor in exploring the huge model space [17]. Second, matrix transformation algorithm in MLMM is different from that in FASTmrEMMA. This difference also exists between FASTmrEMMA and mrMLM of Wang et al. [7].

As described by Wang et al. [7], single-locus genome scan approaches for GWAS require Bonferroni correction for multiple tests. However, this correction is often too conservative to detect important loci for quantitative traits when the number of markers is extremely large. Clearly, FASTmrEMMA is based on a multi-locus model. Owing to the multi-locus nature, Bonferroni correction is replaced by a less stringent selection criterion. Results from analysis of simulated and real data further validated the idea of a less stringent selection criterion in this study.

FASTmrEMMA is a combined method with two steps, each of which needs a critical P-value. In the first step, three critical P-values (0.01, 0.005 and 0.001) were compared to obtain the best one. As a result, the 0.005 critical P-value is the best (Supplementary Table S6). In the second step, a less stringent selection criterion between 0.05 and 0.05/p was adopted, where p is the number of markers. The two critical P-values in FASTmrEMMA have been confirmed by our simulated and real data analysis.

FASTmrEMMA was validated by sensitivity analysis in two aspects. First, various backgrounds (no, ploygenes and epistasis) in the three simulation experiments have validated the new method (Supplementary Table S2). Second, the new method works well for more than 10 QTNs. For example, 14–20 QTNs have been found to be associated with the four traits in Arabidopsis thaliana and then to be closely linked with the 5–11 known genes (Supplementary Table S5).

Conclusion

In FASTmrEMMA algorithm, random-SNP-effect and multi-locus model methods are used to improve the power for QTN detection, and to decrease the false-positive rate, a new matrix transformation in the first step of FASTmrEMMA is constructed to obtain a new genetic model that includes only QTN variation and normal residual error. Additionally, letting the number of nonzero eigenvalues be one and fixing the polygenic-to-residual variance ratio are used to save running time. As a result, FASTmrEMMA has the highest power and accuracy for QTN detection and the best fit for a genetic model, as compared with E-BAYES, SUPER, EMMA, ECMLM and CMLM.

Key Points

• GWAS is to identify a genome-wide set of genetic variants in a population by associating all possible markers with a complex trait.

• Owing to low power and high false-positive rates in a single-marker genome-wide scan, multi-locus GWAS methodologies have been developed, such as FASTmrEMMA.

• We review and assess six GWAS methodologies using both simulated and real data. In the FASTmrEMMA, SNP effects are viewed as being random, the covariance matrix of the polygenic matrix K and environmental noise are whitened and multiple markers potentially associated with a trait are further detected by EMEB.

• FASTmrEMMA is more powerful in QTN detection and model fit, has less bias in QTN effect estimation, and requires a less running time than the other five methods.

Supplementary Data

Supplementary data are available online at http://bib.oxfordjournals.org/.

Funding

National Natural Science Foundation of China (grants 31571268 and 31301229), and Huazhong Agricultural University Scientific & Technological Self-innovation Foundation (Program No. 2014RC020).

Appendix A. Fast multi-locus random-SNP-effect EMMA

Genetic model

We consider the following standard MLM:

$$\mathbf{y}=\mathbf{W}\alpha +\mathbf{X}\beta +\mathbf{Z}\mathbf{u}+\mathit{\epsilon }$$ (A.1)

where $\mathbf{y}$ is an $n\times 1$ phenotypic vector of quantitative trait, and $n$ is the number of individuals; $\mathbf{W}=$$(w_1,w_2,\dots ,w_c)$ is an $n\times c$ matrix of covariates (fixed effects) including a column vector of 1, population structure [2] or principle component [37] may be incorporated into $\mathbf{W}$ and $\mathbf{\alpha }$ is a $c\times 1$ vector of fixed effects including the intercept; X is an $n\times 1$ vector of marker genotypes, and $\beta \sim N(0,{\sigma }_{\beta }^2)$ is random effect of putative QTN; $\mathbf{Z}$ is an $n\times m$ design matrix, $\mathbf{u}\sim {\text{MVN}}_m(\mathbf{0},{\sigma }_g^2\mathbf{K})$ is an $m\times 1$ vector of polygenic effects; $\mathbf{K}$ is a known $m\times m$ relatedness matrix; and $\mathit{\epsilon }\sim MV{N}_n(\mathbf{0},{\sigma }_e^2{\mathbf{I}}_n)$ is an $n\times 1$ vector of residual errors, ${\sigma }_e^2$ is the variance of residual error, ${\mathbf{I}}_n$ is an $n\times n$ identity matrix and MVN denotes multivariate normal distribution. In animal data sets, m is the number of strains, n is the number of animals and Z indicates which strain each animal belongs to (z_ij = 1 if individual i comes from strain j and z_ij = 0 otherwise); in the Arabidopsis thaliana data set of Atwell et al. [29], $m=n$ and $\mathbf{Z}={\mathbf{I}}_n$.

In the current methods, including EMMA [3], CMLM/P3D [18], ECMLM [19], EMMAX [20], FaST-LMM [21], FaST-LMM-Select [22], SUPER [24], GEMMA [4] and GRAMMA-Gamma [23], $\beta$ is treated as a fixed effect, from which it is relatively easy to estimate ${\sigma }_g^2$ and ${\sigma }_e^2$. In this study, we treat $\beta$ as random to make the model more realistic [25, 34, 35]. In this case, three variance components need to be estimated under the assumption that QTN variance is zero, because most SNPs are not associated with the trait of interest. So the variance of $\mathbf{y}$ in the model (A.1) is

$$\begin{array}{c}Var(\mathbf{y})={\sigma }_{\beta }^2\mathbf{X}{\mathbf{X}}^T+{\sigma }_g^2\mathbf{Z}\mathbf{K}{\mathbf{Z}}^T+{\sigma }_e^2{\mathbf{I}}_n\\ ={\sigma }_e^2({\lambda }_{\beta }\mathbf{X}{\mathbf{X}}^T+{\lambda }_g\mathbf{Z}\mathbf{K}{\mathbf{Z}}^T+{\mathbf{I}}_n)\\ ={\sigma }_e^2\mathbf{H}\end{array}$$ (A.2)

where ${\lambda }_{\beta }={\sigma }_{\beta }^2/{\sigma }_e^2$ and ${\lambda }_g={\sigma }_g^2/{\sigma }_e^2$.

Fast multi-locus random-SNP-effect EMMA (FASTmrEMMA)

The key to solve the model (A.1) is to estimate ${\sigma }_{\beta }^2$, ${\sigma }_g^2$ and ${\sigma }_e^2$. Although many algorithms or estimations are available, such as analysis of variance, maximum likelihood (ML), restricted maximum likelihood (REML), minimum norm quadratic unbiased, spectral decomposition [38] and average information [39], they are not feasible for a high number of SNPs. Hence, we proposed a fast and efficient approximation algorithm in this study.

In the first step, we considered the reduced form of the model (A.1), which deleted $\mathbf{X}\beta$,

$$\mathbf{y}=\mathbf{W}\alpha +\mathbf{Z}\mathbf{u}+\mathit{\epsilon }$$ (A.3)

The variance of $\mathbf{y}$ is:

$$\begin{array}{c}Var(\mathbf{y})={\sigma }_g^2\mathbf{Z}\mathbf{K}{\mathbf{Z}}^T+{\sigma }_e^2{\mathbf{I}}_n\\ ={\sigma }_e^2({\lambda }_g\mathbf{Z}\mathbf{K}{\mathbf{Z}}^T+{\mathbf{I}}_n)\end{array}$$ (A.4)

Using EMMA algorithm of Kang et al. [3], the estimate of ${\lambda }_g$, denoted by ${\widehat{\lambda }}_g$, can be easily obtained.

In the second step, we considered the model (A.1), and replaced ${\lambda }_g$ in (A.2) by the ${\widehat{\lambda }}_g$, so

$$\begin{array}{c}Var(\mathbf{y})={\sigma }_e^2({\lambda }_{\beta }\mathbf{X}{\mathbf{X}}^T+{\widehat{\lambda }}_g\mathbf{Z}\mathbf{K}{\mathbf{Z}}^T+{\mathbf{I}}_n)\\ ={\sigma }_e^2({\lambda }_{\beta }\mathbf{X}{\mathbf{X}}^T+\mathbf{B})\end{array}$$ (A.5)

where $\mathbf{B}={\widehat{\lambda }}_g\mathbf{Z}\mathbf{K}{\mathbf{Z}}^T+{\mathbf{I}}_n$. An eigen (or spectral) decomposition of the positive semi-definite matrix $\mathbf{B}$ was

$$\begin{array}{l}\mathbf{B}={\mathbf{Q}}_B{\mathbf{\Lambda }}_B{\mathbf{Q}}_B^T\\ =\left(\begin{array}{cc}{\mathbf{Q}}_1& {\mathbf{Q}}_2\end{array}\right)\left(\begin{array}{cc}{\mathbf{\Lambda }}_r& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}{\mathbf{Q}}_1^T\\ {\mathbf{Q}}_2^T\end{array}\right)\\ =\left(\begin{array}{cc}{\mathbf{Q}}_1& {\mathbf{Q}}_2\end{array}\right)\left(\begin{array}{cc}{\mathbf{\Lambda }}_r^{\frac{1}{2}}& 0\\ 0& 0\end{array}\right)\left(\begin{array}{cc}{\mathbf{\Lambda }}_r^{\frac{1}{2}}& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}{\mathbf{Q}}_1^T\\ {\mathbf{Q}}_2^T\end{array}\right)\\ =\left(\begin{array}{cc}{\mathbf{Q}}_1& {\mathbf{Q}}_2\end{array}\right)\left(\begin{array}{cc}{\mathbf{\Lambda }}_r^{\frac{1}{2}}& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}{\mathbf{Q}}_1^T\\ {\mathbf{Q}}_2^T\end{array}\right)\left(\begin{array}{cc}{\mathbf{Q}}_1& {\mathbf{Q}}_2\end{array}\right)\left(\begin{array}{cc}{\mathbf{\Lambda }}_r^{\frac{1}{2}}& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}{\mathbf{Q}}_1^T\\ {\mathbf{Q}}_2^T\end{array}\right)\\ =\left({\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{\frac{1}{2}}{\mathbf{Q}}_1^T\right)\left({\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{\frac{1}{2}}{\mathbf{Q}}_1^T\right)\end{array}$$ (A.6)

where ${\mathbf{Q}}_B$ is orthogonal, ${\mathbf{\Lambda }}_r$ is a diagonal matrix with positive eigenvalues, $r=Rank(\mathbf{B})$, ${\mathbf{Q}}_1$ and ${\mathbf{Q}}_2$ are the $n\times r$ and $n\times (n-r)$ block matrices of ${\mathbf{Q}}_B$, $0$ is the corresponding block zero matrix.

Let $\mathbf{C}={\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{-\frac{1}{2}}{\mathbf{Q}}_1^T$, the model (A.1) was changed into

$${\mathbf{y}}_c={\mathbf{W}}_c\mathbf{\alpha }+{\mathbf{X}}_c\beta +{\mathit{\epsilon }}_c$$ (A.7)

where ${\mathbf{y}}_c=\mathbf{C}\mathbf{y}$, ${\mathbf{W}}_c=\mathbf{C}\mathbf{W}$, ${\mathbf{X}}_c=\mathbf{C}\mathbf{X}$ and ${\mathit{\epsilon }}_c=\mathbf{C}\mathbf{Z}\mathbf{u}+\mathit{C}\mathit{\epsilon }$. Clearly, the model (A.7) is a new MLM, and ${\mathit{\epsilon }}_c\sim {\text{MVN}}_n(\mathbf{0},{\sigma }_e^2{\mathbf{I}}_n)$.

$$\because \mathit{Var}({\mathbf{y}}_c)=\mathit{Var}(\mathbf{C}\mathbf{y})={\sigma }_e^2\mathbf{C}({\lambda }_{\beta }\mathbf{X}{\mathbf{X}}^T+{\lambda }_g\mathbf{Z}\mathbf{K}{\mathbf{Z}}^T+{\mathbf{I}}_n){\mathbf{C}}^T$$

Let ${\lambda }_g={\widehat{\lambda }}_g$, using equation (A.6) and ${\mathbf{Q}}_1^T{\mathbf{Q}}_1={\mathbf{I}}_r$, yields

$$\begin{array}{l}Var(\mathbf{C}\mathbf{y})={\sigma }_e^2\mathbf{C}({\lambda }_{\beta }\mathbf{X}{\mathbf{X}}^T+{\widehat{\lambda }}_g\mathbf{Z}\mathbf{K}{\mathbf{Z}}^T+{\mathbf{I}}_n){\mathbf{C}}^T\\ ={\sigma }_e^2({\lambda }_{\beta }\mathbf{C}\mathbf{X}{\mathbf{X}}^T{\mathbf{C}}^T+\mathbf{C}\mathbf{B}{\mathbf{C}}^T)\\ ={\sigma }_e^2\left({\lambda }_{\beta }{\mathbf{X}}_c{\mathbf{X}}_c^T+{\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{\begin{array}{c}-\end{array}\frac{1}{2}}{\mathbf{Q}}_1^T\left({\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{\frac{1}{2}}{\mathbf{Q}}_1^T\right)\left({\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{\frac{1}{2}}{\mathbf{Q}}_1^T\right){\left({\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{\begin{array}{c}-\end{array}\frac{1}{2}}{\mathbf{Q}}_1^T\right)}^T\right)\\ ={\sigma }_e^2({\lambda }_{\beta }{\mathbf{X}}_c{\mathbf{X}}_c^T+{\mathbf{I}}_n)\\ ={\sigma }_e^2{\mathbf{H}}_c={\mathbf{V}}_c\end{array}$$ (A.8)

Once the ratio of ${\sigma }_g^2$ and ${\sigma }_e^2$, ${\lambda }_g={\sigma }_g^2/{\sigma }_e^2$, was fixed at ${\widehat{\lambda }}_g$, it is possible to scan each marker on the genome. The evidence for the effectiveness of this approximation is shown in the results section.

Log-likelihood and restricted log-likelihood functions. According to the descriptions for the single-locus genome scan algorithm in previous GWAS studies [3, 4, 40, 41], log-likelihood and restricted log-likelihood functions for the model (A.7) are

$$l_F({\lambda }_{\beta },{\sigma }_e^2,\mathbf{\alpha })=-\frac{n}{2}\text{log}\hspace{0.17em}(2\pi )-\frac{n}{2}\text{log}\hspace{0.17em}({\sigma }_e^2)-\frac{1}{2}\text{log}\hspace{0.17em}\left|{\mathbf{H}}_c\right|-\frac{1}{2{\sigma }_e^2}{\left({\mathbf{y}}_c-{\mathbf{W}}_c\mathbf{\alpha }\right)}^T{\mathbf{H}}_c^{-1}\left({\mathbf{y}}_c-{\mathbf{W}}_c\mathbf{\alpha }\right)$$ (A.9)

and

$$\begin{array}{c}{l}_R({\lambda }_{\beta },{\sigma }_e^2,\mathbf{\alpha })=-\frac{v}{2}\text{log}\hspace{0.17em}(2\pi )-\frac{v}{2}\text{log}\hspace{0.17em}({\sigma }_e^2)+\frac{1}{2}\text{log}\hspace{0.17em}\left|{\mathbf{W}}_c{\mathbf{W}}_c^T\right|\\ -\frac{1}{2}\text{log}\hspace{0.17em}\left|{\mathbf{H}}_c\right|-\frac{1}{2}\text{log}\hspace{0.17em}\left|{\mathbf{W}}_c^T{\mathbf{H}}_c^{-1}{\mathbf{W}}_c\right|-\frac{1}{2{\sigma }_e^2}{\left({\mathbf{y}}_c-{\mathbf{W}}_c\mathbf{\alpha }\right)}^T{\mathbf{H}}_c^{-1}\left({\mathbf{y}}_c-{\mathbf{W}}_c\mathbf{\alpha }\right)\end{array}$$ (A.10)

respectively, where ${\mathbf{H}}_c={\lambda }_{\beta }{\mathbf{X}}_c{\mathbf{X}}_c^T+{\mathbf{I}}_n$, $v=n-a$, $a=rank({\mathbf{W}}_c)\le \min (c,r)$, $c=rank(\mathbf{W})$, $r=rank(\mathbf{C})=rank(\mathbf{B})$, supposing $\mathbf{W}$ is column full rank.

Once $\mathbf{\alpha }$ and ${\sigma }_e^2$ are fixed, the ML and REML estimates for ${\lambda }_{\beta }$ is equivalent to maximizing the following target functions

$$l_F({\lambda }_{\beta }|\mathbf{\alpha },{\sigma }_e^2)\propto -\frac{n}{2}\text{log}\hspace{0.17em}(\frac{2\pi }{n})-\frac{n}{2}-\frac{1}{2}\text{log}\hspace{0.17em}\left|{\mathbf{H}}_c\right|-\frac{n}{2}\text{log}\hspace{0.17em}\left({\mathbf{y}}_c^T{\mathbf{P}}_c{\mathbf{y}}_c\right)$$ (A.11)

$$l_R({\lambda }_{\beta }|\mathbf{\alpha },{\sigma }_e^2)\propto -\frac{v}{2}\text{log}\hspace{0.17em}(\frac{2\pi }{v})-\frac{v}{2}+\frac{1}{2}\text{log}\hspace{0.17em}\left|{\mathbf{W}}_c^T{\mathbf{W}}_c\right|-\frac{1}{2}\text{log}\hspace{0.17em}\left|{\mathbf{H}}_c\right|-\frac{1}{2}\text{log}\hspace{0.17em}\left|{\mathbf{W}}_c^T{\mathbf{H}}_c^{-1}{\mathbf{W}}_c\right|-\frac{v}{2}\text{log}\hspace{0.17em}\left({\mathbf{y}}_c^T{\mathbf{P}}_c{\mathbf{y}}_c\right)$$ (A.12)

where ${\mathbf{P}}_c={\mathbf{H}}_c^{-1}-{\mathbf{H}}_c^{-1}{\mathbf{W}}_c{({\mathbf{W}}_c^T{\mathbf{H}}_c^{-1}{\mathbf{W}}_c)}^{-}{\mathbf{W}}_c^T{\mathbf{H}}_c^{-1}$, and $-$ denotes generalized inverse.

Because it is slow to calculate determinant and inversion in the equations (A.11) and (A.12), a fast computation algorithm should be considered. As described in GEMMA, Zhou and Stephens [4] first obtained the first and second derivatives for ${\lambda }_{\beta }$, and then conducted eigen (or spectral) decomposition. In EMMA, however, Kang et al. [3] first conducted eigen decomposition, and then calculated the derivatives. These two ways are essentially the same. For simplicity, we adopted EMMA method.

It is possible to find ${\xi }_i$ and ${\delta }_s$, such that

$${\mathbf{H}}_c={\lambda }_{\beta }{\mathbf{X}}_c{\mathbf{X}}_c^T+{\mathbf{I}}_n={\mathbf{U}}_{F}diag({\lambda }_{\beta }{\xi }_1+1,\dots ,{\lambda }_{\beta }{\xi }_n+1){\mathbf{U}}_F^T={\mathbf{U}}_{F}diag({\lambda }_{\beta }{\xi }_1+1,1,\dots ,1){\mathbf{U}}_F^T$$ (A.13)

$$\begin{array}{l}{\mathbf{M}}_c{\mathbf{H}}_c{\mathbf{M}}_c={\mathbf{M}}_c({\lambda }_{\beta }{\mathbf{X}}_c{\mathbf{X}}_c^T+{\mathbf{I}}_n){\mathbf{M}}_c\\ =({\mathbf{U}}_R{\mathbf{W}}_R)diag({\lambda }_{\beta }{\delta }_1+1,\dots ,{\lambda }_{\beta }{\delta }_v+1,0,\dots ,0){({\mathbf{U}}_R{\mathbf{W}}_R)}^T\\ ={\mathbf{U}}_{R}diag({\lambda }_{\beta }{\delta }_1+1,1,\dots ,1){\mathbf{U}}_R^T\end{array}$$ (A.14)

where ${\mathbf{M}}_c={\mathbf{I}}_n-{\mathbf{W}}_c{({\mathbf{W}}_c^T{\mathbf{W}}_c)}^{-}{\mathbf{W}}_c^T$,${\mathbf{U}}_F$is an $n\times n$ orthogonal matrix, ${\mathbf{U}}_R$is an $n\times v$ eigenvector matrix corresponding to the nonzero eigenvalues and ${\mathbf{W}}_R$ is an $n\times (n-v)$ eigenvector matrix corresponding to zero eigenvalues.

Note that ${\xi }_i=0\begin{array}{cc}& (i=2,\dots ,n)\end{array}$ and ${\delta }_s=0\begin{array}{cc}& (s=2,\dots ,v)\end{array}$. This is because the nonzero eigenvalues of ${\mathbf{X}}_c{\mathbf{X}}_c^T$ are the same as those of ${\mathbf{X}}_c^T{\mathbf{X}}_c$, which is a positive number. For technical detail the reader is referred to SD1 and SD2 in Supplementary Data.

It should be noted that ${\mathbf{U}}_F$ and ${\mathbf{U}}_R$ are independent of ${\lambda }_{\beta }$. Let ${\mathbf{U}}_R^T{\mathbf{y}}_c={({\eta }_1,\dots ,{\eta }_v)}^T$, then finding the ML and REML estimates for ${\lambda }_{\beta }$ is equivalent to optimizing the following functions with respect to ${\lambda }_{\beta }$(SD3 in Supplementary Data):

$$l_F({\lambda }_{\beta }|\mathbf{\alpha },{\sigma }_e^2)=-\frac{n}{2}\text{log}\hspace{0.17em}(\frac{2\pi }{n})-\frac{n}{2}-\frac{1}{2}\text{log}\hspace{0.17em}\left({\lambda }_{\beta }{\xi }_1+1\right)-\frac{n}{2}\text{log}\hspace{0.17em}\left(\frac{{\eta }_1^2}{{\lambda }_{\beta }{\delta }_1+1}+\sum _{s=2}^v{\eta }_s^2\right)$$ (A.15)

$$l_R({\lambda }_{\beta }|\mathbf{\alpha },{\sigma }_e^2)=-\frac{v}{2}\text{log}\hspace{0.17em}(\frac{2\pi }{v})-\frac{v}{2}-\frac{1}{2}\text{log}\hspace{0.17em}\left({\lambda }_{\beta }{\delta }_1+1\right)-\frac{v}{2}\text{log}\hspace{0.17em}\left(\frac{{\eta }_1^2}{{\lambda }_{\beta }{\delta }_1+1}+\sum _{s=2}^v{\eta }_s^2\right)$$ (A.16)

Estimation of parameter ${\lambda }_{\beta }$. At present three algorithms, Newton–Raphson (NR), Fisher scoring and expectation-maximization, are frequently used to obtain the ML and REML estimates [42]. In this study, we adopted the NR algorithm, which has the form

$${\lambda }_{\beta ,F}^{(t+1)}={\lambda }_{\beta ,F}^{(t)}-\frac{l_F^{\prime }({\lambda }_{\beta ,F}^{(t)}|\mathbf{\alpha },{\sigma }_e^2)}{l_F^{″}({\lambda }_{\beta ,F}^{(t)}|\mathbf{\alpha },{\sigma }_e^2)},\begin{array}{cc}& \end{array}{\lambda }_{\beta ,R}^{(t+1)}={\lambda }_{\beta ,R}^{(t)}-\frac{l_R^{\prime }({\lambda }_{\beta ,R}^{(t)}|\mathbf{\alpha },{\sigma }_e^2)}{l_R^{″}({\lambda }_{\beta ,R}^{(t)}|\mathbf{\alpha },{\sigma }_e^2)}\begin{array}{cc}& \end{array}(t=0,1,\dots ,)$$ (A.17)

where ${\lambda }_{\beta ,F}^{(t)}$ and ${\lambda }_{\beta ,R}^{(t)}$ are the ML and REML estimates at the tth iteration, respectively; and ${\lambda }_{\beta ,F}^{(t+1)}$ and ${\lambda }_{\beta ,R}^{(t+1)}$ are the update estimates, respectively, and the first derivatives of these two functions on ${\lambda }_{\beta }$ were

$$l_F^{\prime }({\lambda }_{\beta }|\mathbf{\alpha },{\sigma }_e^2)=-\frac{{\xi }_1}{2({\lambda }_{\beta }{\xi }_1+1)}+\frac{n}{2}\times \frac{{\delta }_1{\eta }_1^2/{({\lambda }_{\beta }{\delta }_1+1)}^2}{{\eta }_1^2/({\lambda }_{\beta }{\delta }_1+1)+\sum _{s=2}^v{\eta }_s^2}$$ (A.18)

$$l_R^{\prime }({\lambda }_{\beta }\text{|}\alpha ,{\sigma }_e^2)=-\frac{{\delta }_1}{2\left({\lambda }_{\beta }{\delta }_1+1\right)}+\frac{v}{2}\times \frac{{\delta }_1{\eta }_1^2/{({\lambda }_{\beta }{\delta }_1+1)}^2}{{\eta }_1^2/({\lambda }_{\beta }{\delta }_1+1)+{\displaystyle \sum _{s=2}^v{\eta }_s^2}}$$ (A.19)

and the second derivatives on ${\lambda }_{\beta }$ were

$$l_F^{″}({\lambda }_{\beta }|\mathbf{\alpha },{\sigma }_e^2)=\frac{{\xi }_1^2}{2{({\lambda }_{\beta }{\xi }_1+1)}^2}-\frac{n}{2}\times \frac{{\delta }_1^2{\eta }_1^2\left[{\eta }_1^2+2\left(\sum _{s=2}^v{\eta }_s^2\right)\left({\lambda }_{\beta }{\delta }_1+1\right)\right]}{{\left[{\eta }_1^2\left({\lambda }_{\beta }{\delta }_1+1\right)+\left(\sum _{s=2}^v{\eta }_s^2\right){\left({\lambda }_{\beta }{\delta }_1+1\right)}^2\right]}^2}$$ (A.20)

$$l_R^{″}({\lambda }_{\beta }|\mathbf{\alpha },{\sigma }_e^2)=\frac{{\delta }_1^2}{2{({\lambda }_{\beta }{\delta }_1+1)}^2}-\frac{v}{2}\times \frac{{\delta }_1^2{\eta }_1^2\left[{\eta }_1^2+2\left(\sum _{s=2}^v{\eta }_s^2\right)\left({\lambda }_{\beta }{\delta }_1+1\right)\right]}{{\left[{\eta }_1^2\left({\lambda }_{\beta }{\delta }_1+1\right)+\left(\sum _{s=2}^v{\eta }_s^2\right){\left({\lambda }_{\beta }{\delta }_1+1\right)}^2\right]}^2}$$ (A.21)

Using the idea of EMMA [3], the range of ${\lambda }_{\beta }$ is between 1E-05 (corresponding to almost pure environmental effect) and 1E + 05 (corresponding to almost pure single-gene effect), and we divided this range evenly into 100 regions in logarithm scale to compute (A.18) or (A.19). The global ML or REML is searched for by applying the NR algorithm to all the intervals where the signs of derivatives change. This optimization technique for estimating ${\lambda }_g$ has guaranteed the convergence as long as the kinship matrix $\mathbf{K}$ is positive semi-definite. Note that ${\mathbf{X}}_c{\mathbf{X}}_c^T$ is always positive semi-definite.

Estimation of fixed effects $\mathbf{\alpha }$ and residual variance ${\sigma }_e^2$ . Once ${\lambda }_{\beta }$ is known, it is easy to estimate $\mathbf{\alpha }$ and ${\sigma }_e^2$. The ML estimates for $\mathbf{\alpha }$ and ${\sigma }_e^2$ were

$$\begin{array}{c}{\widehat{\mathbf{\alpha }}}_F={\left({\mathbf{W}}_c^T{\widehat{\mathbf{H}}}_{c,F}^{-1}{\mathbf{W}}_c\right)}^{-}{\mathbf{W}}_c^T{\widehat{\mathbf{H}}}_{c,F}^{-1}{\mathbf{y}}_c\\ {\widehat{\sigma }}_{e,F}^2=\frac{1}{n}\left(\frac{{\eta }_1^2}{{\widehat{\lambda }}_{\beta ,F}{\delta }_1+1}+\sum _{s=2}^v{\eta }_s^2\right)\end{array}$$ (A.22)

respectively, where ${\widehat{H}}_{c,F}{}^{-1}=U_{F}diag\left(\frac{1}{{\widehat{\lambda }}_{\beta ,F}{\xi }_1+1},1,\cdots ,1\right)U_F^T$. The REML estimates for $\mathbf{\alpha }$ and ${\sigma }_e^2$ were

$$\begin{array}{c}{\widehat{\mathbf{\alpha }}}_R={\left({\mathbf{W}}_c^T{\widehat{\mathbf{H}}}_{c,R}^{-1}{\mathbf{W}}_c\right)}^{-}{\mathbf{W}}_c^T{\widehat{\mathbf{H}}}_{c,R}^{-1}{\mathbf{y}}_c\\ {\widehat{\sigma }}_{e,R}^2=\frac{1}{v}\left(\frac{{\eta }_1^2}{{\widehat{\lambda }}_{\beta ,R}{\delta }_1+1}+\sum _{s=2}^v{\eta }_s^2\right)\end{array}$$ (A.23)

respectively, where v=n-a and ${\widehat{H}}_{c,R}{}^{-1}=U_{F}diag\left(\frac{1}{{\widehat{\lambda }}_{\beta ,R}{\xi }_1+1},1,\cdots ,1\right)U_F^T$.

Best linear unbiased prediction for parameter $\beta$ . Using $Cov{({\mathbf{y}}_c \beta )}^T$, the best linear unbiased prediction for the $\beta$, $\widehat{\beta }=E(\beta |{\mathbf{y}}_c)$, can be obtained. Based on the above fast and efficient algorithm, the ML or REML estimate is

$$\widehat{\beta }={\widehat{\lambda }}_{\beta }{\mathbf{X}}_c^T{\mathbf{U}}_R{\left(\frac{{\eta }_1}{{\widehat{\lambda }}_{\beta }{\delta }_1+1},{\eta }_2,\dots ,{\eta }_v\right)}^T$$ (A.24)

(SD4 in Supplementary Data), where $\widehat{\beta }$ denotes ${\widehat{\beta }}_F$ or ${\widehat{\beta }}_R$ while ${\widehat{\lambda }}_{\beta }$ is ${\widehat{\lambda }}_{\beta ,F}$ or ${\widehat{\lambda }}_{\beta ,R}$, respectively.

Likelihood ratio test. Although the parameter on QTN in the model (A.1) is $\beta \sim N(0,{\sigma }_{\beta }^2)$, the estimation of ${\lambda }_{\beta }$ is our concern in the above algorithm. Therefore, the null hypothesis might be ${\lambda }_{\beta }=0$[34]. The Likelihood ratio test (LRT) statistic for the ML or REML estimate is

$$D=2(l({\widehat{\lambda }}_{\beta })-l(0))$$ (A.25)

where $l({\widehat{\lambda }}_{\beta })$ is $l_F({\widehat{\lambda }}_{\beta ,F})$ or $l_R({\widehat{\lambda }}_{\beta ,R})$, and $l(0)$ is $l_F(0)=-\frac{n}{2}\text{log}\hspace{0.17em}\left(\frac{2\pi }{n}\right)-\frac{n}{2}-\frac{n}{2}\text{log}\hspace{0.17em}\left(\sum _{s=1}^v{\eta }_s^2\right)$ or $l_R(0)=-\frac{v}{2}\text{log}\hspace{0.17em}\left(\frac{2\pi }{v}\right)-\frac{v}{2}-\frac{v}{2}\text{log}\hspace{0.17em}\left(\sum _{s=1}^v{\eta }_s^2\right)$ while ${\widehat{\lambda }}_{\beta }$ is ${\widehat{\lambda }}_{\beta ,F}$ or ${\widehat{\lambda }}_{\beta ,R}$, respectively.

Under the null hypothesis, the LRT statistic $D$ follows approximately a mixture of two ${\chi }^2$ distributions with an equal weight, denoted by $\frac{1}{2}{\chi }_0^2+\frac{1}{2}{\chi }_1^2$, where ${\chi }_0^2$ is just a fixed number of zero and ${\chi }_1^2$ is a ${\chi }^2$ distribution with one degree of freedom [34], and the P-values can be calculated accordingly. Let P be the P-value for each QTN, it was calculated using

$$\mathrm{P}=\{\begin{array}{c}1\begin{array}{cccc}& & & \begin{array}{ccc}& & D=0\end{array}\end{array}\\ \frac{1}{2}\mathrm{Pr}\left({\chi }_1^2>D\right)\begin{array}{cc}& D>0\end{array}\end{array}$$ (A.26)

Kinship matrix. Many methods for calculating kinship matrix ${\mathbf{K}}_{m\times m}$ from a large number of markers have been proposed, such as identical-by-state approach [2, 3, 7, 26, 43]. Here we adopted the method of Kang et al. [3]. Let S be a $p\times m$ genotypic matrix with elements $s_{oi}\in \{0,0.5,1\}$, the element of kinship matrix $\mathbf{K}$ is defined by

$$k_{ij}=\{\begin{array}{c}1\begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}& \end{array}& & \end{array}& & \end{array}\begin{array}{cc}& \end{array}i=j\\ \frac{1}{p}\sum _{o=1}^p\left(s_{oi}\times s_{oj}+(1-s_{oi})\times (1-s_{oj})\right)\begin{array}{cc}& j<i\end{array},i=2,\dots ,m\\ k_{ji}\begin{array}{ccc}\begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& \end{array}& & \end{array}\begin{array}{cc}& j>i\end{array}\end{array}$$ (A.27)

Time complexity for the first step of FASTmrEMMA. For the single-locus genome scan, FASTmrEMMA is involved in only one eigen decomposition at the beginning, and computational complexity is $O(m{n}^2)$, where $O$ is the big $O$ notation. For each SNP tested, FASTmrEMMA effectively replaces the expensive additional eigen decomposition step in EMMA, and the computational complexity changes from $O(m{n}^2)$ to $O(n^2)$, because the nonzero eigenvalues of ${\mathbf{X}}_c{\mathbf{X}}_c^T$ are the same as those of $X_c^T{X}_c$. After this, as in EMMA, each iteration of the optimization step requires inexpensive operations (computational complexity of $O(n)$) to evaluate both the first and second derivatives of target functions. Therefore, the overall time complexity for the first step of FASTmrEMMA is $O(m{n}^2+p{n}^2+ptn)$, compared with $O(m{n}^2+pm{n}^2+ptn)$ for EMMA [4], where $t$ is the number of optimization iterations required for the NR method (quadratic rate of convergence).

In the GWAS, the number of SNPs is often 1000 times larger than the sample size, and most SNPs are not associated with the trait of interest. In this case, fitting all the genome markers in one model is not feasible. Once we delete these SNPs with zero effects, the reduced model is estimable. The described above can be considered as an initial screening step for FASTmrEMMA. In the first step of FASTmrEMMA, a less stringent criterion for the initial stage screening was adopted, for example, all the SNPs with the ≤0.005 P-values were selected to enter the next step for further evaluation. The majority of markers will be eliminated in the first step. Therefore, the number of markers left in the second stage analysis is often a small subset of all markers, say a few hundred or a few thousand at most, for example, no more than 600 significantly associated SNPs for the four traits in the A. thaliana data sets [29].

In the multi-locus model, we proposed to use the EMEB [28] because EMEB method is a random model approach in which each random marker effect is assigned an empirical distribution with a variance, and therefore is in accordance with treating a marker as a random effect in this study. The linear model is as followed:

$$\mathbf{y}=W\alpha +\sum _{i=1}^q{\mathbf{X}}_i{\beta }_i+\mathit{\epsilon }$$ (A.28)

where $\mathbf{y}$, $\mathbf{W}$, $\mathbf{\alpha }$ and $\mathit{\epsilon }$ are the same as model (A.1); $q$ is the number of the selected QTN in the first step of FASTmrEMMA; ${\mathbf{X}}_i$ and ${\beta }_i$ are an $n\times 1$ vector of marker genotypes and effect for the $i$th QTN, respectively. In the above model, polygenic background is not included because all the potential QTN have been included in the model (A.28).

In the model (A.28), we adopt the normal prior for ${\beta }_i$, $\mathrm{P}({\beta }_i|{\sigma }_i^2)=N(0,{\sigma }_i^2)$ and the scaled inverse ${\chi }^2$ prior for ${\sigma }_i^2$, $\mathrm{P}({\sigma }_i^2|\tau ,\omega )\propto {\left({\sigma }_i^2\right)}^{-\frac{1}{2}\left(\tau +2\right)}\hspace{0.17em}\text{exp}\hspace{0.17em}\left(-\frac{\omega }{2{\sigma }_i^2}\right)$, where we set $(\tau ,\omega )=(0,0)$, which represents the Jeffreys’ prior, $\mathrm{P}({\sigma }_i^2|\tau ,\omega )=1/{\sigma }_i^2$ [44]. The procedure for parameter estimation in EMEB [28] is as follows.

1) Initial-step: To initialize parameters with

$$\begin{array}{l}\mathbf{\alpha }={\left({\mathbf{W}}^T\mathbf{W}\right)}^{-}{\mathbf{W}}^T\mathbf{y}\\ {\sigma }_e^2=\frac{1}{n}{\left(\mathbf{y}-\mathbf{W}\alpha \right)}^T\left(\mathbf{y}-\mathbf{W}\alpha \right)\\ {\sigma }_i^2={\left[{\left({\mathbf{X}}_i^T{\mathbf{X}}_i\right)}^{-1}{\mathbf{X}}_i^T\left(\mathbf{y}-\mathbf{W}\alpha \right)\right]}^2+{\left({\mathbf{X}}_i^T{\mathbf{X}}_i\right)}^{-1}{\sigma }_e^2\end{array}$$

2) E-step: QTN effect can be predicted by

$$E({\beta }_i)={\sigma }_i^2{\mathbf{X}}_i^T{\mathbf{V}}^{-1}(\mathbf{y}-\mathbf{W}\alpha )$$ (A.29)

where $\mathbf{V}=\sum _{i=1}^q{\mathbf{X}}_i{\mathbf{X}}_i^T{\sigma }_i^2+\mathbf{I}{\sigma }_e^2$.

3) M-step: To update parameters ${\sigma }_i^2$, $\mathbf{\alpha }$ and ${\sigma }_e^2$:

$$\begin{array}{l}{\sigma }_i^2=\frac{E\left({\beta }_i^T{\beta }_i\right)+\omega }{\tau +3}\\ \mathbf{\alpha }={\left({\mathbf{W}}^T{\mathbf{V}}^{-1}\mathbf{W}\right)}^{-}{\mathbf{W}}^T{\mathbf{V}}^{-1}\mathbf{y}\\ {\sigma }_e^2=\frac{1}{n}{\left(\mathbf{y}-\mathbf{W}\alpha \right)}^T\left(\mathbf{y}-\mathbf{W}\alpha -\sum _{i=1}^q{\mathbf{X}}_{i}E\left({\beta }_i\right)\right)\end{array}$$ (A.30)

where $E({\beta }_i^T{\beta }_i)=E({\beta }_i^T)E({\beta }_i)+\mathrm{tr}[\mathrm{Var}({\beta }_i)]$,$\mathrm{Var}({\beta }_i)=\mathbf{I}{\sigma }_i^2-{\sigma }_i^2{\mathbf{X}}_i^T{\mathbf{V}}^{-1}{\mathbf{X}}_i{\sigma }_i^2$ and$(\tau ,\omega )=(0,0)$.

Repeat E-step and M-step until convergence is satisfied.

Because the model is multi-locus in nature, Bonferroni correction is replaced by a less stringent selection criterion. Although the general 0.05 critical value may be used for the significance test, we decided to place a slightly more stringent criterion of LOD = 3.0. The criterion is frequently adopted in linkage analysis and is the equivalent of $P=\mathrm{Pr}({\chi }_1^2>3.0\times 4.605)\approx 0.0002$, in which ${\chi }_1^2$ under the null hypothesis, follows a ${\chi }^2$ distribution with one degree of freedom.

Appendix B. The A.thaliana data

We analyzed the well-known A. thaliana data sets published by Atwell et al. [29]. Both phenotypes and genotypes were obtained from http://www.arabidopsis.usc.edu/. A total of 199 Arabidopsis lines and 216 130 SNPs were used for analysis. Four flowering time traits (LD, SDV, 8W GH LN and 8W GH FT) with log-transformation were re-analyzed in this study. We excluded the individuals with missing phenotypes, non-polymorphic SNPs and SNPs with minor allele frequency less than 0.10 and all the six methods (FASTmrEMMA, E-BAYES, SUPER, EMMA, ECMLM and CMLM) were used to analyze these four data sets. A total of approximately 180 000 SNPs for each trait were used to calculate the identity by state matrix as the estimates of relatedness [3].

Appendix C. Simulation experiments

Three Monte Carlo simulation experiments were conducted to validate the new algorithms.

As described by Wang et al. [7] (2016), the SNP genotypes derived from the A. thaliana data sets [29] were also used to perform three simulation experiments. The purpose was to compare FASTmrEMMA with the single-locus model methods (SUPER, EMMA, ECMLM and CMLM) and the multi-locus model method (E-BAYES). In the first simulation experiment, 2000 SNPs on each chromosome were randomly sampled. As a result, all the SNPs between 11226256 and 12038776 bp on Chr. 1, between 5045828 and 6412875 bp on Chr. 2, between 1916588 and 3196442 bp on Chr. 3, between 2232796 and 3143893 bp on Chr. 4 and between 19999868 and 21039406 bp on Chr. 5 were used to conduct simulation studies. The sample size was 199, the number of lines from Atwell et al. [29]. Six QTNs were simulated and placed on the SNPs with allele frequencies of 0.30; their heritabilities of each effect size were set as 0.10, 0.05, 0.05, 0.15, 0.05 and 0.05, respectively; their positions and effects are listed in Supplementary Table S2. All the average and residual variance were set at 10.0. The new phenotypes were simulated by the model: $\mathbf{y}=\mathit{\mu }+\sum _{i=1}^6{\mathbf{x}}_i{b}_i+\mathit{\epsilon }$, where $\epsilon \sim MV{N}_n(0,10\times {\mathbf{I}}_n)$. Each sample was analyzed by the above six methods. For each simulated QTN, we counted the samples in which the LOD statistic exceeded 3.0 for FASTmrEMMA, the P-value was <0.05 for E-BAYES and the P-value ≤5E-6 ($0.05/p$) for the others. A detected, QTN within 2 kb of the simulated QTN was considered a true QTN. The ratio of the number of such samples to the total number of replicates (1000) represented the empirical power of this QTN. The Type I error was calculated as the ratio of the number of false positive effects to the total number of zero effects considered in the full model. To measure the bias of QTN effect estimate, MSE and MAD were defined as $\text{MSE}=\frac{1}{1000}\sum _{i=1}^{1000}{({\widehat{\beta }}_i-\beta )}^2,\text{MAD}=\frac{1}{1000}\sum _{i=1}^{1000}\left|{\widehat{\beta }}_i-\beta \right|$, where ${\widehat{\beta }}_i$ is the estimate of $\beta$ for each QTN in the ith sample. A method with a small MSE (or MAD) is generally more preferable than a method with a large MSE (or MAD).

To investigate the effect of polygenic background on FASTmrEMMA, polygenic effect was simulated in the second simulation experiment by multivariate normal distribution ${\text{MVN}}_n(\mathbf{0},{\sigma }_{pg}^2\mathbf{K})$, where ${\sigma }_{pg}^2$ is polygenic variance, and $\mathbf{K}$ is the kinship coefficient matrix between a pair of lines. The simulated phenotypes were not same as those of Wang et al. [7]. Here ${\sigma }_{pg}^2=2$, so $h_{pg}^2=0.092$. The QTN size (r²), residual variance and others were the same as those in the first simulation experiment. The new phenotypes were simulated by the model: $\mathbf{y}=\mathit{\mu }+\sum _{i=1}^6{x}_i{b}_i+\mathbf{u}+\mathit{\epsilon }$, where polygenic effect $\mathbf{u}\sim MV{N}_n(0,2\times \mathbf{K})$ and $\mathit{\epsilon }\sim MV{N}_n(\mathbf{0},10\times {\mathbf{I}}_n)$.

To investigate the effect of epistatic background on FASTmrEMMA, three epistatic QTN each with ${\sigma }_{epi}^2=1.25$ and $h_{epi}^2=0.05$ were simulated in the third simulation experiment. The first one was placed between 3063784 bp on Chr. 4 and 5227063 bp on Chr. 2; the second one was placed between 5986135 bp on Chr. 2 and 2031781 bp on Chr. 3; and the third one was placed between 2668059 bp on Chr. 3 and 11824678 bp on Chr. 1. The QTN size (r²), residual variance and others were also the same as those in the first simulation experiment. The new phenotypes were simulated by the model: $y=\mathit{\mu }+{\displaystyle \sum _{i=1}^6{\mathit{x}}_i{b}_i}+{\displaystyle \sum _{j\text{=}1}^3\left({\mathit{A}}_j\text{\#}{\mathit{B}}_j\right)b_{jj}}+\mathit{\epsilon }$, where $\mathit{\epsilon }\sim MV{N}_n(\mathbf{0},10\times {\mathbf{I}}_n)$, $b_{jj}$ is the epistatic effect and $A_j\text{\#}{B}_j$ is its incidence coefficient.

Yang-Jun Wen is a Ph D candidate in State Key Laboratory of Crop Genetics and Germplasm Enhancement at Nanjing Agricultural University, China.

Hanwen Zhang is a bachelor student in the Faculty of Applied Science at the University of British Columbia, Canada.

Yuan-Li Ni is a Master student in State Key Laboratory of Crop Genetics and Germplasm Enhancement at Nanjing Agricultural University, China.

Bo Huang is a Master student in State Key Laboratory of Crop Genetics and Germplasm Enhancement at Nanjing Agricultural University, China.

Jin Zhang is an associate professor in State Key Laboratory of Crop Genetics and Germplasm Enhancement at Nanjing Agricultural University, China.

Jian-Ying Feng is a lecturer in State Key Laboratory of Crop Genetics and Germplasm Enhancement at Nanjing Agricultural University, China.

Shi-Bo Wang is a postdoctoral research fellow in the College of Plant Science and Technology at Huazhong Agricultural University, China.

Jim M. Dunwell is a full professor in the School of Agriculture, Policy and Development at the University of Reading, United Kingdom.

Yuan-Ming Zhang is a full professor in State Key Laboratory of Crop Genetics and Germplasm Enhancement at Nanjing Agricultural University, Nanjing, China and Chutian Scholar Professor of Statistical Genomics in the College of Plant Science and Technology at Huazhong Agricultural University, Wuhan, China.

Rongling Wu is Distinguished Professor of Public Health Sciences and Statistics and the Director of the Center for Statistical Genetics at The Pennsylvania State University, USA. He found the Center for Computational Biology at Beijing Forestry University, China.