Lorentz imaging shows hidden states and switching behavior of magnetic vortices under rapid optical excitation and quenching.
Abstract
Understanding the fundamental dynamics of topological vortex and antivortex naturally formed in microscale/nanoscale ferromagnetic building blocks under external perturbations is crucial to magnetic vortex–based information processing and spintronic devices. All previous studies have focused on magnetic vortex–core switching via external magnetic fields, spin-polarized currents, or spin waves, which have largely prohibited the investigation of novel spin configurations that could emerge from the ground states in ferromagnetic disks and their underlying dynamics. We report in situ visualization of femtosecond laser quenching–induced magnetic vortex changes in various symmetric ferromagnetic Permalloy disks by using Lorentz phase imaging of four-dimensional electron microscopy that enables in situ laser excitation. Besides the switching of magnetic vortex chirality and polarity, we observed with distinct occurrence frequencies a plenitude of complex magnetic structures that have never been observed by magnetic field– or current-assisted switching. These complex magnetic structures consist of a number of newly created topological magnetic defects (vortex and antivortex) strictly conserving the topological winding number, demonstrating the direct impact of topological invariants on magnetization dynamics in ferromagnetic disks. Their spin configurations show mirror or rotation symmetry due to the geometrical confinement of the disks. Combined micromagnetic simulations with the experimental observations reveal the underlying magnetization dynamics and formation mechanism of the optical quenching–induced complex magnetic structures. Their distinct occurrence rates are pertinent to their formation-growth energetics and pinning effects at the disk edge. On the basis of these findings, we propose a paradigm of optical quenching–assisted fast switching of vortex cores for the control of magnetic vortex–based information recording and spintronic devices.
INTRODUCTION
A magnetic vortex (1, 2) is one of the fundamental spin configurations occurring in thin micrometer-/nanometer-sized ferromagnetic disk elements due to the confinement of spins imposed by geometrical restrictions (2, 3). It is one kind of topological magnetic defect characterized by two degrees of freedom (4): (i) “chirality” (c = ±1), the in-plane curling magnetization that can be clockwise or counterclockwise along the disk circumference; and (ii) “polarity” (p = ±1), the out-of-plane nanometer-sized core magnetization whose direction is either up or down. This topologically protected magnetic vortex cannot be continuously transferred into a defect-free state and is therefore regarded as very robust quasiparticles against thermal fluctuation (5). Such unique properties make the magnetic vortex a promising candidate for high-density, nonvolatile magnetic memories and spintronic devices (6, 7) because each magnetic vortex can store two bits of information by its chirality and polarity (8, 9).
A fundamental understanding of the magnetization dynamics associated with the precise manipulation of the chirality and polarity of the magnetic vortex in ferromagnetic building blocks is important for its application in magnetic data storage (8). It is well known that the topological magnetic vortex in a ferromagnetic disk can be manipulated by external perturbations, such as pulsed magnetic fields (8, 10, 11), alternating magnetic fields (12, 13), spin-polarized currents (8, 14–16), and field-driven spin waves (17, 18). These external stimuli could drive the gyrotropic motion of the vortex core so that its polarization would be switched through the creation and subsequent annihilation of a magnetic vortex-antivortex pair (12, 19–21). Nevertheless, because of the gyrotropic motion of the vortex core before its switching, it is difficult to precisely determine when the core switching occurs, thus limiting the ultimate investigation of the core switching dynamics that is important for designing vortex-based data storage devices. This gyrotropic motion also intrinsically restricts the speed of the magnetic vortex–core switching.
Recently, researchers have demonstrated the possibility of ultrafast magnetic switching in ferromagnetic thin films via photothermal-assisted femtosecond laser pulse excitation (22–26), where the single pulse rapidly heats up the ferromagnetic films close to their Curie temperatures and reduces the external magnetic field required for the magnetic reversal. The rapid photothermal effect of the ultrashort laser pulse excitation could also generate magnetic defects such as skyrmions in ferromagnetic films (27, 28). In particular, by using the inverse Faraday effect of circularly polarized femtosecond laser (29, 30), it is even possible to realize all-optical magnetization switching in ferromagnetic films (31–35). Researchers have also theoretically predicted the remarkable reduction of the required magnetic switching field for a topological magnetic vortex core at a temperature closely below the Curie point (36) and the possibility of all-optical switching of a magnetic vortex core (37) in ferromagnetic disks. This optically associated switching of the magnetic vortex core does not involve gyrotropic motion and thus has unique advantages in ultrafast magnetic recording. However, direct observation of magnetic vortex switching or change in geometrically confined ferromagnetic disks upon ultrafast laser quenching is rather challenging. Once achieved, it will provide a better fundamental understanding of the effects of topological features, magnetization relaxation dynamics, and geometrical confinement on magnetic vortex switching and its underlying mechanisms.
Here, we report the in situ visualization of femtosecond laser quenching–induced magnetic vortex configurations in symmetric ferromagnetic Permalloy (Py) disks by Lorentz phase imaging of four-dimensional electron microscopy (4D EM) that enables in situ femtosecond laser excitation. Besides the chirality and polarity switching of the magnetic vortex, we observed a plenitude of complex metastable magnetic structures with distinct occurrence frequencies in the Py disks with a femtosecond laser pulse excitation above a fluence of 10 mJ/cm2. We designed different symmetric elements, including circular, square, and regularly triangular disks, to investigate the geometrical confinement effect. The observed magnetic structures consist of a number of newly created topological defects (vortex and antivortex) strictly restricted by the topological winding number, and their spin configurations show mirror or rotation symmetry owing to the geometrical confinement of the disks. Micromagnetic simulations reproduce all the observed magnetic structures, revealing the underlying magnetization dynamics and the formation mechanisms. On the basis of the results, we propose a new paradigm of optical quenching–assisted fast vortex core switching for the control of magnetic vortex–based information processing and spintronic devices.
RESULTS
Metastable magnetic structures induced by femtosecond laser pulse
We study the femtosecond laser pulse–induced magnetic switching in three kinds of symmetric Py (Ni81Fe19) disks, including circle (diameters of 3 and 1.7 μm), square (edge length of 3 μm), and regular triangle (edge length of 1.7 μm) (see Materials and Methods). To resolve the magnetic vortex structures, we record the Fresnel images using a continuous electron beam of 4D EM in the Lorentz phase imaging mode (see Fig. 1A and Materials and Methods). Under out-of-focus conditions of the Lorentz mode, the clockwise and counterclockwise in-plane circling magnetizations of the magnetic vortices exert opposite Lorentz force on the imaging electrons, resulting in black and white contrasts of the vortex core (38–41), as schematically shown in Fig. 1B. Upon femtosecond laser pulse excitation, the electronic temperature of the Py disk jumps thousands of kelvin, and the lattice temperature follows at a slower rate governed by the electron-phonon coupling effect. Then, the Py disk experiences a fast cooling at a quenching rate of about 1012 K/s (42), passing through the silicon nitride substrate below (see the inset of Fig. 1B). Figure 1C presents several typical Fresnel images of the magnetic structures in the circular, square, and triangular Py disks before and after femtosecond laser pulse excitation with a fluence of 12 mJ/cm2 (see also movies S1 to S3). On the basis of the Lorentz contrast, the corresponding spin configurations are schematically depicted in the right panel of each Fresnel image. After each femtosecond laser pulse excitation on the initial single magnetic vortex in all the three geometrical Py disks, the Lorentz contrast in their Fresnel images exhibits a high probability to reversal (see the first three columns in Fig. 1C), implying the switch of the chirality of the magnetic vortex by the rapid optical quenching. Below a threshold fluence of about 10 mJ/cm2, a single femtosecond laser pulse excitation is insufficient to induce an observable change of the initial magnetic vortex in the Py disks, because the pulse-induced transient temperature of the Py disk is substantially lower than its Curie point (~850 K). Note that the observed reversal of the magnetic vortex chirality behaves randomly in the experiment. Besides the random reversal of the magnetic vortex chirality, we also observed, although less frequently, some complex magnetic structures consisting of several newly generated vortices, antivortices, and domains in all the three geometries (see typical ones in the last column of Fig. 1C), which were never observed by magnetic field– or spin current–assisted magnetic vortex switching. The magnetic field– or spin current–assisted switching is caused by the gyrotropic motion of the vortex core and the subsequent creation and annihilation of a vortex-antivortex pair (19, 20); however, the laser quenching–induced switching is due to the rapid photothermal effect, which will be discussed later. The magnetic antivortex is the topological counterpart of a magnetic vortex, which also contains a tiny core magnetized perpendicularly to the plane in the center and enclosed by two adjacent vortex structures (43, 44). It is discernible as a saddle point in the Fresnel image, namely, the cross of two Néel walls showing opposite Lorentz contrast (white and black) (42). As in our work, we did not intend to determine the polarity of the vortex cores; it is possible that the vortex polarity switching may also occur during the ultrafast optical quenching (26, 37).
Fig. 1. Femtosecond laser pulse quenching of a magnetic vortex in Py disks.
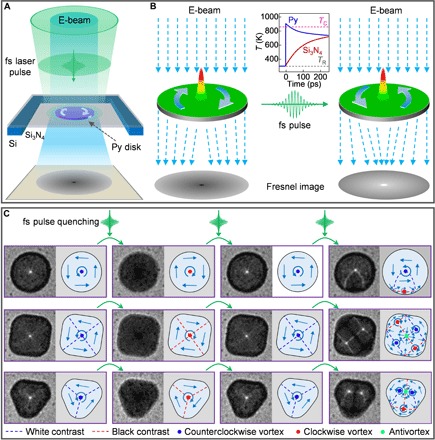
(A) Sketch of imaging the femtosecond laser pulse–induced change of spin configuration in a ferromagnetic Py disk by 4D EM operated in Lorentz phase mode with a continuous electron beam. The green femtosecond laser pulse (520 nm, 350 fs pulse duration) is focused to 40 μm on the sample. (B) Schematic Lorentz contrast reverse mechanism of a magnetic vortex in a circular Py disk before and after a femtosecond laser pulse excitation due to the change of spin chirality. Because of the opposite Lorentz force of the imaging electrons impinging on the sample, the Lorentz contrast of a vortex core can be either black or white. The inset depicts the typical transient temperature evolutions after a femtosecond laser excitation (see Materials and Methods) in both the Py disk and the silicon nitride substrate (TC is the Curie point of the Py disk, TR is the room temperature, and laser fluence is at 12 mJ/cm2). (C) Femtosecond laser pulse–induced variation of a magnetic vortex in circular, square, and regularly triangular Py disks. The right panel of each Fresnel image schematically depicts the corresponding spin configuration. The blue and red dashed lines correspond to the white and black Lorentz contrasts, respectively, while the blue and red dots correspond to the counterclockwise and clockwise vortices, individually. The green dots mark the magnetic antivortex. The same notes are used in all subsequent figures.
To understand the above interesting phenomenon, we repeated the same experiment on the three geometrical Py disks more than 200 times to obtain statistically meaningful measurements of the femtosecond laser pulse–induced metastable magnetic structures so that the underlying mechanism could be retrieved. The typical Fresnel images of the observed metastable magnetic structures are displayed in the middle panel of each subpanel in Fig. 2, while their corresponding spin configurations and occurrence frequency distributions are shown in the panels below and above, respectively. Each Fresnel image was acquired at about 1 s after each femtosecond laser pulse excitation (fluence of 12 mJ/cm2) in our experiment, and the magnetic states created after the rapid quenching do not evolve further until the next femtosecond laser shot. In each statistic histogram, the most frequently observed single clockwise and counterclockwise vortex structures with opposite Lorentz contrast were counted separately, while the other complex magnetic structures with opposite Lorentz contrast but with the same spin configuration were added together. In all three disks, the counterclockwise and clockwise single-vortex states occur randomly with a similar occurrence frequency, which is overwhelmingly higher than that of other complex magnetic structures. This nearly 90% occurrence frequency of the single-vortex state (including both clockwise and counterclockwise ones) also verifies its lowest energy and highest stability in the symmetric Py disks. All the other complex magnetic structures consist of a number of newly generated vortices, antivortices, domains, and pairs of Néel walls, where the antivortex is located between two vortices with the same chirality. Intriguingly, the spatial distribution of their spin configurations exhibits striking mirror or rotation symmetry (see Fig. 2), which is due to the confinement of the geometrical symmetry of the Py disks. For a magnetic structure containing a number of topological defects in a symmetric ferromagnetic disk, the symmetric spin configuration will aid in reducing the total energy of the system. Note that these complex metastable magnetic structures are much more difficult to form in smaller circular Py disks (1.7 μm diameter) under the same quenching condition (see movie S4), where only a single magnetic vortex structure forms, implying that the dimensionality affects the magnetization dynamics and final magnetic states.
Fig. 2. Occurrence frequency distribution of the femtosecond laser pulse–induced magnetic structures in three geometrical Py disks.
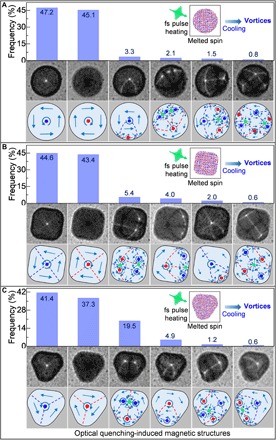
(A to C) Frequency distribution of the femtosecond laser pulse (fluence of 12 mJ/cm2)–induced spin configurations in circular, square, and triangular Py disks, respectively. The bottom panel in each subfigure shows the typical Fresnel images of the experiments, and the middle panel schematically shows their corresponding spin configurations. The most frequent single clockwise and counterclockwise vortex structures with opposite Lorentz imaging contrast were counted separately, while the other magnetic structures with opposite Lorentz imaging contrast but with the same spin configuration were added together. The inset in each subfigure denotes the femtosecond laser pulse quenching process in the Py disks.
To unravel the origin of the different occurrences of the complex metastable magnetic structures, we further carried out the femtosecond laser quenching experiments with a higher laser fluence of 16 mJ/cm2. At this fluence, other more complex, symmetric metastable magnetic structures consisting of a larger number of topological defects were observed in all the three geometries (see figs. S1 to S3). For both the circular and square disks, the magnetic structures that comprise various vortices up to six were observed, while for the triangular one, the most complex magnetic structure only contains four vortices, which is probably due to its lower geometrical symmetry. Note that most of these complex magnetic configurations have never been observed in ferromagnetic disks with other external stimuli, such as annealing, magnetic field, spin-polarized current, and spin wave. Basically, the more complex magnetic configurations (with more topological defects) show a lower occurrence frequency in the femtosecond laser quenching experiment (figs. S1 to S3). The occurrence of additional more complex, symmetric magnetic structures at this high fluence is mainly due to the strong laser heating–induced crystallite change in the Py disk, which will be discussed later.
The magnetic vortex and antivortex are both topological defects with the local magnetization rotating by 360° on a closed loop around the tiny core, which can be characterized by a topological winding number w = 1/2π∮∇α ∙ dS (w = +1 and −1 for vortex and antivortex, respectively), where α is the local orientation of the magnetization vector and S is an arbitrary integral loop containing the tiny core (19). The topological winding number has been theoretically predicted to have a direct impact on the magnetization dynamics (43, 45). Because of the spatial symmetry breaking at the edge of the Py disks, each cross of a pair of Néel walls with opposite Lorentz contrast at the edge can be considered as a half-antivortex, and its topological winding number w turns out to be −1/2. One would find that the sum of the total topological winding numbers for each observed metastable magnetic structure in all the three geometrical disks is equal to 1, which is the same as that of their initial single magnetic vortex state. Namely, the generation of new vortices and antivortices during the femtosecond laser quenching conserves the topological winding number of the Py disks, that is, strictly restricted by the topological invariance. This topological feature is similar to that of the light-induced magnetic network in homogeneous ferromagnetic iron thin films, where the vortex-antivortex generates in pairs and follows the universal behavior within the framework of the Kibble-Zurek mechanism (42).
Micromagnetic simulation of the magnetization dynamics
To understand the formation mechanism and topological feature of the symmetric magnetic structures induced by femtosecond laser pulse quenching, we performed finite-element micromagnetic simulations on these three geometrical Py disks based on the Landau-Lifshitz-Gilbert equation with Langevin dynamics (32) to reveal the underlying magnetization dynamics (see Materials and Methods). For the micromagnetic simulations, we consider the following scenarios: (i) the femtosecond laser pulse only interacts with the magnetization via the photothermal effect; (ii) the femtosecond pulse heats the Py disk above the Curie point and randomizes the local magnetization, namely, melts the electronic spin structures, but without altering the integrity of the lattice; and (iii) each femtosecond laser pulse excitation may result in different random magnetization seeds in the melted spin system. Under these conditions, the optical quenching–induced magnetization dynamics in the Py disks can be understood as follows. Upon a femtosecond laser pulse excitation above the threshold fluence for the Curie temperature, the thermal energy of the electronic system in the Py disk is rapidly increased, creating a hot thermal bath for the spin system. This sharp increase in thermal energy of the spin system leads to a rapid and full demagnetization, namely, spin melt of the initial magnetization in the Py disk within several picoseconds (41, 46–48). The subsequent energy transfer from the electron system to the lattice governed by the electron-phonon coupling (32) leads to a rapid decrease of the temperature to below Curie point, initiating the remagnetization process of the spin system. Compared to the optical writing of skyrmions (28), the remagnetization dynamics of the Py disk under laser pulse excitation relates to the temperature quench process.
We used the exact dimensions of the samples in the micromagnetic simulations, and more than 25 runs of the numerical simulation were performed on each Py disk. The bottom panel of each subfigure in Fig. 3 presents the typical spin configurations in each Py disk generated by the micromagnetic simulation, and their corresponding occurrence frequencies (plotted in pink bars) and energies are plotted together in the top panel. For comparison, the corresponding occurrence frequency distributions of the magnetic structures measured by the experiments are also plotted in blue bars. Here, the single magnetic vortex states with opposite chirality were counted together. All the magnetic structures observed in the experiment (laser fluence of 12 mJ/cm2) are well reproduced by the micromagnetic simulations for all the three geometrical disks, and their occurrence frequencies agree as well (Fig. 3).
Fig. 3. Comparison of micromagnetic simulations with experimental observations.
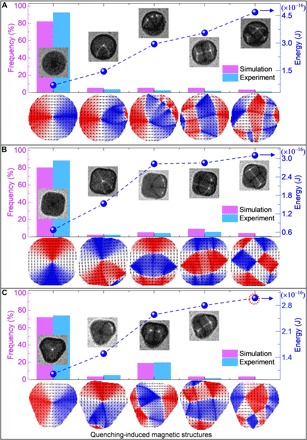
(A to C) Simulation results of the occurrence frequency distribution and energies of the femtosecond laser pulse (fluence of 12 mJ/cm2)–induced magnetic structures in circular, square, and triangular Py disks, respectively. The bottom panel in each subfigure shows the typical results of possible magnetic structures obtained by the micromagnetic simulations (pink bars). The corresponding experiment-determined occurrence frequency distribution of the femtosecond laser pulse–induced magnetic structures is also plotted in blue bars for comparison. The simulation results reproduce the experimental results well (the statistical errors of the histograms are below 5%), with the exception of one magnetic structure in the triangle disk [indicated by the dashed red circle in (C)].
In all three geometrical disks, the single magnetic vortex state always exhibits the highest occurrence due to its lowest energy (~6.98 × 10−17 J for circle, ~7.32 × 10−17 J for square, and ~9.52 × 10−17 J for triangle), while the occurrence of other complex magnetic structures generally decreases with their energy (see Fig. 3). Specifically, for the magnetic structures in the circular disk, their energy nearly increases linearly with an increase in the number of contained topological magnetic defects (vortex), and their occurrence frequency decreases monotonously (Fig. 3A). For both square and triangular disks, the energy increase levels off for the magnetic structures with more than three topological magnetic defects (vortex), and counterintuitively, the magnetic structure containing two vortices with lower energy even exhibits smaller occurrence frequencies than that of the magnetic structure containing three vortices with higher energy (Fig. 3, B and C). This unexpected behavior is probably due to the much smaller energy barrier that the magnetic structure containing two vortices needs to overcome during the magnetization relaxation after the optical quenching. As direct estimation of energy barriers from micromagnetic simulations has been limited to the case of quasi-1D nanowire systems or single-vortex systems in potentials with a high degree of symmetry, we instead use the change in energy required to modify the vortex/antivortex number within the Py disk during application of an applied field, as schematically shown for a square Py disk in fig. S4. The transformation energy is determined by using the minimum field required for transformation from fields applied along the ±x and ±y directions. We note that these energies are larger than the true depinning energies, as they take into account energy changes in the entire disk and may not represent the lowest energy path toward annihilation, and also that the exact values will vary significantly with the pinning region. However, this method can be used to demonstrate the relative differences in pinning energies. We find that the annihilation energy for the two-vortex structure is significantly less than the annihilation energy for other vortex systems. Because of the much smaller energy barrier, the metastable magnetic structure containing two vortices strongly prefers to relax to the single magnetic vortex state, resulting in a lower occurrence than the magnetic structure with three vortices in both square and triangular disks (Fig. 3, B and C). It should be noted that, as measured in single-vortex states or quasi-1D nanowires, spin pinning potentials in magnetic systems induced by both surface roughness and nonuniformities at the sample edge are typically on the order of 1 eV (49, 50), which is significantly larger than thermal fluctuations following the rapid quenching.
To unravel the factors that determine the final magnetic structures, we considered the initial remagnetization process of the random magnetization seeds, especially the role of the spin pinning at the edge defects of the Py disks, in our micromagnetic simulation. In a perfectly circular disk with a smooth edge, the single magnetic vortex state is strongly preferred after a femtosecond laser pulse excitation. Because of the confinement of the geometrical symmetry of the disk and the spin pinning at the edge defects (or edge roughness), the final magnetic structures prefer to form symmetric configuration to reduce the system total energy. For further discussion, three exemplary time-dependent magnetization evolutions for the formation of the single magnetic vortex state and the metastable magnetic structures with two and three vortices in a triangular disk are respectively presented in Fig. 4 (see also movies S5 to S7). After a femtosecond laser pulse–induced randomization of the initial magnetization in the disk, the melted spin system starts to remagnetize when the temperature cools down to below the Curie point in several picoseconds and a number of vortices, antivortices, domains, and half-antivortices at the disk edge are formed. Note that these initially formed topological magnetic defects conserve the topological winding number (w = 1) of the initial single magnetic vortex state in the Py disk. With time lapse, the adjacent vortices and antivortices inside the disk move spirally and approach each other and then annihilate in pairs, while for the half-antivortices at the disk edge, a nearby inside vortex moves toward the center of two adjacent half-antivortices, and they annihilate upon running into one another, as indicated by the colored circles in Fig. 4. Depending on the relative core polarization of the adjacent vortex-antivortex pair, their annihilation process either is a continuous transformation of the magnetization (parallel) or involves nucleation and propagation of a Bloch point, causing a burst-like emission of spin waves (antiparallel) (19). During this incessant vortex-antivortex pair annihilation process, the energy of the spin system continuously decreases, until the system relaxes to the single magnetic vortex state with the lowest energy (see Fig. 4A).
Fig. 4. Typical magnetization dynamics in a Py disk after a femtosecond laser pulse quenching by micromagnetic simulation.
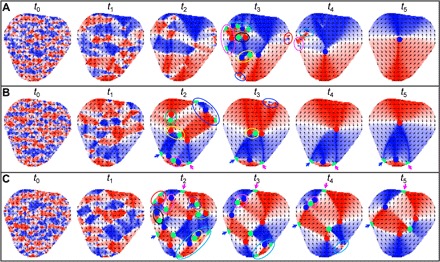
Snapshots of the magnetization dynamics during the formation of different magnetic structures in a triangular Py disk at different times after a femtosecond laser pulse excitation: (A) formation a single magnetic vortex state; (B) formation of a magnetic structure with two vortices; (C) formation of a magnetic structure with three vortices. The laser fluence is 12 mJ/cm2. Note that the precise time scale of the magnetization relaxation process may vary (from hundreds of picoseconds to nanoseconds) with real ferromagnetic disk systems, which exhibit even more complex pinning mechanisms as well as temperature-dependent damping. The vortices and antivortices (including the half-antivortices indicated by the green half dots at the disk edge) in the different colored circles indicate the magnetic vortex-antivortex pairs that annihilate during the magnetization relaxation process. The blue and pink arrows indicate the spin pinning sites at the disk edge.
Because of the spin pinning at the disk edge (indicated by the blue and pink arrows in Fig. 4, B and C; see also fig. S5), the half-antivortices at these pinning sites cannot move freely; thus, the two adjacent half-antivortices at these pinning sites cannot annihilate with a nearby vortex. In such case, the spin system relaxes to a symmetric multivortex state due to the confinement of the symmetric geometry of the disk (Fig. 4, B and C). The magnetization dynamics and the formation mechanisms of other metastable complex magnetic structures, including those in the circular and square Py disks, have similar features (see movies S8 to S13). The strong spin pinning effect at the disk edge could also account for the observation of additional more complex, symmetric magnetic structures in our experiment at a higher laser fluence of 16 mJ/cm2 (see figs. S1 to S3). At this high fluence, the strong heating effect would cause lattice grain growth within the Py disk (see fig. S6), which would induce larger grain boundaries, that is, roughness at the disk edge, and thus more strong spin pinning sites, resulting in more complex magnetic structures (figs. S1 to S3). Thus, pinning processes in these systems play a key role in the population statistics determined in this work. To elucidate the role of pinning in these systems, we have carried out further micromagnetic simulations on the square structure shown in Fig. 3B. To eliminate pinning, we smooth the edges of the structure and then used the previously observed metastable configurations as an initial state. The system is then allowed to relax. We find that, while the single-vortex state and the three highest-energy states are stable in this smoothed geometry, the two-vortex state is not, and relaxes to the single-vortex state. This implies that this state only exists due to strong local pinning effects, and its population is highly dependent on the local edge geometry.
DISCUSSION
Thermally assisted magnetization reversal has been proposed as one of the most promising way to enable high-density magnetic recording (25, 51), where the large anisotropy values required for the stability of the recording media films are transiently reduced by laser heating and the required magnetic switching field markedly declines. Recently, Lebecki and Nowak (36) have theoretically studied the temperature impact on the magnetic switching field of a magnetic vortex core in a circular ferromagnetic disk based on the Landau-Lifshitz-Bloch equation (52) incorporating the thermal effect. As shown in their prediction, the orthogonal magnetic field required for vortex core switching dramatically decreases with increasing temperature due to the lower energy barrier at higher temperature, which may even vanish at a temperature slightly below the Curie point [see figs. 3 and 5 in (36)]. In contrast, our experimental results demonstrate that both the magnetic vortex switching and the final magnetic state are random after a femtosecond laser pulse excitation (see Fig. 2), implying that the purely photothermal switching of a magnetic vortex is possible but uncontrollable, which will seriously hinder the practical application. Nevertheless, a femtosecond laser pulse with a proper fluence could initiate a sharp increase of temperature in the Py disk above its Curie point to induce a transient nonequilibrium paramagnetic state (spin-melted state). During this transient paramagnetic period, if a small external orthogonal magnetic field is applied, then one could easily control the spin direction of the system and initiate the polarization of the magnetic vortex that formed in the subsequent magnetization relaxation process due to the ultrafast quenching.
On the basis of our experimental observations, together with the simulation results, we propose a new paradigm of optical quenching–assisted fast switching of the magnetic vortex polarity for the control of magnetic vortex–based information recording and spintronic devices, as schematically shown in Fig. 5. A femtosecond laser pulse to transiently demagnetize the initial magnetic vortex in the Py disk and a small orthogonal magnetic field pulse (with a duration above tens of picoseconds) to set the polarization of the newly formed magnetic vortex are simultaneously applied. There are several possible approaches to realize this paradigm. For example, through the topological inverse Faraday effect, a small orthogonal magnetic field pulse could be simultaneously generated using a circularly polarized laser pulse for excitation (37). In principle, the strength of this external magnetic field pulse should be much smaller than that (500 mT) of the orthogonal magnetic field required for the conventional quasistatic switching of a magnetic vortex core (53, 54), which could be handily determined by magnetic force microscope measurements. It should be mentioned that, for this proposed optical quenching–assisted, magnetic vortex–based information recording paradigm, the following factors need to be considered carefully: (i) The fluence of the femtosecond laser pulse is crucial. It should be able to instantaneously drive the system above the spin transition temperature, but below the temperature that would cause the crystallite damage in the Py disk. A very strong femtosecond laser pulse excitation would induce lattice change and cause the growth of crystallites in the Py disk (see fig. S6), resulting in additional spin pinning sites that would frustrate the magnetization relaxation. (ii) The dimension and the edge smoothness of the Py disk are also very important. As shown in our results, the small circular Py disks (1.7 μm diameter) strongly prefer the single magnetic vortex state after each femtosecond laser pulse quenching (see movie S4). The smooth disk edge would reduce the spin pinning effects during the magnetization relaxation. Therefore, the proper design of a nanoscale circular Py disk with a smooth edge and uniform small crystallites would be greatly helpful to improve the stability and reliability of the optical quenching–assisted magnetic vortex switching, as well as the scalability of this approach. This would offer the new possibility of magnetic vortex–based high-density information recording with fast writing rates, but consuming much less power.
Fig. 5. A paradigm of the optical quenching–assisted, magnetic vortex–based information recording process.
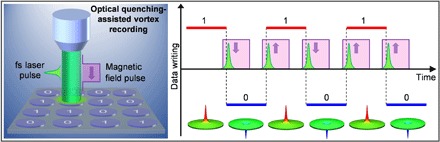
(Left) Schematic of the optical quenching–assisted, magnetic vortex–based information recording system, where a linear polarized femtosecond laser pulse is used to transiently demagnetize the initial magnetic vortex and another synchronized orthogonal small magnetic field pulse is used to set the polarization of the newly formed magnetic vortex. (Right) Sketch for the working mechanism of the optical quenching–assisted, magnetic vortex–based information recording process. The data information “1” and “0” are recorded by the polarity (up and down) of the magnetic vortex. The fluence of the femtosecond laser pulse should be controlled above the threshold for spin melting, but below the threshold for changes in the ferromagnetic disk’s crystallites.
In conclusion, by using the unique ultrafast quenching rate of up to 1012 K/s of a femtosecond laser pulse excitation, we observed a plenitude of new metastable magnetic structures in three types of symmetric, micrometer-sized Py disks by in situ Lorentz electron microscopy. These metastable magnetic structures consist of a number of newly created topological magnetic defects strictly restricted by the topological invariants, which were not observed previously in magnetic field– or spin current–assisted magnetic vortex switching. Because of the confinement of the disk geometrical symmetry, their spin configurations show apparent mirror or rotation symmetry. Micromagnetic simulations revealed the underlying magnetization dynamics of all the observed magnetic structures and the dependence of their occurrence frequencies on their energetics and pinning effects at the disk edge. Our results provide new insights into the fundamental spin switching dynamics in symmetric Py disks under femtosecond laser pulse quenching, which offers guidance for the design of optical quenching–assisted fast switching of topological vortices for vortex-based information recording and spintronic devices.
MATERIALS AND METHODS
Preparation of Py disks
The samples studied in our experiments were prepared by electron beam evaporation of a layer of Py (Ni81Fe19) film (30 nm thickness, ca. 10 nm grain size) onto a silicon nitride membrane (100 nm thickness, 300 μm × 300 μm window area) on a silicon frame with previously prepared symmetric patterns using photolithography and a liftoff process. Three kinds of symmetric disks were prepared: circle (diameters of 3 and 1.7 μm), square (edge length of 3 μm), and regular triangle (edge length of 1.7 μm). The corners of the square and regular triangle disks were intentionally arc-shaped to avoid artificial singularity in spin switching (see Fig. 1C).
Estimation of transient thermal state in the Py disk after femtosecond laser pulse excitation
Since the silicon nitride was almost transparent to the laser wavelength used in our work, upon femtosecond laser pulse excitation, the optical pulse energy was first absorbed by the Py disk, resulting in a rapid rise of the electron temperature and subsequently equilibrating with the spin and lattice on a time scale below 1 ps through the electron-electron and electron-lattice couplings (42, 55). After the femtosecond laser pulse–induced locally equilibrated electron, spin, and lattice system, we described the transient thermal state of the Py disk using a simple single-temperature model in the picosecond time range (42). The relative heat capacities of the Py and silicon nitride layer were taken into account in the model, and the thermal conductivity (~25 W/mK) of the Py was taken from (56), while the thermal boundary resistance between the two layers was estimated from (57). At a laser fluence of 12 mJ/cm2 (above the threshold), the Py disk was initially heated up to a transient peak temperature exceeding the Curie point and then the system cooled down rapidly through the local equilibration between the Py disk and the silicon nitride substrate with a cooling rate of up to ~1012 K/s, followed by subsequent thermal diffusion through the substrate. On longer time scales, the slower lateral heat diffusion across the substrate ultimately brought the system back to room temperature.
Lorentz phase imaging of femtosecond laser pulse–induced magnetic structures
To image the femtosecond laser quenching–induced changes of magnetic structure in the Py disks, we performed out-of-focus (over-focus with a defocus value of about 300 μm) Fresnel phase imaging in 4D EM (58–61) operated under Lorentz-mode conditions (62, 63), which enabled in situ femtosecond laser excitation. To obtain high Lorentz contrast, the images were collected using the continuous electron beam of the 4D EM rather than pulsed electrons. Linearly polarized green femtosecond laser pulses (520 nm, 40 μm focal spot size, 350 fs pulse duration) were used for excitation, which were generated from infrared femtosecond laser pulses (1040 nm, 350 fs pulse duration) by second harmonic generation. The in-plane circular magnetizations (clockwise or counterclockwise) of the magnetic vortices exerted opposite Lorentz forces on the imaging electrons, resulting in contrasts or phase shift of the electron beam related to the vortex core, respectively (39–41). The high-throughput Fresnel phase imaging allowed the investigation of the femtosecond laser quenching–induced magnetization changes at the nanometer scale and the statistical properties of the resulting magnetic structures.
Micromagnetic simulation
Micromagnetic simulations were performed using micromagnetic software (OOMMF) (http://math.nist.gov/oommf/oommf_cites.html). A saturation magnetization (Ms) of 800 kA/m, an exchange stiffness (A) of 13 pJ/m, and a Gilbert damping (α) of 0.01, consistent with typical values of Py, were used. A stopping condition of dM/dt = 0.1 was used to ensure convergence. The parameters used were from (49). The cell size was set to 5 nm × 5 nm × 30 nm. The sample structure for each geometry was determined by creating a binary mask from transmission electron microscopy images for each. To determine possible metastable domain configurations, 25 runs for each geometry were performed using different initial random magnetic configurations and then allowed to relax. Following relaxation, the energies and static domain configurations were recorded.
Supplementary Material
Acknowledgments
We acknowledge Caltech for providing access to the 4D electron microscopy facility for this study. We thank J. S. Baskin for very helpful discussion and help on the Lorentz phase electron microscopy measurement with in situ femtosecond laser excitation. We also thank J. A. Garlow for fruitful discussion on the Lorentz phase imaging measurement. Funding: This work was supported by the Materials Science and Engineering Divisions, Office of Basic Energy Sciences of the U.S. Department of Energy under contract no. DESC0012704. Author contributions: Y.Z. and X.F. conceived the research project. X.F., B.C., and B.-K.Y. carried out the experimental measurements. S.D.P. prepared the samples. X.F. and S.D.P. performed data analysis with input from Y.Z. S.D.P. developed the model and performed the numerical simulations with input from H.Y. All the authors contributed to the discussion and the writing of the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/7/eaat3077/DC1
Fig. S1. Occurrence frequency distribution of femtosecond laser pulse–induced magnetic structures in a circular Py disk at a fluence of 16 mJ/cm2.
Fig. S2. Occurrence frequency distribution of femtosecond laser pulse–induced magnetic structures in a square Py disk at a fluence of 16 mJ/cm2.
Fig. S3. Occurrence frequency distribution of femtosecond laser pulse–induced magnetic structures in a triangular Py disk at a fluence of 16 mJ/cm2.
Fig. S4. Schematic of relative change to the sum of demagnetization and exchange energies associated with the transformation of the indicated state to a lower-energy state estimated by application of a magnetic field applied along the ±x or ±y directions, whichever is lowest.
Fig. S5. Typical magnetic structures in triangular Py disks (edge length of 1.7 μm) determined by micromagnetic simulation to show the pinning sites at the disk edge.
Fig. S6. Annular bright-field images of a circular Py disk after a femtosecond laser pulse quenching with different fluences to show the change of the inside crystallites.
Movie S1. Fresnel imaging of femtosecond laser pulse quenching–induced magnetic structure change in a circular Py disk (diameter of 3 μm) at a fluence of 12 mJ/cm2.
Movie S2. Fresnel imaging of femtosecond laser pulse quenching–induced magnetic structure change in a square Py disk (edge length of 3 μm) at a fluence of 12 mJ/cm2.
Movie S3. Fresnel imaging of femtosecond laser pulse quenching–induced magnetic structure change in a triangular Py disk (edge length of 1.7 μm) at a fluence of 12 mJ/cm2.
Movie S4. Fresnel imaging of femtosecond laser pulse quenching–induced magnetic structure change in a circular Py disk (diameter of 1.7 μm) at a fluence of 12 mJ/cm2.
Movie S5. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a single magnetic vortex structure in the triangular Py disk (edge length of 1.7 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S6. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with two magnetic vortices in the triangular Py disk (edge length of 1.7 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S7. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with three magnetic vortices in the triangular Py disk (diameter of 3.0 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S8. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a single magnetic vortex structure in the circular Py disk (diameter of 3.0 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S9. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with four magnetic vortices in the circular Py disk (diameter of 3.0 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S10. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with four magnetic vortices in the circular Py disk (diameter of 3.0 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S11. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a single magnetic vortex structure in the square Py disk (edge length of 3 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S12. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with three magnetic vortices in the square Py disk (edge length of 3 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S13. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with four magnetic vortices in the square Py disk (edge length of 3 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
REFERENCES AND NOTES
- 1.Shinjo T., Okuno T., Hassdorf R., Shigeto K., Ono T., Magnetic vortex core observation in circular dots of permalloy. Science 289, 930–932 (2000). [DOI] [PubMed] [Google Scholar]
- 2.Wachowiak A., Wiebe J., Bode M., Pietzsch O., Morgenstern M., Wiesendanger R., Direct observation of internal spin structure of magnetic vortex cores. Science 298, 577–580 (2002). [DOI] [PubMed] [Google Scholar]
- 3.Chou K. W., Puzic A., Stoll H., Dolgos D., Schütz G., Direct observation of the vortex core magnetization and its dynamics. Appl. Phys. Lett. 90, 202505 (2007). [Google Scholar]
- 4.Sugimoto S., Fukuma Y., Kasai S., Kimura T., Barman A., Otani Y. C., Dynamics of coupled vortices in a pair of ferromagnetic disks. Phys. Rev. Lett. 106, 197203 (2011). [DOI] [PubMed] [Google Scholar]
- 5.Braun H.-B., Topological effects in nanomagnetism: From superparamagnetism to chiral quantum solitons. Adv. Physiol. Educ. 61, 1–116 (2012). [Google Scholar]
- 6.Cowburn R. P., Spintronics: Change of direction. Nat. Mater. 6, 255–256 (2007). [DOI] [PubMed] [Google Scholar]
- 7.Pigeau B., De Loubens G., Klein O., Riegler A., Lochner F., Schmidt G., Molenkamp L. W., Tiberkevich V. S., Slavin A. N., A frequency-controlled magnetic vortex memory. Appl. Phys. Lett. 96, 132506 (2010). [Google Scholar]
- 8.Yamada K., Kasai S., Nakatani Y., Kobayashi K., Kohno H., Thiaville A., Ono T., Electrical switching of the vortex core in a magnetic disk. Nat. Mater. 6, 270–273 (2007). [DOI] [PubMed] [Google Scholar]
- 9.Höllinger R., Killinger A., Krey U., Statics and fast dynamics of nanomagnets with vortex structure. J. Magn. Magn. Mater. 261, 178–189 (2003). [Google Scholar]
- 10.Xiao Q. F., Rudge J., Choi B. C., Hong Y. K., Donohoe G., Dynamics of vortex core switching in ferromagnetic nanodisks. Appl. Phys. Lett. 89, 262507 (2006). [Google Scholar]
- 11.Lau J. W., Beleggia M., Zhu Y., Common reversal mechanisms and correlation between transient domain states and field sweep rate in patterned Permalloy structures. J. Appl. Phys. 102, 043906–1 (2007). [Google Scholar]
- 12.Van Waeyenberge B., Puzic A., Stoll H., Chou K. W., Tyliszczak T., Hertel R., Fähnle M., Brückl H., Rott K., Reiss G., Neudecker I., Weiss D., Back C. H., Schütz G., Magnetic vortex core reversal by excitation with short bursts of an alternating field. Nature 444, 461–464 (2006). [DOI] [PubMed] [Google Scholar]
- 13.Curcic M., Van Waeyenberge B., Vansteenkiste A., Weigand M., Sackmann V., Stoll H., Fähnle M., Tyliszczak T., Woltersdorf G., Back C. H., Schütz G., Polarization selective magnetic vortex dynamics and core reversal in rotating magnetic fields. Phys. Rev. Lett. 101, 197204 (2008). [DOI] [PubMed] [Google Scholar]
- 14.Liu Y., Gliga S., Hertel R., Schneider C. M., Current-induced magnetic vortex core switching in a Permalloy nanodisk. Appl. Phys. Lett. 91, 112501 (2007). [Google Scholar]
- 15.Yamada K., Kasai S., Nakatani Y., Kobayashi K., Ono T., Switching magnetic vortex core by a single nanosecond current pulse. Appl. Phys. Lett. 93, 152502 (2008). [Google Scholar]
- 16.Yamada K., Kasai S., Nakatani Y., Kobayashi K., Ono T., Current-induced switching of magnetic vortex core in ferromagnetic elliptical disks. Appl. Phys. Lett. 96, 192508 (2010). [Google Scholar]
- 17.Kravchuk V. P., Gaididei Y., Sheka D. D., Nucleation of a vortex-antivortex pair in the presence of an immobile magnetic vortex. Phys. Rev. B 80, 100405 (2009). [Google Scholar]
- 18.Kammerer M., Weigand M., Curcic M., Noske M., Sproll M., Vansteenkiste A., Van Waeyenberge B., Stoll H., Woltersdorf G., Back C. H., Schuetz G., Magnetic vortex core reversal by excitation of spin waves. Nat. Commun. 2, 279 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hertel R., Schneider C. M., Exchange explosions: Magnetization dynamics during vortex-antivortex annihilation. Phys. Rev. Lett. 97, 177202 (2006). [DOI] [PubMed] [Google Scholar]
- 20.Hertel R., Gliga S., Fähnle M., Schneider C. M., Ultrafast nanomagnetic toggle switching of vortex cores. Phys. Rev. Lett. 98, 117201 (2007). [DOI] [PubMed] [Google Scholar]
- 21.Guslienko K. Y., Lee K.-S., Kim S.-K., Dynamic origin of vortex core switching in soft magnetic nanodots. Phys. Rev. Lett. 100, 027203 (2008). [DOI] [PubMed] [Google Scholar]
- 22.Beaurepaire E., Merle J.-C., Daunois A., Bigot J.-Y., Ultrafast spin dynamics in ferromagnetic nickel. Phys. Rev. Lett. 76, 4250–4253 (1996). [DOI] [PubMed] [Google Scholar]
- 23.Ogasawara T., Iwata N., Murakami Y., Okamoto H., Tokura Y., Submicron-scale spatial feature of ultrafast photoinduced magnetization reversal in TbFeCo thin film. Appl. Phys. Lett. 94, 162507 (2009). [Google Scholar]
- 24.Radu I., Vahaplar K., Stamm C., Kachel T., Pontius N., Dürr H. A., Ostler T. A., Barker J., Evans R. F. L., Chantrell R. W., Tsukamoto A., Itoh A., Kirilyuk A., Rasing T., Kimel A. V., Transient ferromagnetic-like state mediating ultrafast reversal of antiferromagnetically coupled spins. Nature 472, 205–208 (2011). [DOI] [PubMed] [Google Scholar]
- 25.Stipe B. C., Strand T. C., Poon C. C., Balamane H., Boone T. D., Katine J. A., Li J.-L., Rawat V., Nemoto H., Hirotsune A., Hellwig O., Ruiz R., Dobisz E., Kercher D. S., Robertson N., Albrecht T. R., Terris B. D., Magnetic recording at 1.5 Pb m−2 using an integrated plasmonic antenna. Nat. Photonics 4, 484–488 (2010). [Google Scholar]
- 26.Le Guyader L., El Moussaoui S., Buzzi M., Chopdekar R. V., Heyderman L. J., Tsukamoto A., Itoh A., Kirilyuk A., Rasing T., Kimel A. V., Nolting F., Demonstration of laser induced magnetization reversal in GdFeCo nanostructures. Appl. Phys. Lett. 101, 022410 (2012). [Google Scholar]
- 27.Finazzi M., Savoini M., Khorsand A. R., Tsukamoto A., Itoh A., Duò L., Kirilyuk A., Rasing T., Ezawa M., Laser-induced magnetic nanostructures with tunable topological properties. Phys. Rev. Lett. 110, 177205 (2013). [DOI] [PubMed] [Google Scholar]
- 28.Berruto G., Madan I., Murooka Y., Vanacore G. M., Pomarico E., Rajeswari J., Lamb R., Huang P., Kruchkov A. J., Togawa Y., LaGrange T., McGrouther D., Rønnow H. M., Carbone F., Laser-induced skyrmion writing and erasing in an ultrafast cryo-lorentz transmission electron microscope. Phys. Rev. Lett. 120, 117201 (2018). [DOI] [PubMed] [Google Scholar]
- 29.Pitaevskii L. P., Electric forces in a transparent dispersive medium. Sov. Phys. JETP 12, 1008–1013 (1961). [Google Scholar]
- 30.Pershan P. S., Van der Ziel J. P., Malmstrom L. D., Theoretical discussion of the inverse Faraday effect, Raman scattering, and related phenomena. Phys. Rev. 143, 574–583 (1966). [Google Scholar]
- 31.Stanciu C. D., Hansteen F., Kimel A. V., Kirilyuk A., Tsukamoto A., Itoh A., Rasing T., All-optical magnetic recording with circularly polarized light. Phys. Rev. Lett. 99, 047601 (2007). [DOI] [PubMed] [Google Scholar]
- 32.Ostler T., Barker J., Evans R. F. L., Chantrell R. W., Atxitia U., Chubykalo-Fesenko O., El Moussaoui S., Le Guyader L., Mengotti E., Heyderman L. J., Nolting F., Tsukamoto A., Itoh A., Afanasiev D., Ivanov B. A., Kalashnikova A. M., Vahaplar K., Mentink J., Kirilyuk A., Rasing T., Kimel A. V., Ultrafast heating as a sufficient stimulus for magnetization reversal in a ferrimagnet. Nat. Commun. 3, 666 (2012). [DOI] [PubMed] [Google Scholar]
- 33.Khorsand A. R., Savoini M., Kirilyuk A., Kimel A. V., Tsukamoto A., Itoh A., Rasing T., Role of magnetic circular dichroism in all-optical magnetic recording. Phys. Rev. Lett. 108, 127205 (2012). [DOI] [PubMed] [Google Scholar]
- 34.Mangin S., Gottwald M., Lambert C.-H., Steil D., Uhlír V., Pang L., Hehn M., Alebrand S., Cinchetti M., Malinowski G., Fainman Y., Aeschlimann M., Fullerton E. E., Engineered materials for all-optical helicity-dependent magnetic switching. Nat. Mater. 13, 286–292 (2014). [DOI] [PubMed] [Google Scholar]
- 35.Lambert C.-H., Mangin S., Varaprasad B. S. D. C. S., Takahashi Y. K., Hehn M., Cinchetti M., Malinowski G., Hono K., Fainman Y., Aeschlimann M., Fullerton E. E., All-optical control of ferromagnetic thin films and nanostructures. Science 345, 1337–1340 (2014). [DOI] [PubMed] [Google Scholar]
- 36.Lebecki K. M., Nowak U., Ferromagnetic vortex core switching at elevated temperatures. Phys. Rev. B 89, 014421 (2014). [Google Scholar]
- 37.Taguchi K., Ohe J.-., Tatara G., Ultrafast magnetic vortex core switching driven by the topological inverse Faraday effect. Phys. Rev. Lett. 109, 127204 (2012). [DOI] [PubMed] [Google Scholar]
- 38.Gomez R. D., Luu T. V., Pak A. O., Kirk K. J., Chapman J. N., Domain configurations of nanostructured Permalloy elements. J. Appl. Phys. 85, 6163–6165 (1999). [Google Scholar]
- 39.Schneider M., Hoffmann H., Zweck J., Lorentz microscopy of circular ferromagnetic permalloy nanodisks. Appl. Phys. Lett. 77, 2909–2911 (2000). [Google Scholar]
- 40.Raabe J., Pulwey R., Sattler R., Schweinböck T., Zweck J., Weiss D., Magnetization pattern of ferromagnetic nanodisks. J. Appl. Phys. 88, 4437–4439 (2000). [Google Scholar]
- 41.N. R. da Silva, M. Möller, A. Feist, H. Ulrichs, C. Ropers, S. Schäfer, Nanoscale mapping of ultrafast magnetization dynamics with femtosecond Lorentz microscopy. arXiv preprint arXiv:1710.03307 1–25 (2017).
- 42.Eggebrecht T., Möller M., Gregor Gatzmann J., da Silva N. R., Feist A., Martens U., Ulrichs H., Münzenberg M., Ropers C., Schäfer S., Light-induced metastable magnetic texture uncovered by in situ Lorentz microscopy. Phys. Rev. Lett. 118, 097203 (2017). [DOI] [PubMed] [Google Scholar]
- 43.Gliga S., Yan M., Hertel R., Schneider C. M., Ultrafast dynamics of a magnetic antivortex: Micromagnetic simulations. Phys. Rev. B 77, 060404 (2008). [Google Scholar]
- 44.Huber E. E. Jr, Smith D. O., Goodenough J. B., Domain-wall structure in permalloy films. J. Appl. Phys. 29, 294–295 (1958). [Google Scholar]
- 45.Thiele A., Steady-state motion of magnetic domains. Phys. Rev. Lett. 30, 230–233 (1973). [Google Scholar]
- 46.B. Koopmans, Spin Dynamics in Confined Magnetic Structures II (Springer, 2003), pp. 256–323. [Google Scholar]
- 47.Koopmans B., Ruigrok J. J. M., Longa F. D., de Jonge W. J. M., Unifying ultrafast magnetization dynamics. Phys. Rev. Lett. 95, 267207 (2005). [DOI] [PubMed] [Google Scholar]
- 48.Bigot J.-Y., Vomir M., Beaurepaire E., Coherent ultrafast magnetism induced by femtosecond laser pulses. Nat. Phys. 5, 515–520 (2009). [Google Scholar]
- 49.Kim J.-S., Boulle O., Verstoep S., Heyne L., Rhensius J., Kläui M., Heyderman L. J., Kronast F., Mattheis R., Ulysse C., Faini G., Current-induced vortex dynamics and pinning potentials probed by homodyne detection. Phys. Rev. B 82, 104427 (2010). [Google Scholar]
- 50.Chen T.-Y., Erickson M. J., Crowell P. A., Leighton C., Surface roughness dominated pinning mechanism of magnetic vortices in soft ferromagnetic films. Phys. Rev. Lett. 109, 097202 (2012). [DOI] [PubMed] [Google Scholar]
- 51.Kryder M. H., Gage E. C., McDaniel T. W., Challener W. A., Rottmayer R. E., Ju G., Hsia Y.-T., Fatih Erden M., Heat assisted magnetic recording. Proc. IEEE 96, 1810–1835 (2008). [Google Scholar]
- 52.Garanin D. A., Fokker-Planck and Landau-Lifshitz-Bloch equations for classical ferromagnets. Phys. Rev. B 55, 3050–3057 (1997). [Google Scholar]
- 53.Okuno T., Shigeto K., Ono T., Mibu K., Shinjo T., MFM study of magnetic vortex cores in circular permalloy dots: Behavior in external field. J. Magn. Magn. Mater. 240, 1–6 (2002). [Google Scholar]
- 54.Thiaville A., García J. M., Dittrich R., Miltat J., Schrefl T., Micromagnetic study of Bloch-point-mediated vortex core reversal. Phys. Rev. B 67, 094410 (2003). [Google Scholar]
- 55.Radu I., Woltersdorf G., Kiessling M., Melnikov A., Bovensiepen U., Thiele J.-U., Back C. H., Laser-induced magnetization dynamics of lanthanide-doped permalloy thin films. Phys. Rev. Lett. 102, 117201 (2009). [DOI] [PubMed] [Google Scholar]
- 56.Avery A. D., Mason S. J., Bassett D., Wesenberg D., Zink B. L., Thermal and electrical conductivity of approximately 100-nm permalloy, Ni, Co, Al, and Cu films and examination of the Wiedemann-Franz Law. Phys. Rev. B 92, 214410 (2015). [Google Scholar]
- 57.Jeong T., Zhu J.-G., Chung S., Gibbons M. R., Thermal boundary resistance for gold and CoFe alloy on silicon nitride films. J. Appl. Phys. 111, 083510 (2012). [Google Scholar]
- 58.Zewail A. H., Four-dimensional electron microscopy. Science 328, 187–193 (2010). [DOI] [PubMed] [Google Scholar]
- 59.Fu X., Chen B., Tang J., Hassan M. T., Zewail A. H., Imaging rotational dynamics of nanoparticles in liquid by 4D electron microscopy. Science 355, 494–498 (2017). [DOI] [PubMed] [Google Scholar]
- 60.Fu X., Chen B., Tang J., Zewail A. H., Photoinduced nanobubble-driven superfast diffusion of nanoparticles imaged by 4D electron microscopy. Sci. Adv. 3, e1701160 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Chen B., Fu X., Tang J., Lysevych M., Tan H. H., Jagadish C., Zewail A. H., Dynamics and control of gold-encapped gallium arsenide nanowires imaged by 4D electron microscopy. Proc. Natl. Acad. Sci. U.S.A. 201708761 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Park H. S., Baskin J. S., Zewail A. H., 4D Lorentz electron microscopy imaging: Magnetic domain wall nucleation, reversal, and wave velocity. Nano Lett. 10, 3796–3803 (2010). [DOI] [PubMed] [Google Scholar]
- 63.Rajeswari J., Huang P., Fulvia Mancini G., Murooka Y., Latychevskaia T., McGrouther D., Cantoni M., Baldini E., Stuart White J., Magrez A., Giamarchi T., Moodysson Rønnow H., Carbone F., Filming the formation and fluctuation of skyrmion domains by cryo-Lorentz transmission electron microscopy. Proc. Natl. Acad. Sci. U.S.A. 112, 14212–14217 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/7/eaat3077/DC1
Fig. S1. Occurrence frequency distribution of femtosecond laser pulse–induced magnetic structures in a circular Py disk at a fluence of 16 mJ/cm2.
Fig. S2. Occurrence frequency distribution of femtosecond laser pulse–induced magnetic structures in a square Py disk at a fluence of 16 mJ/cm2.
Fig. S3. Occurrence frequency distribution of femtosecond laser pulse–induced magnetic structures in a triangular Py disk at a fluence of 16 mJ/cm2.
Fig. S4. Schematic of relative change to the sum of demagnetization and exchange energies associated with the transformation of the indicated state to a lower-energy state estimated by application of a magnetic field applied along the ±x or ±y directions, whichever is lowest.
Fig. S5. Typical magnetic structures in triangular Py disks (edge length of 1.7 μm) determined by micromagnetic simulation to show the pinning sites at the disk edge.
Fig. S6. Annular bright-field images of a circular Py disk after a femtosecond laser pulse quenching with different fluences to show the change of the inside crystallites.
Movie S1. Fresnel imaging of femtosecond laser pulse quenching–induced magnetic structure change in a circular Py disk (diameter of 3 μm) at a fluence of 12 mJ/cm2.
Movie S2. Fresnel imaging of femtosecond laser pulse quenching–induced magnetic structure change in a square Py disk (edge length of 3 μm) at a fluence of 12 mJ/cm2.
Movie S3. Fresnel imaging of femtosecond laser pulse quenching–induced magnetic structure change in a triangular Py disk (edge length of 1.7 μm) at a fluence of 12 mJ/cm2.
Movie S4. Fresnel imaging of femtosecond laser pulse quenching–induced magnetic structure change in a circular Py disk (diameter of 1.7 μm) at a fluence of 12 mJ/cm2.
Movie S5. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a single magnetic vortex structure in the triangular Py disk (edge length of 1.7 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S6. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with two magnetic vortices in the triangular Py disk (edge length of 1.7 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S7. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with three magnetic vortices in the triangular Py disk (diameter of 3.0 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S8. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a single magnetic vortex structure in the circular Py disk (diameter of 3.0 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S9. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with four magnetic vortices in the circular Py disk (diameter of 3.0 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S10. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with four magnetic vortices in the circular Py disk (diameter of 3.0 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S11. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a single magnetic vortex structure in the square Py disk (edge length of 3 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S12. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with three magnetic vortices in the square Py disk (edge length of 3 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).
Movie S13. Micromagnetic simulation on the magnetization relaxation dynamics of the formation of a magnetic structure with four magnetic vortices in the square Py disk (edge length of 3 μm) after a femtosecond pulse quenching (fluence of 12 mJ/cm2).


