Inference on Admixture Fractions in a Mechanistic Model of Recurrent Admixture

Abstract

Signatures of recent historical admixture are ubiquitous in human populations. We present a mechanistic model of admixture with two source populations, encompassing recurrent admixture periods and study the distribution of admixture fractions for finite but arbitrary genome size. We provide simulation-based methods to estimate the introgression parameters and discuss the implications of reaching stationarity on estimability of parameters when there are recurrent admixture events with different rates.

1. Introduction

Admixture among previously isolated populations is a key mechanism influencing the genetic diversity and biological evolution of populations. Since the 1930s population geneticists have extensively investigated genetic diversity patterns in admixed populations from numerous domesticated or wild animal and plant species (Bertorelle et al. 1998; Richards et al.1999; Rosenberg et al. 2002; Garant et al. 2005). This allowed reconstructing the demographic and migratory histories of the studied populations (Long 1991; Chikhi et al. 2001; Hellenthal et al. 2014), detecting traces of natural selection and biological adaptation (Cavalli-Sforza et al. 1971; Tang et al. 2007; Oleksyk et al. 2010; Lohmueller et al. 2011), identifying mutations involved in complex phenotypic traits determination (pathological or not) using admixture mapping approaches (Reich et al. 2005; Smith et al. 2005; Buerkle et al. 2008; Perry et al. 2014), or understanding the genomic architecture of admixed individuals (Tang et al. 2005; Tang et al. 2006; Sankararaman et al. 2008; Price et al. 2009; Bryc et al. 2010; Lawson et al. 2012).

Theoretical approaches to understand the effect of admixture on genetic patterns observed in populations, remain to be more thoroughly explored. A number of mechanistic models have been developed to describe historical admixture processes with a single event of admixture between two source populations. They have been fruitfully used to predict admixture proportions and time since the onset of admixture (Patterson et al. 2012; Pickrell et al. 2012; Lipson et al. 2013; Loh et al. 2013; Hellenthal et al. 2014), and other statistics such as fixation indices (Long 1991), and linkage disequilibrium (Chakraborty et al. 1988; Ewens et al. 1995; Pfaff et al. 2001; Guo et al. 2005; Baird 2006; Loh et al. 2013). However, admixture processes are known to be often more complex than a process with a single event of admixture between two source populations, involving potential recurrent admixture events with varying contributions from several source populations over time (e.g. Crawford et al 2012).

Recent studies have developed mechanistic models of complex historical admixture to better understand the influence of admixture parameters such as the contribution of source populations at each generation, the onset and the duration of admixture (Verdu et al. 2011; Gravel 2012; Goldberg et al. 2014; Goldberg et al. 2015). These authors showed that complex admixture processes may leave an identifiable signature on genetic patterns in admixed populations and individuals. Genetic patterns can further be used to reconstruct previously unknown admixture histories using genetic data. Nevertheless, our ability to accurately infer past admixture histories from observed genetic patterns largely depends upon further theoretical exploration of complex admixture models. For example, identifying whether admixture processes in a hybrid population occur panmictically or follow complex assortative mating is crucial to correctly interpret inferences on past admixture events drawn from the genetic data. In particular, assessing a priori the identifiability and estimability of admixture parameters when complex admixture processes operate is both crucial and challenging.

In this paper, we explore admixture processes derived from the mechanistic models proposed in Verdu and Rosenberg (2011) involving multiple admixture periods (which we refer as recurrent admixture throughout the paper) in the history of admixed populations. Over the long run, our recurrent admixture model leads to a stationary distribution of admixture fractions. We motivate this distribution analytically for single locus and two-locus genomes, and calculate it deterministically for genomes with more than two loci. We develop simulation-based statistical methods to estimate the admixture parameters under historical models using genotyping data, and discuss how reaching the stationarity influences parameter estimability under models with at least two distinct admixture periods over time.

2. A model with recurrent admixture

We consider a process of recurrent admixture every generation between two infinite diploid source populations with fixed and known genome size of L loci. The admixture fraction for an individual is the proportion of alleles in the genome of that individual contributed originally by one of the source populations in a population that evolves as in (Figure 1A). The admixed population H is assumed to be infinite and it is founded at generation t = 0 by random mating of parents from two source populations: A and B. At the founding generation t = 0, the parents of individuals in the admixed population are chosen from source populations A and B independent of each other with constant probabilities a₀ and b₀ respectively. For generations t ≥ 1 after the founding, the parents of the individuals in the admixed population at generation t + 1 are chosen from source populations A, B, and the admixed population H, independent of each other with probabilities a, b, and h respectively. Repeated over generations with constant introgression parameters a, b, and h, this process is a single-stage recurrent admixture model. Verdu and Rosenberg (2011) studied a version of this admixture model under the assumption of unspecified genome size and focused on the probability for a random locus in the genome of a random individual in an admixed population at generation g to ultimately have originated from source population i. Fixing the size of the genome makes the mathematical properties of our model fundamentally different then Verdu and Rosenberg (2011). We refer to their model as unspecified genome size model and discuss its differences from our model in section 3.2.

Figure 1.

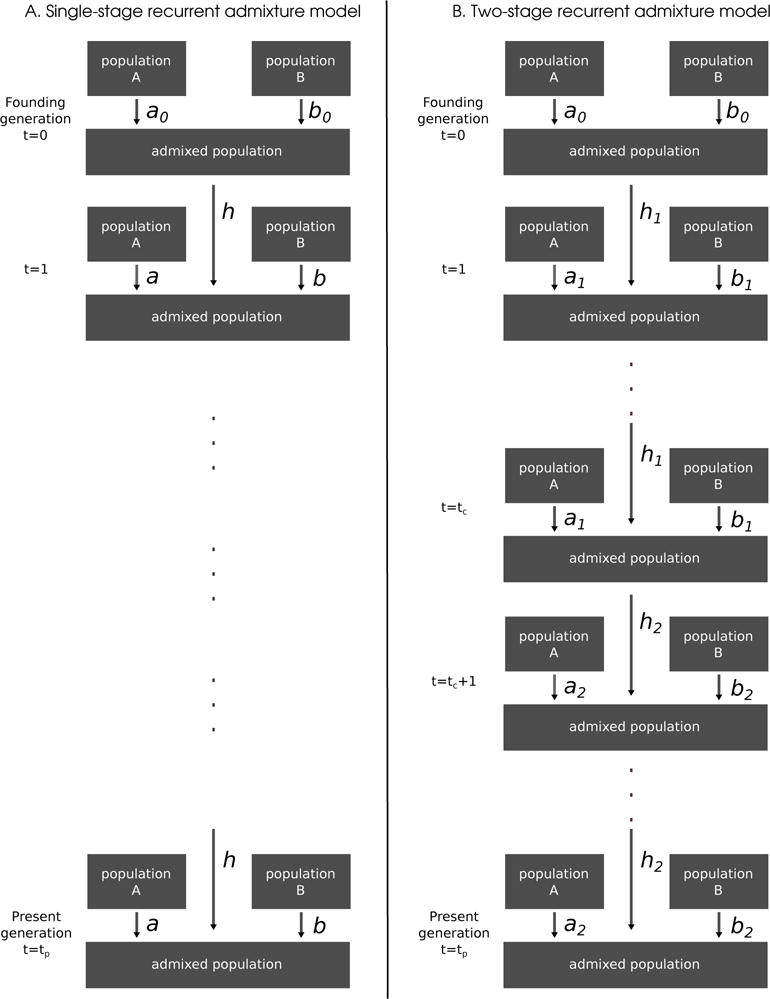
A mechanistic model with: constant recurring admixture (A), and two stage recurring admixture (B) in a diploid population

We assign labels 1 and 0 to alleles originated from source populations A and B respectively, which corresponds to a “diagnostic” locus of the admixture process. For example, as in the case of a locus with two alleles, one of them private to a source population (see Szpiech et al. 2011). The admixture fraction of an individual takes values {0, 1/(2L), 2/(2L), …, 1, where the numerator is the number of alleles in the genome of an admixed individual originating from source population A.

Current hypotheses of admixture in recent history of human populations (Gravel 2012, Liang and Nielsen 2014), predict multiple-stage processes, so we study the properties of the distribution of admixture fractions in a two-stage recurrent admixture model (Figure 1B). In this model, there are two sets of introgression parameter values. Until time t_c, the admixture process runs under the first set of introgression parameters as in the single-stage recurrent admixture model. From generation t_c on, the recurrent admixture process continues with the second set of introgression parameter values until the present generation. We denote the two sets of introgression parameters corresponding to the first and second stage of the recurrent admixture process by (a₁, b₁, h₁) and (a₂, b₂, h₂) respectively (Figure 1B).

3. The stationary distribution of admixture fractions

3.1. Single-stage recurrent admixture model

We motivate the setup for the distribution of admixture fractions using a single-locus biallelic case: Three possible genotypes are 1|1, 0|1, 0|0, (where the vertical bar separates the two alleles in a genotype) and the three admixture fraction values that correspond to these genotypes are 1, 0.5, 0 respectively. We let p_i(t) be the frequency of allele i at generation t in the admixed population H, with the initial frequencies p₁(0) = p and p₀(0) = q such that p+q = 1. At the first generation after the founding, the probability of an allele 1 in the offspring is equal to the probability of the parent coming from population A which contributes allele 1 with probability 1 or population H which contributes allele 1 with probability p. Therefore, the probability of drawing allele 1 as parent of an offspring is hp+a. A similar calculation for allele 0 implies that the probability of drawing allele 0 is hq+b. Under random mating in the hybrid population, the frequency of allele 1 at generation 1 in the admixed population is then given by p₁(1) = (hp+a)² + (hp+a)(hq+b) = hp+a. Calculating the frequency of alleles at each generation recursively, at generation t we have p₁(t) = h^tp + h^t−1a + h^t−2a + … + ha + a. Excluding the first term, the right hand side of this equation follows a geometric series with rate t and at generation t the allele frequencies can be written as geometric sum p₁(t) = h^tp + a(1 − h^t)/(1 − h). Since h < 1, in the limit as t → ∞ the first term h^tp on the right hand side goes to zero, and by the properties of the geometric series, the remaining terms converge to p₁(∞) = a/(1 − h). A similar calculation shows that for allele 0 we have p₀(∞) = b/(1 − h). These probabilities are reminiscient of a result obtained in equation (31) of Verdu and Rosenberg (2011), where for a random locus in the genome of a random individual in the admixed population they derive the expected value of the admixture fraction as a/(1 − h).

The limiting probabilities for admixture fractions {1, 0.5, 0} are given by (a/(1 − h)², (2ab)/(1 − h)², b/(1 − h)²). The time to stationarity depends on the initial allele frequencies p, q and on the parameter values (a, b, h). For the biallelic single locus case, if the initial and equilibrium frequencies of allele 1 are p₁ and p₁(∞) respectively, the convergence rate to stationarity is given by lim_t→∞(|p₁(t + 1) − p₁(∞)|)/(|p₁ (t) − p₁(∞)|), which is equal to h. Since 0 < h < 1, the convergence rate to the limiting frequencies a/(1 − h) and b/(1 − h) is linear in the number of generations t. Figure 2 (panels I and II) shows the effect of different values of (a, b, h) on the time to convergence to the stationary distribution of admixture fractions when the initial frequencies are p = q = 0.5.

Figure 2.

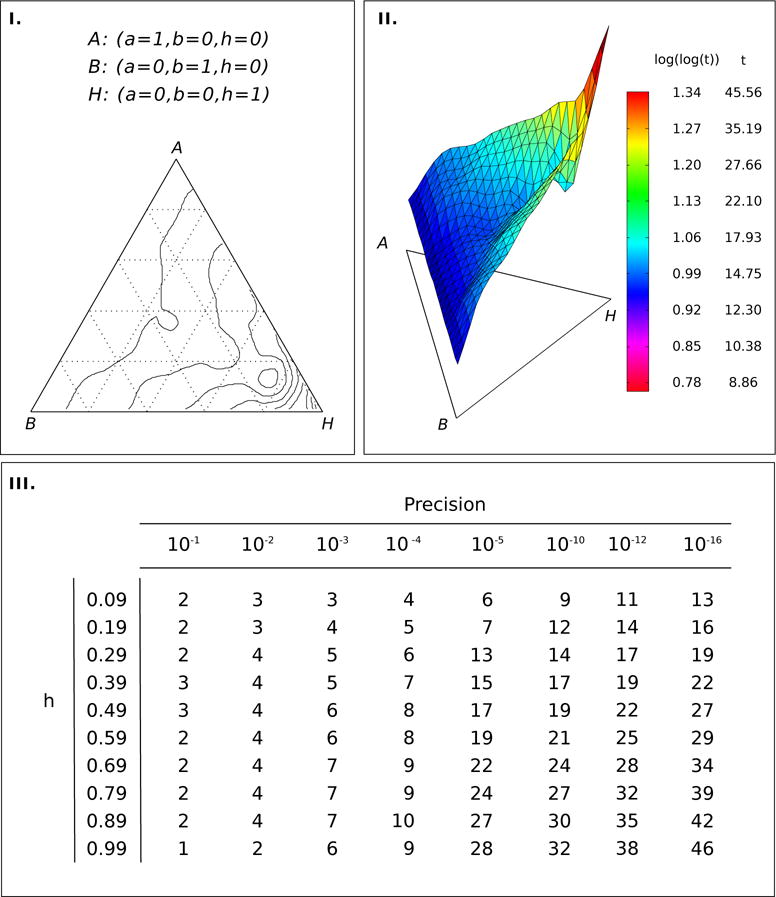
Time to convergence to the stationary distribution in the single-stage admixture model: I.) The contour plot for time to convergence in a two-dimensional simplex with coordinates (a, b, h). II.) The surface of the contour plot. The legend on the right shows the height of the surface in double log scale and the corresponding number of generations (t) to convergence. The convergence is assumed to be attained at accuracy 10⁻¹⁶. Time to convergence is small unless h, the contribution from the hybrid population to itself is close to 1. III. The table entries are time to convergence for different values of h at different accuracies. For example, h = 0.39 and precision 10⁻³ gives the time to convergence as 5 generations. For all cases in the table a = b = (1 − h)/2.

The stationary distribution of admixture fractions can be calculated for multilocus genotypes as well. For a two-locus genome with haplotypes, 11, 01, 10, 00, there are five possible admixture fractions: {1, 0.75, 0.5, 0.25, 0}. We denote the haplotype frequencies at t = 0 by (p₁, p₂, p₃, p₄). At generation t the haplotype frequencies are given by p₁(t + 1) = hp₁(t) + a, p₂(t + 1) = hp₂(t), p₃(t + 1) = hp₃(t), p₄(t + 1) = hp₄(t) + b. At stationarity we have p_i(t_s) = p_i(t_s − 1) and using the recursion we get the probabilities of admixture fractions {1, 0.75, 0.5, 0.25, 0} as $(p_1^2,2(p_1{p}_2+p_1{p}_3)$, $2(p_1{p}_4+p_2{p}_3)+p_2^2+p_3^2$, $2(p_4{p}_2+p_4{p}_3),p_4^2$.

For L > 2, analytical solutions are algebraically cumbersome but the stationary probabilities are easily calculated with forward-in-time deterministic simulations using a tolerance level ε as the criterion of stationarity. The admixture process reaches the stationarity at tolerance level ε at generation t_ε, if t_ε is the first generation at which the maximum difference between any two admixture fractions is smaller than ε for the first time in the process. The main factor that determines the computational cost for the stationary probabilities is L. Even for intermediate L, the number of haplotypes (2^L) is large. Some compuational efficiency is achieved by calculating and storing a matrix of coefficients M that maps genotype probabilities to admixture fractions. When multiplied by a vector of genotype probabilities, M returns the probabilities of admixture fractions. Given L, this matrix is calculated once and it is repeatedly used below in Algorithm 1. Given L, introgression parameters (a, b, h), and the initial frequencies of haplotypes in the hybrid population $p=(p_1,p_2,\dots ,p_{(2^L)})$, Algorithm 1 deterministically calculates the stationary probabilities at a specified tolerance ε.

Algorithm 1.

1. Initialize:

Calculate genotype probabilities: G = pTp where pT is transpose

Calculate probabilities of admixture fractions: ϕ = MG

Set s = (a, 0, …, 0, b), (1 × 2L vector)

While(true), do:

2. Update haplotype probabilities: p = ph + s

3. Update genotype probabilities: G = pTp

4. Update probabilities of admixture fractions: ϕ′ = MG

5. if max |ϕ′ − ϕ| < ε,

break and return ϕ′,

else, set ϕ = ϕ′ and go to step (2)

Figure 2 panel III lists the number of generations to convergence for a specified accuracy in the allele frequencies and is useful in establishing convergence with observed data. For all cases in the figure we use a = b = (1 − h)/2. For example when h = 0.39, at tolerance ε = 10⁻³ we get the time to convergence as 5 generations.

3.2. Differences with the unspecified genome size model in Verdu and Rosenberg (2011)

There are differences between our admixture model and the unspecified genome size model and these differences lead to different distributions of admixture fractions. Consider an example with Parent 1 genotype 0|1, and Parent 2 genotype 1|1. Three offspring genotypes from these two parents are 0|1, 1|0, 1|1, with frequencies 0.25, 0.25, 0.5 and admixture fraction values 0.5, 0.5, 1 respectively. In the unspecified genome size model, the quantity of interest is the distribution of mean admixture fractions of offspring in the admixed population as opposed to the distribution of admixture fractions of all offspring. The mean admixture fraction is (0.5 + 0.5)(0.25) + (1)(0.5) = 0.75, so the model records 0.75 for the offspring of these parents. However, our model calculates the distribution of admixture fractions for all individuals at each generation: the probabilities that an admixture fraction value is equal to 0.5 and 1 are 0.5 and 0.5 respectively.

In the unspecified genome size model, the distribution of the mean admixture fraction for a random locus and each generation the number of possible admixture fraction values increases with 2^t. At generation t, possible admixture fraction values are {0, 1/2^t, …, (2t − 1)/2^t, 1} and the number of admixture fraction does not depend on the number of loci, L. Thus, the support of the distribution of admixture fraction increases with time and thus it is challenging to find the stationary distribution of admixture fractions. We consider a fixed and known number of loci in the genome and the 2^L possible admixture fraction have a nonnegative probability to be in the population at all generations after the first. This makes it easy to calculate the stationary distribution of admixture fractions in our model.

3.3. Two-stage recurrent admixture model

Gravel (2012) and Liang and Nielsen (2014) found support for demographic models in which U.S. African-American populations have experienced a second admixture pulse following a first admixture pulse. This result suggests that complex admixture processes may have occured in human genetic evolution and left an identifiable signature in the genomic make-up of hybrid populations. We expand their two-pulse models to investigate the consequences of a generalized two-stage recurrent admixture process with introgression parameters (a₁, b₁, h₁) in the first stage and (a₂, b₂, h₂) in the second stage by expanding the single stage recurrent admixture model developed in section 3.1. The results that we present in this section extend directly to multi-locus genomes.

We assume that at generation t the introgression parameter values change from (a₁, b₁, h₁) to (a₂, b₂, h₂). In addition to the first admixture process reaching the numerical stationarity at tolerance level ε at generation t_ε, we now assume that the second process reaches the numerical stationarity at generation ℓ_ε (Figure 1B). The second process is assumed to follow the first process immediately and the starting allele frequencies for the second process are the ending allele frequencies from the first process. If the introgression parameter values change at generation t, then at generation t + 1 we have the allele frequencies given by $p_1(t+1)=h_2[h_1^t+a_1((1-h_1^t)/(1-h_1))]+a_2$, and $p_0(t+1)=h_2[h_1^{t}q+b_1((1-h_1^t)/(1-h_1))]+b_2$, where the quantities inside the brackets are p₁(t) and p₀(t) respectively, which become the initial frequencies of alleles for the second recurrent admixture process with introgression parameters (a₂, b₂, h₂). If the total admixture process continues for t + ℓ generations, first for t generations under parameter values (a₁, b₁, h₁) and then for ℓ generations under parameter values (a₂, b₂, h₂), the allele frequencies are given by

$$p_1(t+\ell )=h_2^{\ell }\left[h_1^{t}p+a_1\left(\frac{1-h_1^t}{1-h_1}\right)\right]+a_2\left(\frac{1-h_2^{\ell }}{1-h_2}\right),$$ (1)

$$p_0(t+\ell )=h_2^{\ell }\left[h_1^{t}p+a_1\left(\frac{1-h_1^t}{1-h_1}\right)\right]+b_2\left(\frac{1-h_2^{\ell }}{1-h_2}\right).$$ (2)

Equations 1 and 2 develop an intution on the effect of the first and second admixture processes on the frequency of alleles as follows. If this stationarity has been reached before the second process has started, equations 1 and 2 simplify to

$$p_1(t+\ell |t>t_{\epsilon })=h_2^{\ell }\left(\frac{a_1}{1-h_1}\right)+a_2\left(\frac{1-h_2^{\ell }}{1-h_2}\right),$$ (3)

$$p_0(t+\ell |t>t_{\epsilon })=h_2^{\ell }\left(\frac{b_1}{1-h_1}\right)+b_2\left(\frac{1-h_2^{\ell }}{1-h_2}\right).$$ (4)

if the second process has reached the stationarity, the effect of the first process on the allele frequencies given by the first terms in equations 3, and 4 goes to zero and the second terms converge to the geometric sum $p_1\left(t+\ell |\ell >{\ell }_{\epsilon }\right)=\frac{a_2}{1-h_2}$, and $p_0\left(t+\ell |\ell >{\ell }_{\epsilon }\right)=\frac{b_2}{1-h_2}$. Thus, if the second admixture process has run long enough to reach the stationarity, no effect of the first admixture process can be captured in the allele frequency data and the allele frequencies will carry no information about the first set of introgression parameters, irrespective of how long the first process has run.

Figure 5 shows some examples of how quickly the effect of the first admixture process is erased by the second admixture process in a two-stage recurrent admixture models. We tested six models for which the introgression parameters are given in the upper left corner legend of the figure. The parameterization follows the order (a₁, b₁, h₁), (a₂, b₂, h₂). We started the recurrent admixture at generation 1 after the founding, and ended at generation 50. The horizontal axis of the plot shows the generation t_c at which the admixture was switched from process 1 to process 2 in the sense that the introgression parameters were changed from (a₁, b₁, h₁) to (a₂, b₂, h₂) at that generation. The vertical axis of the plot captures the effect of t_c on the frequencies of admixture fractions at the end of 50 generations using a Sum of Squared Difference statistic (SSD).

Figure 5.

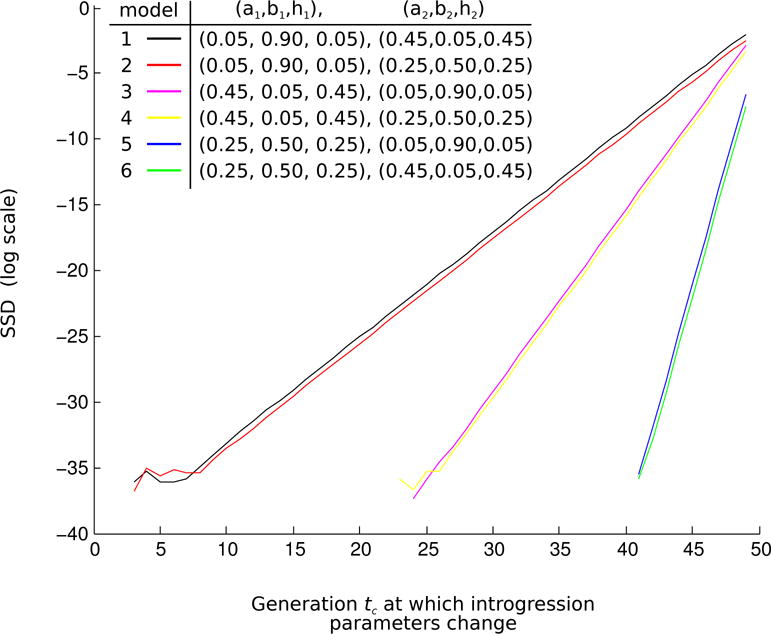
The results of a simulation study from a two-stage admixture model: Six models differing in introgression parameter values for two admixture processes are compared when the switch from process 1 to 2 happens at t_c ∈ {2, 3, …, 48}. The total length of the two admixture processes is 50 generations. The horizontal axis: the generation number t_c. The vertical axis (log scale): the sum of squared differences (SSD) in the admixture fraction frequencies at generation 50, between the model in which the change in the introgression parameters occurs at generation 2 (earliest) and each of the other models with 2 < t_c ≤ 48. The SSD is small in all models indicating that little information remains in the admixture fractions about the first admixture process if a second admixture process acts on the population with parameters different than the first process.

For a model with fixed ((a₁, b₁, h₁), (a₂, b₂, h₂)), SSD for t_c is given by

$$\mathit{SSD}(t_c)={\displaystyle \sum _{i=1}^{2L+1}{[p_i(50|t=t_c)-p_i(50|t=2)]}^2},$$

where p_i(50|t = t_c) and p_i(50|t = 2) denote the frequencies of admixture fractions i at generation 50 when the admixture was switched from process 1 to process 2 at generation t_c and 2 respectively. On average, we would expect SSD to be large if the switch from process 1 to process 2 has occured late in the whole process, because in this case the second process did not act long enough to reshape the frequencies of the admixture fractions that had been determined by the first process. Indeed, for all six models at each value of t_c ∈ {2, 3, …, 48}, we see this effect in figure 5: as t_c increases, the SSD increases.

All SSD values on the vertical axis (log scale) are very small indicating that the information carried in the frequencies of admixture fractions from the first process gets lost in a few generations if a second recurrent admixture process acts on the population. Different parameter combinations of ((a₁, b₁, h₁) relative to (a₂, b₂, h₂)) had very little effect on the magnitude of SSD. We note that models 1 and 2, models 3 and 4, and models 5 and 6 give almost identical results due to symmetry in the admixture parameters.

An implication of these results is that even a few generations of the second admixture process acting on the population is sufficient to erase the information about the introgression parameters of the first admixture process in the case of recurrent admixture.

4. Statistical properties of the distribution of admixture fractions

In this section we describe Bayesian procedures to sample the posterior distribution of introgression parameters under the single-stage recurrent admixture model of section 3.1. If sufficiently long time has passed since the start of the recurrent admixture process and there is no drift, then a sample from the admixed population is effectively from the stationary distribution of admixture fractions. In this case, we first obtain the posterior distribution of admixture fractions given a random sample of admixture fractions from an admixed population, and then we find the introgression parameters that produce this distribution using an optimization algorithm. Statistical inference is peformed in the first step, and mapping this inference to the introgression parameters takes place in the second step.

We let D = (D₁, D₂, …, D_K) be the K ≤ 2L + 1 admixture fractions calculated from L randomly chosen diagnostic biallelic loci independent from each other in the admixed population. We assume that the stationary distribution of admixture fractions, P(X = D_i|ϕ_i) = ϕ_i, has been reached and thus D is multinomially distributed with probabilities ϕ = (ϕ₁, ϕ₂, …,ϕ_K). The minimally informative Bayesian prior on the parameter ϕ for multinomially distributed data is Dirichlet with parameters (1/2, 1/2, …, 1/2). The Dirichlet distribution is the conjugate prior for the multinomial data model, which means that the posterior distribution of ϕ given the data D is also Dirichlet distributed with parameters (D₁ + 1/2, D₂ + 1/2, …, D_K + 1/2). This posterior distribution of population admixture fractions ϕ has the form

$$P(\varphi |D)\propto {\displaystyle \prod _{i=1}^K{\varphi }_i^{D_i+1/2}}.$$ (5)

Estimates of population admixture fractions follow from this posterior distribution. However, we are interested in estimates of introgression parameters and thus our task is to find a procedure to map estimates of admixture fractions to estimates of introgression parameters. If the genome consists of more than one locus¹, there is a vector of introgression parameters (a*, b*, h*) that produces probabilities $\varphi \ast =({\varphi }_1^{\ast },{\varphi }_2^{\ast },\dots ,{\varphi }_K^{\ast })$of admixture fractions through our admixture model. Finding the vector of introgression parameters that produce the probabilities of admixture fractions ϕ* is an optimization problem. We solve this problem by simulated annealing (SA) (see Appendix 1 for algorithm), a well-known optimization metaheuristic. To test the performance of our SA algorithm in finding the true values of introgression parameters given the population distribution of admixture fractions ϕ*, we randomly choose five test introgression parameter sets (a*, b*, h*) from a Dirichlet distribution with parameters (1,1,1) using L = 2, 3, 4, 5, 6 before considering a case with a larger number of loci. The convergence to true parameter values is illustrated in Figure 3.

Figure 3.

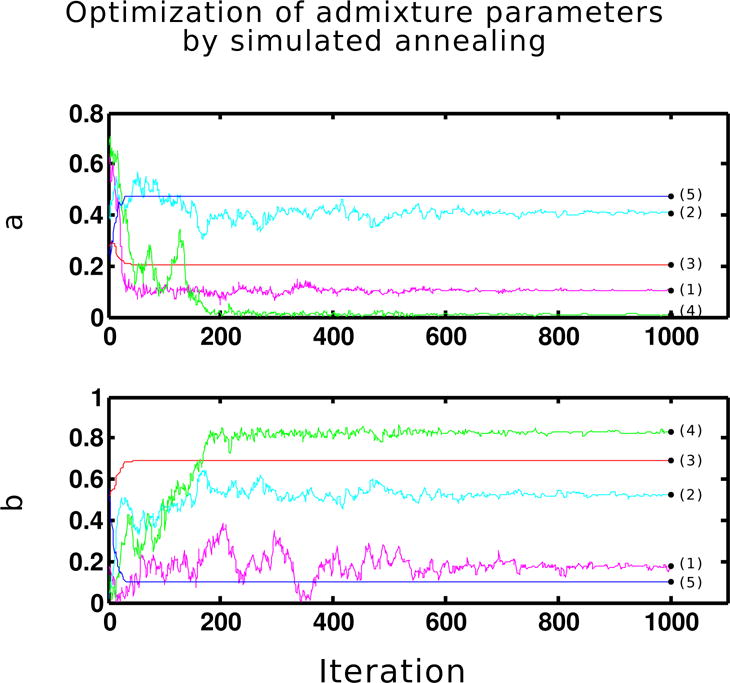
Optimization of introgression parameters (a, b, h) in five randomly generated test cases by simulated annealing algorithm (Appendix 1) given the distribution of admixture fraction. For each test case, a black dot at the end of 1000 iterations indicates the test parameter value under which the admixture fraction are simulated. The number of loci and the parameter values (a, b, h) used in test cases are as follows. (1): L = 6, (0.104, 0.177, 0.719). (2): L = 3, (0.407, 0.526, 0.07). (3): L = 4, (0.204, 0.691, 0.105). (4): L = 2, (0.009, 0.829, 0.162). (5): L = 5, (0.471, 0.101, 0.428).

The simulated annealing algorithm given in Appendix 1 finds introgression parameters that produce a given distribution of population admixture fractions. We do not observe these population admixture fractions, however, only a sample from this population. Therefore, our uncertainty about population admixture fractions will be reflected in our inference on introgression parameters. The posterior distribution of introgression parameters can be obtained in two steps. First, we obtain a random sample ϕ⁽ⁱ⁾, i = 1, 2, …, m of admixture fractions given the data D. This is a sample from the posterior distribution in equation 5, which is a Dirichlet distribution and hence computationally straightforward to sample. Second, we apply the simulated annealing algorithm on each sampled distribution of admixture fractions ϕ⁽ⁱ⁾, and find each set of introgression parameters (a⁽ⁱ⁾, b⁽ⁱ⁾, h⁽ⁱ⁾) producing these distributions of admixture fractions. These (a⁽ⁱ⁾, b⁽ⁱ⁾, h⁽ⁱ⁾) i = 1, 2, …, m values returned by the simulated annealing algorithm are a sample of size m from the posterior distribution of introgression parameters. For the same set of five test parameter sets used in the previous paragraph, Figure 4 shows the posterior samples of size m = 1000 obtained using this method.

Figure 4.

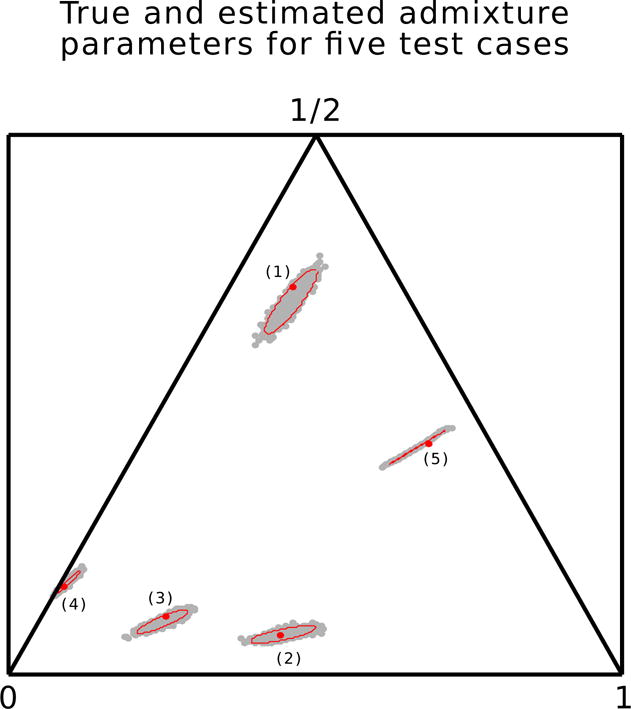
Posterior samples for five test cases. For each test case, the red dot indicates the test parameter value under which the admixture fractions are simulated, the gray cloud of points is a sample of size 1000 from the posterior distribution of parameters (a, b, h), and the red circle is a 95% elliptical interval based on the posterior sample. The number of loci and the parameter values (a, b, h) used in test cases are as follows. (1): L = 6, (0.104, 0.177, 0.719). (2): L = 3, (0.407, 0.526, 0.07). (3): L = 4, (0.204, 0.691, 0.105). (4): L = 2, (0.009, 0.829, 0.162). (5): L = 5, (0.471, 0.101, 0.428).

Any desired α percentile for the introgression parameters can be estimated by one run of the simulated annealing algorithm. First, we determine the lower ϕ(α) from the posterior sample of admixture fractions and find the α(α) of the interval estimates of introgression parameters by applying our simulated annealing algorithm. In particular, an interval of the desired level of credibility can be obtained by running the simulated annealing algorithm two times, once for the lower bound and once for the upper bound.

For our five simulated introgression parameter sets, Figure 4 shows inference on introgression parameters based on a sample of 1000 individuals from the simulated admixed populations. A sample of size 1000 from the posterior distribution is illustrated by clouds of gray dots for each simulated data set. Each cloud of points is obtained by first sampling m = 1000 admixture fraction points from the posterior distribution of admixture fractions and then applying simulated annealing algorithm on each point to find the introgression parameter value producing the given distribution of admixture fractions. 95% credible regions for each introgression parameters is shown by red ellipses, with ℓ = 0.025, u = 0.975 obtained by applying the simulated annealing algorithm twice. These 95% credible regions are precise and they show that our method using the simulating annealing algorithm to obtain interval estimates on introgression parameters works well in practice.

We conclude this section with some remarks on the estimation of introgression parameters in a large genome, that is when L is large. The number of theoretically possible haplotypes is given by 2^L, which grows exponentially. For large L, some haplotypes will either be missing in the population if the population size is smaller than 2^L, or exist at very low frequencies, and thus are unlikely to be sampled when the number of individuals in the sample is small relative to the population size. In these cases, the Bayesian procedure for inference on introgression parameters outlined in this section works well as an approximate method. Intuitively, we assume that the population consists only of haplotypes that are observed in the sample. Formally, this assumption is implemented by assigning a prior probability of zero to any haplotype that is not observed in the sample, resulting in zero posterior probability for these haplotypes. This assignment of zero prior probability to any haplotype not observed in the sample has also a computational advantage. When calculating the distribution of admixture fractions, only the frequencies of genotypes that result from pairing of the observed haplotypes —and not the genotypes that might have resulted from non-observed haplotypes—need to be calculated.

5. Discussion

Our main goals in this work were to better understand a priori the influence of complex admixture processes on the genetic evolution of hybrid populations, use intuitive distributions of admixture fractions, and investigate potentials of inferences for reconstructing the history of admixed populations using genetic data. Although not shown in this paper, we have also studied the joint estimation of duration of the admixture process t and introgression parameters (a, b, h) by simulation. We were confronted with estimability problems in the sense of weak identifiability of parameters. There are many parameter combinations where a process with: 1)little gene flow from source populations (small a, b) that acts for long periods of admixture (large t) or 2)large gene flow from source populations (large a, b) that acts for short periods of admixture (small t), produce practically indistinguishable distributions of admixture fractions. We believe that precise inferences about the introgression parameters require accurate information about the temporal properties of an admixture process. These properties consist either of the duration of admixture, the transient distribution of admixture fractions, and the initial frequencies of alleles, or the stationarity and the stationary distribution of admixture fractions. Using the transient distribution by conditioning on t to make inference on introgression parameters is an interesting idea, but accurate estimates of t from independent sources might not be available in practice.

If the stationarity has been reached, inferences of introgression parameters are considerably facilitated because the stationary distribution of admixture fractions can be calculated as in section 3, and this distribution is independent of initial frequencies of alleles. Statistical tests of stationarity could provide information about whether individuals in the hybrid population randomly mate according to their admixture levels. This is of interest for hybrid reintroduction programs or recurrent biological invasions involving admixture and/or hybridization with endogenous species (Hedrick 1994; Vergeer et al. 2004; Guillemaud et al. 2010; Kerdelhué et al. 2014). In these cases, it is often crucial to understand possible assortative matting mechanisms influencing the reproductive success of hybrids based on their admixture levels in order to predict future population dynamics including survival and expansion, or extinction.

Population genetics methods aiming at inferring the parameters of historical admixture processes using genetic data are increasingly applied to study, in particular, human admixture history at variable geographic and time scales (e.g. Hellenthal et al. 2014; Moreno-Estrada et al. 2013; Gravel et al. 2013; Raghavan et al. 2015; Skoglund et al. 2015; Mallick et al. 2016). These methods schematically rely whether on phylogenetic admixture graphs inferred using the allele frequency spectrum calculated from markers genotyped at the genome-wide scale (Reich et al. 2009; Patterson et al. 2012; Pickrell and Pritchard 2012; Lipson et al. 2013); or on linkage-disequilibrium decay and admixture-haplotype lengths distributions fitted to exponential curves derived under specific complex admixture models (Pool and Nielsen 2009; Moorjani et al. 2011; Gravel et al. 2012; Patterson et al. 2012; Loh et al. 2013; Hellenthal et al. 2014). These authors detailed and extensively warn users about the inherent limitations faced by these approaches. In particular, how poorly these methods may perform when the unknown admixture process underlying the data involves more than two pulses of admixture and/or recurring admixture mechanisms. Here, we demonstrate that if the admixture fractions in a hybrid population have reached stationarity, then drawing inferences about more ancient admixture events may be highly challenging. Moreover, in the simplest case of a single-stage recurrent admixture process, we show that the time needed to reach stationarity, although variable and depending on introgression parameters, can be relatively rapid on the order of 10 to 50 generations (Figure 3). Thus, while recent complex admixture processes may be accurately reconstructed using only present-day genetic data, inferring the parameters of more ancient admixture events might be misleading. In this context, the joint analyses of modern and ancient genetic data become crucial to accurately infer the parameters of more ancient historical processes (e.g. Raghavan et al. 2015; Kilinc et al. 2016; Lazaridis et al. 2014).

Our conclusions rely on the assumption that genetic markers used in the analysis are independent of each other. Independent markers are easier to work with since genetic data phasing still remains a challenging task involving uncertainties. Nevertheless, using linkage-disequilibrium data provides massive amounts of information about the underlying admixture mechanisms, as shown by numerous successful admixture-LD approaches applied to human genomic data (Gravel et al. 2012, 2013; Hellenthal et al. 2014; Malick et al. 2016). Therefore, a natural direction for future theoretical work similar to ours is to focus on LD patterns in hybrid populations having experienced complex admixture processes, to better understand a priori what information can be accurately extracted from real genomic data about historical admixture models and parameters.

Appendix 1: Simulated annealing (SA) algorithm for optimization of parameters given the population admixture fraction

SA is an iterative metaheuristic to minimize a function [27]. The algorithm starts at an arbitrary value (a⁽⁰⁾, b⁽⁰⁾, h⁽⁰⁾) on the parameter space and at each iteration replaces the current value with a proposed random solution (a^(*), b⁽*⁾, h⁽*⁾) with probability 1 if the proposed solution is a better minimizer of the objective function, or with a probability function if it is a worse solution. A temperature parameter T that decreases with time controls the probability of accepting a worse solution decreases with the number of iterations.

We minimize the total variation distance between the distribution of the observed x_o and the proposed x* distribution of admixture fractions. The total variation distance is given by $(1/2){\displaystyle {\sum }_{i=1}^{2L+1}|p(D_i)}-p(x_i^{\ast })|$, where p(D_i) and $p(x_i^{\ast })$ are the probabilities of the admixture fraction i in the observed and the proposed distribution respectively. We set an exponential cooling schedule where temperature at iteration i + 1 iteration is 0.95% of the temperature at iteration i. We set the temperature at the first and final iterations to T₀ = 0.7 and T_f = 0.001 respectively.

1. Initialize

   1. Set T^(c) = T₀ = 0.7, T_f = 0.01, α = 0.95,
   2. Set the estimated probability of admixture fraction i to P(D_i)
   3. Simulate (a^(c), b^(c), h^(c)) ~ Dirichlet(1, 1, 1)
   4. Calculate the current distribution P(x|a^(c), b^(c), h^(c)) analytically
   5. Calculate the current energy:

      $$Ec=(1/2){\displaystyle {\sum }_{i=1}^{2L+1}|P(D_i)-P(x_i|a^{(c)},b^{(c)},h^{(c)})}|$$
2. While T^(c) > T_f repeat:

   1. 6. Propose a new parameter value (a^(p), b^(p), h^(p)) ~ Dirichlet(1, 1, 1)
   2. 7. Calculate the proposed distribution P(x|a^(p), b^(p), h^(p)) analytically
   3. 8. Calculate the proposed energy:

      $Ep=(1/2){\displaystyle {\sum }_{i=1}^{2L+1}|P(D_i)}-P(x_i|a^{(p)},b^{(p)},h^{(p)})|$
   4. 9. Simulate u ~ Unif(0, 1)
   5. 10. If u < e^{−|Ep−Ec|/T(c)}, set (a, b, h) = (a^(p), b^(p), h^(p)), Ec = Ep
   6. 11. Set T^(c) = αT^(c)