Folding artificial mucosa with cell-laden hydrogels guided by mechanics models

Significance

While mucosal folding is a ubiquitous phenomenon observed in many hollow or tubular human tissues/organs, recapitulating the process for tissue engineering has yet to be achieved. Here we fold a cell-laden hydrogel film to recapitulate the folding of a physiologically mimicking artificial mucosa. We attach the cell-laden hydrogel film onto a prestretched tough-hydrogel substrate, which after relaxation induces controlled patterns in the artificial mucosa. A combination of theory and numerical simulations predicts the folding conditions and the morphologies, thereby guiding the design of surface folding. This simple strategy can facilitate the understanding and engineering of mucosa for tissues/organs such as stomach, colon, and intestine. The work also demonstrates a paradigm in tissue engineering via harnessing mechanical instabilities guided by quantitative mechanics models.

Abstract

The surfaces of many hollow or tubular tissues/organs in our respiratory, gastrointestinal, and urogenital tracts are covered by mucosa with folded patterns. The patterns are induced by mechanical instability of the mucosa under compression due to constrained growth. Recapitulating this folding process in vitro will facilitate the understanding and engineering of mucosa in various tissues/organs. However, scant attention has been paid to address the challenge of reproducing mucosal folding. Here we mimic the mucosal folding process using a cell-laden hydrogel film attached to a prestretched tough-hydrogel substrate. The cell-laden hydrogel constitutes a human epithelial cell lining on stromal component to recapitulate the physiological feature of a mucosa. Relaxation of the prestretched tough-hydrogel substrate applies compressive strains on the cell-laden hydrogel film, which undergoes mechanical instability and evolves into morphological patterns. We predict the conditions for mucosal folding as well as the morphology of and strain in the folded artificial mucosa using a combination of theory and simulation. The work not only provides a simple method to fold artificial mucosa but also demonstrates a paradigm in tissue engineering via harnessing mechanical instabilities guided by quantitative mechanics models.

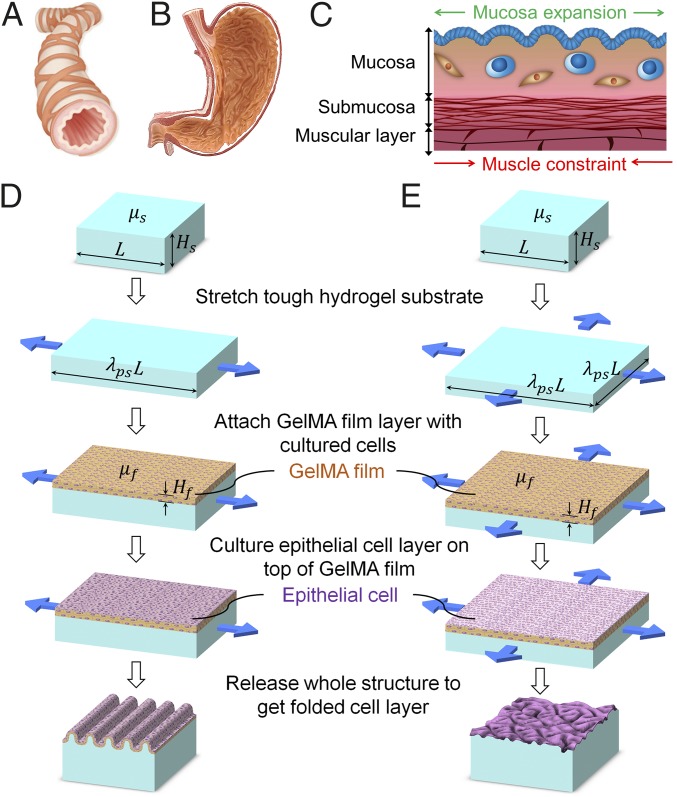
The interior surfaces of many hollow or tubular biological structures such as respiratory, gastrointestinal, and urogenital tracts are not completely smooth, but covered by mucosa with folded structures (1, 2). These surface features can be categorized into uniaxial patterns as found in the bronchus (Fig. 1A) and biaxial patterns as found in the stomach (Fig. 1B) (3, 4). In general, the mucosa consists of one or multiple layers of epithelial cells overlying a stromal layer of loose connective tissue called lamina propria. The stromal compartment contains cell types such as fibroblasts, lymphocytes, and macrophages. Underneath the mucosa is submucosa, another layer of connective tissue, and muscular layer(s) (Fig. 1C) (5). The occurrence of mucosal folding is due to the higher growth rate in the mucosa compared with the underneath muscular layer during development (1, 2, 5–7), which applies compressive strains on the constrained mucosa and consequently induces mechanical instability in the mucosa. The folded mucosa serves important functions. First, in organs such as intestine and colon, the morphological patterns in mucosa significantly increase the surface areas for absorption of nutrients and water (8). Second, the folded mucosa can facilitate the passage of luminal contents, since unfolding of the mucosa allows the tissue/organ to significant expand its luminal diameter without inducing high stresses that may cause injury to the mucosa (5, 9, 10). Given the importance of mucosal folding, recapitulating the phenomenon with cell-laden materials in vitro will not only provide new strategies and design guidelines for engineering a variety of relevant tissues/organs, but also facilitate the understanding of surface morphological development of biological structures. However, while it is possible to grow epithelial cell layers with surface patterns on textured substrates (11–14), existing techniques still cannot reproduce the mucosal folding process induced by compressive strains and mechanical instability. The lack of feasible method as well as suitable biomaterial to reproduce mucosal folding process and physiologically mimicking mucosa has been a grand challenge in the field.

Fig. 1.

(A) Schematic showing the uniaxial patterns developed on the lumen of typical tubular structures such as bronchus. (B) Schematic showing the biaxial patterns developed on the lumen of typical organs such as stomach. (C) The generic structure of the organ wall found in the digestive, respiratory, or reproductive tracts and the mechanism for the formation of pattern. Schematics showing the design of the method to (D) uniaxially and (E) biaxially fold an artificial mucosa.

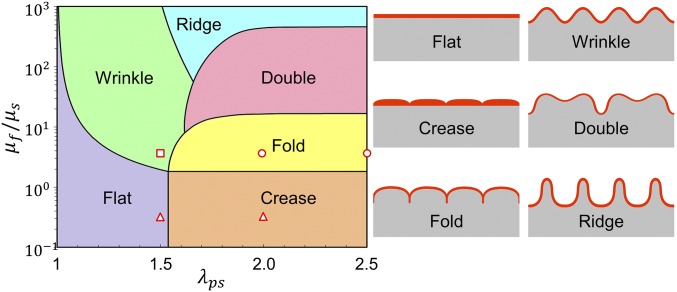
In this paper, we report a simple method to mimic the mucosal folding process induced by compression and mechanical instability using a cell-laden hydrogel film bonded on a prestretched tough-hydrogel substrate. The cell-laden hydrogel acts as an artificial mucosa constituting a human epithelial cell lining on stromal component. Relaxation of the prestretched tough-hydrogel substrate applies controlled compressive strains on the cell-laden layer, which undergoes mechanical instability and evolves into folded patterns. In general, a thin film compressed on a substrate can develop various patterns due to mechanical instability such as wrinkle, crease, period-double, ridge, and fold (15–23) (Fig. 2). The selection of a certain mode of instability pattern depends on the compressive strain applied on the film and the modulus ratio between the film and substrate (20, 24–28). To achieve a desired pattern in the cell-laden hydrogel film, we use a theoretical model and numerical simulation to guide the selection of hydrogel materials and the prestretch ratio in the tough-hydrogel substrate, which in turn determines the compressive strain on the cell-laden hydrogel film (29, 30). The model and simulation further predict the morphology of and the strain distribution in the patterned artificial mucosa. Furthermore, we demonstrate both uniaxial and biaxial patterns achieved in artificial mucosa using the cell-laden hydrogel system and simulation. Overall, the work not only provides a simple method to mimic the folding process of a mucosa but also demonstrates a paradigm in tissue engineering, that is, to achieve morphological patterns of engineered tissues/organs via harnessing mechanical instability of cell-laden scaffolds guided by quantitative mechanics models.

Fig. 2.

A phase diagram for predicting the formation of various instability patterns. In the current study, we select multiple combinations of shear modulus ratio ${\mu }_f/{\mu }_s$ and prestretch ratio ${\lambda }_{ps}$ as indicated by the markers on the phase diagram to achieve various patterns.

Results

Design of the Method for Folding an Artificial Mucosa.

The proposed method to fold an artificial mucosa is schematically illustrated in Fig. 1 D and E to achieve uniaxial and biaxial patterns, respectively. In the first step, we fabricate a substrate of a tough hydrogel, made of interpenetrating polymer networks of polyacrylamide (PAAm) and alginate, with thickness of H_s and length and width of L. The covalently cross-linked PAAm network maintains elasticity while the reversibly cross-linked alginate network dissipates mechanical energy under deformation, leading to a tough and stretchable hydrogel (31, 32). The shear modulus of the tough hydrogel μ_s can be tuned by varying the cross-linking density of PAAm (33). The tough-hydrogel substrate is then bonded to holders made of polydimethylsiloxane (PDMS) on either two or four sides (34) to allow mechanical manipulation of the substrate in later steps. The tough-hydrogel substrate with holders is soaked in PBS overnight to leach out unreacted chemical residuals. Thereafter, the tough-hydrogel substrate is stretched uniaxially along the length direction or biaxially along both length and width directions to a length of λ_psL and maintained at the deformed state (Fig. 1 D and E, respectively), where λ_ps is defined as the prestretch ratio. In a later step, the prestretched tough-hydrogel substrate will be relaxed to apply compressive strain on an artificial mucosa above it, mimicking the role of the muscular layer that constrains mucosal expansion.

In the second step, a hydrogel film of gelatin methacrylate (GelMA) encapsulated with stromal cell line hTERT-immortalized human endometrial stromal cells (tHESCs) is fabricated on the prestretched tough-hydrogel substrate (35). Then a layer of epithelial cell (Ishikawa human endometrial adenocarcinoma cells) is cultured on top of the GelMA film for 3–5 d until it becomes confluent. The GelMA hydrogel is commonly adopted for cell encapsulation applications as well as promoting cell attachments on its surfaces (35), making it suitable to construct the artificial mucosa with epithelial and stromal components. The thickness H_f and shear modulus μ_f of the cell-laden hydrogel film are mainly determined by the GelMA film, which can be tuned as well (35).

In the third step, the prestretched tough-hydrogel substrate is relaxed to its undeformed dimensions (Fig. 1 D and E). Consequently, the relaxation of uniaxially or biaxially prestretched substrate applies a uniaxial or biaxial compressive strain, respectively, on the cell-laden hydrogel film. If the applied compressive strain and mechanical properties of hydrogel film–substrate structure satisfy certain conditions, the cell-laden hydrogel film undergoes mechanical instability and evolves into the desired uniaxial or biaxial patterns (see SI Appendix, Fig. S1 for fabrication of uniaxial pattern).

Theory and Simulation for Folding Artificial Mucosa.

In general, a thin film compressed on a substrate can develop various modes of instability patterns to mimic those found in a native mucosa, including wrinkle, crease, period-double, ridge, and fold (15–22) (Fig. 2). The selection of certain mode of instability pattern depends on the compressive strain applied on the film and the modulus ratio between the film and substrate (20, 24–26). A phase diagram that can predict the instability pattern with input parameters of applied compressive strain and film–substrate modulus ratio has been developed in previous theoretical studies and numerical simulations (19, 36). In Fig. 2, we replot the phase diagram based on the prestretch ratio of the tough-hydrogel substrate λ_ps and the modulus ratio between the cell-laden hydrogel film and tough-hydrogel substrate ${\mu }_f/{\mu }_s$. Guided by the phase diagram (Fig. 2), we first set the shear modulus of the GelMA film (10 wt %) to be 16 kPa and tough-hydrogel substrate to be 4 kPa (i.e., ${\mu }_f/{\mu }_s=4$) and prescribe the prestretch ratios of the substrate to be 2 and 2.5 (see SI Appendix, Fig. S2 A and B for measurement of shear modulus), to achieve the instability pattern of fold in the artificial mucosa (i.e., circular markers in Fig. 2). Thereafter, we either reduce the prestretch ratio to 1.5 to achieve the pattern of wrinkle (i.e., square marker in Fig. 2) or reduce the shear modulus of GelMA film to 1.4 kPa to achieve the pattern of crease (i.e., ${\mu }_f/{\mu }_s=0.35$, triangular markers in Fig. 2) (see SI Appendix, Fig. S2C for measurement of shear modulus). From Fig. 3 A and B, when ${\mu }_f/{\mu }_s=4$ and ${\lambda }_{ps}=\mathrm{2,2.5}$, the pattern of fold indeed forms in the GelMA film on tough-hydrogel substrate. Furthermore, when ${\mu }_f/{\mu }_s=4$ and ${\lambda }_{ps}=1.5$, the pattern of wrinkle occurs (Fig. 3B); when ${\mu }_f/{\mu }_s=0.35$ and ${\lambda }_{ps}=1.5$, the GelMA film maintains flat (SI Appendix, Fig. S3A); and when ${\mu }_f/{\mu }_s=0.35$ and ${\lambda }_{ps}=2$, the pattern of crease appears on the film–substrate structure (SI Appendix, Fig. S3B). These results validate that the phase diagram can guide one to achieve desired instability patterns potentially for tissue engineering by selecting appropriate prestretch ratio and modulus ratio in hydrogels (Fig. 2).

Fig. 3.

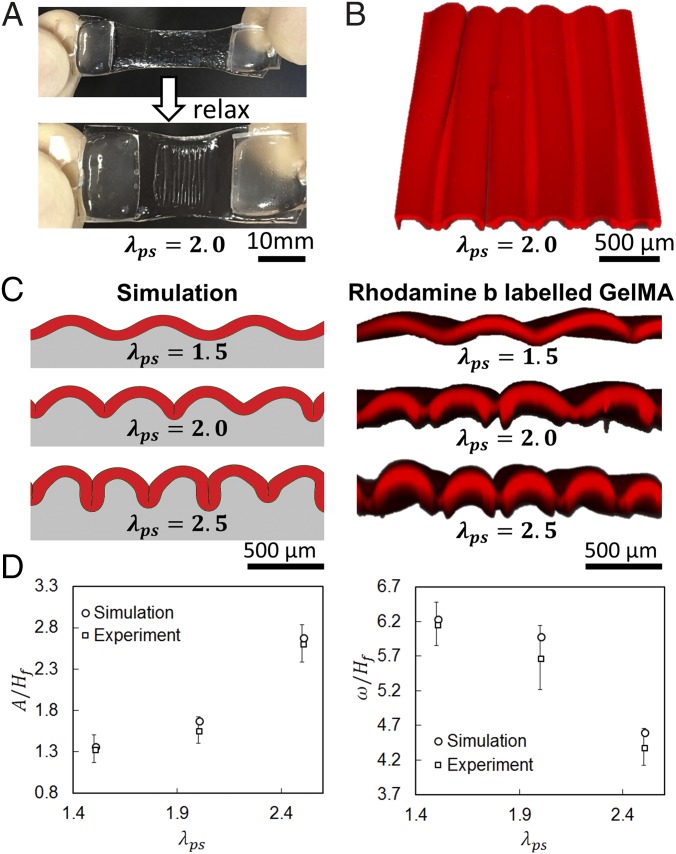
(A) GelMA-coated prestretched tough hydrogel before and after uniaxial relaxaxation. (B) Top view of Rhodamine-B–labeled GelMA (3D confocal reconstruction) showing the surface morphology. (C) Comparison of simulation and experimental results on the patterns formed in GelMA (3D confocal reconstruction of Rhodamine-B–labeled GelMA) on substrates with various prestretch ratios. (D) Comparison of simulation and experimental results on the pattern amplitude and pattern wavelength of the folded GelMA film (experimental data represent mean ± SD, n = 3).

To predict the folding process and the morphology of a folded artificial mucosa on substrates with various prestretch ratios, we further develop a finite-element model to simulate the deformation and instability of the film–substrate structures (See SI Appendix, Supplementary Method for details). In the model, we set both the cell-laden hydrogel film and tough-hydrogel substrate as incompressible neo-Hookean materials with ${\mu }_f/{\mu }_s=4$, ${\lambda }_{ps}=1.5,\mathrm{2,2.5}$, $H_f=100\hspace{0.17em}\mathrm{\mu }\text{m}$ and $H_s=1.5\hspace{0.17em}\text{mm}$, the same as their corresponding values in the experiments. From Fig. 3B, it can be seen that the patterns of the artificial mucosa predicted by the model match well with the experimental results. In Fig. 3C, we further compare the wavelength w (i.e., distance between two adjacent folds) and amplitude A (i.e., distance between the peak and valley of neutral axis on the film; see SI Appendix, Fig. S4 for detailed definition) of the patterns from the model and experiments. The quantified w and A are 380–745 µm and 117–369 µm respectively, and the values are normalized with H_f (81–222 µm). Our results show that the model can quantitatively predict the wavelength w and amplitude A of the folded artificial mucosa.

Uniaxially Folding Artificial Mucosa.

Next we demonstrate the uniaxial folding of the artificial mucosa with relevant cells incorporated. We have encapsulated tHESCs in the GelMA hydrogel film to mimic the stromal compartment in the mucosa. Fig. 4A illustrates the folded GelMA encapsulated with tHESCs and stained for live and dead cells immediately after the folding process, for film–substrate system with modulus ratio ${\mu }_f/{\mu }_s=4$ and prestretch ratios ${\lambda }_{ps}=1.5,\mathrm{2,2.5}$. The cell viability in all cases was over 90%, displaying no significant difference compared with the control case with undeformed GelMA hydrogel film (SI Appendix, Fig. S5).

Fig. 4.

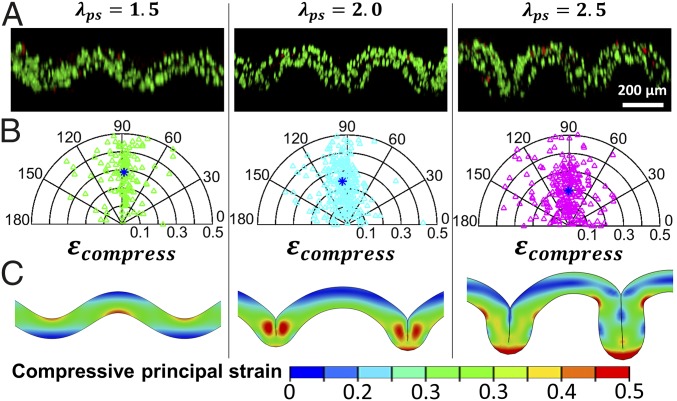
(A) 3D confocal reconstruction of stromal-cells–laden GelMA stained for live and dead cells for the system with modulus ratio ${\mu }_f/{\mu }_s=4$ and prestretch ratio of the substrate ${\lambda }_{ps}=1.5,\hspace{0.17em}2,\hspace{0.17em}\text{and}\hspace{0.17em}2.5$ (substrate is not shown here). Green and red indicate live and dead cells, respectively. (B) Corresponding polar plot for the orientation angles and compressive strains of 150 randomly selected cells in each folded GelMA film shown in A. Blue asterisk indicates the average compressive strain and orientation angle. (C) Corresponding simulation results on contours showing the distribution of compressive principal strains in each folded GelMA film shown in A.

From the z-stack images used to reconstruct Fig. 4A, we discover that upon applied mechanical load, the shape of stromal cells in the folded GelMA hydrogel film is not spherical but ellipsoidal, indicating that the stromal cells have been compressed (or stretched due to incompressibility). We assume that a cell takes a spherical shape with radius r at the undeformed state and deforms into an ellipsoid with axes of a, b, and r due to uniaxial compression. The compressive strain in the cell can be calculated as ${\epsilon }_{\text{compress}}=\left(r-\mathrm{a}\right)/r\equiv 1-{\left(a/b\right)}^{\left(1/2\right)}$ assuming the cell is incompressible (SI Appendix, Fig. S6). In addition, once the cell is deformed into an ellipsoid, it has an orientation angle as illustrated in SI Appendix, Fig. S6. In Fig. 4B, we summarize the compressive strains and orientation angles of 150 randomly selected cells in each folded GelMA hydrogel film on substrate with prestretched ratio of 1.5, 2, or 2.5. The compressive strains of the cells are in the range of 0–0.5 with average compressive strains of 0.29, 0.26, and 0.19 for prestretch ratios of 1.5, 2, and 2.5, respectively (Fig. 4B). The orientation angles of the cells tend to distribute around 90° due to the uniaxial compression on the GelMA hydrogel film by the substrate. We further use our finite-element model to simulate the deformation of folded artificial mucosa on substrates with prestretch ratios of 1.5, 2, and 2.5 (Fig. 4C). The calculated compressive principal strains in the folded artificial mucosa from our model are in the range of 0–0.5, consistent with experimental results (Fig. 4C). It is important to note that the compressive strains in the cells are measured immediately after the folding of the artificial mucosa to quantitatively compare with our model’s predictions. For long-term cell culture, the cell shape is influenced by other factors such as the physical and biochemical properties of the extracellular matrix (ECM) such as stiffness, stress relaxation, topography, and presence of degradable motif (37–41). Those factors should be taken into consideration when investigating cell response to long-term dynamic deformation.

An essential feature of the mucosa is the presence of epithelium, which provides functions such as protection of underlying tissues, regulation of molecular transport, and secretion of mucus. Here we use an epithelial cell line (Ishikawa) to supplement the epithelium on the stromal component to physiologically mimic the native mucosa (SI Appendix, Fig. S7A). We coculture tHESCs in and Ishikawa cells on the GelMA film attached on a prestretched tough-hydrogel substrate. The Ishikawa cells are identified via immunostaining for Cytokeratin 18 (CK-18) (SI Appendix, Fig. S7B). The Ishikawa cells proliferate to form a confluent epithelial sheet after 3–5 d (SI Appendix, Fig. S7C), during which Ishikawa cells and tHESCs are cocultured in the same culture medium. We then relax the substrate to generate the folded pattern as shown in Fig. 5. Both the flat and folded coculture systems exhibit excellent viability of tHESCs and Ishikawa cells as evidenced by live–dead staining (Fig. 5A). The presence of both epithelium and stroma is also confirmed by immunostaining of CK-18 (specific for Ishikawa) and phalloidin staining for F-actin (staining both Ishikawa and tHESCs) (Fig. 5B).

Fig. 5.

(A) Three-dimensional confocal reconstruction of coculture of Ishikawa cells and tHESCs stained for live and dead cells. The transition of flat to folded states after relaxation of the prestretched substrate with ${\lambda }_{ps}=2$ is demonstrated. Note that due to attenuation of fluorescent signal in the hydrogel, two sets of z-stack images are taken at different gains to capture epithelial and stromal components separately before they are integrated into one single 3D reconstruction image. (B) Three-dimensional confocal reconstruction of cocultured artificial mucosa which is fixed and stained. Encapsulated tHESCs are stained with phalloidin for F-actin in GelMA while Ishikawa cells are stained with both CK18 and phalloidin on the surface of GelMA. Nuclei are stained with Hoechst. Note that the staining of phallodin is overexposed to better visualize the encapsulated tHESCs due to signal attenuation in the presence of epithelium.

Biaxially Folding Artificial Mucosa.

In organs such as stomach and urinary bladder, the arrangement of mucosal pattern is not uniaxial but more similar to biaxial zigzag to accommodate the stretching of the organs in multiple directions (Fig. 1B) (42). The development of intestinal villi is also believed to progress through a zigzag state before maturing into individual finger-like structure (43). In human body, such biaxial zigzag pattern is generated by a sequential differentiation of smooth muscle cells to restrict the expansion of epithelium in two perpendicular directions. To fabricate such a biaxial pattern, we coat a GelMA hydrogel film on the PAAm-alginate hydrogel substrate biaxially prestretched to ${\lambda }_{ps}=1.5$. After the prestretched substrate is relaxed, a zigzag pattern of biaxial folds is produced in the GelMA film (Fig. 6A). Our simulation recapitulates consistently the morphological pattern of biaxial folds experimentally observed in the film–substrate system with modulus ratio ${\mu }_f/{\mu }_s=4$ and prestretch ${\lambda }_{ps}=1.5$ (Fig. 6 B and C). To fabricate a physiologically mimicking mucosa with biaxial folds, we further coculture Ishikawa cells on and tHESCs in the GelMA film bonded on a tough-hydrogel hydrogel substrate biaxially prestretched to ${\lambda }_{ps}=1.5$. After the Ishikawa cells have formed a confluent epithelial layer in 3–5 d, we relax the substrate to trigger the instability in the GelMA film (Fig. 6D), with Ishikawa cells forming the epithelium and tHESCs constituting the stromal compartment.

Fig. 6.

(A) GelMA-coated prestretched tough hydrogel before and after equal biaxial relaxation. (B) Simulation result on biaxial folding of the GelMA film on substrate with modulus ratio ${\mu }_f/{\mu }_s=4$ and biaxial prestretch ratio ${\lambda }_{ps}=1.5$. (C) Three-dimensional confocal reconstruction of Rhodamine-B–labeled GelMA film biaxially folded on substrate with modulus ratio ${\mu }_f/{\mu }_s=4$ and biaxial prestretch ratio ${\lambda }_{ps}=1.5$. (D) Three-dimensional confocal reconstruction of coculture of Ishikawa cells and tHESCs in biaxially folded GelMA. Encapsulated tHESCs are stained with phalloidin for F-actin (red) while the Ishikawa cells are stained with both CK18 (green) and phalloidin for F-actin (red) on the surface of GelMA. Nuclei are stained with Hoechst. Note that the staining of phallodin is overexposed to better visualize the encapsulated tHESCs due to signal attenuation in the presence of epithelium. A clipping function is performed to remove part of the image to reveal the underneath structure.

Discussion

Tissue engineering continues to impact tissue replacement, disease modeling, and drug development (44, 45). In particular, the engineering of hollow or tubular organs such as stomach, intestine, and urinary bladder remains important as the treatment of diseases such as stomach cancer and inflammatory bowel disease often necessitates the removal of part of the organ (46–49). Despite the early success of using biomaterials such as collagen and polyglycolic acid to regenerate the mucosa and muscular layer for different organs (48, 50), limited functional improvement such as insignificant change in bladder volume has been recorded after the implantation of tissue-engineered stomach and urinary bladder (49, 51). Therefore, an improved strategy of tissue engineering is desired (47, 52). So far, none of the previous studies has recapitulated the folding process of physiologically mimicking mucosa or reproduced the compressive residual strains in engineered mucosa by learning lesson from the tissue/organ developmental process.

In this paper, we mimic the mucosal folding process induced by compression and mechanical instability using a cell-laden artificial mucosa bonded on a prestretched tough-hydrogel substrate. To quantitatively compare the morphologies and folding conditions of our artificial mucosa with its in vivo biological counterparts, we have summarized the morphologies and conditions of in vivo mucosal folding published in literature (SI Appendix, Table S1). Although the properties of an in vivo mucosa are region- and species-dependent, the moduli (1.4–16 kPa) and thicknesses (81–222 µm) of our artificial mucosa indeed overlap with the corresponding properties of various in vivo mucosa (SI Appendix, Table S1). The prestretches in the substrates to fold our artificial mucosa (1.5–2.5) are also consistent with the effective prestretches of the muscular layers beneath the mucosa in vivo (43, 53). In addition, the folded patterns formed in our artificial mucosa (crease, wrinkle, and fold) and their wavelengths (380–745 µm) have also been observed in various mucosa in vivo (SI Appendix, Table S1). These results validate that our approach of reproducing the mucosal folds is quantitatively consistent with in vivo biological morphologies and conditions. Compared with previous in vitro models of mucosal folding, the current study is of particular in vivo relevance, because it quantitatively guides the folding of artificial mucosa loaded with in vivo relevant cells (i.e., cocultured epithelial and stromal cells).

With our capability of folding an artificial mucosa, we also demonstrate the important role of folded mucosa in accommodating high stretches of underlying tissues. We culture a confluent epithelium (Ishikawa cells) layer on a uniaxially folded GelMA film attached to a tough-hydrogel substrate with ${\mu }_f/{\mu }_s=4$ and ${\lambda }_{ps}=2$ (Fig. 7A and SI Appendix, Fig. S8). As a control case, we culture an epithelium (Ishikawa cells) layer on an unstretched tough-hydrogel substrate to confluency (Fig. 7B). Thereafter, we uniaxially stretch both substrates by a ratio of 2 to mimic the process when a tissue/organ such as stomach or bladder expands its luminal diameter. Nuclei staining reveals much less severe deformation of cells in the folded epithelium layer (Fig. 7C) than the flat epithelium (Fig. 7D), since unfolding of the folded epithelium layer (Fig. 7C) accommodates the excessive stretch from the substrate. In addition, we introduce to both stretched epithelium layers a cell-impermeable dye (FM 1–43) whose fluorescence increases upon binding the endomembrane. Rupture of cell membrane will result in the entry of the dye into the cells, leading to binding with the endomembrane and increase in fluorescence. The flat epithelium layer on stretched substrate shows significant fluorescence, but not the unfolded epithelium layer, indicating the integrity of cell membranes in the unfolded layer. These experiments clearly demonstrate that the folded mucosa protects the epithelium from damage during the expansion of luminal diameter. It is also possible to study other physiologically relevant functions of the folded mucosa with the method developed in the current work. Since we can easily tune the substrate thickness in fabrication and numerical model, the technique can also find use in applications such as microfabricating a biomimetic gut-on-a-chip model (54).

Fig. 7.

Three dimensional confocal reconstruction of Ishikawa cells on (A) folded GelMA film and (B) flat tough-hydrogel substrate. The cells are stained for live (green) and dead (red) cells. The dashed lines indicate the morphology of the GelMA film. Comparison of Ishikawa cells on (C) folded GelMA film and (D) flat tough-hydrogel substrate in response to uniaxial stretch via analysis of nuclei deformation and FM 1–43 dye entry.

There are other morphological patterns induced by mechanical instabilities of film–substrate structures present in biological systems, such as ridge found in intestinal villi (55). To recapitulate these patterns in engineered tissues or organs, we have provided a phase diagram (Fig. 2) to rationally guide the selection of film–substrate modulus ratio and prestretch ratio of the substrate. For example, to generate the pattern of ridge, one needs to select biomaterials that give a much higher film–substrate modulus ratio than that for fold or crease (Fig. 2). Furthermore, one common requirement for creating various patterns is the use of a stretchable substrate with modulus much lower than common elastomers such as PDMS. While many hydrogels can satisfy the requirement of relatively low modulus, they are usually mechanically weak (56, 57). We demonstrate that recently developed tough hydrogels such as PAAm-alginate hydrogel can be a good candidate for the substrate material in future works. The hydrogels can be easily made biodegradable, and tunable with the rate of biodegradation. For in vitro applications like organ-on-a-chip, we likely will not introduce that variable to overcomplicate the design. For tissue replacement, the regeneration process in vivo will replace the biodegradable hydrogel with ECM. In addition, better strategy to adhere the film material onto the substrate without causing delamination is required, such as using one of the novel tissue adhesives recently developed (58).

In this project, we develop the folded mucosa using two well-defined cell lines to eliminate the possible variability associated with primary cells. We expect that the fundamental findings of this study will hold true in samples constructed from normal cells, although the magnitude of the response might differ. For instance, transformed epithelial cells would form a confluent epithelium faster than normal cells due to their higher proliferation rate. The elastic modulus measured with transformed fibroblast is shown to be lower than that of normal cells (59). Besides, we adopt tough hydrogel to replace the smooth muscle layer to impose compressive stress on the mucosa in this study. As our next step, we will improve our design to introduce smooth muscle cells (to generate compressive stress and mechanical pulsation) and submucosa (to supplement vasculature and nerves) to better recapitulate the functions of organ/tissue such as intestine and stomach.

Conclusion

We report a simple method to recapitulate the mucosal folding process using a cell-laden hydrogel film on a tough-hydrogel substrate. Relaxation of the prestretched tough-hydrogel substrate applies controlled compressive strains in the cell-laden hydrogel film containing epithelial and stromal components, which undergoes mechanical instability and evolves into patterned structure. Moreover, we use theory and finite-element simulation to predict critical conditions for mucosal folding and the morphologies of folded artificial mucosa, providing guidance to material selection and design of surface morphologies. This work represents a unique marriage of the fields of mechanics and biomaterials to provide a paradigm in tissue engineering via manipulation of mechanical instabilities of cell-laden scaffolds.

Materials and Methods

All details associated with the finite-element method, cell culture, and characterizations appear in SI Appendix, Supplementary Methods.

The stretchable tough-hydrogel hydrogel contains two components: PAAm and alginate. For PAAm, acrylamide (AAm; A8887; Sigma-Aldrich) was used as the monomer, N,N′-methylenebisacrylamide (MBAA; 146072; Sigma-Aldrich) was used as the cross-linker, ammonium persulfate (APS; 248614; Sigma-Aldrich); and N,N,N′,N′-tetramethylethylenediamine (TEMED; T9281; Sigma-Aldrich) were used as the initiator, respectively. Calcium sulfate (C3771; Sigma-Aldrich) was used as the ionic cross-linker for sodium alginate (A2033; Sigma-Aldrich).