Significance
Assembling 2D materials into vertically stacked heterostructures allows an unprecedented control over their properties. The interaction between the individual crystals plays the crucial role here; thus, the information about the local atomic stacking is of great importance. Still, there are no techniques which would allow investigation of the stacking between such crystals with any reasonable throughput. We present the use of convergent beam electron diffraction (CBED) to investigate the quality of the interface in such heterostructures. We demonstrate that defects such as misorientation, strain, ripples, and others can be visualized, and quantitative information about such structures can be easily extracted. Furthermore, CBED images can be treated as holograms; thus their reconstruction gives 3D profiles of the heterostructures over a large area.
Keywords: graphene, two-dimensional materials, van der Waals structures, electron holography, convergent beam electron diffraction
Abstract
The van der Waals heterostructures, which explore the synergetic properties of 2D materials when assembled into 3D stacks, have already brought to life a number of exciting phenomena and electronic devices. Still, the interaction between the layers in such assembly, possible surface reconstruction, and intrinsic and extrinsic defects are very difficult to characterize by any method, because of the single-atomic nature of the crystals involved. Here we present a convergent beam electron holographic technique which allows imaging of the stacking order in such heterostructures. Based on the interference of electron waves scattered on different crystals in the stack, this approach allows one to reconstruct the relative rotation, stretching, and out-of-plane corrugation of the layers with atomic precision. Being holographic in nature, our approach allows extraction of quantitative information about the 3D structure of the typical defects from a single image covering thousands of square nanometers. Furthermore, qualitative information about the defects in the stack can be extracted from the convergent diffraction patterns even without reconstruction, simply by comparing the patterns in different diffraction spots. We expect that convergent beam electron holography will be widely used to study the properties of van der Waals heterostructures.
Stacking 2D materials into van der Waals heterostructures offers an unprecedented control over the attributes of the resulting devices (1, 2). Initially, the individual layers in the stack were considered to be independent, which offers a reasonable zero-order approximation of the properties of such heterostructures. However, as we gain better and better control over the stacking arrangement between the individual components and the cleanliness of the interfaces, the interaction between the individual crystals becomes more and more important, and can even dominate the performance of the structures.
Still, it is very difficult to extract the detailed information about the stacking. Cross-sectional transmission electron microscopy (TEM) imaging (3) allows atomic-scale information on the structure and chemistry of the buried interface between the individual crystals to be obtained. Unfortunately, this technique requires sophisticated sample preparation, is time-consuming, and only yields data on a thin slice of the sample, which is not necessarily representative of the large-area device. Preferential scattering detection in the scanning TEM has been recently demonstrated to allow determination of atomic stacking for well-aligned graphene/boron nitride heterostructures, but it requires a custom aperture configuration and is based on atomic resolution imaging compared with relaxed density functional theory (DFT) modeling, so is inherently limited to a small field of view (4). Thus, the whole field of van der Waals heterostructures would benefit enormously from a technique which allows one to extract 3D structure for the buried interfaces inside such stacks on a larger scale.
Convergent beam electron diffraction (CBED) (5) has been previously applied to 3D crystals, where it provides a valuable method for studying crystallographic structure (6–9), and measurement of strain (10, 11) and specimen thickness (12, 13) for a nanoscale volume. The choice of the electron beam convergence angle (14, 15), defocusing distance, lens aberrations, and specimen thickness allows precise control of the volume of material analyzed in a single measurement. However, accurate interpretation of a general CBED pattern is not straightforward, requiring careful comparison with simulated structures, which often limits application of the technique. CBED on thin van der Waals heterostructures (1, 2) would deliver a dramatically larger amount of information, which is intuitively easy to interpret and immediately results in both qualitative and quantitative data about the stack. Furthermore, CBED of van der Waals heterostructures can be considered as a hologram, so conventional holographic reconstruction techniques can be applied, thus delivering information about the 3D arrangement between the crystals in the stack (including the local strain, lattice orientations, local vertical separation between the layers, etc.) which is not accessible by conventional TEM imaging (16, 17).
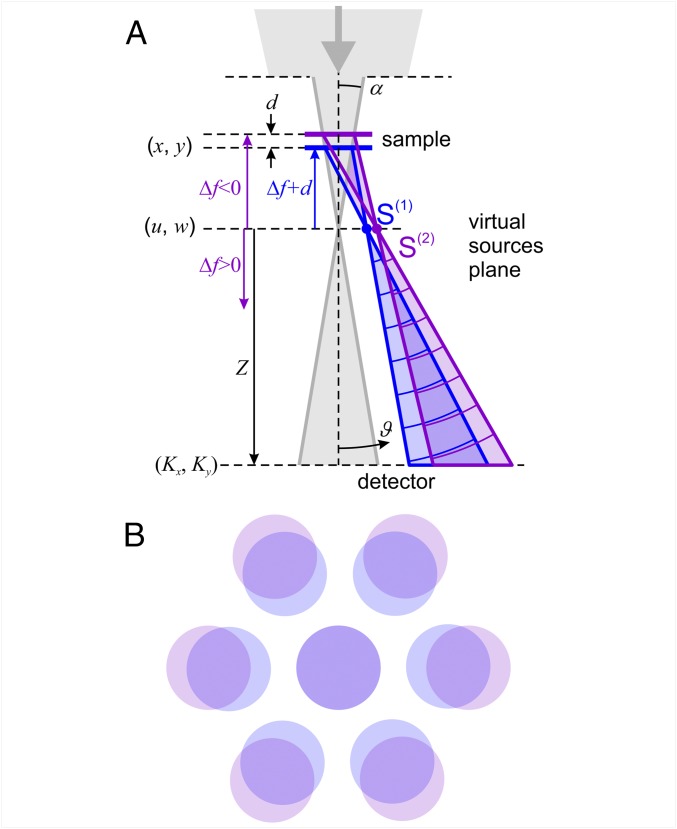
A CBED pattern from a single layer of graphene or hexagonal boron nitride (hBN) consists of finite-sized spots arranged into a sixfold symmetrical pattern. The centers of the spots have the same positions as the diffraction peaks, given by , where is the wavelength, is the diffraction angle, and is the period of the crystallographic planes. The size of a CBED spot on the detector depends on the convergent angle and the diameter of the limiting aperture, and it remains the same independent of the z position of the sample (or defocusing distance). The sample area imaged within a CBED spot corresponds to the illuminated area, whose diameter can be approximated as , where is the convergence semiangle of the electron beam (Fig. 1A). Probing the samples with a convergent (underfocus, ) or divergent (overfocus, ) incident wavefront is achieved by changing the position of the sample.
Fig. 1.
Experimental arrangement for CBED. (A) Schematics of CBED on a bilayer system. Here Δf is the sample z position counted from the focus of the electron beam (in this particular case, underfocus Δf < 0 CBED conditions are shown), Z is the distance from the virtual sources plane to the detector, and S(1) and S(2) are the virtual sources for the first-order CBED spots of bottom (layer 1) and top (layer 2) crystals, respectively, in the heterostructure stack; ϑ is the angular coordinate on the detector. (B) Distribution of CBED spots on a detector in the case of two aligned crystals with slightly different lattice constants.
In case of CBED on a bilayer structure (for instance, graphene/hBN stack—the type of devices we concentrate on in this paper), the electron beams diffracted on each layer interfere at the positions where the CBED patterns of individual layers overlap (Fig. 1B), thus creating a specific interference pattern (Fig. 2). Such interference patterns contain information about the local interatomic spacing (local strain), the vertical distance between the crystal layers, the relative orientation between the layers, etc.
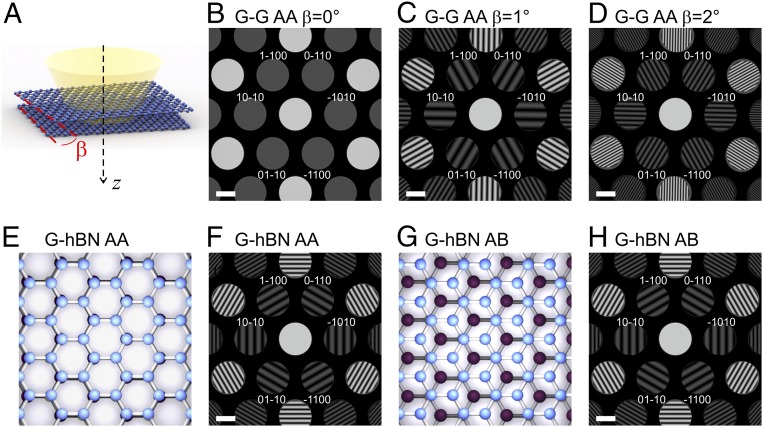
Fig. 2.
Simulated CBED patterns for various 2D bilayer heterostructures. (A) Illustration of a bilayer graphene illuminated by a convergent electron beam with one graphene layer rotated by an angle β. (B–D) Simulated CBED patterns of a double-layer graphene for different β. (E) Sketch of the top view of a graphene–hBN stack with AA atomic stacking in the center of the beam, and (F) the simulated CBED pattern. (G) Sketch of the top view of graphene–hBN with AB stacking in the center of the beam, and (H) the simulated CBED pattern. For these simulations, the distance between the layers is 3.35 Å, Δf = −3 μm, and the imaged area is about 50 nm in diameter. (All scale bars, 2 nm−1.)
Results
Simulated CBED of Perfect Crystals.
Fig. 2 demonstrates modeling of CBED for several typical bilayer heterostructures consisting of perfect crystals (the simulation procedure is described in SI Appendix). The interference pattern in a CBED spot can be interpreted as being created by a superposition of two waves originating from two corresponding virtual sources, as sketched in Fig. 1A. If the two stacked crystals have the same lattice constant and the same orientation (as, for instance, in the case of AA or AB stacked bilayer graphene), then the virtual spots are found almost at the same position, and no interference pattern is observed in CBED spots. A relative rotation between the layers (Fig. 2 A–D), or a slight mismatch of the lattice constants (Fig. 2 E–H), leads to the virtual sources, and, correspondingly, the CBED spots, appearing at slightly different positions, Fig. 1B. As a result, interference between the CBED spots occurs, and a fringed interference pattern is observed where the spots overlap. If the two graphene crystals in the double layer are rotated with respect to each other by a small angle , the CBED patterns from the two crystals will be rotated relative to each other by the same angle. Diffracted electron waves, which originate from the separate layers but arrive at the same point in the CBED detector plane, gain different phases, and the difference is now proportional to the rotation between the layers. As a result, radially distributed interference fringes will be observed, with the period of fringes within a particular CBED spot dependent on the angle of the rotation between the layers (Fig. 2 A–D).
In the case of two crystals with aligned crystallographic directions but with slightly different interatomic spacing (as, for instance, the case for graphene and hBN), the CBED spots will be shifted in the radial direction (Fig. 1B). The hBN has a 1.8% larger basal plane lattice spacing than graphene, and this will result in the appearance of interference patterns with tangentially distributed fringes (Fig. 2 E–H). The period and the tilt of the fringes are unambiguously defined by the lattices’ periods, the probing electron beam wavelength, the position of the sample, the relative rotation between the layers, and the distance between the layers (as shown in SI Appendix). Interestingly, CBED patterns of such bilayer samples are extremely sensitive to the atomic arrangements in the layers. If the local stacking under the center of the electron beam is AA (Fig. 2E), the pattern of interference fringes has maxima at the center of the CBED spots (Fig. 2F). If the local atomic stacking is AB (Fig. 2G), the pattern of interference fringes in the CBED spots is shifted, and, as a result, the intensity distribution in the opposite CBED spots [such as those with Miller indices (1−100) and (−1100)] are not mirror-symmetric (Fig. 2H).
Also, the distance between the layers affects the interference pattern. The phase difference between the electron waves diffracted from the two identical and aligned crystals separated by a distance is given by
| [1] |
where is the electron wavelength (4.2 pm for 80-keV electrons). Since , the phase shift within the CBED spot can be approximated as
| [2] |
where is the lattice period which defines the order of the particular CBED spot. It is clear that, for a bilayer graphene ( Å for the first-order CBED spots), with a typical interlayer distance of about 3.35 Å, the phase difference is negligible (about 0.1 rad) and remains almost constant over the entire CBED spot, and thus no interference fringes should be observed within the CBED spots [as, indeed, has been reported previously (18)]. Further discussion on the period of the interference fringes and examples of the reconstruction of the exact interlayer distances from CBED patterns are provided in SI Appendix.
We should stress that, even in the case of a monolayer, the intensity distribution within each CBED spot is not an image of the sample but a far-field distribution of the intensity of the wave scattered by the sample, which, in fact, is an inline hologram of the sample area.
Simulated CBED for Crystals with Out-of-Plane Atomic Displacements.
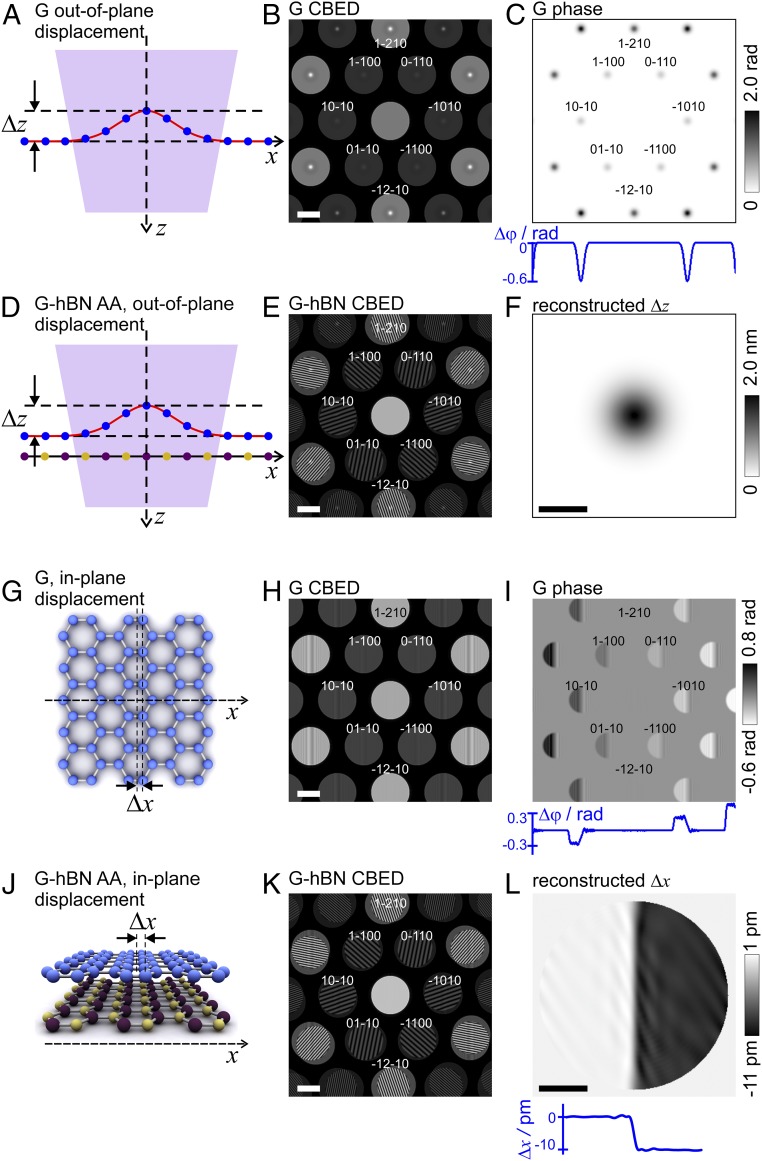
To quantitatively study the relation between the atomic defects and the CBED pattern, we simulated out-of-plane and in-plane displacements of atoms in the graphene lattice and the corresponding phase distributions in the detector (far-field) plane, shown in Fig. 3. When atoms are displaced out of the crystal plane by a distance , the scattered wave gains additional phase shift given by Eq. 1. Because is an even function of , the added phase shift causes equal intensity change (increase or decrease of the intensity) in opposite CBED spots (see SI Appendix for the derivation of the formulae for the phase shift). A simulated CBED pattern of an out-of-plane defect (bubble, Fig. 3A) with a maximum height in the center of 2 nm is presented in Fig. 3B, with the phase distribution in the far field shown in Fig. 3C. Eq. 2 allows estimation of the height of the bubble from the measured phase with 90% precision. The discrepancy is because of the diffraction effects (which are strong for 4-nm-wide bubble) due to perfect coherence of the electron beam assumed in the simulations. This Fresnel diffraction effect can be compensated and the true shape of the bubble restored by performing deconvolution with the free-space propagator as explained in detail in SI Appendix. Such diffraction effects are much less pronounced in the experimental images where electron waves are only partially coherent (SI Appendix, CBED Pattern of an Edge), and where the use of Eq. 2 gives an excellent level of accuracy.
Fig. 3.
Simulated CBED patterns for graphene and graphene–hBN bilayer heterostructures where graphene lattice is deformed. (A) Side view illustration of a graphene layer with atoms displaced out of plane, not drawn to scale. (B) Corresponding simulated CBED pattern where the atoms are displaced out of plane in the form of a bubble. The atomic z positions are shifted by Δz = −ABexp[−(x2 + y2)/(2σ2Β)], AB = 2 nm, and σΒ = 2 nm. (C) The difference of the phases of the wavefronts scattered by graphene with and without the out-of-plane atomic displacement due to the bubble. The blue curve shows the profile through the center of the distribution that is at Ky = 0. (D) Sketch of the side view of a graphene–hBN bilayer with AA stacking area but with atoms in graphene displaced out of plane due to the presence of a bubble. (E) Corresponding simulated CBED pattern for D. The graphene atoms displacement is the same as in B. (F) Reconstructed distribution of the atomic out-of-plane displacement due to the bubble in the graphene layer. (Scale bar, 5 nm.) (G) Sketch of the top view of the graphene layer with atoms displaced laterally (within the crystal plane). (H) Simulated CBED pattern where the atoms positioned at x > 0 are displaced by Δx = −10 pm. (I) The difference between the phases of the wavefronts scattered from graphene with and without in-plane atomic displacement. The blue curve shows the profile through the center of the distribution that is at Ky = 0. (J) Sketch of the side view of a graphene–hBN bilayer, AA stacking area, with atoms in graphene displaced within graphene plane as in H and G. (K) Corresponding simulated CBED pattern for graphene–hBN heterostructures described in J. (L) Reconstructed distribution of the atomic in-plane displacement in the graphene layer. (Scale bar, 5 nm.) For these simulations, the distance between the layers is 3.35 Å, Δf = −2 μm, and the imaged area is about 28 nm in diameter. (Scale bars in B, E, H, and K, 2 nm−1.)
A CBED pattern of a monolayer contains only the amplitude information of the wave, losing the phase part of the signal. Consequently, a direct recalculation of the CBED pattern into the atomic distribution is impossible. However, the CBED pattern intensity distribution unambiguously relates to the atomic 3D displacements, and the atomic displacements, in principle, can be recovered by simulating a matching CBED pattern of a lattice with modeled displacements. The situation is considerably improved in the case of CBED of a bilayer system. Here, the second layer adds a second wavefront that acts as a reference wave. This situation can be considered as a form of off-axis holography, where the wavefront, scattered on one of the crystals, is treated as the object wave, and the wavefront scattered on the other layer is treated as the reference wave. The resulting interference pattern forms an off-axis hologram, which can be reconstructed to give the amplitude and phase distributions of the wavefront at the position of each CBED spot. The reconstruction approach which we use here is based on an established procedure for reconstruction of off-axis holograms (19–21), and involves two Fourier transforms (22) (more details are provided in SI Appendix). From the set of phase distributions recovered for individual CBED spots, the atomic displacements in the layers can be immediately recovered.
Fig. 3D shows a sketch of a bilayer graphene/hBN heterostructure with out-of-plane displacement of atoms in the graphene layer. The corresponding simulated CBED pattern is shown in Fig. 3E. An out-of-plane atomic displacement results in an additional phase shift, which is the same for all CBED spots of the same order. Thus, to extract the out-of-plane atomic displacements, the symmetric component of the CBED signal is extracted by averaging the phase distribution from all CBED spots of the same order, producing . is calculated from by applying Eq. 2 (Fig. 3F).
Simulated CBED of Crystals with In-Plane Atomic Displacement.
When atoms are displaced within the crystal plane by a distance , the additional phase shift is given by
| [3] |
where are the coordinates in the far-field (detector) plane. Fig. 3G shows a sketch of a graphene layer with an in-plane displacement pm for the atoms in the positive semiplane (). The corresponding simulated CBED pattern is shown in Fig. 3H. Because the phase shift is an odd function of , an in-plane displacement gives rise to opposite intensity variation in opposite CBED spots, as shown in Fig. 3H. As follows from Eq. 3, for pm, the maximal phase shift in the first-order CBED spots amounts to ±0.3 rad, which is confirmed by the phase distribution shown in Fig. 3I. In Fig. 3I, vertical interference fringes observed in the center of each CBED spots are due to diffraction on a knife edge. Because infinite coherence is assumed in the simulation, Fresnel fringes appear in the region of about . Again, if we perform deconvolution with the free-space propagator (SI Appendix), this Fresnel diffraction effect can be completely compensated. Such diffraction effects should be much less pronounced in experimental images where electron waves are only partially coherent.
According to Eq. 3, an in-plane displacement does not cause intensity variations (irregularities of fringes) in CBED spots that are orthogonal to the direction of the displacement [note that there is no change in the intensity distributions in (1−210) and (−12−10) spots, Fig. 3 H and I]. To quantitatively reconstruct the in-plane atomic shifts in the direction, the difference between the phase distributions in the opposite CBED spots along the direction should be calculated and divided by 2, thus extracting only the antisymmetric component of the signal. is then calculated from by applying Eq. 3.
Fig. 3J shows a sketch of a graphene/hBN heterostructure with atomic in-plane displacement of some of the graphene atoms (the whole right semiplane is shifted by 10 pm). The corresponding simulated CBED pattern is shown in Fig. 3K. The phase distributions were reconstructed for each CBED spot, and was obtained from the reconstructed phase distributions as described above. Fig. 3L shows the reconstructed which matches the predefined values: 0 for and −10 pm for . An example of a reconstruction when both and occur simultaneously, with more details about the reconstruction procedure, is provided in SI Appendix.
As one can see, it is easy to distinguish between the out-of-plane and in-plane atomic displacements, even without performing a reconstruction, by simply comparing the intensity contrast in the opposite CBED spots of monolayers or the regularity of interference fringes for bilayer samples. An out-of-plane defect will always result in a symmetric phase distribution between the mirror-symmetric CBED spots, and an in-plane defect will result in an antisymmetric one.
Experimental Results.
Fig. 4 shows CBED patterns for three of our samples: aligned graphene on hBN (Fig. 4A), graphene rotated with respect to hBN by a small angle (Fig. 4B), and a multilayered sample (Fig. 4C). As predicted by the simulations (Fig. 2), the interference patterns are tangential and radial in Fig. 4 A and B, respectively. The particular arrangement of the interference patterns (for instance, the number of interference fringes) depends on as well as the misorientation angle between the two crystals, among other parameters. The misorientation angle calculated for this particular sample is 2.5° ± 0.1° (SI Appendix). More examples of experimental CBED patterns for graphene–hBN heterostructures are provided in SI Appendix.
Fig. 4.
Experimental CBED patterns of graphene–hBN samples. (A) CBED pattern where the direction of fringes indicates that there is almost no relative rotation between the layers, Δf = −5 μm, α = 6.93 mrad, which gives the diameter of the imaged area of about 70 nm. (B) CBED pattern of another sample where the direction of fringes indicates a relative rotation between the layers, β = 2.5°, Δf = −3 μm, and α = 8.023 mrad, which gives the diameter of the imaged area of about 48 nm. (C) CBED pattern of graphene/hBN/graphene heterostructure sample, Δf ≈ 0, α = 8.023 mrad; the diameter of the imaged area is about 1 nm (more information on the distribution of the probing wavefront is provided in SI Appendix). The intensity of the central spot is reduced by a factor of 0.002 in A, 0.1 in B, and 0.005 in C. (Scale bars, 2 nm−1.)
Fig. 4C shows a CBED pattern of a three-layer system (hBN sandwiched between two layers of graphene) acquired at Δf ≈ 0. Because is so small, the period of the interference fringes is very large, and no interference fringes are observed within the overlapping CBED spots. From the position of the spots, we measure that the relative rotation between hBN and one of the graphene layers is 2.5°, and the relative rotation between the two graphene layers is 17°. Two of the three layers exhibit unperturbed crystalline structure as evident from the homogeneous intensity within their CBED spots. The intensity variations of opposite contrast in opposite CBED spots of the hBN layer indicate the presence of an in-plane strain (as indicated by the red arrows in Fig. 4C). The contrast variation on the circumference of each CBED discs in Figs. 4 and 5 are attributed to charging of the dust particles at the condenser aperture.
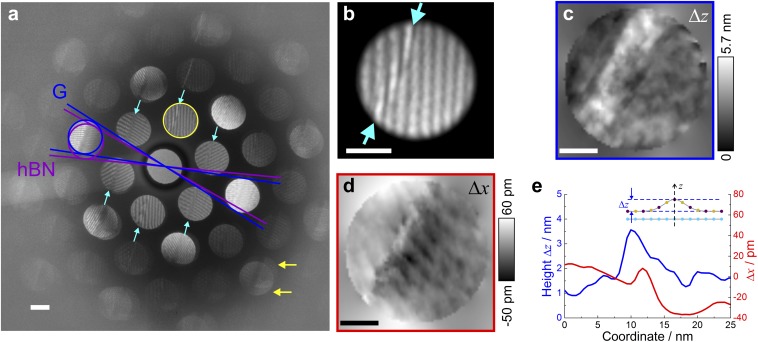
Fig. 5.
Extracting the shape of the out-of-plane ripple from a CBED pattern. (A) Experimental CBED pattern acquired at Δf = −3 μm, with defects in the interference patterns marked by the arrows. The blue and purple lines indicate the relative rotation between graphene and hBN layers, which amounts to 3°. The cyan arrows indicate an out-of-plane ripple observed in the first-order CBED spots. The yellow arrows indicate the separation of CBED spots originating from graphene and hBN layers, where it becomes clear that the ripple is in the hBN layer. The intensity of the central spot is reduced by a factor of 0.1. (Scale bar, 2 nm−1.) (B) Magnified selected spot (circled yellow in A) where irregularities of the fringe pattern can be seen. (Scale bar, 1 nm−1.) (C) The reconstructed distribution of the ripple height Δz. (D) The reconstructed distribution of the lateral shift Δx. (E) Profiles for the magnitude of Δz and Δx profiles perpendicular to the ripple in C and D. (Scale bars in C and D, 10 nm in real space.)
To demonstrate the holographic nature of our CBED patterns, we imaged a ripple defect in stacking between the two layers. Such defects are often associated with basal plane dislocations and have also been referred to as ripplocations (23). Fig. 5A presents a CBED pattern from an area with a stacking fault between slightly misoriented graphene and hBN, which is evident by the presence of a distinctive ridge in the interference patterns in the first- and higher-order CBED spots (see also Fig. 5B). We note that no features are visible in the zero-order spot, suggesting that the defect induces only marginal additional absorption. However, this defect introduces a significant additional phase shift between the electron waves scattered from the top and bottom crystals, which is readily picked up in the CBED interference patterns. If it were not for this interference, quantitative imaging of such a defect would be next to impossible. CBED spots which originate from graphene are found at a slightly larger diffraction angle, allowing differentiation of the spots corresponding to graphene from those for hBN. The overlap between CBED spots from the two crystals is less in the higher diffraction orders, but the intensity contrast due to corrugation is more pronounced in the higher-order CBED spots. Thus, by visual inspection of the high-order CBED spots, the type of corrugation and the layer with the corrugation can be readily identified. For example, in the CBED pattern shown in Fig. 5A, the ripple marked by the cyan arrows in Fig. 5A (also in magnified image in Fig. 5B) manifests itself identically in all of the higher-order CBED spots, which suggests that this is an out-of plane ripple. Also, it is clearly seen in the third-order CBED spots, where the spots from hBN and graphene are sufficiently separated (as indicated by the yellow arrows in Fig. 5A) so that the projection of the ripple exists only in one of the spots (hBN), unambiguously identifying the corrugated layer.
To extract quantitative information about the defect, we performed holographic reconstruction of the CBED pattern image presented in Fig. 5A as described above. The phase unwrapping was applied by using a procedure introduced by Schofield and Zhu (24). Fig. 5C shows the recovered out-of-plane atomic displacements obtained from symmetric component of the CBED picture by averaging the reconstructed phase distributions from all six first-order CBED spots and applying Eq. 1. Fig. 5D shows the recovered in-plane atomic displacements obtained by extracting the antisymmetric component of the phase distribution from two opposite first-order CBED spots and by applying Eq. 3. Fig. 5E compares the out-of-plane and in-plane atomic shifts along the ripple. In our case, the retrieved height of the out-of-plane ripple in hBN layer is about 2 nm. This is reasonable, since out-of-plane ripples are often observed for graphene/hBN stacks due to self-cleansing effects (25).
Discussion
We have demonstrated that single CBED patterns of van der Waals heterostructures allow for direct visualization of the 3D atomic distribution in each individual layer. Even without reconstruction, qualitative information about the type (stretching or out-of-plane rippling) and the extent of lattice deformation can be directly obtained by simple comparison of intensity distributions in the opposite CBED spots. For bilayer materials, a holographic approach can be applied to quantitatively reconstruct the values of 3D atomic displacements.
The resolution provided with our technique depends on the size of the imaged area, that is, on and the corresponding magnification. To evaluate the sensitivity of our method to atomic shifts, we estimate that a phase shift of 0.1 rad is sufficient to cause detectable variations in intensity distribution. Such a phase shift can be caused by out-of-plane atomic shifts of nm or by an in-plane atomic shift of pm (in accordance with Eqs. 2 and 3). Thus, the sensitivity to in-plane atomic displacements is about 100 times higher than the sensitivity to out-of-plane displacements. The sensitivity to spatial position is of the order of 1 nm when the locations of atomic displacements are obtained by comparing intensity distributions from the opposite CBED spots and is a few nanometers when the holographic reconstruction is applied (as discussed in SI Appendix).
Quantitative information in the direction (parallel to the electron beam) is notoriously difficult to obtain from a projection imaging technique such as TEM. Thus, the ability to obtain quantitative information about the relative location of the atomic sheets in the z direction is one of the strengths of our approach. Furthermore, our approach does not require any special sample preparation; it can be applied to any samples being observed in TEM in traditional modes. Classical electron tomography methods used to gain 3D positional data struggle, except when the target is a perfectly crystalline nanoobject that can be imaged along several zone axes (26). Van Dyck et al. (27) have demonstrated that atomic-resolution 3D coordinates could be achieved from only a single projection using a combination of exit wave reconstruction from a focal series of images and a “Big Bang” analysis of the quantitative phase shift for individual atomic columns. Their approach requires a sequence of atomically resolved high-resolution images (to recover the complex-valued exit wave which is a complicated analysis by itself) and only obtains a single z location for each atom column position. By contrast, our approach gains high-resolution z-positional data on the relative position of the two separate layers from a single CBED pattern. Although, currently, the lateral resolution we obtain is poorer than that demonstrated by Van Dyck et al., our approach requires orders of magnitude lower electron exposures, so it has a potential to be applied to heterostructures containing beam-sensitive 2D materials and even overlapping protein membranes (28). In addition, our approach can be further advanced by obtaining many CBED patterns to reconstruct a large area (diffractive imaging). Also, depending on , the area studied by our approach can be tuned from gaining sensitive relative atomic displacements for just a few square nanometers to regions ∼1 μm wide, as is typical of the active area of lithographically patterned 2D heterostructure devices.
Our results demonstrate that CBED on van der Waals heterostructures can be applied to yield a plethora of information about the stacks. This technique has not previously been applied to van der Waals heterostructures, but we have shown that it is highly versatile and can be performed on any conventional TEM instrumentation. We expect that this approach will find a progressive use in the expanding field of 2D materials. Furthermore, it could be extended to the analysis of dopant atoms, local oxidation, or trapped species within the heterostructures, as all of these will affect the interference patterns obtained.
Materials and Methods
The samples were obtained by mechanical stacking of mechanically exfoliated graphene and hBN layers on an Si/SiO2 substrate. By using “pick and lift” technique (29), the whole stack was then transferred on a quantifoil carbon support film for observation in the TEM. CBED was realized in a probe side aberration-corrected scanning TEM at an accelerating voltage of 80 keV and a convergence semiangle, , of ∼6 mrad to 8 mrad. During experiment, the focal lengths of the objective and condenser lenses were kept constant; thus there was no change in the convergence angle. The sample z position was changed by moving the sample along the optical axis. Bilayer structure significantly improves the stability of 2D crystals upon exposure to high-energy electrons, and the electron dose required for CBED imaging is low, so no evidence of knock-on damage was observed during prolonged data acquisition (30, 31).
Supplementary Material
Acknowledgments
This work was supported by the European Union Graphene Flagship Program; European Research Council Synergy Grant “Hetero2D” and European Research Council Starting Grant “EvoluTEM”; the Royal Society; Engineering and Physical Research Council (UK); and US Army Research Office (Grant W911NF-16-1-0279). S.J.H. and E.P. acknowledge funding from the Defense Threat Reduction Agency (Grant HDTRA1-12-1-0013) and the Engineering and Physical Sciences Research Council (UK) (Grants EP/K016946/1, EP/L01548X/1, EP/M010619/1, and EP/P009050/1).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1722523115/-/DCSupplemental.
References
- 1.Geim AK, Grigorieva IV. Van der Waals heterostructures. Nature. 2013;499:419–425. doi: 10.1038/nature12385. [DOI] [PubMed] [Google Scholar]
- 2.Novoselov KS, Mishchenko A, Carvalho A, Castro Neto AH. 2D materials and van der Waals heterostructures. Science. 2016;353:aac9439. doi: 10.1126/science.aac9439. [DOI] [PubMed] [Google Scholar]
- 3.Haigh SJ, et al. Cross-sectional imaging of individual layers and buried interfaces of graphene-based heterostructures and superlattices. Nat Mater. 2012;11:764–767. doi: 10.1038/nmat3386. [DOI] [PubMed] [Google Scholar]
- 4.Argentero G, et al. Unraveling the 3D atomic structure of a suspended graphene/hBN van der Waals heterostructure. Nano Lett. 2017;17:1409–1416. doi: 10.1021/acs.nanolett.6b04360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kossel W, Möllenstedt G. Elektroneninterferenzen im konvergenten Bündel. Ann Phys. 1939;428:113–140. [Google Scholar]
- 6.Goodman P. A practical method of three-dimensional space-group analysis using convergent-beam electron diffraction. Acta Crystallogr A. 1975;31:804–810. [Google Scholar]
- 7.Buxton BF, Eades JA, Steeds JW, Rackham GM. The symmetry of electron diffraction zone axis patterns. Philos Trans R Soc A. 1976;281:171–194. [Google Scholar]
- 8.Tanaka M, Sekii H, Nagasawa T. Space-group determination by dynamic extinction in convergent-beam electron diffraction. Acta Crystallogr A. 1983;39:825–837. [Google Scholar]
- 9.Tanaka M, Saito R, Sekii H. Point-group determination by convergent-beam electron diffraction. Acta Crystallogr A. 1983;39:357–368. [Google Scholar]
- 10.Jones PM, Rackham GM, Steeds JW. Higher-order Laue zone effects in electron-diffraction and their use in lattice-parameter determination. Proc R Soc A. 1977;354:197–222. [Google Scholar]
- 11.Carpenter RW, Spence JCH. Three-dimensional strain-field information in convergent beam electron diffraction patterns. Acta Crystallogr A. 1982;38:55–61. [Google Scholar]
- 12.Kelly PM, Jostsons A, Blake RG, Napier JG. The determination of foil thickness by scanning transmission electron microscopy. Phys Status Solidi A. 1975;31:771–780. [Google Scholar]
- 13.Champness PE. Convergent beam electron diffraction. Mineral Mag. 1987;51:33–48. [Google Scholar]
- 14.Tanaka M, Saito R, Ueno K, Harada Y. Large-angle convergent-beam electron diffraction. J Electron Microsc (Tokyo) 1980;29:408–412. [Google Scholar]
- 15.Morniroli JP. CBED and LACBED characterization of crystal defects. J Microsc. 2006;223:240–245. doi: 10.1111/j.1365-2818.2006.01630.x. [DOI] [PubMed] [Google Scholar]
- 16.Gabor D. A new microscopic principle. Nature. 1948;161:777–778. doi: 10.1038/161777a0. [DOI] [PubMed] [Google Scholar]
- 17.Gabor D. Microscopy by reconstructed wave-fronts. Proc R Soc A. 1949;197:454–487. [Google Scholar]
- 18.Meyer JC, et al. On the roughness of single- and bi-layer graphene membranes. Solid State Commun. 2007;143:101–109. [Google Scholar]
- 19.Leith EN, Upatnieks J. Reconstructed wavefronts and communication theory. J Opt Soc Am. 1962;52:1123–1130. [Google Scholar]
- 20.Leith EN, Upatnieks J. Wavefront reconstruction with continuous-tone objects. J Opt Soc Am. 1963;53:1377–1381. [Google Scholar]
- 21.Mollenstedt G, Wahl H. Electron holography and reconstruction with laser light. Naturwissenschaften. 1968;55:340–341. [Google Scholar]
- 22.Lehmann M, Lichte H. Tutorial on off-axis electron holography. Microsc Microanal. 2002;8:447–466. doi: 10.1017/S1431927602029938. [DOI] [PubMed] [Google Scholar]
- 23.Kushima A, Qian X, Zhao P, Zhang S, Li J. Ripplocations in van der Waals layers. Nano Lett. 2015;15:1302–1308. doi: 10.1021/nl5045082. [DOI] [PubMed] [Google Scholar]
- 24.Schofield MA, Zhu Y. Fast phase unwrapping algorithm for interferometric applications. Opt Lett. 2003;28:1194–1196. doi: 10.1364/ol.28.001194. [DOI] [PubMed] [Google Scholar]
- 25.Kretinin AV, et al. Electronic properties of graphene encapsulated with different two-dimensional atomic crystals. Nano Lett. 2014;14:3270–3276. doi: 10.1021/nl5006542. [DOI] [PubMed] [Google Scholar]
- 26.Van Aert S, Batenburg KJ, Rossell MD, Erni R, Van Tendeloo G. Three-dimensional atomic imaging of crystalline nanoparticles. Nature. 2011;470:374–377. doi: 10.1038/nature09741. [DOI] [PubMed] [Google Scholar]
- 27.Van Dyck D, Jinschek JR, Chen FR. ‘Big Bang’ tomography as a new route to atomic-resolution electron tomography. Nature. 2012;486:243–246, and erratum (2012) 489:460. doi: 10.1038/nature11074. [DOI] [PubMed] [Google Scholar]
- 28.Nair RR, et al. Graphene as a transparent conductive support for studying biological molecules by transmission electron microscopy. Appl Phys Lett. 2010;97:153102. [Google Scholar]
- 29.Wang L, et al. One-dimensional electrical contact to a two-dimensional material. Science. 2013;342:614–617. doi: 10.1126/science.1244358. [DOI] [PubMed] [Google Scholar]
- 30.Zan R, et al. Control of radiation damage in MoS(2) by graphene encapsulation. ACS Nano. 2013;7:10167–10174. doi: 10.1021/nn4044035. [DOI] [PubMed] [Google Scholar]
- 31.Algara-Sillera G, Kurascha S, Sedighi M, Lehtinen O, Kaiser U. The pristine atomic structure of MoS2 monolayer protected from electron radiation damage by graphene. Appl Phys Lett. 2013;103:203107. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.