Universal folding pathways of polyhedron nets

Significance

What makes an object successful at thermal folding? Protein scientists study how sequence affects the pathways by which chained amino acids fold and the structures into which they fold. Here we investigate the inverse problem: Starting with a 3D object as a polyhedron we ask, which ones, among the many choices of 2D unfoldings, are able to fold most consistently? We find that these “nets” follow a universal balance between entropy loss and potential energy gain, allowing us to explain why some of their geometrical attributes (such as compactness) represent a good predictor for the folding propensity of a given shape. Our results can be used to guide the stochastic folding of nanoscale objects into drug-delivery devices and thermally folded robots.

Abstract

Low-dimensional objects such as molecular strands, ladders, and sheets have intrinsic features that affect their propensity to fold into 3D objects. Understanding this relationship remains a challenge for de novo design of functional structures. Using molecular dynamics simulations, we investigate the refolding of the 24 possible 2D unfoldings (“nets”) of the three simplest Platonic shapes and demonstrate that attributes of a net’s topology—net compactness and leaves on the cutting graph—correlate with thermodynamic folding propensity. To explain these correlations we exhaustively enumerate the pathways followed by nets during folding and identify a crossover temperature $T_x$ below which nets fold via nonnative contacts (bonds must break before the net can fold completely) and above which nets fold via native contacts (newly formed bonds are also present in the folded structure). Folding above $T_x$ shows a universal balance between reduction of entropy via the elimination of internal degrees of freedom when bonds are formed and gain in potential energy via local, cooperative edge binding. Exploiting this universality, we devised a numerical method to efficiently compute all high-temperature folding pathways for any net, allowing us to predict, among the combined 86,760 nets for the remaining Platonic solids, those with highest folding propensity. Our results provide a general heuristic for the design of 2D objects to stochastically fold into target 3D geometries and suggest a mechanism by which geometry and folding propensity are related above $T_x$, where native bonds dominate folding.

In the 16th century, the Dutch artist Albrecht Dürer investigated which 2D cuts of nonoverlapping, edge-joined polygons could be folded into Platonic and Archimedean polyhedra. Dürer cuts were later called “nets” but, for a long time, the interest around them was mostly restricted to the field of mathematics (1–3). A newer concept, self-folding origami, adds a modern twist to the ancient art of paper folding. By providing a mechanism to achieve complex 3D geometries from low-dimensional objects—without the need for manipulation of the constituent parts—self-folding brings the concepts pioneered by Dürer to the forefront of many research fields, from medicine (4) to robotics (5).

Several recent works have leveraged physical forces to achieve controllable folding of 3D objects including light (6), pH (7), capillary forces (8), cellular traction (9), and thermal expansion (10). Other works have investigated the relationship between geometric attributes of the object being folded and its propensity for successful folding. In the macroscopic folding of kirigami sheets—origami-like structures containing cuts and creases—the effect of different cut patterns on the material’s stress–strain behavior has been elucidated (11–13) and the “inverse design problem” of finding cuts leading to the folding of a particular target structure has been solved (14). For submillimeter-sized capsules, formed via nonstochastic folding of nets into polyhedra, it has been suggested that nets fold with higher yield when they are compact (8, 15, 16), but the reason for this correlation remains unclear. In natural systems, the canonical example of self-folding occurs for proteins, where a string of amino acids navigate, thermodynamically, from a denatured (unfolded) state to a natured (folded) one. Even after many decades of study, however, a universal relationship between molecular sequence and folded state—which could provide crucial insight into the causes and potential treatments of many diseases—remains out of reach (11–13).

In this work, we study the thermodynamic foldability of 2D nets for all five Platonic solids. Despite being the simplest and most symmetric 3D polytopes, the family of Platonic shapes suffices to demonstrate the rapid increase in design space as shapes become more complex: A tetrahedron has 2 possible net representations, cubes and octahedra each have 11 nets, and dodecahedra and icosahedra have, each, 43,380 distinct edge unfoldings. Here we are interested in the thermodynamic self-folding of these nets. Our goal is to understand how topology affects yield in the stochastic folding of 3D objects. The advantage is threefold. First, by using a collection of sheets folding into the same target shape, we isolate the geometric attributes responsible for high-yield folding. Second, the model allows exhaustive computation of the pathways followed by the nets during folding, elucidating how some nets achieve high yield. Third, by studying increasingly more complex objects—from tetrahedra to icosahedra—we can use the folding mechanisms quantified in the simplest objects to predict, and potentially validate, their occurrence in the more complex shapes.

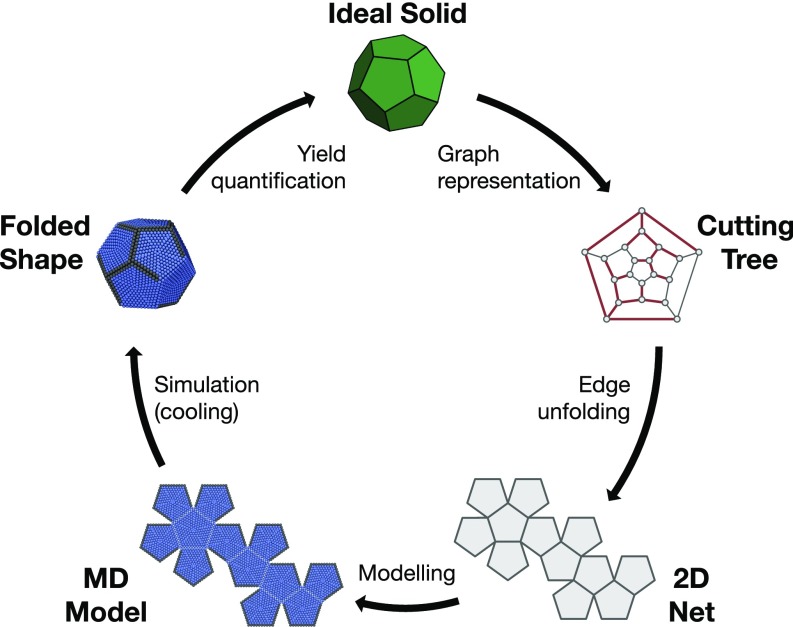
Beginning with a target Platonic shape (Fig. 1), we construct a graph whose vertices and edges correspond to those in the polyhedron. This mapping of the shape to a graph facilitates the exhaustive search of all distinct nets by allowing spanning tree enumeration (3). A set of prechosen edges (the cutting tree) is then cut, in a process called edge unfolding, to create a single, contiguous, and flat 2D sheet of nonoverlapping faces: a net. For the Platonic shapes, whose nets are enumerated (17), this can be repeated exhaustively until all distinct nets are discovered (see Materials and Methods for more details). We note that for other shapes, while the process of computing all nets might become computationally prohibitive, it has been recently demonstrated that a subset of interest for these nets can be computed algorithmically (18). We list all 86,784 nets for the Platonic solids in a database (19).

Fig. 1.

Workflow for polyhedra folding study. Starting with a target 3D polytope (top, and moving clockwise), a graph representation is used to enumerate different permutations of edge cuttings. The vertices (edges) in the so-called cutting tree graph correspond to the vertices (edges) of the polyhedron. Red edges in the cutting tree mark those being cut. From the cutting tree, a planar, hinged connection of nonoverlapping faces (a net) results. Each face of the net is then modeled as a union of spheres rigidly held together, tethered along hinges via harmonic springs. In the MD model shown, gray spheres interact via a Lennard–Jones potential. Blue spheres interact with each other and with gray spheres via a purely repulsive WCA potential. The simulations are initialized at high temperature and brought to low temperature following either a fast quench or a slow annealing protocol. Once the final temperature is reached, the final configuration is compared with the target shape. The folding yield is then calculated as the probability of achieving the desired 3D shape via the particular cooling protocol.

Each net is modeled as a sheet of rigid polygons connected to adjacent polygons via harmonic springs. The polygons are composed of rigidly connected spheres and the influence of thermal fluctuations on a single net, suspended in implicit solvent, is modeled via Langevin molecular dynamics (more details in Materials and Methods). We assign nonspecific, short-ranged attractive (sticky) interactions between all edges not joined by springs of a net so that the polyhedron formed from folding is also the ground-state configuration. This does not guarantee, however, the uniqueness of the ground state and, as we will see, other 3D foldings can arise. Unless explicitly noted otherwise, by “folded state” we refer to the original polyhedron.

As in proteins and other biomolecules, the nonspecificity of the interactions between edges of the nets allows for both native and nonnative contacts. As a consequence, when the system temperature is rapidly decreased (quenched), kinetic traps are possible and net misfolds are observed. This possibility for kinetic traps raises the following question: Among all nets generated by unfolding a polyhedron, which of them show the highest propensity to refold into the original polyhedron?

More Compact, “Leafy” Nets Fold More Reliably

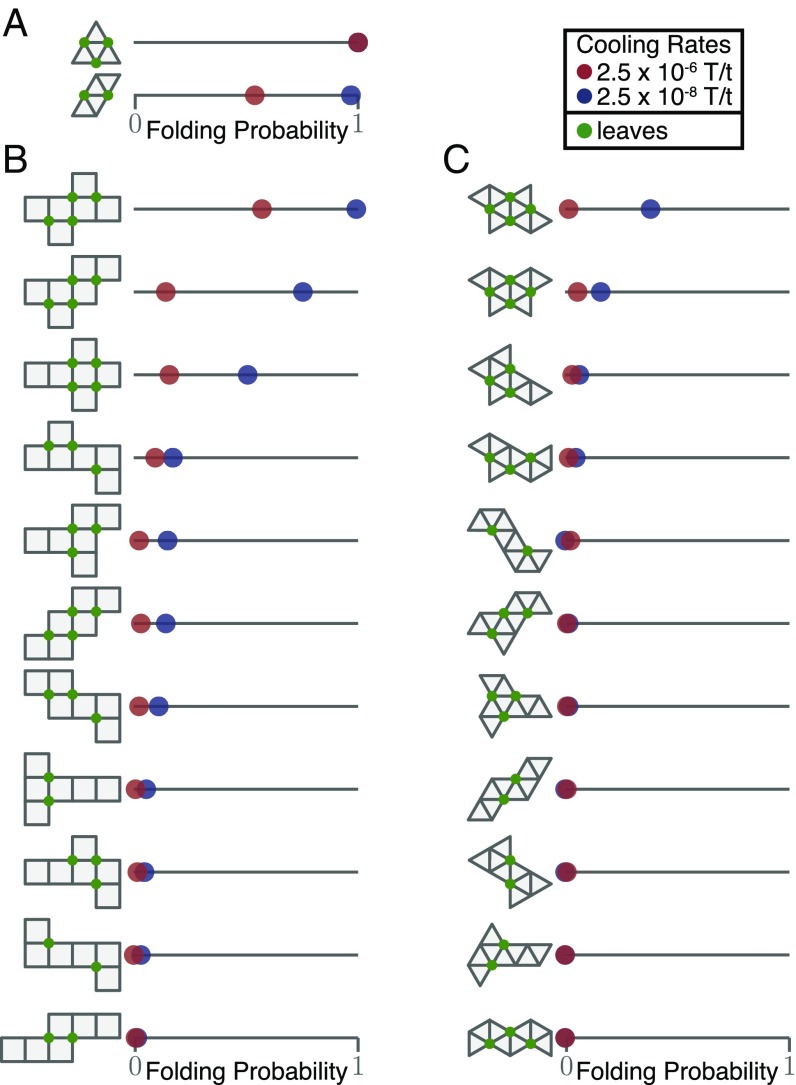
To identify the nets able to fold reliably into their polyhedron of origin we performed hundreds of cooling simulations for each net, using both a fast and a slow cooling protocol (see Materials and Methods section for more details). The two distinct nets for the tetrahedron, hereafter referred to as the triangular net and the linear net (Fig. 2A), showed remarkably different folding propensities for the fast cooling protocol: Of 125 simulations, all triangular nets folded into the target tetrahedron while only 54% of the linear nets succeeded—the other 46% of the experiments resulted in misfolded configurations. In general the slower cooling rate simulations yielded a higher folding probability for each net. This is expected as the net has more time to find the global minimum. Similar simulations for each of the 11 nets of both the cube and the octahedron revealed even larger differences: For the cube nets (Fig. 2B), only 3 of the nets showed greater than 50% success in folding, and only at slow cooling rates; for the octahedron (Fig. 2C), none of the nets achieve higher than 50% success rate for either cooling rate.

Fig. 2.

Effect of net topology on the folding probability for the simplest Platonic solids. Folding yield, defined by the fraction of simulations that reached the folded state, was calculated for two cooling rates. Nets for each polyhedron are ordered from highest to lowest yield at low cooling rate. (A) For the two tetrahedron nets [triangular (Top) and linear (Bottom)], a noticeable difference in folding success rate is visible for rapid cooling rates, but similar folding propensity is found for slower cooling rates. (B and C) For the cube nets (B) 8/11 nets fold poorly (below 50%) even for slow folding reactions while for the octahedron (C) most nets are unable to fold into the original shape. Generally the more compact nets fold better: Nets that have a high number of leaves on their cutting tree and a smaller diameter usually fold best.

The misfolded configurations for the tetrahedron and cube nets were incomplete 3D geometries (showing, for instance, faces collapsed on top of each other or bonds incompatible with the formation of the respective target shape). In contrast, octahedron nets often folded into another 3D shape: a concave, boat-like conformation with the same number of edge–edge contacts as the octahedron: in other words, a degenerate ground state. This competing structure, which is less symmetric than the octahedron, has higher rotational entropy resulting in a lower free energy than the octahedron (see SI Appendix, Fig. S1A for folding probabilities for the boat conformation). A competition between similar degenerate structures was reported for finite clusters of six attractive spherical colloids (20), where symmetry breaking leads to the formation of the same boat-like conformation.

Fig. 2 shows that, despite having the same ground-state energy, not all nets of a polyhedron are equivalent. In general, we observe that the nets that fold most reliably are the most compact and have the highest number of leaves on its cutting graph (green solid circles in nets in Fig. 2). A net is said to be more compact if it has a large number of leaves (the vertices with degree one on the cutting tree) and a small diameter (the longest shortest path between any two faces on the face graph). Exact values for the leaves and diameter are shown in SI Appendix, Table S1. Most strikingly, even nets differing only by the location of a single face can have folding probabilities reduced from 99% to 17%. What causes one shape to fold nearly perfectly every time while a slightly different one fails to do so almost as frequently? And why do net “leafiness” and “compactness” correlate with folding yield?

High-Temperature Folding Happens via Native Contacts

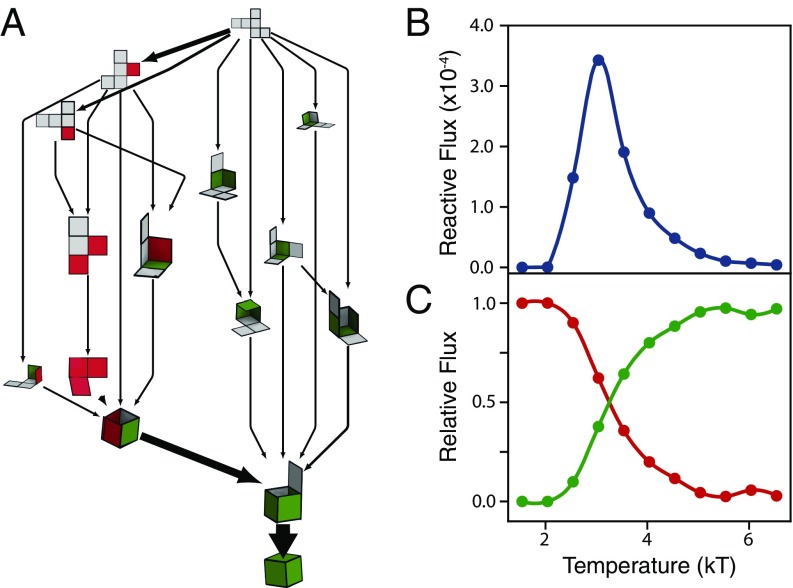
To answer why small differences in net topology can have a large impact on the net’s folding propensity, we used Markov-state models (MSM) (21–23) to compute the pathways through which nets fold into their folded state. Since quench rate was observed to affect the folding propensity of the nets, we run constant temperature simulations of each net while computing the rate of transitions between two states (flux). A representative folding network is shown in Fig. 3A (see SI Appendix, Fig. S2 for other example networks). Arrows represent observed transitions between different states and each arrow has a thickness proportional to the probability flux of the transition being observed (see Materials and Methods for more details). To simplify, we show only the most visited pathways (i.e., those whose combined flux accounts for at least 50% of the total reactive flux between unfolded and folded states). Intermediate configurations can achieve the folded state via the formation of native (green) or nonnative (red) contacts. If a pathway includes native contacts only, every newly formed bond is compatible with the final polyhedron and error correction is not needed. When the folded state is achieved via incompatible bonds, we observe that these nonnative contacts can sometimes have an active role by bringing otherwise far-away native contacts closer together, facilitating folding. In other cases the nonactive contacts contribute only passively and folding occurs sequentially after the misfold occurs until it reaches a point where the nonnative contact must break for folding to continue. In either case, nonnative contacts must eventually break before a folded configuration can be achieved.

Fig. 3.

Folding pathways for a representative cubic net. (A) Intermediate folding states (nets, in the diagram), arise when new bonds between edges are formed. States are connected with an arrow when a pathway from one state to another is observed in the simulation. The thickness of such connection is proportional to the measured probability of this transition being observed. For better visualization, only the most visited states are shown. Red (green) faces correspond to a state where a nonnative (native) contact is formed. The pathways containing only native contacts follow a “sequential” folding process, where one face folds at a time. Nonnative pathways can lead to the native folded shape via one of two mechanisms: (i) Either the misfold helps, bringing otherwise far away faces together, or (ii) the folding proceeds sequentially after the misfold occurs until it reaches a point where the nonnative contact must break for folding to continue. In both cases, if the correct polyhedron is achieved in the end, the nonnative contact is corrected along the pathway. The network represents 55% of the folding flux at $T=3kT$. (B) The total probability flux, defined as the sum of the fluxes along all pathways, for the representative net in A as a function of temperature. The peak around temperature $T=3kT$ shows that there is a temperature at which there is a maximum number of expected transitions from the unfolded to the folded state per unit time. (C) The relative amount of flux that goes through pathways that use the native (green curve) and nonnative (red curve) pathways. The folding seems to happen mostly via native contacts formation when the system is kept at higher temperatures.

The total flux connecting unfolded and folded states (Fig. 3B) first increases with temperature and then decreases to zero at high temperature. At low T the folding flux is low because the states are mostly trapped into a few configurations; i.e., the slow kinetics inhibit bond breaking. As the temperature increases, bonds can now break and the folding/unfolding process occurs at a higher rate. At intermediate $T$, a maximum in reactive flux is observed, meaning that there is a temperature at which there is a maximum number of expected transitions from unfolded to folded state per unit time $\tau$. The representative network shown in Fig. 3A was calculated at that peak temperature. Finally, at high $T$ the unfolded state is preferred and again the flux vanishes. These trends are also true for the other nets studied (SI Appendix, Fig. S3). If we separate the flux into those following native and nonnative contacts, we see (Fig. 3C) that the folding pathways at high temperature mostly follow the formation of native contacts while the behavior inverts for low temperatures, and mostly nonnative contacts are observed. There were only two nets where a crossover temperature was not observed. The triangular tetrahedral net does not exhibit a crossover temperature since it has no traps. The best-folding cubic net also does not have a crossover temperature in the range of temperatures we study; while traps exist, the fraction of native contacts decreases and the temperature decreases but never falls below 50% (SI Appendix, Fig. S3). This $T$ dependency is also observed in colloids, where the assembly of an icosahedron is monomeric at high temperatures, but, at low temperature, particles first aggregate into large clusters (not necessarily compatible with icosahedral symmetry) and those later rearrange into the ground-state structure (24).

To gain an understanding of the mechanisms underlying the observation that native contacts are favored at high temperatures during folding, we calculated the number of degrees of freedom associated with each intermediate.

Nets Follow a Universal Balance Between Entropy and Enthalpy

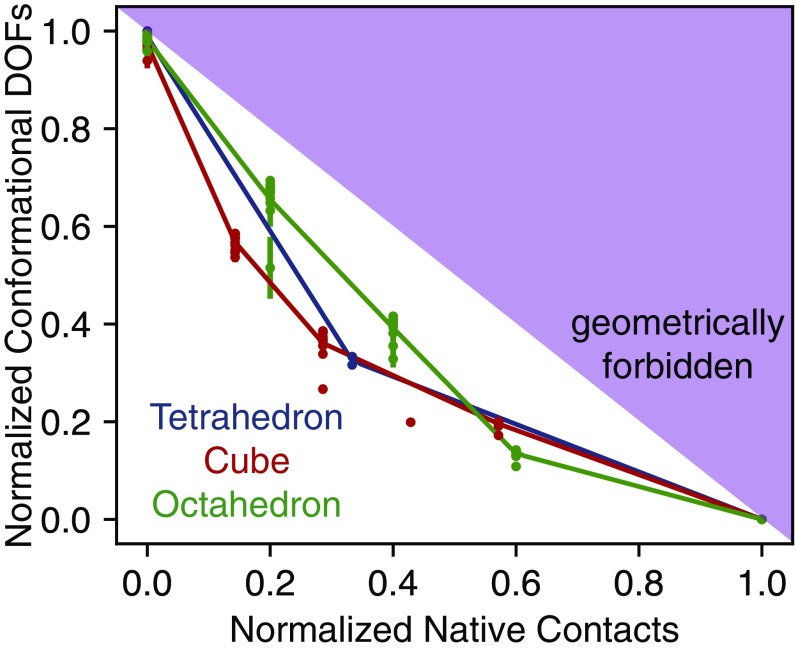
The fact that more compact nets and those with many leaves generally fold with higher yield suggests that nets might fold locally, in a manner that reduces the fewest degrees of freedom, thereby maximizing the conformational entropy along the folding pathways. To test whether this trade-off between maximizing degrees of freedom and forming native contacts occurs at high $T$, we calculate the number $N$ of internal degrees of freedom and the number $Q$ of native contacts as a net folds. We do so for all 24 nets of the tetrahedron, cube, and octahedron. Fig. 4 shows that, remarkably, all nets follow a folding pathway that achieves a narrow balance between reduction of degrees of freedom and gain of potential energy. In practical terms, high-temperature folding happens locally such that, at each step of the process, the system strives to maximize its conformational entropy. From this observation, we hypothesize the following mechanism for the folding of general nets at high temperature. Folding should primarily happen (i) via nearby (local) connections, favoring compact nets with many leaves, and (ii) along one of the optimal trade-off paths, favoring nets with high degeneracy in the number of such optimal paths. Fig. 4 shows that, remarkably, all nets follow a folding pathway that achieves a narrow balance between reduction of degrees of freedom and gain of potential energy. In practical terms, high-temperature folding happens locally such that, at each step of the process, the system strives to maximize its conformational entropy. Importantly, this maximization does not necessarily occur at low temperatures as when intermediate nonnative contacts occur—and stages of the folding are found to lie far away from the narrow balance explained above (SI Appendix, Fig. S4).

Fig. 4.

Projected pathways computed from the MSM of all of the nets onto two order parameters: native contacts and number of internal degrees of freedom. We find that each net will trade its degrees of freedom in approximately the same way. The data points are weighted averages of the number of degrees of freedom over all pathways for each given value of $Q/Q_{folded}$. The lines are drawn to guide the eye. The upper right corner of the plot is a geometrically forbidden region arising from the fact that the net cannot gain a bond without losing at least 1 df. The temperature plotted for each net is given by $T_m+0.5$, and $T_m$ is reported for each net in SI Appendix, Table S1. DOF, degree of freedom.

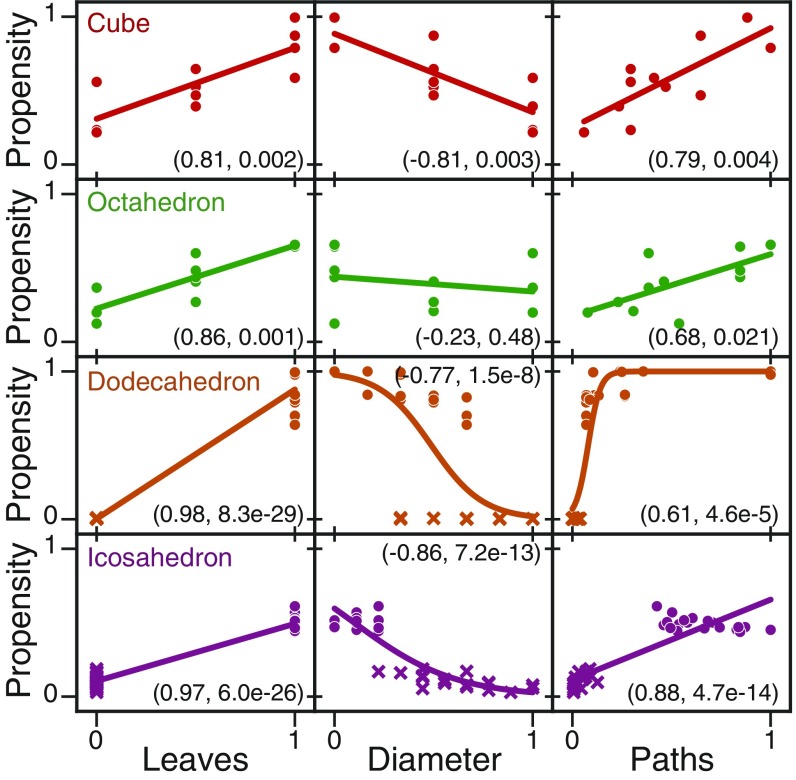
Using this hypothesis we devised an algorithm to generate high-temperature pathways for the 86,760 nets of the dodecahedron and icosahedron, without the need for a full MSM calculation. We do so by first enumerating candidate bonds that can be made if they are next to each other on the net or in the intermediate and then by selecting ones that have the largest number of degrees of freedom (see Materials and Methods for more details). Fig. 5 shows the combined example pathways followed by all 11 nets for the cube (Fig. 5A) and for the octahedron (Fig. 5B), illustrating the pathways that maximize degrees of freedom and using only local, native contacts to fold. We then used these principles to find, among the 86,760 nets, those with high and low folding yields (see SI Appendix, Figs. S5 and S6 for specific nets). The corresponding folding propensities are plotted in Fig. 6. As expected, polyhedra with many leaves and small diameter show higher propensity for correct folding and those nets also have many high-$T$ pathways to the ground state. The correlation between the folding propensity and the leaves may have analogues in other systems as well. The number of leaves is a measure of the amount of local connections that are required to fold from the unfolded state. In the protein-folding literature the contact order is a measure of how far away specific native contacts are on the amino acid sequence and it has been shown that low contact order inversely correlates to folding rate (25).

Fig. 5.

Combined dominant pathways for the 11 nets of the cube (A) and the 11 nets of the octahedron (B) calculated at high temperature. In both cases the dominant pathways are sequential (one face folding at a time) and include only native contacts. As in Fig. 3, arrows indicate transitions between two states, the arrow thickness being proportional to the probability of observing such a transition.

Fig. 6.

Correlation between different geometric and topological quantities calculated for the net and the folding propensity, defined as the average fraction of native contacts formed across all 125 quenching simulations. Leaves are the vertices with degree one on the cutting tree, the diameter is the longest shortest path along the face graph, and the number of high-temperature pathways was calculated by enumerating the number of pathways that maximize the internal degrees of freedom at each step. Each row corresponds to the cube (red), octahedron (green), dodecahedron (orange), and icosahedron (purple), respectively; data for the tetrahedron were omitted because there are only two nets. Pearson coefficients and P values are reported in each panel. We found that the number of leaves provided the strongest linear correlation for both the cube and the octahedron (Pearson coefficients are 0.81 and 0.86, respectively) and so the number of leaves was used to try to predict the nets that would fold with both high and low propensity. In the bottom two rows (dodecahedron and icosahedron), the nets predicted to fold well are plotted with a solid circle and the nets predicted to fold poorly are plotted with a solid “x.” We find that while the number of leaves is a good predictor for the dodecahedron, the icosahedron still folds with relatively low propensity.

Overall, our observations suggest that folding propensity of a net decreases as the number of faces increases. For instance, while the 4-sided tetrahedron folds nearly perfectly, the 20-sided icosahedron is unable to successfully fold. One exception to this trend is the dodecahedron, which folds with higher probability than the octahedron. While the reason for this exception remains elusive, there are two factors that may play a role. The first factor is the number of degrees of freedom retained by the faces sharing a leaf vertex when the leaf edges form a bond. For instance, octahedron nets can make a bond about the leaf vertex, but due to the unique symmetry the loop, retain 1 df (i.e., the resulting intermediate is not rigid), so the intermediate may still enter a trapped state. In the case of the icosahedron, after folding about leaf vertices, the loop retains 2 df. In the case of the other three shapes (i.e., tetrahedron, cube, dodecahedron), folding about leaf vertices renders the loop rigid. This implies that further constraining the net by increasing the rigidity throughout the folding process is important to sufficiently funnel the net’s energy landscape and may boost the folding probability for many nets. The second factor is the complexity that arises in trapped states. There are “tetrahedral motifs” on many octahedral nets, and these motifs can fold into full or partial tetrahedra, as seen in the boat conformation mentioned above (see SI Appendix, Fig. S1A for more examples). For icosahedral nets, there are both tetrahedral and octahedral motifs, and the diversity of the trapped states is further increased for these nets. This is in sharp contrast to the nets of the other three shapes, for which trapped states typically occur when one face folds onto another face.

Discussion and Conclusion

The observed preference for native contact pathways at high temperature is not unique to polyhedron nets. Several small proteins have been observed in simulation to fold via native-only contacts when close to their melting temperature (26). At low $T$ (or high hydrophobicity) the pathways shift to a hydrophobic collapse, in which nonnative contacts form followed by further rearrangements leading to the native state (27). Similarly, colloids assemble via monomeric pathways at high temperature, forming bonds that are compatible with the overall structure in an equivalent process to native contact formation (24). Finally, systems of colloidal sticky spheres prefer to form the same concave, boat-like conformation that we observe for octahedron nets (20).

Our simple model therefore draws connections between the macroscopic irreversible folding of polyhedra (8), assembly of patchy (24) and colloidal (20) particles, and the folding of amino acids (26–28). The identified trade-off between entropy and enthalpy that dictates high-temperature folding provides guiding principles for the assembly of 3D complex geometries from potentially simpler-to-fabricate 2D nets. We demonstrated the judicious pathway engineering via the selection of nets with certain characteristics. We found that nets at high temperature fold through pathways that maximize the internal degrees of freedom, regardless of their propensity to fold, and the more compact nets fold with higher propensity. The compactness measures correlated with the number of pathways connecting the unfolded and folded states, offering some understanding on why these measures work well. In addition to giving insights into the thermodynamics of folding in naturally occurring systems, our results could also provide a route for the fabrication of anisotropic Brownian shells, paving the way for the self-assembly of complex crystals from nanoshells and colloidal shells (29–32) capable of encapsulating cargo. We expect these results to impact future experiments on folding of graphene sheets (13), graphene oxide layers (12), or DNA–origami polyhedral nets (33).

Materials and Methods

Enumeration of Polyhedral Nets.

We create nets from polyhedra via a process known as edge unfolding. In edge unfolding, one cuts along a set of prechosen edges, called the cutting tree, of a polyhedron (e.g., a cube) to create a single, contiguous flat 2D sheet of connected (square) faces: a net. We enumerate all of the nets of each polyhedron by generating random weights for the edges of the skeleton-1 graph of the polyhedron on the interval [0, 1]. The minimal spanning tree was found using Kruskal’s algorithm (34). We then converted the spanning tree to a net and added it to the database if it did not already exist. We ran this loop for many iterations until we found all of the nets for each shape.

Langevin Dynamics and Molecular Dynamics Simulation.

Langevin dynamics are used to model the folding dynamics for each net using HOOMD-Blue (35–38). Each face of the net is approximated by a union of spheres acting as a rigid body, with an edge length of 10 spheres. The spheres are arranged in a hexagonal lattice for triangular faces, a square lattice for square faces, and a hexagonal approximate for the pentagonal faces. For each simulation the drag coefficient, $\gamma$, was set to the inverse of the number of spheres used to create a facet. The spheres in the center of the face interact via a Weeks–Chandler–Andersen (WCA) potential shown in blue in Fig. 1, while the spheres on the free edges of the net interact via a Lennard–Jones potential; both potentials used $ϵ$ and $\sigma$ values of 1.0. The rigid facets are tethered together using harmonic springs along the edges, using a spring constant of 800 and equilibrium distance of 1.0.

Quantifying Yield.

To quantify the folding yield we ran 125 simulations starting from a high temperature and quenched the temperature to near zero ($T=0.1$). We then defined the yield as the fraction of simulations that completely folded into the target polyhedron. To distinguish between nets that had very low probability, we defined the folding propensity as the average fraction of native contacts averaged over all of the quenching simulations we ran. If all nets folded perfectly in all runs, the folding propensity is one but is possibly nonzero even if all nets did not fold at all. We linearly quenched 125 systems from 0.1 ≤ T ≤ T_m + 2.5, where $T_m$ is the folding temperature defined as the maximum melting temperature (temperature at which the net is unfolded 50% of the time) among all nets for a given target shape. We used two different cooling rates to investigate their influence in the folding yield: 2.5 $\times 10^{-6}T/t$ and 2.5 $\times 10^{-8}T/t$. The $T_m$ for each shape is listed in SI Appendix, Table S1.

MSMs and Folding Pathway Calculations.

MSMs (21) have been used to study protein folding (22, 23) and virus capsid assembly (39) and can provide a detailed view into the dynamics and thermodynamics of the folding landscape. In contrast to other methods to compute assembly pathways, which require monotonic order parameters (40) or hierarchical computation of the partition function (41), MSMs require each simulation snapshot to be classified as a discrete state, and the number of transitions between each state is recorded in a matrix. The dihedral angles completely specify the configuration of a net and are therefore a good set of collective variables. We break the “up”/“down” folding degeneracy by keeping track of the dihedral angle on the interval $\left[\mathrm{0,2}\pi \right]$. As the simulation is running we also compute the energy between each pair of free edges (edges not part of a hinge) on the net. If the potential energy between two edges is less than $E_{bond}=-5ϵ$, then the edges are considered to be bonded, and a list of bonded edges is recorded along with the list of dihedral angles. All intermediates are then clustered using DBSCAN (42) with a variation of the Manhattan metric, $d\left(i,j\right)=\underset{\alpha \in \text{Aut}\left(G_{\text{net}}\right)}{min}max|a_{\alpha \left(i\right),k}-a_{j,k}|$, which is a way to compare the dihedral angles of different states taking into account the symmetry of the net. Using the bonding information, we turn the molecular dynamics (MD) model into a graph, $G_{int}$. By looking at the graph automorphisms we can determine whether the symmetry could lead to a relabeling of the vertices of the net. If so, clusters returned by the DBSCAN algorithm were merged.

To build the MSM we ran 125 independent simulations at constant volume and temperature for $12.5\times 10^6$ steps and then branched the trajectories using new random seeds. This process was repeated until we obtained a total of 1,875 ($14\times 125$) trajectories (or, equivalently, $2.3\times 10^{10}$ time steps) for each net and each temperature. Bonded edges and dihedral angles for each hinge were computed every 10 time steps and combined to define a state in the MSM described above. The lag time, $\tau$, was found by the standard protocol of identifying the time at which the eigenvalues of the transition probability matrix become constant (SI Appendix, Fig. S7). We used transition path theory (23, 43, 44) to determine the reactive flux, $f_{ij}$, of all intermediates. The reactive flux is defined as $f_{ij}=q_j^{+}{\pi }_i{P}_{ij}{q}_i^{-}$, where $q_j^{+}$ is the forward committor probability (the probability that the net will fold from state $j$), ${\pi }_i$ is the probability of being in state $i$, $P_{ij}$ is the probability of transitioning to state $j$ given the system is in state $i$, and $q_i^{-}$ is the backward committor probability (the probability that the net is folding, as opposed to unfolding). Finally, the net flux is defined as $f_{ij}^{+}=max\left\{f_{ij}-f_{ji},0\right\}$. The dominant paths were computed via the “bottleneck” algorithm, using the net fluxes (23, 43). The total reactive flux is defined as the sum of the reactive flux out of the unfolded state, $F={\sum }_i{f}_{ui}$, where $u$ is the unfolded state. The folding rate is then $k_{fold}=F/\tau {\pi }_r$, where ${\pi }_r$ is the probability that the pathway is moving forward.

Folding Parameters.

The number of native contacts, $Q$, was calculated by counting the number of edges that were bonded to the correct corresponding edge according to the criteria described above. The nonnative contacts were calculated similarly. The diameter is the graph diameter of the face graph of the net. In general the number of degrees of freedom can be difficult to calculate because it can be difficult to deduce which constraints are redundant in the net. In general one can use the pebble game (45); however, if the linkage is not generic or has point group symmetries, the pebble game can underestimate the number of degrees of freedom (46, 47). First, we applied the pebble game to each intermediate, and then for closed-loop motifs we applied a closed-loop formula to determine the number of degrees of freedom (48); finally, intermediates with high degrees of symmetry were checked by hand, since the pebble game is known to underestimate these cases (46, 47).

Enumerating High-Temperature Pathways.

An exhaustive search was performed to enumerate high-$T$ pathways. Two principles were assumed to be important for the folding pathways at high temperature: local bonds and maximizing number of degrees of freedom. We initialize the algorithm by adding the unfolded state to the queue and creating an empty graph that will contain the pathway information. For each intermediate on the queue, a set of candidate bonds was calculated by finding edges on the intermediate that still needed to be bonded that also had a topological distance of one (local). This intermediate was then added to a queue for further processing, and a link between the current state and the candidate state is made in the graph. Finally, the pathways are taken from the graph and sorted lexicographically by the sequence of degrees of freedom of each intermediate along the pathway. The pathways that have the largest number of degrees of freedom are then returned.