How functional traits influence plant growth and shade tolerance across the life cycle

Significance

Plant species differ in many functional traits—features of specific tissues and allocation of energy among them. While traits have been used in many correlative approaches to describe communities and demography, it has remained unclear how and why traits should influence whole-plant growth. Here, we present a theoretical framework for understanding the effect of traits on plant growth and shade tolerance. This framework captures diverse patterns of growth in relation to size and explains why the effect of traits on growth changes through ontogeny. By disentangling the effects of plant size, light environment, and traits on growth rates, this study provides a theoretical foundation for understanding growth across diverse tree species around the world.

Abstract

Plant species differ in many functional traits that drive differences in rates of photosynthesis, biomass allocation, and tissue turnover. However, it remains unclear how—and even if—such traits influence whole-plant growth, with the simple linear relationships predicted by existing theory often lacking empirical support. Here, we present a theoretical framework for understanding the effect of diverse functional traits on plant growth and shade tolerance by extending a widely used model, linking growth rate in seedlings with a single leaf trait, to explicitly include influences of size, light environment, and five prominent traits: seed mass, height at maturation, leaf mass per unit leaf area, leaf nitrogen per unit leaf area, and wood density. Based on biomass growth and allocation, this framework explains why the influence of traits on growth rate and shade tolerance often varies with plant size and why the impact of size on growth varies among traits. Specifically, we demonstrate why for height growth the influence of: (i) leaf mass per unit leaf area is strong in small plants but weakens with size; (ii) leaf nitrogen per unit leaf area does not change with size; (iii) wood density is present across sizes; (iv) height at maturation strengthens with size; and (v) seed mass decreases with size. Moreover, we show how traits moderate plant responses to light environment and also determine shade tolerance, supporting diverse empirical results.

Functional traits capture core differences in the strategies plants use to acquire and invest resources (1–3). Although most woody plants have the same basic physiological function and key resource requirements (carbon, nutrients, and water), species differ considerably in the rates at which resources are acquired, invested into different tissues, and lost via turnover. During the last two decades, trade-offs related to some prominent traits have been quantified, with values for some leaf, wood, or seed traits now available for up to 10% of the world’s 250,000 plant species (4). As data have accumulated, researchers are increasingly looking to traits to predict patterns in plant growth, demography, life history, and performance (5–8). In this work, we outline the mechanisms by which the growth of individual plants may be influenced by various functional traits, as well as plant size and the light environment.

While the influence of traits on elements of plant physiological function has been increasingly quantified and understood, attempts at using traits to predict demographic rates have met with mixed success (5, 6, 9–11). In seedlings, the trait leaf mass per unit leaf area (LMA)—the central element of the leaf economics spectrum (2)—was found to be tightly correlated with relative growth rate in plant mass (12–14), as predicted from a simple mathematical model of growth rate (described below). LMA and a close correlate leaf lifespan were also linked to height growth rate for small seedlings and saplings (9, 15). These early successes prompted researchers to search for similar relationships in large plants. However, results for saplings and trees showed LMA was not correlated with growth rate (5, 6, 10, 11). Meanwhile, other traits such as wood density (WD) showed strong relationships to growth in large plants (6, 10), but less so in small plants (16). Clearly, traits do not correlate simply and consistently to growth rate.

Recently, it has become clear that the effect of traits on plant growth can be modified by plant size (17–21). A recent metaanalysis of 103 studies reporting >500 correlations provides the most compelling evidence (21). That study showed that the strength of the correlation between some traits (including LMA and maximum height) and growth rate was modified by size, while for other traits (including WD and assimilation rate per leaf area), the sign of the correlation remained the same, irrespective of size. Here, we extend previous work (21) to provide a mechanistic explanation of these empirical patterns via a model of plant growth and allocation.

Interpreting diverse empirical results seeking to link traits to growth rate has been challenging because, until recently (21), we lacked any clear expectations on why the effect of traits may be moderated by size. A widely used equation for seedlings suggests that, all else being equal, a seedling’s relative growth rate in mass is linearly and negatively related to LMA (12–14). An extension of this equation suggests that a similar relationship should hold at larger plant sizes (41). But, as noted above, the prediction for large plants is not supported by empirical results. Meanwhile, theoretical predictions on how other traits should influence growth are largely absent. Without further guidance, many researchers expected traits to map directly onto growth rates (e.g., refs. 3, 5, 11, and 42).

One reason theoretical predictions have been lacking or not been supported is that in existing theory, the effects of traits is realized mainly via influences on net primary productivity (photosynthesis − respiration) (14, 41). By contrast, the physiology of traits such as LMA and WD suggests that they influence allocation of biomass among different tissues and their turnover rates, rather than net primary production (17, 21, 43). A second concern for theory focused on net primary production is that measuring production is really only practical for small plants. On larger plants, growth is measured mainly as increment in either stem diameter or height (44–46). As outlined below, growth in height and diameter also depend on the allocation of biomass and tissue construction costs.

Here, we show how a mechanistic growth model—called plant (47)—can explain diverse empirical phenomena, including a size-dependent effect of traits on growth and an effect of traits on shade tolerance (Table 1), and thereby offer insights into the way traits influence key elements of plant demography across the life cycle. The plant model builds on past approaches to modeling production and allocation of biomass (e.g., refs. 17, 21, 22, 27, and 48–51). Our primary focus in this work is to explain a pattern that has been gradually emerging—that the effect of traits on plant growth is modified by plant size (18, 19, 21). Based on the same decomposition of growth rates as is implemented in the plant model (from refs. 17 and 52), ref. 21 argued conceptually why the effect of traits on growth should change with size. Here, we extend the results of ref. 21 to show, from the point of view of mass production and allocation, how and why the effect of some traits on growth rates changes with size. We consider five prominent traits, each capturing a specific physiological trade-off: seed mass (SM), height at maturation (${\text{H}}_{\mathrm{m}\mathrm{a}\mathrm{t}}$), leaf nitrogen content per unit leaf area (N), LMA, and WD (Table 2).

Table 1.

Empirical phenomena explained in this work

Change in growth rate with increasing size (Fig. 1)

Biomass growth: hump-shaped (22, 23)

Plant mass: increasing (24, 25)

Height: hump-shaped (24, 26, 27)

Stem diameter: hump-shaped (10, 28, 29)

Relative growth rate (all variables): decreasing (19, 30)

Effect of traits on growth rate (Fig. 3)

SM: $\downarrow$ values $\downarrow$ seedling size, & thus $\downarrow$ absolute and $\uparrow$ relative growth rate (21)

$H_{\mathrm{m}\mathrm{a}\mathrm{t}}$: $\downarrow$ values $\downarrow$ growth rate at larger sizes (21)

N*: $\downarrow$ values $\uparrow$ growth rate irrespective of size, but only in high light (21)

LMA†: $\downarrow$ values $\uparrow$ growth rate when small, not at midlarge sizes (21)

WD: $\downarrow$ values $\uparrow$ growth rate, except at largest sizes (21)

Responsiveness of growth rate to changes in light, $E$ (Fig. 3)

N*: $\uparrow$ values respond more

LMA†: $\downarrow$ values respond more

WD: $\downarrow$ values respond more (18)

Effect of size and traits on shade tolerance, WPLCP (Fig. 4)

Size: decreasing (22, 31, 32)

N*: $\downarrow$ values $\uparrow$ shade tolerance (33–35)

LMA†: $\downarrow$ values $\downarrow$ shade tolerance (9, 32, 33, 35)‡ and $\uparrow$LAI (15, 36, 37)

WD: $\downarrow$ values $\downarrow$ shade tolerance (38)

H_mat, height at maturation, LAI, leaf area index; N, leaf nitrogen content per unit leaf area; SM, seed mass.

^*Similar responses occur for maximum photosynthetic rate per leaf area and dark respiration rate per leaf area; here, both related to N.

^†Similar responses occur for leaf lifespan; here, directly related to LMA.

^‡Ref. 35 also finds a relationship between WPLCP and leaf respiration rate expressed per unit leaf area or per unit leaf mass.

Table 2.

Key trade-offs (benefit and cost) for the five traits considered, as encoded into the plant model

Trait	Benefit	Cost	Ref.
SM	$\uparrow$ Size of seedlings	$\downarrow$ Seed production rate	39
${\text{H}}_{\mathrm{m}\mathrm{a}\mathrm{t}}$	$\uparrow$ Growth rate	$\downarrow$ Seed production rate	40
N	$\uparrow$ Photosynthetic rate in high light	$\uparrow$ Respiration rate	2
LMA	$\downarrow$ Leaf turnover rate	$\uparrow$ Cost of building leaf	2
WD	$\downarrow$ Sapwood turnover rate	$\uparrow$ Cost of building stem	3

We also show how our approach can account for related phenomena, including changes in growth and shade tolerance with traits, individual size, and light environment (Table 1). Our view is that trait-based approaches—which aim to explain differences among species—should be integrated within a general model of plant growth and thus should also be able to capture patterns of growth through ontogeny. In absolute terms, growth rates tend to show hump-shaped relationships with size, when expressed as either height (24, 27), diameter (10, 28, 29), or biomass growth (22, 23). In contrast, the growth rate of standing plant mass continues to increase with size (24, 25). Expressed as relative growth rates, all growth measures decrease sharply with size (19, 30). Shade tolerance also varies among species, correlates with traits (9, 32, 33), and tends to decrease with increasing size (22, 31, 32). These diverse phenomena deserve an integrated explanation.

A Framework for Understanding the Effects of Traits on Growth Rate and Shade Tolerance

The plant model builds on the widespread approach used in many vegetation models of explicitly modeling the amounts of biomass in different tissues within a plant (e.g., refs. 17, 22, 27, 49–51, and 53) (Fig. 1A). We consider the masses $M_i$, areas $A_i$, and diameters $D_i$ of tissues, where the subscripts indicates tissue type: a, alive; b, bark and phloem; h, heartwood; l, leaf; r, root; s, sapwood; st, stem total (s+b+h); t, total. The total mass of living tissue is then $M_{\mathrm{a}}=M_{\mathrm{l}}+M_{\mathrm{b}}+M_{\mathrm{s}}+M_{\mathrm{r}}$, and the standing mass of the plant is $M_{\mathrm{t}}=M_{\mathrm{a}}+M_{\mathrm{h}}$. A summary of all variables, units, and definitions is given in Table 3, with further details on the parameter values applied given in SI Appendix, Tables S1 and S2.

Fig. 1.

Conceptual framework linking growth rate to plant size and traits. (A) Shows how the distribution of mass in a typical plant varies with size. (B) Equations describing the rates of biomass growth, and growth in various dimensions of the plant. In the first line the symbol $\mathrm{\Sigma }$ means “sum” across tissues, where $i=\mathrm{l},\mathrm{b},\mathrm{s},\mathrm{r}$. Gray numbers indicate equation numbers referred to in the main text. Insets show how the different metrics change intrinsically with plant height, when applying the “functional-balance” model in Table 4. Colors highlight where the same metric appears repeatedly in different equations. For a list of variable names, see Table 3.

Table 3.

Variable definitions

Symbol	Unit	Description
Traits (constant through ontogeny)
$\omega$	kg	Seed mass (SM)
$H_{\mathrm{m}\mathrm{a}\mathrm{t}}$	m	Height at maturation (${\mathrm{H}}_{\mathrm{m}\mathrm{a}\mathrm{t}}$)
$\nu$	kg$\cdot$m−2	Leaf nitrogen content per unit leaf area (N)
$\varphi$	kg$\cdot$m−2	Leaf mass per unit leaf area (LMA)
$\rho$	kg$\cdot$m−3	Wood density (WD)
State or rate variables (may vary through ontogeny)
$H$	m	Height of a plant
$D$	m	Stem diameter
$M_i$	kg	Mass of tissue type $i$ retained on plant
$A_i$	${\text{m}}^2$	Surface or cross-section are of tissue type $i$
$\frac{\mathrm{d}B}{\mathrm{d}t}$	kg$\cdot$${\text{y}}^{-1}$	Biomass growth rate
$p,\overline{p}$	mol$\cdot$${\text{y}}^{-1}\cdot$${\text{m}}^{-2}$	Photosynthetic rate per unit area
$r_i$	mol$\cdot$${\text{y}}^{-1}\cdot$${\text{kg}}^{-1}$	Respiration rate per unit mass of tissue type $i$
$k_i$	${\text{y}}^{-1}$	Turnover rate for tissue type $i$
Environmental variables (fixed)
$E$		Canopy openness
Other parameters (constant throughout)
${\alpha }_{\mathrm{y}}$		Yield, fraction of carbon fixed into biomass
${\alpha }_{\mathrm{b}io}$	kg$\cdot$mol−1	Biomass per mol carbon
${\eta }_c$		Crown-shape parameter
$\theta$		Sapwood area per unit leaf area
${\alpha }_{\mathrm{l}1}$	m	Height of plant with leaf area of 1${\text{m}}^2$
${\alpha }_{\mathrm{r}1}$	kg$\cdot$m−2	Root mass per unit leaf area
${\alpha }_{\mathrm{b}1}$		Ratio of bark area to sapwood area

For M_i , r_i , k_i and A_i , subscripts refer to: a, alive tissue; b, bark; h, heartwood; l, leaves; r, roots; s, sapwood; st, total stem.

Applying a standard approach, the amount of biomass growth on the plant, $\frac{\mathrm{d}B}{\mathrm{d}t}$, is given by the difference between income (photosynthesis) and losses (respiration and turnover) (49, 54):

$$\frac{\mathrm{d}B}{\mathrm{d}t}={\alpha }_{\mathrm{b}\mathrm{i}\mathrm{o}}\hspace{0.17em}{\alpha }_{\mathrm{y}}(A_{\mathrm{l}}\hspace{0.17em}\overline{p}\left(E\right)-\hspace{0.17em}\sum _{i=\mathrm{l},\mathrm{b},\mathrm{s},\mathrm{r}}{M}_i\hspace{0.17em}{r}_i)-\sum _{i=\mathrm{l},\mathrm{b},\mathrm{s},\mathrm{r}}{M}_i\hspace{0.17em}{k}_i.$$ [1]

Photosynthesis is the product of the average photosynthetic rate per unit leaf area, $\overline{p}\left(E\right)$, and total leaf area, $A_{\mathrm{l}}$. We assume that $\overline{p}$ increases with canopy openness $E$, as per a standard light-response curve (see SI Appendix for details), and respiration and turnover rates of different tissues are constants that potentially differ with traits. The constants ${\alpha }_{\mathrm{y}}$ and ${\alpha }_{\mathrm{b}\mathrm{i}\mathrm{o}}$ account for the yield (fraction of C fixed in biomass) and the conversion of ${\text{CO}}_2$ into units of biomass, respectively. While the plant model can easily accommodate competitive shading via influences on $E$, in this analysis we grew individual plants under a fixed-light environment so that we could better understand trait- and size-related effects. Many vegetation models also use a more detailed physiological model for calculating $\overline{p}$ and $r_{\mathrm{i}}$ (e.g., as functions of temperature), although such detail will not qualitatively alter model behavior.

Classic Model for Mass-Based Relative Growth Rate.

Earlier studies on seedlings related relative growth rate in mass to LMA (12–14, 55), using a model that can be derived from Eq. 1 as a special case of the more-extended model described below. Ignoring all turnover terms, as well as the respiration terms for nonleaf tissues in Eq. 1 and reproduction, biomass growth becomes a linear function of leaf area, making relative growth rate in mass:

$$\frac{\mathrm{d}B}{\mathrm{d}t}\frac{1}{M_{\mathrm{a}}}\approx P_{\mathrm{n}\mathrm{e}\mathrm{t}}\times {\varphi }^{-1}\times \frac{M_{\mathrm{l}}}{M_{\mathrm{a}}},$$ [2]

where $P_{\mathrm{n}\mathrm{e}\mathrm{t}}={\alpha }_{\mathrm{b}\mathrm{i}\mathrm{o}}\hspace{0.17em}{\alpha }_{\mathrm{y}}\hspace{0.17em}\left(\overline{p}\left(E\right)-r_{\mathrm{l}}\right)$, and $\varphi$ is LMA. Although Eq. 2 captures patterns of growth in seedlings in relation to LMA (14), this approximation does not easily extend to the variables that are routinely collected for large trees such as height or stem diameter. The derivations below clarify these links.

Decomposition of Growth Rates into Components.

To model growth in plant height ($H$), leaf area ($A_{\mathrm{l}}$), basal stem area ($A_{\mathrm{s}\mathrm{t}}$), standing mass ($M_{\mathrm{t}}$), or stem diameter ($D$) requires that we account not just for biomass growth, but also for the costs of building new tissues and allocation to reproduction. Mathematically, these growth rates can be decomposed into a product of physiologically relevant terms (17, 21) (Fig. 1B, eqs. 2–7). While other decompositions are possible, the approach used here arises from the idea that multiple aspects of function and allocation decisions are made in relation to the amount of leaf area on a plant (17). Growth rates in plant weight ($\frac{\mathrm{d}{M}_{\mathrm{t}}}{\mathrm{d}t}$; Fig. 1B, eq. 2), total leaf area ($\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}t}$; Fig. 1B, eq. 4), height ($\frac{\mathrm{d}H}{\mathrm{d}t}$; Fig. 1B, eq. 5), stem basal area ($\frac{\mathrm{d}{A}_{\mathrm{s}\mathrm{t}}}{\mathrm{d}t}$; Fig. 1B, eq. 6), and stem diameter ($\frac{\mathrm{d}D}{\mathrm{d}t}$; Fig. 1B, eq. 7) therefore share several terms. Many of these terms also vary intrinsically with size, as shown in Fig. 1B, Insets.

The growth rates of all size metrics (Fig. 1B, eqs. 2–7) depend on the product of biomass growth $\frac{\mathrm{d}B}{\mathrm{d}t}$ (from Eq. 1) and the fraction of biomass allocated to growth of the plant, $\frac{\mathrm{d}{M}_{\mathrm{a}}}{\mathrm{d}B}$, which varies from 0 to 1. The remaining $1-\frac{\mathrm{d}{M}_{\mathrm{a}}}{\mathrm{d}B}$ fraction of mass produced is allocated to reproduction. In plants, $\frac{\mathrm{d}{M}_{\mathrm{a}}}{\mathrm{d}B}$ starts high, 1.0 for seedlings, and then decreases through ontogeny, potentially to zero in fully mature plants (56). Note also that $\frac{\mathrm{d}{M}_{\mathrm{a}}}{\mathrm{d}B}$ is the allocation of biomass after replacing parts lost due to turnover. So a plant with $\frac{\mathrm{d}{M}_{\mathrm{a}}}{\mathrm{d}B}=0$ will continue to produce some new leaves and increase in stem diameter, even if the net amount of live mass $M_{\mathrm{a}}$ is not increasing.

The growth rate in the total standing mass of the plant (Fig. 1B, eq. 2) is then the sum of heartwood formation (= sapwood turnover) and any increment in live mass.

The remaining growth rates (Fig. 1B, eqs. 4–7) all depend on another variable, $\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}{M}_{\mathrm{a}}}$, that accounts for the marginal cost of deploying an additional unit of leaf area, including construction of the leaf itself and supporting bark, sapwood, and roots (Fig. 1B, eq. 3). The inverse of this term, $\frac{\mathrm{d}{M}_{\mathrm{a}}}{\mathrm{d}{A}_{\mathrm{l}}}$, is the whole plant construction cost per unit leaf area, which can be further decomposed as a sum of construction cost per unit leaf area for different tissues, with one of these being the trait $\varphi =\frac{\mathrm{d}{M}_{\mathrm{l}}}{\mathrm{d}{A}_{\mathrm{l}}}$ (Fig. 1B, eq. 3).

The rate of height growth (Fig. 1B, eq. 5) depends on an additional term, $\frac{\mathrm{d}H}{\mathrm{d}{A}_{\mathrm{l}}}$: the growth in plant height per unit growth in leaf area. This variable accounts for the architectural strategy of the plant (17). Some species tend to leaf out more than grow tall, while other species emphasize vertical extension (9).

The rate of stem-basal-area growth (Fig. 1B, eq. 6) can be expressed as the sum of increments in sapwood, bark, and heartwood areas ($A_{\mathrm{s}},A_{\mathrm{b}},A_{\mathrm{h}}$ respectively): $\frac{\mathrm{d}{A}_{\mathrm{s}\mathrm{t}}}{\mathrm{d}t}=\frac{\mathrm{d}{A}_{\mathrm{b}}}{\mathrm{d}t}+\frac{\mathrm{d}{A}_{\mathrm{s}}}{\mathrm{d}t}+\frac{\mathrm{d}{A}_{\mathrm{h}}}{\mathrm{d}t}$. These, in turn, are related to ratios of sapwood and bark area per leaf area and sapwood turnover (Fig. 1B, eq. 6).

Finally, the rate of stem-diameter growth (Fig. 1B, eq. 7) is given by a geometric relationship between stem diameter ($D$) and stem area ($A_{\mathrm{s}\mathrm{t}}$). We make no assumptions about the relationship of stem diameter to height or leaf area: These arise as emergent properties, via integration of stem turnover (Table 4, eqs. 1–10).

Table 4.

Equations for a functional-balance model of plant construction

Variable	Function	Marginal cost	Growth rate	Eq.
Functional-balance assumptions
Height	$H={\alpha }_{\mathrm{l}\mathrm{1}}\hspace{0.17em}{A}_{\mathrm{l}}^{0.5}$	$\frac{\mathrm{d}H}{\mathrm{d}{A}_{\mathrm{l}}}=0.5{\alpha }_{\mathrm{l}\mathrm{1}}{A}_{\mathrm{l}}^{-0.5}$	$\frac{\mathrm{d}H}{\mathrm{d}t}=\frac{\mathrm{d}H}{\mathrm{d}{A}_{\mathrm{l}}}\hspace{0.17em}\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}t}$	1
Sapwood area	$A_{\mathrm{s}}=\theta \hspace{0.17em}{A}_{\mathrm{l}}$	$\frac{\mathrm{d}{A}_{\mathrm{s}}}{\mathrm{d}{A}_{\mathrm{l}}}=\theta$	$\frac{\mathrm{d}{A}_{\mathrm{s}}}{\mathrm{d}t}=\frac{\mathrm{d}{A}_{\mathrm{s}}}{\mathrm{d}{A}_{\mathrm{l}}}\hspace{0.17em}\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}t}$	2
Bark area	$A_{\mathrm{b}}=b\hspace{0.17em}\theta \hspace{0.17em}{A}_{\mathrm{l}}$	$\frac{\mathrm{d}{A}_{\mathrm{b}}}{\mathrm{d}{A}_{\mathrm{l}}}=b\hspace{0.17em}\theta$	$\frac{\mathrm{d}{A}_{\mathrm{b}}}{\mathrm{d}t}=\frac{\mathrm{d}{A}_{\mathrm{b}}}{\mathrm{d}{A}_{\mathrm{l}}}\hspace{0.17em}\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}t}$	3
Root mass	$M_{\mathrm{r}}={\alpha }_{\mathrm{r}\mathrm{1}}\hspace{0.17em}{A}_{\mathrm{l}}$	$\frac{\mathrm{d}{M}_{\mathrm{r}}}{\mathrm{d}{A}_{\mathrm{l}}}={\alpha }_{\mathrm{r}1}$	$\frac{\mathrm{d}{M}_{\mathrm{r}}}{\mathrm{d}t}=\frac{\mathrm{d}{M}_{\mathrm{r}}}{\mathrm{d}{A}_{\mathrm{l}}}\hspace{0.17em}\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}t}$	4
Heartwood area			$\frac{\mathrm{d}{A}_{\mathrm{h}}}{\mathrm{d}t}=k_s{A}_{\mathrm{h}}$	5
Derived quantities
Leaf mass	$M_{\mathrm{l}}=\varphi \hspace{0.17em}{A}_{\mathrm{l}}$	$\frac{\mathrm{d}{M}_{\mathrm{l}}}{\mathrm{d}{A}_{\mathrm{l}}}=\varphi$	$\frac{\mathrm{d}{M}_{\mathrm{l}}}{\mathrm{d}t}=\frac{\mathrm{d}{M}_{\mathrm{l}}}{\mathrm{d}{A}_{\mathrm{l}}}\hspace{0.17em}\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}t}$	6
Sapwood mass	$M_{\mathrm{s}}=\theta \hspace{0.17em}\rho \hspace{0.17em}{\eta }_c\hspace{0.17em}{A}_{\mathrm{l}}\hspace{0.17em}H$	$\frac{\mathrm{d}{M}_{\mathrm{s}}}{\mathrm{d}{A}_{\mathrm{l}}}=\theta \hspace{0.17em}\rho \hspace{0.17em}{\eta }_c\hspace{0.17em}(H+A_{\mathrm{l}}\hspace{0.17em}\frac{\mathrm{d}H}{\mathrm{d}{A}_{\mathrm{l}}})$	$\frac{\mathrm{d}{M}_{\mathrm{s}}}{\mathrm{d}t}=\frac{\mathrm{d}{M}_{\mathrm{s}}}{\mathrm{d}{A}_{\mathrm{l}}}\hspace{0.17em}\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}t}$	7
Bark mass	$M_{\mathrm{b}}=b\hspace{0.17em}\theta \hspace{0.17em}\rho \hspace{0.17em}{\eta }_c\hspace{0.17em}{A}_{\mathrm{l}}\hspace{0.17em}H$	$\frac{\mathrm{d}{M}_{\mathrm{b}}}{\mathrm{d}{A}_{\mathrm{l}}}=b\hspace{0.17em}\theta \hspace{0.17em}\rho \hspace{0.17em}{\eta }_c(H+A_{\mathrm{l}}\hspace{0.17em}\frac{\mathrm{d}H}{\mathrm{d}{A}_{\mathrm{l}}})$	$\frac{\mathrm{d}{M}_{\mathrm{b}}}{\mathrm{d}t}=\frac{\mathrm{d}{M}_{\mathrm{b}}}{\mathrm{d}{A}_{\mathrm{l}}}\hspace{0.17em}\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}t}$	8
Heartwood area	$A_{\mathrm{h}}={\int }_0^t\frac{\mathrm{d}{A}_{\mathrm{h}}}{\mathrm{d}t}\left(t\prime \right)\hspace{0.17em}dt\prime$		$\frac{\mathrm{d}{A}_{\mathrm{h}}}{\mathrm{d}t}=k_{\mathrm{s}}\hspace{0.17em}{A}_{\mathrm{s}}$	9
Heartwood mass	$M_{\mathrm{h}}={\int }_0^t\frac{\mathrm{d}{M}_{\mathrm{h}}}{\mathrm{d}t}\left(t\prime \right)\hspace{0.17em}dt\prime$		$\frac{\mathrm{d}{M}_{\mathrm{h}}}{\mathrm{d}t}=k_{\mathrm{s}}\hspace{0.17em}{M}_{\mathrm{s}}$	10

See Table 3 for a list of variable names and definitions. The first column of the functional-balance assumptions section provides cores assumptions between various size metrics and leaf area. Equations in the center and right columns of the table can be derived from these assumptions.

Shade Tolerance.

Eq. 1 can also be rearranged to obtain a measure of shade tolerance: the “whole-plant-light-compensation point” (WPLCP; refs. 22, 35, and 57). In general, photosynthesis rate per leaf area $\overline{p}$ increases with canopy openness, $E$. The WPLCP is then the value $E=E^{*}$ where photosynthetic gains balance the costs of tissue turnover and respiration, i.e., $\frac{\mathrm{d}B}{\mathrm{d}t}\left(E^{*}\right)=0$. From Eq. 1, this occurs when

$$\overline{p}\left(E^{*}\right)=\frac{{\sum }_{i=\mathrm{l},\mathrm{b},\mathrm{s},\mathrm{r}}\hspace{0.17em}{M}_{\mathrm{i}}\left(\frac{k_{\mathrm{i}}}{y}+r_{\mathrm{i}}\right)}{A_{\mathrm{l}}}.$$ [3]

Graphically, the WPLCP occurs at the point where the photosynthetic production (per unit leaf area) line intersects with the sum of maintenance and respiration costs (per unit leaf area) for each tissue (Fig. 2). Traits influence WPLCP when they affect either photosynthesis, respiration, or turnover. Also, as the amount of stem support increases with plant height, WPLCP also increases with height (22) (Fig. 2).

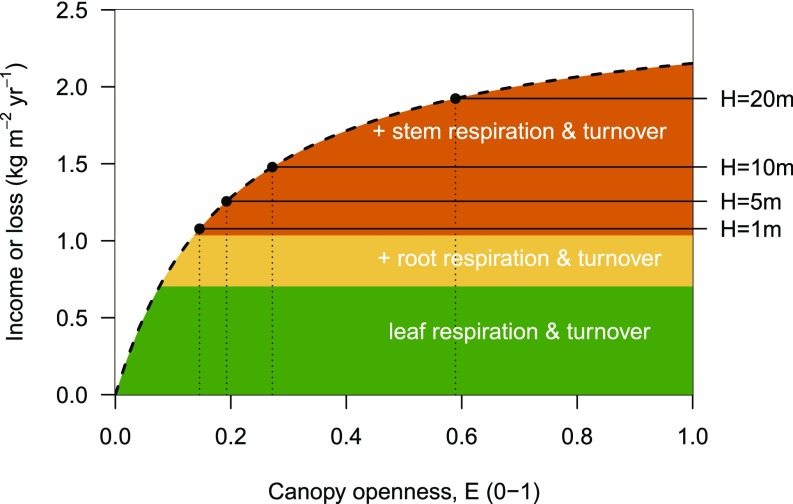
Fig. 2.

Conceptual framework showing how shade tolerance (as measured by WPLCP) is affected by plant size and traits, adapted from ref. 22. From Eq. 3, WPLCP is the canopy openness $E$ where the photosynthetic income per unit leaf area (dashed line) intersects the total respiration and turnover costs per unit leaf area (solid black lines). Colors indicate the contributions from different tissues to total costs. Because the costs of stem tissues increase with height, WPLCP also increases. Traits WD, N, and LMA can alter WPLCP by shifting either income or cost of different tissues (Table 5).

A Functional-Balance Model for Plant Construction.

Since Fig. 1B, eqs. 3–7 and Eq. 3 are derived by using standard rules of addition, multiplication, and differentiation, they may apply to a variety of growth models where biomass allocation is important. However, to make explicit predictions requires that we quantify all of the terms in Fig. 1B via an explicit model of plant construction and function.

The plant package adopts a model of plant construction and function that can be considered a first-order functional-balance or functional-equilibrium model, similar to those implemented in refs. 49 and 50. We could also call it “isometric,” because the assumptions see area-based metrics scaling to the first power of other area-based metrics and to the square power of length-based metrics, such as height (58). Table 4 provides key equations (see ref. 47 for full derivation). In particular, we assume that as a plant grows: (assumption 1) Its height scales to the 0.5 power of its leaf area (Table 4, eq. 1); (assumption 2) the cross-sectional area of sapwood in the stem is proportional to its leaf area (Table 4, eq. 2); (assumption 3) the cross-sectional area of bark and phloem in the stem is proportional to its leaf area (Table 4, eq. 3); (assumption 4) the cross-sectional area of root surface area and therefore mass is proportional to its leaf area (Table 4, eq. 4); and (assumption 5) the vertical distribution of leaf within the plant’s canopy, relative to the plant’s height, remains constant. Assumption 1 accounts for the architectural layout of the plant. Assumptions 2–4 are realizations of the pipe model (59), whereby the cross-sectional area of conducting tissues are proportional to leaf area. To describe the vertical distribution of leaf area within the canopy of an individual plant (assumption 5), we used the model of ref. 48, which can account for a variety of canopy profiles through a single parameter ${\eta }_c$, varying from 0 to 1 (for details, see SI Appendix).

Combined, the functional-balance assumptions from Table 4 lead directly to equations describing the mass of sapwood and bark in relation to leaf and the amount of leaf in relation to height (Table 4). These equations also predict that the amount of live stem tissue supporting each unit of leaf area should increase linearly with height,

$$\frac{M_{\mathrm{b}}+M_{\mathrm{s}}}{A_{\mathrm{l}}}=\left(1+{\alpha }_{\mathrm{b}1}\right)\hspace{0.17em}\theta \hspace{0.17em}\rho \hspace{0.17em}{\eta }_c\hspace{0.17em}H.$$ [4]

Substituting from Table 4, eqs. 1–10 into Fig. 1B, eqs. 5–7 then gives all the necessary terms needed to implement the growth model described in Fig. 1B.

Trait-Based Trade-Offs.

To capture the effects of functional traits on growth rates and shade tolerance requires that trait-based trade-offs be embedded within the model described above. Here, we considered five traits, for which we can posit specific physiological costs and benefits—described in detail below and summarized in Table 2. It is essential that any trait include both a benefit and cost in terms of plant function and/or life history; otherwise, we would expect ever-increasing trait values toward more beneficial values. In postulating potential benefits and costs, we considered only those thought to arise as direct biophysical consequences of varying a trait.

Ontogenetic Traits.

The first two traits considered modify behavior primarily at the start and end of an individual’s growth trajectory and were therefore termed “ontogenetic traits.”

SM:

SM moderates a trade-off between a plant’s rate of seed production per unit mass invested in reproduction and the mass of each offspring (39).

Height at maturation:

${\text{H}}_{\mathrm{m}\mathrm{a}\mathrm{t}}$ moderates an inevitable trade-off between mass invested in reproduction and in growing the plant, i.e., $\frac{\mathrm{d}{M}_{\mathrm{a}}}{\mathrm{d}B}$ in Fig. 1B, eqs. 2–7. We assumed the amount allocated to vegetative growth started high and then decreased once $H>H_{\mathrm{m}\mathrm{a}\mathrm{t}}$ (Fig. 1B). The exact nature of the function is noncritical; what is important is that plants shift from a period of investing mainly in vegetative growth to investing mainly in reproduction. Here, we let the fraction of mass allocated to reproduction vary with $H$ via the function $r_{\mathrm{r}\mathrm{1}}{\left(1.0+\exp \left(r_{\mathrm{r}\mathrm{2}}\left(1-H/H_{\mathrm{m}\mathrm{a}\mathrm{t}}\right)\right)\right)}^{-1}$, where $r_{\mathrm{r}\mathrm{1}}$ is the maximum possible allocation (0–1) and $r_{\mathrm{r}\mathrm{2}}$ determines the sharpness of the transition.

Developmental Traits.

The remaining three traits are termed “developmental traits” because they moderate effects the rate of movement along an individual’s growth trajectory.

Leaf nitrogen per unit leaf area:

We assume that both the maximum photosynthetic capacity of a leaf and leaf respiration rate both vary with N (=$\nu$), as ${\beta }_{\mathrm{l}\mathrm{f}\mathrm{1}}\hspace{0.17em}{\left(\nu /{\nu }_0\right)}^{{\beta }_{\mathrm{l}\mathrm{f}\mathrm{5}}}$ and ${\beta }_{\mathrm{l}\mathrm{f}\mathrm{4}}\hspace{0.17em}\nu$ respectively, where ${\beta }_{\mathrm{l}\mathrm{f}\mathrm{1}}$, ${\nu }_0$ and ${\beta }_{\mathrm{l}\mathrm{f}\mathrm{4}}$, and ${\beta }_{\mathrm{l}\mathrm{f}\mathrm{5}}$ are constants.

LMA:

LMA (=$\varphi$) influences growth by changing $\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}{M}_{\mathrm{a}}}$ (Table 4). In addition, we linked LMA to the rate of leaf turnover ($k_{\mathrm{l}}$), based on a widely observed scaling relationship (2) (SI Appendix, Fig. S1): $k_{\mathrm{l}}={\beta }_{\mathrm{k}\mathrm{l}\mathrm{1}}\hspace{0.17em}{\left(\varphi /{\varphi }_0\right)}^{-{\beta }_{\mathrm{k}\mathrm{l}\mathrm{2}}}$ where ${\beta }_{\mathrm{k}\mathrm{l}\mathrm{1}}$, ${\varphi }_0$ and ${\beta }_{\mathrm{k}\mathrm{l}\mathrm{2}}$ are empirical constants. The rate of leaf respiration per unit area was assumed to be independent of LMA (2); as such, the mass-based rate was adjusted whenever LMA was varied.

WD:

WD (=$\rho$) influences growth by changing $\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}{M}_{\mathrm{a}}}$ (Table 4). In addition, we linked WD to the rate of sapwood and bark turnover, mirroring the relationship assumed for leaf turnover: $k_{\mathrm{b}}=k_{\mathrm{s}}={\beta }_{\mathrm{k}\mathrm{s}\mathrm{1}}\hspace{0.17em}{\left(\rho /{\rho }_0\right)}^{-{\beta }_{\mathrm{k}\mathrm{s}\mathrm{2}}}$ where ${\beta }_{\mathrm{k}\mathrm{s}\mathrm{1}}$, ${\rho }_0$ and ${\rho }_{\mathrm{k}\mathrm{s}\mathrm{2}}$ are empirical constants. The rate of sapwood and bark respiration per unit stem volume was assumed to be independent of WD; as such, the mass-based rate was adjusted accordingly whenever WD was varied. There are currently few data relating sapwood turnover or respiration to WD.

Results

Model Assumptions.

We compared the assumptions outlined in Table 4 to data sourced from the Biomass and Allometry Database (60). SI Appendix, Fig. S2 shows that the three functional-balance assumptions in Table 4 and the relationship in Eq. 4 were all well-supported by the available data. As expected, species differed in elevation, but less so in the slope of the fitted lines, with slopes aligning with those predicted by the functional-balance assumptions (Table 4 and Eq. 4).

Changes in Growth Rate with Size.

Our model suggests an intrinsically size-dependent pattern of biomass-production and growth, which aligns with well-known empirical patterns (Table 1). Fig. 1 shows the predicted patterns for a typical woody plant, obtained by applying the functional-balance model from Table 4. Biomass growth showed a hump-shaped pattern with size, decreasing at larger sizes as the turnover and respiration of sapwood and bark increased. Height growth also showed a hump-shaped pattern with size, first increasing then decreasing. This pattern resulted from systematic changes in the four components of Fig. 1B, eq. 5 with increasing size, including a strong decline in the fraction of plant that is leaf (Fig. 1A), increasing reproductive allocation, and declining biomass growth. In contrast, basal-area growth continued to increase with size, due to an increasing influence of stem turnover. Diameter growth showed a weakly hump-shaped curve, tapering off slightly at larger sizes, in part because of the allometric conversion from basal area to diameter (Fig. 1B, eq. 7) and in part because of increased reproductive allocation in older trees (Fig. 1). All growth measures decreased sharply with size when expressed as relative growth rates.

Changes in Height Growth Rate with Traits.

We analyzed the response of growth rate to five different traits under the assumed trade-offs (Table 2). We considered changes in absolute and relative growth rates for mass, height, stem area, and stem diameter. Across the five different traits, we observed four relatively distinct types of response. These responses are summarized in Table 5 and described in more detail below.

Table 5.

Predicted effects of traits on components of plant function determining growth rate

	Ontogenetic		Development
	SM	$H_{\mathrm{m}\mathrm{a}\mathrm{t}}$	N	LMA	WD
Effect on elements of Eq. 1 and 2 and Fig. 1B, eqs. 1–9
Biomass growth, $\mathrm{d}B/\mathrm{d}t$
Photosynthesis	—	—	$\uparrow$	—	—
Respiration	—	—	$\uparrow$	—	—
Turnover	—	—	—	$\downarrow$	$\downarrow$
Allocation to growth, $\mathrm{d}{M}_{\mathrm{a}}/\mathrm{d}B$	—	$\uparrow$	—	—	—
Leaf deployment, $\mathrm{d}{A}_{\mathrm{l}}/\mathrm{d}{M}_{\mathrm{a}}$
Leaf	—	—	—	$\downarrow$	—
Sapwood	—	—	—	—	$\downarrow$
Predicted effect of trait on growths rate for a small and large plant
Height
Absolute, $\mathrm{d}H/\mathrm{d}t$	$\uparrow$ –	–$\hspace{0.17em}\uparrow$	$\uparrow \hspace{0.17em}\uparrow$	$\downarrow \hspace{0.17em}$–	$\downarrow \hspace{0.17em}\downarrow$
Relative, $\mathrm{d}H/\left(\mathrm{d}t.H\right)$	$\downarrow \hspace{0.17em}$–	–$\hspace{0.17em}\uparrow$	$\uparrow \hspace{0.17em}\uparrow$	$\downarrow \hspace{0.17em}$–	$\downarrow \hspace{0.17em}\downarrow$
Stem area
Absolute, $\mathrm{d}{A}_{\mathrm{s}\mathrm{t}}/\mathrm{d}t$	$\uparrow$ –	–$\hspace{0.17em}\uparrow$	$\uparrow \hspace{0.17em}\uparrow$	$\downarrow \hspace{0.17em}$–	$\downarrow \hspace{0.17em}\downarrow$
Relative, $\mathrm{d}{A}_{\mathrm{s}\mathrm{t}}/\left(\mathrm{d}t.A_{\mathrm{s}\mathrm{t}}\right)$	$\downarrow \hspace{0.17em}$–	–$\hspace{0.17em}\uparrow$	$\uparrow \hspace{0.17em}\uparrow$	$\downarrow \hspace{0.17em}$–	$\downarrow \hspace{0.17em}\downarrow$
Stem diameter
Absolute, $\mathrm{d}D/\mathrm{d}t$	$\uparrow$ –	–$\hspace{0.17em}\uparrow$	$\uparrow \hspace{0.17em}\uparrow$	$\downarrow \hspace{0.17em}$–	$\downarrow \hspace{0.17em}\downarrow$
Relative, $\mathrm{d}D/\left(\mathrm{d}t.D\right)$	$\downarrow \hspace{0.17em}$–	–$\hspace{0.17em}\uparrow$	$\uparrow \hspace{0.17em}\uparrow$	$\downarrow \hspace{0.17em}$–	$\downarrow \hspace{0.17em}\downarrow$
Mass
Absolute, $\mathrm{d}{M}_{\mathrm{t}}/\mathrm{d}t$	$\uparrow$ –	–$\hspace{0.17em}\uparrow$	$\uparrow \hspace{0.17em}\uparrow$	$\downarrow \hspace{0.17em}$–	$\downarrow \hspace{0.17em}\downarrow$
Relative, $\mathrm{d}{M}_{\mathrm{t}}/\left(\mathrm{d}t.M_{\mathrm{t}}\right)$	$\downarrow \hspace{0.17em}$–	–$\hspace{0.17em}\uparrow$	$\uparrow \hspace{0.17em}\uparrow$	$\downarrow \hspace{0.17em}$–	$\downarrow \hspace{0.17em}\downarrow$

Adapted and expanded from ref. 21. Arrows indicate the effect of increased trait value on each component; dashes indicate no effect.

Ontogenetic Traits.

Increasing SM caused seedlings to be larger and the rate of seed production to decrease. The only effect of SM on growth came from changing the plant’s initial size. The plots in Fig. 1, which show changes in growth rate with plant size, also express the expected changes in the growth of seedlings due to changes in seed size. Under similar light conditions, larger seedlings were predicted to have faster absolute growth rates (in all metrics) because of their greater total leaf area. At the same time, relative growth rate was predicted to decrease with size, as the ratio of leaf area to support mass decreases. As plants grow, differences in initial mass decrease in importance relative to other factors influencing growth through the life cycle. As a result, the correlations between SM and growth rate disappeared among larger plants.

Greater ${\text{H}}_{\mathrm{m}\mathrm{a}\mathrm{t}}$ caused a growth advantage at larger sizes by increasing $\frac{\mathrm{d}{M}_{\mathrm{a}}}{\mathrm{d}B}$ (Fig. 3). At smaller sizes, there was no differentiation among species, as all plants focused on growth.

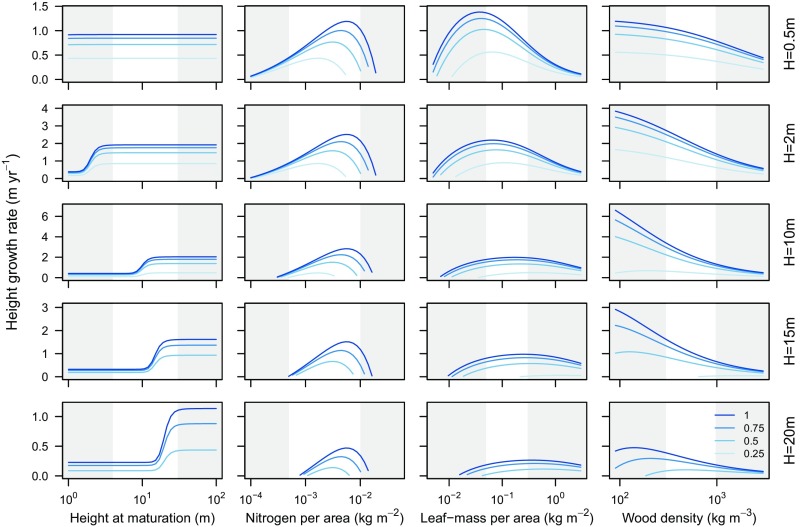
Fig. 3.

Effect of four traits on height growth rate for different-sized plants. Growth rates were simulated by using the plant model, applying the trade-offs describing in Table 2. Each plot shows how growth is influenced by a different trait for plants of a given height and across a series of canopy openness values from completely open (light blue, $E=1$) to heavily shaded (dark line, $E=0.25$). For any given value of trait and $E$, plants were grown to the desired height, and their growth rate was estimated. The white regions indicate trait ranges that are typically observed in real systems. SI Appendix, Figs. S3–S5 show similar plots but with growth measured as stem diameter, stem area, or plant mass. Changes in trait–growth relationships are summarized in Table 5.

Developmental Traits.

The response of growth rate to changes in N is relatively straightforward: There is an optimum value of N that maximizes height growth rate in a given light environment $E$ and does not vary with height (Fig. 3). As $E$ increases, the optimal N also increases. The invariance of the growth–trait relationship with respect to size arises as follows. The direct physiological effect of N is to increase the maximum potential photosynthetic rate of leaves, with a cost of higher respiration rate. Both the cost and benefits of N appear within the term $\frac{\mathrm{d}B}{\mathrm{d}t}$, implying that the direction of correlation between trait and growth rate depends crucially on the change in biomass growth per N. From Eq. 1, $\frac{\partial \left(\frac{\mathrm{d}B}{\mathrm{d}t}\right)}{\partial u}=A_{\mathrm{l}}\hspace{0.17em}\left(\frac{\partial \overline{p}\left(E\right)}{\partial u}-\frac{\partial r_{\mathrm{l}}}{\partial u}\right)$. As both $\overline{p}\left(E\right)$ and $r_{\mathrm{l}}$ are expressed per unit area and independent of height, the optimal value is also independent of height.

Unlike N, the response of growth rate to changes in LMA varies strongly with plant height, with the relationship moving like a wave across the trait spectrum (Fig. 3). As a result, the value of LMA that optimizes plant growth increases with height, while the direction of correlation between height growth rate and LMA shifts from negative to positive, as plants increase in height. Decreasing LMA has two impacts on height growth rate. First, lower LMA increases the leaf deployment per mass invested $\left(\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}{M}_{\mathrm{a}}}\right)$. Second, lower LMA decreases biomass growth $\left(\frac{\mathrm{d}B}{\mathrm{d}t}\right)$, due to increased leaf turnover. Whether lower LMA increases height growth depends on the relative magnitude of these two effects. When plants are small, the effect on leaf deployment rate is larger, and so decreasing LMA increases growth rate. When plants are large, the effect on leaf deployment is diminished because the cost of building other supportive tissues (other terms in Fig. 1B, eq. 3) is larger. Thus, at larger sizes, low LMA no longer increases growth rate (Fig. 3).

Reducing the cost of stem construction, via lower WD, decreases the cost of deploying a unit of leaf area, increasing growth rate (Fig. 3). Unlike LMA, the benefits of cheaper stem construction become more pronounced at intermediate sizes, as a larger fraction of the plant is stem (Fig. 1A).

Changes in Other Growth Rates with Trait.

The results reported above and in Fig. 3 focus on height growth rate. Corresponding results for absolute growth rates in stem diameter (Fig. 1B, eq. 7), stem basal area (Fig. 1B, eq. 6), and above-ground mass (Fig. 1B, eq. 2) are provided in SI Appendix, Figs. S3–S5. For each, plants were grown to a standard diameter, area, or mass. Changes in absolute and relative growth rates with traits therefore showed similar patterns.

We found that for SM, N, LMA, and ${\text{H}}_{\mathrm{m}\mathrm{a}\mathrm{t}}$, the patterns of growth rate in stem diameter, stem area, or above-ground mass with respect to traits mirrored those observed with respect to height growth (Table 5). The only trait where a slightly different response was observed was for WD. Whereas the effect of WD on height growth tended to diminish slightly at larger sizes (Fig. 3), the effect became even stronger when measuring growth rate in stem diameter, stem area, or above-ground mass. Sapwood lost via turnover became heartwood. Whereas the loss of sapwood diverted energy away from the height growth rate, the faster accumulation of heartwood actually accelerated the growth of stem diameter and area.

Responsiveness of Growth Rate to Light.

The predictions in Fig. 3 and SI Appendix, Figs. S3–S5 illustrate how traits impact growth rate under different light environments and at different sizes. An additional outcome that arises directly from these analyses is that traits moderate the responsiveness of growth to changes in light environment. This response arises because individuals with higher potential growth rate naturally have greater potential plasticity in growth. Our results therefore support findings that species with low WD increase growth more substantially with increases in light (Table 1). Variation in LMA also moderates the response of growth to changes in light, with species having the lowest LMA being most responsive. However, unlike for WD, the effect appears only for the smallest size classes.

Shade Tolerance.

Combining Eq. 3 with the functional-balance model in Table 4 leads to the a more specific expression for calculating WPLCP, as the value of $E^{*}$ that gives

$$\overline{p}\left(E^{*}\right)=\varphi c_{\mathrm{l}}+\left(\theta \hspace{0.17em}\rho \hspace{0.17em}{\eta }_c\hspace{0.17em}H\right)\left(b{c}_{\mathrm{b}}+c_{\mathrm{s}}\right)+{\alpha }_{\mathrm{r}\mathrm{1}}{c}_{\mathrm{r}},$$ [5]

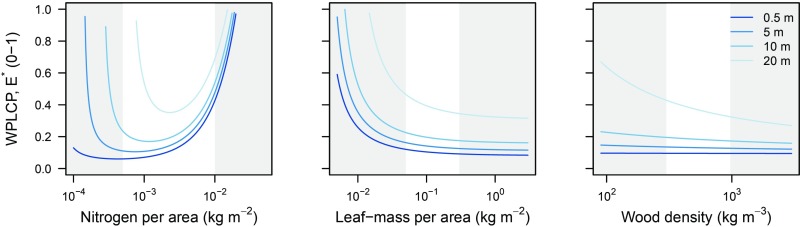
where $c_{\mathrm{i}}=\left(\frac{k_{\mathrm{i}}}{y}+r_{\mathrm{i}}\right)$ for $i=l,s,b,r$. Eq. 5 indicates WPLCP will increase approximately linearly with $H$ and potentially vary with N, LMA, and WD. With some further manipulations, it is possible to show that WPLCP will decrease with LMA if ${\beta }_{\mathrm{k}\mathrm{l}\mathrm{2}}>1$. Likewise, WPLCP will decrease with WD if ${\beta }_{\mathrm{k}\mathrm{s}\mathrm{2}}>1$. The parameters ${\beta }_{\mathrm{k}\mathrm{l}\mathrm{2}}$ and ${\beta }_{\mathrm{k}\mathrm{s}\mathrm{2}}$ give the slope relating tissue turnover rates to LMA and WD, respectively. Since in this analysis, we have assumed ${\beta }_{\mathrm{k}\mathrm{l}\mathrm{2}}>1$ and ${\beta }_{\mathrm{k}\mathrm{s}\mathrm{2}}>1$, species with low LMA and low WD are predicted to be less shade tolerant (Fig. 4). At low LMA (WD), leaf (sapwood) turnover is higher, and thus a greater light income is needed to offset increased turnover. WPLCP also decreases with height because, as size increases, the total amount of carbon needed to offset respiratory and turnover costs in the stem also increases (22). In addition, WPLCP varies with N. At small sizes, WPLCP increases with N across the band of values typically observed in real plants (i.e., high N makes seedlings shade intolerant). At larger sizes, as biomass growth declines to zero, WPLCP begins to increase again for very low values of N. All these results match empirical patterns (Table 1).

Fig. 4.

Effect of three developmental traits on shade tolerance. Plots show the effect of traits on level of canopy openness that causes biomass growth (Eq. 1) to be zero. Different lines indicate relationships for plants with specified height, from short (dark blue, $H=0.5$ m) to tall (light blue, $H=20$ m). The white regions indicate trait ranges that are typically observed in real systems.

Discussion

Using a model relating plant physiological function and mass allocation to prominent traits, we have clarified how traits could impact plant growth across the life cycle. Our approach extends a widely used theoretical model for seedlings, which links mass-based growth rate to the trait LMA (12, 14), to explicitly include influences of size, light environment, and other prominent traits. During recent decades, functional traits have captured the attention of ecologists, in large part because of the ability to organize the world’s plant species along standard dimensions (1). However, it has remained unclear how or whether prominent traits influence growth outcomes (5, 6, 11). Matching growing empirical evidence (Table 1), this study shows when and why the direction or strength of a correlation between traits and growth rate shifts with plant size. Moreover, we show that different traits and trade-offs generate different types of response. Combined with the available empirical evidence, these results demand a shift in our understanding of plant ecological strategies, away from one in which species are thought to have a fixed growth strategy throughout their life (e.g., refs. 8, 11, and 42) to one in which traits define a size-dependent growth trajectory (21). Moreover, we find that growth trajectories and the ranking of traits across them are also moderated by the light environment, while traits that minimize costs of tissue respiration and/or turnover also make plants more shade tolerant (i.e., lower WPLCP), as is empirically observed (9, 32–35). The plant model, used here, builds on and extends several related approaches, wherein emergent outcomes such as height, diameter, and mass growth arise from the interaction of different tissues and traits (e.g., refs. 22, 49, and 50). This approach is quite different from models derived from metabolic scaling theory (MST), which derive everything from a single master “scaling” equation for mass growth and have thus far been unable to account for size-dependent changes in the correlation between traits and growth rate (41, 61). Our approach is also fundamentally different from statistically fitted growth models (e.g., refs. 10, 18, and 19) in that it predicts rather than statistically tests for trait-based effects. Our aim is to both explain observed phenomena (Table 1) and also generate new hypotheses.

LMA Does Not Predict Growth Rates of Large Plants.

The model presented here extends a widely used model for seedlings, linking mass-based growth rate to the trait LMA (12, 14), to larger plants and other traits. Importantly, the seedling model (Eq. 2) can be derived as a special case of the extended model. Unlike Eq. 2, the extended model also predicts a relationship between LMA and growth rate that changes with size. In particular, the correlation shifts from being strongly negative in seedlings to being absent, or even weakly positive, in larger plants (Fig. 3), irrespective of whether growth rate is estimated via height, stem diameter, stem area, or total mass. This shift, which matches empirical evidence (5, 6, 10, 11, 21), occurs because the benefits of cheap leaf deployment diminish with plant size. As seedlings, leaves comprise a large part of the plant (Fig. 1A). Decreasing LMA then has an overwhelmingly positive effect on growth rate because the effect of increasing $\frac{\mathrm{d}{A}_{\mathrm{l}}}{\mathrm{d}{M}_{\mathrm{l}}}$ is large compared with the other terms in Fig. 1B, eq. 3. As plants increase in size, however, the amount of supporting tissue increases (SI Appendix, Fig. S2D), decreasing the benefit of cheap leaf construction. Consequently, the effect of LMA on leaf turnover comes to dominate at larger sizes, and, as such, the effect of LMA on height, diameter, and mass growth shifts from negative to either flat or mildly positive (Table 5).

Generalizing to Other Traits and Trade-Offs.

The list of functional traits known to differ among plant species is ever-increasing (62). While we have focused on understanding the effects of five traits on elements of demography, the framework presented can be extended to generate hypotheses about other traits and trade-offs. The main criteria for including new traits is that a clear trade-off has been established, with benefits and/or costs that ultimately translate into biomass and can therefore be connected with variables in Eqs. 1 and 2 and Fig. 1B, eqs. 1–7. While the list of plant traits that have been measured is extensive, clear trade-offs have been established for only a few of these. A well-developed trade-off must include two opposing forces that operate at some point in the life cycle.

Our framework also highlights what is needed for traits to influence demography. While traits can influence many aspects of plant function, these influences must operate via the pathways outlined in Fig. 1 if the trait is going to impact growth rate or shade tolerance. For example, many studies consider traits related to plant hydraulics, such as vessel size and increased sapwood area per leaf area (63). By altering conductance of water to the leaf, both traits will influence the rate of photosynthesis per leaf area ($\overline{p}$ in Eq. 1), while vessel size might also affect rates of stem turnover ($k_{\mathrm{s}}$ in Eq. 1). The costs of increased sapwood area per leaf area is increased allocation to stem, a factor which is already included in via the parameter $\theta$ (Table 4). The effect of both these traits on growth rate should be expected to vary with plant size.

Implications for Trait-Based Approaches.

There are some broad implications of our work for our understanding of plant ecological strategies and plant growth.

First, our results highlight the importance of allocation decisions and turnover costs in determining demography. Much of current ecosystem research focuses on factors affecting primary production—photosynthesis, respiration, and resultant fluxes of carbon—with less attention devoted to allocation and turnover (ref. 64; for comparisons of models, see refs. 51 and 53). However, four of the five traits considered here do not influence net primary production. In fact, our analysis shows that increased growth rate can occur even at a distinct cost to the plant’s carbon budget. Low LMA results in high leaf turnover, such that individuals with a low LMA have lower biomass growth. It is this property that makes them shade intolerant. And yet they can still achieve a growth advantage (when small).

Second, our results demand a shift away from viewing species as lying on a spectrum from slow to fast growth. When the ranking of growth rates among individuals differing in traits shifts with either plant size or light environment, it is not possible to describe a species via a single point along a spectrum. Such a spectrum is implied by many of the theoretical models used in community ecology, including Grime’s competitive, stress-tolerant and ruderal triangle, the r-K spectrum, and coexistence models base on the Lotka–Volterra system of equations (e.g., refs. 42 and 65). Researchers using functional traits have also tended to describe species as fast or slow growing (8, 66). Our results suggest a more nuanced approach. Plants that are fast growing as seedlings may not be fast growing as saplings or adults or under low light. Plants that are fast growing as adults may not be fast growing as seedlings. This more nuanced perspective reflects observed demographic patterns, where juvenile and adult growth rates are sometimes only loosely correlated (67).

Third, our results suggest that, even if traits define a potential growth trajectory, researchers seeking to link traits to growth rate must probe deeper into the data than simply looking for a linear relationship between traits and average growth, to recover the expected relationships. None of the predicted relationships between traits and growth is linear across the range of sizes and light environments tested. As such, we should not be surprised if the mean growth rate across individuals spanning a range of sizes or light environments is only weakly or not correlated with traits (e.g., refs. 5 and 11). Controlling for size, site, and light environment will be essential for detecting significant patterns (e.g., ref. 21), as will having a clear expectation for the hypothesized relationship.

Plasticity of Traits Through Ontogeny.

While our theory has succeeded in explaining some observed phenomena (Table 1), the test for good theory is that it also makes new predictions that enable the theory to be further refined and tested. To that end, we make a further prediction arising from our results, which is that the trait LMA should increase through ontogeny for all individuals. Such shifts have been observed across a variety of species (23, 68, 69). Since the value of cheap leaf construction diminishes with size, it pays for plants—and especially those with low LMA—to increase their LMA as they grow larger. While a similar prediction was made for a species of Eucalyptus (68), we extend the idea across species. Although trait-based research largely focuses on differences among species, it has long been recognized that traits also vary among individuals within a species and within individuals (1). This hypothesis attempts to give meaning to some of that variation and shows how variation across and within species might be understood within a single framework.

Comparison with Other Frameworks.

As noted above, the plant model is closely related to models used in several other studies, including those by refs. 22, 48–50, 68, 70, and 71. These models have several properties in common, including that they all have growth being driven by the net amount of photosynthetic income; that they have photosynthesis increasing nonlinearly with light and leaf nitrogen content; and that they consider the costs of respiration and turnover in different tissues. Many models also make functional-balance assumptions—for example, linking the cross-section of sapwood to leaf area (22, 48–50, 70). We note that an assumption of exact functional balance is not critical for our results; what matters is that the amount of live biomass (i.e., excluding heartwood) needed to support an extra unit of leaf area increases with height (as shown in SI Appendix, Fig. S2D).

A feature distinguishing our approach (see also refs. 17, 47, and 52) from most of those mentioned above is the explicit linking to trait-based trade-offs. This link enables demographic outcomes and trade-offs to emerge from underlying physiological function. While such a linkage was also made by ref. 50 in the ED model, analyses using ED have focused on ecosystem-level outcomes rather than the growth of individual plants. Because of its underlying similarities, we expect the dynamics reported here to also be present within the ED model. Another study (68) connected a model of growth for a single species to the trait LMA and likewise predicted a gradual flattening out of the relationship between LMA and growth rate with size (as in Fig. 3). Here, we include an additional cost of increased leaf turnover that further penalized low LMA strategies when large.

Perhaps the two most controversial elements of our approach concerns the assumptions about tissue replacement and reproductive allocation. Many vegetation models determine allocation based on net primary production (photosynthesis − respiration), whereas we also subtracted tissues lost via turnover before distributing any surplus. This is because we assume tissues lost via turnover are replaced before mass is allocated to either new growth (i.e., growth that leads to a net increase in $M_{\mathrm{l}},M_{\mathrm{b}},M_{\mathrm{s}}$ or $M_{\mathrm{r}}$) or reproduction (54). This assumption is likely to hold true for most woody plants and perennials, but may not hold for some herbs or annuals, where the switch to reproduction may entail a rundown in the vegetative part of the plant. The second assumption we make is that when mature, plants allocate a substantial fraction of their surplus mass to reproduction. While it remains unclear just how much adult plants might allocate to reproduction, recent reviews suggest that the fraction may be high (40, 56). Moreover, a long line of theoretical models indicates that allocation should increase as plants age (reviewed in ref. 56). Currently, reproductive allocation receives little attention in models focusing on production (e.g., refs. 51 and 53). For example in the ED model, a fixed 30% of net primary production is allocated to reproduction, irrespective of plant size. Yet differences in reproductive allocation offer a clear mechanism explaining correlations between a maximum size and growth rate (e.g., ref. 6).

Another class of model dealing explicitly with size-related effects are those derived from the MST of ecology (41, 61). Several points suggest that our framework provides a better explanation for the growth phenomena in Table 1 than the MST framework. First, the MST model suggests that diameter growth continues to increase with size, whereas empirical data suggest that growth rate declines for larger plants (10, 28, 29). Second, the MST model does not allow for the effects of traits to vary with plant size. Predicted effects are for a linear increase in growth with decreases in either LMA and lower WD, that apply irrespective of size. However, at least for LMA, such effects in large trees have not been observed.

Closing Remarks.

We have shown how diverse phenomena related to plant growth can be understood with a model accounting for processes generating photosynthetic income and allocating this among different tissues. The need to consider effects of plant size, alongside trait-based differences among species, has long been recognized in trait-based research (e.g., refs. 1, 22, 41, 50, and 69). Here, we have provided a framework for achieving this. By disentangling the effects of plant size, light environment, and traits on growth rates, our results provide a solid foundation for understanding and modeling growth across diverse species around the world.

Materials and Methods

Parameters.

Parameters were sourced mainly from ref. 47 (see SI Appendix, Tables S1 and S2 for values). The only exceptions are: (i) parameters affecting the relationships between various size metrics and leaf area, outlined in Table 4, estimated from SI Appendix, Fig. S2; and (ii) parameters describing the function for reproductive allocation, where we set $r_{\mathrm{r}\mathrm{1}}=0.8$ and $r_{\mathrm{r}\mathrm{2}}=10$, implying a relatively rapid transition to reproduction at ${\text{H}}_{\mathrm{m}\mathrm{a}\mathrm{t}}$ (see $\frac{\mathrm{d}{M}_{\mathrm{a}}}{\mathrm{d}B}$ in Fig. 1).

Assumptions.

The functional-balance assumptions listed in Table 4 were evaluated by using data from the Biomass and Allometry Database (60), which includes records for various size metrics from 21,084 individual plants across 656 species. We fit standardized major axis lines (72) to characterize bivariate relationships. We implemented a hierarchical model structure, where the distribution of slopes and intercepts among groups was assumed Gaussian.

Software.

The growth model applied here was implemented as the FF16 physiological module within Version 1.1 of the plant package (47) for R (73). The plant package makes use of supporting packages Rcpp (74) and the Boost Library for C++ (75), via the package BH (76). To encode the trait-based trade-offs described above, we used the plant packages’ ability to provide a “hyperparameterization” function, which causes various parameters to covary with traits (for details, see SI Appendix).