Significance
We apply a statistical thermodynamic formalism to quantify the cooperativity of folding of de novo-designed helical repeat proteins (DHRs). This analysis provides a fundamental thermodynamic description of folding for de novo-designed proteins and permits comparison with naturally occurring repeat protein thermodynamics. We find that individual DHR units are intrinsically stable, unlike those of naturally occurring proteins. This observation reveals local (intrarepeat) interactions as a source of high stability in Rosetta-designed proteins and suggests that different types of DHR repeats may be combined in a single polypeptide chain, expanding the repertoire of folded DHRs for applications such as molecular recognition. Favorable intrinsic stability imparts a downhill shape to the energy landscape, suggesting that DHRs fold fast and through parallel pathways.
Keywords: Ising model, repeat proteins, Rosetta, protein design, DHRs
Abstract
Designed helical repeats (DHRs) are modular helix–loop–helix–loop protein structures that are tandemly repeated to form a superhelical array. Structures combining tandem DHRs demonstrate a wide range of molecular geometries, many of which are not observed in nature. Understanding cooperativity of DHR proteins provides insight into the molecular origins of Rosetta-based protein design hyperstability and facilitates comparison of energy distributions in artificial and naturally occurring protein folds. Here, we use a nearest-neighbor Ising model to quantify the intrinsic and interfacial free energies of four different DHRs. We measure the folding free energies of constructs with varying numbers of internal and terminal capping repeats for four different DHR folds, using guanidine-HCl and glycerol as destabilizing and solubilizing cosolvents. One-dimensional Ising analysis of these series reveals that, although interrepeat coupling energies are within the range seen for naturally occurring repeat proteins, the individual repeats of DHR proteins are intrinsically stable. This favorable intrinsic stability, which has not been observed for naturally occurring repeat proteins, adds to stabilizing interfaces, resulting in extraordinarily high stability. Stable repeats also impart a downhill shape to the energy landscape for DHR folding. These intrinsic stability differences suggest that part of the success of Rosetta-based design results from capturing favorable local interactions.
Linear repeat proteins have proven to be useful model systems in the quest to better understand protein-folding thermodynamics. Due to their repetitive primary structures, these proteins fold into linearly extended modular arrays with approximate translational symmetry from repeat to repeat. Unlike globular proteins, where interactions can span across the protein sequence, the interactions of linear repeat proteins are confined to within or between adjacent repeats (1). This architecture permits the application of nearest-neighbor Ising analysis to extract thermodynamic parameters for folding.
One-dimensional Ising analysis has been successfully applied to a number of linear helical repeat proteins (2–5). This analysis assumes that repeat protein stability can be parsed into intrinsic folding energies of individual repeats and coupling energies at the interfaces between adjacent folded repeats. Previous work characterizing linear repeat proteins derived from naturally occurring folds shows that individual repeats are unstable. In these proteins, stability (and cooperativity) originates in the favorable interfaces between adjacent repeats.
Owing to their modular architectures, repeat proteins have been used in a number of engineering applications. Consensus ankyrin repeats have been used to select for high-affinity binding partners (6–10) and to enhance the activity of engineered cellulases (11). Repeats from transcription activator-like effector proteins (TALEs) have been engineered for genome editing (12, 13). Tetratricopeptide repeat (TPR) domains have been fused to molecular chaperones to increase substrate affinity (14). Expanding to architectures beyond this handful of naturally occurring linear repeat folds would further enable such protein engineering applications. One promising set of templates is the de novo-designed helical repeat proteins (DHRs) (15). This series of constructs comprises a wide variety of native-state architectures that are unrelated to naturally occurring repeat proteins.
Here, we characterize the stability of a series of DHR proteins using nearest-neighbor Ising analysis. We find that, unlike naturally occurring repeat proteins, both the intrinsic folding and interfacial coupling free energies of DHRs are stabilizing, giving rise to extraordinarily high folding stability while maintaining cooperativity. The favorable local stability of DHR repeats suggests a reduced folding barrier. The observation of favorable local stabilities in DHRs provides insights into the success of current Rosetta-based design and suggests mechanisms for further DHR-based protein designs.
Results
Equilibrium Unfolding of DHR Proteins.
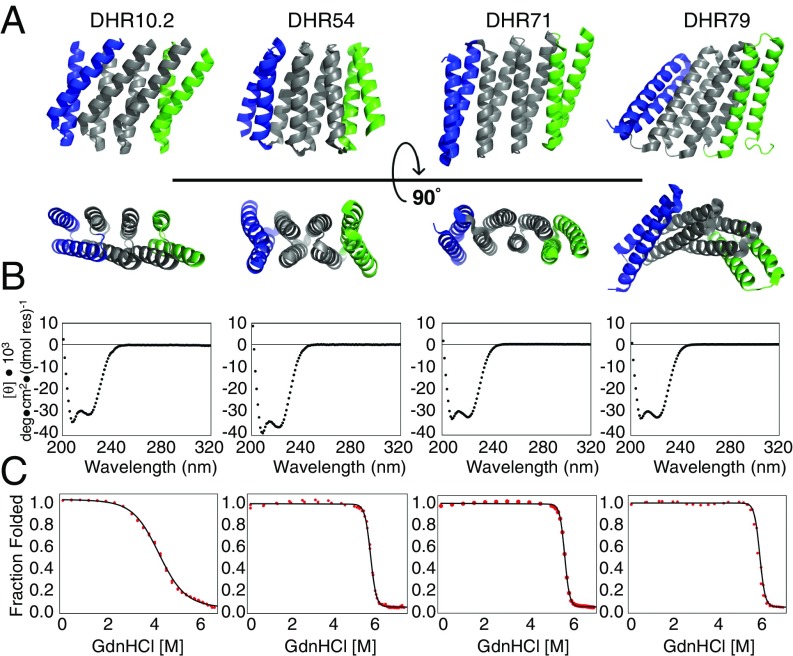
To investigate the thermodynamic folding behavior of Rosetta-designed repeat proteins with novel fold geometries, we chose DHR candidates for characterization based on the following criteria: (i) available small-angle X-ray scattering and crystal structure data that demonstrate that the target structure is adopted, (ii) an absence of cysteine residues to reduce complications associated with disulfide linkages, and (iii) experimental evidence that shows the capped repeat proteins to be monomeric in solution. The proteins DHR9, DHR10.2 (a modified version of DHR10; see below), DHR54, DHR71, and DHR79 (Fig. 1A) satisfy these criteria. These constructs have no detectible sequence similarity to naturally occurring proteins (lowest E-values from BLAST search ranging from 0.026 to 4) and span a broad range of sequence (SI Appendix, Table S1) and structural features (15), including both left- and right-handed superhelical architectures. Far-UV CD spectra for four repeat NR2C constructs (where N and C represent N- and C-terminal polar capping repeats flanking two internal DHR repeats) for each of these DHRs display characteristic minima at 208 and 222 nm, consistent with folded α-helical proteins (Fig. 1B).
Fig. 1.
Structures and stabilities of DHR proteins. (A) Selected DHR proteins have distinct structures not seen in natural repeat proteins, including unique interrepeat twists and radii of curvature between repeating units. (B) Far-UV CD shows characteristic α-helical spectra for DHR proteins. (C) Guanidine-induced denaturation of four-repeat NR2C DHR proteins fit with a two-state unfolding model (black curves) show stable, cooperative folding. Panels in B and C correspond to the DHR proteins shown in A. PDB ID codes are 5CWG (DHR10), 5CWL (DHR54), 5CWN (DHR71), and 5CWP (DHR79).
To measure DHR stability, we monitored guanidine-HCl induced unfolding transitions using CD spectroscopy at 222 nm. NR2C constructs of DHR10.2, DHR54, DHR71, and DHR79 unfold in a single sigmoidal unfolding transition, which is well-fitted with a two-state model (Fig. 1C). DHR9 did not unfold across a range of temperatures, pH, and denaturant concentrations, precluding thermodynamic analysis. The unfolding transitions of DHR54, DHR71, and DHR79 have high slopes and midpoints for unfolding. The steep guanidine unfolding transitions of these three constructs suggest a high level of cooperativity; two-state fits of the unfolding transitions yield m values that are similar to predictions from empirical correlation (SI Appendix, Table S1) (16). In contrast, the unfolding transition of DHR10.2 occurs over a broad range of denaturant concentration and has a low midpoint compared with the other DHRs.
Length and Capping Dependence of Stability.
To determine the effects of variation in repeat number and the sequence substitutions associated with the N- and C-terminal capping repeats on stability, we constructed a series of DHR proteins that delete terminal and internal repeats. For some singly capped constructs, soluble oligomers could be detected by sedimentation velocity analytical ultracentrifugation (SV-AUC). To eliminate oligomerization, glycerol was added to 10% (vol/vol). SV-AUC demonstrates that, in the presence of glycerol, most singly capped constructs are monomeric (SI Appendix, Fig. S1). For DHR10, deletion of the C-terminal repeat leads to formation of soluble oligomers even in the presence of glycerol. To prevent this oligomerization, we made a series of charged substitutions to solvent-exposed hydrophobic residues in the N-terminal capping repeat (V12K, I14E, V16E, L39R). We refer to this series as DHR10.2. All variants of DHR10.2 are monomeric.
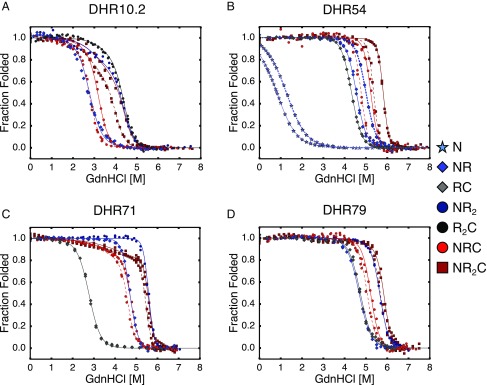
For each of the four DHR series, we measured unfolding curves for constructs with two, three, and four repeats under conditions where constructs remain monomeric. Two repeat constructs contain a single R repeat with either an N-terminal capping repeat (NR) or a C-terminal capping repeat (RC). Three repeat constructs contain one construct with a single R repeat with both N- and C-terminal capping repeats (NRC), or two R repeats with either an N- (NR2) or C-terminal capping repeat (R2C). The four repeat construct contains two R repeats with both N- and C-terminal capping repeats (NR2C). For DHR54, we were also able to purify and characterize a construct containing a single N-terminal capping repeat.
Stabilities of length and capping variants were monitored by guanidine-HCl–induced unfolding transitions by CD spectroscopy at 222 nm as described above (Fig. 2). For all DHR proteins, unfolding midpoints increase as the number of repeats increases (compare DHR54, N to NR and NR2; DHR10.2, DHR71, and DHR79, NR to NR2; and all DHRs, NRC to NR2C). In most cases, midpoints are lower for constructs with capping repeats than internal “R” repeats (compare DHR10.2 NRC and R2C), indicating that capping repeats are generally less stabilizing than internal “R” repeats.
Fig. 2.
Unfolding transitions and nearest-neighbor Ising analysis of DHR proteins of different length and capping architecture. Guanidine-induced unfolding transitions for (A) DHR10.1, (B) DHR54, (C) DHR71, and (D) DHR79 were fitted with a nearest-neighbor Ising model (curves). N-capped constructs are shown in blue, C-capped constructs are shown in gray, and doubly capped constructs are shown in red. Glycerol concentrations are 0% (dash-dotted curves), 10% (solid curves), and 20% (dashed curves). For all constructs, increasing the number of repeats increases stability (based on unfolding midpoints). Conditions: 25 mM NaPO4, 150 mM NaCl, 25 °C.
For the DHR10.2 series, adding a C-terminal capping repeat to NR increases the transition slope and midpoint, whereas adding a C-terminal capping repeat to NR2 increases the slope more than midpoint (compare NR2 to NR2C, Fig. 2A). The C-terminal capping repeat gives rise to a larger slope and midpoint than the N-terminal capping repeat (compare NR2 to R2C), suggesting either greater intrinsic stability for the C-cap or a more stabilizing R:C interface.
For DHR54 and DHR71, the unfolding midpoints for N-terminal capped constructs are higher than those for C-terminal capped constructs (compare NR to RC, Fig. 2 B and C). Whereas for DHR54 capping identity does not affect transition slope, adding a C-terminal capping repeat to DHR71 appears to result in multistate unfolding behavior (compare NR to NRC, and NR2 to NR2C). For DHR79, the N- and C-terminal capped variants are of similar stability (Fig. 2D). In general, longer constructs have steeper transitions, although exceptions described above in which capping repeats unfold before the main transition result in several notable exceptions.
Ising Analysis Quantifies Intrinsic and Interfacial Folding Free Energies for DHRs.
Intrinsic and interfacial folding energies were determined using a 1D Ising model. In this model, the conformations of individual repeats are represented as either folded or unfolded. Thus, for an n-repeat array, there are 2n configurations represented by the model. The energy of each configuration is determined by the intrinsic folding energy of each repeat (ΔGi) as well as the coupling (“interfacial”) free energies (ΔGi − 1,i) between adjacent repeats.
Because the sequences of the N- and C-terminal capping repeats differ from the sequence of central repeats, three intrinsic energies are included in the model (ΔGN, ΔGR, and ΔGC). For all DHRs except DHR54, the model includes only one interfacial free energy (ΔGi − 1,i). Although it is possible that the free energies between central repeats and capping repeats differ, it is not possible to resolve such differences unless the unfolding energy of the lone cap can be measured. Because we were able to measure an unfolding transition for a lone N-cap repeat for DHR54 (Fig. 2B), a separate term for the interfacial energy between a DH54 N-cap repeat and the adjacent R repeat (ΔGN,R) can be fitted.
To account for effects of glycerol on stability, we expanded our standard single-denaturant model to include a linear intrinsic free-energy dependence on glycerol. This model was fitted to DHR guanidine-induced unfolding transitions collected at several glycerol concentrations (2, 3, 17). By including guanidine HCl unfolding transitions at different glycerol concentrations, we were able to extract the intrinsic (ΔGi) and interfacial (ΔGi,i + 1) free energies in the absence of glycerol. For DHR10.2, DHR54, and DHR79, we assumed that N-cap, central, and C-cap repeats have identical m values. For DHR71, fitting required a separate mGdn-HCl for the C-cap repeat.
Fig. 2 shows global fits of the Ising model to four sets of DHR unfolding transitions. There are only six shared thermodynamic parameters (free energies and m values) for the fits in Fig. 2 A and D and seven shared thermodynamic parameters in Fig. 2 B and C. Global fits also include separate baseline parameters for each unfolding transition. For all DHR series, the data are well fitted by the Ising model and result in low and fairly random residuals. The largest nonrandom residuals are associated with the rather long native baselines associated with some of the longer constructs.
All DHRs have favorable interfacial free energies, similar to interfacial energies seen for naturally occurring repeat proteins including ankyrin (3, 17), TPR variants [34PR and 42PR arrays (2, 4)], and TALE repeats (5). The intrinsic folding energies of DHRs are also favorable, in contrast with those of naturally occurring repeats. The majority of the capping repeats also have favorable intrinsic stabilities, although they are typically less stabilizing than the internal repeats. The N- and C-terminal caps of DHR10.2 are intrinsically unstable, as is the C-terminal cap of DHR71, consistent with the multistate transitions seen in Fig. 2 A and C. For all DHRs, glycerol is stabilizing, although the effects of glycerol on stability are significantly lower (and somewhat variable among DHR series) than that of guanidine HCl on a molar basis.
Discussion
By measuring the length and capping dependence on stability of four DHRs families, we have used a 1D Ising model to quantify intrinsic folding free energies and interfacial coupling free energies. Unlike previously studied helical repeat proteins, which were based on naturally occurring folds, these proteins were generated by de novo design. Quantifying the cooperativity of DHRs using the Ising approach provides a vantage point to compare and contrast natural and designed proteins. The surprising finding that DHRs have intrinsically stable repeats has important implications for understanding the energetic basis for the success in Rosetta design, for the distribution of cooperativity in naturally occurring repeat proteins, and for the shape of the energy landscape.
Rosetta Algorithms Design Stable Proteins Through Favorable Local Interactions.
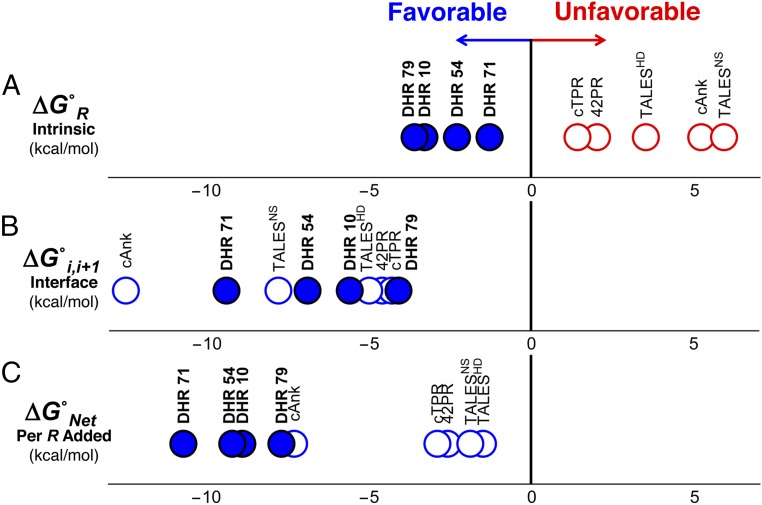
In the past decade, 1D Ising analysis has been used to dissect folding cooperativity in a variety of naturally occurring helical repeat protein families (2–5, 17). These proteins have typically been designed using consensus information obtained from multiple sequence alignments, although for some of these series (4, 5) designs were based on genes with nearly identical sequence repeats. Although exact numbers vary, all of these naturally occurring repeat proteins have unfavorable (i.e., positive) intrinsic folding free energies (unfilled red circles, Fig. 3A), which are offset by favorable (negative) interfacial free energies (unfilled blue circles, Fig. 3B).
Fig. 3.
DHR repeats are intrinsically stable, unlike the repeats of naturally occurring repeat proteins. (A) Intrinsic folding and (B) interfacial coupling free energies determined by Ising analysis for DHR proteins (filled circles) and natural repeat proteins [open circles, TALESNS and TALESHD (5), 42PR (4), cANK (3), and cTPR (4)]. Unfavorable (i.e., positive) free-energy terms are in red, and favorable (i.e., negative) free energies are in blue. DHRs are stabilized by both favorable intrinsic folding and interfacial coupling free energies, whereas natural repeat proteins are destabilized by unfavorable intrinsic folding free energies, which are compensated by large favorable interfacial interactions. (C) Free energy associated with adding a single repeat to a folded array (the sum of intrinsic and interfacial free energies in A and B). Due to their favorable intrinsic folding free energies, DHR proteins are more strongly stabilized by the addition of repeats than natural repeat proteins, resulting in very high overall stability.
The interfacial energies between DHRs are also stabilizing and span roughly the same range as those of naturally occurring repeat proteins (filled blue circles, Fig. 3B). Variation in interfacial free energies among DHRs seems uncorrelated with repeat length, number of interfacial contacts, or surface area buried between repeats (SI Appendix, Table S2). However, intrinsic folding energies for DHRs are favorable (Fig. 3A), in contrast to all previously measured intrinsic energies for natural repeat proteins (2–5, 17). This enhancement of intrinsic stability may reflect a fundamental difference between Rosetta-based de novo design (15) and natural selection. Based on the findings here, it appears that Rosetta-based design is particularly good at enhancing local stability. Whether this enhancement results from backbone selection in the early stages of design, sequence design in the intermediate stages, or selection for funneled energy landscapes is unclear. We note that the fraction of charged residues in the DHR sequences is significantly higher (with an average of 0.45, SI Appendix, Table S1) than the average for all proteins in SWISS-PROT (0.23). An increase in the number of charged residues has been proposed as a mechanism for increased stability in thermophilic proteins (18) and has recently been seen to correlate with high stability in consensus proteins (19).
One consequence of the uniquely stabilizing intrinsic folding energies seen for DHRs is a significant enhancement to overall stability. The stability of a tandem-repeat array depends on both the intrinsic and interfacial stabilities. The sum of the intrinsic and interfacial free energies gives the stability increment of adding a repeat to an existing folded array (Fig. 3C). For naturally occurring repeat proteins, this stability increment derives solely from the interfacial interaction energy and is offset by the intrinsic energy. For DHR arrays, the favorable intrinsic folding energies add to the interfacial energies, giving rise to an exceptionally large stability increase for adding a repeat to an existing array and resulting in very high native-state stabilities.
Differences Between the Energy Landscapes of de Novo-Designed and Naturally Occurring Helical Repeat Proteins.
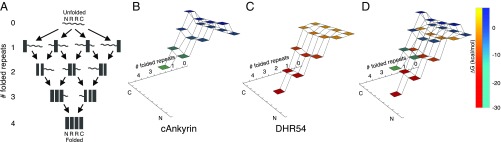
Quantification of the intrinsic and interfacial free energies of repeat proteins using the Ising model allows the energy landscapes of repeat proteins to be represented in meaningful reaction coordinates, scaled using experimentally determined free energies (20, 21). In this representation, the free energies of states where one or more adjacent repeats are folded and paired are plotted as a function of the number of folded repeats and the location of the partly folded structure (N-terminal, C-terminal, or internal; Fig. 4). Ignoring lower probability configurations where unfolded repeats are flanked by folded repeats, there are 10 configurations in the NR2C landscape (Fig. 4A).
Fig. 4.
Stabilizing intrinsic energies diminish the barriers on folding energy landscapes for DHR proteins in the absence of denaturant. (A) Repeat proteins with NR2C repeat sequences can fold along many pathways. (B–D) Free-energy landscapes from experimentally determined intrinsic and interfacial free energies. The vertical dimension (and shading) shows the free energies of partly folded states along the folding pathway shown in A. (B) Consensus ankyrin repeat proteins, which are based on the naturally occurring ankyrin repeat family, have destabilizing intrinsic energies, and as a result, folding the first repeat results in an early barrier. (C) DHR54 proteins have stabilizing intrinsic folding energies and, as a result, lack this early barrier. Moreover, folding of subsequent repeats is strongly downhill. (D) Overlay of consensus ankyrin (blue–green) and DHR54 (orange–red) free-energy landscapes. Landscapes were generated with Mathematica.
For ankyrin consensus repeats, which are based on a naturally occurring repeat family, intrinsic folding energies are unfavorable (3); thus, all conformations with one folded repeat have high energies, resulting in a large barrier that must be crossed during folding (Fig. 4B). Depending on the structure of the transition state for folding, even higher barriers, in which a second repeat is at least partly folded (22) but not yet paired, can further impede folding. In contrast, because the intrinsic folding energies of DHR repeats are favorable, all partly folded configurations are lower in energy than the fully unfolded state under conditions that strongly stabilize folding (Fig. 4 C and D for DHR54). Thus, energy landscapes for DHR folding are comparatively smooth and downhill. Moreover, since addition of each folded DHR54 repeat significantly decreases the free energy, the landscape is also very steep, reflecting a strong driving force for folding.
Unstable Repeats May Be a Result of Natural Selection for Folding Cooperativity.
In addition to reflecting successful Rosetta design principles, the difference between intrinsic stabilities of natural and designed helical repeats may reflect features imposed by natural selection on natural repeat folds. Instability of local repeats enhances cooperativity, suppressing both the equilibrium formation of partly folded states and the transient formation of partly structured species through a zippering mechanism during folding. Such species may be prone to misfolding and aggregation. Naturally occurring repeat proteins may have evolved to minimize such structures by partitioning stability into long-range versus local interactions. Obviously, there is no such pressure on DHRs. Although many of these species are also suppressed in the unfolding transitions of DHR54 and DHR79 (Fig. 2) owing to the strongly destabilizing effects of guanidine on intrinsic stabilities at the transition regions, favorable intrinsic stability would promote conformations where individual repeats are folded relative to the unfolded state. In contrast, for DHR10.2 and DHR71, multistate unfolding is clearly seen for a number of the constructs. This energetic partitioning is consistent with ideas that have emerged from energy landscape theory that natural proteins have been selected to minimize energetic frustration (23–27). Moreover, family-specific functional constraints on naturally occurring repeat proteins may modulate cooperativity to allow for precise conformational fluctuations, as has been suggested for DNA binding by TALE-repeat proteins (5).
Last, it is possible that nature does not select for or against unfavorable intrinsic energies in repeat proteins, but simply selects for global stability above some threshold value (28, 29). Because repeat proteins have very favorable interfacial free energies, global stability can be achieved in combination with modestly destabilizing intrinsic energies. Partitioning stability into interfacial interactions will maintain cooperativity, allowing for functional sequence variation that decreases intrinsic energy. Resolving the intrinsic and interfacial interactions of specific residues will help test these ideas.
Methods
Cloning, Expression, and Purification.
Genes containing DHR repeat constructs were purchased as GeneStrings from GeneArt and cloned with C-terminal His6 tags via Gibson Assembly. DHR constructs were grown in BL21(T1R) cells at 37 °C to an OD of 0.6–0.8, induced with 0.2 mM IPTG, and expressed overnight at 17 °C. Following cell pelleting, resuspension, and lysis in 25 mM sodium phosphate (pH 7.0) and 150 mM NaCl, proteins were purified by affinity chromatography on an Ni-NTA column. Proteins were eluted using 250 mM imidazole and dialyzed into 150 mM NaCl, 0–20% glycerol, and 25 mM NaPO4 (pH 7.0).
CD Spectroscopy.
CD measurements were collected using an AVIV model 400 CD Spectrometer (Aviv Associates). Far-UV CD scans were collected at 25 °C using an 0.1-cm pathlength quartz cuvette, with protein concentrations of 15–30 μM. Buffer scans were recorded and were subtracted from the raw CD data. CD-monitored guanidine unfolding transitions at 222 nm were generated with an automated titrator using 1.5–3 μM protein and a 1-cm pathlength quartz cuvette.
Ising Analysis.
To determine the intrinsic and interfacial free energies for folding of DHR arrays, and to analyze energies of partly folded states, we used a 1D Ising formalism (30, 31). In this model, intrinsic folding and interfacial interaction between nearest neighbors are represented using equilibrium constants κ and τ, respectively, where
| [1] |
| [2] |
| [3] |
| [4] |
For all DHRs, the intrinsic folding free energies of N (solubilizing N-terminal cap), R (consensus repeat), and C (solubilizing C-terminal cap) are independent adjustable parameters. DHR10.2, DHR71, and DHR79 are well described by a simple model where the interfacial interactions of the N:R, R:R, and R:C pairs are identical. DHR54 unfolding transitions are better fitted by a model where the interfacial interactions of the R:R and R:C interface are identical, whereas the N:R pair is different. Glycerol and GdnHCl dependences are built into the intrinsic (but not the interfacial) terms. DHR71 unfolding transitions are better fitted by a model that includes a separate denaturant dependence for the C-terminal cap (mGdnHCl,C, Table 1).
Table 1.
Thermodynamic parameters obtained from Ising analysis
| Construct | ΔGN | ΔGR | ΔGC | ΔGi−1,i | mGdn,i | mglycerol,i | mGdn,C | ΔGN,R |
| DHR10.2 | 1.46 [1.26, 1.67] | −2.51 [−2.90, −2.15] | 0.63 [0.32, 1.00] | −4.80 [−5.10, −4.53] | −1.23 [−1.33, −1.14] | 0.36 [0.33, 0.40] | N/A | N/A |
| DHR54 | −0.45 [−0.58, −0.32] | −2.04 [−2.17, −1.92] | −0.84 [−0.94, −0.74] | −6.76 [−6.98, −6.54] | −1.24 [−1.28, −1.21] | 0.41 [0.39, 0.43] | N/A | −7.72 [−7.95, −7.49] |
| DHR71 | −3.01 [−3.27, −2.75] | −1.41 [−1.61, −1.23] | 3.06 [2.87, 3.29] | −9.93 [−10.50, −9.43] | −1.57 [−1.66, −1.49] | 0.17 [0.15, 0.20] | −0.71 [−0.79, −0.64] | N/A |
| DHR79 | −1.84 [−2.06, −1.64] | −3.48 [−3.83, −3.22] | −1.81 [−2.08, −1.61] | −4.83 [−5.14, −4.55] | −1.12 [−1.18, −1.06] | 0.15 [0.12, 0.18] | N/A | N/A |
Free energies have units of kilocalories/mole. mGdn,i and mglycerol,i have units of kilocalories/mole/[molar GdnHCl] and kilocalories/mole/[molar glycerol]. The 95% confidence intervals shown in brackets are from bootstrap analysis with 2,000 iterations. N/A, not applicable.
Using these equilibrium constants, a partition function q for an n-repeat construct can be constructed by multiplying 2 × 2 transfer matrices:
| [5] |
This representation correlates the each repeat to its neighbor through the separate rows of each matrix. The fraction of folded protein (ffolded) can be obtained by differentiation:
| [6] |
Ising parameters were determined by globally fitting Eq. 6 to guanidine-induced unfolding transitions collected at 0%, 10%, and 20% glycerol. Fitting was performed using the nonlinear least-squares algorithm of the lmfit package (32) using an in-house Python program [written by Marold et al. (4) and adapted to include glycerol dependence by K.G.-S.]. Confidence intervals (95%) were determined by performing 2,000 bootstrap iterations.
Supplementary Material
Acknowledgments
We thank members of the D. Barrick and D. Baker laboratories for their input on this work, and Jeff Gray for helping to initiate these studies. We acknowledge the support of the Center for Molecular Biophysics at Johns Hopkins and Dr. Katherine Tripp for instrumental and technical support. Support to K.G.-S. was provided by NIH Training Grant T32-GM008403. Support for this project was provided by NIH Grant 1R01-GM068462 (to D. Barrick).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1800283115/-/DCSupplemental.
References
- 1.Kloss E, Courtemanche N, Barrick D. Repeat-protein folding: New insights into origins of cooperativity, stability, and topology. Arch Biochem Biophys. 2008;469:83–99. doi: 10.1016/j.abb.2007.08.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kajander T, Cortajarena AL, Main ERG, Mochrie SGJ, Regan L. A new folding paradigm for repeat proteins. J Am Chem Soc. 2005;127:10188–10190. doi: 10.1021/ja0524494. [DOI] [PubMed] [Google Scholar]
- 3.Aksel T, Majumdar A, Barrick D. The contribution of entropy, enthalpy, and hydrophobic desolvation to cooperativity in repeat-protein folding. Structure. 2011;19:349–360. doi: 10.1016/j.str.2010.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Marold JD, Kavran JM, Bowman GD, Barrick D. A naturally occurring repeat protein with high internal sequence identity defines a new class of TPR-like proteins. Structure. 2015;23:2055–2065. doi: 10.1016/j.str.2015.07.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Geiger-Schuller K, Barrick D. Broken TALEs: Transcription activator-like effectors populate partly folded states. Biophys J. 2016;111:2395–2403. doi: 10.1016/j.bpj.2016.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Forrer P, Stumpp MT, Binz HK, Plückthun A. A novel strategy to design binding molecules harnessing the modular nature of repeat proteins. FEBS Lett. 2003;539:2–6. doi: 10.1016/s0014-5793(03)00177-7. [DOI] [PubMed] [Google Scholar]
- 7.Steiner D, Forrer P, Plückthun A. Efficient selection of DARPins with sub-nanomolar affinities using SRP phage display. J Mol Biol. 2008;382:1211–1227. doi: 10.1016/j.jmb.2008.07.085. [DOI] [PubMed] [Google Scholar]
- 8.Plückthun A. Designed ankyrin repeat proteins (DARPins): Binding proteins for research, diagnostics, and therapy. Annu Rev Pharmacol Toxicol. 2015;55:489–511. doi: 10.1146/annurev-pharmtox-010611-134654. [DOI] [PubMed] [Google Scholar]
- 9.Hansen S, et al. Design and applications of a clamp for green fluorescent protein with picomolar affinity. Sci Rep. 2017;7:16292. doi: 10.1038/s41598-017-15711-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wu Y, et al. Rigidly connected multispecific artificial binders with adjustable geometries. Sci Rep. 2017;7:11217. doi: 10.1038/s41598-017-11472-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cunha ES, Hatem CL, Barrick D. Synergistic enhancement of cellulase pairs linked by consensus ankyrin repeats: Determination of the roles of spacing, orientation, and enzyme identity. Proteins. 2016;84:1043–1054. doi: 10.1002/prot.25047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Christian M, et al. Targeting DNA double-strand breaks with TAL effector nucleases. Genetics. 2010;186:757–761. doi: 10.1534/genetics.110.120717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li T, et al. TAL nucleases (TALNs): Hybrid proteins composed of TAL effectors and FokI DNA-cleavage domain. Nucleic Acids Res. 2011;39:359–372. doi: 10.1093/nar/gkq704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cortajarena AL, Kajander T, Pan W, Cocco MJ, Regan L. Protein design to understand peptide ligand recognition by tetratricopeptide repeat proteins. Protein Eng Des Sel. 2004;17:399–409. doi: 10.1093/protein/gzh047. [DOI] [PubMed] [Google Scholar]
- 15.Brunette TJ, et al. Exploring the repeat protein universe through computational protein design. Nature. 2015;528:580–584. doi: 10.1038/nature16162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Myers JK, Pace CN, Scholtz JM. Denaturant m values and heat capacity changes: Relation to changes in accessible surface areas of protein unfolding. Protein Sci. 1995;4:2138–2148. doi: 10.1002/pro.5560041020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wetzel SK, Settanni G, Kenig M, Binz HK, Plückthun A. Folding and unfolding mechanism of highly stable full-consensus ankyrin repeat proteins. J Mol Biol. 2008;376:241–257. doi: 10.1016/j.jmb.2007.11.046. [DOI] [PubMed] [Google Scholar]
- 18.Haney PJ, et al. Thermal adaptation analyzed by comparison of protein sequences from mesophilic and extremely thermophilic Methanococcus species. Proc Natl Acad Sci USA. 1999;96:3578–3583. doi: 10.1073/pnas.96.7.3578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tripp KW, Sternke M, Majumdar A, Barrick D. Creating a homeodomain with high stability and DNA binding affinity by sequence averaging. J Am Chem Soc. March 28, 2017 doi: 10.1021/jacs.6b11323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mello CC, Barrick D. An experimentally determined protein folding energy landscape. Proc Natl Acad Sci USA. 2004;101:14102–14107. doi: 10.1073/pnas.0403386101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Aksel T, Barrick D. Direct observation of parallel folding pathways revealed using a symmetric repeat protein system. Biophys J. 2014;107:220–232. doi: 10.1016/j.bpj.2014.04.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ferreiro DU, Cho SS, Komives EA, Wolynes PG. The energy landscape of modular repeat proteins: Topology determines folding mechanism in the ankyrin family. J Mol Biol. 2005;354:679–692. doi: 10.1016/j.jmb.2005.09.078. [DOI] [PubMed] [Google Scholar]
- 23.Bryngelson JD, Wolynes PG. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci USA. 1987;84:7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 25.Onuchic JN, Luthey-Schulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 26.Onuchic JN, Wolynes PG. Theory of protein folding. Curr Opin Struct Biol. 2004;14:70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 27.Oliveberg M, Wolynes PG. The experimental survey of protein-folding energy landscapes. Q Rev Biophys. 2005;38:245–288. doi: 10.1017/S0033583506004185. [DOI] [PubMed] [Google Scholar]
- 28.Zeldovich KB, Chen P, Shakhnovich EI. Protein stability imposes limits on organism complexity and speed of molecular evolution. Proc Natl Acad Sci USA. 2007;104:16152–16157. doi: 10.1073/pnas.0705366104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Taverna DM, Goldstein RA. Why are proteins marginally stable? Proteins. 2002;46:105–109. doi: 10.1002/prot.10016. [DOI] [PubMed] [Google Scholar]
- 30.Aksel T, Barrick D. Analysis of repeat-protein folding using nearest-neighbor statistical mechanical models. Methods Enzymol. 2009;455:95–125. doi: 10.1016/S0076-6879(08)04204-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Poland D, Scheraga HA. Theory of Helix–Coil Transitions in Biopolymers: Statistical Mechanical Theory of Order–Disorder Transitions in Biological Macromolecules. Academic; New York: 1970. [Google Scholar]
- 32.Newville M, Stensitzki T, Allen DB, Ingargiola A. 2014 LMFIT: Non-Linear Least-Square Minimization and Curve-Fitting for Python (Zenodo). Available at https://zenodo.org/record/11813#.WxVZhkgvyUk. Accessed September 21, 2014.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.