Plant height and hydraulic vulnerability to drought and cold

Significance

As trees worldwide experience mortality or dieback with increasing drought and low tundras grow taller with warming, understanding the link between plant height and climate is increasingly important. We show that taller plants have predictably wider water-conducting conduits, and that wider conduits within species are more vulnerable to conduction-blocking embolisms. These two observations suggest that tall plants in formerly moist areas die because their wide conduits are excessively vulnerable under novel drought conditions. Also, the cold that limits conduit diameter, and therefore height, in tundra plants is relaxed under warming, permitting wider conduits and taller plants. That plant height appears linked to climate via plant hydraulics helps explain why vegetation height differs across biomes and is altering with climate change.

Abstract

Understanding how plants survive drought and cold is increasingly important as plants worldwide experience dieback with drought in moist places and grow taller with warming in cold ones. Crucial in plant climate adaptation are the diameters of water-transporting conduits. Sampling 537 species across climate zones dominated by angiosperms, we find that plant size is unambiguously the main driver of conduit diameter variation. And because taller plants have wider conduits, and wider conduits within species are more vulnerable to conduction-blocking embolisms, taller conspecifics should be more vulnerable than shorter ones, a prediction we confirm with a plantation experiment. As a result, maximum plant size should be short under drought and cold, which cause embolism, or increase if these pressures relax. That conduit diameter and embolism vulnerability are inseparably related to plant size helps explain why factors that interact with conduit diameter, such as drought or warming, are altering plant heights worldwide.

Vegetation height is the most conspicuous biotic attribute of terrestrial landscapes, varying across biomes and as climates change (1). From tundras and deserts to temperate and tropical moist forests, vegetation height becomes predictably taller as temperatures become milder and conditions moister (1–4). As climates change, formerly tall forests worldwide are experiencing dieback or mortality under increasingly erratic rainfall (5, 6). The largest trees, which would be expected to have greater root reach, more stem water storage, and thus more resistance to drought, instead are often especially vulnerable (7–12). At the same time that tall trees die or become shorter, formerly low tundras are growing taller under warming (13–15). Because vegetation height predicts crucial ecosystem services, from primary productivity and carbon sequestration to landscape heat absorption (6), it is essential to understand why changes in climate cause changes in vegetation height (7, 8, 12, 16).

A central link between plant height and climate is water conduction (4, 5, 10, 12). Plants conduct water in narrow conduits under negative pressure. Drought or freezing can break the conductive stream, blocking conduits with gas embolisms (17–19). Abundant embolisms often involve the death of terminal branches or even the whole plant (5, 20). Across species, higher wood density and stomata that close sensitively in response to water deficit are often associated with greater resistance to embolism (7, 12, 21–23). The membranes of pits, small apertures allowing fluid flow between conduits, are also implicated, with thicker membranes and less total interconduit membrane area per conduit volume being associated with greater embolism resistance across species (24–26). Within species, or even within individual stems, conduit diameter is strongly associated with vulnerability to embolism, with wider conduits embolizing more readily than narrow ones (27–33). So, though it remains debated why larger individuals should be more vulnerable to drought and why hydraulic adaptation to climate alters plant size, these phenomena are certain to involve embolism resistance (12, 34).

Of the factors involved in embolism resistance, conduit diameter is manifestly associated with both climate and plant size, but which of these two factors explains most of the variance in mean conduit diameter across individuals remains unclear. Water-conducting conduits are on average narrower in plants of dry or cold areas compared with plants in moist, warm areas (18, 19, 35). Narrow conduits better resist the formation of gas embolisms that block the conductive stream (27–33). Because cold and drought place plants at risk for embolism, biologists have interpreted narrow conduits as key adaptations to these conditions, and climate as the main driver of conduit diameter variation (18, 19, 35).

However, in addition to climate, plant height also predicts conduit diameter. Taller plants consistently have wider conduits than short ones, suggesting that, rather than climate, the main driver of variation in conduit diameter across individuals could be plant height (31, 36–39). Selection favors narrow distal conduits, because diffusion of a given unit of water out of terminal leaf veins, essential in driving the conduction stream, is maximal when conduits are very narrow. This is in line with the general tendency for selection to maximize exchange surface areas relative to fluid volumes, as in the capillaries of animal circulatory systems (38, 40, 41). Hydraulic resistance would accumulate linearly if conduits were of constant diameter, and would lead to a continual decline in water conduction with height growth (17, 31, 36, 38, 39). Because they reduce friction against conduit walls per unit water volume, small increases in conduit diameter from the tip to the base of a plant should counteract this increase in resistance, meaning that taller plants, with their longer pathways, should have predictably wider conduits (42). Hydraulic optimality models such as that of West, Brown, and Enquist (WBE) (38) predict the tip-to-base conduit diameter (D)-widening rate with increase in stem length (SL) that should minimize drops in per-leaf area conductance with height growth, embolism risk, and construction costs (31, 36, 39, 40, 42–45). Modeling the relationship between total plant length and conduit diameter, WBE implies that large sample sizes should converge on a scaling exponent of or somewhat above D ∝ SL^0.2 (36) (SI Appendix, Fig. S1).

Previous attempts to test these predictions and distinguish between climate and plant size have limited sampling to individual clades or to scattershot sampling across flowering plants, or have not properly standardized for height (19, 35, 37, 46). As a result, that size is the main driver of mean conduit diameter across species remains debated, theory regarding hydraulic adaptation to climate does not currently include plant size, and studies of plant hydraulics still do not routinely take plant height or distance from the stem tip into account (18, 47–50).

However, if height is the main driver of variation in mean conduit diameter, then this leads to an important expectation: If taller individuals have predictably wider conduits, and wider conduits within species are more vulnerable to embolism, then taller individuals should be more vulnerable to embolism than shorter conspecifics. Such a finding would provide critical mechanistic insight into studies that document the preferential vulnerability of taller individuals and the effects of climate change on vegetation height (3, 7–12, 16).

To distinguish height versus climate as the main driver of variation in conduit diameter and to test the prediction that taller individuals should be more vulnerable to embolism, we used a two-step procedure. First, we used a comparative approach sampling across biomes and lineages of flowering plants (angiosperms). Angiosperms conduct water in long multicellular conduits known as vessels. We gathered vessel diameter and height data from 19 communities spanning most of angiosperm climate space from the tropics to the north and south temperate zones. Sampling intensively within and across communities enabled comparison of vessel diameter–stem length scaling across differing macroclimatic conditions. This approach unequivocally identified height rather than climate as the main driver of variation in mean vessel diameter. Across biomes, vessel diameter increases with plant height predictably and in agreement with the expected rate, strongly implicating the conduit–height relationship as one favored by selection. Second, we explored the consequences for embolism vulnerability of this universal conduit widening with height. The greater vulnerability of larger individuals has been documented in previous studies (7, 10, 16, 51) but the role of predictable conduit scaling underlying this relationship has never been examined. Our plantation experiment using three species (two angiosperms and one conifer) confirmed our prediction that, with their wider conduits, taller individuals are more vulnerable than shorter conspecifics.

Our results mandate standardizing for plant size in hydraulics studies, and provide key insights for theory regarding plant hydraulic adaptation. Predictions emerging from our work range from expectations regarding plant plastic response to microsite conditions to the relationship between evolutionary and ontogenetic allometry in plant vascular systems. Moreover, finding that height is the main driver of conduit diameter variation allows for a long-overdue integration of plant size into thinking regarding the relationship between hydraulics and climate, helping explain why the largest conspecifics should be preferentially vulnerable and why shifts in climate provoke changes in vegetation height.

Results

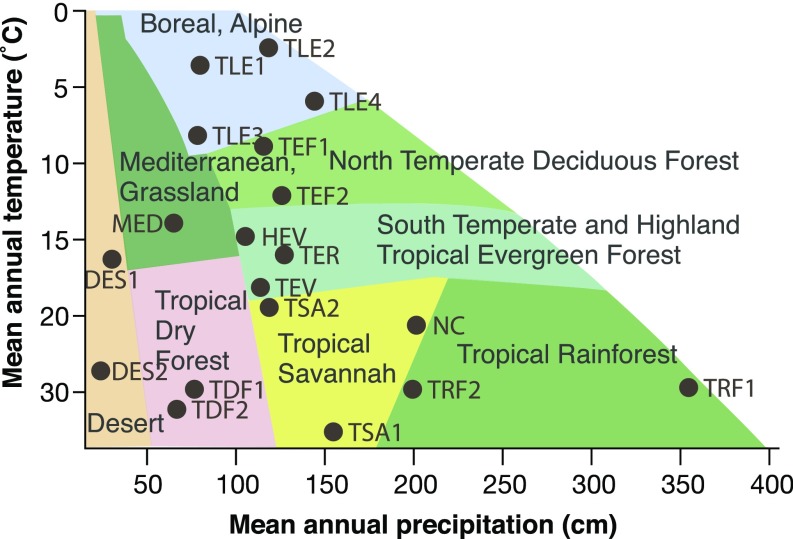
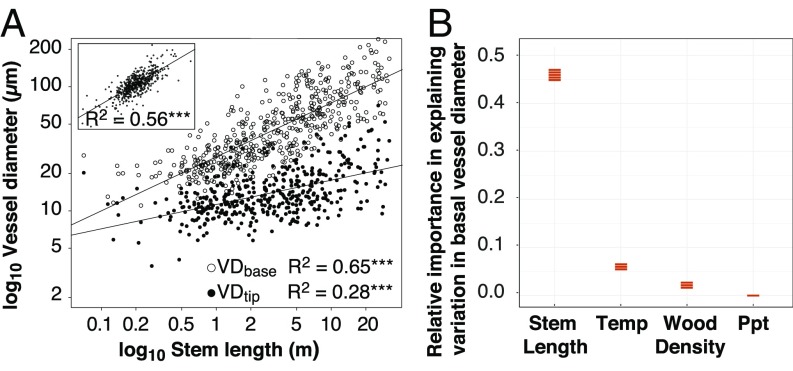
Our comparative sampling included 1,535 samples from 537 species, 43 orders, 140 families, and 374 genera. The 19 communities spanned most of the climates occupied by angiosperms (Fig. 1, SI Appendix, Table S1, and Dataset S1). Although climate is widely regarded as the main driver of variation in mean vessel diameter across individuals (18, 19, 35, 47), our data show unambiguously that the main driver is stem length. To examine the relative abilities of climate and stem length to predict variation in mean vessel diameter at the stem base (VD_base), we used multiple linear regressions that included stem length, climate variables, and wood density. The influence of wood density on conduit scaling has never been examined, but plants with lower wood density are often more vulnerable to embolism (21–23, 52), so density could play a role in predicting VD across species. In the 7 highest-ranked multiple regression models of the 119 fit (SI Appendix, Table S2), stem length was by far the most important explanatory variable (Fig. 2), nearly 10 times more important than temperature variables, as judged by squared standardized coefficients β²_stand (β²_standSL = 0.45 to 0.46 vs. β²_standTemp = 0.05 to 0.07). Temperature, which was positively associated with VD_base, was followed closely by the next most important variable, wood density (β²_standDens = 0.03), whose negative slope meant that plants with low density tend to have wider vessels for a given height. Precipitation (Ppt), traditionally regarded as strongly driving vessel diameter variation (35), had negligible importance values (β²_standPpt < 0.01) so, rather than precipitation, instead plant height, distantly followed by temperature and wood density, drove variation in mean vessel diameter.

Fig. 1.

Sampling across climates and vegetation types. The 19 sampled communities spanned virtually the entire range of angiosperm climates as described by mean annual temperature and precipitation (SI Appendix, Table S1), as well as the world’s major vegetation types from the north temperate zone to the tropics, and from there to the south temperate zone.

Fig. 2.

Stem length as the main driver of variation in vessel diameter across species. (A) Stem base vessel diameter VD_base scales with stem length SL with a slope of 0.44 and at the stem tip with a slope of 0.20, indicating that the widening rate across species is 0.24, coinciding with the rate predicted by optimality models to minimize drops in per-leaf area conductance with height growth, ***P < 0.005. (A, Inset) VD_base–SL regression based on phylogenetically independent contrasts. (B) We fit regression models predicting VD_base given SL, climate variables, and wood density. Orange bars give the ranges of relative importance values (squared standardized coefficients) for each category of variables from the seven best-fitting models (whose cumulative Akaike weights sum 0.95; SI Appendix, Table S2). Although climate is traditionally regarded as the main driver of interspecific variation in mean vessel diameter, stem length is by far the main driver, having a relative importance nearly 10 times larger than temperature, with precipitation not contributing to explanation in any model.

Moreover, our data showed that mean vessel diameter scales with plant height at virtually the exact rate predicted (36, 38, 45), as VD ∝ SL^0.2 (Fig. 2 and SI Appendix, Fig. S1 and Table S3). Because variation in terminal vessel diameter leads to variation in basal vessel diameter given a constant tip-to-base widening rate, to test the prediction that VD ∝ SL^0.2 it was necessary to take the stem tip vessel diameter–stem length widening rate into account. Across our data, species mean VD_base scaled with SL with a slope of 0.44, and VD_tip scaled with SL as 0.20. We calculated the widening ratio (WR), given that if VD_base ∝ SL^a and VD_tip ∝ SL^b, then WR = SL^a/SL^b for a WR of 0.24 (SI Appendix, Table S3). A different means of standardizing for tip vessel diameter (36) involved calculating tapering ratio T for each sample as T = VD_tip/VD_base, computing species averages, and then fitting the slope of T against stem length, which gave a very similar slope of 0.23 (SI Appendix, Table S3).

Given VD–SL scaling across climates, taller plants have predictably wider conduits, and if wider conduits within species are more vulnerable to embolism than narrow ones (19, 27–30, 32, 33, 53–55), then taller plants should be more vulnerable to embolism than shorter conspecifics. Studies in trees 6 to 100 m tall show that taller individuals of a species, or more basal parts within the same individual, are often more vulnerable than shorter individuals or more distal parts (7–10, 27, 29, 30, 32). These studies are consistent with tip-to-base conduit widening and the greater vulnerability of wider conduits. Our plantation experiment focused on plants 47 to 377 cm tall, because the most drought- and cold-prone habitats on Earth fall within this height range, for example the four coldest (mean height 2.0 m) and four driest (mean height 3.3 m) communities in our dataset. As a result, the ≤4 m height range is a crucial one for understanding the role of stature in plant hydraulic adaptation to extreme environments. Moreover, because the conduit diameter–stem length relationship follows a power law-like function (SI Appendix, Figs. S1 and S2), small height changes in plants ≤4 m tall imply marked changes in vessel diameter, meaning height-associated differences in embolism vulnerability should be highly visible to selection.

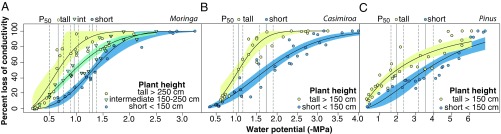
Our experimental plantation included two angiosperms with contrasting wood densities and therefore differing VD_base–SL intercepts, as well as differing thicknesses of intervessel pit membranes (SI Appendix, Fig. S3): Moringa oleifera Lam. (Moringaceae, Brassicales), with low wood density, relatively wide vessels for a given height, and thin pit membranes, and Casimiroa edulis La Llave (Rutaceae, Sapindales), with higher wood density, narrower vessels, and thicker membranes. We also included Pinus ayacahuite Ehrenb. ex Schltdl. (Pinaceae, Pinales), which conducts water in tracheids rather than vessels. In all cases, with their wider conduits (SI Appendix, Fig. S3), taller individuals were significantly more vulnerable to embolism than intermediate or short conspecifics, as assessed by P₅₀, the water potential at which 50% of conductivity was lost. Taller height categories had values of P₅₀ that were always less negative and had 95% confidence intervals that did not overlap with those of shorter categories (Fig. 3), indicating that in taller plants less tension was required to achieve a similar reduction of stem conductivity (SI Appendix, Table S4). Tests in M. oleifera and C. edulis, in which we allowed vessels to embolize and then perfused the vessels with stain, showed within stem segments that wider vessels embolized before narrow ones (SI Appendix, Fig. S3).

Fig. 3.

Vulnerability to embolism increases with plant height. Percent loss of stem hydraulic conductivity (PLC) versus xylem water potential for (A) M. oleifera and (B) C. edulis, both vessel-bearing flowering plants, and (C) the tracheid-bearing conifer P. ayacahuite. P₅₀ is an index of vulnerability, the water potential at which 50% of conductivity is lost, and is less negative (and thus more readily reached) in taller plants. Dashed lines are 95% confidence intervals for P₅₀. Details are in SI Appendix, Table S4.

Discussion

In understanding worldwide shifts in vegetation height as climates change, it is essential to untangle the relationship between climate, plant size, and the diameters of water-conducting conduits. Our data show that plant height, rather than climate, is by far the main driver of variation in species mean vessel diameter across flowering plant lineages and biomes (SI Appendix, Table S2). The effect of plant height on vessel diameter was almost 10 times that of the next most important variable, temperature (Fig. 2). Plants in warmer communities did have on average wider vessels than similar-sized plants in cold communities. Although this pattern is consistent with the traditional account that selection favors narrow, embolism-resistant vessels in cold climates (18), the effect of temperature was very small compared with the effect of plant size. By way of illustration, substituting the mean values in our dataset for plant height (5.67 m), wood density (0.547 g/mm³), and precipitation of the warmest quarter (370.8 mm) in the best-fitting model from SI Appendix, Table S2, the predicted basal vessel diameter would be 43 µm in a tree growing at 3.2 °C mean annual temperature and 70 µm in one growing at 27.3 °C (the extremes of mean annual temperature in our dataset, covering almost all of the mean temperature range occupied by angiosperms). In contrast, using the mean values for density, precipitation, and temperature (17.4 °C), the predicted basal vessel diameter would be 13 µm for a plant 0.11 m tall and 108 µm for one 32.5 m tall (the extremes of height in our dataset, covering just a third of the angiosperm height range). Comparing these ranges—43 to 70 µm across a near-comprehensive range of temperatures and 13 to 108 µm across a comparatively modest range of heights—shows that change in vessel diameter with plant height is vastly more marked than with climate.

That plant height is the main driver of conduit diameter variation means that plant hydraulic adaptation inevitably involves stature (12, 22, 31, 38, 39). A canonical example is provided by cold environments, where narrow conduits are regarded as key adaptations because of their resistance to freezing-induced embolism (18). But taking plant height into account showed that cold communities had height-standardized vessel diameters at the stem base (VD_base–SL residuals) that were not exceptionally narrow (SI Appendix, Fig. S4). They did, however, have vessels that were narrow in absolute terms: Maximum species mean VD_base of the coldest community we sampled, at treeline in the Pyrenees, was just 88.6 µm, versus 244.3 µm in the warm lowland Mexican rainforest. Without highly negative VD–SL residuals, narrow absolute VD_base inevitably requires small plant size. Indeed, median height across the treeline communities was just 1.2 m, versus 12.2 in the rainforests. If selection acts against wide conduit diameters in cold situations (18, 19, 28, 29), then it does so by reducing plant size in the context of a constant conduit diameter–plant height relationship (45, 56).

Given a constant conduit diameter–plant height relationship, our experimental results were congruent with the expectation that the tallest individuals of a species have predictably wider conduits and so, all else being equal, taller individuals should be more vulnerable than shorter conspecifics. Across the 185 individuals that made up our drought experiment, taller size classes, with their predictably wider conduits (SI Appendix, Fig. S3), were significantly more vulnerable than shorter ones of the same species (Fig. 3 and SI Appendix, Table S4). That taller plants have predictably wider conduits, and individuals with wider conduits are more vulnerable to embolism than shorter conspecifics with narrower ones, is consistent with the otherwise puzzling preferential vulnerability of large trees (7–10, 12, 22).

These results point to important considerations for the study of plant hydraulics. One is that comparing variables such as vessel diameter, conductance, or vulnerability to embolism must take into account scaling not only of basal vessel diameter but also terminal twig vessel diameter with height (Fig. 2A); much of the notorious variability about the y axis in intraspecific vulnerability curves is likely accounted for by stem length differences (Fig. 3). Moreover, detailed documentation of vascular allometry can provide models of the plant height–climate relationship with mechanistic detail that is currently “black-boxed” (3, 4, 12), for example, replacing models of bulk flow through a porous medium with explicit modeling of widened conduits (31, 36, 38, 39, 42). In the same vein, our results also highlight the need to study resistance and conductance not only in segments but along the entire conductive pathway.

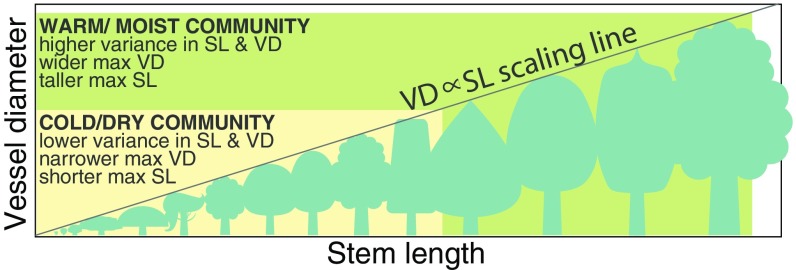
Even more importantly, our data show how plant size must be integrated into thinking regarding plant hydraulic adaptation to climate (Fig. 4) (2, 12, 45). Anatomists have often noted that conduit diameters are predicted both by plant size and climate (45, 57–59), but there has never been an account of how height, conduit diameter, and climate interact simultaneously. Our results point to the following integration, which can be regarded as a rebuilding of Carlquist’s ecological wood anatomy around conduit scaling with plant size as a primary pole of natural selection on plant hydraulic systems (57, 58, 60). Vessel diameter scales predictably with stem length as approximately VD ∝ SL^0.2, the result of selection minimizing the drop in per-leaf area conductance with increasing conductive path length as height increases (31, 38). In general, then, height determines vessel diameter across the array of height ecological strategies, understory to canopy (2, 4), that is found in every community (Fig. 4). Because taller individuals have predictably wider conduits (not only at the stem base but also at the tip; Fig. 2A) and because wider conduits are more vulnerable within species than narrow ones, plants should produce conduits no wider than those permitted by embolism risk given microsite and height ecological strategy. Therefore, maximum height for a given individual should be at least in part determined by the maximum mean conduit diameter permitted by microsite conditions such as water availability, temperature, rooting depth, and soil type (cf. refs. 4, 5, 12, 16, 31, 56, and 61). Across climates, the maximum vessel diameter permitted by selection in drylands and cold environments with short growing seasons (or long growing seasons with many freeze–thaw events) is narrower than in warmer, moister environments. This means that maximum height in drylands and cold environments is necessarily shorter (Fig. 4). That individuals should grow to the maximum mean conduit diameter and therefore plant height that is permitted by microsite conditions and remain there unless conditions change is consistent with observations of trees fluctuating around constant heights for centuries (62, 63). In moist areas that experience frequent freezes per growth season, which act against wide conduits, plant height should be low despite water availability that would otherwise permit taller plants (64). Anthropogenic warming in cool sites should relax selection against wide vessels and permit taller plants, consistent with observed tundra height increase (13–15). At any given site, the tallest plants, which have the widest vessels from tip to base, should be more vulnerable than shorter conspecifics, consistent with the otherwise inexplicable dieback of taller conspecifics under climate change-induced drought in forests worldwide (7–10). Through its elemental relationship with vessel diameter, climate, and wood density, plant size asserts itself as a crucial element in plant hydraulic adaptation.

Fig. 4.

Climate, vessel diameter, and stem length/plant height in plant hydraulic adaptation. Vessel diameter (VD) scales with stem length (SL) similarly across all communities, represented by the diagonal line. The green box denotes a warm and moist community, with wide variance in plant height, represented by the width of the green box and the wide range of plant silhouettes, with a correspondingly wide variance in species mean vessel diameters, represented by the height of the green box. The narrower ranges of height and vessel diameter in a cold, dry community are represented by the yellow box. Because wider vessels are more vulnerable, the maximum vessel diameter permitted in the cold/dry community is narrower, helping explain why maximum plant height in these communities is lower.

Materials and Methods

Teasing apart the relative effects of climate and plant size on vessel diameter variation required sampling across a wide range of angiosperm sizes and climates, so we gathered new data from 352 species, complementing them with previously published data (37) from 185 species. In the field, we sampled either all self-supporting woody species (low-diversity communities) or the 20 commonest species, plus additional species as necessary to cover phylogenetic (excluding monocots) and morphological diversity (habits and wood density), for a range of 18 to 41 species per community. Plants within communities grew in the same general area, except those of the New South Wales temperate rainforest community in Australia, which consisted of small climatically and vegetationally similar localities scattered along the central east coast of the state (coordinates for all collections are given in Dataset S1). We measured heights (SL) of trees and shrubs <8 m with a tape measure, following the longest branch with a flexible tape if very sinuous, in an effort to measure the longest conductive path length per individual. We use “height” and “stem length” interchangeably, indicating a presumably close proxy for the driving variable, the length of the conductive path. We measured the height (base to highest leaf) of individuals >8 m with a TruPulse 200B laser rangefinder (Laser Technology). We collected samples of the outermost basal secondary xylem (wood), as low as possible above buttresses, roots, or basal swellings, usually sampling three individuals per species (88%; one or two samples for the remainder). We also collected the terminal portion of the farthest twig from the base from 1,166 individuals. We cut thin sections for light microscopy, measuring with an ocular micrometer 25 randomly selected vessels, scanning across growth rings when present. We calculated wood density as the oven-dry mass:fresh (or, for material pickled in ethanol, hydrated for 24 h) volume ratio using water displacement (65).

To test for differences in the VD_base–SL relationship across climates, we extracted 19 climate variables from WorldClim v.1.4 (www.worldclim.org) using the R library raster (cran.r-project.org/package=raster) based on the geographical coordinates of the 537 species in the comparative dataset, as well as wood density (Dens). We then examined the association between climate variables and VD_base, VD_tip, SL, and Dens using Pearson correlation (SI Appendix, Table S5). We also calculated the correlations between climate variables and the residual variation of VD_base once SL had been taken into account through simple linear regression.

To compare the relative abilities of climate and stem length to predict variation in mean vessel diameter at the stem base (VD_base), we fitted multiple linear regressions that included SL, climate variables, and Dens, with a model selection process using the Akaike information criterion (66). We fit 119 models with all combinations of from one to four predictor variables including SL, Dens, a precipitation variable, and a temperature variable (SI Appendix, Table S2). These models were based on the 524 species for which we had data for all explanatory variables (wood density was not available for some species). We included in this process the climate variables that were strongly correlated with VD_base (R ≥ 0.4). This was the case for four variables reflecting precipitation and five variables reflecting temperature (SI Appendix, Table S5). To avoid collinearity in models, only one precipitation and one temperature variable could be included at the same time in each model. For each model, we calculated the corrected Akaike information criterion (AICc) and the adjusted R². We also calculated ΔAICc, the difference between model AICc values and the AICc of the best-approximating model (i.e., that with the smallest AICc in the model set), and finally the Akaike weight (w), an index of the probability of a model being the best-approximating model (67). We identified the best-ranked models, representing a 95% confidence set of models (i.e., with cumulative Akaike weights of 0.95; SI Appendix, Table S2). In this set of seven models, the relative importance of explanatory variables was depicted using squared standardized coefficients (β²_stand) (68). We used bootstraps to calculate confidence intervals for these coefficients (69). We checked regression assumptions, including collinearity, which we assessed through variance inflation factors (which were <2) (70).

To test the prediction that taller plants should be more vulnerable to embolism, we used plantations of two flowering plants, M. oleifera and C. edulis, and the conifer P. ayacahuite, which conducts water in tracheids rather than vessels. Including a tracheid-bearing species helped exclude open-conduit artifacts (71–73), because tracheids are much shorter than vessels. We focused on within-species comparisons, because climate change alters maximum vegetation height through its effects on the tallest species at a given site. Conduit diameter predicts embolism risk better within (10, 28–30, 32, 53, 74) than across species (75), presumably because although pit membrane characteristics vary along the lengths of stems (76), these features vary less within than across species (26).

We tested 185 individuals in total, 56 plants 47 to 242 cm tall for C. edulis, 72 plants 69 to 377 cm tall for M. oleifera, and 57 plants 61 to 250 cm tall for P. ayacahuite. We estimated conduit lengths (77) across the different plant height classes examined and tested segments consistently longer than conduit lengths (SI Appendix, Table S6). We imposed the required xylem tensions by drying plants in the soil or removing them from the soil with roots and allowing them to dry at room temperature for varying times (78, 79). We used leaf water potential to determine xylem water potential. To measure leaf water potential, we sealed three leaves per plant in foil laminate bags for an hour to allow equilibrium between xylem and leaf water potential. We measured leaf water potential with a Scholander pressure chamber (PMS Instrument), working with a 0.1- to 7-MPa range of water potentials. After exposing individuals to the required xylem tension, we cut segments of the basal stem underwater. To measure the initial conductivity (K_h), we connected the segments to tubing with a gentle siphon of filtered 10 mM KCl solution at 20 °C and ∼50-cm height [a “Sperry apparatus” (80)]. Water was collected from the end of the stem and weighed on a Sartorius TE1245 analytical balance. Upon constant flow, we took measurements every 30 s for 3 min. To estimate maximum conductivity (K_max), we flushed the segments with filtered 10 mM KCl at a pressure of 1.5 bars until no increase in conductivity was detected. Conductivity was calculated as mass flow rate through the segment, divided by the pressure gradient (m⁴⋅s⁻¹⋅MPa⁻¹). We used the percentage loss of conductivity (PLC) as a measurement of embolism vulnerability, estimated as PLC = 1 − (K_h/K_max) · 100. We divided plants into a tall (>150 cm) and a short (<150 cm) category in C. edulis and P. ayacahuite. In M. oleifera, we divided plants into short (<150 cm), intermediate (150 to 250 cm), and tall (>250 cm) categories. We fit Weibull models to PLC vs. xylem water potential per size class and calculated P₅₀, the water potential at which 50% of conductivity was lost, and 95% confidence intervals using the R package fitplc (cran.r-project.org/package=fitplc).

Finally, we built a phylogeny (SI Appendix, Fig. S5) based on the backbone tree of Soltis et al. (81), using APG IV (82) to place some groups. Some relationships were resolved by reference to phylogenetic studies of specific groups. Using “ape” (ape-package.ird.fr), “phytools” (cran.r-project.org/package=phytools), and branch lengths of one, we tested for significant phylogenetic signal in residuals of the models VD_base–SL (SI Appendix, Table S7) and the first model in SI Appendix, Table S2, based on randomization tests of phylogenetically independent contrasts and using the K statistic (83). Our phylogenetic tree included polytomies, so we repeated calculations 1,000 times using randomly resolved trees. We report ranges for K and P values based on these repetitions. Although phylogenetic signal was statistically significant (P < 0.05; SI Appendix, Table S7), values of K ≤0.18 suggested there was little tendency for closely related species to resemble one another in their VD_base–SL residuals. Consistent with this assessment, the VD_base–SL regressions using independent contrasts calculated by resolving polytomies randomly 1,000 times had a range of slopes very similar (0.381 to 0.393, R² 0.56 to 0.58) to analyses based on raw data (0.435), highlighting that vessel diameter tracks stem length in similar ways regardless of phylogenetic affinity (Fig. 2). All analyses were carried out in R v.3.3.1 (www.r-project.org).