Correlative Multiscale 3D Imaging of a Hierarchical Nanoporous Gold Catalyst by Electron, Ion and X‐ray Nanotomography

Abstract

Tomographic imaging of catalysts allows non‐invasive investigation of structural features and chemical properties by combining large fields of view, high spatial resolution, and the ability to probe multiple length scales. Three complementary nanotomography techniques, (i) electron tomography, (ii) focused ion beam—scanning electron microscopy, and (iii) synchrotron ptychographic X‐ray computed tomography, were applied to render the 3D structure of monolithic nanoporous gold doped with ceria, a catalytically active material with hierarchical porosity on the nm and μm scale. The resulting tomograms were used to directly measure volume fraction, surface area and pore size distribution, together with 3D pore network mapping. Each technique is critically assessed in terms of approximate spatial resolution, field of view, sample preparation and data processing requirements. Ptychographic X‐ray computed tomography produced 3D electron density maps with isotropic spatial resolution of 23 nm, the highest so far demonstrated for a catalyst material, and is highlighted as an emerging method with excellent potential in the field of catalysis.

Introduction

Detailed structural analysis is relevant and important on all length scales in catalysis, where material structure and chemical function of the catalyst are closely linked. Specific features of interest can range from Å to mm, including active sites, metal nanoparticles or clusters, surface composition, and nanoscale porosity further defined as micro‐ (<2 nm), meso‐ (2 to 50 nm) or macropores (>50 nm).1 An excellent example of this is nanoporous gold (np‐Au), a monolithic sponge‐like material which exhibits pores and connecting ligaments of only a few tens of nanometres (typically 10 to 50 nm) depending on the preparation route.2, 3, 4, 5 Such nanoscale porosity is incorporated in a continuous bulk volume which can principally extend in the μm to mm range, therefore forming a hierarchical porous macrostructure. This results in a large fraction of accessible gold surface atoms, particularly at kink and step sites, which makes np‐Au very interesting for catalysis and sensing applications.6, 7 As with all functional materials, it is important to understand physical characteristics such as surface area, porosity, shape and mechanical stability, in order to: (i) define structure–activity relationships;8, 9 (ii) identify and control synthesis parameters which lead to such structures;10, 11 (iii) design future catalysts for target applications.12, 13 When applied to catalysis, analytical methods based on structural imaging or microscopy are therefore required to incorporate large fields of view, high spatial resolution, and to extend across multiple length scales.14, 15, 16 Ideally such techniques should also be non‐invasive, or cause minimal damage or interaction with the sample of interest.17

The characteristic sponge‐like structure of np‐Au has been characterised primarily on the nanoscale using scanning (SEM) or transmission electron microscopy (TEM). These have proven successful in analysing structural stability, ligament coarsening at high temperature, and morphological changes after incorporation of metal oxide dopants such as CeO₂ or TiO₂, for example.6, 11, 18, 19, 20, 21 In particular, modification of np‐Au with metal oxides has been proposed as a method of inhibiting sintering and pore collapse at the elevated temperatures often required for catalysis. Preservation of the pore structure is clearly important for accessibility of reactant molecules and in order to maintain a high surface area, for example. However, SEM and TEM are limited to surface information or samples not thicker than several hundred nanometres. Aside from electron microscopy, synchrotron‐based hard X‐ray ptychography (scanning coherent diffraction imaging) has emerged as a versatile and complementary nanoscale imaging technique.22, 23 Ptychography is a lensless imaging method providing quantitative absorption and phase contrast, with the powerful advantage of avoiding the spatial resolution limit (or diffraction limit) of conventional lens‐based imaging. Although with lower effective spatial resolution than TEM or SEM, hard X‐ray ptychography partly mitigates sample thickness limitations due to the high penetration of X‐rays compared to electrons. This permits larger fields of view, sample sizes on the order of one to several hundred μm,24, 25 avoids potentially damaging preparation of thin TEM lamellae, and even enables in situ studies at above ambient pressure and temperature,26, 27, 28 with the possibility for elemental contrast via resonant imaging around the relevant X‐ray absorption edge of the sample.29 Hard X‐ray ptychography was previously used to study the effect of temperature, gas atmosphere and the presence of CeO₂ and TiO₂ additives on the structure of np‐Au from a two‐dimensional (2D) perspective.26, 27 However, np‐Au contains structural features of interest not only confined to the surface but present throughout the bulk material. These are difficult to accurately observe from a 2D perspective without cutting or sectioning (e.g. preparation of lamellae), which carries the risk of structural damage. In this context, non‐invasive three‐dimensional (3D) imaging methods based on computed tomography are beginning to receive significant attention for characterisation of heterogeneous catalysts,14, 17, 30, 31, 32 including nanoporous gold.8, 33 By revealing both exterior and interior structural features, tomographic analysis can derive surface area, porosity and pore size distribution data from the sample together with pore network mapping in 3D,9, 34, 35, 36 as demonstrated recently for nanoporous silver.37 Such data is highly valuable for modelling physical effects relevant to catalysis, such as gas or liquid diffusion, sintering or structural inhomogeneity.38, 39 In contrast, this data is generally collected from gas adsorption studies (e.g. Brunauer‐Emmett‐Teller or BET analysis), porosimetry measurements (e.g. mercury intrusion), or computational modelling, which involve several assumptions and limitations discussed in detail elsewhere.21, 40, 41, 42 In this context, nanoprobe tomography or ‘nanotomography’ techniques based on electron and X‐ray microscopy are ideal tools for comprehensive multiscale structural analysis.

Here ceria‐doped nanoporous gold (CeO_x/np‐Au) was studied by three nanotomography techniques: (i) electron tomography (ET); (ii) “slice and view” tomography with a focused ion beam—scanning electron microscope (FIB‐SEM‐CT); and (iii) ptychographic X‐ray computed tomography (PXCT). Both ET and FIB‐SEM‐CT are established methods which have previously been used to investigate the pore structure of np‐Au lamella with close to sub‐nm resolution,8, 43, 44 and for extended μm scale cuboid sample volumes, respectively.34, 45 On the other hand, PXCT is an emerging synchrotron‐based method which exploits the high spatial resolution of X‐ray ptychography for 3D imaging.46 While each method has unique features, advantages and limitations, the complementarity of these techniques, particularly the ability to focus on different length scales, the available spatial resolution and the chemical information obtainable, has not been deeply explored. Here we focus on the application of nanotomography specifically in the field of catalysis, taking np‐Au as a case study. The structural information available to each tomographic method, including catalytically relevant properties such as surface area, volume fraction and pore size distribution are presented and compared to results from conventional bulk porosimetry methods. Taking into account the available spatial resolution, field of view and sample preparation requirements, PXCT in particular is brought into focus as a powerful and rapidly developing technique with widespread potential applications in catalysis. While PXCT is a relatively young technique, it has already demonstrated unprecedented 3D isotropic spatial resolutions of 14.6 nm for an integrated circuit sample47 and 31 nm for catalyst particles.17 Here we present an isotropic spatial resolution of 23 nm using PXCT, a new record for a heterogeneous catalyst sample.

Results and Discussion

Suitable samples for nanotomography studies were prepared starting from a single piece of monolithic CeO_x/np‐Au by FIB milling and micromanipulation. An overview of the sample preparation techniques is shown in Figure 1 a. The requirements for each of the three imaging methods were unique: (i) for ET a 300 nm thin lamella was prepared on a TEM lift‐out grid (Figure 1 b); (ii) for PXCT a cylinder of 10 μm diameter and 30 μm height was prepared on a tomography pin sample holder (Figure 1 c);48 (iii) for FIB‐SEM‐CT a cuboid of CeO_x/np‐Au (9.91×11.7×2.62 μm³) was exposed by carving a trench around the monolithic sample directly on a SEM sample holder stub (Figure 1 d).45 Further description of these procedures can be found in the Supporting Information.

Figure 1.

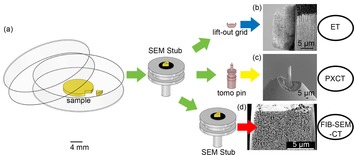
(a) Overview of CeO_x/np‐Au sample preparation procedure via FIB for each of the three nanotomography methods and SEM images (secondary electron detection) of prepared samples: (b) lamella for ET; (c) cylinder for PXCT; (d) cuboid for FIB‐SEM‐CT.

Following sample preparation, CeO_x/np‐Au samples were analysed individually by each of the three nanotomography techniques. The common principle of tomographic and/or 3D image reconstruction is to convert a series of 2D images of the probed samples into 3D data volumes. In the case of PXCT and ET this 2D data is in the form of projected images of the sample at various rotational angles, while FIB‐SEM relies on a series of surface measurements obtained after sequential cutting of sample layers with an ion beam. Figure 2 shows an example of the 2D data obtained for CeO_x/np‐Au by each technique, including an orthographic slice through the phase contrast tomogram acquired by PXCT after ptychographic and tomographic reconstruction, together with a typical SEM image acquired during FIB‐SEM‐CT and a scanning transmission electron microscopy (STEM) overview image of the CeO_x/np‐Au lamella acquired in TEM. Further examples of the 2D data obtained can be found in the Supporting Information. The 2D images clearly indicate the characteristic sponge‐like structure of CeO_x/np‐Au and the presence of pores and ligaments of varying size.8, 11, 18, 26 Notably, the samples appeared to contain finely structured ligaments together with sections of more dense or thicker material, indicative of mild coarsening which may have occurred during the process of ceria addition and low temperature heat treatment (280 °C) to remove organic residues. The presence of a thick layer at the sample exterior was uniquely noticeable during FIB‐SEM‐CT (Figure 1 d and 2 b). This is proposed to be damaged or agglomerated material, resulting from the interaction of Ga⁺ milling at high current (up to 10 nA) during initial sample preparation by FIB, which was necessary to excavate large trenches around the sample region of interest in a timely manner. During the FIB‐SEM‐CT measurement itself and during FIB preparation of the cylinder‐shaped sample for PXCT and lamella for ET, milling was performed at a lower current (50 pA) and no material agglomeration was observed. Complementary energy dispersive X‐ray spectroscopy (EDX) analysis performed during TEM confirmed the presence of ceria (Figure 2 d) with 4.2 wt % or 5.2 At. % Ce within a structure dominant in gold, which is within the range reported previously for this material (2–10 At. % via SEM‐EDX analysis).11 Additional possibilities for analysing and visualising the sample ceria content are discussed later.

Figure 2.

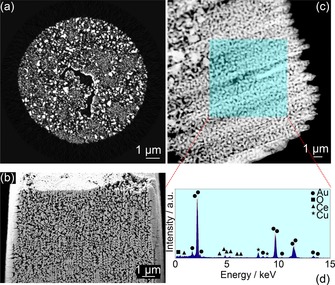
2D perspective of the internal catalyst structure acquired by: (a) PXCT—orthographic slice through the phase contrast tomogram following reconstruction; (b) FIB‐SEM‐CT—secondary electron image of a typical surface exposed during cutting; (c) STEM image of CeO_x/np‐Au and (d) corresponding EDX spectrum acquired from the shaded area.

Following collection of 2D image series by each technique, the data underwent tomographic image reconstruction (in the case of PXCT and ET) or 3D image reconstruction (in the case of FIB‐SEM‐CT), resulting in expansion of the 2D data series into 3D volumes. Volumes were then visualised using Avizo software (FEI). In all cases, the 3D data was first treated to remove the background (air surrounding the catalyst and/or 2D frame padding). The remaining sample volume then underwent threshold segmentation to define separate regions as either “np‐Au” or “pores”, with the help of a watershed contrast gradient to distinguish “grey areas” representing voxels with partial volume effects. Examples of the 3D data obtained by each of the three nanotomography techniques are shown in Figure 3. Full details of the data acquisition, treatment procedure and movies illustrating the 3D volumes can be found as Supplementary Information. 3D rendering clearly shows the propagation of the characteristic sponge‐like structure and porosity throughout the sample. The total probed volume by each method reveals the much greater field of view available to PXCT and FIB‐SEM‐CT compared to ET. As noted previously, a thin lamella is typically a requirement for electron imaging techniques due to the high attenuation experienced, particularly at high tilting angle, in comparison to X‐rays. In this study, the volumes visualised by PXCT and FIB‐SEM‐CT were effectively two orders of magnitude larger than that of ET. To illustrate this, Figure 3 e shows the probed volume from ET to scale with those of PXCT and FIB‐SEM‐CT. The central hole or crack visible in the PXCT volume (Figure 3 a–b) was attributed to a mechanical fracture during FIB preparation, this area was excluded from all further calculations and was not counted when measuring porosity. Similarly for FIB‐SEM‐CT, the approximately 500 nm thick external layer (Figure 2 b) was also discarded before further analysis and did not influence measurement of pore and ligament sizes.

Figure 3.

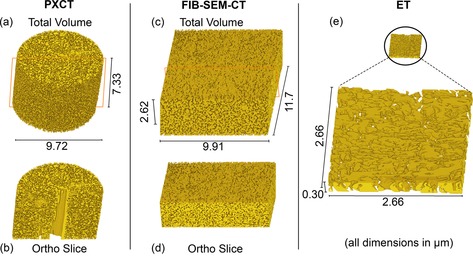
Volume rendering of (a) whole and (b) bisected CeO_x/np‐Au cylinder via PXCT; (c) whole and (d) bisected CeO_x/np‐Au cuboid via FIB‐SEM‐CT; (e) CeO_x/np‐Au lamella to scale (above) and magnified (below) as observed via ET. Ortho slice planes indicated by red lines.

After segmentation of the volumetric data, it was possible to directly analyse the average diameter of the ligaments and pores, subject to the available spatial resolution of each technique. This was accomplished by visualising each material as a collection of discrete subunits, then approximating the ligaments and pores contained in each subunit as spheres or ovoids and measuring the corresponding diameters. Measurement and comparison of the subunit properties was performed by means of label analysis using Avizo software (see Supporting Information). The relevant measurement characteristics are listed in Table 1. Note that in effect distinct regions of the same original sample were measured by each technique, therefore any observed difference in pore characteristics can likely be attributed to sample preparation factors (e.g. beam damage), statistical variance, and/or the characteristics of the measurement technique itself (e.g. spatial resolution limits). The lowest average pore size was derived from ET (61 nm), comparable to literature values of ≈40 nm,7 followed by FIB‐SEM‐CT and PXCT (195.9 and 288.6 nm, respectively). The average pore size was further broken down into distinct regions of porosity, with the distribution profile of ligament and pore sizes for each technique shown in Figure 4. For all three techniques, two distinct regions of pore size were observed, contributing to the average pore size shown in Table 1. For ET porosity was counted in the range of 2 to 200 nm, with maxima at <10 nm and 100 nm. In contrast, PXCT and FIB‐SEM‐CT shared a similar range of pore sizes from 16 to 600 nm, with both showing pore size maxima at around 20 to 30 nm,34 and 200 to 300 nm.21 The significantly lower pore and ligament size derived from ET may primarily result from the much smaller probed volume. Considering that the lamella studied by ET was <300 nm thick, while larger pores were observed between 100 to 600 nm for the monolithic samples, this further implies the unrepresentative sample characteristics of the thin lamella in this case. The sum of the average pore and ligament size for PXCT and FIB‐SEM‐CT was similar (500.5 and 473.2 nm, respectively), but the proportional composition of ligaments was greater for FIB‐SEM‐CT at 277 nm on average (compared to 195 nm for the pores), while PXCT showed a larger proportion of pores at 288 nm on average (compared to 211 nm for the ligaments). As the probed volume was similar for both PXCT and FIB‐SEM‐CT, this discrepancy can potentially be explained by considering the methodology of FIB‐SEM‐CT, a destructive technique which relies on ablation of material layers and was previously shown to cause aggregation or sintering of the sample through 2D analysis (Figure 2 b). In addition, due to the pervasive pore system in np‐Au, the presence of subsurface np‐Au material below the slice being imaged may cause so‐called “shine through” artefacts, leading to oversampling of ligament diameters and undersampling of pores. These artefacts were apparent when considering the poor contrast observed on the image histogram between np‐Au and pores during FIB‐SEM 3D reconstruction (see the Supporting Information).34 PXCT by comparison was found to be non‐invasive, non‐destructive and quantifiably less damaging on the observable length scale to the sample being probed.

Table 1.

Measurement characteristics of volume‐rendered CeO_x/np‐Au from three nanotomography techniques.

Method	Approx. Spatial	Pixel	Probed	Average
	Resolution	Size	Volume	Ligament	Pore Size	Pore
	[nm]	[nm]	[μm3]	Size [nm]	[nm]	Sphericity
PXCT	23[a]	13.3	9.72×9.72×7.33	211±23	288±23	0.57
FIB‐SEM	15‐45[b]	12.8	9.91×11.7×2.62	277±15	195±15	0.62
ET	1‐3[b]	1.3	2.66×2.66×0.30	75±2	61±2	0.81

[a] Half‐period resolution determined by Fourier shell correlation. [b] Full‐period resolution determined by material interface analysis.

Figure 4.

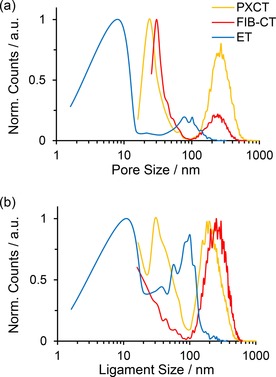
Normalised distribution profile showing (a) pore size and (b) ligament size of CeO_x/np‐Au calculated from three nanotomography techniques.

To understand the differences observed between each technique and assess the quality and reliability of the data obtained, it is also important to consider the spatial resolution of the measurement. Spatial resolution was the primary source of error for the values given in Table 1 and has a strong impact on both image segmentation and measurement of physical characteristics. In this study, the spatial resolution was determined by two separate methods. For PXCT the isotropic half‐period spatial resolution was estimated at 23 nm via Fourier shell correlation using the half‐bit threshold criterion (see the Supporting Information).49 For FIB‐SEM‐CT and ET, the spatial resolution was estimated based on the known pixel size (and slice thickness in the case of FIB‐SEM‐CT) by examining interface regions between np‐Au and pores, then determining the minimum number of pixels which could be visualised across an interface. In this case both methods contained regions where the interface could be defined by a minimum of 3 pixels. Electron‐based imaging techniques such as TEM and ET clearly offer superior spatial resolution close to the atomic scale. In this case the spatial resolution obtained with the microscope given the relatively large field of view and low magnification was around 2 nm, but this may also be influenced by aberration and astigmation effects. High resolution can also be obtained with FIB‐SEM‐CT by reducing the probed volume and decreasing the slice thickness for example, although this limits the practical field of view due to time constraints and may cause difficulties with reconstruction due to sample drift.45 In this study, a beam energy of 30 kV, 50 pA was employed during FIB‐SEM‐CT in order to image a volume comparable to that of PXCT with similar spatial resolution, while limiting damage to the sample.

The effects of spatial resolution can be most clearly observed when considering the size distribution of features shown in Figure 4. ET again showed a distinctly different distribution of both ligament and pore sizes among the three techniques. The results of ET were visibly skewed towards pores and ligaments under 15 nm due to the much higher spatial resolution available, which presumably were not accurately detectable to either PXCT or FIB‐SEM‐CT. However, the pore sizes occurring around 100 nm for ET may be considered somewhat less reliable, as these are within the same order of magnitude as the lamella thickness (300 nm) and are therefore only measurable along the lamella diameter. As a result, ET appears to be ideal for visualising porous features at the smaller end of the hierarchical length scale, such as micro‐ and mesopores. For PXCT and FIB‐SEM‐CT, the high frequency of smaller pores in the range of 20 to 30 nm may simply reflect the lower spatial resolution compared to ET. However, the clear presence of much larger pores of some hundreds of nanometres is notable. FIB‐SEM‐CT and PXCT therefore appear more suitable for investigating meso‐ and macroporosity, where the much larger probed volumes allow reliable determination of features which are not visible on small lamella. Again it should be noted that PXCT proved in this case to match the performance of FIB‐SEM‐CT regarding spatial resolution, while being non‐invasive and non‐destructive towards the sample. FIB‐SEM‐CT naturally requires complete destruction of the sample. It is also important to consider how segmentation and thresholding of individual materials in the raw 3D data can affect the physical properties listed in Table 1 (see thresholding examples in the Supporting Information). With all three techniques, the prevalence of grey areas in the images represent partial volume effects, where the interface between np‐Au and pores occurs below the spatial resolution limit. 3D image segmentation is required to deal with these partial volume effects by undersampling or oversampling the different materials. For example, as already noted for FIB‐SEM‐CT, the presence of shine‐through artefacts and the measurement of sequential surface information can lead to oversampling of material, and by inverse, undersampling of pores. On the other hand, while PXCT showed the highest contrast between material interface regions, manual thresholding is still likely to be biased by the user, in this case towards undersampling of np‐Au and subsequently oversampling of pores, as shown in Table 1. This demonstrates the fact that spatial resolution remains a critical factor in the quality of any imaging technique, and that both technique and sample should be carefully selected based on the size range of the features of interest.

Aside from investigating the 3D morphology of CeO_x/np‐Au, a deeper study of the pore network itself and the structural composition (e.g. presence of ceria) are also relevant in terms of the catalytic properties of the materials.8, 11 Therefore porosity (%), pore volume (V _p/ m³ g⁻¹) and effective surface area (S.A./ m² g⁻¹) of CeO_x/np‐Au were calculated for each of the three techniques, the results are shown in Table 2. In this case, “Volume” refers to the sum of discrete voxels segmented and labelled as either “CeO_x/np‐Au” or “pores”, “Area” refers to the total surface of these segmented materials, ′S.A.′ considers the total catalytically active surface present as a function of the sample mass, and ′V_p′ the cumulative pore volume as a function of the sample mass. Effective surface area and pore volumes or diameters are typically calculated for catalyst samples through BET analysis or other gas adsorption techniques.21 Since the elemental composition (TEM‐EDX analysis) and density of CeO₂/np‐Au are known, and the sample volume can be directly obtained through nanotomography, the effective surface area in this case can be considered a directly quantifiable measurement, in comparison to the bulk or average values normally obtained through porosimetry techniques (see the Supporting Information).

Table 2.

Calculated physical properties of CeO₂/np‐Au following tomographic label analysis.

Method	Sample	CeOx/npAu				Pore			Porosity
		Volume	Area	S.A.		Volume	Area	V p	[%]
		[μm3]	[μm2]	[m2 g−1]		[μm3]	[μm2]	[m3 g−1]
PXCT	Total	205.6	7498	2.06		304	7718	0.083	60
	Sub‐V 1	0.05	2.94	3.3		0.079	3.25	0.089	61
	Sub‐V 2	0.043	2.49	3.3		0.087	2.8	0.115	67
	Sub‐V 3	0.047	1.98	2.41		0.083	2.22	0.101	64
	Sub‐V 4	0.052	2.13	2.32		0.078	2.45	0.085	60
	Sub‐V average	0.048	2.39	2.83		0.082	2.68	0.098	63
	Sub‐V error[a]	±0.015	±0.02	–		±0.015	±0.02	–	–
FIB‐SEM‐CT	Total	190.4	5265	1.56		123.8	5425	0.037	39
	Sub‐V 1	0.089	2.85	1.81		0.039	2.21	0.025	31
	Sub‐V 2	0.083	2.99	2.03		0.045	2.47	0.031	35
	Sub‐V 3	0.081	2.99	2.09		0.047	2.54	0.033	37
	Sub‐V 4	0.09	3.55	2.22		0.038	3.07	0.024	30
	Sub‐V average	0.086	3.1	2.04		0.042	2.57	0.028	33
	Sub‐V error[a]	±0.015	±0.02	–		±0.015	±0.02	–	–
ET	Total	0.998	53.85	3.043		1.104	62.77	0.062	52.5

[a] Based on uncertainty of 20 nm (i.e. approx. 1 pixel) propagated in 2D (μm²) and 3D (μm³).

Aside from the bulk volume, several subvolumes were extracted from PXCT and FIB‐SEM‐CT volume renderings and their properties calculated in the same manner to provide a statistically robust analysis. An illustration of the subvolume selection is shown in Figure 5. Subvolume analysis was not performed for ET due to the smaller probed volume.

Figure 5.

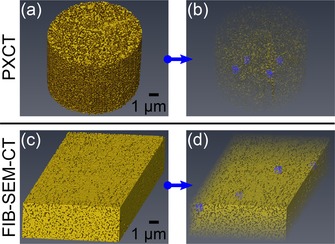
Subvolume extraction showing: (a) PXCT data and (b) selection of four PXCT subvolumes; (c) FIB‐SEM‐CT data and (d) selection of four FIB‐SEM‐CT subvolumes. All subvolumes had dimensions of 500×500×500 nm³ and are highlighted in blue, volumes (b) and (d) rendered with transparency.

For each nanotomography technique, the sum of the volume of CeO_x/npAu and pores indicated in Table 2 was found to be proportional to the probed volume (Table 1), indicating the validity of the voxel counting method. The relevant ratio of material to pores present was indicated by percentage porosity. In this case, PXCT and ET both recorded porosity values close to the range expected in literature (e.g. 60 to 80 %).50, 51 This is interesting considering that the large cylindrical sample for PXCT may be considered more representative of the bulk monolithic gold structure, in comparison to the thin lamella prepared for ET. The porosity calculated by FIB‐SEM‐CT was unusually low and reflects the differences observed previously when measuring ligament and pore sizes (Figure 4). Again this is proposed to be due to the damaging effects of the ion beam which was more extensively used during sample preparation for FIB‐SEM‐CT. Moreover, in comparison to experimental results from previous works,11, 50 it should be noted that the calculated effective surface area values from all three techniques (including subvolumes) were within 1.6 to 3.3 m² g⁻¹, below the minimum value of the range previously reported for a pure np‐Au sample of similar composition (4 m² g⁻¹). This can be explained by considering the relationship between ligament size and surface area, which is known to be inversely proportional.43 The results are therefore in line with the observed porosity, which was close to the minimum expected value of 60 %, therefore indicating larger ligament sizes and subsequently surface area towards the lower end of the scale. It is however critical to reflect that the accuracy of surface area measurements is limited by the spatial resolution. While ET was capable of visualising microporosity, both PXCT and FIB‐SEM‐CT were limited to meso‐ and macroporosity. This is not the case during pore volume analysis by gas adsorption isotherms such as with N₂, which is capable of entering pores well below the resolution limit of PXCT and FIB‐SEM. In general, the subvolume analysis served to highlight minor heterogeneities in the sample, particularly regarding the measured surface area. Apart from statistical variation, this further indicates the presence of some coarsened ligaments.

It is also important to consider possibilities for the detection of ceria within the np‐Au pore network. Ceria and other additives such as titania are known to exert a stabilising effect against sintering and pore collapse, which is relevant given the potential application of np‐Au in catalysis at elevated temperatures.11, 19 In this study, ceria was observed and quantified on a thin lamella via TEM‐EDX mapping during electron microscopy measurements. Similar measurements are likewise possible during FIB‐SEM‐CT. However, observation of metal oxide additives using PXCT would be particularly advantageous, given the extended sample volume and non‐destructive measurement characteristics compared to ET or FIB‐SEM‐CT. As noted previously, the presence of partial volume effects or grey areas was widespread in the images obtained from all three techniques (see histogram data in Supplementary Information). Given that ceria should physically appear at the interface between gold and air, this complicates the direct visualisation of ceria, since the contrast gradients observed may signify a gold‐air, gold‐ceria or ceria‐air interface, or indeed all three. However, PXCT is sensitive to the local electron density of the sample per voxel, and can therefore be used to provide a quantitative assessment of voxels which may contain ceria.52 Figure 6 therefore shows an orthographic slice of the sample following ptychographic and tomographic reconstruction with quantified electron density, and the corresponding histogram values obtained for the complete volume. The electron densities of gold (4.68 Å⁻³) and cerium (IV) oxide (1.87 Å⁻³) were calculated based on their mass densities, here taken as 19.32 g cm⁻³ and 7.22 g cm⁻³, respectively. The electron density of air present in the pores was assumed to be zero, while the sample exterior was excluded from the histogram. It should be noted that in Figure 6 the two peaks observed at around 0.3 and 4 Å⁻³ deviated slightly from the calculated electron density values of air and gold. This further indicates the appearance of partial volume effects resulting from unresolved nanoporosity. Due to the presence of ceria as a minority component and both the mass and electron density of cerium(IV) oxide lying between that of gold and air, it was therefore difficult to definitively visualise ceria with the data quality obtained. Despite this limitation, the accurate visualisation of ceria by PXCT is also technically feasible through use of resonant phase contrast imaging around the Ce L₃ absorption edge (5.72 keV), as demonstrated in the literature for identification of gold and cobalt species,29, 53 and more recently for analysis of ceria density and oxidation state in automotive catalysts.54 As an outlook, while the presence of ceria during PXCT measurements may be indicated by contrast difference in the PXCT images, identification was hindered by the small particle size close to the spatial resolution limit (approximately 10 to 30 nm), and the associated occurrence of partial volume effects also resulting from the gold to pore interface. Definitive observation and quantification of ceria is a challenge which may be addressed using on‐off resonant ptychographic imaging or complementary X‐ray fluorescence nanotomography.

Figure 6.

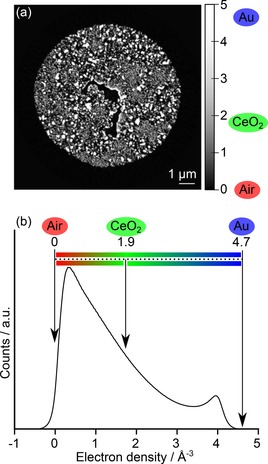
Quantitative electron density of the CeO_x/np‐Au sample visualised as: (a) orthographic slice through the 3D volume with pixel values converted to electron density; (b) the corresponding histogram of the 3D volume following background removal, showing the ideal positions of pure gold, pure ceria and air. Image background was excluded from the electron density counts.

In summary, the close agreement of pore characteristics obtained via nanotomography with those obtained via physical methods confirms the validity of tomographic rendering as a method of interpreting pore characteristics. The central advantage of all nanotomography techniques however may be regarded as the ability to visualise the pore network in 3D space, rather than just obtaining numerical values. Nanotomography should be considered a feasible approach to assist with modelling of porosity in heterogeneous catalysis, and the associated effects which depend on porosity, such as adsorption, diffusion and mass transport for example. In terms of spatial resolution, electron‐based imaging techniques clearly offer superior performance down to the low nm and atomic scale, while PXCT is currently limited to the range of mesoporous features. In addition, data processing workflows for FIB‐SEM‐CT and ET data are often possible using commercial software. PXCT in contrast is a developing method and is comparatively more difficult to access via the synchrotron, while data processing is more complex and requires significant graphical computing resources. However, despite the advantage in spatial resolution and accessibility, both FIB‐SEM‐CT and ET involved destruction of the sample, or preparation of thin lamella, respectively. From this perspective, PXCT in particular is highlighted as a powerful technique due to the ability to measure extended sample volumes non‐invasively. The spatial resolution of hard X‐ray PXCT is uniquely high among X‐ray microscopy methods, and is expected to further improve with ongoing research into optics, detectors and the advent of fourth generation synchrotron light sources. Likewise the total acquisition time for PXCT volumes can be expected to improve potentially by orders of magnitude. In future this will allow either much larger sample volumes to be measured by PXCT, or an increase in spatial resolution for smaller samples, additionally reducing the measurement times to be more in line with modern ET and FIB‐SEM instruments.47 For example, here collection of ET and FIB‐SEM‐CT tomograms took between 30 mins and 6 hours, while PXCT took around 15 hours. In this study PXCT demonstrated the highest resolution currently published for a heterogeneous catalyst sample, providing detailed information about sample porosity, volume fraction and composition in a non‐invasive manner. Moreover, PXCT offers the best potential for further analysis via in situ studies or sequential post‐mortem analysis of catalyst volumes after thermal annealing, for example. This is significantly easier using X‐rays due to flexible range of environmental conditions which may be applied, which are in general not feasible in high vacuum setups for conventional electron microscopy.

Conclusions

Three diverse and complementary nanotomography techniques are presented for 3D analysis of a hierarchically‐porous np‐Au catalyst body. The volume renderings obtained were used to calculate physical properties relevant to catalysis, including information on the pore structure, surface area and volume fraction, along with pore network topology. Considering spatial resolution, non‐invasive sample preparation, and representative nature of the sample structure, PXCT is highlighted as a unique tool for analysis of heterogeneous catalyst samples, by giving access to the meso‐ and macroporous structure of extended sample volumes in a completely non‐invasive manner. This makes PXCT an excellent complement to electron microscopy. Future studies should focus on improving the visualisation of elemental composition and particularly the speciation of ceria additives, for example through resonant phase imaging or complementary fluorescence nanotomography. The potential to measure under in situ conditions along with post mortem analysis of identical sample volumes should also be explored.

Experimental Section

Sample preparation

CeO_x/np‐Au catalyst (4.2 wt %) was prepared by dealloying of an Ag–Au composite, followed by wet impregnation with a ceria precursor solution using the method described in a previous publication.11 A piece of CeO_x/np‐Au was placed on an SEM sample holder stub, then cut and shaped with a Ga⁺ ion beam using a FIB Strata 400S (FEI, USA) to meet the sample requirements for ET and PXCT (see below). The remaining sample on the stub was retained for FIB‐SEM‐CT. A detailed description and illustration of the sample preparation steps can be found in the Supporting Information.

Ptychographic X‐ray computed tomography (PXCT)

For PXCT a cylindrical CeO_x/np‐Au sample (10 μm diameter and 30 μm height) was produced by FIB milling and deposited on an OMNY pin.48 PXCT measurements were carried out at the coherent small angle X‐ray scattering (cSAXS) beamline of the Swiss Light Source at the Paul Scherrer Institute (Villigen, Switzerland), using the flexible tomography nanoimaging endstation (flOMNI), which operates in air and at room temperature.55, 56 In this instrument, differential laser interferometry is used for high‐accuracy positioning of the sample with respect to the illuminating optics.57 The coherent X‐ray illumination onto the sample was determined using an Au‐made Fresnel zone plate (FZP) of 120 μm diameter, a focal length of 50.54 mm, and X‐ray photon energy of 8.7 keV, providing a flux of about 1.4×10⁸ photons s⁻¹. The sample was placed 1 mm downstream from the focus, with illumination diameter on the sample of about 3 μm. Coherent diffraction patterns were recorded using a Pilatus 2 m detector with 172 μm pixel size positioned 7.399 m downstream from the sample.58 A sample field of view of 14×8 μm² (h*v) was recorded per projection with an average distance between points of 0.8 μm which were following a Fermat spiral trajectory.59 The scan was repeated with angular positions ranging from 0 to 180° of the specimen with respect to the incoming X‐ray beam, with a total of 900 equal angular steps. Each individual measurement point had an acquisition time of 0.1 s, leading to a total acquisition time of approximately 15 h for one complete tomogram, including dead time in between acquisitions during sample movements. Ptychographic reconstructions were performed directly after acquisition using the difference map algorithm followed by maximum likelihood optimization as a refinement step.60, 61 Each pair of scans was recorded at different angles and at different positions of the detector and were then combined in the same reconstruction, where two different images could be reconstructed under the same illumination, as introduced in previous work.56 An area of 460×460 detector pixels was used in the ptychographic reconstructions to obtain reconstructed images with a pixel size of 13.32 nm. The phase contrast images were then further processed to correct zero‐ and first‐order terms and were registered in the vertical and horizontal direction.62 The half‐period spatial resolution of the resulting images was estimated to be around 23 nm via Fourier shell correlation of two sub‐tomograms, where each of them was computed with half of the angular projections, using the half‐bit threshold criterion (see Supporting Information).49 The total estimated dose imparted on the specimen for data acquisition was about 8.28×10⁸ Gy.

FIB‐SEM slice and view tomography (FIB‐SEM‐CT)

A piece of CeO_x/np‐Au was placed on a standard SEM sample holder stub. FIB‐SEM slice and view measurements were conducted at the Laboratory of Electron Microscopy (LEM) at Karlsruhe Institute of Technology (Karlsruhe, Germany), using an EsB 1540 dual‐beam FIB‐SEM (Zeiss, Germany) equipped with an external Raith Elphy Plus pattern generator. The sample was placed at a eucentric height, allowing the imaging plane to be scanned with the electron beam under an angle of 54° without changing sample position. A Ga⁺ beam with 30 kV voltage and 0.5 to 10 nA current was used to expose a rectangular prism shaped sample with 8.47 μm width (x direction) and 10.80 μm height (y direction). Slice and view imaging was then performed by sequential Ga⁺ beam erosion of thin layers in z direction with around 15 nm slice thickness, slice width of 14.95 μm, and 50 pA current. In‐lens secondary electron imaging was used to produce a surface map of each exposed slice. During image acquisition, the imaging plane moved stepwise in z direction from the sequential ion‐milling, which eventually resulted in 950 images with a pixel size of 12.78 nm and an effective spatial resolution of around 15–45 nm.

Electron tomography (ET)

For ET a lamella of CeO_x/np‐Au (<300 nm thickness) was produced by FIB milling and attached to a lift‐out grid. Electron tomography measurement was performed using a Fischione tomography holder, on a Titan 80–300 (FEI) microscope operated at an acceleration voltage of 300 kV in STEM mode, at the Institute of Nanotechnology (INT) at Karlsruhe Institute of Technology (Karlsruhe, Germany). The tilt series of high‐angle annular dark‐field (HAADF) STEM images were collected with the Xplore3D software (FEI) over a tilt range of ±60°, with tilt increment of 2°. Alignment of the tilt series was performed in IMOD software using the cross‐correlation function. The aligned tilt series were reconstructed using the Simultaneous Iterative Reconstruction Technique (SIRT) with the Inspect3D software (FEI) and the resultant reconstructed tomogram had a final voxel size of 1.3 nm.

1. D volume rendering and quantitative analysis

Reconstructed data was rendered using the software package Avizo 9.3 (FEI Company). A full description of all image processing and manipulation steps is given in the Supporting Information.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

Supplementary

Supplementary

Y. Fam, T. L. Sheppard, A. Diaz, T. Scherer, M. Holler, W. Wang, D. Wang, P. Brenner, A. Wittstock, J.-D. Grunwaldt, ChemCatChem 2018, 10, 2858.