Weibull regression with Bayesian variable selection to identify prognostic tumour markers of breast cancer survival

Abstract

As data-rich medical datasets are becoming routinely collected, there is a growing demand for regression methodology that facilitates variable selection over a large number of predictors. Bayesian variable selection algorithms offer an attractive solution, whereby a sparsity inducing prior allows inclusion of sets of predictors simultaneously, leading to adjusted effect estimates and inference of which covariates are most important. We present a new implementation of Bayesian variable selection, based on a Reversible Jump MCMC algorithm, for survival analysis under the Weibull regression model. A realistic simulation study is presented comparing against an alternative LASSO-based variable selection strategy in datasets of up to 20,000 covariates. Across half the scenarios, our new method achieved identical sensitivity and specificity to the LASSO strategy, and a marginal improvement otherwise. Runtimes were comparable for both approaches, taking approximately a day for 20,000 covariates. Subsequently, we present a real data application in which 119 protein-based markers are explored for association with breast cancer survival in a case cohort of 2287 patients with oestrogen receptor-positive disease. Evidence was found for three independent prognostic tumour markers of survival, one of which is novel. Our new approach demonstrated the best specificity.

1. Introduction

As large data-rich studies are becoming routinely collected in medical research, there is a growing need for regression techniques designed to cope with many predictors. While the simplest approach is to analyse each variable one at a time, the results are difficult to interpret since confounding from between-predictor associations can cloud the location of true signals leading to elevated false-positive rates. Ideally, when predictors are correlated, multivariate regression should be performed to account for the association structure and enable accurate inference on the subset of variables most likely to represent true effects. However, when the number of covariates is high, traditional Ordinary Least Squares methods suffer from over-fitting – the limited information available is spread too thinly among the covariates leading to unstable parameter estimates with high standard errors.

This inspired the development of LASSO penalised regression by Tibshirani¹ in 1996 whereby a penalty term is included in the likelihood to encourage sparsity. The penalty term modifies the likelihood of the regression coefficients, with a large penalty leading to the exclusion of many variables. Typically, the penalty is tuned through cross-validation such that covariates with negligible predictive effects are removed. The over-fitting problem is thus avoided and prediction improved. Over the years, there have been a number of extensions to the original method, including SCAD,² Elastic Net,³ Adaptive LASSO⁴ and Fused LASSO,⁵ each generating a class of penalties to address specific predictive aims. Some of these methods have been applied in the genomic context to explore multi-SNP models of disease^6,7 or to search for master predictors.⁸ Bayesian versions of the LASSO have been described^9,10 and used for efficient variable selection in genetics. In particular, see Tachmazidou et al.¹¹ for a survival modelling implementation. Extensions of the LASSO framework to model structured sparsity via the group LASSO¹² or to impose additional hierarchical constraints, e.g. when searching for interactions¹³ have also been proposed. Furthermore, techniques have been developed to obtain significance measures for covariates under LASSO regression, including resampling procedures^14,15 and, recently, a formal significance test,^16,17 as well as a modified bootstrap procedure that provides a valid approximation to the LASSO distribution thereby enabling construction of uncertainty intervals.¹⁸

An alternative to penalised regression is Bayesian sparse regression, in which posterior inference is made on the predictors, and subsets of predictors, most likely associated with outcome. Attractive features of Bayesian sparse regression include inference of posterior probabilities for each predictor, posterior inference on the model space and, perhaps most importantly, the possibility of natural incorporation of prior information into the analysis. A variety of formulations and methods for implementing Bayesian variable selection have been developed. George and McCulloch¹⁹ first proposed inducing sparsity via two-component ‘spike and slab’ mixture priors on the effect of each covariate, consisting of a ‘spike’ either exactly at or around zero, corresponding to exclusion from the model, and a flat ‘slab’ elsewhere. Binary indicator variables are used to denote which component each covariate belongs to; the posterior expectation of which provides marginal posterior probabilities of effect. Sparsity is encouraged by placing priors on these indicators which favour the ‘spike’. Such models are typically fitted using MCMC and a number of algorithms have been developed, varying in how the spike and slab components are formulated.^19–21 Notably, an adaptive shrinkage approach proposed by Hoti and Sillanpaa eases the computational challenge through use of single component normal priors, with a hyperprior on the precision that leads to an approximate spike and slab shape, thereby avoiding the use of indicator variables and mixture component switching. A cut-off on the magnitude of effect is used to define whether or not a covariate is included in the model.²²

Whereas these models implement variable selection through priors on each covariate, an alternative approach is to consider the model space as a whole and place priors on the number of included covariates. In 1995, Green²³ demonstrated how classical MCMC methodology can be extended to explore models of differing dimensions using a ‘Reversible Jump’ algorithm in which the Metropolis-Hastings acceptance ratio is modified to account for addition and deletion of covariates during model updates. The level of sparsity is controlled through a prior on the number of included covariates. Reversible Jump has been applied to model selection problems in many areas, including genomics and in particular genetic association analysis,²⁴ meta-analysis^25,26 and predictive model building^27,28 in which the ability to incorporate prior information has been exploited in various ways.

A drawback of Reversible Jump, however, is that the dimension switching leads to a substantial increase in algorithmic complexity. In the case of linear regression, conjugate closed form expressions under the normal likelihood can be exploited to avoid MCMC sampling of covariate effects, allowing the stochastic search algorithm to focus exclusively on the model space, dramatically simplifying the mixing of the algorithm.²⁹ The ‘Stochastic Shotgun Search’ (SSS) algorithm utilises this principle and, in addition, proposes a modified search algorithm that parallelises the exploration of potentially vast model spaces while focusing on areas of high posterior mass.³⁰ This allows rapid identification of models with high posterior mass, at the cost of ‘formal’ posterior inference since the model search space is deliberately restricted. Alternatively, the ‘Evolutionary Stochastic Search’ (ESS) algorithm, developed by Bottolo and Richardson,³¹ similarly utilises conjugate normality to integrate over covariate effects but allows exploration of the entire model space resulting in formal posterior inference on covariate and model probabilities. Sophisticated and efficient implementations of ESS now exist for the analysis of continuous univariate and multivariate outcomes.^32,33 These procedures are very fast and are capable of analysing thousands of predictors simultaneously. Superior power and specificity in comparison to penalised regression style approaches has been shown, which has facilitated the identification of novel genomic associations.^33,34 For a more detailed overview of approaches to Bayesian variable selection, we refer readers to the excellent review by O’Hara and Sillanpaa.³⁵

The Cox semi-parametric proportional hazards model is the most widely used approach for the analysis of right-censored survival data. Cox regression is semi-parametric in that the baseline hazard is ascribed no particular form and is estimated non-parametrically. Working in the Bayesian framework, however, it was natural to choose a fully parametric survival model for the analysis we present in this paper. Whereas a proportional hazards model assumes that covariates multiply the hazard by some constant, so-called ‘accelerated failure time’ models are a class of (typically fully parametric) survival models in which the covariates are assumed to multiply the expected survival time. Consequently, regression parameter estimates from accelerated failure time models are more robust to omitted covariates.³⁶ The Weibull distribution is an appealing choice for fully parametric survival modelling since, uniquely, it has both the accelerated failure time and the proportional hazards property; there is a direct correspondence between the parameters under the two models.³⁷ Therefore, hazard ratios can be inferred as in Cox regression, but while benefiting from the accelerated failure time property. In comparison to Cox regression, when the baseline hazard function describes the data well, the Weibull model offers greater precision in the estimation of hazard ratios. Conversely, however, the non-parametric nature of the baseline hazard under a Cox model affords robustness over a wider range of survival trajectories.

Unfortunately, in the context of Weibull regression for survival analysis, there are no conjugate results to exploit and so we resort to Reversible Jump MCMC, sampling both regression parameters and models. This is, to our knowledge, the first application of a Reversible Jump algorithm to the Weibull model for survival analysis. After exploring performance in comparison to an alternative frequentist variable selection strategy (penalised Cox regression with stability selection), we present a real data application to explore tumour markers of breast cancer survival in a prospective case cohort. Further details of this study and dataset are given below.

2. Data

Breast cancer remains a significant public health problem with more than 45,000 cases diagnosed in the UK in 2012 and, despite significant improvements over the past 30 years,^38,39 continues to be a major cause of mortality amongst women in the western world. Treatment currently consists of surgical excision of the tumour and adjuvant therapies which may include radiotherapy, endocrine therapy, cytotoxic chemotherapy and targeted biological therapies depending on tumour characteristics and patient preference. However, there is substantial heterogeneity in patient response to these therapies, all of which are associated with significant toxicity. There is now a well-established set of pathological prognostic factors for breast cancer including tumour size and grade, lymph node status, oestrogen receptor (ER) status and Human Epithermal growth factor Receptor 2 (HER2) status^40,41 which are widely used in clinical practice to guide treatment decisions. For example, a patient with excellent prognosis may want to avoid exposing themselves to highly toxic therapies. However, our ability to reliably identify patients who can safely forgo adjuvant chemotherapy is limited, impairing optimal clinical decision making. Breast cancer is now known to consist of a variety of molecular subtypes,⁴² and while these tools are of profound clinical utility, there is much scope to expand on this set of prognostic risk factors which do not currently reflect the whole variety of breast cancer leading to suboptimal clinical decisions, particularly the over-prescription of adjuvant chemotherapy.⁴³

We explore a large collection of predominantly protein-based markers related to cancer biology including markers of cancer stem cells and the tumour microenvironment, which may underpin the molecular diversity of tumours.^42,44,45 Our analysis is performed using cases from the ongoing population-based breast cancer cohort of the SEARCH (studies of epidemiology and risk factors in cancer heredity) study; a genetic epidemiology study with a molecular pathology component recruiting individuals resident in the east of England. Ascertainment of breast cancer cases was conducted by the East Anglia Cancer Registry. The study includes both prevalent and incident cases. Prevalent cases are those who were already diagnosed with breast cancer at the time of study commencement. Specifically, these included women diagnosed with invasive breast cancer under the age of 55 between 1991 and mid-1996 and still alive in 1996. Incident cases are those individuals diagnosed after study commencement. These were women under the age of 70 at the time of breast cancer diagnosis after mid-1996. The two different ER subtypes of breast cancer (positive and negative) are recognised as markedly different diseases biologically and pathologically with demonstrated differences in baseline hazard over time.⁴⁶ Therefore, it is sensible to stratify on this characteristic in survival analyses of breast cancer, rather than pool the two conditions, since prognostic markers and effects are expected to differ. In this work, we restrict our analysis to the 2287 ER-positive cases, the larger of the two strata. Follow up work is planned to analyse the ER-negative cases. The SEARCH study is approved by the Cambridgeshire 4 Research Ethics Committee; all participants provided written informed consent.

All analyses modelled breast cancer specific mortality, with survival times left truncated at 10 years. This period was chosen since decisions relating to adjuvant therapy are often taken according to a time horizon of 10 years. Eleven per cent of women suffered breast cancer-specific mortality during this follow-up, among whom the median survival time from baseline was five years. Forty-four per cent of women whose survival times were censored have not yet been followed up for 10 years – the median follow-up time among these women is seven and a half years. Data were available for the following known prognostic risk factors: tumour size and grade, number of positive lymph nodes, HER2 status, use of chemotherapy and hormone therapy, and whether the patient was screen detected (suggesting the cancer was caught at an early stage though screening status is associated with improved outcome independent of stage⁴⁷). These covariates were adjusted for in all analyses. Metastasis is clearly also important for breast cancer prognosis; however, since very few women in SEARCH had metastatic breast cancer at baseline (18/2287), we excluded it from the models to avoid convergence issues. A sensitivity analysis including metastasis showed no change to the results presented in this paper.

2.1. Tumour markers

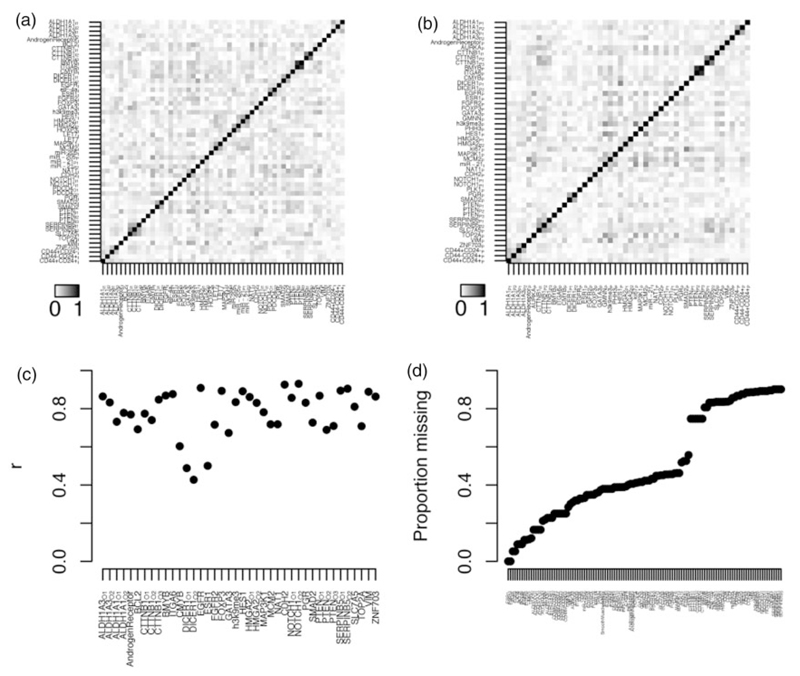
Expression of a particular protein will naturally vary between people, and at different locations in the body, including within tumours. In this experiment, we sought to ascertain expression levels of 73 pre-selected proteins in tumour samples taken at diagnosis (i.e. baseline) using a technique known as immunohistochemistry. Tumour samples were stained with commercially available antibodies which produce a coloration, observable under a microscope, on contact with the protein of interest. Experts scored the stained tumour samples for the proportion of coloured cells in the biopsy (i.e. expressing the protein) on a four-point scale, and for the average intensity of that colour on a six-point scale. In total, intensity scores were taken for 51 proteins, and proportion scores for 45, and both were available for the three CSC markers. In addition, expression of various markers of immune infiltration, including CD8 and FOXP3, were measured in tumour-associated lymphocytes. In situ hybridisation methods for the detection of micro RNAs were implemented as previously described.⁴⁸ In total, 119 tumour markers were available for exploration for association with breast cancer survival. Correlations among the various tumour markers are shown in Figure 1(a) and (b). Unsurprisingly, the two types of scoring (intensities and proportions of expression) are generally strongly correlated when measured for the same protein (Figure 1(c)). Unfortunately, there was substantial missingness among the tumour markers – see Figure 1(d) – with most missing for more than half the patients. There are two main reasons for missingness; by design and technical. Since the amount of biological material available for evaluation of novel tumour markers is limited, it was important to prioritise. Proteins were initially evaluated in a pilot study using only a subset of the available material. Based on preliminary analyses, a judgment was taken whether to proceed to include all available material; hence, in some instances only the data generated as part of the pilot study are available (the tumour markers with >70% missingness). The technical causes of missing data include biological variability, e.g. differences in tumour size, and dropout of samples during processing. This is a well-known unavoidable problem when tissue-microarrays (TMAs)⁴⁹ are used to evaluate large numbers of tumours. Fortunately, the correlation among the tumour markers (Figure 1(a)–(c)) enabled imputation of missing values – a description of how this was conducted, and how the multiply imputed datasets were analysed is given below in the methods.

Figure 1.

Tumour marker correlation structure and missingness. (a) A heatmap representing pairwise Pearson correlation statistics among the various immunohistochemistry (IHC) intensity score tumour markers. (b) A heatmap representing pairwise Pearson correlation statistics among the various IHC proportion score tumour markers. (c) Pearson correlation statistics between IHC intensity and proportion scores for those proteins where both were measured. (d) Proportion of missing values for each tumour marker in the analysis population.

3. Methods

3.1. The Weibull regression model

As noted above, we utilise the Weibull model to develop our sparse Bayesian regression framework for survival analysis. It is instructive to start with a description of the simpler exponential survival model, which the Weibull model extends. Under the exponential model, a patient i’s hazard at time t is modelled as dependent on some P covariate values, denoted by vector x_i, through an exponential link which ensures positivity of the hazard

$${\lambda }_i(t)=e^{\alpha +{\mathit{\text{x}}}_i\mathit{\beta }}={\lambda }_i$$ (1)

where β is a P-length vector of covariate effects, and α denotes an intercept term. Note the lack of dependency on time in equation (1) – under the exponential model, the hazard is assumed constant over time. The corresponding survival function, is straight forward to derive as

$$S(t)=e^{(-{\int }_0^t{\lambda }_i\text{dx})}=e^{-t{\lambda }_i}$$

The assumption that hazard does not depend on time is likely to be overly simplistic for most real world scenarios. The Weibull model extends the exponential model by modifying the survival function with a parameter k as follows:

$$S(t)=e^{{(-t{\lambda }_i)}^k}$$

k > 0, known as the Weibull ‘shape’ parameter, induces a dependency between the hazard and time:

$$\lambda (t)=-\frac{d}{dt}\mathit{\text{log}}(S(t))={\lambda }_{i}k{({\lambda }_{i}t)}^{k-1}$$

If k > 1 the baseline hazard function increases as time progresses, but if k < 1 the hazard decreases.

3.1.1. Likelihood

Let vector t contain the observed survival times of n patients. Typically, a study will not run long enough to observe whether the event occurs for each and every patient, resulting in so-called ‘right-censored’ data. That is, for some patients, we only know their minimum survival time. Therefore, we also introduce an n-length vector of binary indicators d to capture, for each patient i, whether the event was observed during their follow up (in which case d_i = 1), or they were censored, in which case d_i = 0. If the event was observed for patient i (and d_i = 1), then t_i denotes their time to event. Otherwise, t_i denotes their length of follow up. The log-likelihood for parameters α, β and k can be derived as

$$\text{log}(L(\alpha ,\mathit{\beta },k|\mathit{\text{t}},\mathit{\text{X}}))={\displaystyle \sum _{i=1}^n{d}_i\left[\text{log}(k)+k\text{log}({\lambda }_i)+(k-1)\text{log}(t_i)\right]}+{(-t_i{\lambda }_i)}^k$$ (2)

where λ_i is defined in equation (1).

3.2. Sparse Bayesian Weilbull regression

We present a full Reversible Jump MCMC algorithm for fitting Weibull survival models, in order to perform variable selection among the tumour markers. Henceforth, we will refer to this framework, described below, as SBWR (Sparse Bayesian Weibull Regression).

We start by noting that baseline variables age, whether the patient was detected via a screening programme, chemotherapy treatment, hormone therapy, the number of positive lymph nodes and tumour size were excluded from the model selection framework and fixed to be included in the model at all times. Let vector δ denote the log-hazard ratios associated with these ‘fixed effects’, and vector z_i denote the corresponding covariate values for patient i. Going forward, vector x_i will be used to denote patient i’s tumour marker covariates only, and vector β the tumour marker log hazard ratios. P, the length of β therefore now denotes the number of tumour markers we wish to perform variable selection over. Under Reversible Jump, variable selection is facilitated by placing a prior density on β which depends on a latent binary vector γ = (γ₁, … , γ_P) of indices indicating whether each covariate is included in the model. For covariate p, γ_p = 1 indicates inclusion in the model and therefore that β_p ≠ 0. Conditional on the latent variable γ, i.e. that a specific selection of tumour markers are included in the model, patient i’s hazard may now be written as

$${\lambda }_i|\mathit{\gamma }=e^{\alpha +{\mathit{\text{z}}}_i\mathit{\delta }+{\mathit{\text{x}}}_{i,\gamma }{\mathit{\beta }}_{\gamma }}$$

where vector β_γ contains only the non-zero elements of β, and vector x_i,γ contains patient i’s corresponding subset of covariate values. The non-zero coefficients are assigned independent normal priors centred on 0, with a common variance ${\sigma }_{\beta }^2$

$$p({\beta }_p|{\gamma }_p=1,{\sigma }_{\beta })=N(0,{\sigma }_{\beta }^2)\text{for}p=1,\dots ,P$$ (3)

Rather than fixing σ_β, which controls the magnitude of included effects and therefore can have an important impact on the efficiency of the algorithm, we use a flexible hyper-prior to allow adaption to the data at hand. We start by noting that all tumour marker covariates were normalised prior to analysis, so that (during modelling) all hazard ratios correspond to a standard deviation increase in the underlying variable. We chose a relatively informative Uniform(0,2) prior for σ_β. This has an expectation/median at 1, which would correspond to a prior with a 95% credible interval supporting hazard ratios between 0.14 and 7.12. However, this choice equally supports much smaller values of σ_β, (which would result in more pessimistic priors) as well as values up to the maximum of 2, which corresponds to a prior with a 95% credible interval supporting hazard ratios between 0.02 and 50.9 – well outside the range we realistically expect to observe. The ‘fixed effects’ δ were ascribed weakly informative fixed N(0, 100) priors rather than the hierarchical priors in equation (3). Since these covariates have well-established associations with breast cancer survival, they clearly do not have exchangeable effects a priori with the tumour markers, and so should not contribute to estimation of ${\sigma }_{\beta }^2.$

The model selection framework is completed by choosing a prior for γ, the selection of tumour markers included in the model. We used a beta-binomial prior as described by Kohn et al.⁵⁰

$$p(\mathit{\gamma })={\displaystyle \int p(\mathit{\gamma }|\omega )p(\omega )}\text{d}\omega =\frac{\mathit{\text{B}}(p_{\gamma }+a_{\omega },\mathit{\text{P}}-p_{\gamma }+b_{\omega })}{\mathit{\text{B}}(a_{\omega },b_{\omega })}$$ (4)

where B is the beta function and p_γ is the number of non-zero elements in γ. Formally, p_γ = γ^TI_P where I_P is the P × P identify matrix. Conceptually, ω denotes the underlying probability that each covariate has a non-zero effect, i.e. is included in γ. Conditional on ω, all models of the same dimension are assumed, under this setup, equally likely a priori. a_ω and b_ω parameterise a beta hyper-prior on ω. Since all tumour characteristics considered here were carefully selected for possible involvement in disease pathology, we set a_ω = 1 and b_ω = 4 which results in a prior on the probability of a true effect centred at 20%. Note, however, that this is only weakly informative due to the modest magnitudes of a_ω and b_ω relative to the number of tumour markers being analysed; ω should largely be learned from the data.

Finally, we must specify priors for the intercept α and the Weibull shape parameter k. In the spirit of Abrams et al.,⁵¹ who provide a detailed discussion of fitting Weibull models in the Bayesian framework, we place normal priors with very large variance on α and on log(k) (the log scale is used to ensure k > 0) which approximate ‘reference’ uniform priors over the entire real line;

$$\begin{array}{c}p(\alpha )=N(0,{10}^6)\\ p(\mathit{\text{log}}(k))=N(0,{10}^6)\end{array}$$

3.3. Model fitting

As noted above, we cannot calculate the posterior of such a model analytically and so use Reversible Jump MCMC to sample from the required posterior.²³ The Reversible Jump sampling scheme starts at an initial model and corresponding set of parameter values, denote these γ(0) and θ(0), respectively. To sample the next model and set of parameters, which we denote γ(1) and θ(1), we propose moving from the current state to another model and/or set of parameter values, γ* and θ*, by using a proposal function q(γ*, θ*| γ, θ). We then accept these proposed values as the next sample with probability equal to the Metropolis-Hastings ratio:

$$MHR=\frac{P(D|{\mathit{\gamma }}^{*},{\mathit{\theta }}^{*})p({\mathit{\theta }}^{*}|{\mathit{\gamma }}^{*})p({\mathit{\gamma }}^{*})}{P(D|\mathit{\gamma },\mathit{\theta })p(\mathit{\theta }|\mathit{\gamma })p(\mathit{\gamma })}\times \frac{q(\mathit{\gamma },\mathit{\theta }|{\mathit{\gamma }}^{*},{\mathit{\theta }}^{*})}{q({\mathit{\gamma }}^{*},{\mathit{\theta }}^{*}|\mathit{\gamma },\mathit{\theta })}$$

where D is the data, P(D|.) is the Weibull likelihood function described in equation (2), p(θ| γ) is the prior distribution of the parameters conditional on (that is, included in) the model and p(γ) is the model space prior defined in equation (4). Therefore, the proposed model and new parameter values are accepted with a probability proportional to their likelihood and prior. If this new set of values is accepted, the proposed set is accepted as γ(1) and θ(1); otherwise, the sample value remains equal to the current sample value, i.e. γ(1)= γ(0) and θ(1)= θ(0). It can be shown that this produces a sequence of parameter samples that converge to the required posterior distribution.²³ The algorithm was implemented in Java; for technical details, for example, the proposal distributions, we refer readers to the supplementary methods (Available at http://smm.sagepub.com/).

3.4. Post processing

For all SBWR analyses of datasets with 119 covariates, i.e. the SEARCH data and the simulated datasets, the algorithm was run for 1 million iterations, after a burn-in of 1 million iterations, generating samples of all parameters. For the high-dimensional simulated datasets described below, the algorithm was run for 5 million iterations, after a burn-in of 5 million iterations for 10,000 covariates, and 10 million iterations after a burn-in of 10 million iterations for 20,000 covariates. These run lengths were deliberately longer than necessary for convergence, which was assessed using autocorrelation plots of the variable selections (see Supplementary Figure S2), chain plots of parameter values over the RJMCMC iterations (Supplementary Figure S3) and comparison of posterior probabilities obtained using different RJMCMC chains (Supplementary Figure S5). For each tumour marker covariate, complementary output was produced: The marginal posterior probability of inclusion, and the posterior median hazard ratio (and 95% credible interval) conditional on inclusion in the model. Furthermore, we obtain the posterior probability of any particular model, i.e. combination of covariates.

3.5. Multiple imputation for missingness

As noted above, there is substantial missingness among the covariates in the SEARCH breast cancer dataset. Since our algorithm currently cannot handle missingness, we proceeded to impute the missing values prior to analysis using multiple imputation by chained equations (MICE),^52,53 a well-established and popular method of imputing missing data.⁵⁴ The MICE algorithm proceeds as follows. Initially, all missing values are filled in at random. Then, the first covariate with missing values, x₁ say, is regressed on all other covariates (and outcome), restricted to individuals with x₁ observed. The missing x₁ values are then updated with posterior predictive simulations from the resulting fitted model. This process is repeated for each covariate in turn to complete the first ‘cycle’. Subsequently, for each imputed dataset, 10 more ‘cycles’ were run to stabilise results. The entire procedure is then repeated independently M times resulting in a collection of completed datasets, the differences between which reflect uncertainty in the imputed values. We generated 20 imputed datasets in this manner using the STATA package ‘ICE’.⁵⁵ The choice of imputation models fitted for each covariate depends on the nature of its distribution. For the tumour markers, which are measured on an ordered categorical scale, ordinal regression was used to generate their posterior predictive distributions within each ‘cycle’. Likewise, ordinal regression was used for tumour size and grade, and positive lymph nodes. For the binary variables chemotherapy and screen detection, logistic regression was used, and for morphology – an unordered categorical variable – multinomial logistic regression was used.

3.5.1. Bayesian analysis of multiply imputed datasets

To analyse multiply imputed datasets in a Bayesian framework, we follow the approach suggested by Gelman⁵⁶ which is to (i) simulate many draws from the posterior distribution in each imputed dataset and (ii) mix all resulting draws into a single posterior sample. This final ‘super’ posterior therefore reflects the imputation uncertainty due to the heterogeneity among the chain-specific posteriors which have been pooled together.

3.6. Complementary pairs stability selection

In the following sections, we will compare our method against a stability selection strategy utilising penalised regression of the LASSO form.¹ Stability selection was recently popularised by Meinshausen and Buhlmann¹⁴ and aims to improve the selection of variables provided by penalised regression methods by adding a resampling step which involves repeating the variable selection procedure (in our case, LASSO regression) in a large number of datasets randomly sampled from the original. For each subsample analysis, the covariates selected and rejected by LASSO are recorded. ‘Selection probabilities’ are then calculated across the results of all sub-sampled datasets. Intuitively this provides a measure of significance for each covariate since the strongest signals should be more robust to perturbations of the data. Theoretical results have been derived which offer upper bounds on the number of ‘noise’ variables for various thresholds on these selection probabilities, allowing inference of statistically significant predictors.¹⁴ These results were recently improved upon by Shah and Samworth,¹⁵ who propose sub-sampling exactly half the data for each subset analysis and, each time this is done, analysing both halves (i.e. the two complementary pairs) of the partitioned dataset. They provide a novel set of theoretical results to estimate the rate of ‘noise’ variables selected at different thresholds on the resulting selection probabilities. Their method leads to less conservative selections of covariates – a known issue with stability selection.¹⁵

4. Simulation study

In this section, we used simulated data to investigate the performance of SBWR posterior probabilities in identifying true signal variables from noise variables. We compared performance against the selections provided by LASSO Cox regression with the penalty parameter set to the optimum under 10-fold cross-validation, and against the selection probabilities from Lasso Cox regression under Complementary Pairs Stability Selection (CPSS).

4.1. Generation of the simulated data

Initially, simulated datasets were designed to have the same number of patients and covariates as the SEARCH breast cancer dataset, and the same real-life correlation structure as amongst the tumour markers. Hence, the covariate matrix of 119 tumour markers among the 2287 ER-positive patients was used from the SEARCH dataset in each replicate simulated dataset. We chose to ignore the missingness in the real data for the simulation study, simply to avoid the computational burden that would have arisen if multiple imputation chains were analysed for each replicate simulated dataset. Missing covariate values were filled in, arbitrarily, from the first multiple imputation chain.

4.1.1. Generation of simulated survival outcomes

We simulated outcome data according to the Generalized gamma parametric survival model, a flexible framework encompassing four of the commonly used parametric survival models (exponential, Weibull, log-normal and gamma) as special cases.^57,58 In comparison to the Weibull, the Generalized gamma uses an extra parameter to model the hazard function, thus enabling a wider range of survival trajectories to be captured. Using the parameterisation of Prentice,⁵⁷ in terms of three parameters µ, σ and q, the probability density function (PDF) is:

$$f(t)=\frac{\left|q\right|}{\sigma t\Gamma q^{-2}}\mathit{\text{exp}}\left(q^{-2}\left(qw-e^{qw}\right)\right){(q^{-2})}^{q^{-2}}$$

when q ≠ 0 and where w = (log(t) − µ)/σ. When q = 0 the PDF is:

$$f(t)=\frac{1}{\sqrt{2\pi }\sigma t}\mathit{\text{exp}}\left\{-\frac{1}{2{\sigma }^2}{\left(\mathit{\text{log}}\left(t\right)-\mu \right)}^2\right\}$$

When q = 1, the Generalised gamma reduces to the Weibull with k = 1/σ and λ = exp(−µ). For a more detailed description of the Generalized gamma and its relationship with other survival models, we recommend referring to Cox et al.⁵⁸ and Jackson et al.⁵⁹ To capture associations between predictors and outcome, the parameter µ may be substituted for the standard linear predictor. Therefore, to induce associations between the covariates and outcome in the simulated data, we drew survival times from a Generalised gamma distribution with

$$\mu =\alpha +\mathit{\beta }\mathit{\text{X}}$$

where the covariate matrix X is that of the real data from the first imputation chain, and β is a vector of 119 tumour marker effects on survival. Note that the effects in a Generalized gamma model do not correspond to hazard ratios since hazards are no longer proportional under the more complex likelihood. Since, however, the Generalized gamma model has the accelerated failure-time property, they do still correspond to differences in expected survival time. For the covariate effects, β, 12 were randomly selected (approximately 10%) to have ‘true’, i.e. non-zero, effects. This random selection was only carried out once and used for all the simulation scenarios described below. We wished to use realistic effect magnitudes and so assigned these parameters the 12 largest coefficients from one-at-a-time Generalized gamma regressions of each tumour marker in the real data. That is, effect sizes observed in the real data were used, but arbitrarily re-assigned to different covariates. The absolute values of the 12 non-null elements of β ranged from 0.25 to 0.38 (note that all covariates were standardised to have unit variance). To determine realistic values for the remaining parameters α, σ and q, we fitted a Generalized gamma regression model including an intercept term only (i.e. the ‘null’ model) in the real data. The resulting estimates of α, σ and q (3.28, 0.80, and –2.19 respectively) were used in the subsequent simulations. As noted above, the Generalized gamma is equivalent to the Weibull when q = 1. Since we are using q = −2.19, the simulated survival times are not Weibull distributed. This was done on purpose so that the simulation setup does not give an unfair advantage to SBWR, the only of the three methods to use the parametric Weibull likelihood, rather than the semi-parametric Cox likelihood.

Survival times were drawn from a Generalized gamma distribution according to the resulting linear predictor and parameters described above, and truncated at 10 years to mimic the actual SEARCH data. Survival status was set to ‘survived’ where the survival time exceeded 10 years (before truncation), and ‘died’ otherwise. Using the same parameters, survival outcomes were re-drawn 20 times to create 20 replicate simulated datasets of 2287 ‘patients’ each. This process was repeated to generate additional simulated datasets in which the covariate effect sizes used for the simulations were halved to create a harder problem for the regression models, and again setting all covariate effects to zero to examine performance under the null. Generalized gamma simulation draws and regression model fitting was carried out using the excellent R package ‘flexsurv’, developed by Jackson et al.⁵⁹

4.1.2. High-dimensional data simulations

We also expanded the simulation setup to explore the performance of our method in much larger datasets, that is with more covariates than samples. To this end, we duplicated the covariate matrix described above, X, multiple times column-wise (i.e. to add covariates). Each time a duplicate was added, the rows were randomised such that none of the newly added covariates would be co-linear with their counterparts in any other instance of X. This process was repeated until P = 10, 000 and P = 20, 000 covariates were present, resulting in two new high-dimensional covariate matrices with 2287 ‘patients’ each. For clarity, these consist of 119-covariate wide blocks within which the correlation structure is that among the SEARCH tumour markers. Covariates within each block, however, are independent of covariates in all other blocks.

To investigate performance in the so-called ‘needle in a haystack’ setting, outcomes were drawn exactly as above, with the same effects at the same 12 tumour markers (arbitrarily using the first instance of X). All other covariates were assigned null effects such that only 12/10,000 and 12/20,000 covariates had effects in the resulting high-dimensional simulated datasets. As above, outcomes were drawn 20 times, and the process repeated for ‘full size’, ‘half size’ and no effects.

4.2. Analysis of simulated datasets

All simulation analyses were carried out on Intel Xeon E5-2640 2.50 GHz processors.

4.2.1. LASSO penalised Cox regression

Each simulated dataset was analysed using LASSO penalised Cox regression as implemented in the excellent R package ‘glmnet’.⁶⁰ 10-fold cross-validation was used to choose the penalisation coefficient, and the selection of variables at the resulting optimum was recorded. These analyses took less than a minute per replicate for 119 covariates, around 19 minutes for 10,000 covariates and around 28 minutes for 20,000 covariates.

4.2.2. LASSO Penalised Cox Regression with CPSS

Each simulated data set was also analysed using LASSO penalised Cox regression under CPSS. In summary, 50 sets of complementary pairs were used as recommended by Shah and Samworth.¹⁵ For each of the resulting 100 sub-datasets, as above, the LASSO penalisation coefficient was optimised under 10-fold cross-validation. The resulting covariate selection probabilities were recorded. These took about 3 minutes per replicate for 119 covariates, around 18 hours for 10,000 covariates and around 25 hours for 20,000 covariates.

4.2.3. Sparse Bayesian Weilbull regression

For the simulations, we assumed a complete lack of prior information and set a = 1 and b = 1 in the beta-binomial prior on model space. This corresponds to a naive, weakly informative, uniform prior on the probability for a covariate to be truly causal. For the analysis of datasets with 119 covariates, 2 million RJMCMC iterations were run which took around 1 hour/replicate. For analyses of datasets with 10,000 covariates, 10 million iterations were run (about 9 hours/replicate), and for the datasets with 20,000 covariates, 20 million iterations were run (about 28 hours/replicate).

4.3. Receiver operator characteristic analysis for selection of true effects

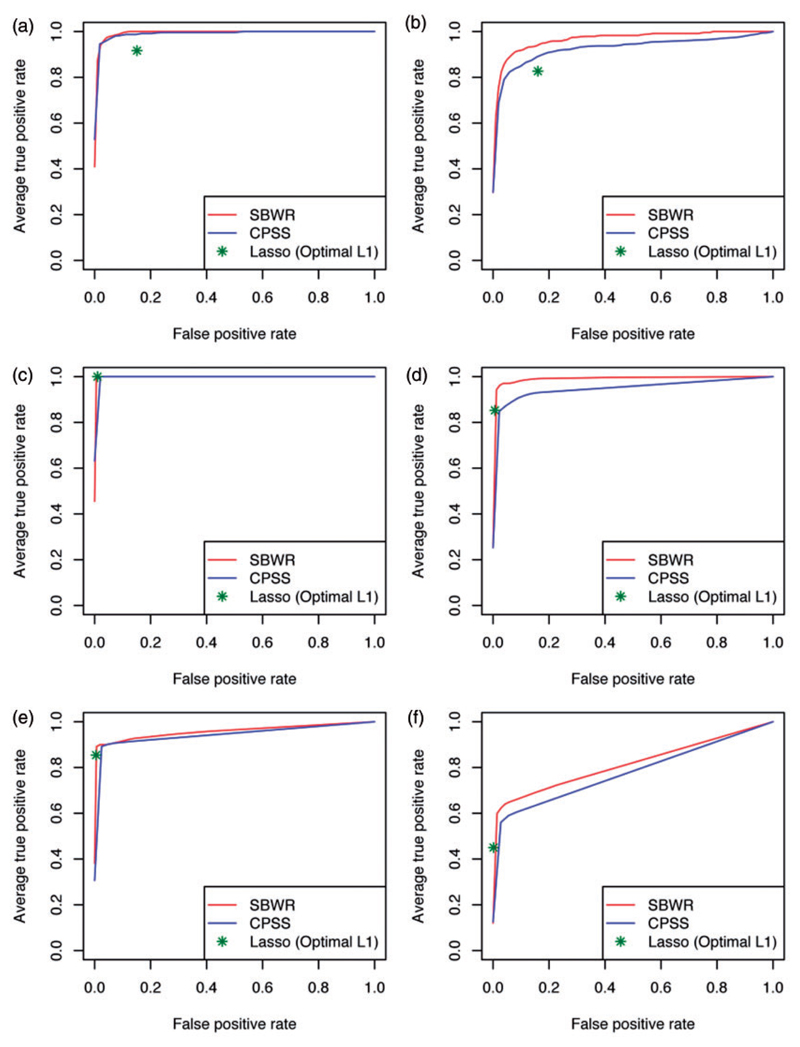
We used receiver operator characteristic (ROC) analysis to assess the ability of each approach to discriminate the 12 true signal variables from the noise variables in the simulated datasets. The resulting ROC curves for the different scenarios are shown in Figure 2 and the corresponding areas under the ROC curve (AUCs) in Table 1. When the number of covariates was equivalent to the SEARCH dataset (i.e. 119) and ‘full size’ effects were simulated, the CPSS and SBWR selection probabilities demonstrated excellent, and equal, performance, and both gave modest improvements over the simple LASSO. Both CPSS and SBWR achieved average AUCs of 0.99 for discriminating the 12 true signal variables from the noise variables, compared to 0.92 for the LASSO selections. Under the harder ‘half size’ log-HR scenario, the posterior probabilities from SBWR demonstrated marginally better discrimination than the CPSS selection probabilities (average ROC AUC 0.97 vs. 0.93). Again, both beat the LASSO selections – this time by a more substantial margin – which achieved an average ROC AUC of 0.86. Relative performance was similar in the high-dimensional simulated datasets of 10,000 and 20,000 covariates. SBWR and CPSS selection probabilities consistently outperformed the LASSO selections for discriminating the 12 true effects, with equal performance for the ‘full size’ effect scenario, and a marginal improvement in SBWR performance for the‘half size’ effect scenario. Under ‘full size’ simulated effects, the ability of SBWR and CPSS to discriminate the 12 signal variables from noise remained excellent up to 20,000 covariates, with average ROC AUCs > 0.95, and LASSO also performed well (AUCs > 0.92). When ‘half size’ effects were used the performance of all methods remained strong up to 10,000 covariates, but deteriorated by 20,000 covariates – SBWR and CPSS AUCs dropped to 0.82 and 0.78, respectively, while the mean LASSO AUC dropped to 0.72.

Figure 2.

ROC analysis of simulation results. Performance of association measures from CPSS and SBWR, and the LASSO selections when the penalty parameter is set to the optimum under cross-validation, in distinguishing 12 signals from noise in datasets ranging from 119 to 20,000 covariates. Panels (a), (c) and (e) show results from datasets simulated to have 12 ‘full-size’ effects, and panels (b), (d) and (f) when 12 ‘half-size’ effects were simulated. Each ROC curve is vertically averaged over the results from the analysis of 20 replicate datasets. CPSS: Complementary Pairs Stability Selection; SBWR: Sparse Bayesian Weibull Regression.

Table 1.

Comparison of methods in simulated data.

	LASSO	CPSS	SBWR
ROC AUCs
119 covariates, ‘full size’ effects	0.92 (0.04)	0.99 (0.01)	0.99 (0.01)
119 covariates, ‘half size’ effects	0.86 (0.06)	0.93 (0.05)	0.97 (0.03)
10,000 covariates, ‘full size’ effects	0.99 (0.00)	1.00 (0.00)	1.00 (0.00)
10,000 covariates, ‘half size’ effects	0.95 (0.05)	0.95 (0.03)	0.99 (0.01)
20,000 covariates, ‘full size’ effects	0.92 (0.02)	0.95 (0.02)	0.96 (0.04)
20,000 covariates, ‘half size’ effects	0.72 (0.05)	0.78 (0.03)	0.82 (0.15)
Selection rates under the null
119 covariates	0.60 (0.49)	0.48 (0.32)	0.14 (0.25)
10,000 covariates	9.2E – 4 (0.03)	6.9E – 4 (5.0E-3)	1.6E – 6 (2.1E – 5)
20,000 covariates	0 (0)	1.8E – 4 (1.8E-3)	0 (0)

CPSS: Complementary Pairs Stability Selection; SBWR: Sparse Bayesian Weibull Regression

The top part of the table presents areas under the receiver operator characteristic curve (ROC AUCs) for detection of the 12 true effects among the variables analysed. Results are averaged over the analysis of 20 replicate datasets for each simulation scenario, with the standard deviation across replicates included in brackets. The bottom part of the table presents mean selection rates of each method under the null, over all covariates and all simulation replicates, with the standard deviation included in brackets.

4.4. Performance under the null

Table 1 also includes median, and 2.5th to 97.5th percentile ranges, of the CPSS and SBWR selection probabilities, and mean selection probabilities from the LASSO analyses across covariates and simulation replicates under the null. There was no obvious cause for concern with any of the methods. When 119 covariates were analysed, SBWR demonstrated the smallest selection rates (mean 0.14 compared to 0.48 from Lasso under CPSS, and 0.60 from Lasso), though it should be kept in mind these selection probabilities from Lasso and CPSS do not have the same interpretation as posterior probabilities. Performance of all methods under the null was superior in the high dimensional data, with mean rates all under 1E – 3.

5. Tumour markers of breast cancer survival in SEARCH

In this section, we apply SBWR to explore a collection of tumour markers for association with breast cancer survival using data from 2287 ER-positive women collected as part of the SEARCH study. In the first instance, we restricted the analysis to the 75 tumour markers for which the majority of values were observed rather than imputed (i.e. those with missingness less than 50% – see Figure 1(d)). Analyses were also conducted using LASSO Cox regression with CPSS, and standard Weibull regressions including each tumour marker one-at-a-time, a straight forward strategy that might typically be used here, and all tumour markers at once in a ‘saturated’ model.

To account for data missingness, 20 multiply imputed datasets were analysed independently using SBWR, and posterior results pooled, as described in the methods. Similarly, LASSO regressions under CPSS were performed in each multiply imputed dataset, and the resulting selection probabilities were averaged. For the one-at-a-time and ‘saturated’ Weibull regressions, results from each imputation chain were combined using Rubin’s rules, as is standard practice.⁶¹ Known predictors number of positive lymph nodes, tumour size and grade, detection by screening, chemotherapy, hormone therapy and morphology were fixed to be adjusted for in the SBWR and LASSO models at all times, and adjusted for in the one-at-a-time regressions, in addition to age of diagnosis and study entry delay as possible confounders. In all frameworks, the tumour markers were analysed as ordinal continuous, assuming additive relationships with log-Hazards across all levels of the scales used in their measurement. Number of positive lymph nodes, tumour size, tumour grade and diagnosis age were also modelled as ordinal continuous variables using the levels derived by Wishart et al.⁴⁰ to provide the best fitting additive relationship with log-hazards using an independent collection of 5694 breast cancer patients (see Table 3 for the categorisations).

Table 3.

SBWR results, for the fixed effects and top tumour markers associated breast cancer survival in SEARCH.

	HR	95% CrIa	MPPIb	Imputed
Fixed parameters
Intercept	−7.32	(−8.07, −6.63)		–
log(beta) Hyperprior SD (σβ)	0.24	(0.12, 0.71)		–
Weibull scale	1.74	(1.54, 1.96)		–
Number positive nodesc     (0, 1, 2–4, 5–9, 10+)	1.61	(1.45, 1.79)		8.4%
Tumour size, mmc     (<10, 10–19, 20–29, 30–49, 50+)	1.26	(1.09, 1.45)		3.8%
Tumour gradec     (Low, Intermediate, High)	1.47	(1.14, 1.89)		10.5%
Morphology – Ductular	–	–		0%
Morphology – Lobular	1.55	(1.10, 2.16)		–
Morphology – Other	1.06	(0.64, 1.68)		–
HER2	1.47	(0.97, 2.18)		10.8%
Detection by screening	0.79	(0.55, 1.11)		6.1%
Hormone therapy	2.20	(1.38, 3.86)		<0.01%
Study entry delay, years	0.88	(0.79, 0.98)		0%
‘Top’ tumour markers
PGRP	0.86	(0.80, 0.93)	0.92	5.2%
PDCD4O2	0.75	(0.62, 0.89)	0.84	43.2%
AURKAP	1.30	(1.11, 1.51)	0.68	31.0%
CD8P	0.92	(0.85, 0.98)	0.30	32.9%
GATA3I	0.80	(0.68, 0.94)	0.30	41.6%
BCL2P	0.94	(0.90, 0.98)	0.26	9.0%

^aCredible Intervals (CrI): For the tumour markers, these were calculated conditional on inclusion in the model.

^bMarginal Posterior Probabilitiy of Inclusion in the model – may be interpreted as the posterior probability an association exists with survival, adjusted for all other covariates in the model.

^cModelled as ordinal continuous.

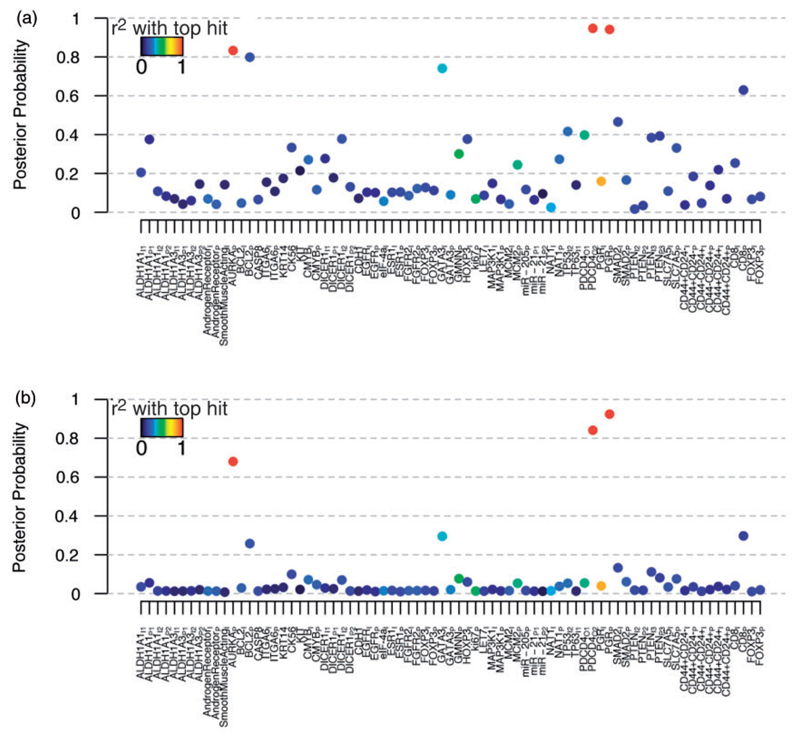
Evidence of association for each tumour marker under SBWR and CPSS are shown in Figure 3(a) and (b). Under SBWR, there was strong evidence of protective effects at PDCD4 (HR: 0.75 (0.62, 0.89), MPPI = 84%) and the proportion score for PGR (HR: 0.86 (0.80, 0.93), MPPI = 92%) and of a risk effect of AURKA (HR: 1.30 (1.11, 1.51), MPPI = 68%). These three tumour markers were selected simultaneously in most of the top 20 models, providing strong evidence they represent independent effects on survival (Table 2). The Bayesian false discovery rate among these three tumour markers was estimated to be 19% which, while larger than we might have hoped, is to be expected since none of their posterior probabilities are decisive (please see the supplementary methods for a formal definition of the Bayesian false discovery rate). There was another ‘band’ of tumour markers for which there was suggestive evidence of association: the intensity score for GATA3, the proportion score for BCL2 and the proportion score for CD8 had similar posterior probabilities between 26% and 30%. However, the false discovery rate estimate increases to 45% when these tumour markers are included in the selection. Detailed results for these top six tumour markers under SBWR, in addition to the fixed effects and key model parameters, are presented in Table 3. The posterior distribution across the number of tumour markers included by SBWR had a large weight at 5 and above, the posterior probability of which was 63% (Supplementary Figure S1). This suggests that while the model may not be able to clearly discriminate among the more weakly associated tumour markers, there is more signal here than that captured by the top three associations alone, and that a future predictive model may benefit from leniency in which tumour markers are included. Interestingly, key prognostic factors tumour grade and HER2 had weaker effects upon inclusion of the tumour markers, suggesting that part of their association with survival may be through the tumour markers measured in this study (Supplementary Table S1). Variable selection auto-correlation plots (Supplementary Figure S2) and trace plots (Supplementary Figure S3) were consistent with convergence. Results were indistinguishable using more optimistic beta-binomial prior parameter choices of a_ω = 1, b_ω = 3 (centring the prior proportion of signals on 1/3) and a more pessimistic choice of a_ω = 1, b_ω = 9 (centring the prior proportion of signals on 0.1) – see Supplementary Figure S4 –, as well as between different chains and starting values (Supplementary Figure S5). Furthermore, the results for the top tumour markers were consistent between inclusion or exclusion of imputed data (Supplementary Figure S6).

Figure 3.

Association of tumour markers with breast cancer survival in the SEARCH dataset. In all panels, each tumour marker is coloured according to its strongest pairwise correlation with one of the three top hits – PDCD4, PGR and AURKA. (a) Selection probabilities from LASSO Cox regression with CPSS. (b) SBWR posterior probabilities. CPSS: Complementary Pairs Stability Selection; SBWR: Sparse Bayesian Weibull Regression.

Table 2.

Top 20 models from the SBWR analysis of the SEARCH dataset, inferred by SBWR.

AURKAP	BCL2P	CK56	GATA3I	PDCD4O2	PGRP	SMAD2I	PTENI3	PTENP3	SLC7A5P	CD8P	Posterior probability
•				•	•						4.5%
				•	•						2.5%
•				•	•					•	2.0%
•	•			•	•						1.3%
•			•	•	•						1.2%
				•	•					•	1.2%
•				•	•		•				0.7%
					•	•					0.6%
•			•		•						0.6%
•				•	•				•		0.5%
	•			•	•						0.5%
•	•			•							0.5%
•	•			•						•	0.5%
			•		•						0.4%
•					•						0.4%
•				•	•			•			0.4%
			•	•	•						0.4%
				•	•	•					0.3%
•				•	•	•					0.3%
•		•		•	•						0.3%

Encouragingly, the CPSS analysis ascribed the strongest selection probabilities to the same top three tumour markers as SBWR. Furthermore, the estimated percentage of ‘noise’ variables among these proteins was similar to the Bayesian false discovery rate estimate at 21%. There was somewhat less separation among the CPSS selection probabilities (Figure 3(a)) such that other markers, which were assigned weaker evidence under SBWR, achieved similar selection probabilities to the top three signals. In the one-at-a-time regressions (Supplementary Figure S7a), as under SBWR, there was strong evidence for PDCD4 and the proportion score for PGR with p-values for association that easily surpassed a multiplicity adjusted Bonferroni threshold of 6:7 × 10⁻⁴ (p = 4:6 × 10⁻⁵ and 1:1 × 10⁻⁶, respectively; Figure 3(a)). However, the intensity score for PGR, which was ruled out under SBWR as confounded by its strong association with the proportion score, also reached significance (p = 1.9 × 10⁻⁴). AURKA, which obtained strong evidence of association under SBWR, was not significant falling short of the Bonferroni threshold (p = 1.05 × 10⁻³). As, in this application, the number of predictors is smaller than the number of subjects, we also estimated a saturated Weibull model which included all 75 tumour markers simultaneously. In the saturated regression (Supplementary Figure S7b), the proportion score for PGR also reached significance (p = 0.024). The only other marker to reach significance was an intensity score for GATA3 (p = 0.040); we expect this is a spurious result arising from overfitting due to use of the saturated model. The fact that AURKA and PDCD4 both received p-values greater than 0.05 is likely reflective of the increase in power using sparse models under SBWR and LASSO.

Finally, we repeated the SBWR and CPSS analyses of SEARCH, extending to the complete set of 119 tumour markers, i.e. including tumour markers for which more than 50% of values were imputed. Inference was unchanged for the previously analysed 75 tumour markers, and there was no compelling evidence for any of the newly included tumour markers (Supplementary Figure S8).

6. Discussion

As large data-rich studies become common place in medical research, there is a growing need for regression tools that can facilitate variable selection over many predictors. Attractive features of developing solutions in the Bayesian sparse regression framework include adequate reflection of uncertainty in the selection of covariates through inference of posterior probabilities for each predictor and possible model and, perhaps most importantly, that prior information can potentially be incorporated, for example through additional modelling of the causal probability, ω, in the spirit of Quintana and Conti⁶². We present, to our knowledge, the first implementation of a Bayesian variable selection algorithm for survival analysis under the Weibull model.

Over a range of realistic simulation scenarios, our method generally demonstrated similar performance, and at times a marginal improvement in specificity, in comparison to an alternative frequentist variable selection strategy – penalised Cox regression with stability selection (specifically CPSS¹⁵). Our simulation study also shows that our method can cope with high-dimensional data up to 20,000 predictors, with computational times similar to the stability selection-based approach (approximately one day for n = 2287 on an Intel Xeon E5-2640 2.50GHz processor).

Subsequently, we conducted a real data application in which 119 prospectively measured immunohistochemical tumour markers were explored for their association with survival among 2287 ER-positive breast cancer cases. Three proteins stood out with evidence of independent effects: PDCD4, PGR and AURKA. Discrimination, i.e. separation between the top signals and other tumour markers, was clearer when using SBWR in comparison to CPSS, consistently with the specificity improvements observed in some of the simulation scenarios. We also compared our results with those from a univariate strategy that might typically be used to analyse such data, highlighting some of the benefits of multivariate modelling.

Of the top three proteins, two are becoming increasingly recognised as powerful prognostic factors in ER-positive breast cancer. Indeed most schemes for clinical classification of subgroups of breast tumours based on molecular profiles include PGR^46,63,64 and, more recently, by using PGR expression at a higher threshold, it has been proposed that it ought to be used to identify indolent ER-positive ‘luminal A’ tumours in the clinical setting.⁶⁵ Following numerous high-resolution molecular profiling studies over the past decade, tumour cell proliferation has been confirmed as the most powerful predictor of outcome in ER-positive tumours.^66,67 There are potentially dozens of methods for measuring tumour cell proliferation including assaying different molecular markers of cell cycle. We have previously conducted a systematic comparison of the relative prognostic power of a panel of six proteins associated with cell-cycle including AURKA.⁶⁸ This study, based on the SEARCH dataset, identified AURKA as most strongly associated with outcome, outperforming the other investigated markers including marker combinations.⁶⁸ Moreover, at the level of mRNA, AURKA has been identified as a prototypical marker of proliferation and selected for optimal classification of breast tumours into distinct molecular subgroups.⁶⁹ PDCD4 has not been investigated as a potential prognostic marker in breast cancer previously. However, studies in lung⁷⁰ and salivary gland tumours⁷¹ have shown an association with outcome. It is a well-known tumour suppressor and thought to inhibit the translation of proteins by interacting with eukaryotic translation factor 4A (eIF4A).⁷² The strong independent association between PDCD4 and outcome revealed by this analysis is a novel finding which highlights PDCD4 as a potentially useful clinical marker of outcome requiring further evaluation. Interpretation of these results should, however, be mindful of the estimated false discovery rate, 19%, suggesting that up to one of the three proteins is expected to be a false positive.

A further caveat to our real data application is that our treatment of missing data may be sub-optimal. Missing data were imputed using the well-established technique of multiple imputation using chained equations,⁵⁴ after which posteriors were pooled from individual analyses of 20 chains as suggested by Gelman.⁵⁶ However, after a simulation study on the practical performance of this approach, Zhou and Reiter⁷³ concluded that 100 or more chains should be used to achieve adequate coverage of the target posterior. We did not do so here due to the computational time required to run our algorithm that many times, and since sensitivity analyses using less chains showed no substantive difference in estimates and inference. We also note that, while it was advisable for penalised regression, and our approach due to the prior framework, in general one should be very careful normalising predictors by their standard deviation.⁷⁴ In our case, however, none of the top three markers had extreme standard deviations prior to normalisation (ranging from 0.85 to 1.72), so our key results should not be meaningfully impacted by this issue.

Although our algorithm was technically challenging to develop, since both models and parameters are sampled during Reversible Jump MCMC, the framework used for variable selection is relatively simplistic. First, we specified independent priors for all covariate effects. Ideally, a multivariate normal prior would be used to reflect that correlated covariates are likely to have correlated effects. Zellner⁷⁵ proposed the use of ‘g-priors’ in which a multivariate normal is used as a prior for the regression coefficients with a correlation structure informed by that of the covariate matrix. In the context of linear regression, g-priors also preserve the ability to use conjugate results for coefficient effects and have been successfully implemented in the ESS sparse Bayesian regression framework.^31–33 It is worth noting, however, that the SSS algorithm also uses independent priors,³⁰ and the use of independent priors in the work we present here did not prove problematic. Nevertheless, we intend to incorporate a g-prior option in the future. Second, the parametric assumptions imposed on the hazard function under the Weibull model might be too restrictive for some problems. Haneuse et al.⁷⁶ have proposed a flexible Bayesian approach for capturing much more complex hazard functions, including to account for potentially time varying predictor effects. Future work could also involve incorporating their ideas into our algorithm resulting in a considerably more flexible tool for survival analysis.

Although the runtimes of our algorithm when applied to high-dimensional datasets of 20,000 covariates were similar to those from a state-of-the-art implementation of LASSO, there is certainly room for improvement. An alternative strategy might be to avoid Reversible Jump altogether and induce sparsity via independent double-exponential Laplacian priors on the Weibull covariate effects, a so-called Bayesian LASSO model due to demonstrated similarity of results with the LASSO.⁷⁷ This would sacrifice the arguably more natural prior setup of the beta-binomial which, for example, allows direct specification of priors on the proportions of associated covariates. However, removing Reversible Jump from the MCMC algorithm could considerably improve efficiency. Another way we might improve efficiency would be to employ Evolutionary Monte Carlo scheme which has proved effective for exploring parameter spaces consisting of hundreds of thousands of predictors.^31,33 We plan to investigate both strategies in future work.

Our method of variable selection is relevant both to breast cancer research and clinical practice. Cancer research has been transformed by the introduction of high-throughput technologies which enable scientists to interrogate all expressed genes in a tumour and, more recently, the sequence of the entire cancer genome at single nucleotide resolution in a single experiment.⁷⁸ This has led to a proliferation of large datasets comprising hundreds to tens of thousands of molecular features. The emergence of such abundant data poses a strategic problem for the cancer biologist: How best can a shortlist of molecules of probable importance be distilled from such a multitude? One approach has been to use a combination of biological knowledge and statistical inference.⁷⁹ However, an alternative may be to use a legitimate endpoint such as disease-specific survival to infer which of a set of molecules influences the clinical behaviour of a tumour and is, therefore, likely to reflect its biological characteristics. Variable selection which accounts for the relative contribution of each of a large number of predictors represents a powerful method for identifying candidate molecules which warrant further biological investigation. Those molecules which are confirmed by such work to play a key role in tumour progression would represent lucrative targets for novel therapies.

Accurate risk prediction in breast cancer is important since many therapies have a modest effect on mortality and the absolute benefit of such toxic therapies is dependent on absolute risk of relapse or death.⁴³ Therefore, even modest improvements in risk-prediction can influence treatment decisions. Current clinical methods heavily rely on conventional clinical parameters to estimate risk such as tumour size and grade, which are already measured rigorously and are not likely to be much improved.⁴¹ However, molecular characteristics of tumours are not much utilised and represent an important avenue for improving our approach. The impact of abundant molecular data on clinical practice has been facilitated by studies over the past decade which used frequentist approaches to compile risk-prediction signatures for certain clinical endpoints.⁸⁰ These methods have had varying success and do not systematically account for the relative contribution of different variables. Through systematic consideration of multivariate models which account for the dependencies between covariates, our method of variable selection is likely to highlight not only molecules of biological importance but also to improve current risk-prediction methods. These benefits will extend to all common solid tumours in addition to breast cancer.

In summary, we present a new implementation of a Reversible Jump MCMC algorithm for Bayesian variable selection in survival analysis under the Weibull regression model. We demonstrate equal, or marginally superior, sensitivity and specificity to an alternative state-of-the-art approach over a range of realistic simulation scenarios with up to 20,000 covariates. In a real data application, in which our method demonstrated superior specificity over alternative approaches, we present evidence for three possible prognostic tumour markers of breast cancer survival. Despite the conceptual limitations listed above, in practice our software proved reliable, robust and efficient across the range of analyses presented here. Furthermore, our current implementation offers enormous flexibility for incorporation of prior information on effect magnitudes (individual priors can be specified for every covariate), and on relative probabilities of effect – the model space may be partitioned into as many components as required, each with an individual prior on the expected number of effects. This could, for example, be utilised to reflect that a subset of features lie in a known pathway for the disease being modelled. We have incorporated the algorithm, which was developed in java, into a freely available and easy to use R package called ‘R2BGLiMS’. For download and installation instructions, please look under ‘Other R packages’ on our software page http://www.mrc-bsu.cam.ac.uk/software/, or, alternatively, direct download of ‘R2BGLiMS’ is available via github https://github.com/pjnewcombe/R2BGLiMS.