A Methodology for Individual-Specific Modeling of Rat Optic Nerve Head Biomechanics in Glaucoma

Abstract

Glaucoma is the leading cause of irreversible blindness and involves the death of retinal ganglion cells (RGCs). Although biomechanics likely contributes to axonal injury within the optic nerve head (ONH), leading to RGC death, the pathways by which this occurs are not well understood. While rat models of glaucoma are well-suited for mechanistic studies, the anatomy of the rat ONH is different from the human, and the resulting differences in biomechanics have not been characterized. The aim of this study is to describe a methodology for building individual-specific finite element (FE) models of rat ONHs. This method was used to build three rat ONH FE models and compute the biomechanical environment within these ONHs. Initial results show that rat ONH strains are larger and more asymmetric than those seen in human ONH modeling studies. This method provides a framework for building additional models of normotensive and glaucomatous rat ONHs. Comparing model strain patterns with patterns of cellular response seen in studies using rat glaucoma models will help us to learn more about the link between biomechanics and glaucomatous cell death, which in turn may drive the development of novel therapies for glaucoma.

Introduction

Glaucoma is the leading cause of irreversible blindness, affecting an estimated 70 million people worldwide [1]. Blindness in glaucoma patients is initiated by loss of retinal ganglion cell (RGC) axons, which transmit visual information from the retina to the brain. Elevated intraocular pressure (IOP) is a main and causative risk factor [2,3], leading to the hypothesis that biomechanical insult is a key driver leading to RGC axon degeneration [4]. Current therapies all focus on lowering IOP, although this is not always effective at preventing further vision loss.

The optic nerve head (ONH) is the location where RGC axon bundles exit the eye. In the human eye, axons pass through pores in a connective tissue web called the lamina cribrosa, which spans the scleral canal. The ONH has been identified as an early and primary region of glaucomatous damage for several reasons, including posterior bowing and remodeling of the lamina cribrosa [5–7], remodeling of the surrounding sclera [2,8–16], sectoral RGC axonal injury corresponding to the ONH [17,18], and disruption of RGC axonal transport at the level of the lamina cribrosa [19,20]. However, the pathways by which biomechanical insult results in RGC death are not well understood. Commonly proposed possibilities include direct mechanical insult to RGC axons, nutrition scarcity due to IOP-induced remodeling or obstructed capillaries [7,21], and decreased support from ONH resident cells (i.e., astrocytes) to RGCs due to mechanical activation [22–26]. This lack of understanding has prompted many studies on ONH biomechanics in several species, particularly in humans and monkeys [27–41]. As IOP is elevated, stress and strain are increased within the ONH in complex patterns due to the intricate anatomy and mechanical behavior of ONH tissues. Although constantly improving imaging technologies are making it more possible to measure strain in vivo [42,43], computational modeling remains a key tool for understanding the complex biomechanics of the ONH. The previous modeling studies on the human have identified scleral stiffness as the most important factor in glaucoma-related ONH biomechanics [37,39], and more recent studies have begun to explore the impact of lamina cribrosa and peripapillary scleral microstructure [43,44].

In distinction to biomechanical studies, much of what we know about cellular behavior and degeneration in glaucoma has come from rodent model studies [45]. The rat is a particularly useful animal model for mechanistic glaucoma studies for several reasons. (1) Acute and chronic ocular hypertensive experimental glaucoma models exist for the rat and present with similar ONH pathophysiology as that seen clinically [25,46–49]. (2) Regional patterns of rat RGC loss and astrocyte activation offer unique opportunities for study. In experimental glaucoma rat studies, the RGC axons in the superior optic nerve tend to die first [45]. In addition, it was recently shown that mechanosensitive ONH astrocytes activate and reorient their processes in the inferior nerve before those in the superior nerve [25]. (3) Rodent experimental glaucoma models are necessary for high subject-number studies because they are less expensive and easier to manage than monkey models. (4) Rodent experimental glaucoma studies allow for better control of factors that may influence RGC death (versus human).

However, there are substantial differences between rat and human ONH anatomy [45,50] (Fig. 1). (1) The rat lacks a connective tissue lamina cribrosa spanning the neurovascular scleral canal. (2) The central retinal vein (CRV) and artery (CRA) pass through the sclera on the inferior side of the nerve, rather than within the center of the optic nerve. (3) There is a vascular plexus between the optic nerve and the sclera of the neurovascular canal, referred to as the perineural vascular plexus (PNVP). (4) There is an additional canal in the sclera, the inferior arterial canal (IAC), which is separated from the neurovascular canal by a scleral sling. (5) Bruch's membrane extends into the nerve tissue on its superior side creating a BM overhang. These differences are likely to affect rat ONH biomechanics, and although several studies on rodent ONH biomechanics have been conducted [42,52–55], no computational modeling study has been done to date.

Fig. 1.

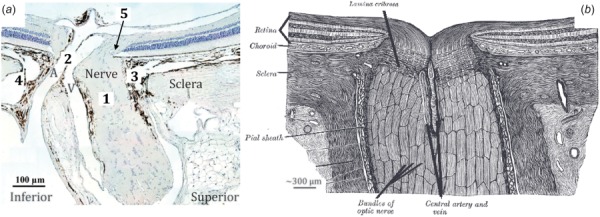
Histologic section of the rat (a) (modified from Ref. [45]) and schematic drawing of the human (b) ONH (modified from Ref. [51]) illustrating their anatomical differences, including five key differences of particular interest (1)-(5) as described in the text. Abbreviations: CRA (A) and CRV (V).

Therefore, there is a need for an in-depth characterization of the IOP-induced biomechanical environment in the rat ONH that will allow us to better interpret results from rat glaucoma studies. For example, comparing strain patterns in the ONH with patterns of biological response from rat experimental glaucoma studies could help us to determine the pathway between biomechanical insult and RGC death. This knowledge would assist in novel therapy development and early identification of at-risk patients. Our goal is to fill this need by using recently available data sets describing normal and glaucomatous rat ONH tissue anatomy [50,56] to build individual-specific finite element (FE) models of rat ONHs. We here present a method for building these models as well as initial results on strain patterns in the rat ONH.

Methods

Building Model Geometry.

Three-dimensional (3D) digital reconstructions of ONHs from normotensive, ostensibly normal rat eyes were built from histomorphometric data sets, collected as previously described [50,56]. Animals were male Brown Norway rats between 9.5 and 10.5 months of age. After animals were sacrificed via CO₂ euthanasia, eyes were perfusion-fixed in situ while experiencing an estimated IOP of 10 mmHg and an estimated arterial pressure in the range of 40-100 mmHg. The justification for these values is given below. Eyes were enucleated and each ONH was removed using a 3 mm trephine and embedded in paraffin. The resulting block was serial sectioned at 1.5 μm thickness using an automated microtome starting at the vitreoretinal interface and proceeding through the ONH. After each section was cut, the block surface was stained with a 1:1 (v/v) mixture of Ponceau S and acid fuchsin stains, then imaged at a resolution of 1.5 × 1.5 μm per pixel using a custom device. The images were then aligned and stacked into a digital 3D reconstruction of the ONH. In this work, we provide information on reconstructions of three rat eyes (MR04OD, MR05OD, and MR10OS) from three separate rats.

Using custom software (multiview [5]), tissue boundaries were manually delineated (Fig. 2). BM, the anterior scleral surface, the posterior scleral surface, neural boundary, outer posterior pia mater surface, and the side branches of the CRV were delineated by viewing radial sections through the ONH. The anterior scleral canal opening, posterior scleral canal opening, and BM opening were also delineated in this view. The CRA, main CRV lumen, and IAC were delineated by viewing transverse sections through the ONH. We chose to disregard the long posterior ciliary arteries which feed into the CRA just posterior to the globe. Depending on their placement within or just outside the sclera, different sections along their lengths were either considered part of the sclera or were not included in delineation. We also did not include delineations of the dura mater because we decided to focus on tissues primarily influenced by IOP. The dura mater will be included in future studies that focus on changes in cerebrospinal fluid pressure. The resulting 3D point clouds describing tissue geometry were imported into Rhino 5 SR 14 (Robert McNeel and Associates, Seattle, WA).

Fig. 2.

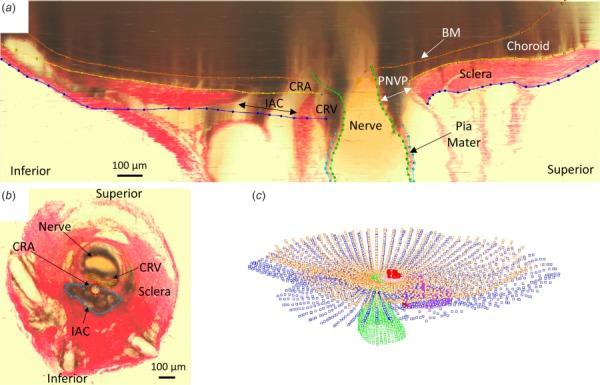
Manual delineation of tissue boundaries: (a) Radial section through rat ONH with tissue boundaries delineated: BM, anterior scleral boundary, posterior scleral boundary, neural boundary, posterior pia mater outer boundary. (b) Transverse section normal to nerve axis with tissue boundaries delineated: CRV, CRA, IAC. (c) Point clouds produced from delineation of radial sections and cross sections.

Nonuniform rational basis spline surfaces were fit to the point clouds and were joined to create volumes representing each tissue (Fig. 3) using Rhino. Nonuniform rational basis spline curves and surfaces are useful for representing complex geometries, such as those of biological tissues, because they offer a high degree of accuracy for representing free form geometry with lower memory requirements than faceted approximations of geometry. The Rhino T-Splines plugin (Autodesk, Inc., San Rafael, CA) was used to build tissue geometries that were particularly difficult to represent, i.e., the three connecting branches of the CRV. Curves and surfaces were smoothed to make them more amenable to meshing. Smoothing of the original point cloud data occurred at several steps in the geometry building process. First, the chosen settings within Rhino fitting functions affected the smoothness of the resulting curve or surface. For example, forcing a curve to pass directly through every point in a given set often produced a jagged curve, so this requirement was usually relaxed. In addition, after the initial fitting of original point cloud data, curves and surfaces were sometimes smoothed using the built-in Rhino function “smooth” and T-Splines function “flatten.” In addition to the outer surfaces of the IAC, CRA, and CRV which required smoothing in all three eyes, smoothing was done as needed to remove features such as small “wrinkles” or “sharp” sections within curves and surfaces, while taking care not to edit more prominent features of tissue morphology. Also, since tissues near the edges of the histomorphometric reconstructions were more prone to artifacts (tissue curling, bending, etc.) than those in the center, geometry outside of a 1.5 mm diameter cylinder centered at the center of BM opening was removed from the model. Boolean operations were used in areas where tissues intersected each other. For example, since the CRA passes through the BM, choroid, sclera, and IAC, the CRA geometry was subtracted from each of those tissues. This ensured that adjacent tissues shared common surfaces and helped to produce conforming meshes between tissues. In cases where the thickness of the tissue could not be determined from the reconstructions, a constant thickness was assumed. Specifically, we made thickness measurements of the CRV wall (3 μm), CRA wall (10 μm), and anterior pia mater (20 μm) from the previously gathered histology slides of the rat ONH. The anterior pia mater was defined as being anterior to the posterior scleral surface. For model MR05OD only, which was the first model built before the above procedure had been refined, the posterior pia mater was also given a constant thickness of 20 μm; revising this model to make the small corrections to posterior pia mater thickness would have been labor intensive and would have likely had very small effects on model results. The BM was given a thickness of 3 μm based on published data on the human BM [57–59]. After each model geometry was completed, a custom Rhino.Python script was used to project the volume boundaries back onto the original reconstruction sections to ensure that ONH anatomy was accurately represented (Fig. 4 and Supplemental Fig. 2 which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). In addition, a custom script was written to calculate the minimum distance between each delineation point and its respective tissue surface, representing the error between the manual delineations and the resulting model geometries. Tissue volumes were then exported to Trelis 16.3.6 (computation simulation software, llc) for meshing.

Fig. 3.

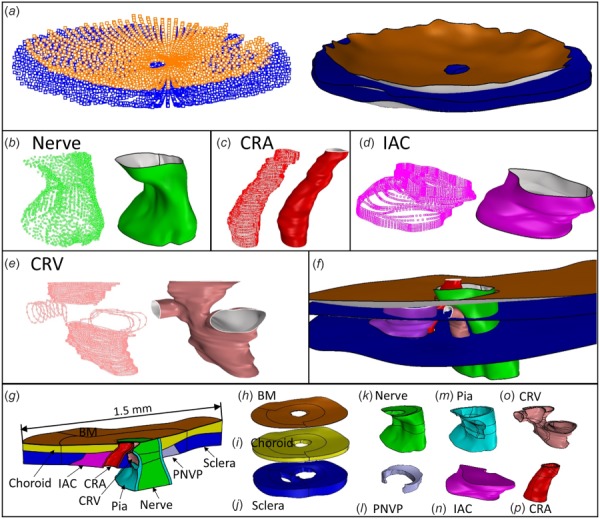
Overview of geometry building process. See text for abbreviations. (a)-(e) Point cloud and surface fit of (a) BM and sclera, (b) optic nerve, (c) CRA, (d) IAC, (e) CRV. (f) Intersecting tissue surfaces before Boolean operations were performed. (g) Superior-Inferior cut view of MR05OD model geometry. (h)-(p) Individual tissue volumes (not to scale): (h) BM, (i) choroid, (j) sclera, (k) optic nerve, (l) PNVP, (m) pia mater, (n) IAC, (o) CRV, and (p) CRA.

Fig. 4.

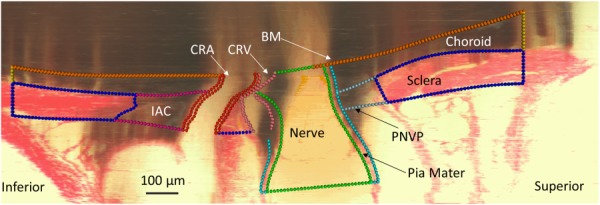
Projection of model tissue outlines onto digital section to ensure accurate representation of individual-specific tissue geometry. Note that the “shadow-like” appearance in parts of the section is an artifact of the reconstruction process. It occurs because highly pigmented tissue within the semitransparent paraffin block can be seen even before it is cut by the microtome.

Meshing and Constraints.

Because the model geometry was so complex, most of the model was meshed using tetrahedral elements. However, due to the thinness of BM, it could not be meshed using tetrahedral elements without either using an unreasonably high mesh density or producing skewed element shapes. Meshing the entire volume of the choroid and sclera with tetrahedra also produced too many elements. To overcome these problems, we divided each ONH model into an inner region containing tissues with complex geometry (nerve, pia mater, CRV, CRA, PNVP, and IAC) and an outer region containing only tissues with simpler geometry (sclera, choroid, and BM) (Supplemental Fig. 1 which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). The outer region was meshed with eight-node hexahedral elements. The inner region was meshed with a combination of six-node wedge elements and four-node tetrahedral elements. Since this meshing scheme created a nonconforming mesh between the simple region and complex region, tied constraints were implemented at these boundaries. A general contact without friction was also implemented between inner surfaces of the CRV vessel wall in the model of MR05OD because its CRV geometry resulted in contact between opposite sides of the CRV wall.

Material Properties.

Since it has been established that connective tissues in the eye, especially the sclera, contain organized layers of collagen [44,60], nonlinear, anisotropic material models are appropriate for modeling their mechanical behavior. However, to our knowledge, the mechanical behavior of rat ONH tissues has not been characterized. Therefore, as a first-pass effort, we modeled all tissues as isotropic, neo-Hookean solids. All tissues were assumed to be nearly incompressible and were thus given a Poisson's ratio value of 0.49. We used tissue stiffness values (Table 1) from the previous modeling studies on the human ONH for the sclera, pia mater, optic nerve, and central retinal vessels [39–41,61]. For BM and the choroid, we assumed values from the literature [27,57,59,62]. We assumed that the PNVP and IAC had the same material properties as the choroid, all highly vascularized tissues.

Table 1.

Tissue elastic modulus values

Tissue	Elastic modulus (MPa)	Tissue	Elastic modulus (MPa)
BM	7	Choroid	0.1
Sclera	3	PNVP	0.1
Pia mater	3	IAC	0.1
CRA wall	0.3	Optic nerve	0.03
CRV wall	0.3

Loads.

Our 3D point cloud data represents the ONH geometry at perfusion fixation pressures. We used a “relative displacement” approach to account for the preexisting stress and strain in the ONH at perfusion fixation. This approach provides a more accurate solution than neglecting the effects of prestress without having to implement more involved, iterative methods [63]. As prescribed by this approach, we treated the model geometry created from 3D point cloud data as the unloaded ONH geometry. We applied loads (IOP, CRA blood pressure (BP), and CRV BP) equal to those experienced by the ONH during perfusion fixation and assumed that the resulting model state represented the preloaded reference configuration, i.e., was under the stress and strain experienced by the ONH at perfusion fixation. Next, we applied additional loads to bring the model to a glaucomatous loading state, and we calculated the change in strain relative to the preloaded reference configuration.

Preloaded Reference State.

Intraocular pressure at fixation was estimated to be 10 mmHg based on the previous experience with the IOP of anesthetized rats [64], and CRA BP at fixation was in the range of 40 mmHg-100 mmHg as measured by a pressure transducer connected to the perfusion line. We assumed the lower end of the CRA fixation BP range, and thus applied a large CRA BP in the second step of our model simulation to reach glaucomatous conditions. This corresponds to a “worst case scenario” in our model because applying a larger CRA BP is more likely to cause high strains within adjacent sections of the optic nerve. For example, in the cases of MR04OD and MR05OD, a small portion of anterior optic nerve tissue was in contact with the CRA and experienced strain due to expansion of the CRA. Finally, we assumed that CRV BP closely followed IOP [65]. In summary, we took the pressures experienced by the eye during perfusion fixation to be 10 mmHg IOP, 10 mmHg CRV BP, and 40 mmHg CRA BP. IOP was applied to the anterior surfaces of BM, the optic nerve, the CRA, and the CRV, while CRA BP and CRV BP were applied to each vessel lumen.

Glaucomatous Loading State.

A daytime (light phase) IOP of approximately 30 mmHg and above will usually produce glaucomatous damage in a rat, depending on duration of exposure [64,66,67]. We estimated that blood pressure in the CRA of an awake rat is likely around 110 mmHg [68,69]. It is difficult to determine CRV pressure, but we assumed that it closely follows IOP. Therefore, the pressure loads applied in the second step of our model simulation were 20 mmHg IOP, 20 mmHg CRV BP, and 70 mmHg CRA BP, representing the increases in respective pressures over the preloaded reference state. All strains reported herein thus represent a change in strain from the preloaded reference configuration.

Boundary Conditions.

We utilized a submodeling approach to apply realistic boundary conditions to the edges of each ONH FE model [36,37,41,70]. Submodeling involves solving a less detailed “full model” (in our case, the entire posterior half of the eye) that encompasses the true region of interest or “submodel” (in our case, the ONH). Displacements from the full model were mapped to nodes on the edges of the submodel and applied as boundary conditions using the abaqus (Dassault Systèmes, Providence, RI) submodeling feature. We built a posterior eye model with simplified ONH geometry that included a choroid, sclera, optic nerve, PNVP, and IAC (Fig. 5). We did not include the CRA and CRV because that level of detail would have required a much denser mesh. Since the long axis and the diameter of the rat eye only differ by about 2% [50], we modeled the posterior eye as a half sphere with a diameter of 6.41 mm [50]. The choroid and sclera had constant thicknesses of 100 μm and 60 μm, respectively [50]. To generate a simplified ONH geometry, we measured the cross section of the optic nerve, PNVP and IAC at the level of the anterior choroid, anterior sclera, and posterior sclera in 5 ONH geometries: three that were used in this study and two additional geometries. The nerve and PNVP cross sections were represented as ellipses, and the IAC cross sections were represented as half ellipses. To measure the dimensions of each tissue cross section, points were laid on the cross section boundary, a plane was fit through the points, and the points were projected to the plane using Rhino. A matlab (The Mathworks, Inc., Natick, MA) script was used to fit an ellipse through those points, and the major and minor axes were recorded as well as their center locations relative to BM opening. Each of these measures were averaged and used to create generalized tissue cross sections for the posterior eye model. Tissue volumes were generated by lofting a surface through the generalized cross sections. We applied boundary conditions to nodes on the flat, anterior surface of the posterior eye model. Nodes were allowed to move in the r direction, but were fixed in the z and θ directions. The z-axis was coincident with the central axis of the half sphere (Fig. 5). As in the submodels, we applied IOP in two loading steps: 10 mmHg and an additional 20 mmHg. IOP was applied to the anterior surface of the choroid and optic nerve. The material properties for each tissue were the same as for the submodel.

Fig. 5.

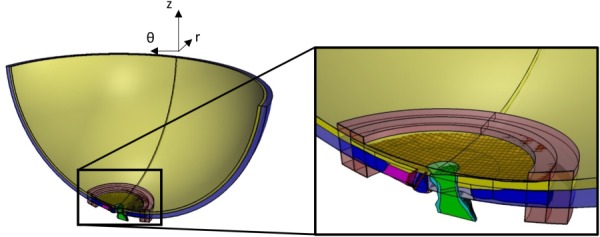
Superior-Inferior cut plane view illustrating a match between individual-specific model geometry (opaque) with generic posterior eye geometry (semitransparent). Tissue colors are the same as in Fig. 3. Transparent red blocks on anterior choroid and posterior sclera are the very soft material used to interpolate displacement values to any protruding individual-specific model edges.

Submodel/Posterior Eye Model Registration.

Matching between the submodel and the posterior eye model was done via a combination of manual and automatic adjustments. First, the submodel geometry was manually translated and rotated until it closely matched the posterior eye geometry. We focused on matching the anterior scleral surfaces of the two models, especially at the edges of the submodel, and then tried to line up the nerve, PNVP, and IAC. Next, for the submodel and posterior eye model, we overlaid points on the outer, anterior surface of the sclera, the PNVP cross section boundary at the level of the sclera, and the IAC cross section boundary at the level of the sclera. These points were imported into matlab and an automatic surface registration algorithm [71] was used to make small adjustments. We then inspected the fit and manually made fine adjustments as necessary. Since there were differences in scleral and choroidal thickness and surface contour between ONH models, it was impossible to produce matches which resulted in the entire submodel edge being contained within the posterior eye model geometry. For this reason, we added blocks of very soft material (elastic modulus of 0.01 MPa) to the anterior choroidal surface and posterior scleral surface of the posterior eye model where submodel boundaries sometimes protruded. This provided a way to interpolate displacement values to the nodes at these protruding edges.

All simulations were run using abaqus 2016 on a virtual machine with an Intel Xeon CPU E5-26900 v3 at 2.60 GHz with 50 GB of RAM. Results were postprocessed using the abaqus2matlab toolbox [72], a custom matlab script, and paraview (Kitware, Inc., Clifton Park, New York).

Results

Model Geometry.

Average errors between the manual delineations and the resulting model geometries for MR04OD, MR05OD, and MR10OS were 5.8 μm, 5.5 μm, and 5.0 μm, respectively, indicating that the model geometries closely matched the original delineations. Figure 4 shows an example of the good agreement between the MR05OD model geometry and the true ONH anatomy as illustrated by projecting points from the model edges back onto the original reconstruction sections. Supplemental Fig. 2 which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection shows model point projections on multiple sections from all three ONH reconstructions.

Mesh Sensitivity.

We evaluated model sensitivity to mesh density by solving the MR05OD model with low-, medium-, and high-density meshes which had node counts of 87,429, 175,941, and 340,016. In three out of the four quantified strain measures (listed below), the error between the high- and medium-density meshes was substantially lower than the error between the medium- and low-density meshes (Table 2). In these three cases, error decreased to at most 1/5 of the original value. The exception was the relative error for average third principal strain, which increased from 0.56% to 1.17%. However, the relative error in all quantified strain measures between the medium-density mesh and high-density mesh was less than 2% of the medium density mesh strain values. For these reasons, we decided that the medium-density mesh was sufficient, and we ensured that the mesh density of each model was approximately at that of the medium-density mesh or greater. The resulting node counts for each model were 221,937 for MR04OD, 175,941 for MR05OD, and 412,175 for MR10OS.

Table 2.

Mesh density study results

	Low density mesh	Medium density mesh	High density mesh
First principal strain mean	3.81%	3.96%	3.98%
First principal strain 95th percentile	5.78%	5.85%	5.86%
Third principal strain mean	–4.21%	–4.24%	–4.29%
Third principal strain fifth percentile	–6.80%	–6.83%	–6.84%

Optic Nerve Strain Patterns.

For the most part, patterns of strain were consistent between models, with first and third principal strain concentrations occurring in the inferior side of the anterior half of the nerve (Fig. 6). In two of the models, the nerve tissue came into contact with the CRA and strain concentrations were observed at this interface. The level of strain that occurred around the BM overhang on the superior side of the nerve varied between models. MR04OD experienced the most consistent elevation of strain along the BM overhang edge, while MR05OD presented with less strain near the BM overhang.

Fig. 6.

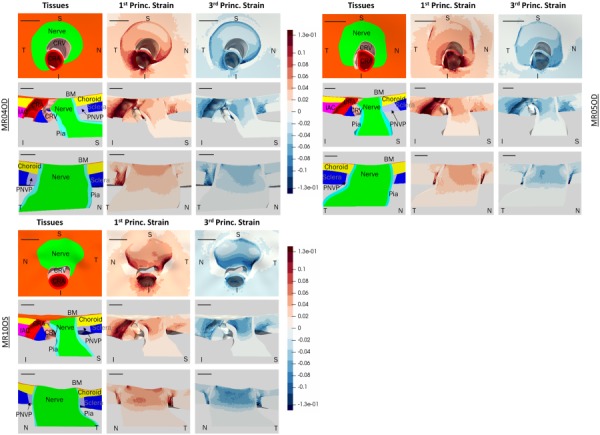
Computed first and third principal strain patterns for three different rat ONH models: MR04OD (top left), MR05OD (top right), and MR10OS (bottom left). Superior (S), inferior (I), nasal (N), and temporal (T) directions are indicated. Top rows show en face view, middle rows show S-I cut view, and bottom rows show T-N cut view. Tissue colors are the same as in Fig. 3. All scale bars are 100 μm. All three models have primary strain concentrations along the inferior side of the anterior nerve. MR10OS and MR04OD have more prominent strain concentrations around the BM overhang edge than MR05OD. MR10OS has particularly high strain concentrations in the inferior nerve as seen from the en face view.

We quantified the average and 95th percentile first principal strain and average and fifth percentile third principal strain in the anterior nerve, defined as nerve tissue from the level of the BM to the level of the posterior scleral surface (about 150 μm posterior to BM) (Table 3). The 95th and fifth percentile values were chosen for quantification because they are a measure of the most extreme strains in the tissue, which are most likely to invoke a cellular response, while avoiding potential numerical errors associated with the 100th and first percentile values, e.g., due to badly shaped elements. The second principal strain magnitudes were much lower than first or third principal strain values, so we focused on reporting the first and third principal strains. MR04OD and MR05OD had similar strain values but the values of MR04OD and MR10OS differed by as much as 27%.

Table 3.

Computed first and third principal strains in the anterior optic nerve

	First principal strain		Third principal strain
Model	Mean	95th percentile	Mean	Fifth percentile
MR04OD	3.65%	5.74%	–4.23%	–6.61%
MR05OD	3.96%	5.85%	–4.24%	–6.83%
MR10OS	4.38%	7.11%	–5.70%	–8.40%

In earlier stages of methods development, we ran model simulations that did not include a preloading step, and therefore, did not account for the effects of prestress (data not shown). However, adding in a preloading step did not significantly alter the overall strain patterns calculated by each model. Including the effects of prestress will likely be more important for future versions of the models that account for the nonlinear stiffening behavior of the sclera (see below).

Discussion

Our methodology is capable of producing rat ONH finite element models which closely adhere to the true, complex rat ONH anatomy. This is made evident when the tissue boundaries of our models are overlaid on the original digital rat ONH reconstructions (Fig. 4 and Supplemental Fig. 2 which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). This was consistent with our finding that the highest average error between model geometry and the tissue delineations was only 5.8 μm.

As expected, our initial results predict different strain patterns and higher strain magnitudes than those previously reported in human ONH modeling studies. The human ONH has a higher degree of anatomical symmetry, with ONH tissues being arranged in an approximately axisymmetric pattern around the central retinal vessels. The rat ONH is somewhat symmetric about the sagittal plane, but is not axisymmetric like the human ONH. This affected strain patterns in the rat ONH models, with main strain concentrations occurring in the inferior nerve and, in the case of MR04OD and MR10OS, in the nerve tissue in contact with the BM overhang. We also expected that rat ONH strains would be higher than in the human, since the rat ONH lacks the biomechanical support of a collagenous lamina cribrosa as in the human ONH. Our models confirmed this expectation, with predicted strains at an IOP load of 20 mmHg (10 mmHg-30 mmHg) similar to those seen in the human ONH at an IOP load of 45 mmHg [41] (5 mmHg-50 mmHg). For example, in the prelaminar neural tissue of the human ONH models, the first principal strain median and 95th percentile values ranged from approximately 2% to 4% and 5% to 9%, respectively, while the third principal strain median and fifth percentile values ranged from approximately –4% to –5% and –9% to –13%. In all cases except for the third principal fifth percentile strains, the human values were about the same as those of the rat despite the human ONH being subjected to approximately double the IOP load that our rat ONH models were.

This difference is likely due to the existence of a collagenous lamina cribrosa in the human ONH. It is also possible that other anatomical differences contributed to the generally higher strain levels in the rat. For example, scleral stiffness and thickness have previously been shown to strongly influence ONH strain in the human eye. Although the rat eye is only about 4 times smaller in diameter than the human eye, the rat sclera is 5-10 times thinner than the human sclera [50]. In addition, the IAC creates an additional “weak point” in the rat sclera that does not exist in the human sclera. The strains we predicted were also similar to those determined by a recent experimental study on strains in the mouse astrocytic lamina under an IOP elevation from 10 to 30 mmHg [42], which estimated mean strains in the nasal-temporal and superior-inferior direction to be 5.21% and 3.74%, respectively.

Although we expected our models to produce asymmetric stress and strain patterns in the optic nerve, we were surprised by the predominantly inferior localization of the strain concentrations. Since the BM was modeled with a large modulus (7 MPa) compared to the optic nerve (0.03 MPa), we expected to see the highest strain concentrations where the BM overhang contacted the nerve. In addition, the previous rat glaucoma studies have reported a preferentially superior pattern of RGC axonal degeneration [25,26], leading us to predict that we would also see the highest levels of strain in the superior nerve. However, it was recently shown that astrocytes, known to be mechanosensitive, will reorient their processes in response to a chronic IOP elevation [26]. A follow-up study, which exposed rats to an acute IOP elevation, demonstrated that astrocytes in the inferior optic nerve tended to reorient their processes before those in the superior optic nerve [25]. This does seem to match with the prediction of our models that the most prominent strain concentrations occurred in the inferior nerve. As mentioned earlier, it is possible that these large strains primarily occur in the inferior nerve due in part to the inferior placement of the CRA, CRV, and IAC causing a weak region of the sclera just inferior to the scleral canal. At this point, we have only qualitatively compared patterns of strain between models, but plan to perform in-depth quantification of regional nerve strain levels in future work.

Limitations.

The models presented here have several limitations, primarily due to simplifications made in the assumed tissue constitutive relations. First, the stiffnesses that we used in our model were either derived from measurements from other species or were educated estimates. It is likely that the values we chose are at least within the correct ranges for each tissue, but in the future, it will be important to determine properties that are specific to the rat ONH. In addition, the assumption that the tissues behave as isotropic neo-Hookean solids falls short from modeling true soft tissue behavior in several ways. Notably, it does not capture the nonlinear stiffening behavior that soft tissues are known to exhibit as they experience increased strain. However, it is still useful to compare our model results to the previous studies on the human ONH which also utilized linear elastic material models. Second, modeling tissues as isotropic give them an unrealistically high bending stiffness since connective tissues generally have a higher tensile strength than compressive strength. Third, the isotropic assumption also fails to account for differences in in-plane stiffness which likely exist due to organization of collagen fibers. The isotropic assumption is especially likely to cause error in the modeled scleral and pia mater behavior. We have plans to include the effects of collagen fibers in the sclera in future modeling attempts and are interested to see if this will change the strain patterns we currently observe. Note that a representation of the pia mater with a lower compressive modulus could potentially decrease the strain concentration we currently see in the inferior nerve.

In this study, we have only presented results from three models. The previous studies have shown that eye-to-eye variations in geometry can have noticeable effects on ONH strain values [41], and we already saw differences in the models reported here. Modeling efforts are ongoing and we plan to model eight normal rat ONH geometries in total.

Although the histomorphometric method used to build the rat ONH digital reconstructions accurately preserves important anatomic and morphologic relationships, it is known that tissue fixation and tissue embedding cause differential shrinkage of tissue constituents which may distort ONH tissues prior to digital reconstruction and modeling [6]. Currently, there is no strategy to identify, quantify, and correct for these effects in our reconstructions. Their effects on the predicted stress and strain levels and patterns in our models are therefore unknown.

The computed results have not been experimentally validated. Although extremely challenging, it is possible that optical coherence tomography could be used to track the deformation of tissue landmarks during in vivo inflation testing of a rat eye and such displacements compared with computed values in the future.

Conclusion

We developed a method for creating individual-specific models of rat ONHs utilizing 3D point cloud data sets and presented initial strain results from three ONH models utilizing tissue properties similar to those used in earlier modeling studies on the human ONH [40,41]. Our models predicted more asymmetric strain patterns than in the human, higher strain magnitudes than in the human, and strain concentrations that align with recently reported patterns of astrocyte activation and reorientation. Applying this method to additional normotensive and glaucomatous rat ONHs and comparing their strain results to patterns of cell response from rat experimental glaucoma studies will help us to learn more about how biomechanics affects glaucoma pathophysiology.

Funding Data

• National Institutes of Health (NIH). NEI: T32EY007092, NEI: R01EY-010145, NEI: R01EY-016866, and EY011610.

• Research to Prevent Blindness (RPB). P30 EY010572 (OHSU).

• Georgia Research Alliance.

• Legacy Devers Good Samaritan Foundation.

• Sears Medical Trust.

• The Alcon Research Institute.

Nomenclature

BM =

Bruch's membrane

CRA =

central retinal artery

CRV =

central retinal vein

IAC =

inferior arterial canal

IOP =

intraocular pressure

ONH =

optic nerve head

PNVP =

perineural vascular plexus

RGC =

retinal ganglion cell