Electromyography-Driven Forward Dynamics Simulation to Estimate In Vivo Joint Contact Forces During Normal, Smooth, and Bouncy Gaits

Abstract

Computational models that predict in vivo joint loading and muscle forces can potentially enhance and augment our knowledge of both typical and pathological gaits. To adopt such models into clinical applications, studies validating modeling predictions are essential. This study created a full-body musculoskeletal model using data from the “Sixth Grand Challenge Competition to Predict in vivo Knee Loads.” This model incorporates subject-specific geometries of the right leg in order to concurrently predict knee contact forces, ligament forces, muscle forces, and ground contact forces. The objectives of this paper are twofold: (1) to describe an electromyography (EMG)-driven modeling methodology to predict knee contact forces and (2) to validate model predictions by evaluating the model predictions against known values for a patient with an instrumented total knee replacement (TKR) for three distinctly different gait styles (normal, smooth, and bouncy gaits). The model integrates a subject-specific knee model onto a previously validated generic full-body musculoskeletal model. The combined model included six degrees-of-freedom (6DOF) patellofemoral and tibiofemoral joints, ligament forces, and deformable contact forces with viscous damping. The foot/shoe/floor interactions were modeled by incorporating shoe geometries to the feet. Contact between shoe segments and the floor surface was used to constrain the shoe segments. A novel EMG-driven feedforward with feedback trim motor control strategy was used to concurrently estimate muscle forces and knee contact forces from standard motion capture data collected on the individual subject. The predicted medial, lateral, and total tibiofemoral forces represented the overall measured magnitude and temporal patterns with good root-mean-squared errors (RMSEs) and Pearson's correlation (p²). The model accuracy was high: medial, lateral, and total tibiofemoral contact force RMSEs = 0.15, 0.14, 0.21 body weight (BW), and (0.92 < p² < 0.96) for normal gait; RMSEs = 0.18 BW, 0.21 BW, 0.29 BW, and (0.81 < p² < 0.93) for smooth gait; and RMSEs = 0.21 BW, 0.22 BW, 0.33 BW, and (0.86 < p² < 0.95) for bouncy gait, respectively. Overall, the model captured the general shape, magnitude, and temporal patterns of the contact force profiles accurately. Potential applications of this proposed model include predictive biomechanics simulations, design of TKR components, soft tissue balancing, and surgical simulation.

Introduction

Estimating the forces applied to our joints by muscles, ligaments, and articulating surfaces as well as their contribution to joint loading is fundamental in understanding joint damage, function, and disease. Knee joint loading is an important parameter in the design and implantation of total knee replacement (TKR) components, as excessive joint loading can cause component wear and eventually lead to failure [1–3]. Excessive joint contact forces are also an important contributor to the development of osteoarthritis [4]. Knowledge of joint loading during daily activities is essential for understanding mechanisms of injury in the development of tissue engineered biomaterials [5], as well as developing, evaluating, and optimizing injury prevention strategies. Joint loads can be measured in vivo using instrumented TKRs [6,7] during dynamic activities. However, implementation of such devices is not common because it is invasive and expensive. Furthermore, the results are subject-specific and may not transfer to a healthy population. Thus, computational models for dynamic simulation [8–11] are more commonly used to estimate joint loads and muscle forces. Accurate prediction of joint loads under dynamic conditions requires accurate estimates of muscle forces, component and skeletal alignment, and ligament stiffness [12]. The resulting system is overdetermined with more muscles crossing the joint than degrees-of-freedom (DOF). The most common approach to solving this redundancy problem is static optimization [1,13]. In this approach, inverse dynamics is used to minimize a cost function such as muscle activation, contact energy, or muscle stress one frame at a time to find muscle forces that reproduce computed joint moments [14]. While this approach is computationally efficient, the physiological form of the cost function is unknown and this method may not account for variability in an individual's muscle activation patterns. Activation of a muscle can be task dependent and can vary for the same joint kinematics and kinetics. Another approach uses electromyography (EMG) signals in conjunction with a muscle model to estimate task-specific muscle forces [15–17]. The reliance of EMG-driven models on measured muscle activity takes into account an individual's activation patterns and muscle cocontraction. With the EMG-driven approach, no assumptions are required about the form of the cost function being minimized. However, “flexibility” still remains in the solution process as the absolute amplitude of each muscle excitation is difficult to determine, the number of EMG measurements is often limited, and EMG data are typically unavailable from deep muscles. Hybrid approaches [18,19] that combine EMG-driven models with either static optimization or computed muscle control take advantage of both optimization and EMG-driven approaches.

During the development of musculoskeletal models various assumptions are made, a few of these are phenomenological rather than established in biological or physiological evidence. To increase the accuracy of these models, additional studies measuring in vivo joint loading, joint kinematics, and musculoskeletal geometry are required. Such studies will provide a better understanding of the impact of size, age, morphology, or surgical history on model predictions and help define model limitations. Current musculoskeletal models often simplify or ignore the effects of soft tissue. However, coupling soft tissue deformation and muscle loading in concurrent simulation is essential for realistic prediction of osteokinematic, and more importantly, arthrokinematic motion and joint loading. The strength and ultimate goal of musculoskeletal modeling is to predict outcomes of an intervention or surgery. Despite these potential advantages, predictive musculoskeletal simulation has not been widely explored in clinical applications [20]. These simulations are not widely used due to high demand for computational efficiency [21], difficulty in defining relevant objective functions [22], and the complex computer programming required to build these simulations.

This paper presents a dual stage modeling method to predict tibiofemoral contact forces during three styles of overground gait. This study differs from earlier research in several respects. During the first stage, kinematic data are the sole input into the model, while the knee joint (tibiofemoral and patellofemoral) is allowed 6DOF. The knee joint is constrained by contact between articulating surfaces and ligament forces. In the second forward dynamics stage, muscle and joint loads are predicted in a single computational step using an EMG-driven feedforward with feedback trim motor control strategy. Traditional inverse dynamics optimization calculates moments about a knee modeled as a simple hinge or as a hinge with secondary motion prescribed based on flexion angle. The method proposed in this paper is conducive to models with 6DOF knee joints. Because ground reaction forces (GRFs) are not used as an input to the model, this method provides a foundation for predictive biomechanical simulation, testing different motor control strategies and incorporating proprioceptive feedback during movement.

The objective of this study was development of an EMG-driven, full-body, musculoskeletal model with subject-specific leg geometries including deformable contacts, ligaments, 6DOF knee joint, and a shoe-floor model that can concurrently predict muscle forces, ligament forces, and joint contact forces. Model predictions of tibiofemoral joint contact forces were evaluated against the subject-specific in vivo measurements from the instrumented TKR for three distinctly different styles of overground gait.

Methods

Experimental Data.

The data for this study were collected from an 83-year-old male subject (mass = 70 kg and height = 172 cm) with an instrumented TKR that measures the six loading components acting on the tibial tray. The experimental data were sourced from the sixth edition of the Grand Challenge Competition to Predict in vivo Knee Loads [6,23] and include motion capture marker trajectories (modified Cleveland Clinic marker set), GRFs and moments, EMG signals, dynamometer measurements, knee joint forces, geometries of the right leg bones and prosthetic, fluoroscopic, computed tomography, and magnetic resonance images. Motion capture marker trajectories, EMG, GRFs, and knee joint loads were collected simultaneously in a motion capture laboratory while the subject completed three different styles of overground gait: normal, smooth, and bouncy. One gait cycle for each gait style was chosen for modeling. The descriptions of the gait styles [24] were smooth: reduced superior–inferior translation of the pelvis during the gait cycle and bouncy: increased superior–inferior translation of the pelvis during the gait cycle. GRF data were sampled at 1000 Hz and passed through a low-pass filter with a 50 Hz cut-off frequency. Motion capture data were sampled at 120 Hz and passed through a low pass filter with 6 Hz cut-off frequency. Measured total knee contact forces were distributed into medial and lateral components using an experimental regression equation [25].

Knee Model.

The subject-specific knee model was created using the implanted component geometries and bone geometries segmented from computed tomography images of the subject (Fig. 1) in the multibody dynamic analysis program ADAMS (MSC Software Corporation, Santa Ana, CA). The right knee joint allowed 6DOF for the tibiofemoral and patellofemoral joints. The motion for both joints was constrained by a compliant contact force model with viscous damping [26,27], ligament forces, and the patellar tendon. The tibial insert was divided into medial and lateral geometries, with contacts created between each geometry and the femoral component. The contact force in the medial and lateral tibial inserts by means of a compliant contact was defined as

$$F_c=k{\delta }^n+B(\delta )\dot{\delta }$$ (1)

Fig. 1.

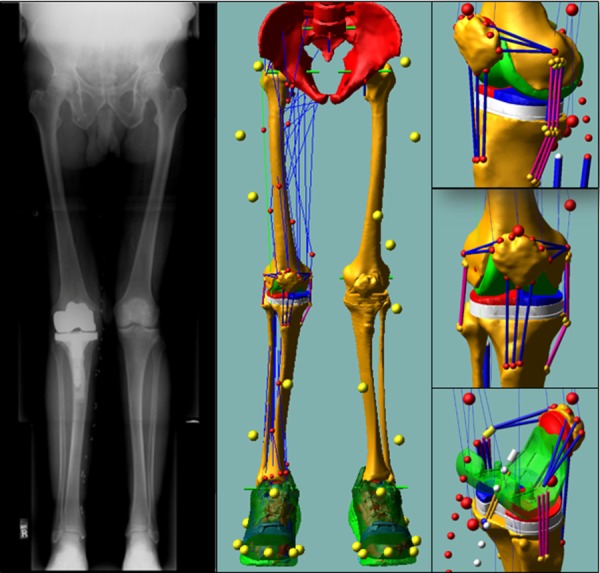
The knee model used subject-specific bone and knee prosthetic component geometries including ligaments and the patellar tendon. The knee model was integrated into a generic full-body model which included 44 muscle-tendon actuators acting about the hip, knee, and ankle. The standing radiograph was used to confirm limb alignment in the coronal plane.

where $F_c$ is the contact force, $\delta$ is the interpenetration distance between the geometries in contact, $\dot{\delta }$ is the velocity of interpenetration, $k$ is the contact stiffness, $n$ is the nonlinear power exponent, and $B(\delta )$ is a damping coefficient. The values implemented in this model were derived from a previous study [26] where $k=\mathrm{30,000}\mathrm{N}/{\mathrm{m}\mathrm{m}}^n$, $n=3/2$, and $B=40\mathrm{N}\mathrm{s}/\mathrm{m}\mathrm{m}$.

The ligaments were modeled as multiple bundles with origin and insertion site footprints based on anatomical studies [28–37]. The posterior cruciate ligament was separated into two bundles [38]. Three bundles were used for the lateral collateral ligament [29]. Five bundles were used for the medial collateral ligament, two deep and three superficial [30,39,40]. Three bundles each were used for the lateral and medial patellofemoral ligaments. The anterior cruciate ligament was not included in the model as the TKR surgery involved resection of this ligament. A generic piecewise function [41] defining the force-length relationship of ligaments was used to model each bundle. Ligament bundle stiffness and zero-load length values were used to scale the generic force-length relationship for each bundle. Ligament bundle stiffness values were obtained from the literature [41–45] and have been verified in a previous knee joint model [46]. The zero-load lengths for each ligament bundle were determined from open-chain knee flexion-extension joint range-of-motion trials where ligament force was assumed to be small (under 20 N). To prevent the superficial medial collateral ligament bundles penetrating into the bone and component geometries, wrapping was incorporated into the ligament. The quadriceps muscles inserted on the patella and the patellar tendon were modeled using three bundles with the same piecewise function used for the ligaments.

Shoe-Floor Contact Model.

The shoe-ground interface was modeled using deformable contacts between the shoe and force plate geometries. The shoe geometries were obtained by three-dimensional scanning shoes of the same size, model, and made used by the subject during the motion capture measurements. The shoe geometries were divided into three rigid bodies: (1) the region containing the heel and midfoot, (2) the region containing the metatarsals, and (3) the region containing the phalanges (Fig. 2). The regions were defined by visually inspecting the compliance and the geometry of the shoe during gait. Regions were attached to each other using six-axis springs. The shoe was attached to the body of the foot segment via a six-axis spring. A hinge joint was applied where the midfoot region joins the toe region to model the metatarsophalangeal joints. The six-axis springs serve as representative models for shoe compliance as well as relative movement of the foot within the shoe. Contacts were defined between the three rigid bodies and the force plates. The same shoe model was applied to both feet. Simple box representations were used to model the force plates.

Fig. 2.

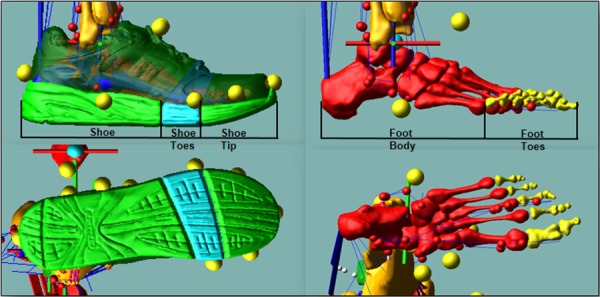
Shoe and foot model. The shoe geometry is divided into three rigid bodies: the shoe, shoe toes, and shoe tip. The foot geometry is divided into two rigid bodies: the foot body and foot toes. Deformable contacts are defined between the three shoe parts and the force plate.

Generic Musculoskeletal Model.

The generic full-body musculoskeletal model consisted of 21 rigid body segments, 53 revolute joints, and 44 right leg muscles. The lower limb extremity model is based on the model by Arnold et al. [47]. Regression equations from the U.S. Air Force's Generator of Body Data were used to determine generic joint center locations, mass, and inertial properties based on subject height, weight, and gender [48]. The generic bone geometries for the right leg were scaled to match the subject-specific bone geometries. These scaling factors were also used to scale muscle origins, muscle insertions, and muscle via points for the right leg. Each joint center was represented by three orthogonal revolute joints with the exception of the ankle and the metatarsophalangeal joint. The ankle was modeled using two hinge joints that defined the talocrural and the talocalcaneal axes [49]. The metatarsophalangeal joint was modeled using a single revolute joint. The hip joint center and the knee joint center were obtained using the symmetrical center of rotation estimation method [50] and symmetrical axis of rotation approach [51] applied to their respective joint range of motion trials. The scaled hip and knee joint center from the generic model were replaced by the symmetrical center of rotation estimation and symmetrical axis of rotation approach method joint centers. The relative motion between the head and the neck joint were fixed for this study. For each marker, a three-axis spring was defined between the body segment and the corresponding motion marker to allow relative movement between them. Markers defining the modified Cleveland clinic marker set locations were manually adjusted relative to their attached segment by minimizing the forces in the springs. The subject-specific femur and tibia along with the femoral and tibial components were manually aligned to the scaled generic model. Ellipsoidal wrapping surfaces and via points [47] (Fig. 3) were used to define muscle-tendon paths inhibited by bones and deeper muscles. Using wrapping surfaces allows the model to reflect more accurately operating lengths, muscle moment arms, and force production ability for muscles in the lower limb.

Fig. 3.

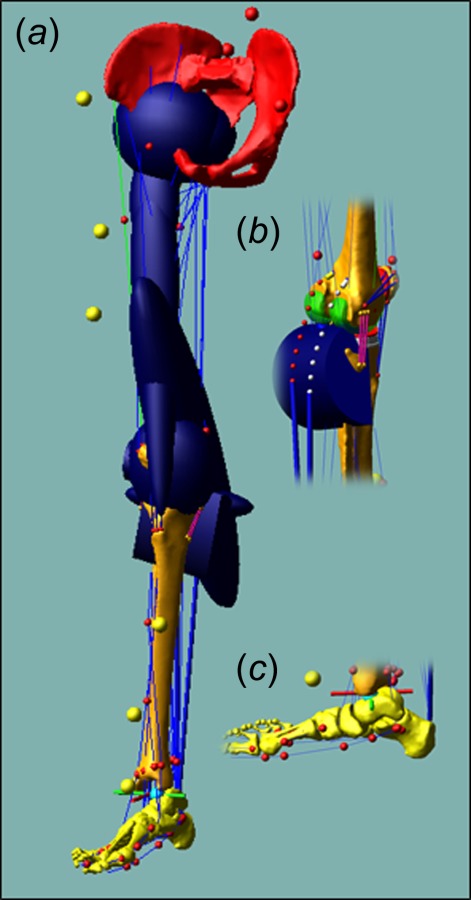
Three-dimensional model of the lower limb: (a) bony geometries including the wrapping surfaces for the pelvis, femur, and tibia, (b) wrapping surfaces for the medial and LG, and (c) via points for ankle plantar flexors

Subject-Specific EMG-Driven Muscle Model.

Surface EMG data were collected for 16 lower extremity muscles (Table 1) on the right side. These muscles were adductor magnus (AddM), biceps femoris long head (BFLH), gluteus maximus (GMAX), gluteus medius (GMED), gracilis (GRA), lateral gastrocnemius (LG), medial gastrocnemius (MG), peroneus longus (PL), rectus femoris (RF), sartorius (SAR), semimembranosus (SM), soleus (SO), tensor fasciae lata (TFL), tibialis anterior (TA), vastus medialis (VM), and vastus lateralis (VL). After evaluating EMG patterns of the BFLH, GMED, and VM for all measured trials, it was determined that the EMG signals were in error and EMG signals for these muscles were replaced by average activations from an age-matched population during normal gait. Muscle activation for vastus intermedius (VI) was estimated as the average of VM and VL activation values. Semitendinosus was assumed to have the same activation as SM. Biceps femoris short head (BFSH) was presumed to have the same activation as BFLH [16]. To generate subject-specific and trial-specific muscle forces, recorded EMG for normal, smooth, and bouncy gait trials were high-pass filtered using a fourth-order Butterworth filter with a cutoff frequency of 30 Hz, rectified. They were then low-pass filtered with a cutoff frequency of 4 Hz to obtain linear envelopes for each muscle similar to the procedure described by Lloyd and Besier [16]. The linear envelopes were normalized to the peak values obtained from a series of available isometric and quasi-static force tasks. Two types of model parameter values were implemented: (1) activation dynamics parameter values and (2) contraction dynamics parameter values. The EMG-to-activation model is a first-order dynamic model based on the work of Thelen [52] and Winters [53]. The activation and deactivation time constants are assumed to be 10 ms and 40 ms, respectively [54]. For the Hill-type muscle-tendon model, initial parameter values, including optimal muscle fiber length, tendon slack length, and peak isometric muscle force, were taken from Arnold et al. [47] and scaled according to subject height and bone geometries. A custom Hill-type muscle model [47] with an inextensible tendon [55] was implemented in Simulink (The MathWorks, Inc., Natick, MA). Previously implemented EMG-driven models [16,17,56] tune or calibrate their models to identify the set of muscle parameters reproducing moments computed from inverse dynamics and no such calibration was performed on these models.

Table 1.

Muscles with feedforward signal and feedback trim and their corresponding EMG signal inputs

Measured EMG	Muscle model
AddM	AddM distal
	AddM ischial
	AddM middle
	AddM proximal
BFLHa	BFLH
	BFSH
LG	LG
MG	MG
GMAX	GMAX superior
	GMAX middle
	GMAX inferior
GMEDa	GMED anterior
	GMED middle
	GMED posterior
GRA	GRA
PL	PL
RF	RF
SAR	SAR
SM	SM
	Semitendinosus
SO	SO
TFL	TFL
TA	TA
	VIb
VL	VL
VMa	VM

^aReplaced by average activations from a similar age matched population.

^bEqual to the average of the signals from the medial and lateral vasti.

Gait Simulation.

The experimental motion capture data for three gait styles (normal, smooth, and bouncy) were used as inputs in inverse kinematics analyses. During these analyses, measured marker trajectories drove motion constraints connected to three-axis springs associated with the corresponding body segments, during which, muscle-tendon lengths for the right leg and joint angles for the left leg and upper body were recorded. During inverse kinematics, the knee joint was constrained by ligament forces and contact forces, and the shoe ground interface contact constraints were included. For forward dynamics simulations (Fig. 4), the motion constraints were eliminated and muscle forces drove the right leg. Joint torques drove the upper body and left leg. Feedback controllers produced joint torques tracking inverse kinematics joint angles for the upper body and contralateral limb. A feedforward with feedback trim control scheme (Fig. 4) was used to produce muscle forces for the right limb. The feedforward muscle scheme incorporated experimental EMGs when available (Table 1) with a Hill-type muscle model to produce feedforward muscle forces. A feedback trim scheme was used to modulate the feedforward muscle force such that muscle-tendon lengths from the inverse kinematics step were maintained. The feedback trim controller adds to feedforward muscle forces if these forces are insufficient to maintain inverse kinematics musculotendon lengths during forward dynamics simulations to produce the total muscle force. In other words, muscle force is augmented if the forward dynamics length is greater than inverse kinematics length at a given time-step. Similarly, the feedback trim controller will decrease muscle force if the current forward dynamics musculotendon length is too short. For muscles without measured EMG signals, the feedforward muscle forces come only from passive muscle properties. The feedback controller parameters were scaled based on physiological cross-sectional area in order to account for muscle size. As motion and EMGs were the inputs to the modeling scheme, tibiofemoral joint contact forces could be compared to measured forces.

Fig. 4.

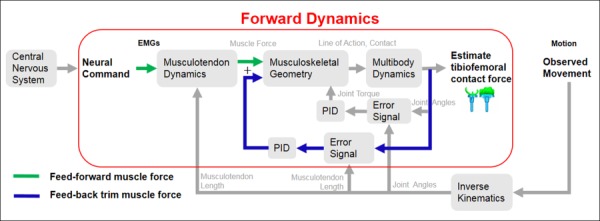
Feedforward with feedback control scheme for calculating muscle forces and joint contact forces. The feedforward muscle scheme incorporates experimental EMG in conjunction with musculotendon (activation and contraction) dynamics to produce feedforward muscle forces. The feedback muscle scheme uses the error between the current muscle length and the desired muscle length to produce feed-back trim muscle forces. The predicted muscle forces are the sum of the feedforward muscle forces and calculated feed-back trim muscle forces.

Model Evaluation.

The model predicted results were resampled to a time interval from 0% to 100% gait cycle using cubic spline interpolation. Differences between the measured and predicted forces were assessed by calculating Pearson's correlation coefficient (P²), root-mean-squared errors (RMSEs), and the coefficient of determination (R²). Pearson's correlation coefficient is used as a measure of shape differences. Values may range between −1 and 1, with values of 1 indicating a complete positive correlation, and 0 no correlation. The RMSE is used as a measure of magnitude differences. The coefficient of determination is used as a measure of both magnitude and shape differences. The total muscle force, which is the output of the feedback trim controller, is used in the forward dynamics simulations. Comparison of normalized experimental EMG and predicted total and feedforward muscle forces is used to evaluate the contribution of the feedforward muscle force to the total muscle force required for forward dynamics simulation.

Results

The model predictions of medial, lateral, and total tibiofemoral contact forces followed the measured temporal patterns with good Pearson's correlation (p²) during normal (0.92 < p² < 0.96), smooth (0.81 < p² < 0.93), and bouncy (0.86 < p² < 0.95) gaits, respectively (Fig. 5). The temporal patterns of the stance phase were well predicted in both compartments for all three trials with the predicted terminal stance phase having the least correlation. Much of this trend is attributed to the shoe-floor model and a premature heel strike on the contralateral limb. On average, the greatest agreement between the measured and predicted forces was in normal gait. For normal gait, the RMSEs between predicted and measured medial, lateral, and total contact forces were 0.15 body weight (BW), 0.14 BW, and 0.21 BW and the R² were 0.9, 0.85, and 0.93, respectively. The greatest differences were observed in bouncy gait, with RSMEs between predicted and measured medial, lateral, and total contact forces of 0.21 BW, 0.22 BW, and 0.33 BW, respectively. The corresponding R² values were 0.85, 0.64, and 0.87.

Fig. 5.

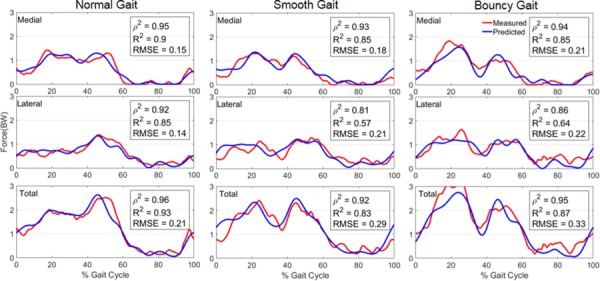
Medial, lateral, and total tibiofemoral contact forces compared with in vivo measurements obtained during three modifications of gait. Contact force is scaled to bodyweight with 1 BW equal to 686 N.

The predicted pattern and timing of the feedforward and total muscle forces were compared along with the measured EMG signals for the primary muscles involved during gait. In general, the total muscle forces used to drive the forward dynamics simulations were similar to the feedforward muscle forces generated by the Hill-type muscle models for the major muscles of gait (Fig. 6) (for additional muscles see Supplemental Information available under “Supplemental Materials” tab for this paper on the ASME Digital Collection). An exception was the MG where feedforward muscle forces during terminal stance are decreased by the feedback trim controller, particularly for bouncy gait. Feedforward forces for the VL were also decreased during the loading response phase of gait. For the GMED, the feedback trim controller added muscle force during mid-stance and terminal stance, indicating that the feedforward force for this muscle was not sufficient to maintain the muscle lengths derived during inverse kinematics. Measured EMG signals for the GMAX and VL muscles increased from normal to smooth gait and again from smooth to bouncy gait. There was a corresponding match in both feedforward and total muscle forces for these muscles. The ground reaction force RMSEs were less than 0.08 BW for the anterior–posterior and medial–lateral shear directions and less than 0.22 BW in the vertical direction for the three different styles of gait.

Fig. 6.

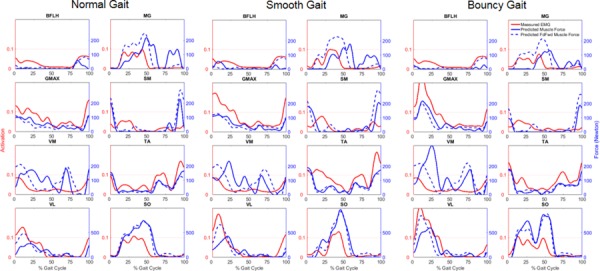
Comparison of normalized experimental EMG and predicted total and feedforward muscle forces for the muscles of BFLH, MG, GMAX, SM, GMED, TA, VL, and SO for the three versions of gait. Note: scale for muscle forces of VL and SO (bottom row) is greater than scale for other muscles.

Discussion

Various studies have demonstrated the potential of EMG-driven musculoskeletal models [15–17] in estimating muscle forces, providing understanding of normal and pathological movements, and complementing interpretations obtained via standard motion capture studies. Our primary objective for this paper was to describe our EMG-driven, subject-specific musculoskeletal modeling methodology. This methodology has the capability of concurrently simulating joint contact mechanics, shoe-ground interactions, and muscle forces. The second objective for this paper was to provide a comparison between our predictions of joint contact forces to known values recorded for a subject for three distinctly different styles of gait with the goal of validating our model. The sixth grand challenge data set provides a unique opportunity to evaluate our modeling method by providing data for a subject with an instrumented TKR which continuously measured six loading components on the tibial tray. Experimental data were collected for three gait styles: normal, smooth, and bouncy. A subject-specific knee model was created from the experimental data and incorporated into a generic full-body musculoskeletal model. The muscle force estimates were based on subject specific muscle activation patterns derived from recorded EMG and knee contact forces were used as a means for indirect validation of muscle force estimates.

Thanks in large part to the publicly available data set provided by the Grand Challenge Competition to Predict In-Vivo Knee Loads, musculoskeletal modeling and simulation techniques have seen notable advancements in recent years. An array of musculoskeletal modeling methods has been used to predict muscle forces and the resulting contact forces during movement including EMG-driven models [17], static and dynamic optimization techniques [8–11], hybrid methods [18,19], and parametric methods [57] to solve the muscle redundancy problem. The 2012 “Grand Challenge” winner [17] introduced an EMG-driven model which estimated muscle forces by solving an inverse dynamics based optimization problem. However, the modeling approach prescribed motion to the pelvis, assumed two DOF at the knee, and used GRFs as model inputs. We have extended this approach by developing a full-body musculoskeletal model that is torque driven for the upper body and left leg, and includes a 6DOF knee joint and a shoe-floor contact model in lieu of GRFs as an input. Our knee contact force predictions (RSMEs: medial = 0.15 BW and lateral = 0.14 BW in normal gait) are slightly better than those obtained using the previous EMG-driven model (RSMEs: medial = 0.16 BW and lateral = 0.22 BW in normal gait). The 2016 “grand challenge” winner [9] introduced a full-body model with a simple knee contact model that used an inverse dynamics based optimization method to estimate muscle forces. However, the modeling approach assumed three DOF at the knee and used GRFs as model inputs. Our joint contact load prediction errors (RSMEs: medial = 0.18 BW and lateral = 0.21 BW in smooth gait; medial = 0.21 BW and lateral = 0.22 BW in bouncy gait) are comparable and even slightly better to that obtained using the proposed approach (RSMEs: medial = 0.22 BW and lateral = 0.27 BW in smooth gait; medial = 0.20 BW and lateral = 0.25 BW in bouncy gait); the results obtained were also more accurate than those that have been acquired using forward dynamic simulations or traditional optimization [8–11] in the 2016 competition. Only one [10] of the 2016 competitors modeled normal gait using a one DOF knee model, our joint load predictions errors (RSMEs: medial = 0.15 BW and lateral = 0.14 BW in normal gait) are better than that obtained (RSMEs: medial = 0.26 BW and lateral = 0.63 BW in normal gait) using an inverse dynamics based optimization model.

Our knee model, shoe-floor contact model, and simulation technique include several unique features. Typically, during inverse kinematics or inverse dynamics, the knee joint is constrained by a single DOF (flexion–extension) joint and secondary DOFs are constrained to be functions of knee flexion–extension. This assumption removes any interdependence of contact forces on the muscles as well as muscle force influence to motion in the frontal and transverse planes. In this study, during both the inverse kinematics and forward dynamics simulations, the knee was constrained by ligament forces and tibiofemoral and patellofemoral contact forces allowing 6DOF. Accurately modeling the shoe-ground interface is important for accurate prediction of joint contact forces. Our shoe-floor contact model included three rigid shoe segments per shoe, translational motion between the foot and shoe, and deformable contact between shoe and ground geometries. In the absence of experimental knee contact forces, evaluations of the predicted GRF against measured GRF may offer indirect validation of joint load predictions. Also, the proposed framework is more conducive for predictive musculoskeletal simulations where, in the absence of experimental data or in efforts to predict new motions, contact with the environment (e.g., ground) must be modeled.

The feedforward with feedback trim control scheme allows simultaneous estimates of muscle forces, ligament forces, and medial and lateral knee contact forces. Hill-type muscle models rely on accurate estimation of subject-specific model parameters, such as optimal muscle fiber length, tendon slack length, and peak isometric muscle force. Given the errors associated with EMG measurement and Hill-type muscle models, a true EMG-driven forward dynamics model is not reasonably possible. To reduce sensitivity to measurement and model parameter uncertainty, a feedback trim controller is employed to ensure that the model tracks measured kinematics by reducing the error between the current forward dynamics musculotendon length and the inverse kinematics recorded musculotendon length. Muscle activation can be task dependent, even for gait. This is evidenced by the different activation profiles, for similar joint angles, of the GMAX, VL, and TA during the different styles of gait (Fig. 6). Hence, we believe that in order to produce better physiological estimates of muscle forces, EMG data as model inputs should be used. The computational performance is relatively quick for both inverse kinematics and forward dynamics taking under 25 min on a desktop PC (Windows 7, 3.4 GHz Intel Core i7-4770 CPU, 16 GB RAM), when compared to dynamic optimization based approaches. The faster simulation time facilitates sensitivity analyses and predictive simulations, promoting understanding of causes for movement deviation, and ultimately assisting assessment of treatment options in response to clinical questions. However, the major challenge of applying this methodology in the clinical setting remains subject-specific geometry generation.

In order to accurately interpret the results of this study, multiple limitations in methodology must be noted. First, a single gait trial from each gait style from a single subject was analyzed. Data from additional trials and subjects are necessary in order to assess the extent to which these results can be generalized. In the multibody framework, joint loading predictions were estimated using a compliant contact force model with viscous damping rather than a finite element model which could better represent component deformation. Cosimulating multibody dynamics and linear or nonlinear finite element methods to predict refined estimates of deformation and stress is an area we are pursuing. The muscle modeling parameters and architecture parameters were based on a published generic musculoskeletal model [47] and assumed linear scaling. Inclusion of magnetic resonance image-based subject-specific muscle parameter prediction [58] and more complex muscle-tendon dynamics models such as equilibrium or damped-equilibrium models [55] would improve feedforward muscle force predictions. Our models used a feedforward with feedback trim control scheme to predict forward dynamics muscle forces. The maximum EMG signal from various trials was used to normalize EMG data, but the accuracy of the EMG normalization is unknown. The feedforward control scheme relies on experimental EMG traces, when available, coupled with Hill-type models to estimate muscle force. The EMG signals from three muscles (VM, GMED, and BFLH) were replaced with age-matched average EMG signals from normal gait, contributing to errors in model force predictions, especially for smooth and bouncy gaits. The feedback trim controller will add to feedforward muscle forces if this force is insufficient to maintain inverse kinematics musculotendon lengths during forward dynamics simulations. The feedback trim controller is necessary for forward dynamics simulations, but it has no physiological basis and may reduce cocontraction of antagonistic muscles. Magnetic resonance images were not available for this subject and ligament attachment footprints in the model were obtained in relation to anatomical landmarks. Hence, incorrect attachment sites and zero-load length determination could affect model predictions. Precisely modeling the shoe-floor interface is critical in accurately predicting joint loading. Errors in prediction of vertical GRF and a premature heel strike on the contralateral limb indicate that improvements in the foot/shoe/floor model are necessary. Experimental measurement of foot/shoe motion and subject specific shoe compliance is recommended for future studies.

In summary, this study presented an EMG-driven musculoskeletal model with subject-specific joint anatomy to predict in vivo TKR mechanics during walking. Joint loading predictions agreed well with in vivo measurements obtained via an instrumented TKR. Thus, the proposed framework is conducive for application in predictive biomechanics simulations, design of TKR components, soft tissue balancing, and surgical simulation.