Statistical Characterization of Human Brain Deformation During Mild Angular Acceleration Measured In Vivo by Tagged Magnetic Resonance Imaging

Abstract

Understanding of in vivo brain biomechanical behavior is critical in the study of traumatic brain injury (TBI) mechanisms and prevention. Using tagged magnetic resonance imaging, we measured spatiotemporal brain deformations in 34 healthy human volunteers under mild angular accelerations of the head. Two-dimensional (2D) Lagrangian strains were examined throughout the brain in each subject. Strain metrics peaked shortly after contact with a padded stop, corresponding to the inertial response of the brain after head deceleration. Maximum shear strain of at least 3% was experienced at peak deformation by an area fraction (median±standard error) of 23.5±1.8% of cortical gray matter, 15.9±1.4% of white matter, and 4.0±1.5% of deep gray matter. Cortical gray matter strains were greater in the temporal cortex on the side of the initial contact with the padded stop and also in the contralateral temporal, frontal, and parietal cortex. These tissue-level deformations from a population of healthy volunteers provide the first in vivo measurements of full-volume brain deformation in response to known kinematics. Although strains differed in different tissue type and cortical lobes, no significant differences between male and female head accelerations or strain metrics were found. These cumulative results highlight important kinematic features of the brain's mechanical response and can be used to facilitate the evaluation of computational simulations of TBI.

Introduction

Traumatic brain injury (TBI) of varying severity is prevalent in both the civilian and the military populations [1]. Mild TBIs and concussions are an increasingly prominent health concern for both active youths and adults in the military and in impact sports [2,3], particularly with the links established to chronic traumatic encephalopathy [4,5] and post-traumatic stress disorder [6]. Injurious stretching of axonal tracts [1], cerebral vasculature [7], and other intracranial tissues—a result of rapid accelerations of the head—is implicated in both the primary and secondary effects of nonpenetrating TBI. However, the roles of various factors such as the magnitude, frequency, and location of mechanical trauma in brain injury and neurological outcomes have yet to be fully elucidated. Recent work has shown that even at subconcussive levels, repetitive impacts to the head can result in metabolic shifts [8,9], short- and long-term cognitive impairment [10,11], and morphologic changes [12,13], substantiating the need for further research in the biomechanical response of the brain to various levels and frequencies of external forces.

Experimental data are necessary to quantify how the brain deforms in response to inertial loading; however, brain deformation cannot be studied in a live human subject during an injury-level impact. Instead, physical models, animal models, and cadavers have been largely employed to date [14–16]. Gel-filled surrogates have been used to estimate the deformation response of the brain to angular head acceleration [14,15]. In those studies, patterns of deformation were compared to histopathology results from a baboon model and a porcine model of diffuse axonal injury, leading to threshold estimates of injury. Tagged magnetic resonance imaging (MRI) was previously used to measure the deformation response of the brain to a rapid skull indentation of 1–2 mm in rat pups [16]. Although animal models have advantages for studying the relationship between known inertial conditions and injury, accounting for the differences between animal and human brain geometry and structure to translate the animal tissue response to human brain motion and injury remains a challenge.

Deformations have also been measured from clusters of neutral density targets implanted in human cadavers and tracked with high-speed bi-planar X-ray. Zou et al. [17] estimated rigid-body displacement and brain deformation from six low-severity impact tests acquired by Hardy et al. [18]. Hardy et al. later conducted an additional 35 impact tests on eight cadaver heads for impacts ranging from 38 to 291 g and 2370 to 24,206 rad/s² [19]. Maximum principal strain and maximum shearing strain, estimated from tracked displacements, provide considerable information about how the postmortem brain deforms across a wide range of loading conditions. However, the strain resolution is sparse due to the need to implant neutral density trackers into the brain, in addition to various limitations of bi-planar imaging with radiopaque markers. More recent in situ work in the cadaveric brain has shown that more sophisticated imaging techniques can provide three-dimensional (3D) tissue deformation data at high impact rates [20]. Nonetheless, the extent of the changes in material properties and physiology on the deformation response of the postmortem brain remains unclear and may vary depending on experimental conditions, confounding validation of models that ideally predict brain deformations in living adults of varying age and size.

To better understand the mechanisms of brain injury and predict the mechanical response of the brain to head motion, both experimental and computational approaches are therefore necessary. The observed mechanical behavior of brain tissue is highly dependent on the kinematics and kinetics of motion [21,22]. Computational models that are validated at a range of length scales and rates, from high-energy to subconcussive impacts, therefore provide better confidence in the model performance. Importantly, models that utilize strain thresholds such as maximum principal strain [23,24] and cumulative strain damage measure [21,25] to estimate brain injury [26] and functional deficits [27] are best validated against experimentally observed tissue strains in the whole brain. Therefore, in this study, we aimed to measure the in vivo strain response of the brain during a low-rate rotational motion of the head.

The brain deformation response of the live human brain to very low-level impacts has been measured using tagged MRI. Two-dimensional (2D) deformations were measured in three subjects during a mild linear head acceleration of 2–3 g [28] and in three subjects during mild angular head acceleration of approximately 244–370 rad/s² [29]. These experiments provided high resolution spatiotemporal strain measurements in the live human in one to two slices; the number of slices was limited because the subject had to repeat the motion 72–144 times to acquire a single slice of data. More recently, our group implemented a novel double-trigger tagged MRI sequence [30] that allows us to acquire a single slice of data in eight head rotations. This makes it possible to obtain a sufficient number of slices to provide full-brain coverage in a single imaging session. However, no study has yet examined full-brain biomechanics using these MRI techniques in a larger population sample of healthy humans.

The current study extends prior work by (1) acquiring an image volume spanning the whole brain, (2) determining strain in different anatomical regions, and (3) performing measurements in a cohort of 34 healthy human volunteers (17 females, 17 males). We report the population-wise brain deformations for various tissues and regions of the brain as identified by segmentation of high-resolution anatomic images. Additionally, we examined bias of the tagged MRI analysis, as well as the precision of displacement and strain measures. This in vivo study takes important steps toward understanding the mechanical behavior of the entire human brain and the association of that behavior to known loading conditions, while providing information-rich datasets achieved within single imaging sessions for the development of more biofidelic brain models.

Methods

Healthy human volunteers, with no history of spinal cord injury, head injury, or other musculoskeletal conditions that limit head motion, were recruited for the measurement of brain deformations under mild angular acceleration of the head and neck. Informed consent was obtained from each volunteer prior to scanning under an approved protocol by an Institutional Review Board at the National Institutes of Health. Total MRI scanning was restricted to be no longer than 2 h per session and consisted of anatomical MRI scans and tagged MRI within a head-rotation device.

Anatomical Images.

Volunteers were positioned head-first and supine in a 3-T Siemens Biograph mMR (Erlangen, Germany) for structural scans prior to tagged MRI of brain motion. A T1-weighted Magnetization-Prepared Rapid Acquisition Gradient Echo (MPRAGE) was acquired using either a 16- or 32-channel head coil. The echo time, inversion time, and repetition time were 3.03 ms, 1100 ms, and 2530 ms, respectively. The spatial resolution was 1 mm isotropic (256 × 256 × 176).

Head Rotation Device.

For tagged MRI under mild head angular acceleration, volunteers lay with their head secured within an MRI-compatible, rotational head support (superficially modified from a previously published design [29], with an added angular sensor, for use in the current MRI system). Images in this configuration were acquired with a six-channel receive-only body array coil, which was positioned over the rotational head support, and two three-channel receive-only spine coil arrays inlaid within the examination table. Participants voluntarily released a latch that permitted a head rotation of approximately 32 deg about the inferior-superior axis toward the left shoulder. An off-axis counterweight encouraged head rotation. Impact between the counterweight and a padded stop generated a rapid deceleration of the head of approximately 200 rad/s², which is in the range of 10–15% of the angular accelerations experienced by soccer players when heading a ball [31]. The angular position of the head support was measured using an MRI-compatible optical position sensor (Micronor, Camarillo, CA), which was set to record at 1176 samples/s (every 0.85 ms) and provided an angular resolution of 8191 counts per full 2π turn or 0.046 deg. Tracking of angular kinematics permitted the identification of initial impact, or contact, as the time frame during which head deceleration occurred, while the full rebound period was defined as all times after contact. Peak accelerations during contact and rebound could then be compared across subjects.

Tagged Magnetic Resonance Imaging During Mild Angular Acceleration.

To visualize tissue deformations, MRI tagging and the acquisition of sequential image frames was synchronized to the angular position during each voluntarily initiated head rotation. MRI tagging noninvasively places a spatial pattern on the image, referred to as “tag lines,” that moves and deforms with the object being imaged. Multiframe images were acquired using a double-triggered, tagged MRI pulse sequence to reduce unwanted motion artifacts, as previously described [30]. Briefly, the first optically gated trigger activated a 1–1 Spatial Modulation of Magnetization (SPAMM) tagging preparation [32], which generated tag lines spaced at 8 mm and oriented at 30 deg, every time the subject initiated a head rotation (Fig. 1). During each head rotation, when the head support rotated through 28.5 deg, a segmented cine gradient echo acquisition was initiated via a second trigger signal sent from the angular position encoder [30]. Because tag lines were applied only once, and at an angle at the initiation of head rotation, the tag lines of the multiframe, cine acquisition are approximately aligned to the readout direction [30] in the x or y direction (Fig. 1). The position-controlled double-trigger system permitted repeatable synchronization of the image acquisition in coordination with the measurement of the kinematics of each head rotation [30].

Fig. 1.

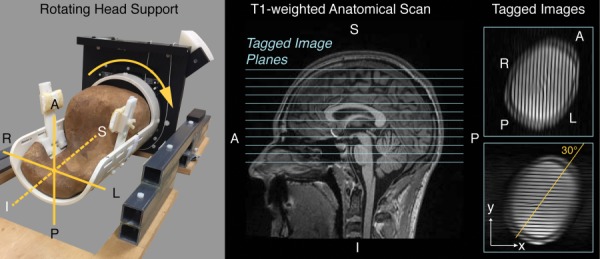
Head support device showing right to left rotation direction (arrow) for tagged image acquisitions during mild head acceleration. The head support pivots about a superior (S) to inferior (I) axis (dotted line), so that subjects' heads were rotated toward their left shoulder. Axial tagged image planes of 8 mm thickness were acquired 10 mm apart (center-to-center) as indicated on the T1-weighted image of a representative subject to provide adequate volume coverage of brain tissues. Tag lines, which are applied immediately after the volunteer initiates the rotation, were aligned at 30 deg from the anterior (A) to posterior (P) and left (L) to right (R) axes to provide sensitivity to in-plane motion in the x and y directions after the approximately 30 deg rotation [30].

Images were acquired in the axial image orientation with a base resolution of 160 × 24 (readout by phase encode) and was reconstructed to 160 × 160 [30]; the corresponding nominal voxel size was 1.5 by 1.5 mm², with 8 mm thick slices. The temporal resolution between image frames was 18.06 ms; the echo time and the repetition time were 1.67 and 3.01 ms, respectively, with six lines of data in the phase-encode direction acquired per image frame. Although up to 13 frames were collected depending on the subject, only ten image frames were analyzed collectively across all subjects.

Since a segmented cine acquisition was used, four head rotations were required to generate a single multiframe tagged image set using the double-triggered acquisition [30]. Two tagged multiframe image sets, with tag lines in orthogonal orientations, were needed to track each component of motion and estimate deformation within an anatomic slice. Sufficient slices were acquired to cover the cerebral cortex at a spacing of 1 cm between slice centers. The total number of axial slices varied across subjects, ranging from 10 to 13, to provide a full-volume tagged image set.

A 2 mm isotropic MPRAGE (128 readout by 128 phase encode by 88 slices) and a set of tagged images with the subject's head stationary (termed “reference” tagged images) were acquired to aid the registration of the tagged images during motion to the 1 mm MPRAGE. The echo time, inversion time, and repetition time were 3.03 ms, 1100 ms, and 2530 ms, respectively.

For the reference tagged images, the acquisition matrix was 160 × 80 (reconstructed to 160 × 160), providing a nominal in-plane pixel size of 1.5 × 1.5 mm² in axial slices, corresponding in number to those for tagged MRI under rotation, with 8 mm slice thickness and 10 mm center-to-center slice separation. The reference tagged images were also used to estimate bias of the strain measurements over time. The temporal resolution in this stationary condition was 83.7 ms; the pulse echo and repetition times were 1.67 and 3.1 ms, respectively, with 27 segments.

Image Segmentation and Registration.

Brain segmentation was performed using the subject-specific sparse dictionary learning algorithm [33] applied to the 1 mm isotropic resolution MPRAGE scans. Segmented regions consisted of the whole brain, cortical gray matter, cerebral white matter, and deep gray matter, which included the caudate, thalamus, and putamen. Brain tissue volumes were also estimated from the segmentation of T1-weighted MPRAGE images of 1 mm isotropic spatial resolution. Lobar parcellation (FreeSurfer, Charlestown, MA) was performed to divide cortical gray matter into left and right frontal, parietal, occipital, and temporal lobes.

Because tagged MRI data were acquired with a different coil and with the subject's head within the head rotation device, the subject's head was in a different position than the 1 mm MPRAGE used for high-resolution segmentation. To map the segmentation labels into the tagged image space, first the 1 mm MPRAGE was rigidly registered to the 2 mm MPRAGE. Then, the reference tagged image, which was acquired in the same imaging space as the 2 mm MPRAGE, was rigidly registered to the first frame of the tagged data, which was acquired just prior to impact [30]. The resulting transformation matrices were concatenated and the segmentation labels were transformed to the tagged image space using nearest-neighbor interpolation.

Tissue Displacements and Strain.

All subsequent data analyses were performed in matlab (Mathworks, Natick, MA), unless otherwise noted. Motion was tracked between tagged image frames using harmonic phase (HARP) analysis [34] and shortest-path HARP refinement [35], using the first frame as the reference configuration. For each voxel, a displacement vector (u) was computed between the voxel center in the first, or reference frame, to its location in subsequent image frames. The Lagrangian strain tensor (E) was then computed from the displacement vectors [36] at each reference point as

$$\mathit{E}=\frac{1}{2}\left[\nabla \mathit{u}+{(\nabla \mathit{u})}^{\mathrm{T}}+\left(\nabla \mathit{u}\right){\left(\nabla \mathit{u}\right)}^{\mathrm{T}}\right]$$ (1)

where ${\left(·\right)}^{\mathrm{T}}$ is the transpose and ∇ is the gradient operator. Maximum shear strain (${\gamma }_{\mathrm{m}\mathrm{a}\mathrm{x}}$) was then computed as an invariant measure of the tissue deformation as

$${\gamma }_{\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{1}{2}\left(E_1-E_2\right)$$ (2)

where E₁ and E₂ are the first and second principal strains (or eigenvalues of the 2D strain tensor E), respectively. Displacements and strains were computed for each frame after Refs. [30] and [37], with frame times reported here as the end time of each 18.06 ms-long frame.

Experimental Studies and Subject Groups.

Of the total 42 subjects imaged during head rotations under the approved protocol, subjects excluded from analysis include those for whom consistent head rotations (defined as a standard deviation of peak acceleration of less than 30 rad/s²) could not be achieved, often due to voluntary or reflexive resistance to the rotation motion (five subjects). Within the data set for each subject, an imaging plane was excluded from analysis if one or both tagged images contained artifacts that would skew HARP analysis (e.g., blurred tag lines and failed phase unwrapping). Subjects were also excluded from the analysis here if over 30% of the brain volume was thus eliminated (three subjects). Displacements, strains, and area fractions were estimated as described previously for a total of 34 subjects (17 females and 17 males) that remained after exclusions (Table 1). Subgroups of volunteers selected from this primary subject pool were used in separate studies to evaluate bias and precision, which are described further below. Subjects reported no adverse effects immediately after imaging and at the 1 week follow-up.

Table 1.

Demographics of consented volunteers (mean ± standard deviation) included in this study.

	n	Age (year)	Height (cm)	Weight (kg)
All	34	30.9 ± 8.2	171.8 ± 10.0	71.5 ± 14.4
Female	17	29.3 ± 6.7	164.9 ± 5.6	64.7 ± 13.3
Male	17	32.4 ± 9.5	178.6 ± 8.6	78.3 ± 12.2
Female versus male (p)		0.34	<0.001	<0.001

Note: Statistically significant p values are indicated in bold.

Experimental data were collected by one of three investigators (DDC, AKK, and YL). Tagged MRI was analyzed for comparison of strain metrics across subjects and among the various tissues of interest. Strains in regions of interest were quantified on a frame-by-frame basis and also with respect to the peak strain measured within a voxel over the course of all frames.

To compare between subjects, area fraction was defined as the percentage of voxels of interest in which the strain metric exceeded a specified threshold. Area fractions were calculated for E₁, E₂, and γ_max for the total brain, each brain tissue type, and each cortical lobe. Accelerations during head rotation were calculated from the angular position using the manufacturer's controller and data acquisition software (zapview and pcs monitor v1.0.0, Micronor).

Additionally, E₁, E₂, and γ_max area fractions were computed separately for each image slice for every subject with available kinematics data during initial impact and rebound, permitting a comparison of peak accelerations, which were averaged across the associated head rotations. The areas used for these correlations included all brain tissues as well as cortical gray matter, deep gray matter, and white matter separately. Data points that represented regions of interest containing fewer than 100 pixels (225 mm²) within that slice were excluded from this analysis, as 10 × 10 pixels represented a conservative estimate of the confidence in HARP tracking within an area. This cutoff also excluded the superior- and inferior-most slices that contained small regions of interest, which were expected to be dominated by partial volume effects.

Bias and Precision Studies.

Three subjects were randomly sampled from the primary study to evaluate bias and noise, totaling three subjects (2 females and 1 male). HARP tracking was applied to tagged reference scans in which subjects lay still with no head accelerations. Because tracking between tagged frames of stationary brain tissue should produce maps of zero displacement and strain throughout, this study enabled a quantification of the bias and root-mean-square (RMS) noise inherent to the tagged imaging and image analysis methods, removed from motion quantification.

To assess precision, or within-scan reproducibility, three subjects (1 female and 2 males) were scanned during a separate session. Instead of performing the full-volume brain tagging protocol as described earlier, the head rotation experiment was repeated five times for a single slice. Since orthogonally tagged images were acquired in independent experiments, a total of 25 combinations of these scans could be analyzed for displacements and strains. The precision of within-scan displacement and strain measures could then be computed as the pooled variance across all combinations

$$s_p^2=\left({\sum }_i\left(N_i-1\right)s_i^2\right)/\left({\sum }_i(N_i-1)\right)$$ (3)

where s_p² is the pooled variance, s_i² is the variance in displacement or strain across all combinations within the ith pixel, and N_i is the number of pixels of interest within the slice.

Statistical Analyses.

Subject demographics (i.e., age and sex), brain tissue volumes, and peak accelerations, which are presented as mean±standard deviation unless otherwise noted, were not normally distributed in our subject pool (Kolmogorov–Smirnov test). Wilcoxon rank sum tests were used to identify any differences in demographics, tissue volumes, and acceleration metrics between the female and male cohorts. Kendall's τ rank correlation was used to test the relationships among demographics data and brain tissue volumes, as well as between strain area fractions and peak accelerations. A significance level (α) of 0.05 was used for all comparisons, with conservative Bonferroni correction for multiple comparison of the tissue volumes of interest.

Strain area fractions for peak strain and strain on a frame-by-frame basis were compared among the regions of interest for all subjects. Kolmogorov–Smirnov test confirmed that strain area fractions did not fit into normal distributions. Differences in strain area fractions across tissue types and cortical lobes were evaluated using Friedman's test, controlling for subject effects with α = 0.05 for tests of area fraction of peak strain. In separate tests of strain area fractions by frame, a conservative Bonferroni correction was used to determine statistical significance over multiple comparisons (nine frames). Significant effects of tissue type or cortical lobe were then evaluated post hoc using a Dunn–Sidak correction. Wilcoxon rank sum tests were then used to compare peak and frame-by-frame strain area fractions between the male and female cohorts, with a conservative Bonferroni correction for multiple comparisons across three tissue types or eight cortical lobes and also across nine frames for by-frame comparisons.

Results

Bias and Precision.

In the analysis of bias using the reference tagged images, tracking of apparent motion while the head remained stationary provided a range of absolute displacement and strain mean biases of 0.000–0.018 mm and 0.000–0.038%, respectively. RMS across the analyzed reference tagged images ranged 0.061–0.075 mm and 0.876–1.103%, respectively. HARP analysis of both the reference tagged images and the tagged images of head rotation was performed with the same filtering, tracking, and refinement parameters [34,35], permitting the estimation of bias from reference scans. The precision of the displacement and principal strains were estimated to be 0.374 mm and 1.081%, respectively; the precision of γ_max was estimated to be 0.742%. Based on the observed bias and precision, a threshold of 3% strain was chosen for subsequent area fraction analyses.

Population Strain Metrics.

Segmentations of brain tissue into cortical gray matter, cerebral white matter, and deep gray matter were used to estimate the tissue volumes from the MPRAGE images acquired at 1 mm isotropic resolution (Table 2). Volumes of the overall brain tissue, cortical gray matter, and cerebral white matter were significantly different between the male and female cohorts (p < 0.01). Height (p < 0.001) and weight (p < 0.01), but not age (p = 0.27), were also significantly different between female and male cohorts (Table 1).

Table 2.

Estimated brain tissue volumes (mean ± standard deviation).

	Total brain tissues (cm3)	Cerebral gray matter (cm3)	White matter (cm3)	Deep gray matter (cm3)
All	1160.4 ± 109.0	546.1 ± 59.3	401.8 ± 52.8	53.4 ± 5.2
Female	1100.4 ± 105.5	521.8 ± 53.0	374.4 ± 50.0	51.9 ± 5.3
Male	1220.5 ± 75.6	570.5 ± 56.3	429.1 ± 40.7	54.9 ± 4.8
Female versus male (p)	<0.001	0.018	<0.001	0.068

Note: Statistically significant p values are indicated in bold.

The angular position, velocity, and acceleration measurements for the representative subject and across all subjects are associated with each imaged MRI frame (Fig. 2). The representative subject (shown in Figs. 1, 2, and 5) was chosen based on the criterion that the area fraction at the 3% threshold of the peak E₁, E₂, and γ_max was closest to the mean value across all subjects. Average values of peak angular acceleration during contact with the padded stop and in the rebound period were −195 ± 38 and 81 ± 36 rad/s², respectively (Table 3) and ranged across subjects from −117 to −255 rad/s² and from 34 to 207 rad/s², respectively (Supplemental Figure S1 is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection.). Peak accelerations during contact and rebound were not significantly different between male and female cohorts. Negative angular acceleration at contact indicated deceleration as head rotation was halted by the rubber stop. One subject was excluded from kinematics analysis (*, Table 3) due to a data recording error that did not otherwise affect tagged image acquisitions.

Fig. 2.

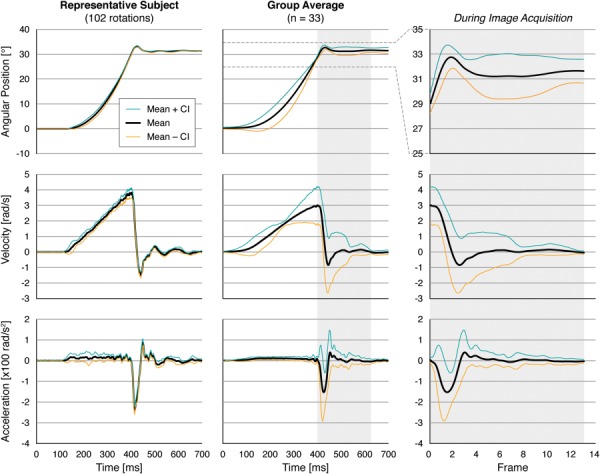
Position, velocity, and acceleration (mean±95% CI) of the head cradle were recorded during mild angular accelerations of the head for the representative subject (left column). The average kinematics traces (n = 33) were then aggregated across subjects for which positions were measured (middle and right columns). Tagged MRI acquisition (light gray background) was triggered prior to contact of the head cradle to the rubber stop and spanned up to 13 frames of 18.06 ms each.

Fig. 5.

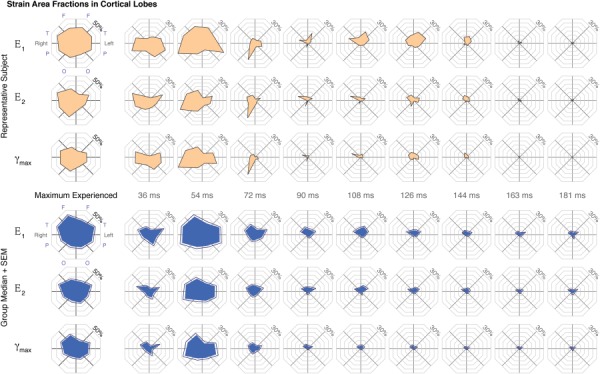
Area fractions of peak and by-frame maximum shear strain (γ_max) in the cortical lobes were calculated at a 3% threshold for all subjects (n = 34). The representative and group median (+ standard error of the mean (SEM)) values plotted on a polar plot with octants representing the frontal (F), temporal (T), parietal (P), and occipital (O) lobes of left and right hemispheres.

Table 3.

Peak accelerations (mean ± standard deviation) in the direction of rotation, during and after initial contact

		During contact (rad/s2)		During rebound (rad/s2)
Peak acceleration	n	Within-subject average	Within-subject SD	Within-subject average	Within-subject SD
All	33	−195 ± 38	21 ± 9	81 ± 36	12 ± 6
Female	16*	−194 ± 41	20 ± 9	80 ± 30	12 ± 6
Male	17	−197 ± 36	22 ± 10	82 ± 43	13 ± 7
Female versus male (p)		0.783	0.428	0.863	0.890

Additionally, strain area fractions in all of the regions showed significant negative correlations with peak angular acceleration during contact (Table 4). So, the measured area fractions increase as the acceleration magnitude increased. Only data pairs in which the region of interest used to compute area fraction was greater than 225 mm² were considered in this comparison.

Table 4.

Correlations between peak contact acceleration and peak strain area fraction.

		Versus peak contact acceleration
Region of interest	Strain area fraction	τ	p
Total brain tissues	E1	−0.440	<0.001
	E2	−0.365	0.002
γmax	−0.430	<0.001
Cortical gray matter	E1	−0.472	<0.0001
	E2	−0.380	0.001
γmax	−0.430	<0.001
White matter	E1	−0.389	0.001
	E2	−0.362	0.002
γmax	−0.412	<0.001
Deep gray matter	E1	−0.234	0.054
	E2	−0.134	0.275
γmax	−0.255	0.035

Note: Statistically significant p values are indicated in bold.

As observable in the representative subject, displacements and strains mapped to the segmented anatomy showed a spatiotemporally varying response to the mild acceleration of the head (Fig. 3(a)). Strain area fraction measured at a 3% threshold peaked at frame 3 (approximately 54 ms after the subject rotated through 28.5 deg, which initiated the image acquisition). This is the first full frame to occur entirely after the peak angular acceleration measured by the angular position sensor (Fig. 3(b)).

Fig. 3.

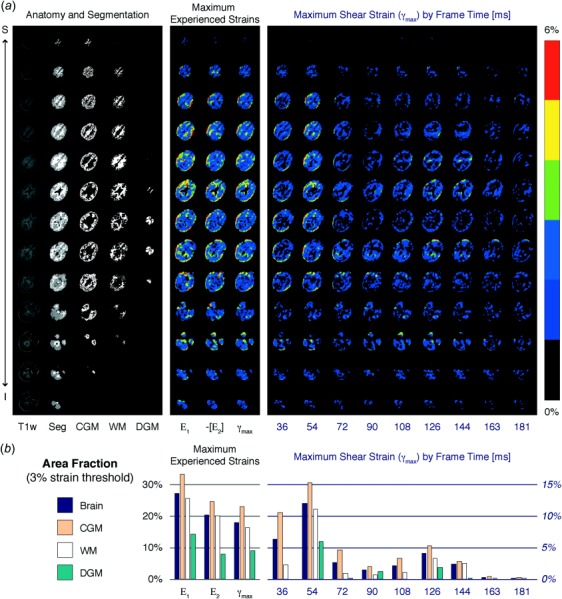
Anatomic images and strain maps are shown for a representative subject. (a) Registered anatomy from the T1-weighted (T1w) MPRAGE image and whole brain segmentation (Seg) permitted the identification and grouping of brain tissues of interest (cortical gray matter (CGM), white matter (WM), and deep gray matter (DGM)). The maximum values for in-plane principal strain (E₁, E₂) and maximum shear strain (γ_max) experienced by each voxel through all frames were determined and mapped to the segmented anatomy. Because E₁ and E₂ were primarily tensile and compressive, respectively, −[E₂] is shown to permit visualization with E₁ and γ_max on the same color scale. γ_max maps are shown as a function of time. (b) Area fractions of peak E₁, E₂, and γ_max and area fraction of γ_max by frame were computed for a threshold of 3% absolute strain in the whole brain and tissue types of interest. Corresponding with the greater proportion of areas of higher strain within the strain maps, strain area fractions peaked at frame 3 (54 ms) and were greatest in the cortical gray matter, followed by the white matter and deep gray matter.

Areas of higher strain, and therefore, values for area fractions evolved within the total brain tissue with time, with the highest strain and strain area fractions at 54 ms (Fig. 4). Area fractions of maximum-experienced E₁, E₂, and γ_max showed significant tissue type effects by Friedman's test (p < 0.001), indicating that there were significant differences among cortical gray matter, white matter, and deep gray matter. Comparing frame by frame with Friedman's test, the tissue type effect was again consistently significant for all strain area fractions (p < 0.001), with values significantly greatest in the cortical gray matter (p < 0.001) and significantly greater in white matter than deep gray matter only at frames spanning 36–72 ms (p < 0.005) as indicated by post hoc comparisons.

Fig. 4.

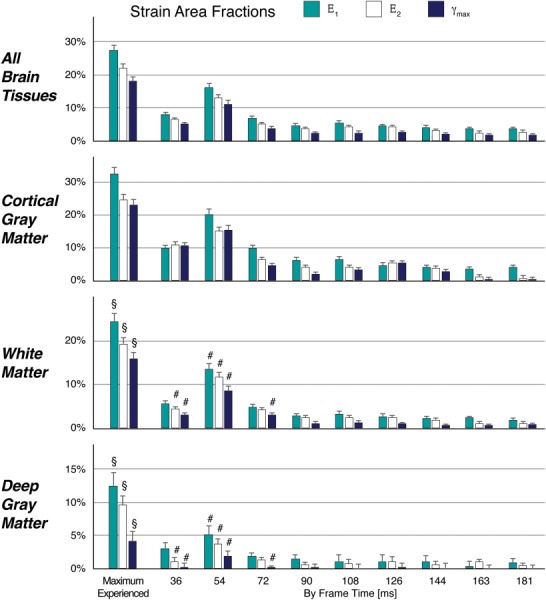
Area fractions (n = 34, median±standard error) of in-plane principal strains (Ε₁, Ε₂) and maximum shear strain (γ_max) were calculated at a 3% threshold for peak strains (Max) and on a by-frame basis in all brain tissues, cortical gray matter, cerebral white matter, and deep gray matter. The effect of tissue type on Ε₁, Ε₂, and γ_max area fractions was significant (all p < 0.0001), with metrics greatest within the cortical gray matter for all frames and peak strains (not indicated on graphs). The area fractions of white matter and deep gray matter were significantly different in peak strains (§, all p < 0.02) and in some frames associated with the initial impact (#, p < 0.005). These strain metrics are consistent with axes of rotation that lay within the brain during angular acceleration, with the highest strains furthest from the axis of rotation.

Strains within the cortical gray matter were broken down further by hemisphere and lobe into eight cortical regions (Fig. 5). E₁, E₂, and γ_max area fractions showed a significant cortical lobe effect for peak and by-frame measures (p < 0.005) by Friedman's tests, with post hoc comparisons identifying significantly different pairings among the cortical lobes. With peak γ_max (Fig. 5), the left temporal cortex, followed by right temporal and frontal cortex, showed the highest area fractions, and the right occipital and left frontal cortex showed the least (p < 0.005).

Comparing the area fraction among frames, the greatest differences between lobes generally occurred during the times associated with contact and rebound accelerations (Fig. 5). With a mild angular acceleration toward the left shoulder, strain area fractions averaged across all subjects were greatest in the temporal lobes at approximately 36 ms (E₁ and γ_max greatest in the left and E₂ greatest in the right temporal lobe), followed quickly by the right parietal cortex at 54 ms, which coincides with the time frame between the peak contact and peak rebound accelerations of the head cradle (Fig. 5). Over the same time frames (36–72 ms), strain area fractions were least in the left frontal cortex (p < 0.05 versus left temporal, right parietal, and right temporal cortex).

The sex-balanced cohort of volunteers also permitted the comparison of the peak strains between male and female groups (Fig. 6). Male subjects on average had a tendency to experience strains exceeding 3% within a greater volume of all brain tissues, as well as within each of the tissue types, although these differences were not statistically significant. Broken down by cortical lobe, strain area fractions trended higher in the right parietal cortex in males and in the occipital and left temporal cortex in females, but differences were not statistically significant.

Fig. 6.

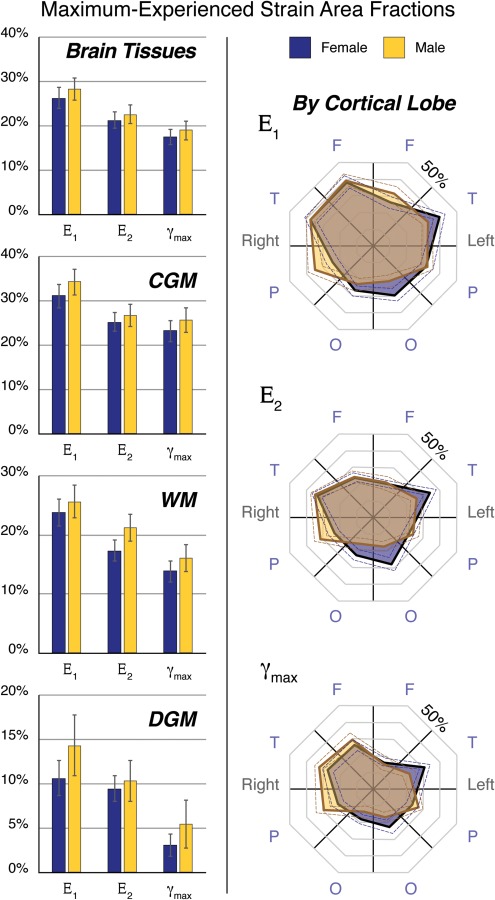
Area fractions of peak strains in female and male groups were compared across tissue type and cortical lobes. Males tended to show higher strain metrics in all tissue types, although these differences were not statistically significant. Female subjects tended toward higher strain area fractions in the occipital cortex, while male subjects showed higher strains in the parietal cortex.

Discussion

This work builds upon previously established MRI techniques [30], head acceleration devices [28–30], and other research [28,31,38], by our group and collaborators, and culminates in this sizeable data set (n = 34, 17 females, ages 22–49) of in vivo brain deformations in which tissue strains in various regions of the brain can be compared and demographic comparisons can also be performed. Mild angular accelerations of approximately 160–240 rad/s² permitted the measurement of tissue displacement and strain in this cohort of volunteers. In addition, we characterized the within-scan repeatability (precision) of this technique, as well as the RMS error of the combined MRI tagging and HARP analysis without loading (bias), as applied to human brain deformations.

Area Fraction as an Aggregate Strain Metric.

Principal strains E₁ and E₂ indicate the most tensile and most compressive strains, or changes in tissue dimension, experienced in the plane of the image by brain tissue. Likewise, the maximum shear strain indicates the greatest distortion experienced by tissue and, mathematically, is an invariant function of in-plane principal strains (Eq. (2)). Physiologically, shear strains represent the tissue deformations associated with diffuse axonal injury [1] and brain injury resulting from angular accelerations [39,40]. Additionally, because each subject is expected to have different brain morphology and kinematics, a strain measure that is more representative of region and aggregate behavior than a single maximum or percentile value was needed. The area fraction of strains exceeding a particular strain threshold [29] provides a robust, aggregate measure of the magnitude of strains experienced within a particular volume of interest.

Analysis of the cohort of volunteers focused on a 3% strain threshold for area fraction and was guided by the component studies reported in this work. An analysis of reference tagged images, under which no brain deformations would be expected, produced strain maps with an RMS error of up to 1% in absolute strain. Additionally, precision (or immediate repeatability) of tissue displacements and strains was measured using repeated tagged scans and shown to be most conservatively estimated to approximately 0.4 mm and 1% strain. Because strains in the brain were not expected to appreciably exceed 6% [29] with the mild angular accelerations in this study, the selection of 3% strain for area fraction was well justified for exceeding the noise in the system while remaining sensitive to strain variations between tissue types and cortical lobes. Correlation of peak accelerations to strain area fractions also showed significant relationships between acceleration and greatest strain area fraction, as measured at a 3% strain cutoff (Table 4).

Strains Reflect Inertial Response of Brain Tissues to Mild Rotational Acceleration.

The analysis of strain area fractions showed that the cortical gray matter consistently experienced the highest tensile, compressive, and shear strains. This pattern is consistent with the head motion that the subjects experienced—a rotation about an axis that lay closely in line with their spine and brain stem. As a result, the strains under angular acceleration and moment of inertia would be expected to be greatest in the tissues furthest from the axis of rotation. Additionally, a slight increase in strain during the later rebound period (108–144 ms) is observable in individual subjects (Fig. 5). This indicates a continued motion of the brain after the initial impact and rebound (36–72 ms) but at reduced magnitudes due to energy dissipation. These results are consistent with the viscoelastic oscillations that have been previously reported experimentally and in simulations of the brain response to similar motions [29,41]. Averaging across subjects appears to mask this effect because the timing and magnitude of these oscillations differ between subjects, as was also demonstrated by the lack of correlation between rebound accelerations and strain area fractions (Table 4). Whether the differences between subjects are due to differences in individual reactions to the head motion, differences in head structural anatomy, or differences in the intrinsic material properties of their brain tissues, however, cannot be determined from the current data, though it is worth further examination.

Since cortical gray matter exhibited the highest strains, a further decomposition of the volumes of interest into specific cortical lobes allowed a more detailed assessment of where the highest strains were experienced. The effect of cortical lobe was significant in peak and frame-by-frame strain measures, indicating that while strains were generally higher in the cortical gray matter, the magnitude of these strains was not evenly distributed across all of the cortex. The highest strains consistently lay in the right frontal and temporal lobes, while the left frontal and occipital lobes of both hemispheres experienced the least strain. In terms of the impact of the head, during a rotation toward the left shoulder and with an impact closest to the left temple, these locations reflect areas of higher strains associated with the regions directly adjacent to the impact location and on the opposing side of the brain. The more diffuse location and lower magnitude of deformations in the same regions may indicate that there is a smaller linear acceleration component to the head motion, in addition to the noninjurious mild angular acceleration used in this study. With the initial impact of the head after a leftward rotation, high strains may be expected around the location of the impact—the left temporal cortex—at a time frame consistent with our experimental results (36 ms, Fig. 5). Immediately after impact, high strains may be expected in the right temporal, parietal, and/or frontal cortex, depending on the exact orientation of the subject's head upon impact. In our experimental data, the highest strains lie in the right hemisphere cortical gray matter from 54 to 72 ms (Fig. 5), while the occipital cortex is relatively shielded from high strains throughout the impact and rebound. Although the predominant motion in this study was rotational, the slight increase in strain in cortical regions adjacent to and opposite of the impact location could indicate both a small linear component of the acceleration, which may be expected if the centroidal axis of the head did not align with the rotational axis. Variations in head geometry among the subjects may also influence the observed strain variations and point to the role of skull geometry in constraining the rotational motion of the brain. However, in part because the strains measured in this study are multislice 2D strain fields but the geometry of the skull and brain are fully represented in 3D, a direct comparison or association between skull morphology and full-volume brain strains is beyond the scope of this study.

Differences in head kinematics and head geometries may also explain some of the variation observed between female and male cohorts. The use of the counterweight on the head support (Fig. 1), which was the same for all subjects, may have helped achieve similar accelerations in male and female cohorts, despite significantly different heights, weights, and brain volumes (Tables 1 and 2). However, even though peak accelerations were similar (Table 3), strain metrics tended to be larger in males (Fig. 6), although these differences did not reach statistical significance. It is likely that, with the larger overall brain volume in the male cohort, a sex dimorphism consistent with the literature [42], the same head accelerations resulted in slightly higher strains due to the differences in brain mass distribution. Larger brain volumes, given the same accelerations, would be expected to achieve a greater angular momentum, and therefore, experience a greater inertial response. Interestingly, strains in the cortical gray matter showed a tendency toward higher shear strains for females in the occipital cortex and for males in the parietal cortex (Fig. 6). These tendencies in different cortical lobes, although statistically insignificant, may be because the axis of rotation passes through different regions of the brain when constrained by the geometry of the head support. Additionally, these geometrical effects could be compounded with differences in biomaterial properties of brain tissue between males and females; for example, one study has found lower stiffness in the temporal and occipital cortex in males in comparison to females [43].

Interestingly, strains observed in this study as well as other experimental observations of mild head accelerations [28–30] indicated maximum tissue strains of 5% to 6% in the living brain under noninjurious accelerations, while cadaveric tissue strains measured at accelerations of 1–2 orders of magnitude greater produced strains in a similar range of no more than 9% [19]. Therefore, a computational model that predicts in vivo strains of 5% observed here under noninjurious head rotations could be expected to predict tissue strains much greater than 9% at higher, injurious accelerations. This inconsistency, whether it be rooted in nonlinear scaling between levels of acceleration or the transfer function from cadaveric to living tissue, is also seen in the recent observation that some commonly used brain injury risk models may overestimate risk when data from noninjurious sled tests are used as input [44]. Further investigations into the source of these seeming incongruities are necessary, particularly in comparing in vivo to cadaveric in situ biomechanics and assessing the role of aging in the material properties of brain tissue. To address the mapping of biomechanical behaviors at subconcussive levels in living subjects to that at higher impact rates in cadavers, cadaveric brain studies with MRI tagging under rotational accelerations are ongoing within our group.

Future Work to Refine In Vivo Studies and Address Limitations.

The variability inherent to in vivo volunteer studies is compounded in this study by the need to repeat head rotations many times for coverage of the full brain volume. Because motion artifacts may affect phase tracking in the HARP analysis [34,35], images suspected to have such artifacts were eliminated from analysis. Slight variations among the 10–13 image planes and out-of-plane motion also preclude a straightforward three-dimensional analysis of the brain deformations at this time. The estimation of full 3D strain tensor fields will likely require regularization across slices and kinematics of the skull [45] to aid in distortion-free tracking of motion [46,47]. Full 3D strain fields would also permit an examination of the role of the 3D morphology of the brain, skull, and other head and neck geometries.

Improvements to the spatial and temporal resolution of strain measurement in the full volume of living brain are possible with longer scan times and more refinements to HARP analysis. Total imaging time and subject comfort during scans may limit the extent of these improvements, without further acceleration of the acquisition protocol. Incorporation of other MRI contrast mechanisms with tagging could also improve insight into the relationship between brain structure and mechanical behavior. Diffusion tensor imaging, magnetic resonance angiography, and T₂-weighted images were also acquired as part of the approved imaging protocol but were not analyzed for this study. In particular, diffusion tensor imaging data in combination with three-dimensional strains would enable the evaluation of stretch along and transverse to white matter tracts as a further step toward brain modeling and injury prediction [26,48]. Additionally, improved segmentation techniques would allow in vivo deformations to be mapped with respect to blood vessels, the meninges, and other intracranial structures, permitting a better understanding of their role in the brain's response to accelerations [49]. Integration of the results of MRI tagging and MR elastography [50–52] could also lead to a more comprehensive understanding of the brain's mechanical behaviors and improved design of computational models of brain biomechanics.

Nonetheless, the in vivo brain deformation data presented here can be used not only to establish and validate subject-specific or population-based brain models [53] but also to supplement and refine already established brain models built upon in vivo findings [23,24]. The heterogeneous strain patterns observed suggests that the properties of brain tissue are also heterogeneous, emphasizing further the importance of anisotropic and heterogeneous material properties of brain tissues [54] to the improvement of computational models. Importantly, in vivo human data, measured at subconcussive impacts such as those in this and prior studies [29,30,55], can be used in conjunction with cadaveric in situ data [18,20] to design computational models that can predict brain biomechanics and injury under a wide range of rotational accelerations.

Conclusions

The MRI tagging data and analyses presented in this study represent advances in the study of brain biomechanics and brain injury. The use of noninvasive imaging combined with HARP analysis permitted visualization of in vivo tissue motion throughout the brain volume under mild angular accelerations (∼200 rad/s²), leading to a rich MRI data set that relates brain motion to head kinematics and brain morphology for each of the 34 volunteers, evenly split between males and females and ranging in age from 22 to 49.

Maximum shear strains were consistently greatest immediately after peak acceleration in the cortical gray matter, followed temporally by maximum strains in deeper, subcortical white matter. The decrease in strains from the cortical layer to the deep brain is consistent with the effects of rotational inertia of the brain under an angular acceleration. After deceleration of the head, the brain continues to move within the skull, resulting in oscillatory strains even after the peak and rebound accelerations associated with the initial impact ended. However, the magnitude of these tissue strains diminishes over time due to a viscoelastic damping effect [29].

Finally, these strain data, and the displacements from which they were derived, combined with the morphological images and segmentation that were also acquired in this study, provide valuable experimental data for the design and validation of high-fidelity computational models of the brain [23,41], as well as the development of subject-specific models of brain biomechanics [53]. Such computational models permit the study of the effects of higher accelerations and other injurious conditions that cannot be studied in live human subjects. Although experimentally derived biomechanics of cadaveric and animal tissue provide useful inputs for simulation models, knowledge of the in vivo mechanical behavior of the entire human brain provides complementary information that is important for achieving high biofidelity in simulations of traumatic brain injury.

Funding Data

• National Institute of Neurological Disorders and Stroke (R01NS055951).

• The Department of Defense in the Center for Neuroscience and Regenerative Medicine.

• The National Institutes of Health Intramural Research Program.