Modeling Skeletal Muscle Stress and Intramuscular Pressure: A Whole Muscle Active–Passive Approach

Abstract

Clinical treatments of skeletal muscle weakness are hindered by a lack of an approach to evaluate individual muscle force. Intramuscular pressure (IMP) has shown a correlation to muscle force in vivo, but patient to patient and muscle to muscle variability results in difficulty of utilizing IMP to estimate muscle force. The goal of this work was to develop a finite element model of whole skeletal muscle that can predict IMP under passive and active conditions to further investigate the mechanisms of IMP variability. A previously validated hypervisco-poroelastic constitutive approach was modified to incorporate muscle activation through an inhomogeneous geometry. Model parameters were optimized to fit model stress to experimental data, and the resulting model fluid pressurization data were utilized for validation. Model fitting was excellent (root-mean-square error or RMSE <1.5 kPa for passive and active conditions), and IMP predictive capability was strong for both passive (RMSE 3.5 mmHg) and active (RMSE 10 mmHg at in vivo lengths) conditions. Additionally, model fluid pressure was affected by length under isometric conditions, as increases in stretch yielded decreases in fluid pressurization following a contraction, resulting from counteracting Poisson effects. Model pressure also varied spatially, with the highest gradients located near aponeuroses. These findings may explain variability of in vivo IMP measurements in the clinic, and thus help reduce this variability in future studies. Further development of this model to include isotonic contractions and muscle weakness would greatly benefit this work.

1. Introduction

While healthy skeletal muscle provides stabilization and locomotion for the human body, muscle weakness is a debilitating condition that can lead to injury, disability, and even death [1,2]. Determination of individual muscle force in vivo is a major clinical challenge, as current methods either do not measure force (electromyography) or are subject to variability from contributions of multiple muscles (torque measurements). Intramuscular pressure (IMP), which is correlated with muscle force, has benefitted from recent improvements in pressure microsensor technology and thus could be used as an approach to estimate muscle force [3–5]. However, variations in IMP across multiple patients and various muscles make this force estimation a challenge [6]. A validated finite element model could provide the necessary correlation between muscle force and IMP, thus improving the use of pressure microsensors as a tool to estimate muscle force.

The robust function and complex mechanical behavior of skeletal muscle are driven by the active properties and passive structure [7,8]. Specifically, muscle structure facilitates active force transmission from contractile fibers through passive constituents to the skeletal system [9]. Thus, understanding and modeling physiological function requires studying muscle as not only a contractile tissue, but a passive structure as well. This is particularly evident for studies of intramuscular pressure, as fluid pressurization is dictated by its environment.

Previously, a finite element model of skeletal muscle was developed that accurately predicted both muscle force and intramuscular pressure under passive stretch [10]. This model characterized the complex passive response of the tissue by incorporating hyperelasticity, viscoelasticity, poroelasticity, and anisotropy. However, this model did not incorporate muscle activation. This work further develops this approach by incorporating muscle activation through an inhomogeneous geometry and validation of IMP under active conditions. The goals of this work were to identify how fluid pressurization is distributed within active skeletal muscle to potentially identify ideal microsensor insertion location and to gain further insight into what conditions dictate this pressurization.

2. Methods

2.1. Experiment.

Eight New Zealand White Rabbit muscles (n = 8) were passively stretched and stimulated under isometric conditions at a total of fifteen different muscle lengths. Passive data were identified from eleven muscle lengths at which muscle slack did not occur. Experiments were conducted on anesthetized animals with the approval of the University of California San Diego Institutional Animal Use and Care Committee by isolating and attaching the distal tibialis anterior tendon to an actuator and load cell. Active isometric contraction involved maximal stimulation of the peroneal nerve. Muscle stress was calculated as force measured by the load cell from either stretch (passive) or activation (active) divided by the physiological cross-sectional area [11]. Intramuscular pressure was measured with a pressure microsensor [3] inserted into the muscle midbelly the longitudinal direction (parallel to muscle fibers).

2.2. Constitutive Model

2.2.1. Skeletal Muscle.

Two similar constitutive models were simultaneously utilized for skeletal muscle in this study (Table 1), representing the contractile and passive-only components of the tissue. As contractile components of skeletal muscle (sarcomeres) are capable of generating active force and supporting passive loads, we will denote this constituent as “excitable.” All other muscle volumes that are not capable of generating force (fluid, extracellular matrix, etc.) will be entitled “passive.” The separation of excitable and passive constituents provides an opportunity to study the relationship between contractile components and fluid in skeletal muscle. As the tissue-level passive properties of skeletal muscle are attributed to both the active actin–myosin complex [12–14] and the extracellular matrix [15,16], it is difficult to elucidate exactly how to assign properties to these constituents. Thus, for both previous modeling efforts [10] and the current model, the passive responses from the extracellular matrix and contractile elements are coupled into a continuum model. Previously, passive skeletal muscle was modeled as a hypervisco-poroelastic material with an anisotropic compressible solid phase [10]. For the current model, the assumption was made that the excitable constituent did not contain a fluid component, and as such the constitutive approaches for the excitable and passive constituents are very similar, with the only exception being that the excitable constituent did not include a permeability/poroelasticity. Thus, it is assumed that the excitable tissue is comprised of solid material only as a compressible hyperviscoelastic material [17–20], while passive tissue was modeled as compressible hypervisco-poroelastic material [21].

Table 1.

Constitutive model parameter values for skeletal muscle. Note that the excitable and passive constituents have the same constitutive model and parameters with the exception of poroelasticity, which was only utilized for the passive constituent.

Mooney–Rivlin SED			Prony series viscoelasticity		Ellipsoidal fiber distribution
c1 (kPa)	c2 (kPa)	k (kPa)	gi	τi (s)	ξlong (kPa)	βlong	ξtrans (kPa)	βtrans	Permeability (mm4/N s) (passive)
0.05	0.5	5	1.33, 0.476, 0.295, 0.167	0.1, 1, 10, 100	Optim	Optim	15	3	0.074

While the full constitutive approach has been previously outlined [10], in brief, an isotropic, compressible (or coupled) Mooney–Rivlin strain energy density function was utilized for the ground matrix [22], which characterizes isotropic and symmetric behavior of the tissue in response to tensile, compressive, and shear deformations. Viscoelastic effects were modeled using a three-term Prony series [23]. As skeletal muscle exhibits a higher stiffness in tension (it is not tension-compression symmetric) [24], tensile anisotropic and nonlinear properties of passive muscle were largely dictated by three-dimensional (3D) tension-only reinforcing fibers with an ellipsoidal fiber distribution (EFD) [25]. Previously, the longitudinal EFD properties were optimized to experimental data and the transverse EFD parameters were fixed based on the assumption of an increase in modulus of one order of magnitude over longitudinal properties [26]. While this formulation yielded excellent model validation to both muscle stress and intramuscular pressure under passive conditions [10], they were optimized in this study for improved agreement with experimental data under both passive and active conditions. A constant, isotropic hydraulic permeability was assumed based on prior experimental and finite element analysis of skeletal muscle [21].

The total stress within a biphasic finite element model that includes an active component can be decomposed into active stress ${\mathit{\sigma }}^{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}$, passive stress within the porous solid ${\mathit{\sigma }}^{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{d}}$, and fluid pressure $p$ (Eq. (1), where $\mathit{I}$ is the identity matrix). Muscle activation was modeled using prescribed uniaxial contraction (Eq. (2)) [27]. Here, $J$ is the Jacobian or volume ratio, $T_0$ is the maximum activation stress, $c\left(t\right)$ is a load curve that defines the stress as a function of time, and $\mathit{n}$ is the unit vector that dictates the direction of active contraction, which is the physiological pennation angle. The load curve $c\left(t\right)$ was chosen to replicate the increase of force of fully fused isometric skeletal muscle [8]

$${\mathit{\sigma }}^{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}={\mathit{\sigma }}^{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}+{\mathit{\sigma }}^{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{d}}-p\mathit{I}$$ (1)

$${\mathit{\sigma }}^{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}=J^{-1}{T}_{0}c\left(t\right)\mathit{n}\otimes \mathit{n}$$ (2)

2.2.2. Aponeurosis and Tendon.

Aponeurosis and tendon were modeled as nearly incompressible hyperviscoelastic with a transversely isotropic Mooney–Rivlin strain energy function [28] and a Prony series viscoelastic formulation [29] (Table 2). This formulation is outlined in greater detail in Ref. [10].

Table 2.

Constitutive model parameter values for tendon/aponeurosis. These parameters are identical to previously utilized values [10].

Mooney–Rivlin SED							Prony series viscoelasticity
c1 (kPa)	c2 (kPa)	k (kPa)	c4	c5 (kPa)	λmax	k (kPa)	gi	τi (s)
10,000	500	50	40	100,000	1.03	500,000	0.203, 0.133, 0.191	0.33, 47.5, 2500

2.3. Finite Element Model.

To represent the longitudinal contractile structure of skeletal muscle, inhomogeneous geometry of the New Zealand White Rabbit tibialis anterior was developed. The excitable and passive components of the tissue, which are separate components both in geometry and constitutive modeling approach, were connected directly through mesh structure, along with aponeurosis and tendon tissue. Thus, no contact conditions were necessary between these three constituents. As skeletal muscle is comprised of roughly 80% fluid [30], it was assumed that 80% of the tissue by volume is unable to generate contractile force. The remaining 20%, while not entirely comprised of contractile material, is capable of generating active force. Thus, the model was divided into 80% passive constituent, and 20% excitable constituent. The mesh is comprised of solely hexahedral elements; thus, inhomogeneity was achieved by denoting one out of every five longitudinal strings of elements as excitable (Fig. 1). To achieve a physiologically relevant isometric contractile stress for whole muscle, the stress in the excitable constituent must exceed experimentally measured values of isometric muscle fiber stress. This is to account for the fact that the excitable component comprises only 20% of the model muscle volume. In muscle at the microscale, for example, the stress in a maximally contracting single myofibril (up to 1 MPa) exceeds the stress in a maximally contracting muscle fiber or whole muscle (roughly 200 kPa), as the muscle is comprised of noncontractile components (fluid, etc.) [31,32].

Fig. 1.

Inhomogeneous finite element geometry of skeletal muscle, showing excitable (dark longitudinal constituent), passive (light longitudinal constituent), and aponeurosis/tendon (located at ends of tissue): (a) Whole New Zealand White Rabbit tibialis anterior muscle model and (b) cross-sectional view of the rabbit tibialis anterior model

The finite element geometry for the rabbit tibialis anterior is outlined elsewhere [10], but in short, it was developed by segmentation and hexahedral meshing of μCT images of an in vitro New Zealand White Rabbit tibialis anterior. The pennation angle of 2.5 deg [11] was applied globally by specifying the orientation of the constitutive model. First, Piola–Kirchhoff stress (engineering stress) was calculated by summing the total reaction force at the distal nodes and dividing by undeformed physiological cross-sectional area of the model. This stress measure was calculated to match experimental procedures for measured stress, which is necessary for model validation. This approach was the same for both active isometric and passive conditions. Model pressure was calculated as fluid pressure from 90 midbelly elements of the passive constituent. Again, this output did not change between active and passive simulations. The muscle mesh utilized in this study (18,646 elements) was compared against a denser mesh (46,400 elements) under active isometric conditions to ensure mesh density convergence. Isometric activation was simulated using an active stress of 500 kPa ($T_0$ from Eq. (2), determined based on applied active stress from the results) for the denser mesh and for the same reaction force using the less dense mesh, only a 0.80% difference of mean fluid pressure between the two models was observed at $t=0.5$ s.

2.4. Verification of Transverse Stiffness Parameters.

To investigate the role of transverse fiber stiffness in model behavior, with an emphasis on fluid pressure, variations in transverse EFD parameters were applied. The tensile model stiffness is largely dictated by these tension-only EFD parameters by design, as skeletal muscle tensile stiffness is roughly two orders higher in tension versus compression [26,33–36]. While the longitudinal fiber parameters were determined through nonlinear optimization, the transverse parameters were not simultaneously optimized. Previous finite element modeling of passively stretched muscle utilized a value of ∼33 kPa for ξ_trans based on the assumption of the transverse orientation being one order of stiffness higher than the longitudinal [10]. However, the reported values for transverse tensile linear modulus of skeletal muscle from literature range from roughly 20 kPa to nearly 800 kPa [24,26]. Additionally, there remains uncertainty to the role of transverse stiffness in model fluid pressurization. To study this, two ξ_trans parameter values were directly compared: 33 kPa from the previous study and 15 kPa utilized in this study. A value of 15 kPa was used in this study as it yielded improved agreement to experimental data of uniaxial transversally stretched passive muscle (Fig. 4).

Fig. 4.

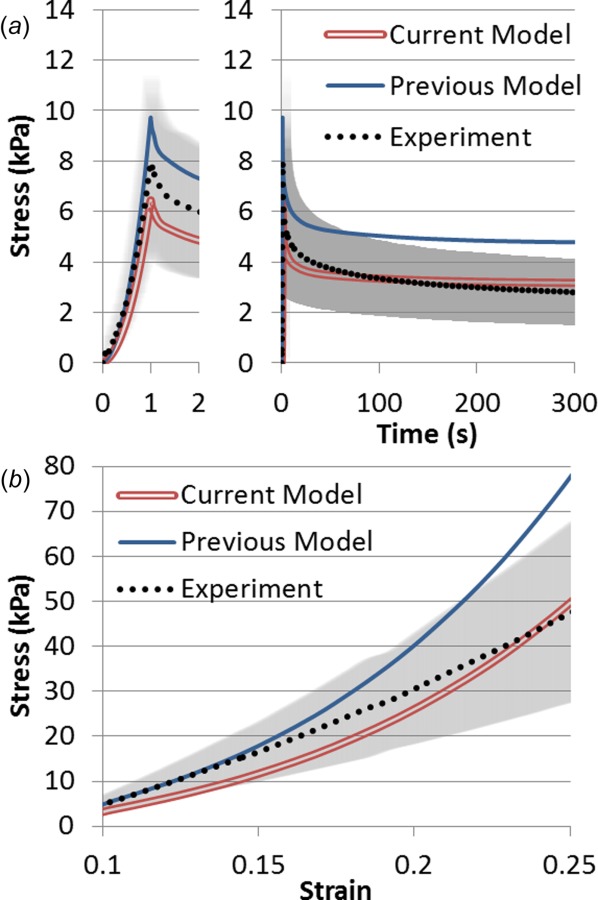
Comparison of two models to experimental data (mean with standard deviation in gray) of rabbit tibialis anterior muscle subject to transverse extension. The current model assumes a ξ_trans value of 15 kPa while previous modeling utilized 33 kPa. (a) Stress relaxation step of 0.1 strain ramp (shown left) and 300 s of relaxation (shown right). (b) Constant rate pull to 0.25 strain at a rate of 0.01 s⁻¹.

A simplified finite element geometry of 2560 cubic hexahedral elements using the same inhomogeneous nature as presented in Fig. 1 was developed to compare model behavior to experimentally analyzed excised muscle samples [26]. The mean Cauchy stress in the direction of elongation (transverse) was compared to the experimentally calculated Cauchy stress. Experimental samples underwent 0.1 tensile strain at a rate of 0.1 s⁻¹ followed by a 300 s relaxation period, and finally a constant rate pull step to 0.25 tensile strain at 0.01 s⁻¹. The goals of this approach were to (1) improve the accuracy of the material parameters used in this study, and (2) investigate how these parameters affect model fluid pressure. The above whole muscle finite element model was thus employed with each of these two parameter values under active contraction at three muscle lengths to investigate the role of transverse stiffness in model fluid pressure. The three lengths include one on the ascending limb (−0.2 fiber strain from optimal length), optimal length, and one on the descending limb (0.2 fiber strain from optimal length). Optimal length is defined as the length at which isometric stress is maximum, as determined from experimental data (Fig. 2). The specified contractile internal stress (Eq. (2)) will remain the same for both conditions, although changes to the constitutive approach may result in differences in reaction force at the model boundary.

Fig. 2.

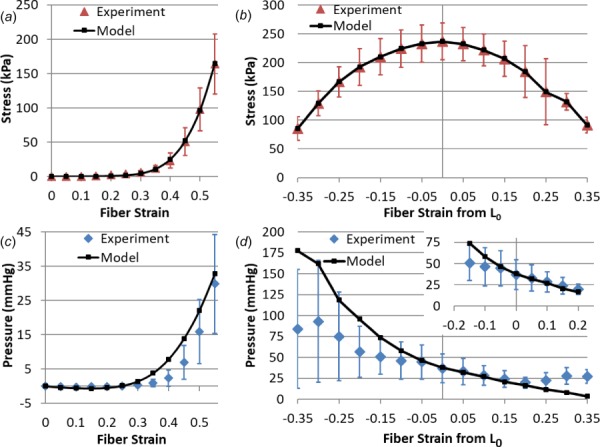
(a) Model fit to experimental stress under (a) passive stretch and (b) active isometric conditions. The corresponding experimental data and model predictions for IMP are shown under (c) passive stretch and (d) active isometric conditions. Physiological in vivo muscle lengths are highlighted in the top right inset of (d), showing model predictive capabilities. All experimental data presented as mean and standard deviation. Active data show the change in stress/pressure as a result of contraction, and are thus calculated as passive stress/pressure subtracted from total stress/pressure. Note that for muscle lengths below zero in (a) and (c), the tissue does not support passive tensile load, and thus slack occurs.

2.5. Optimization and Validation.

To ensure that passive model behavior was consistent with passive experimental data following changes to the constitutive model and inhomogeneity from previously published modeling efforts [10], the same optimization approach was used. In short, a nonlinear least squares optimization algorithm was implemented in matlab (lsqnonlin) that applied an inverse finite element approach. This optimization varied ξ_long and β_long parameters to fit model stress (force divided by PCSA as outlined above) to the passive experimental stress. This was completed at increments of 5% fiber strain over a total of eleven data points, which are identified as muscle lengths in which the tissue is capable of supporting passive tensile load (no longer slack). Passive model pressure was compared against experimental IMP data for validation at these same points.

Active isometric stress from the FE model was optimized to experimental data by varying the $T_0$ parameter from Eq. (2). This was done for each of the fifteen experimental data points under active isometric contraction (±35% of optimal length in 5% increments). For the data used in this study (Fig. 2), slack length was observed as 85% of optimal length (−15% strain). For each fit, the muscle was passively stretched to the corresponding experimental length followed by 300 s of relaxation to reach steady-state [23,37] before activation was applied per the activation curve. Active model stress and fluid pressure were calculated by subtracting the steady-state stress and fluid pressure values from the maximum stress and pressure during contraction. Thus, data presented for active conditions are the change in stress/pressure from passive conditions. Experimental and model pressures were compared for an independent validation. Statistical analysis of agreement between model outputs and experimental data was completed by calculating the root-mean-square error (RMSE, Eq. (3), where $y^e$ are experimental data and $y^m$ are model data) and normalized root-mean-square error (NRMSE, Eq. (4))

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{\sum _{i=1}^{15}{\left(y_i^e-y_i^m\right)}^2}{15}}$$ (3)

$$\mathrm{N}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\frac{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}{\mathrm{m}\mathrm{a}\mathrm{x}\left(y^e\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(y^e\right)}$$ (4)

3. Results

The optimized passive parameters for longitudinal EFD properties showed a highly nonlinear longitudinal stiffness, which is consistent with previous investigations of skeletal muscle longitudinal tensile behavior [4,23,26,35,38] (Table 3). Optimized applied stress ($T_0$ from Eq. (2)) in the excitable constituent for isometric activation varied for each data point and ranged from 229 to 604 kPa. These values were expected to be higher than the whole muscle specific tension as the excitable constituent comprises only a fraction of the total muscle volume [32,39,40].

Table 3.

Optimized longitudinal EFD parameters

Ellipsoidal fiber distribution
ξlong (kPa)	βlong
2.76	10.9

Model optimization to experimental stress data under both passive and active conditions was confirmed visually (Figs. 2(a) and 2(b)) and resulted in small statistical error values (NRMSE values less than 1%, Table 4). The model was able to match experimental intramuscular pressure readings under passive tension by visual analysis (Fig. 2(c)) and through statistical measures (12% NRMSE, Table 4). While this was not as strong under active contraction, visual and statistical agreement with experimental intramuscular pressure data (NRMSE of 48%) still shows predictive capability of the model. Visually, model pressures decreased with increasing stretch similar to experimental data (Fig. 2(d)). The model agreement with transverse data was stronger at muscle lengths that occur in vivo (Fig. 2(d) inset, RMSE 9.97 mmHg and NRMSE of 37%) [41,42].

Table 4.

Statistical analysis of model agreement to experimental data of sensor insertion in the longitudinal or transverse orientations. Root-mean-square error (RMSE, Eq. (3)) and normalized root-mean-square error (NRMSE, Eq. (4)). Note that for passive and active stress, the model was fit to experimental data (hence the smaller errors) and that all pressure comparisons are independent validation.

Statistic	Passive stress (kPa)	Passive pressure (mmHg)	Active stress (kPa)	Active pressure (mmHg)
RMSE	1.26	3.53	0.119	35.3
NRMSE	0.765%	11.7%	0.0786%	48.1%

Intramuscular pressure exhibited inhomogeneity within the model (Fig. 3). Fluid pressure was highly transient in the distal region near the larger aponeurosis, which had pressure gradients of nearly 100 mmHg across less than 15 mm (Fig. 3(a)). While the proximal region also exhibited pressure gradients, they were not as drastic (Fig. 3(b), ranging from 0 mmHg to ∼30 mmHg). Fluid pressure gradients decreased with time as pressure equilibrated.

Fig. 3.

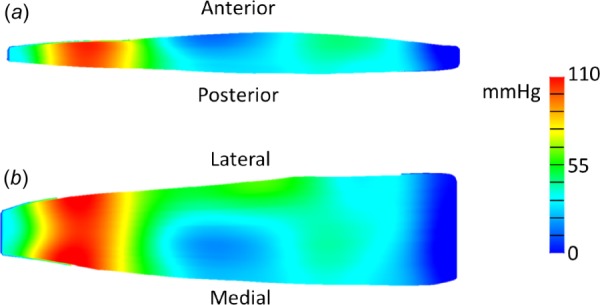
Color maps of fully activated finite element model at optimal length after one second of maximum contraction. (a) Image of two-dimensional sagittal midbelly slice of the model showing fluid pressure distribution. (b) Image of two-dimensional coronal midbelly slice showing fluid pressure distribution. The distal region exhibited the highest variability in fluid pressure.

The transverse stiffness parameter comparison showed that current modeling approaches (a value of 15 kPa for ξ_trans) had a stronger agreement to experimental tensile stress data than previous approaches (33 kPa for ξ_trans) (Fig. 4). This was observed both under stress relaxation (Fig. 4(a)) (NRMSE of 3.8% for the current approach versus 22% for the previous approach) and constant rate pull (Fig. 4(b)) (NRMSE of 8.3% for current versus 26% for previous). Transverse parameter stiffness affected fluid pressurization within the model under active contraction, particularly at short muscle lengths. Specifically, increases in transverse stiffness lead to increases in fluid pressure in excess of 20% on the ascending limb for the same active stress generation (Table 5).

Table 5.

Comparison between the previous modeling approach (ξ_trans of 33 kPa) and current approach (ξ_trans of 15 kPa) at three muscle lengths: the ascending limb (strain of −0.2), optimal length (zero strain), and the descending limb (strain of 0.2). Fluid pressure increased with increases in transverse stiffness, particularly on the ascending limb, yet measured whole model stress had little dependence on transverse stiffness.

	Stress (kPa)				Pressure (mmHg)
Strain from L0	Exp	Current model	Previous model	Model % difference	Exp	Current model	Previous model	Model % difference
−0.2	192	192	190	1.1%	56.7	95.6	117	23%
0	237	237	236	0.19%	36.8	38.0	40.3	6.0%
0.2	184	184	184	0.17%	19.6	16.5	17.2	4.2%

4. Discussion

This work presents the first whole muscle finite element model to predict both intramuscular pressure and muscle stress under active contraction conditions. Previous modeling efforts either did not include activation [10] or used an idealized two-dimensional geometry and lacked time-dependent effects [43]. This work has developed the foundation for future endeavors to evaluate intramuscular pressure distributions within skeletal muscle, study how disease and degradation affect muscle force and intramuscular pressure, and how variations in geometry or activation affect force and IMP. Investigations of diseased muscle may require a separation of muscle extracellular matrix and muscle fiber passive constituents through either geometry or constitutive modeling. This could be achieved from a constitutive standpoint by decoupled anisotropic strain energy terms, and geometrically by either a multidomain meshing approach similar to other studies [18] or with one-dimensional (1D) muscle fiber elements. Inhomogeneity would provide another layer of complexity, which could again be defined either geometrically through meshing or by changes in constitutive parameter values as a function of location. Measuring and modeling IMP may provide unique insight into how the material properties and mechanical function of muscle are affected by a diseased versus healthy state. Future work to investigate the role of muscle weakness, fibrosis, fatigue, and isotonic contractions on fluid pressurization would benefit the IMP field.

While the model presented here simulated isometric contractions, it remains to be seen how strong the predictive capabilities of this approach is for dynamic contractions. Concentric (shortening) and eccentric (lengthening) as well as submaximal contractions would greatly improve the clinical applicability of this work. The inclusion of fluid and viscoelasticity in this model suggests an application to dynamic conditions would be appropriate, as the constitutive framework for this model is reflective of a transient state. However, limited experimental data exist for IMP under eccentric and/or concentric conditions [5], particularly for current IMP measurement tools. Future studies are needed to generate a clear understanding of IMP in dynamic and submaximal conditions before the efficacy of this model can be evaluated.

Although the NRMSE error value of 48% for longitudinal active data may seem quite high, experimental standard deviations are similarly ∼50%. Additionally, the model showed predictive capability within experimental standard deviation (less than 25 mmHg and as low as 6.5 mmHg) for data from −0.15 to 0.2 strain (Fig. 2(d) inset), which are muscle lengths experienced in vivo [41]. The relatively straightforward inhomogeneous approach in this work was chosen based on the experimentally measured volume of tissue comprised of solid muscle in contrast and fluid content, specifically a 20/80 split of excitable to passive only [30,44]. Previous finite element modeling efforts of skeletal muscle have utilized similar three-dimensional inhomogeneous assumptions about contractile constituents [18,45,46], homogeneous assumptions [17,20,28,43,47–52], and a combination of three-dimensional and one-dimensional elements [42,53,54]. The approach implemented here is clearly a macroscopic geometric approximation of skeletal muscle, but it does justify insight into the inhomogeneous behavior of the tissue, particularly for intramuscular pressure (Fig. 3). Further increases in accuracy of inhomogeneous IMP distributions would surely need to be accompanied by mesh refinement or depending on the scale of study alterations to the geometric approach. While it remains to be seen exactly how other approaches, such as a passive three-dimensional mesh reinforced with one-dimensional contractile elements are able to model intramuscular pressure behavior, this current approach shows predictive capabilities, especially in the physiological range of strain.

Model fluid pressure exhibited a high level of spatial dependence during immediate contraction (Fig. 3). While this variability decreased with time even during contraction, the combination of transience and inhomogeneity manifests in a highly dynamic pressure distribution. This could support previous experimental findings noting the difficulty with repeatability of intramuscular pressure measurements [6], particularly under dynamic conditions when sensor movement occurs [5]. Under steady-state conditions, fluid can equilibrate and thus the model pressure distribution is uniform. However, it remains unclear if this modeling observation is physiologically accurate, as current experimental intramuscular pressure studies do not provide the necessary spatial measurements to correlate with a finite element model. Future work to experimentally investigate regional IMP in muscle simultaneously would provide valuable insight into this spatial fluid distribution and provide strong validation data for this model. Additionally, dynamic muscle conditions are critical to proper in vivo function [8] and thus should not be neglected for the sake of simplicity.

Our model further supports experimental findings of increases in fluid pressure with passive muscle tension [4]. In fact, some studies have suggested that fluid content in muscle may play a role in passive stiffness either through poroelasticity [21,55] or modeling muscle fibers as volumes filled with incompressible fluid [56,57]. However, the length dependency of fluid pressure in our model under contractile conditions suggests that variability of intramuscular pressure in vivo may be dependent on other physiological conditions (in this case muscle length) in addition to muscle force.

When muscle is passively stretched, the transverse direction compresses due to the Poisson effect. When muscle actively contracts, the transverse direction expands, again due to the Poisson effect. Thus, when muscle is stretched and contracts, the Poisson effect enacts opposing deformations, which when combined result in a small net volumetric deformation (Fig. 5). A small net volumetric deformation will result in a small fluid pressure. Or, more generally, it is well known that fluid is pressurized from changes in volume in a biphasic material. Our model suggests that as muscle is lengthened, contraction must overcome larger and larger opposing deformations to pressurize the fluid. Thus, the observed decreases in change in fluid pressure with muscle stretch are expected within our model.

Fig. 5.

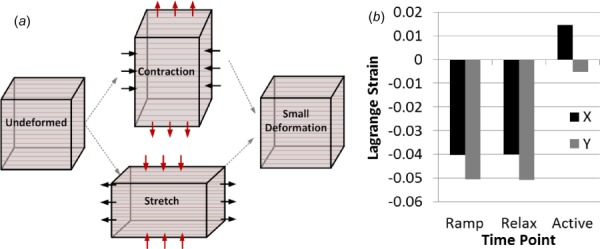
(a) The deformations resulting from passive stretch and active contraction both enact the Poisson effect, where the longitudinal strain (horizontal arrows) results in strain in the transverse plane (vertical arrows). As these deformations oppose each other, the result is a smaller resultant volumetric deformation, which yields low fluid pressurization. (b) Model transverse strains (x and y directions, as elongation occurs in the z direction) for three time points when stretched to optimal length, after initial ramp elongation, at the end of stress relaxation, and at maximum contraction. Passive elongation results in negative transverse strains, which is then counteracted by shortening due to active contraction.

This is supported by recent experimental work by Ateş et al. of human in vivo IMP measurements in the tibialis anterior [58]. Specifically, increases in ankle torque were observed with increasing joint angle (increasing muscle length), but IMP was not found to increase in similar fashion. As discussed by Ateş et al., TA moment arm changes cannot account for increasing torque in this case; thus, the isometric force–length relationship (increasing) and IMP–length relationship (no increase) were not observed to be the same, similar to our model. Further experimental work to identify exactly how muscle length and activation level contribute to intramuscular pressure readings, such as eccentric or concentric contractions, would further elucidate the accuracy of our modeling approach. Additionally, it remains unclear how contraction velocity may similarly affect model results.

While passive stretch of in vitro whole skeletal muscle is largely dictated by longitudinal mechanical properties, in vivo muscle fibers are connected through fascia to surrounding muscle fibers and other tissues. As a result, force generation is transmitted laterally throughout skeletal muscle [9]. Thus, while the transverse tensile properties play a limited role in in vitro passive muscle stiffness, they contribute to the mechanical function of skeletal muscle in vivo. In our model, the transverse tensile stiffness also plays a key role in fluid pressurization (Table 5). This was particularly evident on the ascending limb when muscle is at short lengths, as there is no prestretch to overcome and thus transverse tensile strains are larger. Stiffer fibers would result in less expansion and thus more fluid pressurization. However, at longer muscle lengths, the role of transverse stiffness seems to be less important to fluid pressurization (Table 5). This appears to be due to the fact that contraction must “overcome” stretch to pressurize fluid (Fig. 5), as outlined above. The agreement between experiment and model data for transverse muscle stiffness (Fig. 4) is thus critical for future applications of this work to in vivo modeling and to the use of this model for clinical recommendations.

5. Conclusions

This work presents the first whole muscle finite element model of skeletal muscle that predicts both intramuscular pressure and muscle force under passive and active conditions. This work also modeled active skeletal muscle with a hyperporo-viscoelastic constitutive approach, utilized inhomogeneity, and confirmed physiological accuracy in regard to choosing parameter values. The transverse tensile stiffness was shown to play a key role in fluid pressurization at short muscle length. At longer lengths, passive stretch and muscle contraction enacted opposing Poisson effects, which led to low fluid pressurizations. Future use of this model to study spatial distribution of fluid pressure within skeletal muscle will guide the clinical use of the pressure microsensors for accurately measuring intramuscular pressure. Further model development to include more complex muscle activation as well as the effects of muscle weakness or disease would also be highly beneficial.

Funding Data

• Eunice Kennedy Shriver National Institute of Child Health and Human Development (R01HD31476).