Numerical Parametric Study of Paravalvular Leak Following a Transcatheter Aortic Valve Deployment Into a Patient-Specific Aortic Root

Abstract

Paravalvular leak (PVL) is a relatively frequent complication after transcatheter aortic valve replacement (TAVR) with increased mortality. Currently, there is no effective method to pre-operatively predict and prevent PVL. In this study, we developed a computational model to predict the severity of PVL after TAVR. Nonlinear finite element (FE) method was used to simulate a self-expandable CoreValve deployment into a patient-specific aortic root, specified with human material properties of aortic tissues. Subsequently, computational fluid dynamics (CFD) simulations were performed using the post-TAVR geometries from the FE simulation, and a parametric investigation of the impact of the transcatheter aortic valve (TAV) skirt shape, TAV orientation, and deployment height on PVL was conducted. The predicted PVL was in good agreement with the echocardiography data. Due to the scallop shape of CoreValve skirt, the difference of PVL due to TAV orientation can be as large as 40%. Although the stent thickness is small compared to the aortic annulus size, we found that inappropriate modeling of it can lead to an underestimation of PVL up to 10 ml/beat. Moreover, the deployment height could significantly alter the extent and the distribution of regurgitant jets, which results in a change of leaking volume up to 70%. Further investigation in a large cohort of patients is warranted to verify the accuracy of our model. This study demonstrated that a rigorously developed patient-specific computational model can provide useful insights into underlying mechanisms causing PVL and potentially assist in pre-operative planning for TAVR to minimize PVL.

Introduction

Transcatheter aortic valve replacement (TAVR) is a less-invasive treatment for patients with severe aortic stenosis [1]. It has been established as a standard of care in aortic stenosis patients with high risk of surgical mortality or who are not suitable for surgery [2,3]. Recently, this revolutionary therapy has been approved by U.S. Food and Drug Administration (FDA) to treat intermediate-risk patients [4], with the advantages of less trauma and shorter recovery time. Despite the progress made, there remain several potential TAVR limitations that need to be minimized [5]. Among them, paravalvular leak (PVL) remains a frequent complication of TAVR associated with increased mortality [6]. The 2-year follow-up of PARTNER 2 trial demonstrated that TAVR resulted in higher incidence of PVL than surgical aortic valve replacement with >25% of TAVR patients having at least mild PVL [7]. Moreover, even mild PVL post-TAVR was associated with 10–15% higher mortality at 2 years than patients with none or trace PVL in earlier PARTNER analyses [8]. Valve undersizing or under-expansion, valve malalignment (either too high or too low), and severe global and focal aortic valve calcification with malapposition are the main causes of PVL [6,9]. However, currently, there is no effective method to pre-operatively predict and prevent PVL.

The severity of PVL after TAVR can be assessed by several imaging modalities, such as angiography, echocardiography, cardiac magnetic resonance [10], and multislice computed tomography (MSCT) [11]. Aortic root angiography is an established tool for qualitative and semiquantitative assessment of PVL. The downside of this tool is that it relies on the subjective interpretation of unidimensional images [6]. Echocardiography remains the least costly and most widely available diagnostic method. However, it is important to realize that quantification of PVL after TAVR still remains challenging, since several regurgitant jets often co-exist. The Valve Academic Research Consortium (VARC) published the VARC-2 criteria for the assessment of aortic regurgitant and/or PVL after TAVR [12]. VARC-2 classifies PVL severity into three levels: mild, moderate, and severe. The evidence supporting these criteria for the assessment of PVL is limited and requires further validation [13,14].

Computational models [15–19] have greatly improved our understanding of the structural mechanics of the transcatheter aortic valve (TAV) deployment; however, there is still a lack of studies on the post-TAVR hemodynamics with the consideration of device-tissue interaction. Only a few studies investigated the PVL after TAVR. De Jaegere et al. [20,21] validated a computational model of PVL prediction in 60 patients who underwent CoreValve (Medtronic, Minneapolis, MN) deployment. The predicted PVL from the model was compared with the observed data from angiography and echocardiography. The impact of device sizing and implantation depth on PVL was investigated in a subset of cases. However, a fixed 32 mmHg transvalvular pressure during diastole used in their model seems unphysiological and may underestimate the severity of PVL. Saeedi [22] investigated the energetic and hemodynamic characteristics of PVL after TAVR. A 26 mm Edwards SAPIEN valve was modeled in an idealized aortic root geometry, and the PVL orifices were numerically created at different locations. Therefore, their findings may not reflect the clinical practice in real patient anatomies. Bosmans et al. [23] developed a finite element (FE) model to study the self-expandable TAV stent implantation in 10 patients. The deformed geometries of the stent and displacement of calcifications from simulations were compared to the follow-up MSCT scans for validation. A max-flow algorithm, which creates a one-dimensional connected graph to represent the flow network based on the distance between the stent and aortic root, was used to estimate the severity of PVL. This analysis corresponded well to the clinical data when no regurgitation was observed but suffered from inaccuracy for PVL patients, which may be due to the inaccurate estimations of the one-dimensional model.

Clearly, there still lacks accurate preprocedural computational models for the prediction of post-TAVR PVL. In this study, we developed computational models to perform a parametric investigation of the impact of various TAVR shape, deployment and modeling strategies on PVL. Since accurate modeling of TAV deployment is essential in simulating post-TAVR aortic flow, nonlinear FE method was used to simulate a self-expandable CoreValve system deployment into a patient-specific aortic root, modeled with human aortic tissue properties. Subsequently, computational fluid dynamics (CFD) simulations were performed using the post-TAVR geometries from the FE simulation, and a parametric investigation of the impact of the factors such as the TAV skirt shape, TAV orientation, and deployment height on PVL was conducted.

Methods

Patient-Specific Aortic Root Model and Transcatheter Aortic Valve Geometry.

In this study, a clinical case that a 26 mm CoreValve was implanted in a 91-year-old female patient was studied. The patient-specific three-dimensional (3D) geometry of the aortic root including the calcified native leaflets was reconstructed from de-identified pre-operative MSCT images, collected from Columbia University Medical Center, using Avizo software (VSG, Burlington, MA). Institutional Review Broad approval to review patient images was obtained for the study. HyperMesh software (Altair Engineering, Troy, MI) was used to generate a high-quality FE mesh of the 3D aortic root model (Fig. 1(a)), which included aortic root, native leaflets, calcification, mitral-aortic intervalvular fibrosa, fibrous trigones, and left ventricular outflow tract (LVOT). It can be seen (Fig. 1) that for this patient, each native aortic leaflet has one large chunk of calcification attached to the aortic side. There is an additional small piece of calcification on the right coronary leaflet and left coronary leaflet (LCL). A large chunk of calcification also appears just above the noncoronary leaflet (NCL). Calcification was modeled such that the volume of 3D elements in HyperMesh was similar to that was quantified using the material statistics tool with a density greater than 850 Hounsfield units in Avizo. The CoreValve stent geometry used in this study was created using the illustrations in the literature [24].

Fig. 1.

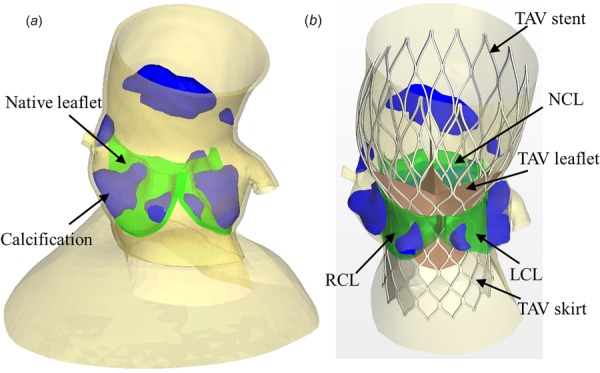
(a) Pre-TAVR aortic root geometry from CT scans used for FE simulations of TAV deployment and (b) post-TAVR geometry obtained from FE simulation results. TAV skirt and leaflets were added to accommodate CFD simulations.

Finite Element Modeling of CoreValve Deployment.

Three-dimensional solid elements were used to model the TAV stent and the aortic root in ABAQUS explicit 6.13 (SIMULIA, Providence, RI) fe software. The modified anisotropic hyperelastic Holzapfel-Gasser-Ogden (MHGO) material model [25] was adopted to characterize mechanical behaviors of the human tissues, including native leaflets, aortic sinus, and ascending aorta. The tissues were assumed to be composed of a matrix material with two families of embedded fibers, each consisting of a preferred direction. The strain energy function W can be expressed as

$$W=c_1\left\{\text{exp}\hspace{0.17em}\left[c_2\left({\overline{\mathit{I}}}_1-3\right)\right]-1\right\}+\frac{k_1}{2k_2}\sum _{i=1}^2\left[\text{exp}\hspace{0.17em}\left\{k_2{[\kappa {\overline{\mathit{I}}}_1+\left(1-3\kappa \right){\overline{\mathit{I}}}_{4i}-1]}^2\right\}-1\right]+\frac{1}{D}{\left(J-1\right)}^2,i=1,2$$ (1)

where the strain invariant ${\overline{\mathit{I}}}_1$ is used to describe the matrix material and the strain invariant, ${\overline{\mathit{I}}}_{4i}$ is used to describe the properties of the fiber families. $c_1$, $c_2$ and $k_1$, $k_2$ are the matrix and fiber parameters, respectively, $D$ is a material constant to enforce incompressibility, and $J$ is the determinant of the deformation gradient. In addition, if $\rho \left(\mathrm{\Theta }\right)$ is the orientation density function, then $\kappa =1/4{\int }_0^{\pi }\rho \left(\mathrm{\Theta }\right){\mathrm{s}\mathrm{i}\mathrm{n}}^3\mathrm{\Theta }d\mathrm{\Theta }$, ranging from 0 to 1/3, determines the level of dispersion in the fiber directions [26]. Local coordinate systems were defined for each leaflet and sinus to include fiber orientations for each region. The mean fiber directions are assumed symmetric with respect to the circumferential axis of the local coordinate system. The parameter $\theta$ defines the angle between one of the mean local fiber direction and the circumferential axis of the local coordinate system. The anisotropic material model was implemented into abaqus with a user subroutine VUANISOHYPER [27–29].

The isotropic hyperelastic Ogden model [30] was used to characterize the mechanical properties of the human mitral-aortic intervalvular fibrosa and fibrous trigones obtained from uniaxial testing. Calcification was assumed to be homogeneous and to have a Young's modulus of 12.6 MPa [31] and a Poisson's ratio of 0.3. Details of the determination of material parameters for aged human tissues from biaxial mechanical tests were described in previous publications [32,33] and the material parameters used in this study are listed in Table 1.

Table 1.

Material parameters of noncalcified human aortic sinus, ascending aorta, leaflet, myocardium, anterior mitral leaflet, and mitral-aortic intervalvular fibrosa

	c1 (kPa)	c2	$k_1$ (kPa)	$k_2$	$\kappa$	D (kPa−1)	$\theta$ (deg)
Sinus	1.7553	13.7077	10.5507	80.3790	0.0006	0.0005	20.06
Ascending aorta	4.1755	3.4649	3.7711	15.9276	0.0864	0.0005	70.95
Leaflet	0.9627	6.3928	12.7250	48.6769	0.0711	0.0005	28.04
Myocardium	0.0374	15.3875	6.0798	98.3666	0.1440	0.0005	6.78
Mitral leaflet	0.1245	13.6655	11.0069	84.8478	0.0800	0.0005	13.09
Ogden model	μ1 (kPa)	α1	μ2 (kPa)	α2	μ3 (kPa)	α3
Fibrosa	2069.4	12.5	94.8	12.5	3182.6	12.5

Eight-node hexahedral elements (C3D8I) were used to model the TAV stent. Initially, the stent was positioned coaxially with the aortic root. The stent was modeled using the properties of nitinol with austenite elasticity of 50 GPa, austenite Poisson's ratio of 0.3, martensite elasticity of 25 GPa, and martensite Poisson's ratio of 0.3 [34]. The TAV leaflets were not included in the deployment FE model because the effects of TAV leaflets on the biomechanical interaction between the stent and native tissue during the stent expansion were negligible. The crimped geometry of the self-expanding CoreValve stent was obtained by applying a displacement field in the radial direction to a cylindrical sheath outside the stent, and the deployment of the stent was simulated by applying a displacement field in the axial direction to the sheath away from the aortic root. The top of the ascending aorta was constrained to allow only rotational degrees-of-freedom. The friction coefficient between the stent and aortic root was assumed to be 0.1 [35].

Computational Fluid Dynamics Modeling of Aortic Flow.

The deformed aortic root and stent geometries after deployment were extracted from the FE simulation and used to create CFD models. The inner surface of the aortic root was used to extract fluid domain. A skirt was added to the TAV stent in the CFD model to mimic the impermeable porcine pericardium skirt seal of the CoreValve. The TAV leaflets were created by virtually reproducing the closed shape of CoreValve leaflets and attached to the stent [36] for CFD simulations. It was demonstrated later that the detailed closing shape of the leaflets has a negligible effect on the PVL. The geometries of the aortic root, calcification, TAV stent, leaflets, and skirt in the deployed configuration are depicted in Fig. 1(b). The post-TAVR hemodynamics was simulated in Star-CCM+ (CD-adapco, Melville, NY) cfd software. The physics model employed an incompressible Newtonian fluid with a reference density $\rho =1056\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$ and dynamic viscosity $\mu =0.0035\mathrm{P}\mathrm{a}·\mathrm{s}$ for blood properties. The largest leakage gap size is around 2–3 mm in our models, considering a peak regurgitant jet velocity of 5 m/s, therefore the peak Reynolds number exceeds 3000. This suggests the flow is in the transitional or low-Re turbulent flow regime. Turbulence modeling was performed using the K-Omega SST model with all y+ wall treatment and low Reynold number damping modification, since the Reynolds number is not very high through the small leakage channel [37]. The Navier–Stokes equations for 3D flow were solved by a second-order segregated iterative method (SIMPLE algorithm). Since the purpose of this paper was to evaluate PVL when TAV was closed, only diastolic phase was modeled (simulation time T = 0.516 s). The transient feature of the flow was modeled using the implicit unsteady solver with a time-step of 0.5 ms. Convergence criteria for all the flow parameters were set to 10⁻⁵.

High-density hexahedral core meshes with prism layer meshes near the wall boundary were generated. Volumetric control was used to generate dense meshes with the shortest edge length less than 0.1 mm in the vicinity of the contact region between the stent and aortic root. Approximately 2.3–2.8 ×10⁶ cells per model were found to be sufficient to provide mesh-independent results. Figure 2 illustrates the mesh configuration in three cross sections. The LVOT, right (RCA) and left coronary artery (LCA) boundaries were extended to eliminate the boundary effect on the results of the CFD simulations [38].

Fig. 2.

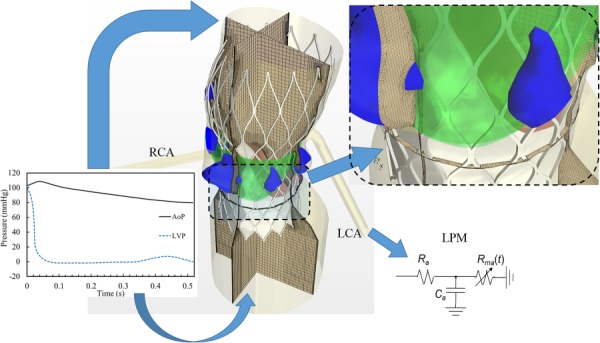
Computational fluid dynamics mesh and boundary conditions. Physiological pressure waveforms were used at the LVOT and ascending aorta as the pressure outlet and pressure inlet boundary conditions, respectively. Lumped parameter model was used at each coronary outlet.

Physiological pressure waveforms were applied to the ascending aorta and LVOT as the pressure inlet and outlet boundary conditions, respectively since the patient-specific pressure waveform is unknown after TAVR (Fig. 2). Lumped parameter model established previously [39] was implemented at the coronary arteries to couple the local pressure with the flow rate. This model has been validated [39] to be able to capture physiological coronary blood flows.

Transcatheter Aortic Valve Models.

It is known that valve mal-alignment is a main cause of PVL [6,9]. To quantify the impact of valve deployed orientation on PVL, simulations of two different TAV orientations were performed. Rotation #1 (denoted as r1) consisted of the TAV leaflet commissures aligned with the native leaflet commissures (Fig. 3(a)). For Rotation #2 (denoted as r2), the TAV leaflet commissures were aligned with the center of the native leaflets. The impact of TAV vertical placement on PVL was assessed by FE simulations of TAV deployment into three different heights: 5 mm higher than the optimum (denoted as h1), the optimum (denoted as h2), and 5 mm lower than the optimum (denoted as h3). The optimal implant position is defined as the stent nadir is approximately 4 mm–6 mm below the aortic annulus according to the manufacturer's guideline of CoreValve System [40]. Note that in Fig. 3(b), the TAV leaflets were simplified using planar seals. This simplification has a negligible effect on the PVL assessment, which will be discussed later. In addition, as shown in Fig. 3(c), the impact of the skirt shape was modeled by considering three different shapes: realistic scallop shape of the skirt (denoted as s1), the modified skirt with 2.5 units of stent cell height (denoted as s2), and the modified skirt with 2 units of stent cell height (denoted as s3). The impact of stent thickness on the modeling accuracy was assessed as well, which was ignored in a previous study [23]. Two scenarios were considered: (1) A TAV stent of 0.35 mm in strut thickness with the skirt mounted on the inner surface of the stent is denoted as a brick stent; and (2) a shell stent, as shown in Fig. 3(d), with zero strut thickness, modeled as a surface, and the skirt on the stent outer surface.

Fig. 3.

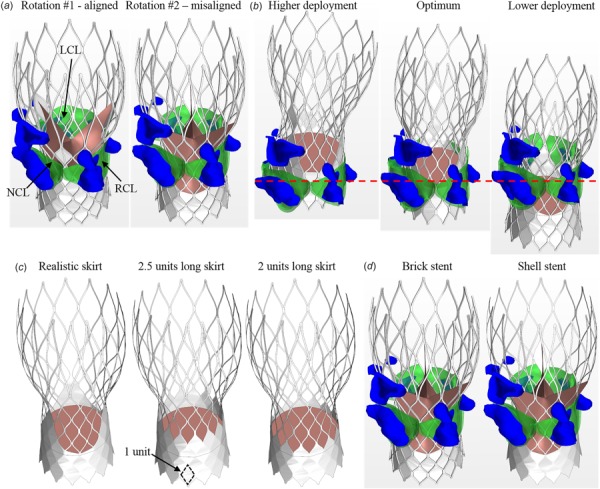
TAV models with (a) two different orientations: r1 and r2, (b) three different deployment heights: h1, h2, and h3, (c) three skirt shapes: s1, s2, and s3, and (d) brick stent and shell stent

Results

Flow Rate and Pressure Waveforms.

The representative coronary artery flow rate and pressure waveforms from one simulation are shown in Fig. 4(a). It can be seen that the flow rate of LCA is approximately twice that of RCA, which is consistent with physiological observations [41,42]. We found that coronary flow rates do not change among different TAV models since the pressure in the domain is almost unchanged. For the pressure waveforms, it can be seen that the coronary pressure has the same trend as the aortic pressure and the LCA pressure is slightly higher than the RCA pressure. Figure 4(b) shows the PVL flow rate waveform from the TAV model with an optimal deployment height and aligned orientation. Since the PVL is driven by the pressure difference between the ascending aorta and LVOT, as expected, the leaking flow rate is proportional to the pressure drop (shown as the dotted line).

Fig. 4.

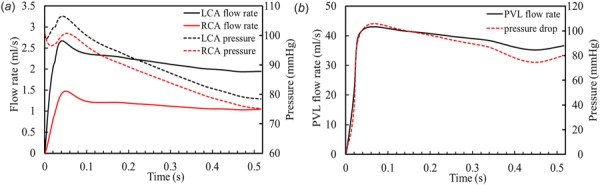
(a) The representative coronary artery flow rate and pressure waveforms from the simulation. (b) PVL flow rate curve calculated from the simulation of brick-s1-r1-h2 model. The dotted line represents the pressure drop between the ascending aorta and LVOT.

The Effect of Stent Thickness and Skirt Shape.

To simplify the model, the TAV leaflets at the closed configuration were modeled as a planar seal (as shown in Fig. 3(b)). It was found that this simplification has a negligible effect on the evaluation of PVL, i.e., less than 4% difference in leaking volume compared to the fully closed realistic TAV leaflet configuration. Therefore, the planar seal was used in the following TAV models to save time and effort in the model setup. This may be critical to streamline the process as a tool for surgical planning in the future. First, we evaluated the impact of the skirt shape (Fig. 3(c)) on PVL. Their corresponding PVL flow rates are depicted in Fig. 5(a). It can be seen that the model with a shorter skirt height (the s3 model) caused the largest leakage, while the other two models have the similar leaking flow rates. The leaking flow velocity profiles are shown in Fig. 5(b). We found that a strong regurgitant jet streamed through the gap right below the LCL. In the s1 and s2 models, the leakage pathway has a smaller cross-sectional area compared to the case of s3, marked by the dash line circles in Fig. 5(b). This caused smaller PVL volumes in the s1 and s2 models.

Fig. 5.

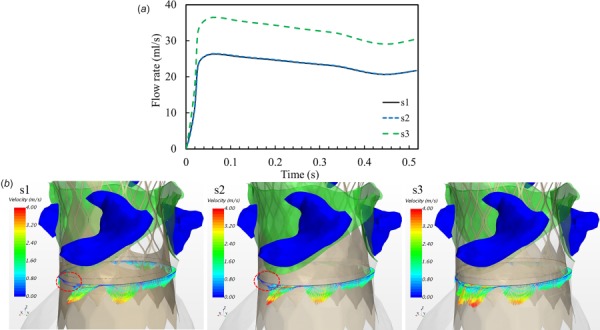
(a) Paravalvular leak flow rate curves from three TAV models with different skirt shapes as shown in Fig. 3(c) and (b) velocity vector profiles in a vertical cross section illustrate the leaking flow through the gaps between the aortic root and TAV stent

Since the thickness of the stent is only 0.35 mm, one may consider modeling the stent as a zero thickness baffle to simplify volume mesh generation. However, this simplification may cause a significant error in evaluation of PVL. The regurgitant velocity vectors through a vertical cross section from the brick stent and shell stent models (Fig. 3(d)) are illustrated In Fig. 6. Note that dense meshes were generated in the vicinity of the leakage zone to ensure at least 10 cells across the gap. Due to the inclusion of the brick stent, the velocity vectors were disturbed and appeared more irregular than that in the shell stent model. Another notable observation is that the cross section area of the leakage is larger in the brick stent model with the skirt mounted on the inner surface of the stent. The averaged regurgitant flow rates are 24.6 ml/s and 42.4 ml/s (corresponding regurgitant volumes are 12.7 ml/beat and 21.9 ml/beat) for the shell stent and brick stent models, respectively (see Fig. 8(d)). This large difference in the regurgitant flow rate demonstrates the importance of incorporating stent thickness in the model in order to accurately assess the severity of PVL.

Fig. 6.

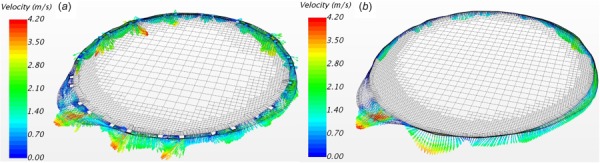
Regurgitant velocity vectors of a vertical cross section from (a) the brick stent (brick-s1-r2-h3) model and (b) shell stent (shell-s1-r2-h3) model

Fig. 8.

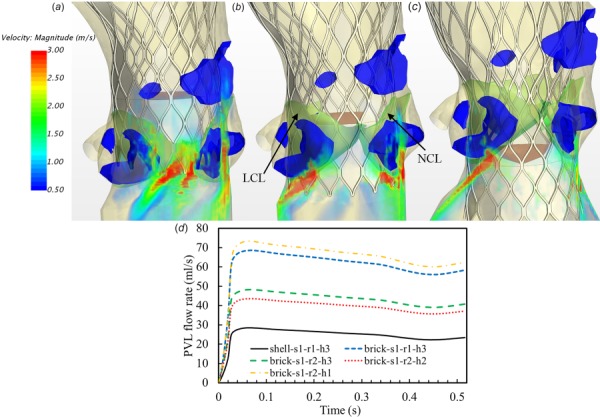
Volume rendering of velocity fields from the models with different deployment heights (a) higher than the optimum, h1 (brick-s1-r2-h1 model), (b) around the optimum, h2 (brick-s1-r2-h2 model), (c) lower than the optimum, h3 (brick-s1-r2-h3 model), and (d) corresponding PVL flow rate curves from five TAV models in Figs. 6–8

The Effect of Transcatheter Aortic Valve Orientation.

The CoreValve device has a longer skirt in the region between the leaflet commissures and a shorter skirt around the nadir of the leaflet attachment, thus the orientation of TAV may affect PVL. Volume-rendering velocity fields from two models with different orientations (Fig. 3(a)) are depicted in Fig. 7. It can be seen that the TAV model with aligned orientation had a larger leakage than the one with misaligned orientation. Marked by the black circle in the figure, there was a strong leaking jet through the gap just below the LCL (see Fig. 7(a)), while a smaller and weaker jet was observed (see Fig. 7(b)). As expected, the longer skirt located adjacent to the leaking pathway increased flow resistance, thus led to a smaller jet in the model of r2. The averaged regurgitant flow rates for the aligned and misaligned models are 60.4 ml/s and 42.4 ml/s (corresponding regurgitant volumes are 31.2 ml/beat and 21.9 ml/beat), respectively (see Fig. 8(d)). This indicates that the TAV orientation could significantly affect PVL for CoreValve patients under certain situations.

Fig. 7.

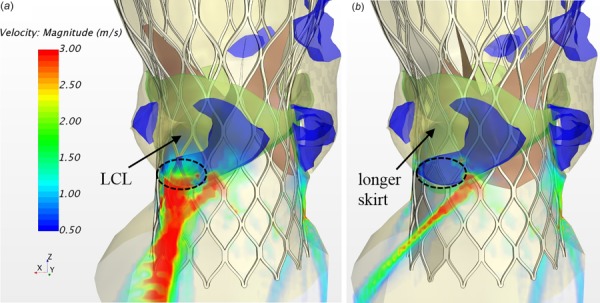
Volume rendering of velocity fields from the models of (a) aligned orientation r1 (brick-s1-r1-h3 model), and (b) misaligned orientation r2 (brick-s1-r2-h3 model)

The Effect of Deployment Height.

Three FE simulations of TAV deployment were conducted in order to accurately capture the tissue-device interaction due to the different deployment heights. Volume rendering velocity fields from the models with three deployment heights and the misaligned TAV orientation (r2) (Fig. 3(b)) are shown in Fig. 8. The model with higher than the optimal deployment exhibited overwhelmingly strong regurgitant jets downstream the TAV as shown in Fig. 8(a). The majority of PVL occurred through the commissure regions between the LCL and NCL, and the NCL and RCL. The optimal and lower deployments resulted in a similar regurgitant flow field, with the majority of the leakage through the midregion of the LCL and NCL, as shown in Figs. 8(b) and 8(c). The corresponding averaged regurgitant flow rates for these three models are 64.5 ml/s, 38.4 ml/s, and 42.4 ml/s (corresponding regurgitant volumes are 33.3 ml/beat, 19.8 ml/beat, and 21.9 ml/beat), respectively (see Fig. 8(d)).

Comparison of Paravalvular Leak from the Simulation and Clinical Data.

Doppler echocardiography is usually used clinically for the assessment of PVL. PVL severity is defined based on the VARC-2 classification [12]. It is noted that the resultant classification may not be consistent using different criteria, such as regurgitant volume, regurgitant fraction, and effective regurgitant orifice area (EROA). Here, the PVL grade was classified based on EROA. Clinically, EROA of this patient is calculated by the proximal isovelocity surface area method based on echo measurements [43]. In the simulations, EROA was calculated according to the formula $\mathrm{E}\mathrm{R}\mathrm{O}\mathrm{A}=(\mathrm{R}\mathrm{V}/\mathrm{V}\mathrm{T}\mathrm{I})$ [44], where RV is the regurgitant volume and $\mathrm{V}\mathrm{T}\mathrm{I}$ is the velocity time integral of regurgitant jets. Regurgitant volume was calculated by integrating the volumetric flow rate over time. The quantitative comparison of PVL calculated from the models and clinical data is summarized in Table 2. It can be seen that the shell stent models underestimate the severity of PVL, whereas in general, the brick stent models are in good agreement with the clinical data.

Table 2.

Comparison of PVL metrics calculated from the simulations with clinical data

Case	EROA (cm2)	PVL grade	Regurgitant volume (ml/beat)
Clinical data	0.12	Mild-moderate	N/A
Shell-s1-r1-h3	0.088	Mild	21.5
Shell-s1-r2-h3	0.052	Mild	12.7
Shell-s2-h3	0.048	Mild	11.8
Shell-s3-h3	0.067	Mild	16.4
Brick-s1-r1-h3	0.127	Mild-moderate	31.2
Brick-s1-r2-h3	0.089	Mild	21.9
Brick-s1-r1-h1	0.135	Mild-moderate	32.9
Brick-s1-r2-h1	0.136	Mild-moderate	33.3
Brick-s1-r1-h2	0.080	Mild	19.6
Brick-s1-r2-h2	0.081	Mild	19.8

Discussion

In this study, the influences of skirt shape, TAV orientation, stent and skirt modeling, and deployment height of CoreValve on PVL were investigated using computational models. These factors are related to the valve design and the device-host interaction.

Calcification amount and distribution play a key role in PVL outcome after TAVR. Calcification may cause incomplete or non-uniform expansion of the stent. However, whether the extent or the distribution of calcification is a predictor of the grade of PVL is still debatable. Some studies have shown a significant correlation [45–47], while other studies did not [11,48]. From an engineering analysis perspective, heavy focal calcification could cause elliptical, asymmetric deformed shape of TAV, which may lead to central and paravalvular leakage [49]. However, the severity of the leakage is heavily dependent on the nature of the complex interaction between the stent and the host tissue, i.e., native leaflets, calcification and aortic annulus, and factors such as TAV type, deployment height, and device/annulus sizing ratio. Thus, a strong correlation between calcium burden and PVL may not be established by a statistical regression analysis. As shown in this study, the patient has a large chunk of calcification in each leaflet, accompanied with a bulky calcification attached to the ascending aorta above the NCL. The resultant PVL jets were not distributed equally among the leaflets. Conversely, PVL depends on the deployment height and TAV orientation. Therefore, a computational model based on pre-TAVR imaging scans may serve as a patient-specific pre-operative planning tool to predict the clinically relevant outcome and guide the physicians to select the proper deployment strategy during the procedure that best fits the individual patient. In the future, by applying this computational model to a large cohort of PVL patients, we expect that a correlation between the optimal TAV deployment position and the calcification distribution and anatomic characteristics of the patient could be established.

The computational model developed in this study may also assist the design of next-generation TAVs. For instance, the impact of skirt length and shape on PVL could be studied. The longer skirt could reduce the grade of PVL; however, it may cause coronary obstruction in certain situations. Therefore, a proper length of the skirt considering these two competitive factors should be used in practice. This conjecture was reflected in the newer Medtronic CoreValve Evolut R, which has an extended skirt of the inflow tract to provide better seal [50]. The significant smaller leakage in the shell stent model compared to its brick stent counterpart may suggest that a skirt wrapping along the outer surface of the stent could lessen PVL. This was reflected in the new generation of Edwards SAPIEN 3 TAV and CoreValve Evolut Pro devices, which have an outer skirt to the exterior of the stent at the inflow tract to minimize PVL [51,52]. By examining the PVL results from different deployment heights in Fig. 8, we found that lower deployment seems to help reduce PVL and the majority of regurgitant jets originated right below the native leaflets. Under-expanded stent at the inflow tract due to leaflet calcifications and dilated LVOT created large gaps for the leaking. It is conjectured that a flared inflow shape of the stent may alleviate the likelihood of PVL from this region.

The effect of skirt shape and stent thickness on PVL may be estimated by analyzing the laminar flow through an annular pipe. The flow rate through an annular pipe [53] can be calculated as

$$Q=\frac{\pi }{8\mu }\frac{\Delta P}{\Delta L}\left[r_2^4-r_1^4-\frac{{(r_2^2-r_1^2)}^2}{\mathrm{l}\mathrm{n}\left(r_2/r_1\right)}\right]$$ (2)

where $r_2$ and $r_1$ are the outer and inner radii of the annulus, respectively, $\Delta P$ is the pressure drop and $\Delta L$ is the pipe length. It can be seen from Eq. (2) that the flow rate is inversely proportional to the length of an annulus, which is largely determined by the skirt length in the PVL case. Assume that the leakage channel has an inner diameter of 22 mm, which is similar to the deformed diameter of the implanted TAV in this study, a gap thickness ($r_2-r_1)$ of 0.3 mm, and a channel length of 15 mm, we calculated that the flow rate is 32 ml/s with a 80 mmHg pressure drop. If the thickness of the stent strut is considered, then the gap thickness should increase to 0.65 mm, which would result in a flow rate of 321 ml/s. This estimation may explain why the brick stent model has a substantial increase in PVL compared to the shell stent model. Note that the stent strut may partially block the leakage channel; thus, the gap is not uniform as shown in Fig. 6(a); therefore, Eq. (2) only serves as a rough estimation. In clinical practice, the leakage channels are irregular; thus, a CFD simulation is warranted to accurately calculate the leaking volume after TAVR.

Since the sealing skirt was treated as rigid in our CFD simulations, the validity of this assumption needs to be justified. It is known that the skirt is made from the porcine pericardium for the CoreValve. In Fig. 9(a), we could see that the pressure on the upper skirt spreads in a wide range from −75 to 75 mmHg depending on its location. Here, the positive value means the pressure pointing to the root center (expanding the leakage channel), while the negative value means the pressure force pointing outward (shrinking the leakage channel). By extracting the pressure load on the skirt from CFD simulations, we conducted FE simulations to check the bending deflection of the skirt as a clamped plate. Here, Tissue FE models were developed with four layers of C3D8I elements through the thickness of 0.15 mm, which is a typical value for a thin porcine pericardium (Fig. 9(b)). The MHGO hyperelastic material model was used with the optimized material parameters for flexural deformation from our previous paper [54]. We found that the maximum skirt deflection is small (∼0.14 mm) compared to the largest leakage gap size (∼2.1 mm) due to the low pressure (∼5 mmHg) exerted on the skirt in the vicinity of strong leaking jets. However, the skirt deflection can be larger (∼0.51 mm) in certain regions of small leakage channel size (∼0.5 mm) due to the high pressure (∼75 mmHg) exerted on the skirt. Even for the worst-case scenario, the altered leakage gap size is still smaller than half of the largest gap size. It indicates that the skirt deflection would not significantly change the distribution of leaking jets, since the original largest leakage gap remains the largest. Although the accurate estimation of regurgitant volume due to skirt bending can only be determined by fluid–structure interaction simulations, considering the low pressure load on the majority of skirts, based on the formula (2), we estimated that the variation of regurgitant volume can be less than 20%. Note that the skirt bending is negligible for Edwards SAPIEN valves due to the stiffer polyethylene terephthalate material used.

Fig. 9.

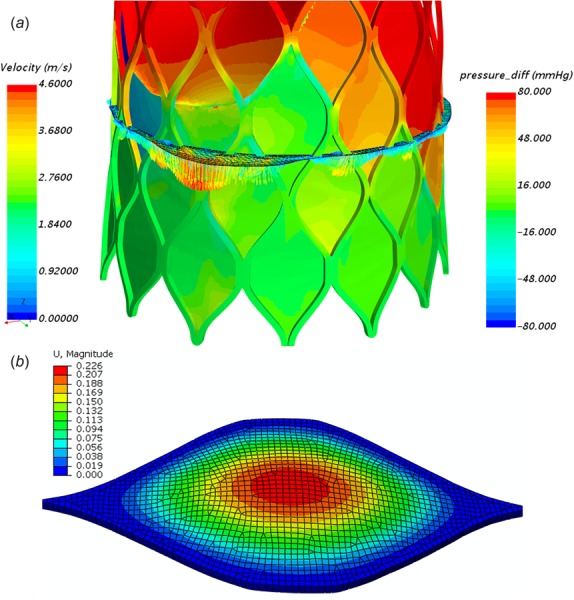
(a) Pressure distribution on the skirt with a regurgitant flow velocity profile to show the distribution of regurgitant jets from the brick-s1-r1-h3 model. (b) A corresponding FE simulation to show the skirt bending under a pressure load of 10 mmHg.

The interpretation of the results from this study should consider the following limitations. First, our computational model was constructed and validated with one patient data. It remains to be seen whether similar results can be obtained for a larger number of patients undergoing TAVR. However, the conclusions drawn based side-by-side comparisons from the parametric study are still valid. Also, the current simulation was performed with a CoreValve device, additional TAVR valve devices and sizes, such as Edwards SAPIEN 3 valves, may need to be incorporated into our model. Moreover, it is commonly accepted that when considering blood flow through large blood vessels, one can treat blood as an incompressible Newtonian fluid [55]. However, when the blood flows through smaller vessels or gaps, the blood flow may no longer be considered Newtonian, and its cellular nature needs to be taken into account. Leakage gaps in this study can have a size as low as 0.1 mm, but are still at least one order of magnitude larger than blood cells. Besides, due to the high shear rate and strong leakage jets, the shear-thinning behavior of blood should reach a plateau with a constant apparent viscosity of 0.0035 Pa·s [56]; thus, the blood may be treated as a Newtonian fluid. Since the TAV leaflets were fully sealed in the model, central leakage was not considered in this study.

Conclusions

In conclusion, we have developed a computational framework utilizing FE and CFD to investigate the severity of PVL in a CoreValve patient. The simulation results are quantitatively close to the clinical measurement. The analysis of the effects of skirt shape, TAV orientation and deployment height on PVL provided useful insights into the deployment strategies for individual patient and may facilitate next-generation TAV designs. Because of the scallop shape of the skirt, the difference of PVL due to TAV orientation can be as large as 40%. Although the stent thickness is small compared to the aortic annulus size, we found that inappropriate modeling of it can lead to an underestimation of PVL up to 10 ml/beat. Further investigation in a large cohort of patients is needed to verify the accuracy of our model. This study also demonstrated that a rigorously developed patient-specific computational model could potentially serve as a tool to assist in pre-operative planning for TAVR deployment strategies to minimize PVL.

Funding Data

• National Institutes of Health (NIH) (HL104080 and HL127570).

• American Heart Association Post-doctoral Fellowship (15POST25910002).