Abstract
Cerebrospinal fluid (CSF) dynamics are thought to play a vital role in central nervous system (CNS) physiology. The objective of this study was to investigate the impact of spinal cord (SC) nerve roots (NR) on CSF dynamics. A subject-specific computational fluid dynamics (CFD) model of the complete spinal subarachnoid space (SSS) with and without anatomically realistic NR and nonuniform moving dura wall deformation was constructed. This CFD model allowed detailed investigation of the impact of NR on CSF velocities that is not possible in vivo using magnetic resonance imaging (MRI) or other noninvasive imaging methods. Results showed that NR altered CSF dynamics in terms of velocity field, steady-streaming, and vortical structures. Vortices occurred in the cervical spine around NR during CSF flow reversal. The magnitude of steady-streaming CSF flow increased with NR, in particular within the cervical spine. This increase was located axially upstream and downstream of NR due to the interface of adjacent vortices that formed around NR.
Introduction
Cerebrospinal Fluid Importance and Therapeutic Applications.
Dynamic motion of cerebrospinal fluid (CSF) plays an important role in central nervous system (CNS) physiology. CSF is a water-like fluid that surrounds the brain and spinal cord (SC) and pulsates in an oscillatory manner with each cardiac and respiratory cycle [1–3]. A detailed understanding of CSF dynamics could improve treatment of CSF-related CNS diseases and lead to novel CSF-based therapeutics. The importance of CSF dynamics has been investigated in several CNS diseases that include Alzheimer's disease [4,5], syringomyelia [6,7], Chiari malformation [8,9], astronaut vision impairment due to space flight [10], and hydrocephalus [11]. CSF can also serve as a conduit for drug delivery to the brain, as solutes delivered to the CSF bypass the blood brain barrier thereby providing relatively direct access to neuronal and glial cells [12,13]. CSF-based therapeutics are presently under development for brain hypothermia [14], CSF filtration [15–18], and control of intracranial CSF pressure oscillations [19].
The efficacy of many of these treatments depends, in part, on transport within the spinal subarachnoid space (SSS). Among the least studied factors is the effect of structures within the SSS on flow and transport, yet the structures appear to strongly affect transport. For example, Stockman found that simplified nerve roots (NR) increased longitudinal transport by five to ten times compared the same channel without NR [20,21]. Tangen et al. found that simplified microstructures increased vorticity and rostral transport of intrathecal drugs [22], and Tangen et al. noted mixing of subarachnoid hemorrhage around NR [23,24]. Accordingly, this study focuses on the effects of more highly resolved NR.
Previous Numerical Models of Spinal Subarachnoid Space Cerebrospinal Fluid Dynamics.
Computational fluid dynamics (CFD) has an advantage in that it is capable of achieving CSF pressure and flow field resolution that may be difficult in vivo with magnetic resonance imaging (MRI) or other invasive techniques. In addition, parameters can be varied that may not be possible to vary in vivo. One challenge has been accurately representing the complex CSF space geometry that includes feature sizes that range over five-orders of magnitude from microns to tens of centimeters. In addition, these features are attached to deforming dural and pial boundaries. Numerical studies of CSF dynamics in the spine (Table 1) can be roughly stratified in terms of:
Table 1.
Summary of previous spinal CSF dynamics numerical studies with key information on the numerical method, anatomic/physiologic feature investigated and the feature impact on CSF dynamics
| Study | Numerical method | Three-dimensional (3D) | Subject-specific | Full spine | TM | NR | AT | Anatomic/physiologic feature investigated | Feature impact on CSF dynamics |
|---|---|---|---|---|---|---|---|---|---|
| Khani et al. (present study) | Finite volume | x | x | x | x | x | NR and nonuniform CSF flow | Steady-streaming flow and CSF vortices created during flow reversal | |
| Tangen et al. [22] | Finite volume | x | x | x | x | x | x | Impact of AT on CSF pressure and solute spread | AT increase pressure drop but have little impact on drug spread to cervical spine |
| Khani et al. [25] | Finite volume | x | x | x | x | Nonuniform CSF flow in a nonhuman primate | Laminar, inertial dominated CSF flow found throughout nonhuman primate spine | ||
| Hsu et al. [26,27] | Finite volume | x | x | x | x | Impact of CSF pulse freq. and mag. on drug spread | Increased CSF pulse frequency and magnitude increase drug spread | ||
| Cheng et al. [28] | Finite volume | x | x | x | x | FSI between CSF and SC | Caused up to 2 mm of SC displacement | ||
| Tangen et al. [29] | Finite volume | x | x | x | x | Infusion settings, drug chemistry and anatomy | Drug dispersion is impacted by infusion, chemistry and anatomy | ||
| Tangen et al. [23] | Finite volume | x | x | x | x | Lumbar CSF drainage after subarachnoid hemorrhage | Body position and CSF drainage rate impact blood removal from CSF | ||
| Kuttler et al. [30] | Finite volume | x | x | x | Impact of slow or fast bolus dose | Pulsation and breathing dominated long-term bolus spread (not bolus speed) | |||
| Pizzichelli et al. [31] | Finite element | x | x | x | Catheter position and angle and tissue permeability | Injection perpendicular to cord increased penetration to the cord tissue | |||
| Haga et al. [32] | Finite element | x | x | x | Catheter position, angle, and injection flow rates | Catheter position, angle and injection flow rates impact solute distribution | |||
| Heidari Pahlavian et al. [33,34] | Finite volume | x | x | x | Comparison of in vivo and in vitro MRI with CFD results | in vitro MRI compared well with CFD results, in vivo compared poorly with CFD | |||
| Heidari Pahlavian et al. [35] | Finite volume | x | x | x | Presence of NR and DL | Increased peak CSF velocities, mixing and bi-directional flow | |||
| Stockman [20] | Lattice Boltzmann | x | x | x | NR, DL, and AT | Increased nonstreamwise components of CSF velocity | |||
| Pahlavian et al. [9] | Finite volume | x | x | x | Pulsatile motion of cerebellar tonsils | Increased peak CSF velocities, mixing, and bidirectional flow | |||
| Bertram et al. [36] | Finite element | x | x | SC and dura compliance | Pressure wave propagation impacted by the elastic properties of tissue | ||||
| Bertram et al. [37] | Finite element | x | x | SC tethering due to arachnoiditis | Increased tensile radial stress and decreased pressure in the SC material | ||||
| Elliott et al. [38] | Finite difference | x | x | Posttraumatic syringomyelia | Stress induced by syrinx fluid sloshing diminishes as syrinx expands | ||||
| Elliott [39] | Analytic | x | x | Syrinx filling due to CSF wave mechanics | Syrinx filling impacted by CSF flow obstruction and tissue properties | ||||
| Jain et al. [40] | Lattice Boltzmann | x | x | Highly resolved direct numerical simulation | Onset of transitional CSF flow in Chiari patients | ||||
| Cheng et al. [41] | Finite volume | x | x | Arachnoiditis permeability | Increased bidirectional flow, peak CSF pressure timing shifted | ||||
| Rutkowska et al. [42] | Finite volume | x | x | Presence of tonsillar herniation | Increased peak CSF velocities, gradient, and bidirectional flow | ||||
| Yiallourou et al. [43] | Finite volume | x | x | Presence of tonsillar herniation | Increased peak systolic CSF velocities, flow jets near foramen magnum | ||||
| Clarke et al. [44] | Finite volume | x | x | Presence of tonsillar herniation | Increased magnitude of peak pressure | ||||
| Shaffer et al. [45] | Finite volume | x | x | Tonsillar descent | Increased longitudinal impedance to CSF flow and correlated with tonsillar descent | ||||
| Martin et al. [46] | Finite volume | x | x | Tonsillar descent | Increased peak CSF velocities, pressure gradient, and longitudinal impedance | ||||
| Roldan et al. [47] | Boundary element | x | x | Tonsillar descent | Increased peak CSF velocities near the CVJ and peak pressure gradient along SSS | ||||
| Linge et al. [48] | Finite volume | x | Tonsillar descent & surgery impact | Increase peak CSF velocities, velocity heterogeneity and CSF pressure gradient | |||||
| Linge et al. [49] | Finite volume | x | Presence of tonsillar herniation | Increased peak CSF velocities and pressure gradient near the tonsils | |||||
| Linge et al. [50] | Finite volume | x | Increase in cardiac rate | Increased pressure gradient, increased magnitude of bi-directional flow | |||||
| Bilston et al. [51] | Finite volume | Decreased arachnoiditis permeability | Increased pressure gradient along the SSS | ||||||
| Loth et al. [52] | Finite volume | x | x | Cross-sectional geometry and SC motion | Pressure gradient waveform dependent on CSF flow waveform and cross-sectional area |
Note: 3D—model constructed in three-dimensional, TM—tissue motion included in model, AT—arachnoid trabeculae included in model, NR—nerve roots included in model.
-
(a)
Numerical method applied: finite volume, finite element, finite difference, analytic, and lattice Boltzmann methods.
-
(b)
Anatomic domain and physiological accuracy: partial/entire SSS length, simplified two-dimensional/three-dimensional (3D), subject-specific based on MR imaging.
-
(c)
Microstructure and tissue motion: spinal cord NR and/or arachnoid trabeculae (AT), prescribed boundary motion, and fluid–structure interaction.
-
(d)
Focus of the investigations: impact of NR and AT on CSF mixing [35], fluid structure interaction of dynamically deforming spinal cord tissue [41], intrathecal drug solute [31–32] and blood [29] transport, and anatomic alterations within disease states such as Chiari malformation and syringomyelia [46]. Several studies have included anatomically idealized NR. Only three studies included arachnoid trabeculae [20,22,53] (note: study by Gupta et al. focused on intracranial SAS and not included in Table 1).
Objectives.
There is a need to understand the impact of realistic geometry on CSF flow patterns. An anatomically accurate and validated model will allow testing and optimization of CNS therapeutics that could lead to more rapid application for clinical use and reduced cost for nonhuman primate studies. To address these needs, the objectives of this study were to build upon the body of CSF modeling work (Table 1) by: (1) MRI measurements of SSS geometry and flow distribution in a patient, and (2) CFD simulation of unsteady CSF flow in a SSS model with and without anatomically realistic spinal cord NR based on the MRI measurements. We hypothesized that the presence of NR increases nonuniformity of axial flow velocities and promotes steady-streaming within the SSS.
Materials and Methods
Ethics Statement.
In this study, all the MRI data collection development was approved by the local Institutional Review Board in Amiens, France and satisfied all local and international regulations for human subject research. All data were de-identified before transferring to the University of Idaho for further analysis.
Subject Selection.
A 23-yr female was chosen for this study as a representative healthy subject to define the CSF space geometry and flow for the numerical model. The subject did not have any history of spinal deformity or CSF-related disorders.
Magnetic Resonance Imaging Cerebrospinal Fluid Flow Measurement and Quantification.
A General Electric 3T scanner was used to obtain all MRI measurements (signa hdxt, software 15.0_M4_0910.a, Boston, MA) using our previously published methodology [25]. CSF flow rate was measured at three vertebral levels, C2-C3, C7-T1, and T10-T11 (Figs. 1(a) and 1(b)), using phase-contrast MRI with retrospective electrocardiogram gating with 32 cardiac phases [46]. Each slice had a thickness of 5.0 mm and an in-plane resolution of 0.54 × 0.54 mm2. The slice orientation was approximately perpendicular to the spine and placed vertically by intersection with a vertebral disk (Fig. 1(a)). CSF flow waveforms were interpolated between the measurement locations to obtain a smooth distribution of CSF flow rate along the entire spine [25]. Zero flow was assumed at the spine termination. Flow at the foramen magnum was assumed to have identical shape as C2–C3 but with 40% reduction in amplitude based on our previous publications with quantification of axial distribution of CSF flow in humans [33,43] and nonhuman primates [25].
Fig. 1.
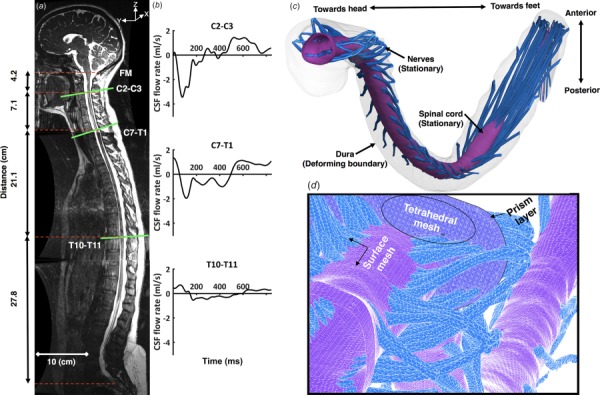
Summary of numerical modeling approach based on subject specific MRI measurements: (a) T2-weighted MR image of the entire spine for the human analyzed (open-source 3D geometry from Ref. [54]). Axial location and slice orientation (lines) of the phase-contrast MRI scans are obtained in this study. Slice axial distance is indicated by dotted lines; (b) The CSF flow rate based on in vivo PCMRI measurement at C2–C3, C7–T1, and T10–T11; (c) three-dimensional CFD model of the SSS; and (d) volumetric and surface mesh visualization with zoom of the upper cervical spine (top).
Magnetic Resonance Imaging Cerebrospinal Fluid Space Geometry Protocol and Segmentation.
The freely downloadable open-source 3D spine geometry with spinal cord NR given previously by Sass et al. was used for this study [54]. In brief, high-resolution MR images were collected within three regions to define the complete intrathecal CSF space geometry (Fig. 1(a)). Three-dimensional fast imaging employing steady-state acquisition (3D FIESTA) was used to collect geometric measurements with improved CSF signal. In-plane voxel spacing was 0.547 × 0.547 mm2, and slice thickness was 1 mm with slice spacing set at 0.499 mm. Echo times were 1.944, 2.112, 2.100, and repetition times were 5.348, 5.762, 5.708 for the craniocervical, thoracic, and lumbosacral volumes, respectively. Total imaging time for the three levels was ∼45 min.
The open-source program, itk-snap (Version 3.4.0, University of Pennsylvania, Philadelphia, PA) [55], was used to segment the MRI data. A single operator segmented the complete spine. The final model includes the 31 pairs of dorsal and ventral NRs, the spinal cord, and dural wall (Fig. 1(c)). Axial position of NR was placed based on the MR imaging. However, the structure and orientation of each NR was idealized based on cadaveric measurements as described by Sass et al. [54].
Computational Model.
The computational domain with nonuniform unstructured grid was generated within ANSYS icem cfd software (ANSYS Academic Research, Release 17.2 University of Idaho, Moscow, ID) and consisted of approximately 13.7 × 106 tetrahedral elements (Fig. 1(d)). The commercial finite volume CFD solver ANSYS fluent (ANSYS Academic Research, Release 17.2) was used to solve the continuity (Eq. (1)) and Navier–Stokes (Eq. (2)) equations
| (1) |
| (2) |
where ρ is the density, μ is the dynamic viscosity, and and p describe the velocity and pressure fields, respectively. CSF was considered to be an incompressible Newtonian fluid with viscosity and density equivalent to water at body temperature [53,56] (ρ = 993.3 kg/m3 and μ = 0.6913 mPa·s). The laminar viscous model was used.
A zero pressure-outlet boundary condition was defined at the foramen magnum. No-slip boundary conditions were imposed at the dural and pial walls. The pial boundary was stationary. Dural boundary motion was modeled based on the in vivo MRI flow measurements. The nonuniform deformation of the computational mesh was implemented at each time-step, as described by Khani et al., by a user-defined function [25]. In summary, this method split the dura into 1 mm segments (606 segments total), and the dural spatial–temporal displacement was modeled to reproduce the interpolated CSF flow rates at each axial level. This resulted in a nonuniform circumferential displacement in the radial direction. In brief, the method involved: (1) interpolation of MRI CSF flow measurements onto 1 mm slice intervals of size, , along the spine; (2) determination of the centroid of each slice, (3) dividing the slice into N pie-shaped radial sections depending on the number of nodes present at the dura wall, (4) movement of each node on the dura surface by a value, , for each radial section based on its radial distance, , from the centroid of the slice: where is the difference in CSF flow rate across each slice section, and is the time-step (see Ref. [25]).
Second-order momentum and pressure gradient solvers were used with default values for under relaxation factors. The convergence criteria for velocity, continuity, and momentum were set to 1 × 106. Total simulation time was 30 h for two cycles (results are presented for the second cycle only) in parallel mode with 141 GB RAM and 30 processors at a clock speed of 2.3 GHz.
Numerical Sensitivity Studies.
Computational fluid dynamics results were verified by numerical sensitivity studies for time-step size, cycle, and mesh resolution (Table 2) with respect to velocity and cyclic mean velocity (Fig. 2) using an improved methodology from that of Khani et al. [25]. For these studies, we quantified sensitivity of z-velocity and cyclic mean z-velocity (steady-streaming) at three locations within the model for a “coarse,” “medium,” “fine,” and “X-fine” mesh with wall prism layers (Figs. 2(a) and 2(b)). Based on these results, a single “fine” mesh was carried forward for completion of subsequent cycle and time-step sensitivity studies. Time-step sensitivity was then checked with time-step resolution given by fractions of the cardiac cycle, T = 0.84 s, for T/168, T/84, and T/42. Cycle sensitivity was checked over three complete cardiac cycles.
Table 2.
Numerical sensitivity studies—values show the maximum relative error for velocity in the z-direction for the three axial planes analyzed (Fig. 2)
| Sensitivity study | Parameter to study | Constant parameters | Maximum error (%) |
|---|---|---|---|
| Grid size | MS = 2 mm, GS = 0.06 M, PS = 0.1 mm, PN = 3 | TS = CT/84 | 68 |
| MS = 1 mm, GS = 0.6 M, PS = 0.1 mm PN = 3 | CN = 2 | 15.7 | |
| MS = 0.5 mm, GS = 3.7 M, PS = 0.05 mm PN = 4 | 4.4 | ||
| MS = 0.25 mm, GS = 29.5 M, PS = 0.025 mm, PN = 6 | |||
| Time Step Size | CT/42 | GS = 3.7 M | 51 |
| CT/84 | CN = 2 | 18 | |
| CT/168 | 2.7 | ||
| CT/336 | |||
| Cycle number | 1 | GS = 3.7 M | 16.1 |
| 2 | TS = CT/84 | 3.7 | |
| 3 | 3.06 | ||
| 4 |
GS = grid size, PS = prism size, PN = prism number, MS = mesh size, CN = cycle number, M = million cells, CT = cycle time in seconds, TS = time step size
Fig. 2.
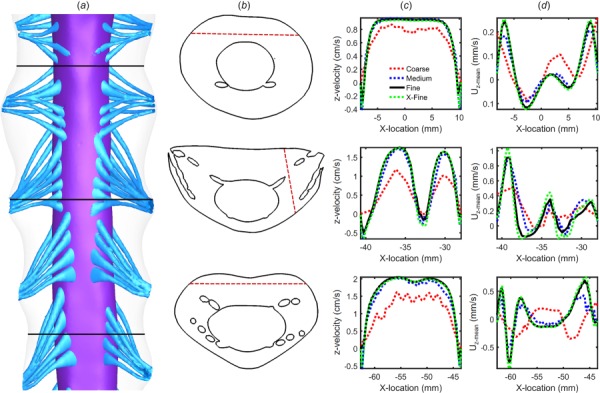
Numerical sensitivity study for velocity and cyclic mean velocity results: (a) 3D geometry of the sensitivity study and axial plane positions, (b) line location along each plane, (c) simulated peak systolic z-velocity component along each line for the four grids (coarse, medium, fine, and X-fine), and (d) simulated cross-sectional mean velocity, Uz-mean, along each line for the four grids
Computational Fluid Dynamics Model Comparison With In Vivo Magnetic Resonance Imaging Cerebrospinal Fluid Flow Measurements.
Dural wall motion was set to reproduce the local CSF flow rate waveform measured by MRI along the spine. The simulated flow rates were compared to the MRI flow rates at three axial locations (Fig. 1(b)). Percent error was defined as the maximum difference between the unsteady flow rate produced by the CFD model, , and the corresponding flow rate measured by MRI, , divided by the mean of the absolute value of CSF flow rate over the cardiac cycle, .
Geometric and Hydrodynamic Quantification.
Based on the 3D reconstruction and meshing, the following geometric and hydrodynamic parameters were calculated along the spine at 1 mm intervals using our previously described methods [25]. Reynolds number based on hydraulic diameter was calculated as , where is the absolute value of the peak flow rate from the flow rate waveform at each cross section, DH is hydraulic diameter, Acs is the cross-sectional area, and v is the kinematic viscosity. Reynolds number for external flow around NR was quantified as: where NR cylinder diameter, , was given by the axial distribution of NR diameters along the spine provided by Sass et al. [54] (ranging from 0.5 to 1.5 mm) and free-stream velocity, , was approximated based on the maximum value of the peak CSF velocity quantified for each axial slice. Stokes–Reynolds number (Reynolds number based on the Stokes layer thickness ) was calculated as . To assess possibility of instabilities in an oscillatory flow around cylinders, Keulegan–Carpenter number was computed as: , and the value of beta is given by, . Flow instabilities occur for values of K > 2 under a given as shown experimentally by Honji [57] and theoretically by Hall [58]. Womersley number was quantified as , where is the angular velocity. The following indicators of the possible presence of turbulent flow were quantified, (1) maximum Reynolds number Re > 2300 at each location along the spine, and (2) Stokes–Reynolds number Reδ > 550 for conditional turbulence in oscillatory flow or for a given Womersley number and Reδ < 550 for weak turbulence [59]. Mean cross-sectional CSF velocity at peak systolic and diastolic flow, , was computed at 1 mm slice intervals along the spine where , with Qpeak defined as the maximum flow rate at peak systole and diastole at each slice.
Quantification of Steady-Streaming Cerebrospinal Fluid Flow.
Oscillatory flow (zero mean flow) can result in steady-streaming due to nonlinear cumulative effects of convective acceleration [60]. To help quantify steady-streaming of CSF, the cyclic mean velocity in the z-direction, , was computed for each node in the computational mesh. A positive value for indicates steady-streaming in the rostral direction. was visualized at multiple axial slices and for a midsagittal slice.
The axial distribution of steady-streaming, , was estimated by computing the cross-sectional average of magnitude
| (3) |
where is cell volume, and the summations were conducted over every cell in the cross section. was calculated for z-slices at 1 mm intervals along the spine. To understand the effect of NR on steady-streaming, and were compared for cases with and without NR. To further quantify the magnitude of steady-streaming flow, a nondimensional fraction of the specified flow rate amplitude was defined as:
| (4) |
where was divided by two to obtain a unidirectional steady-streaming flow rate, because the positive flow is always equal the negative flow for a closed SSS.
Results
Numerical Sensitivity Studies.
Numerical sensitivity study was confirmed based on an assumed error threshold of <5% under increasing degrees of resolution. Maximum z-velocity error for the fine versus X-fine grid was 4.4% and medium versus fine grid was 15.7% (Table 2 and Fig. 2). error was similar (<5% between the fine versus X-fine grid). Thus, subsequent sensitivity studies were carried out with the fine grid. A time-step size of 0.01 s (T/84) produced a maximum error of 2.7% for z-velocity and was selected for future studies. Similarly, cycle sensitivity results for unsteady z-velocity showed that z-velocity variation after the first cycle was negligible (∼3.6%). Thus, the results for the final CFD study were analyzed based on the second cycle with a fine grid and time-step size of 0.01 s (T/84).
Reproduction of Magnetic Resonance Imaging-Derived In Vivo Cerebrospinal Fluid Flow Measurements.
The results showed a maximum flow rate error of 2.3% (Fig. 3). This degree of error is similar to previous CSF flow studies [61]. The flow rate waveforms applied to the model had a similar amplitude to previous in vivo MRI studies [52,62–64]. For those studies, mean velocity at peak systole near C2 vertebral level was ∼2.5 cm/s. In the present model, the mean velocity at C2 was ∼2.4 cm/s with NR and stroke volume at that location was 0.77 cm3.
Fig. 3.
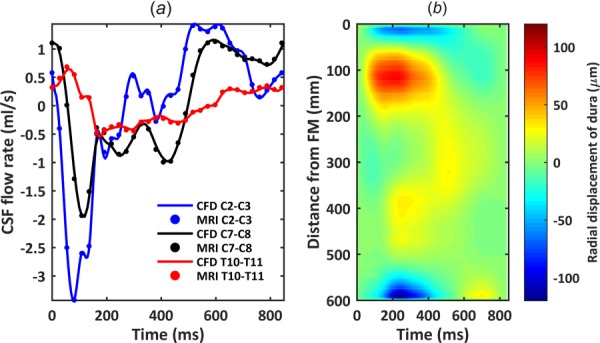
Comparison of numerical model axial flow rate distribution with subject specific PCMRI measurements: (a) CSF flow waveforms measured by PCMRI at three axial locations along the spine. Dots indicate experimental data and lines denote CFD results. Note: negative, or peak systolic, CSF flow is in the caudal direction. (b) Spatial–temporal distribution of the average dura radial displacement along the spine.
Hydrodynamic Parameters.
Hydrodynamic results are reported in detail for the 3D model with NR only. CSF volume within the SSS from the FM to spinal sac was 97.3 ml at the beginning of cardiac systole (t = 0). Spinal cord and NR volumes were constant at 19.9 and 5.8 ml, respectively. Peak CSF velocity showed maximum values in the cervical spine of 3.9 and 2.9 cm/s for the cases with and without NR, respectively (Fig. 4(a)). Cross-sectional area was reduced with NR by up to 13.8% (Fig. 4(b)). Maximum of the cross-sectional mean velocities, , from MRI data (interpolated flow) were present at the cervical spine near the C4–C5 level (Fig. 3(a)). Minimum occurred in the lower thoracic spine about 40 cm below the FM (∼T11 to T12). Hydraulic diameter, omitting the filum terminale, had a minimum value of 3.4 mm occurring at a distance of 95 mm caudal to the FM within the cervical spine (Fig. 4(c)—y-axis left). Hydraulic diameter was larger at both the FM and within the thoracic spine than elsewhere. Womersley number ranged from 22.96 to 1.64 (Fig. 4(c)—y-axis right). Local maxima for Womersley number were present within the FM level (α = 23.0) and at the thoracic spine (α = 16.1). Womersley number had local minima within the cervical spine and just rostral to the intrathecal sac. Maximum Re with NR was 184 (Fig. 4(d)) and located in the cervical spine where the SSS had a relatively small hydraulic diameter and peak flow rate was maximum. Maximum , and Keulegan–Carpenter number was 78.2, 14.2, and 30.8 (), respectively (Figs. 4(e) and 4(f)).
Fig. 4.
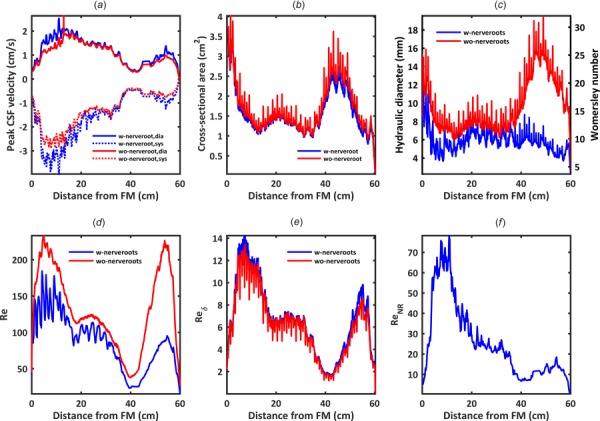
Hydrodynamic parameter distribution computed along the spine in terms of: (a) peak CSF velocity, (b) cross-sectional area, (c) hydraulic diameter and Womersley number, α, (d) Reynolds number, for internal flow within a tube, Re, (e) Stokes–Reynolds number based on Stokes-layer thickness, , and (f) Reynolds number for external flow over a NR, ReNR
Cerebrospinal Fluid Flow, Velocities, and Flow Features.
Comparison of flow rates at the three MRI slice locations (Fig. 3(a)) showed that CFD results were nearly identical to MRI measurements (error < 2.3%), verifying the dural motion inputs. Peak flow rates at C2–C3, C7–C8, and T10–T11 were 3.44, 1.95, and 0.53 ml/s, respectively. Stroke volumes at these locations were 0.77, 0.69, and 0.25 ml, respectively. Spatial–temporal distribution of dura radial displacement over the cardiac cycle showed that maximum dural displacement was 122.52 μm and located at 595 mm below the FM (Fig. 3(b)). Average dural displacement along the entire spine was 16.41 μm. Note, interpolated values of dural displacement should not be used for model validation purposes. The empirical data are only derived from MRI measurements at the three axial levels investigated.
Velocity profiles at T = 90 ms (peak systole, Fig. 5) in the coronal, sagittal, and axial planes exhibited peaks in the cervical spine. Note: peak systolic timing was obtained for CSF flow at C2–C3. Depending on the timing, the velocity profile changes due to nonuniform deformation of the dura. The axial distribution of peak CSF velocities over the entire cardiac cycle is shown in Fig. 4(a). As expected, spinal cord NR decreased nearby velocities and resulted in “jets” between dorsal and ventral NR pairs in the cervical spine (Fig. 5(c), C5–C6 level). Note, to better visualize results along the entire spine, Fig. 5 and similar figures are contracted at ½ scale in the z-direction (maximum spine curvature with respect to the z-axis is <15 deg). At peak flow (Fig. 6(a)), the CSF velocity profile on the posterior side of the spinal cord and between NR showed a characteristic “m-shaped” profile (Fig. 6(b)).
Fig. 5.
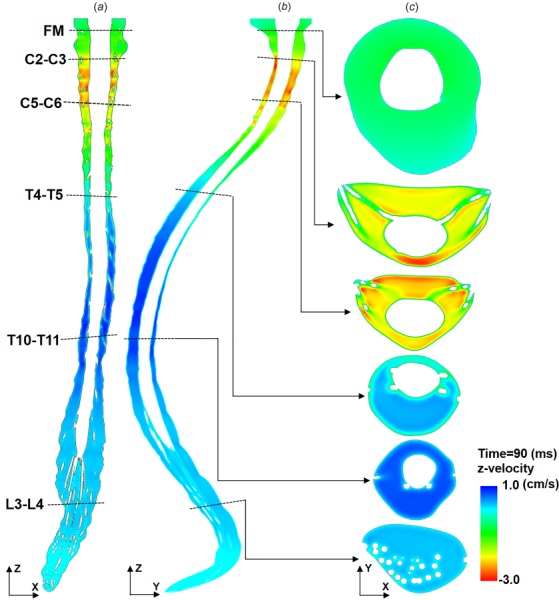
Thru-plane CSF velocity profiles simulated by CFD at T = 90 ms (peak systole) for three different views: (a) coronal, (b) sagittal, and (c) axial at six slice locations. Note: peak systolic timing was obtained for CSF flow at C2–C3. The axial distribution of peak CSF velocities over the entire cardiac cycle is shown in Fig. 4(a). Also, to help visualize the entire spine, z-scaling of the geometry is set at 0.5 with respect to x- and y-dimensions. Thus, spine curvature appears greater than without scaling.
Fig. 6.
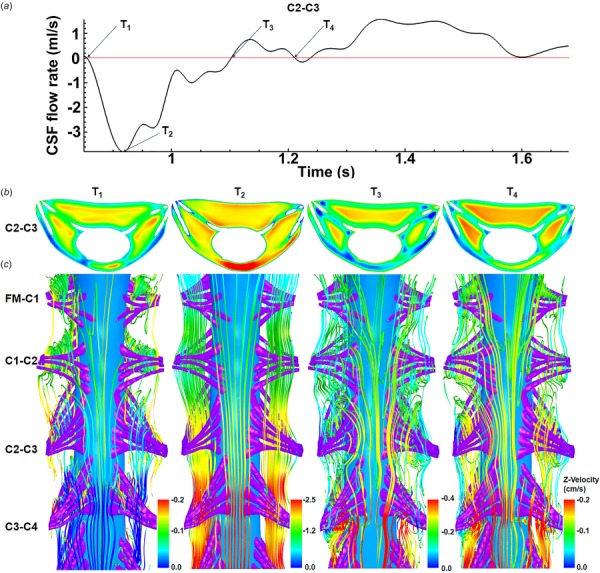
Vortices form around SC NR in the cervical spine at time-points corresponding to CSF flow reversal. (a) CSF flow rate at C2–C3 section, (b) velocity contour for C2–C3 section, and (c) streamlines showing vortices that form around NR pairs (FM-C1, C1–C2, C2–C3, and C3–C4) at four different time steps. The interfaces of these vortices are located upstream and downstream of NR pairs. Note: velocity contours and streamlines are colored with different scales.
Recirculation and vortices occurred upstream, downstream, within, and around dorsal and ventral NR bundles within the cervical spine depending on the location and phase of the cycle (Fig. 6(c)). Vortices were not present in the thoracic and lumbar spine where the NRs are oriented in a streamwise direction. These vortices formed at time points corresponding to flow reversal (Fig. 6(a) at T1, T3, and T4). Vortices did not form at peak flow rate (T2) when flow streamlines were more uniformly axial.
Steady-Streaming Cerebrospinal Fluid Velocity Quantification.
The presence of spinal cord NR was found to have a large impact on and . Overall, NR resulted in greater steady-streaming velocity magnitude and more complex steady-streaming velocity profiles (compare Figs. 7 and 8). The coronal velocity profile (Fig. 7(a)) indicated rostral streaming near NR. With NR present, the sagittal velocity profile (Fig. 7(b)) exhibits a large region of caudally directed steady-streaming in the posterior SSS in the middle thoracic spine and anterior SSS in the cervical spine. In addition, streaming “pockets” were visualized on axial slices (Fig. 7(c)) and were located laterally between dorsal and ventral NR at the interface of adjacent vortices (Fig. 6(c)). These features changed considerably without NR present (Fig. 8(a)). For example, CSF streaming pockets were still present (Fig. 8(b)), albeit, located anterolaterally to the spinal cord and with a lesser steady-streaming velocity magnitude (Fig. 8(c)). Similar to NR, rostral-directed streaming was present in the dorsal thoracic SSS and somewhat in the ventral cervical SSS (Fig. 8(b)). Relatively little steady-streaming was present in the lumbar spine.
Fig. 7.
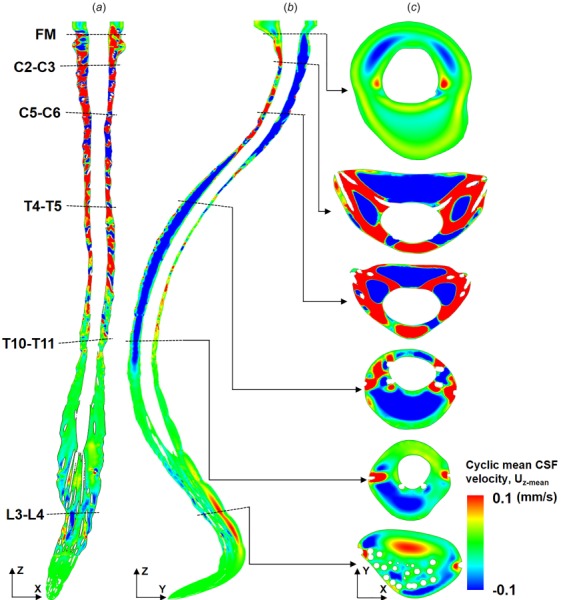
Presence of SC NR result in a complex distribution of cyclic mean CSF velocities within the SSS. Cyclic mean CSF velocity profiles simulated by CFD for three different views: (a) coronal, (b) sagittal, and (c) axial at six slice locations. Note: Cyclic mean CSF velocity is calculated based on one complete CSF flow cycle.
Fig. 8.
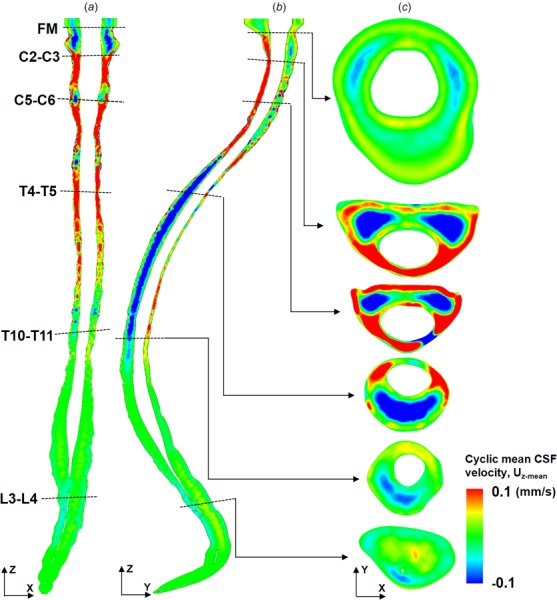
Cyclic mean CSF velocities decrease and change profiles without NR present in the numerical model. CSF cyclic mean velocity profiles, Uz-mean, for the case without SC NRs at three different views: (a) coronal, (b) sagittal, and (c) axial at six slice locations. Compare profiles to Fig. 7 to see impact of NR.
The presence of NR increased steady-streaming CSF velocity magnitude, , to a great degree within the cervical spine and to a lesser degree in the thoracic and lumbar spine (Fig. 9). Average value for was 0.11±0.12 and 0.05±0.04 mm/s (mean ± stdev) for the model with versus without NR (120% greater with NR). The region of greatest difference in values was the cervical spine that had up to 5× larger value of with NR compared to without. On closer inspection, it was noted that the local regions of elevated were located between spinal cord NR in the region located from C1 to T2 (see vertical dotted lines in Fig. 9). These localized increases were not present elsewhere along the spine. (Fig. 9—right axis) showed a nearly identical trend as . The average value for was 0.023±0.026 and 0.012±0.009 (mean ± stdev) for cases with and without NR.
Fig. 9.
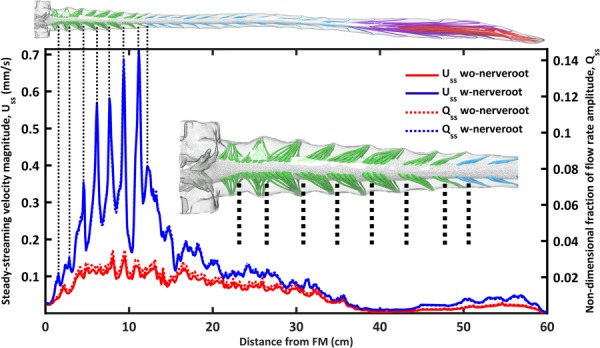
Steady-streaming velocity magnitude, Uss, and nondimensional fraction of flow rate amplitude, Qss, increases with NR compared to without NR. Dotted lines indicate that maximum Uss occurs upstream/downstream of NRs in the cervical spine at the interface of adjacent vortices (see vortices in Fig. 6(c)).
Discussion
The presence of spinal cord NR has an important impact on CSF flow dynamics in terms of velocities and steady-streaming effects.
Moving Boundary Mesh to Reproduce Subject Specific Cerebrospinal Fluid Flow Distribution.
Spatial–temporal interpolation of MRI-measured flow rates resulted in simulated velocities that were in opposing directions along the spine at some time points (Figs. 5(a) and 5(b) plotted at T = 90 ms). Maximum deformation of the dura was 122.52 μm and located in the cervical spine (Fig. 3(b)). This value is lower than the threshold that is possible to detect by current 3T anatomic MR imaging resolution. Therefore, because dural motion was specified and verified based on CSF flow waveforms, uncertainty remains about the validity of the exact velocity profile results.
Spinal Cord Nerve Roots Impact Cerebrospinal Fluid Hydrodynamics.
The presence of NR decreased , Re, and (Fig. 4). NR increased cross-sectional mean velocity and area by up to 13.8%, as dictated by the reduction in cross-sectional flow area. Peak CSF velocities increased by up to 70%, indicating that the velocity increase was greater than what can be attributed to reduction in cross-sectional area with NR (Fig. 4(b)). Axial distribution of these parameters had larger variation in the cervical spine due to the transverse orientation of NR that resulted in local reduction in SSS cross-sectional area (Figs. 1(c) and 4(b)). In the thoracic and lumbar spine, NR were oriented parallel to the flow direction and, therefore, had a smaller impact on axial variation in Re. Assessment of Re likely indicated laminar flow (<184 for model with NR). Re increased without NR present due to a larger hydraulic diameter in that case, in particular in the dural sac of the lumbar spine (Fig. 4(c)).
The measured values for hydrodynamic parameters in this study are within the range of previously published studies [52,65] (Table 1). In specific, maximum Re was reported to be 187 by Heidari Pahlavian et al. [35], 150–450 by Loth et al. [52], and 140 by Martin et al. [46] in CFD models of the cervical spine. These values support that CSF flow is likely laminar. These and the value measured for our subject, Re < 250, suggest that the flow, were it steady, would be laminar. Although it should be noted that SSS geometry is complicated with multiple levels of anatomic complexity that include tiny anatomic structures such as arachnoid trabeculae and denticulate ligaments. Anatomic complexity can lead to flow instabilities at Re > 600 in a stenosis [66], at Re in the range of 200–350 in aneurysms [67,68], in the heart [69], and within CSF in the SSS [40,70]. Sources of flow instability related to nerve roots are discussed in the section of Vortices Form Around Cervical Spinal Cord NR During Cerebrospinal Fluid Flow Reversal. In addition, the unsteadiness of the flow presents a different set of turbulent transition criteria. The Stokes–Reynolds number, , was less than 14.2, which is below the threshold of 550 for conditional turbulence in oscillatory flow [59]. On the other hand, the Womersley number was greater than 5, which places the flow in the weakly turbulent flow regime. Weak turbulence is characterized by instabilities that appear during flow acceleration and disappear during deceleration [59]. Generally, for pulsatile flow, the instabilities appear on deceleration and disappear during acceleration. This is due to the unfavorable pressure gradient in deceleration and a favorable pressure gradient in acceleration.
Velocity profiles showed similar presence of localized flow jets (Fig. 5) similar to previously published studies [8,43,65]. However, the NR in this study were modeled as anatomically realistic individual rootlet fibers. Previous studies [22,35] idealized NR as airfoil- or rod-shaped structures.
Vortices Form Around Cervical Spinal Cord Nerve Roots During Cerebrospinal Fluid Flow Reversal.
The finding of transient vortices in the vicinity of NR during deceleration (Fig. 6(c)) may be consistent with the appearance of instabilities in oscillatory flow around cylinders. Such instabilities have been documented in a number of experiments for large β and small K, and the critical Keulegan–Carpenter number for these limits has been calculated as: given by Hall [58]. Thus, for the current results, for which , Kcr has a value of 1.18. The value for the current results, , is well above this threshold. However, the results do not conform to the large β and small K limits. Therefore, the occurrence of Honji-type instabilities [57] in the SSS is uncertain. If such instabilities exist, the flow rate waveform applied in our study had multiple points of flow reversal and, therefore, multiple periods during which vortex formation could affect mixing. Honji rolls have also been shown to induce transverse streaming [71], which would tend to increase longitudinal dispersion. We hypothesize that this and other factors causing flow reversal and vortical structures, e.g., medical device interventions or abdominal maneuvers, etc., could be leveraged to increase flow mixing to a therapeutic degree, in particular within the cervical spine. Further, the presence of adjacent vortices may be leveraged to increase axial solute transport within the SSS due to “blinking” vortex formation [72,73].
The observed vortical structures around NR in our model (Fig. 6) are in a different location than the vortices reported by Pahlavian et al. [35] and Tangen et al. [29] who found vortices located between axial NR (e.g., between C1 and C2 NR). The difference in vortex location is likely due to the more idealized NR geometry applied by Pahlavian et al. that modeled NR as airfoil-shaped structures with a greater thickness than this study. Also, Tangen et al. had all NR in the model oriented relatively orthogonal to the primary flow direction (see Fig. 4, Tangen et al.). This resulted in vortex formation throughout the spine. In our model, vortices were only observed in the cervical spine where NR were oriented relatively orthogonal to the primary flow direction (Fig. 6(c)) and did not appear in the lumbar or thoracic spine (Fig. 1(c)). It should be noted that our current model lacked denticulate ligaments located between NR pairs. These ligaments may impact flow to some degree and therefore could alter where vortices are located in the present model.
Nerve Roots Increase Steady-Streaming Cerebrospinal Fluid Dynamics.
Nerve roots increased steady-streaming velocity magnitude, , to a great degree within the cervical spine and to a lesser degree in the thoracic and lumbar spine (Fig. 9). Local elevation of Uss was located within the spaces above or below NR (see spikes in the blue curve for the case with NR, Fig. 9). These values coincided with more complex mean z-velocity profiles and increased the value of Uz-mean for the case with NR (Fig. 7) compared to without NR (Fig. 8). We hypothesize that these regions are due to adjacent “blinking” vortices [73,74] that touch in the space above or below NR. It may be possible to leverage the location of this increased steady-streaming transport to assist solute spread in the SSS (e.g., inject medication at this location).
To put numbers in context, the maximum value of was only 0.15 mm/s without NR and 0.71 mm/s with NR (Fig. 9) compared to mean velocities (at peak systole) up to ∼25 mm/s. Thus, for the presented model boundary conditions, was more than 35× smaller than transient velocities. In addition to steady-streaming, Tangen et al. [22,29] found CSF pulsation magnitude to play an important role on SSS transport. CSF pulsation magnitude in combination with flow reversals might be optimized to increase SSS mixing.
Uz-mean profiles (Figs. 7 and 8) show that NR impact the distribution of cyclic mean CSF velocities around the spinal cord (axial orientation), but the overall streaming structures in the sagittal orientation are similar both with and without NR. For example, the caudal directed flow in the posterior thoracic spine with NR (Fig. 7(b)—negative value ) was still present in the model without NR (Fig. 8(b)). Also, in the coronal orientation (Fig. 7(a) and 8(a)), rostral-streaming flow was located laterally with and without NR present. Thus, since the overall posterior versus anterior steady-streaming flow profiles were relatively unaffected by the presence of NR, it is possible that posterior versus anterior steady-streaming profiles may be due to eccentricity of the flow cross section and spine curvature. However, NR did affect steady-streaming velocity profiles lateral to the spinal cord (Figure 7(c) versus 8c). We hypothesize that changing eccentricity and spinal curvature (kyphosis/lordosis) could be applied strategically to direct steady-streaming solute transport. Steady-streaming of CSF flow has been previously reported by Kuttler et al. [30] in an eccentric SSS. However, quantitative results were not provided in that study and therefore are not comparable to this work. Kuttler applied the steady-streaming velocity field as a “frozen flow field” and used it with the molecular diffusion equation to solve for drug transport along the SSS. This approach should be tested against in vitro experiments for validation.
Limitations
This study included one healthy adult volunteer as a platform to analyze the impact of NR on the CSF flow field. As such, the results are subject-specific. We expect that the exact values could change considerably with alterations in flow waveform shape and amplitude as well as overall SSS geometry for different subjects. Shifting of the brain and/or spinal cord position due to posture changes was not analyzed. This study did not take into account the impact of other fine structures within the SSS, such as arachnoid trabeculae, blood vessels, and denticulate ligaments.
We sought to verify the model with in vivo subject specific measurements of CSF flow rate at three axial locations along the spine. Results showed <2.3% error. A more accurate model would measure flow rate at additional axial levels. Our approach was to deform the dura to match MRI-derived CSF flow. In reality, it is possible that the dura does not deform at all, but rather, veins within the CSF are compressed. With current MR imaging techniques, it is difficult to verify which is the exact location of deformation. The MRI measurements conducted in this study did not allow direct validation of steady-streaming velocity results as these were <1 mm/s. This value is below MRI velocity detection limits that typically are set at 5 cm/s for phase-contrast MR imaging studies.
A source of error in the comparison of Uss between cases with and without NR is that cross-sectional area was reduced with NR, which increased the cross-sectional mean velocities (given that CSF flow rate was imposed identically across the two simulations). Maximum percent area of the SSS occupied by the NR was 13.8% (average percent NR area over the entire SSS was 5.5%). Therefore comparison of Qss, which is normalized by the imposed flow rate, is more valid. Qss increased a maximum of 434% with NR compared to without NR (average increase in Qss was 91%). This supports that the relatively small change in SSS cross-sectional area due to NR does not on its own account for the relatively large increase in Qss with NR.
The z-slice orientation through the model was orthogonal to the z-axis. Thus, since the spine has curvature, the values for Uss are not computed exactly in the streamwise direction. We estimated that the maximum angle of the spine with respect to the z-axis is <15 deg (omitting lumbar spine where nearly zero flow velocities were present). This would result in a maximum Uss error of 3.4%. Note: To help visualize the entire SSS, Figs. 5, 7, and 8 are scaled at 0.5× in the z-axis, making the spine curvature appear more curved than actual.
Conclusion
A subject-specific model of the complete SSS with anatomically realistic NR and accurate reproduction of nonuniform flow rate was used to investigate the impact of NR on CSF dynamics. NR were found to alter CSF dynamics in terms of velocity field, steady-streaming and vortical structures. Vortices occurred in the cervical spine upstream and downstream of NR during CSF flow reversal. Steady-streaming increased with NR, in particular within the cervical spine. These findings suggests that future studies should investigate how solute transport within the SSS could be increased and/or controlled by: (a) delivery of solutes either upstream or downstream of NR, (b) control of CSF pulse magnitude and/or number of flow reversals per cardiac cycle, and (c) changing eccentricity or spinal curvature (kyphosis/lordosis).
Appendix: Quantitative Solution Verification Using Factor of Safety Method
To further verify the numerical results, the following factor of safety method was applied as developed by Xing and Stern [75,76]. The accuracy of this method has been evaluated for uncertainty estimates [77]. The use of the L2 norm and factor of safety method has an advantage over methods based on local error estimates, as applied above and in a number of previous CSF simulations [9,35,78,79], as the former accounts for the errors across the whole solution domain and convergence of errors on three not two grids. As such, we present the methodology to assist researchers in verification of numerical results.
Let S1, S2, S3 represent the X-fine, fine, and medium grid solutions for velocity, respectively. The relative difference between the fine grid solution and correlation value, A, is calculated as:
| (A1) |
The solution verification study requires the use of the following equations:
| (A2) |
| (A3) |
| (A4) |
| (A5) |
The grid refinement ratio is 2. This value was specified in ansys by dividing the maximum mesh size by two for each simulation (see Table 2, mesh size values). Evaluation of the convergence ratio , order of accuracy pG for point variables on the velocity profiles can be problematic when the solution changes and both go to zero so that their ratio is ill-defined. This was overcome by using the following Separate L2 norms of and for and [80], i.e.,
| (A6) |
| (A7) |
where < > is used to denote a profile-averaged quantity (with ratio of solution changes based on L2 norms), and is used to denote the L2 norm defined below:
| (A8) |
| (A9) |
In Eqs. (A6) and (A7), n is the number of points on the velocity profiles, which is the same for the three meshes. Monotonic convergence is achieved when 0 < < 1. The ratio of the estimated order of accuracy to the theoretical order of accuracy is defined as
| (A10) |
where is the nominal order of accuracy of the numerical schemes applied, which is set to be 2.
The estimated numerical error, , and grid uncertainty, , are defined as
| (A11) |
| (A12) |
Using , the exact solution can be estimated as . Grid uncertainty is an estimate of an error such that the interval ±UG contains the true value of numerical error at least 95 times out of 100, i.e., at the 95% confidence level. An uncertainty interval thus indicates the range of likely magnitudes of δRE. A lower UG value indicates a more accurate solution.
Factor of Safety Method Results.
The factor of safety method gives additional confidence in the velocity results (Table 3). For the mean velocity profiles, grid uncertainties decreased with grid refinement for all three profiles (Figs. 2(c) and 2(d)), although the magnitudes for group 1 (X-fine, fine, medium) were the same order-of-magnitude as for group 2 (fine, medium, and coarse). A similar trend was observed for z-velocity, but the difference between grid uncertainties for groups 1 and 2 was much greater. Grid uncertainties for group 1 were one order-of-magnitude smaller than that for group 2, which suggests that the z-velocity is much more sensitive to grid refinement than the mean velocity profile.
Table 3.
Verification of results by factor of safety method—values show the global error for velocity in the z-direction for the three axial planes analyzed (Fig. 2)
| Parameter | Study group | Grid uncertainty (%S1) |
|---|---|---|
| Mean velocity, Uz-mean | Group 1 (X-fine, fine, medium) | 0.72 |
| 1.06 | ||
| 0.34 | ||
| Group 2 (fine, medium, coarse) | 1.09 | |
| 1.02 | ||
| 0.59 | ||
| Z-velocity | Group 1 (X-fine, fine, medium) | 1.13 |
| 2.69 | ||
| 0.728 | ||
| Group 2 (fine, medium, coarse) | 10.64 | |
| 36.94 | ||
| 1.5 |
Contributor Information
Mohammadreza Khani, Neurophysiological Imaging and Modeling , Laboratory, , Department of Biological Engineering, , University of Idaho, , Moscow, ID 83844 , e-mail: Khan0242@vandals.uidaho.edu.
Lucas R. Sass, Neurophysiological Imaging and Modeling , Laboratory, , Department of Biological Engineering, , University of Idaho, , Moscow, ID 83844 , e-mail: sass8026@vandals.uidaho.edu
Tao Xing, Department of Mechanical Engineering, , University of Idaho, , Moscow, ID 83844 , e-mail: xing@uidaho.edu.
M. Keith Sharp, Biofluid Mechanics Laboratory, , University of Louisville, , Louisville, KY 40292 , e-mail: keith.sharp@louisville.edu
Olivier Balédent, Bioflow Image, , CHU Nord Amiens-Picardie, , Amiens 80054, France , e-mail: Olivier.Baledent@chu-amiens.fr.
Bryn A. Martin, Neurophysiological Imaging and Modeling , Laboratory, , Department of Biological Engineering, , University of Idaho, , Moscow, ID 83844 , e-mail: brynm@uidaho.edu
Funding Data
• This work was supported by an Institutional Development Award (IDeA) from the National Institute of General Medical Sciences (NIGMS) of the National Institutes of Health (NIH) under Grant #P20GM1033408 and #4U54GM104944-04TBD, The National Institute of Mental Health Grant #1R44MH112210-01A1, and University of Idaho Vandal Ideas Project.
Nomenclature
- A =
area
- CFD =
computational fluid dynamics
- CNS =
central nervous system
- CSF =
cerebrospinal fluid
- FM =
Foramen magnum
- HD =
hydraulic diameter
- MRI =
magnetic resonance imaging
- P =
perimeter
- PCMRI =
phase-contrast magnetic resonance imaging
- Q =
flow rate
- Re =
Reynolds number based on hydraulic diameter
- ReNR =
Reynolds number based on nerve root diameter
- =
Stokes–Reynolds number based on Stokes-layer thickness
- ROI =
region of interests
- SC =
spinal cord
- SSS =
spinal subarachnoid space
- U =
velocity
- V =
cell volume
- 3D =
three-dimensional
- α =
Womersley number
- δ =
Stokes layer thickness
- μ =
dynamic viscosity (Pa⋅s)
- ν =
kinematic viscosity (m2s−1)
- ρ =
density (Kg/m3)
- ω =
angular velocity (Rad/s)
References
- [1]. Yildiz, S. , Thyagaraj, S. , Jin, N. , Zhong, X. , Heidari Pahlavian, S. , Martin, B. A. , Loth, F. , Oshinski, J. , and Sabra, K. G. , 2017, “ Quantifying the Influence of Respiration and Cardiac Pulsations on Cerebrospinal Fluid Dynamics Using Real-Time Phase-Contrast MRI,” J. Magn. Reson. Imaging, Press, 46(12), pp. 431–439. 10.1002/jmri.25591 [DOI] [PubMed] [Google Scholar]
- [2]. Chen, L. , Beckett, A. , Verma, A. , and Feinberg, D. A. , 2015, “ Dynamics of Respiratory and Cardiac CSF Motion Revealed With Real-Time Simultaneous Multi-Slice EPI Velocity Phase Contrast Imaging,” Neuroimage, 122, pp. 281–287. 10.1016/j.neuroimage.2015.07.073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Baledent, O. , Henry-Feugeas, M. C. , and Idy-Peretti, I. , 2001, “ Cerebrospinal Fluid Dynamics and Relation With Blood Flow: A Magnetic Resonance Study With Semiautomated Cerebrospinal Fluid Segmentation,” Invest. Radiol., 36(7), pp. 368–377. 10.1097/00004424-200107000-00003 [DOI] [PubMed] [Google Scholar]
- [4]. Wostyn, P. , Audenaert, K. , and De Deyn, P. P. , 2009, “ More Advanced Alzheimer's Disease May Be Associated With a Decrease in Cerebrospinal Fluid Pressure,” Cerebrospinal Fluid Res., 6(1), p. 14. 10.1186/1743-8454-6-14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Takizawa, K. , Matsumae, M. , Hayashi, N. , Hirayama, A. , Yatsushiro, S. , and Kuroda, K. , 2017, “ Hyperdynamic CSF Motion Profiles Found in Idiopathic Normal Pressure Hydrocephalus and Alzheimer's Disease Assessed by Fluid Mechanics Derived From Magnetic Resonance Images,” Fluids Barriers CNS, 14(1), p. 29. 10.1186/s12987-017-0077-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6]. Martin, B. A. , Labuda, R. , Royston, T. J. , Oshinski, J. N. , Iskandar, B. , and Loth, F. , 2010, “ Spinal Subarachnoid Space Pressure Measurements in an In Vivo Spinal Stenosis Model: Implications on Syringomyelia Theories,” ASME J. Biomech. Eng., 132(11), p. 111007. 10.1115/1.4000089. [DOI] [PubMed] [Google Scholar]
- [7]. Yeo, J. , Cheng, S. , Hemley, S. , Lee, B. B. , Stoodley, M. , and Bilston, L. , 2017, “ Characteristics of CSF Velocity-Time Profile in Posttraumatic Syringomyelia,” Am. J. Neuroradiol., 38(9), pp. 1839–1844. 10.3174/ajnr.A5304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8]. Bunck, A. C. , Kroeger, J. R. , Juettner, A. , Brentrup, A. , Fiedler, B. , Crelier, G. R. , Martin, B. A. , Heindel, W. , Maintz, D. , and Schwindt, W. , 2012, “ Magnetic Resonance 4D Flow Analysis of Cerebrospinal Fluid Dynamics in Chiari I Malformation With and Without Syringomyelia,” Eur. Radiol., 22(9), pp. 1860–1870. 10.1007/s00330-012-2457-7 [DOI] [PubMed] [Google Scholar]
- [9]. Pahlavian, S. H. , Loth, F. , Luciano, M. , Oshinski, J. , and Martin, B. A. , 2015, “ Neural Tissue Motion Impacts Cerebrospinal Fluid Dynamics at the Cervical Medullary Junction: A Patient-Specific Moving-Boundary Computational Model,” Ann. Biomed. Eng., 43(12), pp. 2911–2923. 10.1007/s10439-015-1355-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Zhang, L. F. , and Hargens, A. R. , 2014, “ Intraocular/Intracranial Pressure Mismatch Hypothesis for Visual Impairment Syndrome in Space,” Aviat. Space. Environ. Med., 85(1), pp. 78–80. 10.3357/ASEM.3789.2014 [DOI] [PubMed] [Google Scholar]
- [11]. Bradley, W. G., Jr. , Scalzo, D. , Queralt, J. , Nitz, W. N. , Atkinson, D. J. , and Wong, P. , 1996, “ Normal-Pressure Hydrocephalus: Evaluation With Cerebrospinal Fluid Flow Measurements at MR Imaging,” Radiology, 198(2), pp. 523–529. 10.1148/radiology.198.2.8596861 [DOI] [PubMed] [Google Scholar]
- [12]. Simpson, K. , Baranidharan, G. , and Gupta, S. , 2012, Spinal Interventions in Pain Management, 1st ed., Oxford University Press, Oxford, UK. [Google Scholar]
- [13]. Papisov, M. I. , Belov, V. V. , and Gannon, K. S. , 2013, “ Physiology of the Intrathecal Bolus: The Leptomeningeal Route for Macromolecule and Particle Delivery to CNS,” Mol. Pharm., 10(5), pp. 1522–1532. 10.1021/mp300474m [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Rassoli, A. , Nabaei, M. , Fatouraee, N. , and Nabaei, G. , 2017, “ Numerical Modeling of the Brain Hypothermia by Cooling the Cerebrospinal Fluid,” Tehran Univ. Med. J., 75(1), pp. 31–38.http://www.ingentaconnect.com/content/doaj/16831764/2017/00000075/00000001/art00005 [Google Scholar]
- [15]. Kumar, P. , Srivatsava, M. V. , Singh, S. , and Prasad, H. K. , 2008, “ Filtration of Cerebrospinal Fluid Improves Isolation of Mycobacteria,” J. Clin. Microbiol., 46(8), pp. 2824–2825. 10.1128/JCM.00210-08 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Urwin, S. C. , and Hunt, P. , 2000, “ Cerebrospinal Fluid Filtration in Guillain-Barre Syndrome,” Anaesthesia, 55(5), pp. 489–518. 10.1046/j.1365-2044.2000.01425-24.x [DOI] [PubMed] [Google Scholar]
- [17]. Finsterer, J. , and Mamoli, B. , 1999, “ Cerebrospinal Fluid Filtration in Amyotrophic Lateral Sclerosis,” Eur. J. Neurol., 6(5), pp. 597–600. 10.1046/j.1468-1331.1999.650597.x [DOI] [PubMed] [Google Scholar]
- [18]. Brizzi, M. , Thoren, A. , and Hindfelt, B. , 1996, “ Cerebrospinal Fluid Filtration in a Case of Severe Pneumococcal Meningitis,” Scand. J. Infect. Dis., 28(5), pp. 455–458. 10.3109/00365549609037939 [DOI] [PubMed] [Google Scholar]
- [19]. Luciano, M. G. , Dombrowski, S. M. , Qvarlander, S. , El-Khoury, S. , Yang, J. , Thyagaraj, S. , and Loth, F. , 2017, “ Novel Method for Dynamic Control of Intracranial Pressure,” J. Neurosurg., 126(5), pp. 1629–1640. 10.3171/2016.4.JNS152457 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Stockman, H. W. , 2007, “ Effect of Anatomical Fine Structure on the Dispersion of Solutes in the Spinal Subarachnoid Space,” ASME J. Biomech. Eng., 129(5), pp. 666–675. 10.1115/1.2768112 [DOI] [PubMed] [Google Scholar]
- [21]. Stockman, H. W. , 2006, “ Effect of Anatomical Fine Structure on the Flow of Cerebrospinal Fluid in the Spinal Subarachnoid Space,” ASME J. Biomech. Eng., 128(1), pp. 106–114. 10.1115/1.2132372 [DOI] [PubMed] [Google Scholar]
- [22]. Tangen, K. M. , Hsu, Y. , Zhu, D. C. , and Linninger, A. A. , 2015, “ CNS Wide Simulation of Flow Resistance and Drug Transport Due to Spinal Microanatomy,” J. Biomech., 48(10), pp. 2144–2154. 10.1016/j.jbiomech.2015.02.018 [DOI] [PubMed] [Google Scholar]
- [23]. Tangen, K. , Narasimhan, N. S. , Sierzega, K. , Preden, T. , Alaraj, A. , and Linninger, A. A. , 2016, “ Clearance of Subarachnoid Hemorrhage From the Cerebrospinal Fluid in Computational and In Vivo Models,” Ann Biomed Eng., 44(12), pp. 3478–3494. 10.1007/s10439-016-1681-8 [DOI] [PubMed] [Google Scholar]
- [24]. Tangen, K. , Linninger, A. , and Narasimhan, N. S. , 2016, “ Clearance of Subarachnoid Hemorrhage from the Cerebrospinal Fluid in Computational and In Vitro Models,” Cerebrovasc. Dis., 44, p. 202. [DOI] [PubMed] [Google Scholar]
- [25]. Khani, M. , Xing, T. , Gibbs, C. , Oshinski, J. N. , Stewart, G. R. , Zeller, J. R. , and Martin, B. A. , 2017, “ Nonuniform Moving Boundary Method for Computational Fluid Dynamics Simulation of Intrathecal Cerebrospinal Flow Distribution in a Cynomolgus Monkey,” ASME J. Biomech. Eng., 139(8), p. 081005. 10.1115/1.4036608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. Hsu, Y. , Harris, T. J. , Hettiarachchi, H. D. M. , Penn, R. , and Linninger, A. A. , 2011, “ Three Dimensional Simulation and Experimental Investigation of Intrathecal Drug Delivery in the Spinal Canal and the Brain,” 21st European Symposium on Computer Aided Process Engineering (ESCAPE), Chalkidiki, Greece, May 29–June 1, pp. 1525–1529. 10.1016/B978-0-444-54298-4.50084-2 [DOI] [Google Scholar]
- [27]. Hsu, Y. , Hettiarachchi, H. D. , Zhu, D. C. , and Linninger, A. A. , 2012, “ The Frequency and Magnitude of Cerebrospinal Fluid Pulsations Influence Intrathecal Drug Distribution: Key Factors for Interpatient Variability,” Anesth. Analg., 115(2), pp. 386–394. 10.1213/ANE.0b013e3182536211 [DOI] [PubMed] [Google Scholar]
- [28]. Cheng, S. , Fletcher, D. , Hemley, S. , Stoodley, M. , and Bilston, L. , 2014, “ Effects of Fluid Structure Interaction in a Three Dimensional Model of the Spinal Subarachnoid Space,” J. Biomech., 47(11), pp. 2826–2830. 10.1016/j.jbiomech.2014.04.027 [DOI] [PubMed] [Google Scholar]
- [29]. Tangen, K. M. , Leval, R. , Mehta, A. I. , and Linninger, A. A. , 2017, “ Computational and In Vitro Experimental Investigation of Intrathecal Drug Distribution: Parametric Study of the Effect of Injection Volume, Cerebrospinal Fluid Pulsatility, and Drug Uptake,” Anesth. Analg., 124(5), pp. 1686–1696. 10.1213/ANE.0000000000002011 [DOI] [PubMed] [Google Scholar]
- [30]. Kuttler, A. , Dimke, T. , Kern, S. , Helmlinger, G. , Stanski, D. , and Finelli, L. A. , 2010, “ Understanding Pharmacokinetics Using Realistic Computational Models of Fluid Dynamics: Biosimulation of Drug Distribution Within the CSF Space for Intrathecal Drugs,” J. Pharmacokinet. Pharmacodyn., 37(6), pp. 629–644. 10.1007/s10928-010-9184-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31]. Pizzichelli, G. , Kehlet, G. , Evju, Ø. , Martin, B. A. , Rognes, M. E. , Mardal, K. A. , and Sinibaldi, E. , 2017, “ Numerical Study of Intrathecal Drug Delivery to a Permeable Spinal Cord: Effect of Catheter Position and Angle,” Comput. Methods Biomech. Biomed. Eng., Press., 20(15), pp. 1599–1608. 10.1080/10255842.2017.1393805 [DOI] [PubMed] [Google Scholar]
- [32]. Haga, P. T. , Pizzichelli, G. , Mortensen, M. , Kuchta, M. , Pahlavian, S. H. , Sinibaldi, E. , Martin, B. A. , and Mardal, K. A. , 2017, “ A Numerical Investigation of Intrathecal Isobaric Drug Dispersion Within the Cervical Subarachnoid Space,” PLoS One, 12(3), p. e0173680. 10.1371/journal.pone.0173680 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Heidari Pahlavian, S. , Bunck, A. C. , Loth, F. , Shane Tubbs, R. , Yiallourou, T. , Kroeger, J. R. , Heindel, W. , and Martin, B. A. , 2015, “ Characterization of the Discrepancies Between Four-Dimensional Phase-Contrast Magnetic Resonance Imaging and In-Silico Simulations of Cerebrospinal Fluid Dynamics,” ASME J. Biomech. Eng., 137(5), p. 051002. 10.1115/1.4029699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34]. Heidari Pahlavian, S. , Bunck, A. C. , Thyagaraj, S. , Giese, D. , Loth, F. , Hedderich, D. M. , Kroger, J. R. , and Martin, B. A. , 2016, “ Accuracy of 4D Flow Measurement of Cerebrospinal Fluid Dynamics in the Cervical Spine: An In Vivo Verification against Numerical Simulation,” Ann. Biomed. Eng., 44(11), pp. 3202–3214. 10.1007/s10439-016-1602-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35]. Heidari Pahlavian, S. , Yiallourou, T. , Tubbs, R. S. , Bunck, A. C. , Loth, F. , Goodin, M. , Raisee, M. , and Martin, B. A. , 2014, “ The Impact of Spinal Cord Nerve Roots and Denticulate Ligaments on Cerebrospinal Fluid Dynamics in the Cervical Spine,” PLoS One, 9(4), p. e91888. 10.1371/journal.pone.0091888 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Bertram, C. D. , Brodbelt, A. R. , and Stoodley, M. A. , 2005, “ The Origins of Syringomyelia: Numerical Models of Fluid/Structure Interactions in the Spinal Cord,” ASME J. Biomech. Eng., 127(7), pp. 1099–1109. 10.1115/1.2073607 [DOI] [PubMed] [Google Scholar]
- [37]. Bertram, C. , Bilston, L. , and Stoodley, M. , 2008, “ Tensile Radial Stress in the Spinal Cord Related to Arachnoiditis or Tethering: A Numerical Model,” Med. Biol. Eng. Comput., 46(7), pp. 701–707. 10.1007/s11517-008-0332-0 [DOI] [PubMed] [Google Scholar]
- [38]. Elliott, N. S. J. , Lucey, A. D. , Lockerby, D. A. , and Brodbelt, A. R. , 2017, “ Fluid-Structure Interactions in a Cylindrical Layered Wave Guide With Application in the Spinal Column to Syringomyelia,” J. Fluids Struct., 70, pp. 464–499. 10.1016/j.jfluidstructs.2016.11.007 [DOI] [Google Scholar]
- [39]. Elliott, N. S. , 2012, “ Syrinx Fluid Transport: Modeling Pressure-Wave-Induced Flux Across the Spinal Pial Membrane,” ASME J. Biomech. Eng., 134(3), p. 031006. 10.1115/1.4005849 [DOI] [PubMed] [Google Scholar]
- [40]. Jain, K. , Ringstad, G. , Eide, P. K. , and Mardal, K. A. , 2017, “ Direct Numerical Simulation of Transitional Hydrodynamics of the Cerebrospinal Fluid in Chiari I Malformation: The Role of Cranio-Vertebral Junction,” Int. J. Numer. Method Biomed. Eng., 33(9), p. e02853. 10.1002/cnm.2853 [DOI] [PubMed] [Google Scholar]
- [41]. Cheng, S. , Stoodley, M. A. , Wong, J. , Hemley, S. , Fletcher, D. F. , and Bilston, L. E. , 2012, “ The Presence of Arachnoiditis Affects the Characteristics of CSF Flow in the Spinal Subarachnoid Space: A Modelling Study,” J. Biomech., 45(7), pp. 1186–1191. 10.1016/j.jbiomech.2012.01.050 [DOI] [PubMed] [Google Scholar]
- [42]. Rutkowska, G. , Haughton, V. , Linge, S. , and Mardal, K. A. , 2012, “ Patient-Specific 3D Simulation of Cyclic CSF Flow at the Craniocervical Region,” AJNR Am. J. Neuroradiol., 33(9), pp. 1756–1762. 10.3174/ajnr.A3047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43]. Yiallourou, T. I. , Kröger, J. R. , Stergiopulos, N. , Maintz, D. , Martin, B. A. , and Bunck, A. C. , 2012, “ Comparison of 4D Phase-Contrast MRI Flow Measurements to Computational Fluid Dynamics Simulations of Cerebrospinal Fluid Motion in the Cervical Spine,” PLoS ONE, 7(12), p. e52284. 10.1371/journal.pone.0052284 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44]. Clarke, E. C. , Stoodley, M. A. , and Bilston, L. E. , 2013, “ Changes in Temporal Flow Characteristics of CSF in Chiari Malformation Type I With and Without Syringomyelia: Implications for Theory of Syrinx Development Clinical Article,” J. Neurosurg., 118(5), pp. 1135–1140. 10.3171/2013.2.JNS12759 [DOI] [PubMed] [Google Scholar]
- [45]. Shaffer, N. , Martin, B. A. , Rocque, B. , Madura, C. , Wieben, O. , Iskandar, B. , Dombrowski, S. , Luciano, M. , Oshinski, J. , and Loth, F. , 2013, “ Cerebrospinal Fluid Flow Impedance Is Elevated in Type I Chiari Malformation,” ASME J. Biomech. Eng., 136(2), p. 021012. 10.1115/1.4026316 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46]. Martin, B. A. , Kalata, W. , Shaffer, N. , Fischer, P. , Luciano, M. , and Loth, F. , 2013, “ Hydrodynamic and Longitudinal Impedance Analysis of Cerebrospinal Fluid Dynamics at the Craniovertebral Junction in Type I Chiari Malformation,” PLoS One, 8(10), p. e75335. 10.1371/journal.pone.0075335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47]. Roldan, A. , Wieben, O. , Haughton, V. , Osswald, T. , and Chesler, N. , 2009, “ Characterization of CSF Hydrodynamics in the Presence and Absence of Tonsillar Ectopia by Means of Computational Flow Analysis,” AJNR Am. J. Neuroradiol., 30(5), pp. 941–946. 10.3174/ajnr.A1489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48]. Linge, S. O. , Mardal, K.-A. , Helgeland, A. , Heiss, J. D. , and Haughton, V. , 2014, “ Effect of Craniovertebral Decompression on CSF Dynamics in Chiari Malformation Type I Studied With Computational Fluid Dynamics: Laboratory Investigation,” J. Neurosurg. Spine, 21(4), p. 559. 10.3171/2014.6.SPINE13950 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49]. Linge, S. O. , Haughton, V. , Lovgren, A. E. , Mardal, K. A. , Helgeland, A. , and Langtangen, H. P. , 2011, “ Effect of Tonsillar Herniation on Cyclic CSF Flow Studied With Computational Flow Analysis,” AJNR Am. J. Neuroradiol., 32(8), pp. 1474–1481. 10.3174/ajnr.A2496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50]. Linge, S. , Mardal, K.-A. , Haughton, V. , and Helgeland, A. , 2013, “ Simulating CSF Flow Dynamics in the Normal and the Chiari I Subarachnoid Space During Rest and Exertion,” Am. J. Neuroradiol., 34(1), pp. 41–45. 10.3174/ajnr.A3282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51]. Bilston, L. E. , Fletcher, D. F. , and Stoodley, M. A. , 2006, “ Focal Spinal Arachnoiditis Increases Subarachnoid Space Pressure: A Computational Study,” Clin. Biomech. (Bristol, Avon), 21(6), pp. 579–584. 10.1016/j.clinbiomech.2006.01.009 [DOI] [PubMed] [Google Scholar]
- [52]. Loth, F. , Yardimci, M. A. , and Alperin, N. , 2001, “ Hydrodynamic Modeling of Cerebrospinal Fluid Motion Within the Spinal Cavity,” ASME J. Biomech. Eng., 123(1), pp. 71–79. 10.1115/1.1336144 [DOI] [PubMed] [Google Scholar]
- [53]. Gupta, S. , Soellinger, M. , Grzybowski, D. M. , Boesiger, P. , Biddiscombe, J. , Poulikakos, D. , and Kurtcuoglu, V. , 2010, “ Cerebrospinal Fluid Dynamics in the Human Cranial Subarachnoid Space: An Overlooked Mediator of Cerebral Disease—I: Computational Model,” J. R. Soc. Interface, 7(49), pp. 1195–1204. 10.1098/rsif.2010.0033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54]. Sass, L. R. , Khani, M. , Natividad, G. C. , Tubbs, R. S. , Baledent, O. , and Martin, B. A. , 2017, “ A 3D Subject-Specific Model of the Spinal Subarachnoid Space With Anatomically Realistic Ventral and Dorsal Spinal Cord Nerve Rootlets,” Fluids Barriers CNS, 14(1), p. 36. 10.1186/s12987-017-0085-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55]. Yushkevich, P. A. , Piven, J. , Hazlett, H. C. , Smith, R. G. , Ho, S. , Gee, J. C. , and Gerig, G. , 2006, “ User-Guided 3D Active Contour Segmentation of Anatomical Structures: Significantly Improved Efficiency and Reliability,” Neuroimage, 31(3), pp. 1116–1128. 10.1016/j.neuroimage.2006.01.015 [DOI] [PubMed] [Google Scholar]
- [56]. Gupta, A. , Church, D. , Barnes, D. , and Hassan, A. , 2009, “ Cut to the Chase: On the Need for Genotype-Specific Soft Tissue Sarcoma Trials,” Ann. Oncol., 20(3), pp. 399–400. 10.1093/annonc/mdp021 [DOI] [PubMed] [Google Scholar]
- [57]. Honji, H. , 1981, “ Streaked Flow Around an Oscillating Circular-Cylinder,” J Fluid Mech., 107(1), pp. 509–520. 10.1017/S0022112081001894 [DOI] [Google Scholar]
- [58]. Hall, P. , 1984, “ On the Stability of the Unsteady Boundary-Layer on a Cylinder Oscillating Transversely in a Viscous-Fluid,” J. Fluid Mech., 146(1), pp. 347–367. 10.1017/S0022112084001907 [DOI] [Google Scholar]
- [59]. Hino, M. , Sawamoto, M. , and Takasu, S. , 1976, “ Experiments on Transition to Turbulence in an Oscillatory Pipe-Flow,” J. Fluid Mech., 75(2), pp. 193–207. 10.1017/S0022112076000177 [DOI] [Google Scholar]
- [60]. Sanchez, A. L. , Martinez-Bazan, C. , Gutierrez-Montes, C. , Criado-Hidalgo, E. , Pawlak, G. , Bradley, W. , Haughton, V. , and Lasheras, J. C. , 2018, “ On the Bulk Motion of the Cerebrospinal Fluid in the Spinal Canal,” J. Fluid Mech., 841, pp. 203–227. 10.1017/jfm.2018.67 [DOI] [Google Scholar]
- [61]. Clarke, E. C. , Fletcher, D. F. , Stoodley, M. A. , and Bilston, L. E. , 2013, “ Computational Fluid Dynamics Modelling of Cerebrospinal Fluid Pressure in Chiari Malformation and Syringomyelia,” J. Biomech., 46(11), pp. 1801–1809. 10.1016/j.jbiomech.2013.05.013 [DOI] [PubMed] [Google Scholar]
- [62]. Linninger, A. A. , Tsakiris, C. , Zhu, D. C. , Xenos, M. , Roycewicz, P. , Danziger, Z. , and Penn, R. , 2005, “ Pulsatile Cerebrospinal Fluid Dynamics in the Human Brain,” IEEE Trans. Biomed. Eng., 52(4), pp. 557–565. 10.1109/TBME.2005.844021 [DOI] [PubMed] [Google Scholar]
- [63]. Greitz, D. , 1993, “ Cerebrospinal Fluid Circulation and Associated Intracranial Dynamics: A Radiologic Investigation Using MR Imaging and Radionuclide Cisternography,”" Acta Radiol. Suppl., 386, pp. 1–23.http://europepmc.org/abstract/med/8517189 [PubMed] [Google Scholar]
- [64]. Greitz, D. , Franck, A. , and Nordell, B. , 1993, “ On the Pulsatile Nature of Intracranial and Spinal CSF-Circulation Demonstrated by MR Imaging,” Acta Radiol., 34(4), pp. 321–328. 10.1177/028418519303400403 [DOI] [PubMed] [Google Scholar]
- [65]. Bunck, A. C. , Kroger, J. R. , Juttner, A. , Brentrup, A. , Fiedler, B. , Schaarschmidt, F. , Crelier, G. R. , Schwindt, W. , Heindel, W. , Niederstadt, T. , and Maintz, D. , 2011, “ Magnetic Resonance 4D Flow Characteristics of Cerebrospinal Fluid at the Craniocervical Junction and the Cervical Spinal Canal,” Eur. Radiol., 21(8), pp. 1788–1796. 10.1007/s00330-011-2105-7 [DOI] [PubMed] [Google Scholar]
- [66]. Ahmed, S. A. , and Giddens, D. P. , 1984, “ Pulsatile Poststenotic Flow Studies With Laser Doppler Anemometry,” J. Biomech., 17(9) , pp. 695–705. 10.1016/0021-9290(84)90123-4 [DOI] [PubMed] [Google Scholar]
- [67]. Valen-Sendstad, K. , and Steinman, D. A. , 2014, “ Mind the Gap: Impact of Computational Fluid Dynamics Solution Strategy on Prediction of Intracranial Aneurysm Hemodynamics and Rupture Status Indicators,” AJNR Am. J. Neuroradiol., 35(3), pp. 536–543. 10.3174/ajnr.A3793 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68]. Valen-Sendstad, K. , Mardal, K. A. , Mortensen, M. , Reif, B. A. P. , and Langtangen, H. P. , 2011, “ Direct Numerical Simulation of Transitional Flow in a Patient-Specific Intracranial Aneurysm,” J. Biomech., 44(16), pp. 2826–2832. 10.1016/j.jbiomech.2011.08.015 [DOI] [PubMed] [Google Scholar]
- [69]. Tagliabue, A. , Dede, L. , and Quarteroni, A. , 2017, “ Complex Blood Flow Patterns in an Idealized Left Ventricle: A Numerical Study,” Chaos, 27(9), p. 093939. 10.1063/1.5002120 [DOI] [PubMed] [Google Scholar]
- [70]. Jain, K. , and Universität Siegen, 2016, “ Transition to Turbulence in Physiological Flows: Direct Numerical Simulation of Hemodynamics in Intracranial Aneurysms and Cerebrospinal Fluid Hydrodynamics in the Spinal Canal,” universi—Universitätsverlag Siegen, Siegen, Germany.
- [71]. An, H. W. , Cheng, L. A. , and Zhao, M. , 2011, “ Direct Numerical Simulation of Oscillatory Flow Around a Circular Cylinder at Low Keulegan-Carpenter Number,” J. Fluid Mech., 666, pp. 77–103. 10.1017/S0022112010003691 [DOI] [Google Scholar]
- [72]. Kin, E. , and Sakajo, T. , 2005, “ Efficient Topological Chaos Embedded in the Blinking Vortex System,” Chaos, 15(2), p. 23111. 10.1063/1.1923207 [DOI] [PubMed] [Google Scholar]
- [73]. Aref, H. , 2002, “ The Development of Chaotic Advection,” Phys. Fluids, 14(4), pp. 1315–1325. 10.1063/1.1458932 [DOI] [Google Scholar]
- [74]. Daitche, A. , and Tel, T. , 2009, “ Dynamics of Blinking Vortices,” Phys. Rev. E, 79(1), p. 016210. 10.1103/PhysRevE.79.016210 [DOI] [PubMed] [Google Scholar]
- [75]. Xing, T. , and Stern, F. , 2010, “ Factors of Safety for Richardson Extrapolation,” ASME J. Fluids Eng., 132(6), p. 061403. 10.1115/1.4001771 [DOI] [Google Scholar]
- [76]. Xing, T. , and Stern, F. , 2011, “ Closure to Discussion of 'Factors of Safety for Richardson Extrapolation' (2011, ASME J. Fluids Eng., 133, p. 115501),” ASME J. Fluids Eng., 133(11), p. 115502. 10.1115/1.4005030 [DOI] [Google Scholar]
- [77]. Phillips, T. S. , and Roy, C. J. , 2014, “ Richardson Extrapolation-Based Discretization Uncertainty Estimation for Computational Fluid Dynamics,” ASME J. Fluids Eng., 136(12), p. 121401. 10.1115/1.4027353 [DOI] [Google Scholar]
- [78]. Kurtcuoglu, V. , Soellinger, M. , Summers, P. , Poulikakos, D. , and Boesiger, P. , 2007, “ Mixing and Modes of Mass Transfer in the Third Cerebral Ventricle: A Computational Analysis,” ASME J. Biomech. Eng., 129(5), pp. 695–702. 10.1115/1.2768376 [DOI] [PubMed] [Google Scholar]
- [79]. Kurtcuoglu, V. , Soellinger, M. , Summers, P. , Boomsma, K. , Poulikakos, D. , Boesiger, P. , and Ventikos, Y. , 2007, “ Computational Investigation of Subject-Specific Cerebrospinal Fluid Flow in the Third Ventricle and Aqueduct of Sylvius,” J. Biomech., 40(6), pp. 1235–1245. 10.1016/j.jbiomech.2006.05.031 [DOI] [PubMed] [Google Scholar]
- [80]. Wilson, R. V. , Stern, F. , Coleman, H. W. , and Paterson, E. G. , 2001, “ Comprehensive Approach to Verification and Validation of CFD Simulations—Part 2: Application for RANS Simulation of a Cargo/Container Ship,” ASME J. Fluids Eng., 123(4), pp. 803–810. 10.1115/1.1412236 [DOI] [Google Scholar]


