Abstract
We study a novel fuzzy clustering method to improve the segmentation performance on the target texture image by leveraging the knowledge from a prior texture image. Two knowledge transfer mechanisms, i.e. knowledge-leveraged prototype transfer (KL-PT) and knowledge-leveraged prototype matching (KL-PM) are first introduced as the bases. Applying them, the knowledge-leveraged transfer fuzzy C-means (KL-TFCM) method and its three-stage-interlinked framework, including knowledge extraction, knowledge matching, and knowledge utilization, are developed. There are two specific versions: KL-TFCM-c and KL-TFCM-f, i.e. the so-called crisp and flexible forms, which use the strategies of maximum matching degree and weighted sum, respectively. The significance of our work is fourfold: 1) Owing to the adjustability of referable degree between the source and target domains, KL-PT is capable of appropriately learning the insightful knowledge, i.e. the cluster prototypes, from the source domain; 2) KL-PM is able to self-adaptively determine the reasonable pairwise relationships of cluster prototypes between the source and target domains, even if the numbers of clusters differ in the two domains; 3) The joint action of KL-PM and KL-PT can effectively resolve the data inconsistency and heterogeneity between the source and target domains, e.g. the data distribution diversity and cluster number difference. Thus, using the three-stage-based knowledge transfer, the beneficial knowledge from the source domain can be extensively, self-adaptively leveraged in the target domain. As evidence of this, both KL-TFCM-c and KL-TFCM-f surpass many existing clustering methods in texture image segmentation; and 4) In the case of different cluster numbers between the source and target domains, KL-TFCM-f proves higher clustering effectiveness and segmentation performance than does KL-TFCM-c.
Keywords: Fuzzy C-means (FCM), Transfer learning, Knowledge transfer, Image segmentation, Data heterogeneity
1. Introduction
The effectiveness of clustering methods is often largely influenced by noise existing in target data sets. Usually, the greater the noise amplitude, the more negative the impact is. However, noise is nearly unavoidable and particularly impacts image segmentation [1–5], which motivates our research. Specifically, we address the issue that the segmentation performance of classic fuzzy C-means (FCM) [6–8], one of the most popular clustering approaches, is highly degraded by noise. While there have been numerous attempts to address this challenge, such as Ref. [1,2,9–15], most have not transcended the scope of traditional learning modalities and cannot achieve the required performance. In contrast, transfer learning [16,17], a state-of-the-art machine learning technique which will be introduced in the next section, has triggered an increasing amount of research interest owing to its distinctive advantages [18–42]. In brief, transfer learning helps one algorithm to improve the processing efficacy in the target domain, e.g. the image to be segmented, through the use of information in the source domain, e.g. another referenced image [16,22].
We pursue transfer learning as a means to improve the segmentation performance of FCM on target texture images in this manuscript. Specifically, the knowledge-leveraged prototype transfer (KL-PT) mechanism is introduced in response to the questions “What in the source domain can be enlisted as the knowledge?” and “How is such knowledge properly learned in the target domain?”. Further, to the challenge of performing knowledge transfer when the numbers of clusters in the source and target domains are inconsistent, the knowledge-leveraged prototype matching (KL-PM) mechanism is presented based on FCM. After that, via these two mechanisms, and with a three-stage-interlinked framework, i.e. knowledge extraction, knowledge matching, and knowledge utilization, the knowledge-leveraged transfer fuzzy C-means (KL-TFCM) approach is developed for the purpose of target texture image segmentation. In addition, by means of the strategies of maximum matching degree and weighted sum, KL-TFCM is differentiated into two specific versions: KL-TFCM-c and KL-TFCM-f, i.e. the crisp and flexible forms of the KL-TFCM, respectively. In summary, the contributions of our effort s are as follows:
KL-PT is devoted to leveraging the insightful knowledge, i.e., the cluster prototypes, of the source domain to guide the fuzzy clustering in the target domain, with the desirable adjustability of the referable degree between the source and target domains.
KL-PM strives to self-adaptively determine the pairwise relationships with regard to the cluster prototypes between the source and target domains, particularly when the numbers of clusters in the two domains are inconsistent.
By organically incorporating the strength of FCM, KL-PM, and KL-PT, and using the delicate three-stage-interlinked frame-work of knowledge transfer, we develop two versions of KL-TFCM methods, i.e., KL-TFCM-c and KL-TFCM-f, for the effective segmentation on target texture images. Both of them strive to properly leverage knowledge across domains, even though there is a certain extent of data inconsistency/heterogeneity between the source and target domains, e.g. the data distribution diversity and cluster number difference.
Benefiting from the more flexible strategy to generate cluster representatives from the source domain, compared with KL-TFCM-c, KL-TFCM-f exhibits better noise-tolerance as well as clustering effectiveness, particularly when the numbers of clusters differ in the source and target domains; this facilitates its generally preferable segmentation performance on target texture images.
Moreover, for knowledge-leveraged transfer clustering, our proposed KL-PT and KL-PM mechanisms are also suitable for other classic fuzzy clustering models, e.g., maximum entropy clustering (MEC) [43,44], fuzzy clustering by quadratic regularization (FC-QR) [43,45], and possibilistic C-means (PCM) [43,46] ; this additionally highlights our efforts in this manuscript.
The reminder in this manuscript is organized as follows. Section II reviews the theories and methods related to our research. Section III introduces, step-by-step, the knowledge transfer mechanisms regarding KL-PT and KL-PM, the KL-TFCM framework, and the two specific algorithms—KL-TFCM-c and KL-TFCM-f. Section IV evaluates the performance of KL-TFCM in texture image segmentation. Section V concludes and indicates areas of future work.
2. Related work
First, to facilitate understanding, common notations used throughout this paper are listed in Table 1.
Table 1.
Common notations used throughout this manuscript.
| Symbol | Use | Meaning | |
|---|---|---|---|
| X = {x1,...xN} ∈ RN×D | Eq. (1) | The target data set with N data instances and D dimensions | |
| XT = {x1,T,...xNT,T} ∈ RNT × D | Eqs. (5) and (12) | The data set in the target domain with NT data instances and D dimensions | |
| U = [μij]C×N | Eq. (1) | The C × N membership matrix with μij indicating the membership degree of xj(j = 1,..., N) belonging to cluster i(i = 1,…, C) | |
| UT = [μij,T]CT×NT | Eqs. (5) and (12) | The generated CT ×NT membership matrix in the target domain with μij,T indicating the membership degree of xj(j = 1,..., NT) belonging to cluster i (i = 1,…, CT) | |
| PT&S = [pjk]CT×CS | Eq. (5) | The matching degree matrix with pjk indicating the matching degree of the jth estimated cluster prototype in the target domain to the kth cluster prototype in the source domain; CT and CS denote the cluster numbers in the target and source domains respectively | |
| V = [v1,···,vC]T | Eq. (1) | The cluster prototype matrix with vi = [vi1, ···, viD]T (i = 1,..., C) signifying the ith cluster prototype (centroid) | |
| VT = [v1,T, ···, vCT,T]T | Eqs. (4),(5),(11), and (12) | The cluster prototype matrix in the target domain with vj,T = [vj1,T, ···, vjD,T]T (j = 1,..., CT) signifying the jth cluster prototype (centroid) | |
|
|
Generated in the knowledge matching stage, and used in the knowledge utilization stage | The raw cluster prototypes in the target domain estimated by KL-PM with signifying the jth raw cluster prototype (centroid) | |
| VS = [v1,S, ···, vCS,S]T | Eqs. (4),(5), and (11) | The cluster prototype matrix in the source domain with vk,S = [vk1,S, ···, vkD,S]T (k = 1,..., CS) signifying the kth cluster prototype (centroid) | |
| ṼS = [ṽ1,S, ···, ṽCT,S]T | Eqs. (9)–(12); Generated in the knowledge matching stage, and used in the knowledge utilization stage | The employed cluster representatives from the source domain for the eventual knowledge utilization in the target domain with ṽ j,S = [ṽj1,S, ···, ṽjD,S]T (j = 1,..., CT) denoting the jth cluster representative in the source domain |
2.1. Classic FCM
FCM attempts to group a set of given data instances, X = {x1,...xN} ∈ RN×D, into C disjoint clusters by means of the membership matrix U = [μij]C×N and the cluster prototypes V = [v1, ···, vC]T. For this purpose, FCM adopts the following objective function:
| (1) |
where m > 1 is the fuzzifier, i.e. the weighting exponent that controls the fuzziness of partitions.
Via the Lagrange optimization, it is easy to derive the following updating rules for the cluster prototype vi and membership degree μij:
| (2) |
| (3) |
Via the iterative procedure, the final fuzzy membership matrix U is attained, and then the cluster that each data instance should belong to can be determined in terms of the maximum probability principle.
As mentioned in Introduction, one disadvantage of FCM is its sensitivity to noise existing in target data sets which often incurs its inefficiency in target image segmentation.
2.2. Transfer learning based clustering and related methods
A. Transfer learning
Transfer learning [16–42] has recently become one of the hot topics in pattern recognition. Transfer learning focuses on improving the learning performance of intelligent algorithms on the target data set, i.e. the target domain, by referring to some beneficial information from the related data set, i.e. the source domain. Transfer learning is suitable for the situation where the target data are insufficient or distorted by noise or outliers, whereas some beneficial information from relevant data sets is available. Although the most common form of transfer learning entails only one source domain and one target domain, the number of source domains can be selected as needed.
The referable information between the source and target domains generally exhibits two types—raw data and knowledge. Due to the correlation between domains, some data in the source domain are certainly available supplements for those in the target domain. This is termed instance-transfer [16,33,34] in transfer learning. However, because of the difference of data distributions across domains, not all raw data in the source domain are beneficial to the target domain. To avoid the negative transfer [16,17,35], i.e. the phenomenon that source domain data or tasks contribute to the reduced performance of learning in the target domain, extracting knowledge instead of raw data from the source domain is a safe choose. In transfer learning, knowledge is referred to as a category of advanced information from the source domain, such as feature representations [16,17,25,36,37], parameters [16,21,39], and relationships [16,38], which is usually obtained from certain specific perspectives and via some reliable theories and precise procedures. Compared with raw data, knowledge is usually regarded as being more insightful as well as possessing stronger anti-noise capability. In some cases where the original data in the source domain are not accessible, for instance, because of privacy protection, it could be the only feasible pathway for transfer learning to extract knowledge rather than raw data from the source domain.
In general, there have been three categories of transfer learning [16,17] so far, i.e. inductive transfer learning, transductive transfer learning, and unsupervised transfer learning. In inductive transfer learning, it is required to induce an objective predictive model based on the labeled data in the target domain and with the assistance of the data or knowledge from the source domain. Many transfer classification [17,18,21,39] and regression [26–28] methods belong to this category. Conversely, in transductive transfer learning, there is no labeled data in the target domain while lots of labeled data in the source domain are usually available. Some approaches of domain-adaptation-based transfer classification [40–42] are the representatives of this category. As for unsupervised transfer learning, such as the research of transfer clustering [31,32] and transfer dimensionality reduction [29,30], it is label-independent in both of the source and target domains. So far, existing work on unsupervised transfer learning is comparatively little, and this encourages our research in this manuscript. One can refer to [16,17] for the more complete surveys on transfer learning.
B. Transfer clustering
As is mentioned above, clustering specializes in grouping a set of data instances so that objects in the same group (namely, a cluster) are more similar to each other than to those in other groups (clusters). The practical effectiveness of clustering methods depends strongly on the data quantity and quality in the target data set. Conventional clustering techniques can achieve desirable clustering performance only in relatively ideal situations in which data are relatively sufficient and have little distortion by noise or outliers. Such conditions, however, are difficult to achieve in practice. Transfer learning based clustering has emerged as an approach to address this challenge [31,32,47].
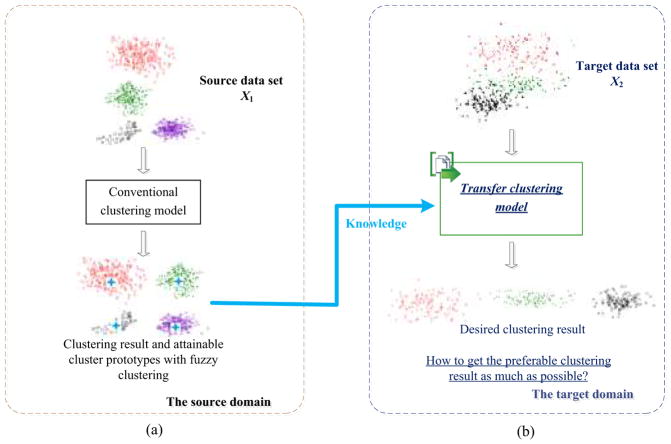
We use a simple example having only one source domain along with the target domain, as shown in Fig. 1, to explain how clustering is associated with transfer learning. As is evident in Fig. 1 (b), noise interference causes the examples in the target data set (X2) to be mixed together so that the three potential clusters, indicated by red, green, and black, are difficult to distinguish using conventional clustering methods. Suppose that another comparatively low-noise data set (X1) is now available, as shown in Fig. 1 (a), in which the data essence can be relatively easily captured by usual clustering approaches. Regardless of the apparent distinction of cluster numbers in X1 and X2, there are intrinsic connections between these two data sets, e.g., the three potentially embedded clusters in X2 also exist in X1, although their individual data distributions are visually different, possibly due to noise. In such case, transfer learning is an appropriate strategy conducive to improving the clustering performance on X2 by taking X2 and X1 as the target and source domains, respectively. If any fuzzy clustering method, e.g., FCM, is performed on X1, the cluster prototypes (centroids) can be attained, as marked with small, blue stars in Fig. 1 (a). These achieved cluster prototypes in X1 are reasonably regarded as a type of knowledge for guiding and improving the clustering accuracy on X2. This is exactly the central idea of our knowledge-leveraged transfer clustering in this literature.
Fig. 1.
Outline of knowledge-leveraged transfer clustering.
To date there have been few studies that connect transfer learning and clustering. The two well-known ones are the self-taught clustering (STC) [31] and transfer spectral clustering (TSC) [32]. STC was a collaborative learning-based transfer clustering approach, which simultaneously clustered the target and auxiliary data with allowing the feature representation from the auxiliary data to influence the target data via the common features. Benefiting from the new data representation, STC worked well on the target data. As for TSC, it assumes that the embedded information regarding features could connect different clustering tasks of different data sets and hence mutually improve the clustering performance of both sets. As such, both the data manifold information of clustering tasks and the feature manifold information shared between related clustering tasks were involved in TSC. In addition, the collaborative clustering strategy was also recruited in TSC for controlling the knowledge transfer among tasks. Nevertheless, it should particularly be pointed out that, although STC and TSC have proved their respective advantages, both are restricted in the condition that the cluster numbers in the source and target domains are the same. That is, neither of them can be used for such transfer scenario wherein the number of clusters in one domain is different from that in the other. In addition, we have recently been attempting to establish the bridge between transfer learning and partition-based clustering [1,2,10]. For example, we introduced the concept of cluster prototype-based knowledge transfer [47] for many sof-tpartition clustering models, such as FCM, soft subspace clustering [10,48], and maximum entropy clustering [43,44]. Our research in this manuscript also belongs to this category.
C. Methods associated with transfer clustering
Despite the fact that transfer clustering only emerged in recent years, it is not isolated from other mainstream techniques in pattern recognition, such as multi-task clustering [49,50], co-clustering (collaborative clustering) [13,51,52], semi-supervised clustering [53,54,55], and supervised clustering [56,57,58].
Multi-task clustering concurrently performs clustering tasks with interactions among these tasks so that all of them achieve better performance versus clustering separately. For example, the learning shared subspace for multitask clustering (LSSMTC) [49] focused on learning a subspace shared by all the tasks, through which the knowledge of the tasks can be transferred to each other. Moreover, as the derivative of LSSMTC, the multi-task clustering via domain adaptation (MTC-DM) [50] was proposed in order to address the issue of distribution differences among tasks according to the frontier research in domain adaptation. As revealed in [16,17], transfer learning is actually one of the extensions of multi-task learning. The most noticeable difference between transfer clustering and multi-task clustering lies in that the former merely cares about the task occurred in the target domain whereas conventional multi-task clustering utilizes the data in all tasks directly. Thus, when multi-task clustering is used, a high noise level in one data set can cause negative consequences among tasks.
Co-clustering performs clustering on the data instances and attributes simultaneously on the target data set. Therefore, it is also capable of being regarded as a special type of multi-task clustering, in the sense of two collaborative clustering tasks from the perspectives of examples and features separately. In this aspect, considerable work has also been conducted. For instance, the dual-regularized co-clustering (DRCC) [51] was developed via semi-nonnegative matrix tri-factorization as well as manifold information. That is, by constructing two graphs on the data points and features respectively, the co-clustering was formulated as semi-nonnegative matrix tri-factorization with two graph regularization terms, requiring that the cluster labels of data points are smooth to the data manifold, whereas those of features are smooth to the feature manifold. In addition, by treating the contingency table as an empirical joint probability distribution between two discrete random variables which take values over the rows and columns, the information-theoretic co-clustering (ITCC) [52] was put forward with maximizing mutual information between the clustered random variables subject to the constraints on the cluster numbers of row and column. As revealed in both STC [31] and TSC [32], co-clustering is sometimes involved in transfer clustering when feature-based knowledge is shared between the auxiliary and target data.
Semi-supervised clustering and supervised clustering are the other two categories of clustering techniques associated with transfer clustering. Both attempt to improve the clustering performance on target data sets via the assist of given prior information. This is consistent with the intention of transfer clustering. We briefly review them as follows.
Semi-supervised clustering aims to enhance the clustering performance using some side information, i.e. must-link and/or cannot-link constraints, on the target data set. The existing research on semi-supervised clustering can be subdivided into two major groups, i.e. similarity-based methods and search-based methods. The similarity-based method creates a modified distance function that incorporates the knowledge with respect to the given side information and use a conventional clustering model to cluster the data. For example, the K-means clustering in conjunction with one modified distance function was used to compute clusters in [54], and one shortest path algorithm [55] was developed by modifying the Euclidian distance function based on the prior knowledge of pairwise constraints. Conversely, the search-based method modifies the clustering algorithm itself but does not change the distance function. For instance, the constrained K-means clustering (CKM) [53] was developed by profitably manipulating the search procedure of classic K-means so as to make use of the pairwise must-link and cannot-link constraints.
Supervised clustering is to automatically adapt a clustering algorithm that learns a parameterized similarity measure with the aid of a training set consisting of numerous labeled examples. Differing from semi-supervised clustering, the learned parameterized similarity measure in supervised clustering is usually used to cluster future data sets rather than the current one for training. For instance, the support vector machine-based supervised clustering approaches [56,57] were studied by learning the item or item-pair based similarity measure to optimize the performance of correlation clustering on a variety of performance measures. In addition, a supervised fuzzy C-means clustering method (SFCM) [58] was presented by defining a multivariate Gaussian-based distance measure of which the parameters needs to be trained using the given labeled examples.
However, it should be pointed out that the applicable data scenes of semi-supervised clustering, supervised clustering, and transfer clustering are markedly different, regardless of the fact that the prior information, in the form of either raw data or advanced knowledge, is involved in all of them. Specifically, semi-supervised clustering usually serves only one data set. It gets some beneficial supervision information from one data set and eventually boosts clustering on the same data set. In supervised clustering, a training set is given in which all examples are labeled. One parameterized distance measure, which aims to group future data sets, is then learned via these training data. Here the training set and future data sets are from the same domain in supervised clustering. As for transfer clustering, as already disclosed, the prior information is obtained from the source domain/domains but is used in the target domain, and there usually exist different degrees of data inconsistency between the source and target domains. Therefore, both semi-supervised clustering and supervised clustering can be regarded as the special cases of transfer learning in which the target and auxiliary data possess the same distribution.
3. Knowledge-leveraged transfer fuzzy C-Means (KL-TFCM) for texture image segmentation
Now coming back to the intent of this paper, we focus on exploring the promising fuzzy clustering schema for target texture image segmentation, based on transfer learning. Two points need to be clarified before introducing our work. First, only one source domain is considered throughout our current research. The multiple-source-domain-oriented model will be continued in the future. Second, we always suppose that the data in the source domain are relatively pure and sufficient so that we can achieve desirable, insightful knowledge to assist the clustering in the target domain.
Let us begin with one realistic scenario, as shown in Fig. 2, so as to intuitively illustrate how transfer clustering occurs in the texture image segmentation. Fig. 2 (c) is the target image to be segmented. It is distinctly intractable to deal with such image as it has been rather polluted by noise, and conventional clustering methods usually cannot gain insights into the essence, i.e. Fig. 2 (b). In such case, transfer learning can be adopted to obtain valuable information from another correlative texture image, i.e. Fig. 2 (a), in order to assist the eventual clustering on Fig. 2 (c). In the context of transfer learning, Fig. 2 (c) is the target domain and Fig. 2 (a) is the only source domain. What could be regarded as beneficial information (i.e. referable knowledge) across two domains are the intrinsic characteristics of common textures between Fig. 2 (a) and (b), similarly between Fig. 2 (a) and (c). Certainly, due to the noise distortion in Fig. 2 (c), the texture characteristics between Fig. 2 (a) and (c) are not distinctly consistent even if they are essentially the same textures, which actually depend on the referable degree between these two images (domains). Moreover, we also face two other challenges:
Fig. 2.
Illustration of transfer clustering occurred in texture image segmentation.
What can be recruited for effectively embodying the intrinsic texture characteristics in the referenced source image, so as to attain the desirable, valuable knowledge for transfer clustering on the target texture image?
How can one self-adaptively learn knowledge from the source domain, in answer to the probable data inconsistency (data heterogeneity) between the source and target domains, e.g., the data distribution diversity as well as the cluster number difference between Fig. 2 (a) and (c)?
For addressing the above issues, we detail our countermeasures as follows.
3.1. Self-adaptive, knowledge-leveraged transfer mechanisms across domains
As we know well, the resultant cluster centroids, V = [v1, ···, vC]T, are also referred to as the cluster prototypes in fuzzy clustering, e.g. FCM, which means that each of them is able to represent the objects in its matching cluster [43]. Based on this, suppose under the condition that the texture features in the source texture image can be effectively captured and be subsequently used to constitute the target data set, then the centroids (prototypes), denoted as VS = [v1,S, ···, vCS,S]T, of all embedded clusters can conveniently be obtained using a certain conventional fuzzy clustering method. As disclosed in [47], the achieved VS = [v1,S, ···, vCS,S]T can be regarded as the knowledge that is capable of depicting the substance of all textures in the source image. With these cluster centroids acting as the knowledge, we can benefit from two features: (1) A cluster centroid is also referred to as a cluster prototype in fuzzy clustering, which suffices to indicate its nice representability to one cluster, and also to all the affiliated objects in one cluster; (2) A cluster centroid is synthetically generated via reliable theories as well as rigorous procedures, which facilitates its robustness when facing nosy situations.
For the challenge of potential data heterogeneity between the source and target domains, as already mentioned, a mechanism with capability of flexibly controlling the referable degree between these two domains should be feasible to address. To this end, we present the following knowledge-leveraged prototype transfer (KL-PT) formulation.
A. The KL-PT mechanism
Let us first cope with a relatively simple scenario, i.e. the cluster numbers in the source and target domains are the same, denoted as C. Suppose VS = [v1,S, ···, vC,S]T and VT = [v1,T, ···, vC,T]T signify the cluster prototypes in the source and target domains, respectively. Then the formula of the knowledge-leveraged prototype transfer (KL-PT) mechanism can be expressed as
| (4) |
where λ ≥ 0 is the regularization coefficient.
Eq. (4) measures the total gap between the estimated cluster prototypes in the target domain and the referenced ones in the source domain. In the sense of texture image segmentation, here VT refers to the texture prototypes in the target image that need to be estimated by our own method, whereas VS signifies the texture prototypes in the source image that are given for reference. The parameter λ controls the overall, referable degree between VT in the target domain to VS in the source domain. The larger the value of λ, the greater the overall referable degree between VT and VS is, and the smaller the expected total difference between VT and VS is.
B. The knowledge-leveraged prototype matching (KL-PM) mechanism
KL-PT in the form of Eq. (4) assumes that the cluster numbers in the source and target domains are equal, which sometimes restricts its practicability. For example, the potential texture numbers in Fig. 2 (a) and (c) are different: the former is 7 and the latter is 5. Key to this situation is to appropriately differentiate the importance of each cluster prototype in the source domain so as to correctly utilize them as the knowledge for transfer clustering in the target domain. To this end, adapting from [47], we introduce another transfer clustering mechanism termed knowledge-leveraged prototype mat ching (KL-PM), which can be formulated as
| (5) |
in which the notations of xi,T (i = 1,..., NT) ∈ XT, UT, PT&S, VT, and VS are the same as those listed in Table 1. NT denotes the data size in the target domain; CS and CT signify the cluster numbers in the source and target domains separately; m1 > 1 and m2 > 1 are two fuzzifiers controlling the model fuzziness; and β > 0 is the regularization parameter.
Eq. (5) includes two terms. The first, originating from classical FCM, aims to divide the data in the target domain into CT groups with overall minimum intra-cluster deviation as well as maximum inter-cluster separation. The second attempts to determine the appropriate values of pjk, 1 ≤ j ≤ CT, 1 ≤ k ≤ CS, i.e. the matching degrees of cluster prototypes between the target and source domains.
By the Lagrange optimization, the updating equations of vj,T, μij,T, and pjk in Eq. (5) can easily be derived as
| (6) |
| (7) |
| (8) |
After the iterative procedure, two desired outcomes regarding the target domain are obtained. One is the current estimate of cluster centroids, VT = [v1,T,..., vCT,T]T in the target domain. As they still need to be refined in our method, we call them the raw cluster prototypes of the target domain and designate them as . The other outcome is the eventual matching degrees PT&S = [pjk]CT×CS. Via these matching values, the appropriate pairwise relationships regarding the cluster prototypes in the source and target domains are achieved. Large values of pjk indicate that the jth cluster prototype in the target domain strongly matches the kth one in the source domain.
Next, we continue discussing how to extract knowledge from the source domain, based on the matching degrees, PT&S, so as to implement knowledge transfer in the case of inconsistent cluster numbers between the source and target domains. Given our assumption that the data in the source domain are sufficient, which implies that the number of embedded clusters in the source domain are more than or at least equal to that in the target domain, two ways are available here, and we call them the so-called crisp and flexible forms, respectively. In either case, the CT cluster representatives, denoted as ṼS = [ṽ1,S, ···, ṽCT,S]T, are achieved in the source domain, and regarded as the final knowledge for transfer learning in the target domain.
-
The crisp form
In this case, for each , i.e. each of the raw cluster prototypes in the target domain, we directly designate the cluster prototype in the source domain that owns the maximum matching degree to as ṽj,S ∈ ṼS. Namely,(9) -
The flexible form
Here all of the ṽj,S ∈ ṼS, j ∈ [1, CT], are synthetically generated by means of the weighted sums:(10) That is, for each in the target domain, in terms of VS = [v1,S, ···, vCS,S]T as well as the matching degrees, pjk(k = 1,..., Cs), we synthesize a virtual product as the referable object in the source domain, via the strategy of the weighted sum.
So far, even if there is data inconsistency between the source and target domains, via the strategies of extracting the cluster representatives from the source domain as well as controlling the referable degree between these two domains, transfer clustering is now available for target texture image segmentation. Accordingly, the KL-PT mechanism in the form of Eq. (4) can be rewritten as
| (11) |
That is, in the case of different cluster numbers between the source target domains, KL-PT substitutes the CT cluster representatives, ṼS = [ ṽ1,S, · · · , ṽCT,S]T, for the original cluster prototypes, VS = [ v1,S, · · · , vCS,S]T, for the knowledge transfer across domains.
3.2. The proposed KL-TFCM
A. The complete framework of KL-TFCM
Now, by means of the two knowledge transfer mechanisms—KL-PM in the form of Eq. (5) and KL-PT in the form of Eq. (11), and based on FCM, we can propose our novel clustering model, referred to as knowledge-leveraged transfer fuzzy C-means (KL-TFCM), for texture image segmentation. The eventual formulation of KL-TFCM is:
| (12) |
where, xi,T (i = 1, …, NT) ∈ XT, ṽj,S ∈ ṼS, vk,S ∈ VS, pjk ∈ PT&S, UT, and VT are the same as those listed in Table 1, and CS, CT, NT, and λ are the same as those in Eq. (4) or (5).
Eq. (12) is also composed of two terms. The first term aims at partitioning the target data into CT groups with optimal intercluster purity, while the second is devoted to suitably and flexibly exploiting the final knowledge, ṼS = [ ṽ1,S, · · · , ṽCT,S]T, from the source domain. The parameter λ ≥ 0 determines the referable degree across the two domains. Greater values of λ indicate that the target domain should learn much from the source domain, i.e. VT should be much closer to ṼS; conversely, smaller values of λ mean that the overall similarity between VT and ṼS is not strongly enforced.
Once again, via the Lagrange optimization, the updating equations regarding cluster prototype vj,T and membership μij,T in Eq. (12) are also deduced:
| (13) |
| (14) |
It should be noted that KL-TFCM is proposed based on KL-PM and KL-PL and that KL-PM is always performed before KL-TFCM in the same target domain. Therefore, as mentioned in Section 3.1-B, the raw cluster prototypes, , achieved by KL-PM in the target domain can be further refined in our subsequent procedure. For this purpose, we initialize at the beginning of the iterative optimization with respect to Eqs. (13) and (14).
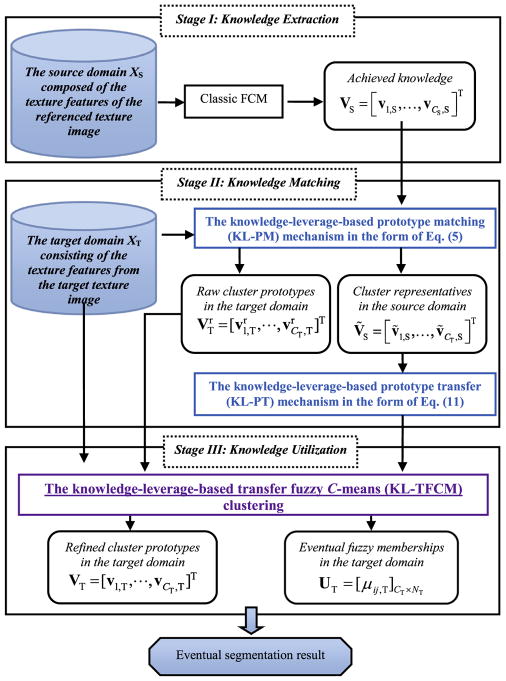
Last but not least, to facilitate understanding, it is worth summarizing the complete framework of KL-TFCM developed for target texture image segmentation. As illustrated in Fig. 3, this complete framework involves three stages: knowledge extraction, knowledge matching, and knowledge utilization.
Fig. 3.
Complete framework of KL-TFCM for texture image segmentation.
-
Stage I: Knowledge extraction
In this stage, the texture features in the reference texture image are first extracted in order to compose the source domain data set XS. Then, via classic FCM, the prototypes (centroids), VS = [v1,S, · · · , vCS,S]T, of all embedded clusters (i.e. all contained textures) are obtained as the knowledge for reference in the target domain.
-
Stage II: Knowledge matching
The texture features of the target texture image are used to compose the target domain data set XT. By KL-PM in the form of Eq. (5), the currently estimated, raw cluster prototypes, , in the target domain as well as the final matching degrees, PT&S, between the source and target domains are obtained. Subsequently, in terms of PT&S, and via the crisp or flexible form, the CT cluster representatives, ṼS = [ ṽ1,S, · · · , ṽCT,S]T, in the source domain can be attained. After that, the rewritten KL-PT knowledge transfer mechanism in the form of Eq. (11) becomes feasible.
-
Stage III: Knowledge utilization
Based on the joint action of KL-PM and KL-PT in the form of Eq. (11), KL-TFCM is now available for target texture image segmentation, no matter whether there is the difference of cluster numbers between the source and target domains or not. In KL-TFCM, the cluster representatives, ṼS = [ ṽ1,S, · · · , ṽCT,S]T, from the source domain are regarded as the final knowledge for transfer clustering in the target domain. Initializing and using Eqs. (14) and (13) alternately, the eventual partitions on XT, i.e. the segmentation result of the target texture image, can be determined.
B. Detailed core algorithms
In light of the two ways for generating the cluster representatives, ṼS = [ ṽ1,S, · · · , ṽCT,S]T, from the source domain, i.e. using the crisp or flexible form, we categorize KL-TFCM into two specific versions—KL-TFCM-c and KL-TFCM-f, corresponding to Eqs. (9) and (10), respectively. The detailed procedure is listed as follows
Algorithms.
Knowledge-leveraged transfer fuzzy C-means clustering (KL-TFCM)-c/-f
| Inputs: | The target domain data set XT constituted by extracting texture features from the target texture image; the source domain data set XS composed of texture features from the referenced texture image; the cluster numbers CT and CS in the target and source domains, respectively; the convergence threshold ε; the fuzzifiers m, m1, m2 and parameters λ, β in Eq. (1), (5), or (12); and the maximum number of iterations max_iter |
| Outputs: | The eventual partitions on XT, i.e. the segmentation result of target texture image |
| Stage I: Knowledge extraction | |
| Step I-1: | Set the iteration index t = 1, initialize the fuzzy memberships in Eq. (1) and compute the cluster prototypes , i = 1, …, CS, using Eq. (2) in the source domain XS; |
| Step I-2: | Compute the fuzzy memberships , i = 1, …, CS, j = 1, … NS, using Eq. (3); |
| Step I-3: | Compute the cluster prototypes , i = 1, …, CS, using Eq. (2); |
| Step I-4: | If or t > max_iter, go to Step I-5; otherwise, set t = t + 1 and go to Step I-2; |
| Step I-5; | Step I-5: Set the cluster prototypes in the source domain XS. |
| Stage II: Knowledge matching | |
| Step II-1: | Set the iteration index t = 1, initialize the fuzzy memberships and the matching degrees in Eq. (5), and compute the cluster prototypes , j = 1, …, CT, using Eq. (6) in the target domain XT; |
| Step II-2: | Compute the fuzzy memberships , i = 1, …, NT, j = 1, …, CT, using Eq. (7); |
| Step II-3: | Compute the matching degrees , j = 1, …, CT, k = 1, …, CS, using Eq. (8); |
| Step II-4: | Compute the cluster prototypes , j = 1, …, CT, using Eq. (6); |
| Step II-5: | If or t > max_iter, go to Step II-6; otherwise, set t = t + 1 and go to Step II-2; |
| Step II-6: | Set the raw cluster prototypes and the final matching degrees ; |
| Step II-5: | Generate the CT cluster representatives, ṼS = [ ṽ1,S, · · · , ṽCT,S]T, of the source domain as the final knowledge for the target domain, according to: Case-c: the crisp form, i.e. Eq. (9); Case-f: the flexible form, i.e. Eq. (10). |
| Stage III: Knowledge utilization | |
| Step III-1: | Set the iteration index t = 1, initialize the cluster prototypes in Eq. (12), and compute the fuzzy memberships using (14) in the target domain XT; |
| Step III-2: | Compute the cluster prototypes , j = 1, …, CT, using (13); |
| Step III-3: | Compute the fuzzy memberships , i = 1, …, NT, j = 1, …, CT, using (14); |
| Step III-4: | If or t > max_iter, go to Step III-5; otherwise, t = t + 1 and go to Step III-2; |
| Step III-5: | The final memberships matrix UT in the target domain is achieved, i.e. ; |
| Step III-6: | Determine the eventual partitions on the target texture image according to the eventual memberships UT. |
Let us analyse the computational cost of KL-TFCM in stages. The time complexity of the first stage is O (ma x_tria · max_iter · (NS · CS + CS)), the second stage is O (ma x_tria · max_iter · (NT · CT + CT + CS · CT)), and the final stage is O (ma x_tria · max_iter · (NT · CT + CT)), in which, max_tria and max_iter are, respectively, the maximal numbers of trials and iterations; NS and NT are separately the data sizes in the source and target domains; and CS and CT signify the cluster numbers of the source and target domains, respectively.
4. Experimental studies
4.1. Setup
In this section, we focus on evaluating the real-world segmentation performance of texture images of our research. In addition to KL-TFCM-c and KL-TFCM-f, eight other correlative algorithms are enlisted for performance comparison, including classic FCM, STC [31], TSC [32], LSSMTC [49], CombKM [49], DRCC [51], CKM [53], and SFCM [58]. All of these competitive algorithms have been briefly introduced in Section II, except for CombKM. As described in [49], CombKM refers to the K-means performed on the combined data set constituted by merging the data of all tasks together. These algorithms are good representatives of the state-of-the-art approaches associated with our research. Among these, FCM, SFCM, KL-TFCM-c, and KL-TFCM-f belong to fuzzy clustering; KL-TFCM-c, KL-TFCM-f, STC, and TSC belong to transfer clustering; Both STC and TSC also belong to co-clustering; LSSMTC and CombKM belong to multi-task clustering; and DRCC, CKM, and SFCM are, respectively, the member of co-clustering, semi-supervised clustering, and supervised clustering.
For measuring the clustering effectiveness of these involved approaches, two well-accepted validity metrics, i.e. NMI (Normalized Mutual Information) [48] and RI (Rand Index) [48], are employed. Both NMI and RI take values within the interval [0,1]. The greater the value of NMI or RI, the better performance the corresponding algorithm indicates. Their definitions are briefly reviewed as follows.
| (15) |
where Ni,j is the number of agreements between cluster i and class j, Ni is the number of data points in cluster i, Nj is the number of data points in class j, and N signifies the data capacity of the whole dataset.
| (16) |
where f00 denotes the number of any two sample points belonging to two different clusters, f11 denotes the number of any two sample points belonging to the same cluster, and N is the number of all the sample points.
The grid search strategy [48] was enlisted for partial parameter settings during our experiments. The values or trial ranges of core parameters involved in the recruited algorithms are listed in Tables 2 and 3. The experimental results of matching approaches are reported in terms of the means and standard deviations of NMI and RI after twenty times of random initialization based running on the target data sets.
Table 2.
Parameter settings in transfer clustering algorithms.
| Settings | Transfer clustering algorithms | ||
|---|---|---|---|
|
| |||
| KL-TFCM-c/-f | TSC | STC | |
| Core parameters | The fuzzifers m, m1, , where N and D are the data size and data dimension in the target dataset, respectively; Parameters β4 ∈ {0.1, 0.5, 1, 5, 10, 50, 100, 500, 1000} and λ* ∈ {0, 0.005,0.1,0.5,0.7, 1, 1.5, 5, 10, 50, 100}; ṽj,S ∈ ṼS, j ∈ [1, CT], Case-c: Eq. (9) and Case-f: Eq. (10) | Parameters K = 27, λ = 3, and step = 1. | Trade-off parameter λ = 1 |
| For the details regarding parameters in TSC and STC, please refer to [31,32]. | |||
Note:
* denotes that the optimal settings need to be eventually determined by the grid search.
Table 3.
Parameter settings in other algorithms.
| Settings | Other algorithms | |||||
|---|---|---|---|---|---|---|
|
| ||||||
| Classic fuzzy clustering | Multi-task clustering | Co-clustering | Semi-supervised clustering | Supervised clustering | ||
|
| ||||||
| FCM | LSSMTC | CombKM | DRCC | CKM | SFCM | |
| Core parameters | The fuzzifier , where N and D are the data size and data dimension, respectively; C equals the number of clusters. | Task number T = 2; Regularizer l * ∈ {2, 22, 23, 24} ∪[100: 100: 1000]; Regularizer λ* ∈ {0.25, 0, 5, 0.75} | K equals the number of clusters | Regularizer λ* = μ* ∈ {0.1,1,10, 100,500,1000} See [51] for the detailed parameters | K equals the number of clusters | The fuzzifier , where N and D are the data size and data dimension, respectively; |
Note:
* denotes that the optimal settings need to be eventually determined by the grid search.
All of our experiments were implemented via MATLAB 2010b on a PC with Intel i5-3317 U 1.70 GHz CPU and 16GB RAM.
4.2. Texture image segmentation
A. Constitution of the transfer Scenarios of Texture Image Segmentation
For constituting the experimental texture images, the well-known Brodatz texture [59] repository was enlisted in our research. Specifically, thirteen basic textures: D3, D6, D21, D31, D33, D41, D45, D49, D53, D56, D93, D96, and D101, in this repository were used to synthesize the texture images acting as the source or target domains for transfer clustering in our experiments.
It should be noted that, for achieving the balance of good readability and appropriate paper length, we show our experimental studies in two parts: the major contents are shown in Section IV and the others are given in the Appendix as supplementary material.
To perform our experiments, we have first generated two data scenarios suitable for transfer clustering, as illustrated in Figs. 4 and A1, respectively. Specifically, for transfer learning, TI_S 1, Fig. 4 (a), was enlisted as the only source domain and TI_T 1_1 to TI_T 1_8, Fig. 4 (b)–(i), as the target domains respectively. All these synthetic texture images were rescaled to 100 × 100 resolution, and to some of them the Gaussian noise with different standard deviations was added in order to simulate multiple noisy data situations. In our experiments, TI-T 1_1 to TI-T 1_8 (i.e. Fig. 4 (b)–(i)) belong to two types of target domains. That is, each of TI-T 1_1 to TI-T 1_4 owns the same texture number as that in TI-S 1 (i.e. 7 clusters), but has an inconsistent data distribution, whereas the numbers of clusters in TI-T 1_5 to TI-T 1_8 are 3, 4, 5, and 6, respectively, which are all different from that in TI-S 1. In addition, the noise amplitudes in these target domain images are also different. For example, the standard deviations of Gaussian noise in TI-T 1_1, TI-T 1_4, and TI-T 1_5 to TI-T 1_8 are 0.1, while in TI-T 1_2 and TI-T 1_3 are 0.2 and 0, respectively. Please refer to Fig. 4 for the details regarding the texture arrangement, cluster number, and noise level in each target texture image. The situations are similar in Fig. A1 in which TI_T 2_1, TI_T 2_2, and TI_S 2 all have 7 clusters, whereas TI_T 2_3 to TI_T 2_6 have from 3 to 6 clusters. These two transfer scenarios enable us to extensively investigate the performance of all employed algorithms in the realistic applications of target texture image segmentation.
Fig. 4.
Artificial scenario 1 for transfer clustering. (a) TI_S 1: the image acting as the source domain; (b)–(e) TI_T 1_1 to TI_T 1_4: the target domain images owning the same cluster number as that in TI_S 1, but different data distributions; (f)–(i) TI_T 1_5 to TI_T 1_8: the target domain images whose cluster numbers are different from that of TI_S 1.
The Gabor filter [60] was used to extract intrinsic texture features of all texture images in terms of the filtering bank with 6 orientations (at every 30°) and 5 frequencies (starting from 0.46). As such, the data sets corresponding to all texture images were produced, with the data dimensionality and data size being 30 and 10,000, respectively. Note that for the purpose of good readability, we use consistent nomenclature designating these data sets as the names of their associated texture images.
B. Comparisons of segmentation results
The ideal segmentation results regarding all target texture images are first illustrated in Figs. 5 and A2, respectively, where the small squares with the same colors in each subfigure signify the same textures which should be grouped into the same clusters.
Fig. 5.
Illustrations of ideal segmentation of employed texture images. (a) for TI_T 1_1 and TI_T 1_2; (b) for TI_T 1_3 and TI_T 1_4; (c) for TI_T 1_5; (d) for TI_T 1_6; (e) for TI_T 1_7; (f) for TI_T 1_8.
In contrast, the actual segmentation results as well as the scores of NMI and RI achieved by the ten competitors are shown in Figs. 6, 7, A3, and A4 and Tables 4 and A1. Based on these outcomes, we make the following observations.
Fig. 6.
Segmentation results of ten clustering approaches on target texture images TI_T 1_1 to TI_T 1_4.
Fig. 7.
Segmentation results of five clustering approaches on target texture images TI_T 1_5 to TI_T 1_8.
Table 4.
Performance comparisons of ten involved algorithms on TI_T 1_1 to TI_T 1_8.
| Data sets | Validity Metrics | FCM | LSSMTC | CombKM | DRCC | CKM | SFCM | STC | TSC | KL-TFCM-c | KL-TFCM-f |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TI_T1_1 | NMI-mean | 0.4151 | 0.2508 | 0.2500 | 0.2480 | 0.3762 | 0.4468 | 0.4986 | 0.5133 | 0.6287 | 0.6336 |
| NMI-std | 0.0052 | 0.0191 | 0.0308 | 0.0213 | 0.0068 | 0.0295 | 0 | 0.0066 | 0.0084 | 0.0049 | |
| RI-mean | 0.8268 | 0.7893 | 0.7532 | 0.7905 | 0.8342 | 0.7882 | 0.8690 | 0.8772 | 0.9055 | 0.9063 | |
| RI-std | 0.0087 | 0.0043 | 0.0154 | 0.0037 | 0.0021 | 0.0126 | 0 | 0.0022 | 0.0020 | 0.0011 | |
| TI_T1_2 | NMI-mean | 0.3027 | 0.2331 | 0.2311 | 0.2264 | 0.2999 | 0.2836 | 0.3696 | 0.3470 | 0.5362 | 0.5350 |
| NMI-std | 0.0048 | 0.0237 | 0.0481 | 0.0188 | 0.0169 | 0.0444 | 0 | 0 | 0.0140 | 0.0091 | |
| RI-mean | 0.7777 | 0.7695 | 0.7063 | 0.7783 | 0.8156 | 0.6630 | 0.7839 | 0.7708 | 0.8600 | 0.8569 | |
| RI-std | 0.0052 | 0.0050 | 0.0287 | 0.0015 | 0.0021 | 0.0764 | 0 | 0 | 0.0170 | 0.0124 | |
| TI_T1_3 | NMI-mean | 0.6039 | 0.6087 | 0.6092 | 0.3422 | 0.5738 | 0.5713 | 0.6511 | 0.6104 | 0.6200 | 0.6198 |
| NMI-std | 0.0359 | 0.0326 | 0.0240 | 0.0241 | 0.0513 | 0.0312 | 0 | 5.77e–004 | 0.0037 | 0.0032 | |
| RI-mean | 0.8553 | 0.8710 | 0.8611 | 0.7849 | 0.8463 | 0.8534 | 0.8877 | 0.8726 | 0.8643 | 0.8644 | |
| RI-std | 0.0185 | 0.0112 | 0.0268 | 0.0204 | 0.0270 | 0.0195 | 0 | 2.31e–004 | 0.0010 | 0.0008 | |
| TI_T1_4 | NMI-mean | 0.4557 | 0.4789 | 0.4261 | 0.2413 | 0.4109 | 0.2836 | 0.5497 | 0.5511 | 0.6136 | 0.6147 |
| NMI-std | 0.0197 | 0.0013 | 0.0193 | 0.0143 | 0.0015 | 0.0240 | 0 | 0 | 0.0006 | 0.0011 | |
| RI-mean | 0.8178 | 0.8185 | 0.8082 | 0.7848 | 0.7956 | 0.6598 | 0.8472 | 0.8496 | 0.8754 | 0.8757 | |
| RI-std | 0.0044 | 0.0028 | 0.0073 | 0.0013 | 2.96e–04 | 0.0363 | 0 | 0 | 0.0005 | 0.0008 | |
| TI_T1_5 | NMI-mean | 0.4644 | – | 0.5557 | – | 0.4103 | – | – | – | 0.6006 | 0.6501 |
| NMI-std | 0.0002 | – | 0.0201 | – | 0.0021 | – | – | – | 0 | 7.06e–05 | |
| RI-mean | 0.7817 | – | 0.7310 | – | 0.6895 | – | – | – | 0.8021 | 0.8360 | |
| RI-std | 0.0001 | – | 0.0220 | – | 0.0012 | – | – | – | 0 | 5.90e–05 | |
| TI_T1_6 | NMI-mean | 0.2680 | – | 0.5087 | – | 0.5082 | – | – | – | 0.7398 | 0.7628 |
| NMI-std | 0.0050 | – | 0.0690 | – | 0.0055 | – | – | – | 1.35e-16 | 1.11e–16 | |
| RI-mean | 0.6872 | – | 0.6578 | – | 0.7943 | – | – | – | 0.9103 | 0.9168 | |
| RI-std | 0.0020 | – | 0.0888 | – | 0.0028 | – | – | – | 1.35e-16 | 1.35e–16 | |
| TI_T1_7 | NMI-mean | 0.2910 | – | 0.5769 | – | 0.4239 | – | – | – | 0.7227 | 0.7278 |
| NMI-std | 0.0080 | – | 0.0189 | – | 0.0014 | – | – | – | 7.85e-17 | 0 | |
| RI-mean | 0.7325 | – | 0.7347 | – | 0.7911 | – | – | – | 0.9085 | 0.9054 | |
| RI-std | 0.0033 | – | 0.0476 | – | 7.03e–04 | – | – | – | 0 | 0 | |
| TI_T1_8 | NMI-mean | 0.2038 | – | 0.5728 | – | 0.5190 | – | – | – | 0.6827 | 0.6914 |
| NMI-std | 0.0225 | – | 0.0329 | – | 0.0019 | – | – | – | 0.0005 | 1.11e–16 | |
| RI-mean | 0.7399 | – | 0.7941 | – | 0.8615 | – | – | – | 0.9010 | 0.9032 | |
| RI-std | 0.0059 | – | 0.0160 | – | 6.58e–04 | – | – | – | 0.0002 | 0 |
-
Transfer clustering using the same number of clusters but with inconsistent data distributions in the source and target domains:
Due to the existing noise interference, classic FCM did not obtain acceptable clustering effectiveness and segmentation results on any noisy images, e.g., TI_T 1_1, TI_T 1_2, TI_T 1_4, TI_T 2_1, and TI_T 2_2. Conversely, benefiting from the reference information across the source and target domains, all of the transfer clustering algorithms, i.e. STC, TSC, KL-TFCM-c, and KL-TFCM-f, obtain relatively good performance on TI_T 1_1 to TI_T 1_4 and TI_T 2_1 to TI_T 2_2, compared with the other non-transfer-clustering algorithms. This demonstrates the merit of transfer clustering in the practice of target texture image segmentation.
As far as the transfer clustering approaches are concerned, the clustering effectiveness as well as the segmentation performance of both KL-TFCM-c and KL-TFCM-f on real-world data are better than those of STC and TSC in all of the noisy data conditions, except on TI_T 1_3 (i.e. Fig. 4 (d)) where the data are never distorted by noise. KL-TFCM-c and KL-TFCM-f rank Nos. 2 and 3, respectively, and are only a little worse than STC. This distinctly reflects the superiority regarding our KL-PM and KL-PT based three stages of knowledge transfer, i.e. knowledge extraction, knowledge matching, and knowledge utilization. As such, regardless of the data distribution diversities in the source and target images, the knowledge from the source domain, i.e. the texture characteristics in TI_S 1 and TI_S 2 can be extensively, appropriately referenced by KL-TFCM-c/-f on the target domain images. This is consequently conducive for them to having insights into the ground truth of texture characteristics in these target images, even if these images were distorted by noise. That is, with the self-adaptive knowledge reference from the source domain, both KL-TFCM-c and KL-TFCM-f demonstrate excellent anti-noise properties.
Comparing KL-TFCM-c/-f with the multi-task and co-clustering algorithms: CombKM, LSSMTC, and DRCC, our KL-TFCM-c/-f algorithms are also superior on all target images due to their different mechanisms. More specifically, because of the existing noise interference as well as the potential data distribution diversities between the target and source domains, the raw data in the source domain could not directly provide valuable information to the target domain data. As evidence of this, CombKM and LSSMTC, two multi-task clustering methods directly utilizing the raw data in the source domain, were prone to encountering unexpectedly negative interactions between tasks instead of both gaining performance improvements. DRCC, one of pure co-clustering approaches, was devoted to constructing the manifold structures on both data instances and features, and then to simultaneously smoothing these two types of manifolds. However, DRCC generally did not achieve relatively satisfactory clustering and segmentation performance throughout all experiments, probably due to its sensitivity to our adopted strategy with respect to texture feature extraction. On the contrary, with the cluster prototypes rather than the raw data in the source domain acting as the reference in the target domain, both KL-TFCM-c and KL-TFCM-f exhibit more robust clustering effectiveness than do the other methods. This demonstrates the significance of our own work.
CKM was enlisted as the representative of semi-supervised clustering in our experiments, and SFCM of supervised clustering. To perform CKM, we randomly selected 100 labeled examples from the source domain and converted them into the pairwise constraints as the supervision. As for SFCM, all examples along with their labels in the source domain were used to train the parameterized distance measure for fuzzy clustering, and then we used this distance measure with the learned parameters to group the data in the target domain. However, as could be predicted, neither CKM nor SFCM worked well when facing such two domains having distinctly different data distributions. Due to the data inconsistency between the source and target domains, in CKM, many of the 100 selected examples from the source domain equaled essentially to outliers to the data in the target domain, which decreased the performance of CKM instead of facilitating clustering. In SFCM, likewise, because of the data inconsistency across two domains, the learned distance measure in the source domain became inapplicable in the target domains. This incurred the overall inefficiency of SFCM in nearly all of the transfer data scenes.
-
Transfer clustering when source and target domains have different numbers of clusters:
TI_T 1_5 to TI_T 1_8 (Fig. 4 (f)–(i)) and TI_T 2_3 to TI_T 2_6 (Fig. A1 (d)–(g)) were used to further verify the effectiveness and reliability of our approach for handling another type of data heterogeneity existing in transfer learning: differences in the numbers of clusters and in the data distributions between the source and target domains. In such cases, LSSMTC, CDRCC, SFCM, STC, and TSC, cannot be applied, as they strictly require the cluster number consistency between the source and target domains. In contrast, our proposed KL-TFCM-c and KL-TFCM-f approaches are applicable for such situations and, compared with classic FCM, CombKM, and CKM, both of them achieved quite considerable performance improvements. This indicates, again, that the proposed, three-stage-interlinked knowledge transfer framework in our research is effective at coping with the data inconsistency between the source and target domains, and accordingly facilitating the clustering of both KL-TFCM-c and KL-TFCM-f on target texture images.
When KL-TFCM-c and KL-TFCM-f are compared only with each other, their performance differences are evident which, how46 ever, is not notable in the cases of the first type of transfer clustering. Specifically, KL-TFCM-f generally features better clustering performance versus KL-TFCM-c on all of TI_T 1_5 to TI_T 1_8 and TI_T 2_3 to TI_T 2_6. This implies that, for generating the cluster representatives, ṼS = [ ṽ1,S, · · · , ṽCT,S]T, of the source domain in our work, the strategy of weighted sum, i.e. the so-called flexible form (see Eq. (10)), appears more efficient than the maximum matching strategy, namely, the crisp form (see Eq. (9)), when the numbers of clusters in the source and target domains are different.
All of these experimental results indicate that, our proposed, three-stage-based transfer clustering algorithms—KL-TFCM-c and KL-TFCM-f, generally feature better clustering and segmentation performance than many existing, popular clustering methods in both two types of texture image segmentation, i.e. one possesses the same cluster number but different data distributions in the source and target domains, while the other has inconsistent cluster numbers between the two domains. In addition, KL-TFCM-f appears more effective and reliable than KL-TFCM-c in the latter case.
5. Conclusions
Motivated by target texture image segmentation, we propose the three-stage-based transfer clustering framework as well as the two corresponding algorithms designated as KL-TFCMc and KL-TFCM-f. Two embedded, dedicated knowledge transfer mechanisms—KL-PT and KL-PM are simultaneously designed. KL-PT provides the way to flexibly learn the valuable knowledge even in the presence of noise in the source domain. KL-PM is devoted to mining the appropriate pairwise relationships of clustering prototypes between the source and target domains even if their numbers of clusters are different. Benefiting from the joint action of KL-PT and KL-PM, and via the three-stage-interlinked knowledge transfer, both KL-TFCM-c and KL-TFCM-f generally feature preferable clustering effectiveness and segmentation performance on almost all of the involved target texture images. As far as our KL-TFCM-c and KL-TFCM-f are concerned, due to the more flexible, efficient mechanism for generating the cluster representatives from the source domain, the latter performs better than the former in the case of different cluster numbers between the source and target domains.
In the future, two aspects of work are worth continuing. One is the more practical mechanism regarding parameter settings. The grid search strategy is now used in our work to determine the optimal values of parameters via two well-established validity indices: NMI and RI. Both of them are label-dependent [61]. From the viewpoint of practicability, a novel validity index independent of any label information will be perused in our future research. The other is the multiple source domains based knowledge transfer mechanism for fuzzy clustering which, in our opinion, is a very promising prospect.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grants 61572236 and 61673194, by Natural Science Foundation of Jiangsu Province under Grant BK20160187, by the R&D Frontier Grant of Jiangsu Province under Grant BY2013015-02, and by the Fundamental Research Funds for the Central Universities under Grants JUSRP51614A and JUSRP11737. Research reported in this publication was also supported by National Cancer Institute of the National Institutes of Health, USA, under award number R01CA196687. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health, USA.
In addition, we would like to thank Bonnie Hami, MA (USA) for her editorial assistance in the preparation of this manuscript.
Appendix
Table A1.
Performance comparisons of ten involved algorithms on TI_T 2_1 to TI_T 2_6.
| Data sets | Validity Metrics | FCM | LSSMTC | CombKM | DRCC | CKM | SFCM | STC | TSC | KL-TFCM-c | KL-TFCM-f |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TI_T2_1 | NMI-mean | 0.0670 | 0.1250 | 0.0491 | 0.1745 | 0.1572 | 0.1812 | 0.2593 | 0.2723 | 0.3444 | 0.3372 |
| NMI-std | 0.0033 | 0.0217 | 0.0020 | 0.0221 | 0.0056 | 0.0083 | 0.0213 | 0.0059 | 0.0062 | 0.0095 | |
| RI-mean | 0.7501 | 0.6545 | 0.5101 | 0.6901 | 0.7671 | 0.6898 | 0.7979 | 0.8000 | 0.8158 | 0.8111 | |
| RI-std | 0.0051 | 0.0108 | 0.0339 | 0.0045 | 0.0036 | 0.0125 | 0.0072 | 0.0023 | 0.0057 | 0.0090 | |
| TI_T2_2 | NMI-mean | 0.0217 | 0.0903 | 0.0330 | 0.1016 | 0.1190 | 0.1061 | 0.2077 | 0.2403 | 0.2804 | 0.2839 |
| NMI-std | 0.0011 | 0.0014 | 0.0037 | 0.0086 | 0.0152 | 0.0067 | 0.0073 | 0.0041 | 0.0227 | 0.0199 | |
| RI-mean | 0.7422 | 0.7015 | 0.5855 | 0.7147 | 0.7543 | 0.6831 | 0.7830 | 0.7845 | 0.7958 | 0.7984 | |
| RI-std | 0.0012 | 0.0059 | 0.0033 | 0.0134 | 0.0037 | 0.0178 | 0.0024 | 0.0082 | 0.0113 | 0.0087 | |
| TI_T2_3 | NMI-mean | 0.3207 | – | 0.4122 | – | 0.1201 | – | – | – | 0.4685 | 0.5036 |
| NMI-std | 0.0100 | – | 0.0008 | – | 0.0167 | – | – | – | 0.0002 | 0 | |
| RI-mean | 0.6977 | – | 0.7542 | – | 0.6042 | – | – | – | 0.7757 | 0.7886 | |
| RI-std | 0.0066 | – | 0.0006 | – | 0.0123 | – | – | – | 0.0001 | 0 | |
| TI_T2_4 | NMI-mean | 0.1005 | – | 0.3032 | – | 0.1355 | – | – | – | 0.3755 | 0.4179 |
| NMI-std | 0.0146 | – | 0.0023 | – | 0.0046 | – | – | – | 0.0173 | 0.0005 | |
| RI-mean | 0.6564 | – | 0.7104 | – | 0.6660 | – | – | – | 0.7448 | 0.7633 | |
| RI-std | 0.0063 | – | 0.0011 | – | 0.0019 | – | – | – | 0.0058 | 0.0001 | |
| TI_T2_5 | NMI-mean | 0.1249 | – | 0.2691 | – | 0.1597 | – | – | – | 0.3081 | 0.3465 |
| NMI-std | 0.0077 | – | 0.0124 | – | 0.0067 | – | – | – | 0.0449 | 0.0150 | |
| RI-mean | 0.7052 | – | 0.7378 | – | 0.7064 | – | – | – | 0.7587 | 0.7623 | |
| RI-std | 0.0049 | – | 0.0158 | – | 0.0089 | – | – | – | 0.0224 | 0.0082 | |
| TI_T2_6 | NMI-mean | 0.1727 | – | 0.3022 | – | 0.1846 | – | – | – | 0.3419 | 0.3851 |
| NMI-std | 0.0078 | – | 0.0131 | – | 0.0249 | – | – | – | 0.0216 | 0.0069 | |
| RI-mean | 0.7394 | – | 0.7677 | – | 0.7393 | – | – | – | 0.7877 | 0.7938 | |
| RI-std | 0.0069 | – | 0.0361 | – | 0.0052 | – | – | – | 0.0076 | 0.0008 |
Fig. A1.
Artificial scenario 2 for transfer clustering. (a) TI_S2: the image acting as the source domain; (b)–(c) TI_T2_1 to TI_T2_2: the target domain images owning the same cluster number as that in TI_S2, but different distributions; (d)–(g) TI_T2_3 to TI_T2_6: the target domain images whose cluster numbers are different from that of TI_S2.
Fig. A2.
Illustrations of ideal segmentation of employed texture images. (a) for TI_T2_1 and TI_T2_2; (b) for TI_T2_3; (c) for TI_T2_4; (d) for TI_T2_5; (e) for TI_T2_6.
Fig. A3.
Segmentation results of ten clustering approaches on target texture images TI_T2_1 to TI_T2_2.
Fig. A4.
Segmentation results of five clustering approaches on target texture images TI_T2_3 to TI_T2_6.
References
- 1.Zhu L, Chung FL, Wang ST. Generalized fuzzy C-means clustering algorithm with improved fuzzy partitions. IEEE Trans Syst, Man, Cybern, Part B. 2009;39(3):578–591. doi: 10.1109/TSMCB.2008.2004818. [DOI] [PubMed] [Google Scholar]
- 2.Jiang Y, Chung FL, Wang S. Enhanced fuzzy partitions vs data randomness in FCM. J Intell Fuzzy Syst. 2014;27(4):1639–1648. [Google Scholar]
- 3.Wang L, Pan C. Robust level set image segmentation via a local correntropy--based K-means clustering. Pattern Recognit. 2014;47(5):1917–1925. [Google Scholar]
- 4.Kim S, Yoo CD, Nowozin S, Kohli P. Image segmentation using higher-order correlation clustering. IEEE Trans Pattern Anal Mach Intell. 2014;6(9):1761–1774. doi: 10.1109/TPAMI.2014.2303095. [DOI] [PubMed] [Google Scholar]
- 5.Ji Z, Liu J, Cao G, Sun Q, Chen Q. Robust spatially constrained fuzzy c-means algorithm for brain MR image segmentation. Pattern Recognit. 2014;47(7):2454–2466. [Google Scholar]
- 6.Bezdek JC. Pattern Recognition With Fuzzy Objective Function Algorithms. Plenum Press; New York: 1981. [Google Scholar]
- 7.Havens TC, Bezdek JC, Leckie C, Hall LO, Palaniswami M. Fuzzy c-means algorithms for very large data. IEEE Trans Fuzzy Syst. 2012;20(6):1130–1146. [Google Scholar]
- 8.Wu J, Xiong H, Liu C, Chen J. A generalization of distance functions for fuzzy c-means clustering with centroids of arithmetic means. IEEE Trans Fuzzy Syst. 2012;20(3):557–571. [Google Scholar]
- 9.Ma J, Tian D, Gong M, Jiao L. Fuzzy clustering with non-local information for image segmentation. Int J Mach Learn Cybern. 2014;5(6):845–859. [Google Scholar]
- 10.Wang J, Wang S, Chung F, Deng Z. Fuzzy partition based soft subspace clustering and its applications in high dimensional data. Inform Sci. 2013;246:133–154. [Google Scholar]
- 11.Jiang Y, Chung FL, Wang S, Deng Z, Wang J, Qian P. Collaborative fuzzy clustering from multiple weighted views. IEEE Trans Cybern. 2015;45(4):688–701. doi: 10.1109/TCYB.2014.2334595. [DOI] [PubMed] [Google Scholar]
- 12.Huang HC, Chuang YY, Chen CS. Multiple kernel fuzzy clustering. IEEE Trans Fuzzy Syst. 2012;20(1):120–134. [Google Scholar]
- 13.Pedrycz W. Collaborative fuzzy clustering. Pattern Recognit Lett. 2002;23(14):1675–1686. [Google Scholar]
- 14.Pedrycz W. Fuzzy clustering with a knowledge-based guidance. Pattern Recognition Lett. 2004;25(4):469–480. [Google Scholar]
- 15.Chung FL, Wang ST, Deng ZH, Chen S, Hu DW. Clustering analysis of gene expression data based on semi-supervised visual clustering algorithm. Soft Comput. 2006;10(11):981–993. [Google Scholar]
- 16.Pan SJ, Yang Q. A survey on transfer learning. IEEE Trans Knowl Data Eng. 2010 Oct22(10):1345–1359. [Google Scholar]
- 17.Lu J, Behbood V, Hao P, Zuo H, Xue S, Zhang G. Transfer learning using computational intelligence: a survey. Knowl-Based Syst. 2015;80:14–23. [Google Scholar]
- 18.Tao JW, Chung F-L, Wang ST. On minimum distribution discrepancy support vector machine for domain adaptation. Pattern Recognit. 2012;45(11):3962–3984. [Google Scholar]
- 19.Sun Z, Chen YQ, Qi J, Liu JF. Adaptive localization through transfer learning in indoor Wi-Fi environment. Proceedings of 7th International Conference on Machine Learning and Applications; 2008. pp. 331–336. [Google Scholar]
- 20.Bickel S, Brückner M, Scheffer T. Discriminative learning for differing training and test distributions. Proceedings of 24th International Conference on Machine Learning; 2007. pp. 81–88. [Google Scholar]
- 21.Gao J, Fan W, Jiang J, Han J. Knowledge transfer via multiple model local structure mapping. Proceedings of 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2008. pp. 283–291. [Google Scholar]
- 22.Qian P, Jiang Y, Deng Z, Hu L, Sun S, Wang S, Muzic RF., Jr Cluster Prototypes and Fuzzy Memberships Jointly Leveraged Cross-Domain Maximum Entropy Clustering. IEEE Trans Cybern. 2016;46(1):181–193. doi: 10.1109/TCYB.2015.2399351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Deng ZH, Jiang YZ, Chung FL, Ishibuchi H, Wang ST. Knowledge-Leverage based fuzzy system and its modeling. IEEE Trans Fuzzy Syst. 2013;21(4):597–609. [Google Scholar]
- 24.Deng Z, Choi K-S, Jiang Y, Wang S. Generalized hidden-mapping ridge regression, knowledge-leveraged inductive transfer learning for neural networks, fuzzy systems and kernel methods. IEEE Trans Cybern. 2014;44(12):2585–2599. doi: 10.1109/TCYB.2014.2311014. [DOI] [PubMed] [Google Scholar]
- 25.Dong A, Chung F-L, Deng Z, Wang S. Semi-supervised SVM with extended hidden features. IEEE Trans Cybern. 2015 doi: 10.1109/TCYB.2015.2493161. [DOI] [PubMed] [Google Scholar]
- 26.Yang P, Tan Q, Ding Y. Bayesian task-level transfer learning for non-linear regression. Proceedings of International Conference on Computer Science and Software Engineering; 2008. pp. 62–65. [Google Scholar]
- 27.Mao W, Yan G, Bai J, Li H. Regression transfer learning based on principal curve. Lect Note Comput Sci. 2010;6063:365–372. [Google Scholar]
- 28.Deng Z, Jiang Y, Choi KS, Chung FL, Wang S. Knowledge-leveraged TSK fuzzy system modeling. IEEE Trans Neural Netw Learn Syst. 2013;24(8):1200–1212. doi: 10.1109/TNNLS.2013.2253617. [DOI] [PubMed] [Google Scholar]
- 29.Wang Z, Song YQ, Zhang CS. Transferred dimensionality reduction. Lect Notes Comput Sci. 2008;5212:550–565. [Google Scholar]
- 30.Pan SJ, Kwok JT, Yang Q. Transfer learning via dimensionality reduction. Proc AAAI’08. 2008;2:677–682. [Google Scholar]
- 31.Dai W, Yang Q, Xue G, Yu Y. Self-taught clustering. Proc 25th Int Conf Machine Learning. 2008:200–207. [Google Scholar]
- 32.Jiang WH, Chung FL. Machine Learning and Knowledge Discovery in Databases. Springer; Berlin Heidelberg: 2012. Transfer spectral clustering; pp. 789–803. [Google Scholar]
- 33.Liao X, Xue Y, Carin L. Logistic regression with an auxiliary data source. Proceedings of 21st Int’l Conference on Machine Learning; 2005. pp. 505–512. [Google Scholar]
- 34.Huang J, Smola A, Gretton A, Borgwardt KM, Schölkopf B. Correcting sample selection bias by unlabeled data. Proceedings of 19th Annual Conference on Neural Information Processing Systems; 2007. [Google Scholar]
- 35.Rosenstein MT, Marx Z, Kaelbling LP. To transfer or not to transfer. Proceedings of Conference on Neural Information Processing Systems (NIPS ’05) Workshop Inductive Transfer: 10 Years Later; 2005 Dec. [Google Scholar]
- 36.Raina R, Battle A, Lee H, Packer B, Ng AY. Self-taught learning: transfer learning from unlabeled data. Proceedings of 24th Int’l Conference on Machine Learning; 2007. pp. 759–766. [Google Scholar]
- 37.Jebara T. Multi-task feature and kernel selection for SVMs. Proceedings of 21st Int’l Conference on Machine Learning; 2004 July. [Google Scholar]
- 38.Mihalkova L, Huynh T, Mooney RJ. Mapping and revising Markov logic networks for transfer learning. Proceedings of 22nd Association for the Advancement of Artificial Intelligence (AAAI) Conference on Artificial Intelligence; 2007. pp. 608–614. [Google Scholar]
- 39.Evgeniou T, Pontil M. Regularized multi-task learning. Proceedings of the 10th ACM SIGKDD Int’l Conference on Knowledge Discovery and Data Mining; 2004. pp. 109–117. [Google Scholar]
- 40.Daumé H., III Frustratingly easy domain adaptation. Proceedings of the 45th Annual Meeting of the Associations for Computational Linguistics; 2007. pp. 256–263. [Google Scholar]
- 41.Ben-David S, Blitzer J, Crammer K, Pereira F. Analysis of representations for domain adaptation. Proceedings 20th Annual Conference on Neural Information Processing Systems; 2007. pp. 137–144. [Google Scholar]
- 42.Blitzer J, McDonald R, Pereira F. Domain adaptation with structural correspondence learning. Proceedings of Conference on Empirical Methods in Natural Language; 2006. pp. 120–128. [Google Scholar]
- 43.Miyamoto S, Ichihashi H, Honda K. Algorithms For Fuzzy Clustering. Springer; 2008. [Google Scholar]
- 44.Wang S, Chung KL, Deng Z, et al. Robust maximum entropy clustering with its labeling for outliers. Soft Compt. 2006;10(7):555–563. [Google Scholar]
- 45.Miyamoto S, Umayahara K. Fuzzy clustering by quadratic regularization. Proceedings of the 1998 IEEE International Conference on Fuzzy Systems and IEEE World Congress on Computational Intelligence; 1998. pp. 1394–1399. [Google Scholar]
- 46.Krishnapuram R, Keller M. A possibilistic approach to clustering. IEEE Trans Fuzzy Syst. 1993;1(2):98–110. [Google Scholar]
- 47.Deng Z, Jang Y, Chung F-L, Ishibuchi H, Choi K-S, Wang S. Transfer prototype-based fuzzy clustering. IEEE Trans Fuzzy Syst. 2016;24(5):1210–1232. [Google Scholar]
- 48.Deng Z, Choi KS, Chung FL, Wang S. Enhanced soft subspace clustering integrating within-cluster and between-cluster information. Pattern Recognit. 2010;43(3):767–781. [Google Scholar]
- 49.Gu QQ, Zhou J. Learning the shared subspace for multi-task clustering and transductive transfer classification. Proceedings of the 9th IEEE International Conference on Data Mining; 2009. pp. 159–168. [Google Scholar]
- 50.Zhang Z, Zhou J. Multi-task clustering via domain adaptation. Pattern Recognit. 2012;45(1):465–473. [Google Scholar]
- 51.Gu QQ, Zhou J. Co-clustering on manifolds. Proceedings of the 15th International Conference on KDD; 2009. pp. 359–368. [Google Scholar]
- 52.Dhillon IS, Mallela S, Modha DS. Information-theoretic co-clustering. Proceedings of the 9th ACM SIGKDD Int. Conf. on KDD’03; 2003. pp. 89–98. [Google Scholar]
- 53.Wagstaff K, Cardie C, Rogers S, Schrödl S. Constrained k-means clustering with background knowledge. Proceedings of the Eighteenth International Conference on Machine Learning; 2001. pp. 577–584. [Google Scholar]
- 54.Xing EP, Ng AY, Jordan M, Russell S. Advances in Neural Information Processing. Vol. 15. MIT Press; 2003. Distance metric learning, with application to clustering with side-information. [Google Scholar]
- 55.Klein D, Kamvar SD, Manning C. From instance-level constraints to space-level constraints: making the most prior knowledge in data clustering. Proc. ICML’02; Sydney, Australia. 2002. [Google Scholar]
- 56.Finley T, Joachims T. Supervised clustering with support vector machines. Proceedings of the Twenty-second International Conference on Machine Learning; 2005. pp. 217–224. [Google Scholar]
- 57.Finley T, Joachims T. Supervised k-means clustering. Cornell Computing and Information Science. 2008:1813–11621. [Google Scholar]
- 58.Abonyi J, Szeifert F. Supervised fuzzy clustering for the identification of fuzzy classifiers. Pattern Recognit Lett. 2003;24:2195–2207. [Google Scholar]
- 59.Randen T. Brodatz Texture. http://www.ux.uis.no/~tranden/brodatz.html.
- 60.Kyrki V, Kamarainen JK, Kalviainen H. Simple Gabor feature space for invariant object recognition. Pattern Recognit Lett. 2004;25(3):311–318. [Google Scholar]
- 61.Desgraupes B. Clustering Indices. University Paris Ouest, Lab Modal’X; 2013. [Google Scholar]