Abstract
BACKGROUND:
Routinely collected data from large population health surveys linked to chronic disease outcomes create an opportunity to develop more complex risk-prediction algorithms. We developed a predictive algorithm to estimate 5-year risk of incident cardiovascular disease in the community setting.
METHODS:
We derived the Cardiovascular Disease Population Risk Tool (CVDPoRT) using prospectively collected data from Ontario respondents of the Canadian Community Health Surveys, representing 98% of the Ontario population (survey years 2001 to 2007; follow-up from 2001 to 2012) linked to hospital admission and vital statistics databases. Predictors included body mass index, hypertension, diabetes, and multiple behavioural, demographic and general health risk factors. The primary outcome was the first major cardiovascular event resulting in hospital admission or death. Death from a noncardiovascular cause was considered a competing risk.
RESULTS:
We included 104 219 respondents aged 20 to 105 years. There were 3709 cardiovascular events and 818 478 person-years follow-up in the combined derivation and validation cohorts (5-year cumulative incidence function, men: 0.026, 95% confidence interval [CI] 0.025–0.028; women: 0.018, 95% 0.017–0.019). The final CVDPoRT algorithm contained 12 variables, was discriminating (men: C statistic 0.82, 95% CI 0.81–0.83; women: 0.86, 95% CI 0.85–0.87) and was well-calibrated in the overall population (5-year observed cumulative incidence function v. predicted risk, men: 0.28%; women: 0.38%) and in nearly all predefined policy-relevant subgroups (206 of 208 groups).
INTERPRETATION:
The CVDPoRT algorithm can accurately discriminate cardiovascular disease risk for a wide range of health profiles without the aid of clinical measures. Such algorithms hold potential to support precision medicine for individual or population uses. Study registration: ClinicalTrials.gov, no. NCT02267447
“Big data” has the potential to support personalized or precision medicine through more complex risk-prediction algorithms with more predictors.1–3 These data can be used to accurately assess disease risk across subgroups with distinct characteristics or health profiles — including situations where a health profile represents only a fraction of the overall population.
Furthermore, compared with more commonly used clinical data or epidemiology studies, large population health surveys have the potential to generate predictive algorithms that are more patient-oriented, have the potential to perform better across socioeconomic groups, and can be used for both population and clinical purposes.
First, population health surveys emphasize sociodemographic profile and health behaviours. These patient-oriented risks are common for multiple chronic diseases.4 Risks are all ascertained using self-response questions and validated for use in a broad community setting. This allows people to calculate their own risk in a nonclinical setting — reducing the burden on clinicians to collect and perform risk calculation. Second, algorithms developed using entire populations should be better calibrated (i.e., predictive risk closely approximating real or observed risk) and generalizable (i.e., better performing in a wide range of settings). As well, there are opportunities to recalibrate risk algorithms using population data that are not feasible with clinical data.5,6 Third, population-based algorithms can be more easily used for population planning. Examples of population uses include estimating the future incidence of cardiovascular disease events in populations and estimating the future burden of health behaviours (e.g., smoking, physical activity, alcohol and diet).7,8 A precision population health approach tailors preventive strategies for specific subgroups at risk.9,10 For example, subgroups with a low socioeconomic position typically have higher cardiovascular disease risk and may benefit from a wider range and more intensive interventions for effective prevention and health promotion.11–13
We developed and validated a prognostic cardiovascular disease risk algorithm — the Cardiovascular Disease Population Risk Tool (CVDPoRT) — using routinely collected data from population health surveys. The CVDPoRT has 2 potential uses: patient-oriented, individual cardiovascular disease risk assessment in the community setting, including assessment by patients or their clinicians; and population cardiovascular disease risk assessment for planning and research, including the evaluation of preventive strategies.9,10
Methods
Study design and participants
The CVDPoRT was derived and validated using population-based secondary data. There were 4 steps:
Model derivation — creation of the CVDPoRT risk algorithm using respondents to the combined Ontario sample of the 2001, 2003 and 2005 Canadian Community Health Surveys.
Model validation — validation of the CVDPoRT using the 2007 Canadian Community Health Survey.
Final model generation — combination of validation and derivation data to estimate the final application the CVDPoRT algorithm using the same model specification as the original derivation model.
Derivation of the application model — creation of a parsimonious model (fewer predictors) that maintains discriminative ability, calibration and overall model performance.
The protocol for development and validation of the CVDPoRT was registered and published (ClinicalTrials.gov, no. NCT02267447).14 We adhered to the protocol without deviation from the published analysis plan with 2 exceptions: only the 2007 Canadian Community Health Survey was used for validation (as opposed to both 2007 and 2009), and additional sensitivity testing and exploratory analyses were performed after algorithm development, as described in the “Statistical analysis” section. Here we report analyses of the primary study outcome described in the protocol.
Respondents were excluded if they were not eligible for Ontario’s universal health insurance program, were pregnant, self-reported a prior history of heart disease or stroke, or were younger than 20 years at the time of survey administration.
Data sources
Predictors were ascertained using self-responses from the Canadian Community Health Surveys. The Canadian Community Health Survey uses a multistage stratified cluster design that represents about 98% of the Canadian population over the age of 12 years and attains an average response rate of 80.5%.15
To ascertain cardiovascular disease events, we individually linked the survey respondents to 2 population-based databases: hospital-admission records from the Canadian Institute for Health Information Discharge Abstract Database, and deaths from the Office of the Registrar General of Ontario Vital Statistics Database. 16,17 All cardiovascular disease events and deaths were coded as International Statistical Classification of Diseases and Related Health Problems, 10th revision (ICD-10) codes (or ICD-9 codes for deaths before 2003 and hospital discharges before 2002).
Outcomes
The primary outcome of interest was 5-year incidence of a major cardiovascular disease event resulting in hospital admission or death from cardiovascular disease (diagnostic codes and criteria as presented in Appendix 1, available at www.cmaj.ca/lookup/suppl/doi:10.1503/cmaj.170914/-/DC1).16 Respondents were followed from the survey administration date until the earliest of the following: incident event, death due to causes other than cardiovascular disease (defined as a competing risk), loss to follow-up (defined as loss of health care eligibility) or end of study (Dec. 31, 2012).
Statistical analysis
We followed guidelines by Harrell18 and Steyerberg19 in the development of our analysis plan, which was constructed before any model fitting or any descriptive analyses involving the exposure–outcome associations. Key considerations in our approach were full prespecification of the predictor variables, use of flexible functions for continuous predictors, and preservation of statistical properties through avoidance of data-driven variable-selection procedures.
Table 1 shows the 21 predictor variables that were identified, including 7 sociodemographic, 8 behavioural,7,8,21 5 general health and chronic conditions, and 1 design variable.9,22 The model included interactions between age and smoking, alcohol, diet, physical activity, body mass index (BMI), diabetes and hypertension.
Table 1:
Predictor variables for the Cardiovascular Disease Population Risk Tool
| Variable | Scale | Initial variable specification* | Variable form, full model† | Variable form, reduced model‡ |
|---|---|---|---|---|
| Demographic | ||||
| Age | Continuous | 5 knot spline Valid range: 20–101 (women), 20–102 (men) |
Unchanged | Unchanged |
| Sex | Dichotomous | Stratified: female, male | NA | NA |
| Health behaviours | ||||
| Pack-years of smoking§ | Continuous | 3 knot spline Valid range: 0–79 (women), 0–109 (men) |
Unchanged | Unchanged |
| Smoking status§ | Categorical | 4 categories:
|
Unchanged | Unchanged |
| Alcohol (no. of drinks in the past wk)§ | Continuous | 3 knot spline Valid range: 0–26 (women), 0–53 (men) |
Linear (women), 3 knot spline (men) | Unchanged |
| Former drinker§ | Dichotomous | Yes/no | Unchanged | Excluded (men) |
| Fruits and vegetables (average daily consumption)§ | Continuous | 3 knot spline Valid range: 0–13 (women), 0–12 (men) |
Unchanged | Unchanged |
| Potato (average daily consumption)§ | Continuous | 3 knot spline Valid range: 0–2 Linear (women), 3 knot spline (men) |
Excluded (women) | |
| Juice (average daily consumption)§ | Continuous | 3 knot spline Valid range: 0–5 (women), 0–6 (men) |
Linear | Excluded (women) |
| Leisure physical activity (metabolic equivalent of task [MET], kcal/kg/d)§ | Continuous | 3 knot spline Valid range: 0–11 (women), 0–13 (men) |
3 knot spline (women), linear (men) | Excluded (men) |
| General health | ||||
| Self-perceived stress | Ordinal | 5 categories:
|
2 categories
|
Excluded |
| Sense of belonging to local community | Ordinal | 4 categories:
|
4 categories (women), linear (men) | Excluded |
| Sociodemographic | ||||
| Ethnicity | Categorical | 7 categories:
|
2 categories:
|
Excluded |
| Immigrant | Dichotomous | Yes/no | Unchanged | Excluded |
| % of lifetime in Canada | Continuous | 3 knot spline 0–100 |
Linear | Excluded |
| Education | Categorical | 4 categories:
|
Unchanged | Unchanged |
| Neighbourhood social and material deprivation (Pampalon’s deprivation index20) | Ordinal | 3 categories:
|
Linear | Excluded |
| Chronic conditions | ||||
| Diabetes§ | Dichotomous | Yes/no | Unchanged | Unchanged |
| High blood pressure§ | Dichotomous | Yes/no | Unchanged | Unchanged |
| Body mass index§ | Continuous | 3 knot spline 10–48 (women), 9–44 (men) |
Unchanged | Unchanged |
| Design | ||||
| Survey year | Ordinal | 4 categories 2001, 2003, 2005, 2007 |
Unchanged | Unchanged |
Note: df = degrees of freedom.
df = 61.
df = 48 for women; df = 47 for men.
df = 36 for women; df = 37 for men.
Age interaction included.
Data cleaning, model specification and model estimation are presented in Appendix 2, available at www.cmaj.ca/lookup/suppl/doi:10.1503/cmaj.170914/-/DC1. Models were estimated using a proportional hazards model for the subdistribution of a competing risk, with death from a noncardiovascular disease cause considered as a competing risk.23
Performance in the derivation and validation cohorts was assessed using measures of discrimination (ability to differentiate between individuals with high and low risk), and calibration (agreement between predicted and observed risk).9,24–26 Subgroups were examined using predefined criteria for clinically or policy relevant standards of calibration (< 20% difference between observed and predicted estimates for categories with prevalence higher than 5%).7,9
The CVDPoRT differs from existing cardiovascular disease algorithms in its use of the competing risk approach. To facilitate algorithm comparison and to examine the role of competing risks for cardiovascular disease prediction, we conducted sensitivity analyses in which we used a standard Cox model, but otherwise maintained all predictor specifications.
We used the step-down procedure described by Ambler and colleagues27 to identify a parsimonious model for applications where parsimony may be more important than accuracy. This procedure involves deleting variables to a desired degree of accuracy based on contribution to model R2.
Ethics approval
The use of data in this project was authorized under section 45 of Ontario’s Personal Health Information Protection Act, which does not require review by a research ethics board.
Results
Participants
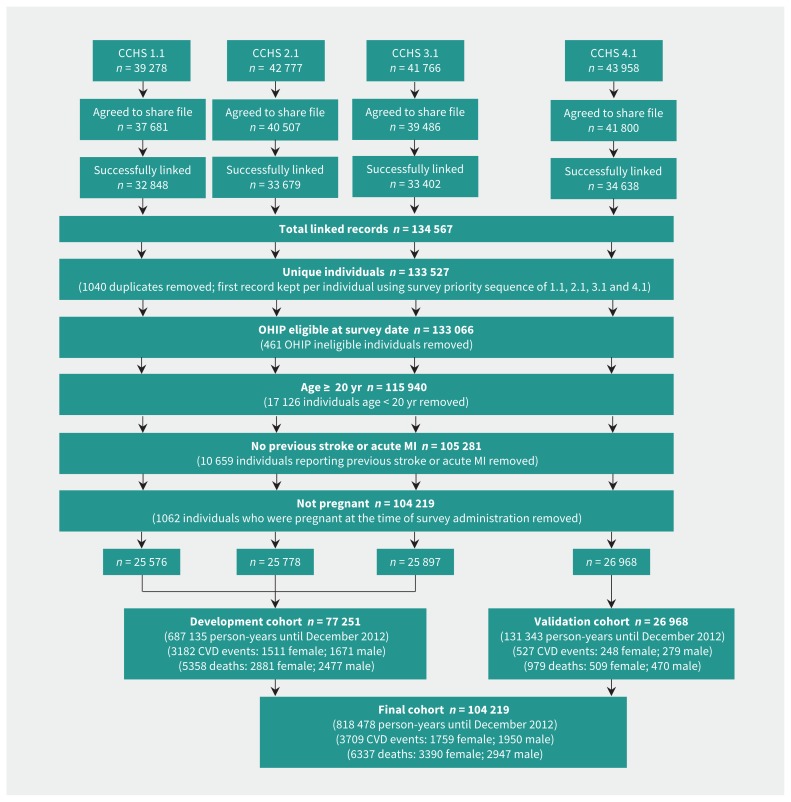
The combined derivation and validation cohort consisted of 104 219 respondents, 818 478 person-years follow-up, with 3709 cardiovascular disease events until Dec. 31, 2012. The number of noncardiovascular disease deaths (events from competing risk) in the combined cohort was 2947 for men and 3390 for women (Figure 1). Pack-years of smoking had the most missing data (2.5% of the study population), with other health behaviours having less than 1% missing data (Table 2). A total of 2.7% of participants were lost to follow-up; 1.2% of participants were lost to follow-up in the validation data set.
Figure 1:
Study flow diagram showing Canadian Community Health Survey (CCHS) cohorts linked for the Cardiovascular Disease Population Risk Tool. CVD = cardiovascular disease, MI = myocardial infarction, OHIP = Ontario Health Insurance Plan.
Table 2:
Population characteristics of all predictors that were prespecified and included in the model
| Characteristic | Median (IQR) or no. (%) | |||
|---|---|---|---|---|
|
| ||||
| Female cohort | Male cohort | |||
|
|
|
|||
| Derivation n = 42 185 (377 635 person-years) |
Validation n = 14 801 (72 317 person-years) |
Derivation n = 35 066 (309 500 person-years) |
Validation n = 12 167 (59 026 person-years) |
|
| Age, yr | 48.0 (35.0–63.0) | 51.0 (37.0–64.0) | 46.0 (35.0–59.0) | 49.0 (36.0–62.0) |
|
| ||||
| Smoking | ||||
|
| ||||
| Current | 9533 (22.6) | 2884 (19.5) | 9409 (26.8) | 2935 (24.1) |
|
| ||||
| Pack-years | 15.5 (7.0–28.5) | 16.2 (3.5–28.9) | 18.8 (8.5–34.0) | 18.8 (8.2–36.0) |
|
| ||||
| Former smoker < 5 yr ago | 2947 (7.0) | 916 (6.2) | 2933 (8.4) | 921 (7.6) |
|
| ||||
| Pack-years | 11.9 (3.9–27.8) | 10.9 (3.5–29.9) | 17.9 (6.0–36.0) | 15.0 (4.6–35.0) |
|
| ||||
| Former smoker ≥ 5 yr ago | 7928 (18.8) | 3059 (20.7) | 8750 (25.0) | 3270 (26.9) |
|
| ||||
| Pack-years | 6.5 (1.0–18.5) | 7.2 (1.7–19.5) | 12.0 (2.5–27.0) | 13.0 (3.8–28) |
|
| ||||
| Nonsmoker | 15 843 (37.6) | 6019 (40.7) | 8724 (24.9) | 3235 (26.6) |
|
| ||||
| Missing | 5934 (14.1) | 1923 (13.0) | 5250 (15.0) | 1806 (14.8) |
|
| ||||
| Alcohol | ||||
|
| ||||
| Current drinker | 33 063 (78.4) | 11 693 (79.0) | 30 178 (86.1) | 10 466 (86.0) |
|
| ||||
| No. of drinks in the previous week | 1 (0–4) | 1 (0–4) | 3 (0–9) | 4 (0–10) |
|
| ||||
| Former drinker | 6217 (14.7) | –* | 3642 (10.4) | –* |
|
| ||||
| Nondrinker | 2839 (6.7) | 3090 (20.9) | 1188 (3.4) | 1679 (13.8) |
|
| ||||
| Missing | 66 (0.2) | 18 (0.1) | 58 (0.2) | 22 (0.2) |
|
| ||||
| Diet | ||||
|
| ||||
| Fruit and vegetables, servings/d | 3.4 (2.3–5.0) | 3.7 (2.4–5.3) | 2.6 (1.7–3.8) | 2.7 (1.7–4.1) |
|
| ||||
| Potato consumption, servings/d | 0.3 (0.1–0.6) | 0.3 (0.1–0.4) | 0.3 (0.1–0.6) | 0.3 (0.1–0.6) |
|
| ||||
| Juice consumption, servings/d | 1.0 (0.1–1.0) | 0.4 (0.1–1.0) | 1.0 (0.3–1.0) | 1.0 (0.1–1.0) |
|
| ||||
| Physical activity | ||||
|
| ||||
| Energy expenditure, kcal/kg/d | 1.3 (0.5–2.7) | 1.4 (0.5–2.7) | 1.6 (0.6–3.1) | 1.6 (0.6–3.1) |
|
| ||||
| Body mass index | 24.7 (21.8–28.1) | 24.9 (22.1–28.9) | 26.2 (23.9–28.9) | 26.4 (24.1–29.3) |
|
| ||||
| Self-perceived stress | ||||
|
| ||||
| Not at all/not very | 14 769 (35.0) | 5340 (36.1) | 13 082 (37.3) | 4787 (39.3) |
|
| ||||
| A bit | 17 286 (41) | 6292 (42.5) | 14 276 (40.7) | 4983 (41.0) |
|
| ||||
| Quite a bit/extremely | 10 072 (23.9) | 3098 (20.9) | 7645 (21.8) | 2352 (19.3) |
|
| ||||
| Missing | 58 (0.1) | 71 (0.5) | 63 (0.2) | 45 (0.4) |
|
| ||||
| Sense of belonging | ||||
|
| ||||
| Very strong/somewhat strong | 27 552 (65.3) | 10 118 (68.4) | 21 768 (62.1) | 7977 (65.6) |
|
| ||||
| Somewhat weak/very weak | 13 850 (32.8) | 4373 (29.5) | 11 981 (34.2) | 3848 (31.6) |
|
| ||||
| Missing | 783 (1.9) | 310 (2.1) | 1317 (3.8) | 342 (2.8) |
|
| ||||
| Ethnicity | ||||
|
| ||||
| White | 38 089 (90.3) | 12 894 (87.1) | 31 369 (89.5) | 10 577 (86.9) |
|
| ||||
| Black | 519 (1.2) | 280 (1.9) | 432 (1.2) | 206 (1.7) |
|
| ||||
| Chinese | 590 (1.4) | 229 (1.5) | 570 (1.6) | 217 (1.8) |
|
| ||||
| Aboriginal | 685 (1.6) | 432 (2.9) | 516 (1.5) | 348 (2.9) |
|
| ||||
| South Asian, Arab, West Asian | 867 (2.1) | 440 (3.0) | 901 (2.6) | 411 (3.4) |
|
| ||||
| Japanese, Korean, Southeast Asian, Filipino | 503 (1.2) | 206 (1.4) | 423 (1.2) | 166 (1.4) |
|
| ||||
| Other, multiple origin, unknown, Latin American | 854 (2.0) | 218 (1.5) | 788 (2.2) | 166 (1.4) |
|
| ||||
| Missing | 78 (0.2) | 102 (0.7) | 67 (0.2) | 76 (0.6) |
|
| ||||
| Immigration status | ||||
|
| ||||
| Immigrant | 8544 (20.3) | 3163 (21.4) | 7153 (20.4) | 2594 (21.3) |
|
| ||||
| Fraction of life lived in Canada | 0.60 (0.36–0.73) | 0.60 (0.36–0.73) | 0.59 (0.35–0.74) | 0.60 (0.38–0.75) |
|
| ||||
| Nonimmigrant | 33 591 (79.6) | 11 618 (78.5) | 27 868 (79.5) | 9565 (78.6) |
|
| ||||
| Missing | 50 (0.1) | 20 (0.1) | 45(0.1) | 8 (0.1) |
|
| ||||
| Education | ||||
|
| ||||
| Less than secondary school graduation | 8330 (19.7) | 2388 (16.1) | 6486 (18.5) | 1966 (16.1) |
|
| ||||
| Secondary school graduation | 8754 (20.8) | 2749 (18.6) | 6567 (18.7) | 2048 (16.8) |
|
| ||||
| Some postsecondary education | 3099 (7.3) | 935 (6.3) | 2587 (7.4) | 897 (7.4) |
|
| ||||
| Postsecondary graduation | 21 711 (51.5) | 8658 (58.5) | 19 079 (54.4) | 7204 (59.2) |
|
| ||||
| Missing | 291 (0.7) | 71 (0.5) | 347 (1.0) | 52 (0.4) |
|
| ||||
| Neighbourhood deprivation | ||||
|
| ||||
| Low | 8189 (19.4) | 2658 (18.0) | 7255 (20.7) | 2285 (18.8) |
|
| ||||
| Moderate | 26 229 (62.2) | 9231 (62.3) | 21 760 (62.1) | 7664 (63.0) |
|
| ||||
| High | 6890 (16.3) | 2471 (16.7) | 5313 (15.2) | 1900 (15.6) |
|
| ||||
| Missing | 877 (2.1) | 441 (3.0) | 738 (2.1) | 318 (2.6) |
|
| ||||
| Diabetes status | ||||
|
| ||||
| Yes diabetes | 2159 (5.1) | 949 (6.4) | 2041 (5.8) | 952 (7.8) |
|
| ||||
| No diabetes | 40 004 (94.8) | 13 846 (93.5) | 33 004 (94.1) | 11 201 (92.1) |
|
| ||||
| Missing | 22 (0.1) | 6 (0.04) | 21 (0.1) | 14 (0.1) |
|
| ||||
| Hypertension status | ||||
|
| ||||
| Yes hypertension | 8089 (19.2) | 3344 (22.5) | 5659 (16.1) | 2471 (20.3) |
|
| ||||
| No hypertension | 34 060 (80.7) | 11 435 (77.3) | 29 333 (83.7) | 9643 (79.3) |
|
| ||||
| Missing | 36 (0.1) | 22 (0.1) | 74 (0.2) | 53 (0.4) |
|
| ||||
| Survey cycle | ||||
|
| ||||
| 1 | 13 932 (33.0) | – | 11 644 (33.2) | – |
|
| ||||
| 2 | 14 093 (33.4) | – | 11 685 (33.3) | – |
|
| ||||
| 3 | 14 160 (33.6) | – | 11 737 (33.5) | – |
Note: IQR = interquartile range.
Former drinkers and nondrinkers were combined in 1 category in Canadian Community Health Survey 2007/08.
Model specification and development
The predictors, along with their initial and final degrees of freedom are shown in Table 1. Partial correlation plots are presented in Appendix 3, available at www.cmaj.ca/lookup/suppl/doi:10.1503/cmaj.170914/-/DC1.
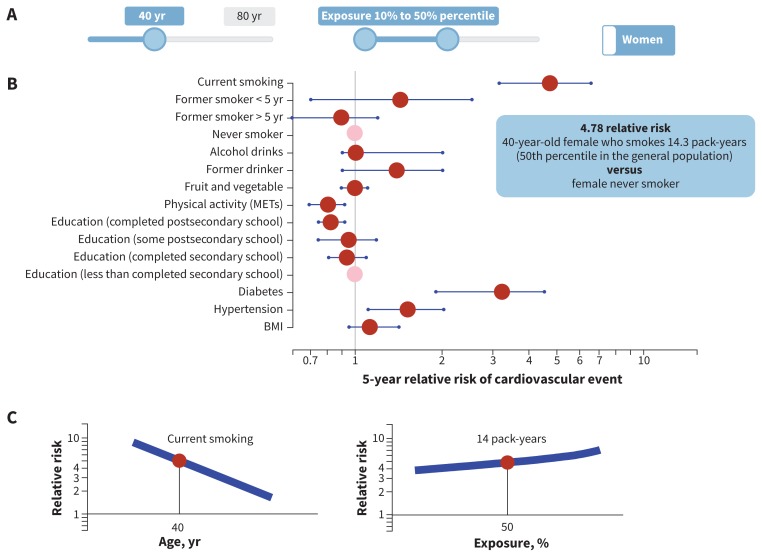
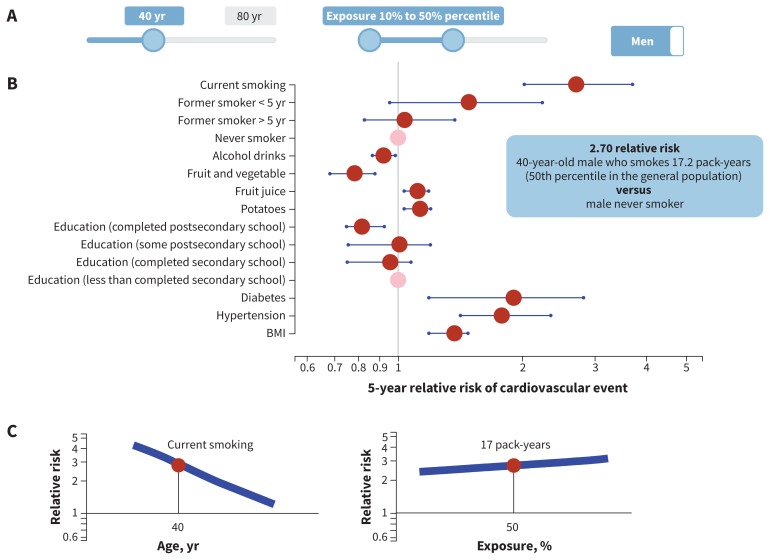
The female and male full models had 48 degrees of freedom and 47 degrees of freedom, respectively, with 20 predictors (10 continuous) and 13 interaction terms (Table 1). The final (reduced) model for females had 36 degrees of freedom with 12 predictors (6 continuous) and 9 interaction terms; the model for males had 37 degrees of freedom with 12 predictors (7 continuous) and 9 interaction terms (Table 1). The complete model specifications, estimated coefficients and the survey questionnaire are available in Appendices 4 and 5, available at www.cmaj.ca/lookup/suppl/doi:10.1503/cmaj.170914/-/DC1, and at https://github.com/Ottawa-mHealth/predictive-algorithms. Figures 2 and 3 show the predicted risk for median exposure compared with a reference for each predictor for females and males. An interactive relative risk plot is available at www.projectbiglife.ca, and shows the influence of age and exposure–outcome relations.
Figure 2:
Relative risk by median risk exposure for 40-year-old women. A) The sliders reflect age (range 20–80 yr), exposure level for each risk (range 10th–90th percentile, reflecting percentile exposure level in the total population) and sex-specific algorithm (male, female). B) Point estimate (red dot) and 95% confidence interval (blue line) of 5-year relative risk of cardiovascular event by exposure variable. Reference group for continuous variables = lower number from the exposure slider (10th percentile in this example), with the exception of smoking, where reference group = nonsmoker. Reference group for categorical variables = pink dot. C) Visualization for impact of age interaction and exposure level on relative risk for selected exposure: y-axis = relative risk, x-axis = age or percentile exposure. In this example, selected exposure = current smoker, age = 40, percentile exposure for pack-years = 50th. Blue line represents range of relative risk by age or percentile of exposure. See www.projectbiglife.ca for an interactive version of this figure. BMI = body mass index, MET = metabolic equivalent of task.
Figure 3:
Relative risk by median risk exposure for 40-year-old men. A) The sliders reflect age (range 20–80 yr), exposure level for each risk (range 10th–90th percentile, reflecting percentile exposure level in the total population) and sex-specific algorithm (male, female). B) Point estimate (red dot) and 95% confidence interval (blue line) of 5-year relative risk of cardiovascular event by exposure variable. Reference group for continuous variables = lower number from exposure slider (10th percentile in this example), with the exception of smoking, where reference group = nonsmoker. Reference group for categorical variables = pink dot. C) Visualization for impact of age interaction and exposure level on relative risk for selected exposure: y-axis = relative risk, x-axis = age or percentile exposure. In this example, selected exposure = current smoker, age = 40, percentile exposure for pack-years = 50th. Blue line represents range of relative risk by age or percentile of exposure. See www.projectbiglife.ca for an interactive version of this figure. BMI = body mass index.
Model performance
Table 3 presents summary indicators of model performance. The model showed good ability to correctly rank order (discriminate) people with different risk levels (women: C statistic 0.86, 95% confidence interval [CI] 0.85–0.87; men: 0.82, 95% CI 0.81–0.83). Discrimination remained stable across development, validation and pooled data. Predictive risk closely approximated observed risk (calibration slope for women: 0.9734, SE 0.0698; for men: 0.9295, SE 0.0731) (Appendix 8, available at www.cmaj.ca/lookup/suppl/doi:10.1503/cmaj.170914/-/DC1).
Table 3:
Summary statistics showing goodness of fit for the Cardiovascular Disease Population Risk Tool in the initial development model, the validation model, the final model derived from the combined data and the parsimonious model after applying the step-down procedure*
| Variable | Development | Validation | Combined | Reduced |
|---|---|---|---|---|
| Male model | ||||
| Discrimination | ||||
| C-statistic (95% CI) | 0.82 (0.81–0.83) | 0.79 (0.76–0.81) | 0.82 (0.81–0.83) | 0.82 (0.81–0.83) |
| Ratio of 95 to 5 risk percentile | 298.2 (0.0963/0.0003) | 468.7 (0.0770/0.0002) | 345.3 (0.0914/0.0003) | 337.8 (0.0913/0.0003) |
| Calibration | ||||
| Observed v. predicted, % | 0.08 | 1.38 | 0.28 | 0.28 |
| 5-year cumulative incidence (observed) (95% CI) | 0.027 (0.026–0.029) | 0.023 (0.020–0.025) | 0.026 (0.025–0.028) | 0.026 (0.025–0.028) |
| 5-year risk (predicted) | 0.027 | 0.022 | 0.026 | 0.026 |
| Overall performance | ||||
| Brierscaled score | 0.025 | 0.022 | 0.024 | 0.024 |
| Nagelkerke R2 | 0.096 | 0.086 | 0.089 | 0.089 |
| Female model | ||||
| Discrimination | ||||
| C–statistic (95% CI) | 0.87 (0.86–0.88) | 0.85 (0.83–0.87) | 0.86 (0.85–0.87) | 0.86 (0.85–0.87) |
| Ratio of 95 to 5 risk percentile | 645.0 (0.0811/0.0001) | 810.5 (0.0709/0.0001) | 482.3 (0.0794/0.0002) | 477.5 (0.0794/0.0002) |
| Calibration | ||||
| Observed v. predicted, % | 0.30 | 7.13 | 0.39 | 0.38 |
| 5-year cumulative incidence (observed) (95% CI) | 0.018 (0.017–0.019) | 0.017 (0.015–0.019) | 0.018 (0.017–0.019) | 0.018 (0.017–0.019) |
| 5-year risk (predicted) | 0.018 | 0.016 | 0.018 | 0.018 |
| Overall performance | ||||
| Brierscaled score | 0.017 | 0.016 | 0.017 | 0.017 |
| Nagelkerke R2 | 0.124 | 0.126 | 0.117 | 0.117 |
Note: CI = confidence interval
Three types of performance tests were examined:28 1) Discrimination is the ability of a prediction model to differentiate between those who do and do not develop the outcome of interest. C-statistic is a rank order statistic for predictions against true outcomes.18,29 The statistic ranges from 0 to 1: a value of 0.5 indicates the model is no better than random prediction, a value of 1 indicates the model perfectly predicts those who will develop the outcome of interest and those who will not. Ratio of 95 to 5 risk percentiles is a test of discrimination. A higher ratio indicates a more discriminating algorithm. For example, a ratio of 100 indicates that the absolute risk is 100 times higher for a person in the 95th percentile than for a person in the 5th percentile. The ratio can be used to gauge the potential absolute benefit of treatment for different individuals in the development and validation cohorts. For an intervention with the same relative benefit, a risk ratio of 100 indicates that 1 person will have 100 times the absolute benefit of the comparative person. 2) Calibration reflects agreement between the observed outcomes and predictions. Calibration (or accuracy) describes how well the predicted probability of disease agrees with the observed outcome. Observed versus predicted (O v. P) is the relative difference between the observed incidence and predicted risk. A 1% difference in O v. P indicates 1% more cardiovascular events were observed than predicted. This table shows overall O v. P. Appendices 6 and 7, available at www.cmaj.ca/lookup/suppl/doi:10.1503/cmaj.170914/-/DC1, show O v. P for specific subgroups. This table presents an absolute measure of O v. P as the observed 5-year cumulative incidence and the predicted 5-year risk. A graphical assessment of calibration is presented in Appendix 8, available at www.cmaj.ca/lookup/suppl/doi:10.1503/cmaj.170914/-/DC1 (calibration plots). 3) Overall performance measures. Brierscaled score is a measure of overall agreement between observed and predictive risk with values between 0 and 1.30 This scaled Brier score happens to be very similar to the Pearson R2 statistic.31 Nagelkerke R2 is a measure of amount the model explains the variation of risk between respondents in the development or validation data with values from 0 to 1.32,33 Larger R2 values indicate that more of the variation is explained by the model, to a maximum of 1.
There was close agreement between predicted and observed numbers of cardiovascular disease events within the overall population (5-year observed cumulative incidence function v. predicted risk in men: 0.28%; in women: 0.38%) (Table 3). Among men, the algorithm was well-calibrated in 110 of 111 predefined policy-relevant subgroups, with observed versus predicted risk being greater than the predefined difference of 20% only for people with no leisure time physical activity (0 metabolic equivalents of task [METs]) (Appendix 7, available at www.cmaj.ca/lookup/suppl/doi:10.1503/cmaj.170914/-/DC1). Among women, the algorithm was well-calibrated in 96 of 97 predefined policy-relevant subgroups, with observed versus predicted risk being greater than the predefined difference of 20% only for the lowest level of sense of belonging (Appendix 6, available at www.cmaj.ca/lookup/suppl/doi:10.1503/cmaj.170914/-/DC1).
A sensitivity analysis, in which algorithms were generated using a Cox proportional hazards model without competing risks, found slightly improved calibration in several subgroups, particularly those at higher risk deciles and for people older than age 70 years, but differences did not reach significance and the models had similar discrimination (men: C statistic 0.84 v. 0.82; women: 0.87 v. 0.86) (Appendix 9, available at www.cmaj.ca/lookup/suppl/doi:10.1503/cmaj.170914/-/DC1).
Interpretation
The CVDPoRT was developed and validated using large population health surveys that are routinely collected and contain only self-reported risk factors. The CVDPoRT has a high discrimination and shows good calibration in a wide range of sociodemographic groups — including education, ethnicity, immigration status, area deprivation and social cohesion — despite omission of risk factors such as lipid levels and measured blood pressure. We attribute the favourable performance of the CVDPoRT to greater model specification and complexity compared with other commonly used cardiovascular disease risk algorithms.
The algorithm was developed for population and individual uses. For population uses, health surveys (which are available in more than 100 countries) can be used to predict the number of people who will develop cardiovascular disease.7,9 How risk varies across populations — whether risk is diffused or concentrated — is a cornerstone of modern population planning.34 Multivariable predictive algorithms are the most robust approach to describe population risk, and their use improves the assessment of population strategies. 10 Although the World Health Organization and others currently measure burden of disease without including an equity perspective, 35 the inclusion of sociodemographic factors in the CVDPoRT allows a straightforward assessment of cardiovascular disease risk, burden and intervention effectiveness by socioeconomic status.7,8
For individual use, the CVDPoRT’s discrimination is exceeded only by QRISK3 — an algorithm that was also developed using “big” data; however, QRISK3 used clinical data that focused on clinical measures (lipids, blood pressure and disease states).36,37 Clinicians and patients appear to favour health behaviour interventions over medications for patients at low and medium risk,38 but existing cardiovascular risk algorithms seldom assess the role of health behaviours beyond smoking.2,39 This means that clinicians have difficulty communicating the degree to which health behaviours contribute to cardiovascular risk, as well as the potential benefit from behavioural interventions.40,41 The CVDPoRT allows patients to assess their risk outside the clinic setting with only self-reported measures — with predictive accuracy that is better than that assessed using the algorithms currently recommended in Canada for the clinical setting.42 Complex algorithms with many predictors are not necessarily more burdensome to patients — rather the opposite if, for example, calculations can be performed with partial responses using adaptive questionnaires (see the CVDPoRT online calculator at www.projectbiglife.ca). The CVDPoRT predictors are centred, which allows patients to calculate their cardiovascular disease risk as each question is answered with unbiased calculations. The concept of assessing risk incrementally as more information is available is a central concept to clinical decision-making, and facilitated when algorithms are derived using big data, but has not yet been widely adopted in chronic disease predictive algorithms.43,44 Personalized risk communication follows personalized risk assessment with a range of cardiovascular disease risk measures such as heart age.45 See Box 1 for an example of CVDPoRT for individual use.
Box 1: Example of the Cardiovascular Disease Population Risk Tool for individual use*.
45-year-old woman
Health behaviours
Smoker with 20 pack-years
Never drinker
Diet: 3 fruits and vegetables (average daily consumption)
Physical activity unknown
Sociodemographic
Some postsecondary education
Chronic conditions
No diabetes
No high blood pressure
Body mass index 26
5-year cardiovascular disease risk 0.8%
Heart age 51 years†
40 000 additional examples are available at https://github.com/Ottawa-mHealth/predictive-algorithms.
See Appendix 2 (available at www.cmaj.ca/lookup/suppl/doi:10.1503/cmaj.170914/-/DC1) for calculation of heart age.
The use of large, routinely collected population health surveys provides 2 perspectives that are relevant for precision medicine. First, large databases provide sufficient statistical power to develop and validate predictive algorithms with a larger set of risk factors and greater specification of those risks, which in turn generate distinct risk estimates for a wide range of health profiles or populations.
Second, the high discriminating ability of the CVDPoRT suggests that sociodemographic factors and health behaviours have an important role in precision medicine. For example, although smoking is included in most clinical cardiovascular disease risk algorithms, it is typically considered as a categorical measure (i.e., current, former or never smoker). This is despite the fact that smoking is the most important cardiovascular disease risk factor, there is a clear continuous dose–response relationship, there is clear attenuation of risk with age, and there are clear recommendations that continuous measures should not be categorized in predictive algorithms.41,46,47
A concern with complex algorithms is the lack of improved discrimination in the overall population when predictors are added beyond 4 or 5 basic exposures.48,49 In precision medicine there is less emphasis on the overall population and more on the value of prediction “within” individuals (clinical uses) or subgroups (population uses).50–53 We emphasized calibration across subgroups as a measure of the CVDPoRT’s value for precision medicine.53,54 Commonly, calibration is assessed across deciles of predictive risk. Large data allowed us to assess CVDPoRT calibration for more than 200 predefined, policy-relevant subgroups.
The CVDPoRT maintained very good calibration (191 of 205 subgroups) and was developed with few missing follow-up data, but we recommend recalibration of the CVDPoRT for most new settings. Fortunately, population-based data and health surveys provide opportunities to assess and recalibrate risk algorithms that are not available in the clinical setting.7,55 Surveys that are similar to the Canadian Community Health Survey are available in many countries worldwide. Increasingly, these surveys are being linked to health outcomes, enabling calibration assessment and, if required, recalibration. Additionally, unlinked cardiovascular disease events are even more available worldwide; these events can be compared with predicted cardiovascular disease events — calculated using the CVDPoRT and local population health surveys — to enable recalibration to the local population.5 The need for recalibration would not indicate that the CVDPoRT has poor predictive accuracy; rather, it would signal that factors beyond those included in the CVDPoRT are influencing baseline risk in the new population. Recalibration adjusts for these factors — conserving the purpose of the CVDPoRT to discriminate risk based on health behaviours (smoking, alcohol, diet and exercise).
Cardiovascular disease has predictors that span sociodemographic (e.g., ethnicity, social position, immigrant status), environmental (e.g., air pollution), distal (e.g., health behaviours), proximal (e.g., BMI, hypertension, lipids and other diseases) and genetic risks. To our knowledge, previous cardiovascular disease algorithms have not considered the full range of predictors or, more specifically, have not considered discriminating and well-calibrated risk prediction for people exposed to those predictors. In the example of CVDPoRT and QRISK3 algorithms, there are several important differences in the predictors used, which suggests that a combined algorithm that considers the range of predictors and interactions from both algorithms could be even more discriminating and well-suited for precision medicine in clinical and population settings. Clearly, such an algorithm would require large data, suggesting there is a role for linking larger clinical and population data to provide a wider range of predictors that can be assessed.2 That stated, it may be overly challenging to see improved discrimination beyond that shown in our study or QRISK studies, and calibration may not improve for subpopulations. In our study, we found that a more parsimonious CVDPoRT algorithm has essentially the same predictive ability as our fully prespecified algorithm.
Limitations
A potential limitation is misclassification error resulting from use of self-reported predictors and routinely collected outcomes. Although more accurate risk factor ascertainment could improve discrimination and calibration, the CVDPoRT already has a high discrimination and favourable calibration. Other studies have also found that chronic diseases can be accurately assessed using self-reports, with only modest classification differences when cardiovascular risk assessment is performed with and without clinical and laboratory measures.56,57
Conclusion
The CVDPoRT discriminately assesses cardiovascular disease risk using information that focuses on sociodemographic and behavioural risks. For the clinical setting, the CVDPoRT can be completed by individuals in the community, without assistance of a clinician or use of clinical measures (e.g., cholesterol and blood pressure), to help inform subsequent clinical decisions. In the population setting, the CVDPoRT can assess cardiovascular disease risk using population health surveys that are available in many countries and settings.
Acknowledgements
The authors thank Anan Bader Eddeen for analysis support; Mahsa Jessri for scientific advice regarding diet measures; Yulric Sequeira for developing the online web calculator, visualization tools and application programming interface; and Robert Talarico for assistance with integrating the online tool with the Cardiovascular Disease Population Risk Tool algorithm.
Footnotes
Competing interests: None declared.
This article has been peer reviewed.
Contributors: Douglas Manuel conceived the study and developed the design in consultation with the other authors. Meltem Tuna completed the analysis. All authors contributed to interpretation of the data. Douglas Manuel drafted the manuscript, and all authors contributed substantially to its revision. All authors (with the exception of Jack Tu) approved the final version to be published and agreed to be accountable for all aspects of the work.
Funding: Funding for this study was provided by the Canadian Institutes of Health Research (grant TCA 118349). Jack Tu held a Tier 1 Canada Research Council Chair in Health Services Research. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.
Data sharing: Data were linked using unique encoded identifiers and analyzed at the Institute for Clinical Evaluative Sciences (ICES). The data set from this study is held securely in coded form at ICES. Although data-sharing agreements prohibit ICES from making the data set publicly available, access may be granted to those who meet prespecified criteria for confidential access, available at www.ices.on.ca/DAS.
Resources to implement, validate and redevelop CVDPoRT are available at https://github.com/Ottawa-mHealth/predictive-algorithms. These files include the algorithm specified in Predictive Modelling Markup Language, validation data, bootstraps file of 500 predictor coefficients to calculate model uncertainty and other resources.
Disclaimer: This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long-Term Care (MOHLTC). The opinions, results and conclusions reported in this paper are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred.
References
- 1.Collins GS, Reitsma JB, Altman DG, et al. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD statement. BMJ 2015;350:g7594. [DOI] [PubMed] [Google Scholar]
- 2.Damen JAAG, Hooft L, Schuit E, et al. Prediction models for cardiovascular disease risk in the general population: systematic review. BMJ 2016;353:i2416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rumsfeld JS, Joynt KE, Maddox TM. Big data analytics to improve cardiovascular care: promise and challenges. Nat Rev Cardiol 2016;13:350–9. [DOI] [PubMed] [Google Scholar]
- 4.Salvador-Carulla L, Cloninger CR, Thornicroft A, et al. 2013 Geneva Declaration Consultation Group. Background, structure and priorities of the 2013 Geneva Declaration on Person-centered Health Research. Int J Pers Cent Med 2013;3: 109–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hajifathalian K, Ueda P, Lu Y, et al. A novel risk score to predict cardiovascular disease risk in national populations (Globorisk): a pooled analysis of prospective cohorts and health examination surveys. Lancet Diabetes Endocrinol 2015; 3:339–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Masconi KL, Matsha TE, Erasmus RT, et al. Recalibration in validation studies of diabetes risk prediction models: a systematic review. Int J Stat Med Res 2015;4:347–69. [Google Scholar]
- 7.Manuel DG, Perez R, Sanmartin C, et al. Measuring burden of unhealthy behaviours using a multivariable predictive approach: life expectancy lost in Canada attributable to smoking, alcohol, physical inactivity, and diet. PLoS Med 2016;13:e1002082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Manuel DG, Perez R, Bennett C, et al. Seven more years: the impact of smoking, alcohol, diet, physical activity and stress on health and life expectancy in Ontario. Toronto: Institute for Clinical Evaluative Sciences and Public Health Ontario; 2012. [Google Scholar]
- 9.Manuel DG, Rosella LC, Hennessy D, et al. Predictive risk algorithms in a population setting: an overview. J Epidemiol Community Health 2012;66:859–65. [DOI] [PubMed] [Google Scholar]
- 10.Manuel DG, Lim J, Tanuseputro P, et al. Revisiting Rose: strategies for reducing coronary heart disease. BMJ 2006;332:659–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Manuel DG, Rosella LC. Commentary: assessing population (baseline) risk is a cornerstone of population health planning — looking forward to address new challenges. Int J Epidemiol 2010;39:380–2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tugwell P, de Savigny D, Hawker G, et al. Applying clinical epidemiological methods to health equity: the equity effectiveness loop. BMJ 2006;332:358–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Murdoch TB, Detsky AS. The inevitable application of big data to health care. JAMA 2013;309:1351–2. [DOI] [PubMed] [Google Scholar]
- 14.Taljaard M, Tuna M, Bennett C, et al. Cardiovascular Disease Population Risk Tool (CVDPoRT): predictive algorithm for assessing CVD risk in the community setting. A study protocol. BMJ Open 2014;4:e006701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Béland Y. Canadian community health survey — methodological overview. Health Rep 2002;13:9–14. [PubMed] [Google Scholar]
- 16.Kennedy CC, Brien SE, Tu JV. An overview of the methods and data used in the CCORT Canadian Cardiovascular Atlas project. Can J Cardiol 2003;19:655–63. [PubMed] [Google Scholar]
- 17.Tu JV, Chu A, Donovan LR, et al. The Cardiovascular Health in Ambulatory Care Research Team (CANHEART): using big data to measure and improve cardiovascular health and healthcare services. Circ Cardiovasc Qual Outcomes 2015;8:204–12. [DOI] [PubMed] [Google Scholar]
- 18.Harrell FE., Jr Regression modeling strategies: with applications to linear models, logistic regression and survival analysis. New York: Springer-Verlag New York; 2001:1–568. [Google Scholar]
- 19.Steyerberg EW. Clinical prediction models: a practical approach to development, validation, and updating. London (UK): Springer; 2009. [Google Scholar]
- 20.Pampalon R, Hamel D, Gamache P, et al. A deprivation index for health planning in Canada. Chronic Dis Can 2009;29:178–91. [PubMed] [Google Scholar]
- 21.Manuel DG, Perez R, Bennett C, et al. A $4.9 billion decrease in health care expenditure: the ten-year impact of improving smoking, alcohol, diet and physical activity in Ontario. Toronto: Institute for Clinical Evaluative Sciences; 2016. [Google Scholar]
- 22.Rosella LC, Manuel DG, Burchill C, et al. PHIAT-DM team. A population-based risk algorithm for the development of diabetes: development and validation of the Diabetes Population Risk Tool (DPoRT). J Epidemiol Community Health 2011;65:613–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fine JP, Gray RJ. A proportional hazards model for the subdistribution of a competing risk. J Am Stat Assoc 1999;94:496–509. [Google Scholar]
- 24.Cook NR. Statistical evaluation of prognostic versus diagnostic models: beyond the ROC curve. Clin Chem 2008;54:17–23. [DOI] [PubMed] [Google Scholar]
- 25.Cook NR. Methods for evaluating novel biomarkers — a new paradigm. Int J Clin Pract 2010;64:1723–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ganna A, Ingelsson E. 5-year mortality predictors in 498 103 UK Biobank participants: a prospective population-based study. Lancet 2015;386:533–40. [DOI] [PubMed] [Google Scholar]
- 27.Ambler G, Brady AR, Royston P. Simplifying a prognostic model: a simulation study based on clinical data. Stat Med 2002;21:3803–22. [DOI] [PubMed] [Google Scholar]
- 28.Moons KG, Altman DG, Reitsma JB, et al. Transparent Reporting of a multivariable prediction model for Individual Prognosis or Diagnosis (TRIPOD): explanation and elaboration. Ann Intern Med 2015;162:W1–73. [DOI] [PubMed] [Google Scholar]
- 29.Harrell F. Hmisc Package. Nashville (TN): Department of Biostatistics, Vanderbilt University; 2018. Available: http://biostat.mc.vanderbilt.edu/wiki/Main/Hmisc (accessed 2018 May 28). [Google Scholar]
- 30.Rufibach K. Use of Brier score to assess binary predictions. J Clin Epidemiol 2010;63:938–9. [DOI] [PubMed] [Google Scholar]
- 31.Hu B, Palta M, Shao J. Properties of R(2) statistics for logistic regression. Stat Med 2006;25:1383–95. [DOI] [PubMed] [Google Scholar]
- 32.Nagelkerke NJ. A note on a general definition of the coefficient of determination. Biometrika 1991;78:691–2. [Google Scholar]
- 33.Royston P. Explained variation for survival models. Stata J 2006;6:83–96. [Google Scholar]
- 34.Rose G. The strategy of preventive medicine. Oxford (UK): Oxford University Press; 1992:xii + 135 p. [Google Scholar]
- 35.Lim SS, Vos T, Flaxman AD, et al. A comparative risk assessment of burden of disease and injury attributable to 67 risk factors and risk factor clusters in 21 regions, 1990–2010: a systematic analysis for the Global Burden of Disease Study 2010. Lancet 2012;380:2224–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Siontis GC, Tzoulaki I, Siontis KC, et al. Comparisons of established risk prediction models for cardiovascular disease: systematic review. BMJ 2012;344: e3318. [DOI] [PubMed] [Google Scholar]
- 37.Hippisley-Cox J, Coupland C, Brindle P. Development and validation of QRISK3 risk prediction algorithms to estimate future risk of cardiovascular disease: prospective cohort study. BMJ 2017;357:j2099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Schulte JM, Rothaus CS, Adler JN. Starting statins — polling results. N Engl J Med 2014;371:e6. [DOI] [PubMed] [Google Scholar]
- 39.Hippisley-Cox J, Coupland C, Vinogradova Y, et al. Predicting cardiovascular risk in England and Wales: prospective derivation and validation of QRISK2. BMJ 2008;336:1475–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mons U, Müezzinler A, Gellert C, et al. CHANCES Consortium. Impact of smoking and smoking cessation on cardiovascular events and mortality among older adults: meta-analysis of individual participant data from prospective cohort studies of the CHANCES consortium. BMJ 2015;350:h1551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Patnode CD, Evans CV, Senger CA, et al. Behavioral counseling to promote a healthful diet and physical activity for cardiovascular disease prevention in adults without known cardiovascular disease risk factors: updated evidence report and systematic review for the us preventive services task force. JAMA 2017;318:175–93. [DOI] [PubMed] [Google Scholar]
- 42.Anderson TJ, Grégoire J, Pearson GJ, et al. 2016 Canadian Cardiovascular Society guidelines for the management of dyslipidemia for the prevention of cardiovascular disease in the adult. Can J Cardiol 2016;32:1263–82. [DOI] [PubMed] [Google Scholar]
- 43.Sackett DL, Haynes RB, Guyatt GH, et al. Clinical epidemiology: a basic science for clinical medicine. Toronto: Little, Brown and Company; 1991: 1–441. [Google Scholar]
- 44.Weed LL. Physicians of the future. N Engl Med 1981;304:903–7. [DOI] [PubMed] [Google Scholar]
- 45.Ng E, Sanmartin C, Manuel DG. Hospitalization rates among economic immigrants to Canada. Health Rep 2017;28:3–10. [PubMed] [Google Scholar]
- 46.The health consequences of smoking — 50 years of progress: a report of the surgeon general. Washington (DC): U.S. Department of Health and Human Services; 2014. [Google Scholar]
- 47.Altman DG, Royston P. The cost of dichotomising continuous variables. BMJ 2006;332:1080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lloyd-Jones DM. Cardiovascular risk prediction: basic concepts, current status, and future directions. Circulation 2010;121:1768–77. [DOI] [PubMed] [Google Scholar]
- 49.Austin PC, Pencinca MJ, Steyerberg EW. Predictive accuracy of novel risk factors and markers: a simulation study of the sensitivity of different performance measures for the Cox proportional hazards regression model. Stat Methods Med Res 2017;26:1053–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pepe MS, Janes H. Reporting standards are needed for evaluations of risk reclassification. Int J Epidemiol 2011;40:1106–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kerr KF, Bansal A, Pepe MS. Further insight into the incremental value of new markers: the interpretation of performance measures and the importance of clinical context. Am J Epidemiol 2012;176:482–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bansal A, Pepe MS. When does combining markers improve classification performance and what are implications for practice? Stat Med 2013;32:1877–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kerr KF, Wang Z, Janes H, et al. Net reclassification indices for evaluating risk-prediction instruments: a critical review. Epidemiology 2014;25:114–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Janes H, Pepe MS, Bossuyt PM, et al. Measuring the performance of markers for guiding treatment decisions. Ann Intern Med 2011;154:253–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ueda P, Woodward M, Lu Y, et al. Laboratory-based and office-based risk scores and charts to predict 10-year risk of cardiovascular disease in 182 countries: a pooled analysis of prospective cohorts and health surveys. Lancet Diabetes Endocrinol 2017;5:196–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Ning F, Zhang L, Dekker JM, et al. DECODE Finnish and Swedish Study Investigators. Development of coronary heart disease and ischemic stroke in relation to fasting and 2-hour plasma glucose levels in the normal range. Cardiovasc Diabetol 2012;11:76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Gaziano TA. Know your risk: But how? Indian J Med Res 2008;128:221–4. [PubMed] [Google Scholar]