The Globe’s Eccentric Rotational Axis: Why Medial Rectus Surgery is More Potent Than Lateral Rectus Surgery

Abstract

Purpose

Tables typically recommend greater lateral rectus (LR) than medial rectus (MR) surgical doses for horizontal strabismus of any given magnitude, a difference unexplained by mechanical models that assume globe rotation about its center. We tested this assumption during horizontal ductions.

Design

Prospective observational study.

Participants

Eighteen adult subjects with normal binocular vision.

Methods

Surface coil magnetic resonance imaging at 390 or 430 μm resolution was obtained using 2 mm thick contiguous axial planes while subjects fixated targets in central, right, and left gaze. Angular displacements of lines connecting the corneal apex through the minor lens axis to the retina were measured to approximate clinical ductions. Globe centers were calculated from their area centroids. Apparent lens and globe-ON junction rotations around the globe center were then compared with clinical ductions.

Main outcome measures

Apparent angular rotations of lenses and globe-ON junctions during horizontal ductions.

Results

Globe-ON junctions appeared to rotate significantly less around globe centers than did lenses for abduction (20.6±4.7° versus 27.4±7.4°, p<0.001) and adduction (25.3±6.7° versus 31.9±8.3°, p<0.001). Both rotations differed significantly from clinical adduction (27.9±8.3°, p <0.007), but only in abduction was globe-ON junction rotation significantly less than clinical abduction (28.6±9.4°, p<0.001). The true geometric globe rotational center was 2.2±0.5 mm medial and 0.8±1.0 mm posterior to geometric globe center and was displaced farther medially and posteriorly during adduction. This eccentricity imbues each mm of MR recession with approximately 30% more trigonometric rotational effect than equivalent LR recession.

Conclusion

The medial and posterior eccentricity of the normal ocular rotational axis profoundly influences horizontal rectus action. The proximity of the globe’s rotational axis to the MR shortens its lever arm relative to the LR, explaining why mechanical effects of smaller MR recessions are equivalent to larger LR recessions.

Both simple^1–3 and complex^4–8 models of the biomechanical effects of extraocular muscle (EOM) action assume that the globe rotates about its geometric center. With this assumption, mechanical factors that determine idealized globe rotation in response to applied force are limited to the lever arm of each EOM insertion with respect to globe center^{2, 9}, the pulling direction of the EOM relative to its pulley^{6, 7, 10–16}, and the tangency of the EOM insertion to the globe¹⁷.

The eye is not, however, an isolated sphere of uniform density rotating in a frictionless environment. Instead, it is a non-uniform structure constrained by and attached to orbital tissues. The sclera and cornea vary in thickness from anterior to posterior¹⁸, while the lens, ciliary body, and vitreous body all have slightly different viscosities and densities¹⁹. In addition, while the four rectus EOMs have a relatively balanced distribution of insertions, the superior oblique and inferior oblique insertions are asymmetrically placed relative to the globe’s geometric center^{5, 20}. Finally, in the posterior orbit, the globe-optic nerve (ON) junction is asymmetrically medial to the globe’s geometric center.

Any eccentricity of the globe’s axis of rotation changes the lever arm for each EOM and thus their respective torques even at identical EOM tensions, introducing a potentially important biomechanical nuance to the contributions of each EOM to duction. Analogous to the larger and smaller gears on a bicycle, displacements in EOM insertions along the globe surface closer to the rotational axis would rotate the globe more degrees per mm, while displacements of EOM insertions along the globe surface farther from the rotational axis would have less angular effect.

If the globe rotates about its geometric center, all structures on the globe surface should appear to move the same number of degrees of arc with respect to the globe center. For this study, we compared the apparent angular rotation of the lens with that of the globe-ON junction during abduction and adduction to determine if the globe does indeed rotate about its geometric center.

Methods

Subjects

Eighteen adult volunteers (average age 59±12 years; 5 males, 13 females) were prospectively recruited through advertising for this study. Each subject consented in writing to a protocol conforming to the tenets of the Declaration of Helsinki that was approved by the University of California, Los Angeles Institutional Review Board. Every subject was evaluated with a comprehensive eye examination to verify normal motility, normal binocular alignment, and normal corrected vision.

Magnetic Resonance Imaging (MRI)

Using a 1.5-T General Electric Signa scanner (Milwaukee, WI) enhanced with a dual-phased surface coil array (Medical Advances, Milwaukee, WI), high resolution T2 fast spin echo axial MRI was performed²¹ as subjects fixated a fiber optic target in central gaze and various right and left gaze positions. Images were obtained in contiguous 2-mm slices over a 10-cm or 11-cm field of view, yielding 390- or 430-μm in plane resolution.

Analysis

Digital MRI images for each gaze position were converted into image stacks and quantified with the ImageJ program (W. Rasband, National Institutes of Health, Bethesda, Maryland). For each gaze position, the rotation of midline structures of the face away from scanner vertical was measured to vertically align the midline for all gaze positions (Fig. 1). To measure duction, the angular displacement from scanner vertical of a line from the apex of the cornea through the minor axis of lens to the retina was measured for each gaze position; the change in angle of that line in the various gaze positions approximated clinical measurements of duction.

Fig. 1.

T2 weighted axial magnetic resonance image of a normal subject in central gaze. Dashed white lines from the retina through the minor axis of the lens and corneal apex approximate the visual axes. The angular change in the dashed lines between gaze positions was used to measure clinical duction.

Then, the geometric globe center was measured by manually outlining the largest globe cross-section that did not include cornea and using the “Area Centroid” function of ImageJ to define the center of that globe cross-section with sub-pixel resolution. Similarly, the largest cross-section of the lens and the breadth of the attachment of the ON onto the globe were manually outlined (Fig. 2) and the “Area Centroid” function was used to define the centers of the lens and globe-ON junction, respectively.

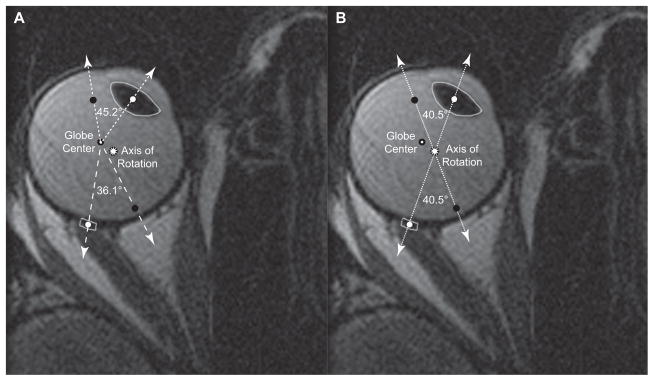
Fig. 2.

Two copies of the same axial magnetic resonance image of a normal right eye in adduction, but differently labeled according to rotational axis location. White dots represent centers of the lens and the globe-optic nerve (ON) junction in this gaze position, while black dots represent where the centers of the lens and the globe-ON junction were in central gaze. A. When adduction is assumed about globe center, the lens appears to rotate more (45.2°) than the globe-ON junction (36.1°), implying that the ocular rotational axis must be eccentric. B. The true axis of rotation, defined by the intersection of the lines between the lens center and globe-ON junction center in the different gaze positions, was offset medially more than 2 mm and posteriorly almost 1 mm from the geometric globe center. By definition, both lens and globe-ON junction rotated the same angle (40.5°) around the true rotational axis.

Once the globe center, lens center, and globe-ON junction were defined for each gaze position, geometry using the globe center as the common origin allowed calculation of the apparent angular rotation of the lens and globe-ON junction for each gaze position. Paired t-tests were then used to compare rotations of the lens and globe-ON junction with each other and with clinical ductions.

Results

Recruitment was halted after 18 subjects because there were no meaningful changes to the results after the tenth subject. Each subject completed imaging in five positions of gaze: central gaze, smaller and larger angles of right gaze, and smaller and larger angles of left gaze. Globe axial length averaged 24.5±1.2 mm. Table 1 summarizes the average clinical ductions and apparent lens and globe-ON junction rotations for the different gaze positions if oculocentric rotation is assumed. Overall, globe-ON junctions appeared to rotate significantly less around geometric globe centers than did the lenses in abduction (20.6±4.7° versus 27.4±7.4°, p<0.001) and adduction (25.3±6.7° versus 31.9±8.3°, p<0.001). Both rotations differed significantly from clinical adduction (27.9±8.3°, p<0.007 for both), but only the globe-ON junction rotation appeared significantly less than clinical abduction (28.6± 9.4°, p<0.001).

Table 1.

Apparent Angular Rotation Around Ocular Geometric Center

	Clinical Duction	Lens Rotation	Globe-ON Rotation
Larger Abduction	31.3 ± 8.7°	31.0 ± 6.9°	23.6 ± 3.4°
Smaller Abduction	25.8 ± 9.4°	23.7 ± 6.2°	17.6 ± 3.8
Smaller Adduction	25.4 ± 8.5°	28.3 ± 6.8°	22.4 ± 6.9°
Larger Adduction	30.5 ± 7.3°	35.5 ± 8.3°	28.1 ± 5.1°

For each gaze position, the globe-optic nerve (ON) junction rotated significantly less around the globe’s geometric center than did the lens (p < 10⁻⁶ for all comparisons, mean ± standard deviation).

The foregoing differences imply that the globe does not rotate about its geometric center, but about a different rotational center for which computed rotations for every part of the eye are indeed equal. The intersection of lines connecting the lens center and globe-ON junction in central gaze and in eccentric gaze occurred at the true globe rotational center and represent the point about which the lens and globe-ON junction appeared to have equal rotational change (Fig. 2). Table 2 summarizes the average displacements of the true globe rotational axis from geometric globe center for each of the different gaze positons studied. Overall, globe rotational axis was eccentric by 2.2±0.5 mm medial and 0.8±1.0 mm posterior to geometric globe center during horizontal gaze changes and was displaced farther medially and posteriorly during adduction than abduction. There was minimal correlation between the magnitude of the eccentricity of the axis of rotation and axial length.

Table 2.

Eccentricity of Ocular Rotation Axis from Geometric Center Medial Posterior

	Medial	Posterior
Larger Abduction	+2.0 ± 0.5 mm	−0.3 ± 0.8 mm
Smaller Abduction	+2.1 ± 0.6 mm	−0.6 ± 1.1 mm
Smaller Adduction	+2.3 ± 0.4 mm	−1.2 ± 1.0 mm
Larger Adduction	+2.3 ± 0.3 mm	−1.2 ± 0.8 mm

mean ± standard deviation

Greater proximity of the globe’s rotational axis to the medial rectus (MR) insertion than the lateral rectus (LR) insertion implies a shorter lever arm for the MR than the LR. Thus, each mm of movement of the MR insertion in its arc along the globe surface generates a greater angular effect than a corresponding mm of movement of the LR insertion. Table 3 summarizes the predicted differences in globe rotation for 1 to 6 mm of surgical recession for the MR versus the LR, assuming a 24 mm diameter globe and typical EOM insertion locations⁵. The eccentric location of the globe’s rotational axis imbues each mm of MR recession with more than 30% greater rotational effect than the equivalent LR recession.

Table 3.

Predicted Globe Rotation after Surgical Recession

Recession (mm)	MR Globe Rotation (°)	LR Globe Rotation (°)	MR v LR % Effect
1.0	5.3	4.0	132%
2.0	5.3	4.0	132%
3.0	5.4	4.0	134%
4.0	5.5	4.0	136%
5.0	5.6	4.0	138%
6.0	5.6	4.0	138%

This table assumes that the globe rotates by an angle determined by the arc change on the ocular surface produced by the recession. Because the medial rectus (MR) insertion is closer to the eccentric rotational axis, each mm change in MR position rotates a 24-mm diameter globe more than 5°, compared with only 4° for each mm change in lateral rectus (LR) position. The differential effect increases because with larger recessions the MR insertion approaches the globe’s axis of rotation, further shortening its lever arm.

Discussion

The commonly held assumption that the globe rotates about its geometric center must be discarded because this study demonstrates the ocular rotational axis to be consistently and highly significantly eccentric in all 18 orthotropic subjects examined. This eccentricity was about 2 mm medial and 1 mm posterior to geometric globe center, a functionally important displacement relative to the average 12 mm globe radius.

One obvious suspect as a structural cause for the medial eccentricity of the ocular rotational axis might be the asymmetric medial insertion of the ON. MRI has demonstrated that the ON tethers the globe during large adduction, exerting substantial active posterior and medial traction onto the globe-ON junction when the redundancy of ON length has been exhausted ^{22, 23}. This traction is sufficient to retract the globe and has been argued as a potential cause of ON atrophy in patients with normal tension glaucoma²². However, globe translation during gaze changes^{12, 22} would not affect the present determination of ocular rotational axis because the geometric center of the globe in each image set was defined as the origin for all calculations, eliminating the effects of translation.

Until now, the basis for lower surgical dosages advocated for the MR versus the LR^{5, 24} to accomplish the same change in horizontal binocular alignment has been poorly understood. Explanations based on differences in EOM length-tension curves caused by the different lengths of the EOMs in central gaze fail to account for the fact that EOM “length” is entirely dependent on gaze position; the EOM lengthens during contralateral duction and shortens during ipsilateral duction. Although this study was not designed to assess EOM lengths, in a prior study careful MRI measurements have revealed remarkable similarities in the lengths of all of the rectus EOMs in the contracted (MR length 37.6±1.5 mm, LR length 37.9±2.1 mm) and relaxed (MR length 45.8±1.6 mm, LR length 46.0±1.9 mm) states²⁵. With nearly identical relaxed and contracted lengths²⁵, the length-tension curves of the MR and LR should be quite similar, so that explanation fails to account for the difference in surgical dosing.

On the other hand, MRI analysis has demonstrated a much greater change in MR volume during contraction and relaxation than was found for the LR²⁵, strong evidence that, for an identical horizontal change in gaze, the MR exerts greater contractile force²⁶. Since the final resting positon of the globe after a change of gaze depends on the balance of all oculorotary forces, this finding implies that a smaller change in LR force completely balances a larger change in MR force. Biomechanically, the only way these asymmetric contractile forces could balance is if the LR has a greater mechanical advantage provided by a longer oculorotary lever arm than does the MR. This is precisely the situation that results from medial eccentricity of the ocular rotational axis. Thus, each mm change in the arc of the LR insertion on the globe surface rotates a 24 mm diameter globe 4° around the globe’s eccentric rotational axis, compared with more than 5° per mm for a similar change in position of the MR insertion (Table 3).

Moreover, the identical argument can be extended to the effect of resection, where larger surgical doses are also required for LR than MR. Another way of viewing the significance of this phenomenon is to consider its implications for a recess-resect operation in the same eye, where it may be assumed that the post-operative MR and LR tensions each remain about the same as pre-operatively. In the case of recess-resect, the eccentric rotational axis implies an approximately 30% stronger surgical effect on the MR, simultaneous with a 30% weaker effect on the LR, than would be the case for the traditional oculocentric rotational assumption. Since eye position is determined by the difference in forces between agonist and antagonist muscles, the effect of eccentric rotational axis on binocular alignment is about 60%!

The foregoing semi-quantitative analysis, which of course assumes appropriate balance of MR and LR tensions such that the entire change in ocular rotation is accomplished by this maneuver, provides a simple mechanical explanation for the necessity of larger surgical dosages for the LR than the MR to create the same change in horizontal binocular alignment. Of course, as is the case for all EOM surgery, other mechanical and biological factors ultimately contribute to final binocular alignment. Nevertheless, the biomechanical effect of eccentric rotational axis has profound implications for computational modeling of binocular alignment. While no prior computer model of strabismus considers this effect, it must be included in realistic future efforts. Being now recognized for horizontal ductions, the concept of eccentric ocular rotational axis could in future studies be explored other rotational directions. More detailed characterization of the three-dimensional location of the globe’s rotational axis could include quasi-sagittal imaging during vertical gaze changes to permit calculation of the vertical position of the axis relative to the globe’s geometric center.

In conclusion, MRI provides compelling evidence that the normal eye does not rotate around its geometric center. Instead, the axis of rotation is medially and posteriorly eccentric, and displaces farther medially and posteriorly with increasing adduction. This shift may be related to the ON insertion, although other factors influencing eccentricity deserve biomechanical study. The eccentric location of ocular rotational axis towards the MR and away from the LR insertion profoundly affects the mechanical advantages of each muscle, explaining on geometric grounds why smaller MR recessions and resections can be equivalent to larger LR surgeries.