Repeatability and Reproducibility of Ultrasonic Attenuation Coefficient and Backscatter Coefficient Measured in the Right Lobe of the Liver in Adults with Known or Suspected Nonalcoholic Fatty Liver Disease

Abstract

Objective

To assess the repeatability and reproducibility (R&R) of ultrasonic attenuation coefficient (AC) and backscatter coefficient (BSC) measured in the livers of adults with known or suspected nonalcoholic fatty liver disease (NAFLD).

Methods

Institutional review board approved this HIPAA-compliant prospective study; informed consent was obtained. 41 research participants with known or suspected NAFLD were recruited and underwent same-day sonograms of the right liver lobe with a clinical scanner by a clinical sonographer. Each participant underwent two scanning trials, with participant repositioning between trials. Two transducers were used in each trial. For each transducer, machine settings were optimized by the sonographer but then kept constant while three data acquisitions were obtained from the liver without participant repositioning and then from an external calibrated phantom. Raw radio-frequency echo data were recorded. AC and BSC were measured within 2.6–3.0 MHz from a user-defined hepatic field of interest from each acquisition. The R&R were analyzed using random effects models.

Results

Mean AC and log-transformed BSC (logBSC) were 0.94 dB/cm-MHz and −27.0 dB, respectively. Intraclass correlation coefficient (ICC) was 0.88–0.94 for AC and 0.87–0.95 for logBSC acquired without participant repositioning. For between-trial repeated scans with participant repositioning, the ICC was 0.80–0.84 for AC and 0.69–0.82 for logBSC after averaging results from three within-trial images. The variability introduced by the transducer was less than the repeatability error.

Conclusions

Hepatic AC and BSC measures using a reference phantom technique on a clinical scanner are repeatable and reproducible between transducers in adults with known or suspected NAFLD.

INTRODUCTION

Under technical development for decades, quantitative ultrasound (QUS) now is emerging as a noninvasive means to objectively assess human diseases and conditions, with promising potential applications, for example, in liver fat quantification (1–3), spontaneous preterm birth prediction (4–5), and breast cancer treatment monitoring (6). Ultrasonic attenuation coefficient (AC, dB/cm-MHz) and ultrasonic backscatter coefficient (BSC, (cm-sr)⁻¹) are two fundamental QUS parameters derived from the raw radio-frequency (RF) echo data. AC is a measure of ultrasound energy loss in tissue and provides a numerical parameter analogous to the obscuration of tissue structures assessed qualitatively from B-mode images. BSC is a measure of ultrasound energy returned from tissue and provides a quantitative parameter analogous to the “echogenicity” assessed qualitatively from B-mode images. Quantitative definitions of AC and BSC are presented herein. The two parameters promise to be clinically useful quantitative imaging biomarkers (QIBs), a term defined by RSNA’s Quantitative Imaging Biomarker Alliance (QIBA) as “a characteristic derived from one or more in vivo images and objectively measured according to a ratio or interval scale as an indicator of normal biological processes, pathogenic processes, or response to a therapeutic intervention” (7).

Nonalcoholic fatty liver disease (NAFLD) is one of the most common types of chronic liver diseases worldwide (8). Noninvasive assessment of disease severity in NAFLD is an area of intense research (9). Magnetic resonance imaging-measured proton density fat fraction (MRI-PDFF) is emerging as an accurate and reproducible quantitative biomarker for assessment and quantification of liver fat content in patients with NAFLD (9–13), but MRI is not widely available globally and it can provoke anxiety or be unsafe in some patients. The controlled attenuation parameter (CAP) measured by Fibroscan (Echosens, Paris, France) has promise for objective assessment of liver fat in NAFLD, but this method has several limitations including low accuracy to distinguish between different grades of hepatic steatosis (14–15). Also, CAP is a proprietary algorithm provided by a single manufacturer used on a specialized device, and is not available on other clinical ultrasound systems. Current conventional ultrasound image-based assessment of liver fat is not accurate and lacks objectivity and precision due to system and reader variability. Recent studies using AC and BSC have shown promise in fat quantification (1–3).

For AC and BSC to play an important role as clinically useful QIBs, both technical and clinical performance of the parameters need to be evaluated rigorously. Repeatability and reproducibility (R&R) are two technical performance metrics that address QIB precision. Repeatability is “the measurement of precision with conditions that remain unchanged between replicate measurements (repeatability conditions)” (7), while reproducibility is “the measurement of precision with conditions that vary between replicate measurements (reproducibility conditions)” (7). The measurement location in the liver, operator, and measurement systems are examples of reproducibility conditions. A previous study showed good repeatability and operator/transducer reproducibility of AC and BSC in homogeneous liver-mimicking phantoms (16). Further, previous work showed that AC and BSC may accurately diagnose hepatic steatosis in adults with known or suspected NAFLD (1). However, R&R of AC and BSC in in vivo human NAFLD has not been examined. Therefore, the study’s purpose is to assess R&R of AC and BSC in adults with known or suspected NAFLD.

MATERIALS AND METHODS

Study Design and Participants

Institutional review board approval was obtained for this Health Insurance Portability and Accountability Act-compliant study. 41 adult research participants with known or suspected NAFLD were prospectively recruited between September 2015 and November 2016 from UCSD’s NAFLD Research Center. Other than known or suspected NAFLD, the only inclusion criterion was willingness to participate. Written informed consent was obtained. Demographic and anthropometric data were acquired by research coordinators. Data from contemporaneous hepatic MRI research studies and/or from clinical-care liver biopsies were recorded if available to help characterize the participant cohort.

Ultrasonic Data Acquisition

A clinical ultrasound system (Siemens S3000, Issaquah, WA) was used that allowed recording of direct post-beamformed RF echo data acquisition under terms of a research agreement. Two experienced, registered diagnostic medical sonographers (A and B) performed a research protocol for liver assessment on 41 participants, 20 scanned by A, termed Group A, and 21 scanned by B, termed Group B.

Each participant underwent two repeated scanning trials (Figure 1), separated by 5–10 minutes, between which the participant left the table and then was repositioned on the scanning table (referred to as participant repositioning). Each trial comprised two data acquisition sequences, one utilizing the 4C1 transducer (1–4 MHz nominal), the other the 6C1HD transducer (1.5–6 MHz nominal). Each sequence comprised four data acquisitions: three in the right liver lobe using a lateral intercostal approach, and one in calibrated reference phantom P2 (details available in the Reference Phantom Subsection). A data acquisition means a single operator button press that recorded a B-mode image and RF data. Twelve liver images were collected per participant (Figure 1): two repeated trials × two transducers/trial × three repeated acquisitions/transducer.

Figure 1.

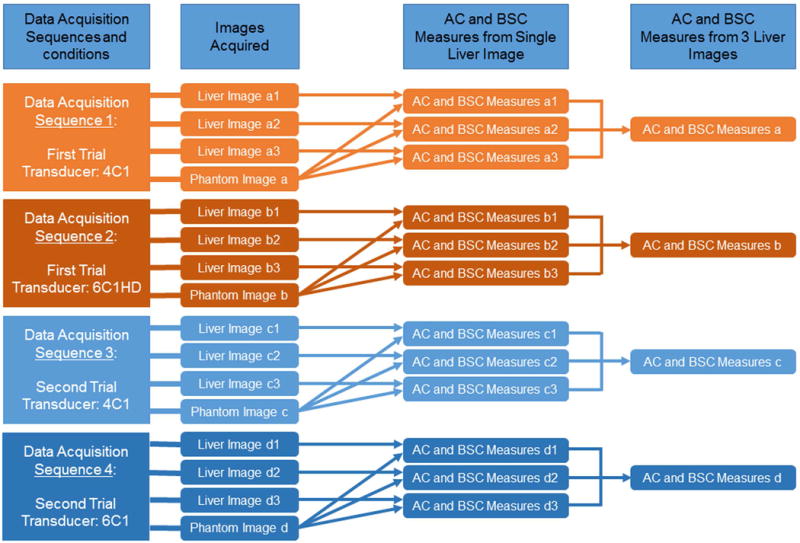
Diagram of the design for data acquisition and processing. The machine settings remained constant within each data acquisition sequence (e.g., the same machine settings were used for acquiring liver images a1, a2, and a3, and phantom image a), but were allowed to be changed from one acquisition sequence to the next or between participants.

In keeping with standard clinical practice, the sonographer adjusted system settings in each participant for a given transducer to optimize right hepatic lobe visualization, and then acquired B-mode/RF data for that trial. Participants suspended breathing after shallow inspiration prior to each data acquisition. Since each acquisition was obtained during a separate breath hold about 15 seconds apart, minor repositioning of the transducer was unavoidable, although the sonographer attempted to replicate the same liver location.

Definitions of AC and BSC

Attenuation refers to the loss of wave amplitude due to all mechanisms (e.g., absorption and scattering). For ultrasonic wave propagation in human soft tissues, the amplitude decay may be modeled as $A(z)=A_0-\alpha fz$, where _A0 is the initial ultrasonic wave amplitude in decibel (dB), _A(z) is the amplitude (in dB) after the wave propagates a distance z (in cm), f is the ultrasonic frequency in MHz, and α is the attenuation coefficient (AC; in dB/cm-MHz). αfz represents the total loss of wave amplitude.

BSC is a measure of the ability of tissue to scatter ultrasound waves, and provides a quantitative parameter analogous to the “echogenicity” assessed qualitatively from B-mode images. The BSC is defined as the differential scattering cross section per unit volume for a scattering angle of 180° (i.e., backscattering direction). The logarithmically transformed version of BSC is denoted in this paper as logBSC in dB, where $\mathit{logBSC}=10lo{g}_{10}\left(\mathit{BSC}/{\mathit{BSC}}_0\right)$, with ${\mathit{BSC}}_0=1 {\left(cm-sr\right)}^{-1}$.

Reference Phantom

The reference phantom P2 was purchased from CIRS, Inc. (Norfolk, VA). The model/project number of the phantom was 1409–00. The phantom was housed in a plastic cylinder with inside dimension of 15 +/− 1 cm and a height of 20 +/− 0.5 cm. The bottom was potted in an acoustically absorbing polymer, 2 cm thick, while the top had a Saran laminate membrane approximately 200 microns thick. The top also had a water-well extending approximately 2 cm above the membrane surface.

The calibrated speed of sound for phantom P2 was 1540 m/s between 2 and 4 MHz. The calibrated AC for phantom P2 was 0.69 dB/cm-MHz between 2 and 4 MHz. The calibrated BSC was frequency depenent. The BSC was 2.5×10⁻⁴ (cm-sr)⁻¹ at 2.8 MHz (i.e., logBSC = −36.0 dB), and the logBSC versus frequency plot between 2 and 4 MHz is shown in Figure 3. The QUS technique does not require multiple phantoms spanning the range of human liver AC and BSC values. Only a single phantom with fixed AC and BSC is needed.

Figure 3.

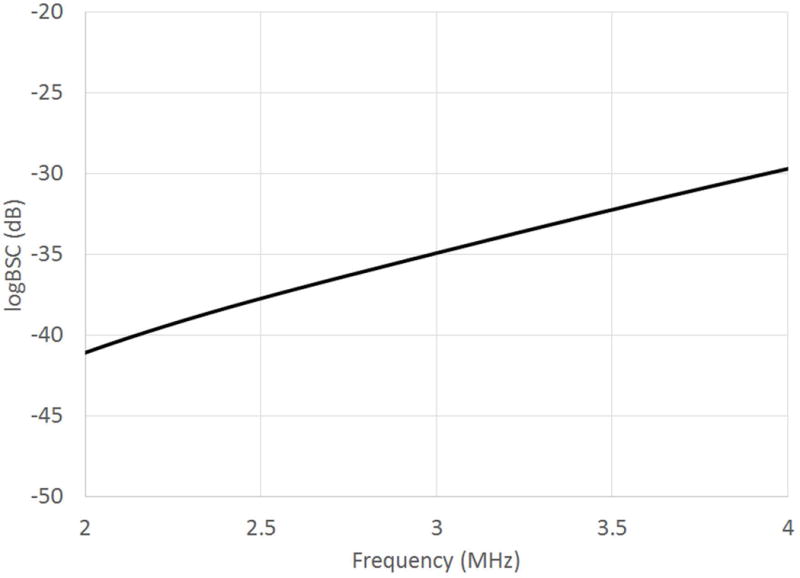
LogBSC versus frequency plot for the reference phantom.

AC and BSC Computation

AC and BSC frequency spectra were derived from the RF data of the liver and phantom using established methodologies (16), (25). To do so, the liver and phantom RF data were transferred to a PC for offline processing (MATLAB, The MathWorks, Natick, MA). The liver B-mode image was reconstructed from the RF data. A field of interest (FOI) was drawn on each B-mode reconstruction, outlining the region inside the liver boundary (Figure 2) to gate the RF data. The FOI was required by the AC and BSC algorithms; the liver AC and BSC were computed by comparing the RF data of the liver with those of the calibrated phantom. The RF data outside the liver cannot be used, or the resultant AC and BSC would correspond to extrahepatic tissues rather than the liver. To keep the FOI drawing simple, which is likely to be relevant for possible future clinical applications of this technology, no effort was made to exclude any hepatic vessels. FOIs were drawn under the supervision of an expert radiologist by a physician fellow with two years’ experience in radiology body imaging research and by a medical physicist with four decades’ experience in ultrasound research.

Figure 2.

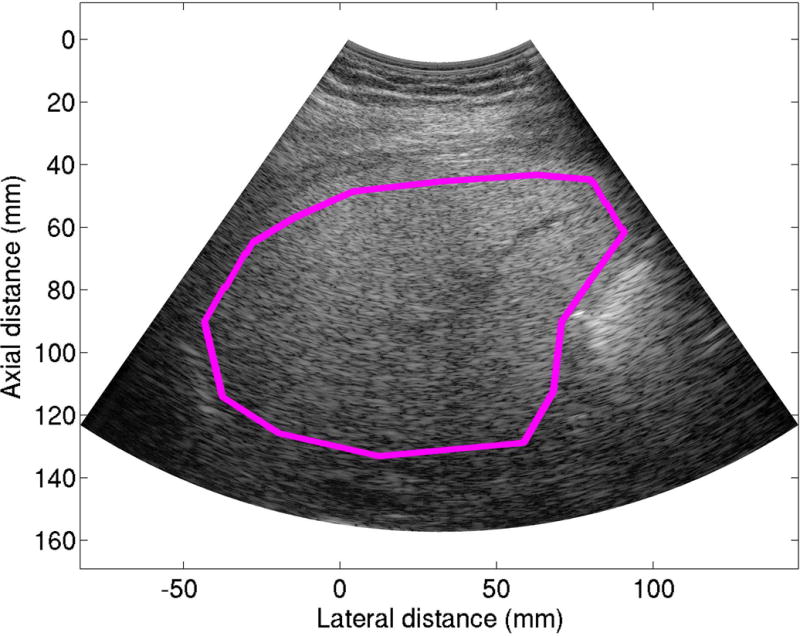
A representative liver B-mode image reconstructed from the RF data acquired from a 32 year old male. The pink field of interest line was drawn on the reconstructed B-mode image to delineate the liver boundary.

The delineated FOI was analyzed to yield the AC and BSC estimates as described below. For both AC and BSC estimates, the FOI was subdivided into overlapping sub-Regions of Interest (sub-ROIs). The AC sub-ROIs had a dimension of 20 mm × 40 A-lines (axial × lateral; axial size equivalent to 20 pulse lengths). The lateral and axial overlaps between adjacent AC sub-ROIs were both set to be 50% (16). The BSC sub-ROIs had a dimension of 7.7 mm × 40 A-lines (axial × lateral; axial size equivalent to 15 wavelengths at 3 MHz). The lateral and axial overlaps between adjacent BSC sub-ROIs were both set to be 75% (16). An AC spectrum was generated from each AC sub-ROI, and the results from all AC sub-ROIs within the FOI were averaged to yield the AC spectrum of the entire FOI. The BSC spectrum for the FOI was calculated likewise.

The spectral difference method was used to calculate the liver AC for an AC sub-ROI. Briefly, the AC sub-ROI was further divided into axial sections with a 50% axial overlap between adjacent axial sections, where each section represented a different depth. The liver power spectrum $S_{\mathit{Liver}}(f,z)$ was then estimated at each depth z by averaging the squared moduli of the fast Fourier transforms of all the A-lines in the sub-section corresponding to that depth. The phantom power spectrum $S_{\mathit{Phantom}}(f,z)$ was also estimated for each depth for which the liver power spectrum was estimated, using a similar approach except that more A-lines were used for the phantom power spectrum estimate to reduce noise. More A-lines was a result of laterally extending the sub-ROIs and sub-sections for the phantom (not exceeding the phantom edge), taking advantage of the spatial uniformity of the phantom. Finally, the AC spectrum for an AC sub-ROI was estimated by $A{C}_{\mathit{Liver}}\left(f\right)=A{C}_{\mathit{Phantom}}\left(f\right)-\frac{\gamma \left(f\right)}{4\times 8.686f}$, where $\gamma \left(f\right)$ is the slope of the straight line that fits log spectrum difference $\log \left(S_{\mathit{Liver}}(f,z)\right)-\log \left(S_{\mathit{Phantom}}(f,z)\right)$ as the function of depth, and the phantom AC, $A{C}_{\mathit{Phantom}}\left(f\right)$, was calibrated a priori.

The liver BSC was computed for each BSC sub-ROI without needing to further divide the BSC sub-ROI (a reason why BSC sub-ROI was smaller than AC sub-ROI). Instead, a single liver power spectrum estimate $S_{\mathit{Liver}}\left(f,z\right)$ was obtained for the BSC sub-ROI by averaging the squared moduli of the fast Fourier transforms of all the A-lines in the sub-ROI. The phantom power spectrum corresponding to the same depth, $S_{\mathit{Phantom}}\left(f,z\right)$, was obtained similarly from the phantom RF data, except that the phantom sub-ROI was extended laterally to reduce noise, similar to what was done for the AC estimate. The BSC spectrum for the BSC sub-ROI was then estimated using $BS{C}_{\mathit{Liver}}\left(f,z\right)=\frac{S_{\mathit{Liver}}\left(f,z\right)}{S_{\mathit{Phantom}}(f,z)}BS{C}_{\mathit{Phantom}}(f){10}^{2zf\left[A{C}_{\mathit{Liver}}(f)-A{C}_{\mathit{Phantom}}(f)\right]/10}$, where $BS{C}_{\mathit{Phantom}}(f)$ was calibrated a priori, and the factor ${10}^{2zf\left[A{C}_{\mathit{Liver}}(f)-A{C}_{\mathit{Phantom}}(f)\right]/10}$ compensated for the attenuation effects.

AC and BSC spectra were frequency-averaged over a 2.6–3.0 MHz bandwidth, yielding single AC and BSC measures per image. The bandwidth was chosen because it was a narrow range around the 2.8-MHz center frequency of the transducers with optimal signal-to-noise ratio. Averaging the measures from three images in an acquisition sequence yielded a three-image measure. Both the single-image and three-image measures were analyzed.

Statistical Analysis

Statistical analysis was performed using R (version 3.3.2, The R Foundation for Statistical Computing, Vienna, Austria). Participant characteristics were summarized descriptively. The BSC was log-transformed ( $\mathit{logBSC}=10lo{g}_{10}\mathit{BSC}$) for R&R assessment because logBSC was normally distributed. AC and logBSC were assessed separately.

The between-image repeatability, between-trial repeatability and between-transducer reproducibility were assessed for single-image measures. The between-trial repeatability and between-transducer reproducibility were assessed for three-image measures. The repeatability was analyzed separately for various conditions because repeatability might depend on the conditions.

The repeatability was assessed using a one-way random effects model (19)

$$Y_{ij}=\mu +{\mu }_i+{\epsilon }_{ij},\left(i=1,\dots ,n_S;j=1,\dots ,k\right)$$ (1)

where there are $n_S$ participants, $Y_{ij}$ is the $j$th repeated measure from participant $i$, $\mu$ is the overall mean, and ${\mu }_i~N\left(0, {\sigma }_S^2\right)$ and ${\epsilon }_{ij}~N\left(0,{\sigma }_E^2\right)$ are jointly independent random variables representing the random effects of the participants and replicates, respectively.

Following RSNA’s QIBA suggestions, several repeatability metrics (Table 1) were calculated: repeatability standard deviation (SD) ${\sigma }_E$, coefficient of variation (CV) for AC, repeatability coefficient ( $RC=2.77{\sigma }_E$) (17), and intraclass correlation coefficient (ICC) for absolute agreement. Two ICC forms were estimated: ICC(1,1) and ICC(1,k), representing values calculated from a single measure and from an average of k repeated measures, respectively (18). In this study, k=3.

Table 1.

R&R Metrics and their Representations using Random Effects Model Parameters

R&R Metrics	Between-participant SD	Repeatability SD	RC	ICC (1, 1)	QIBA-Reproducibility SD	Gauge-Reproducibility SD	RDC
Model Representation	${\sigma }_S$	${\sigma }_E$	$2.77{\sigma }_E$	${\sigma }_S^2/\left({\sigma }_S^2+{\sigma }_E^2\right)$	$\sqrt{{\sigma }_T^2+{\sigma }_{ST}^2+{\sigma }_E^2}$	$\sqrt{{\sigma }_T^2+{\sigma }_{ST}^2}$	$2.77\sqrt{{\sigma }_T^2+{\sigma }_{ST}^2+{\sigma }_E^2}$

The reproducibility was assessed using a two-way random effects model (19)

$$Y_{\mathit{ijr}}=\mu +{\alpha }_i+{\beta }_j+{\left(\alpha \beta \right)}_{ij}+{\epsilon }_{\mathit{ijr}},\left(i=1,\dots ,n_S;j=1,\dots ,n_T;r=1,\dots ,k\right)$$ (2)

where there are $n_S$ participants and $n_T$ transducers, $Y_{\mathit{ijr}}$ is the $r$th repeated measure from participant $i$ with transducer $j$, and ${\alpha }_i~N\left(0,{\sigma }_S^2\right)$, ${\beta }_j~N\left(0,{\sigma }_T^2\right)$, $(\alpha {\beta }_{ij})~N\left(0,{\sigma }_{ST}^2\right)$ and ${\epsilon }_{\mathit{ijr}}~N\left(0,{\sigma }_E^2\right)$ are jointly independent random variables representing the random effects of the participants, transducers, subject by transducer interactions, and replicates, respectively.

There are two widely used definitions of reproducibility. One includes the repeatability effect, while the other does not. Reproducibility that includes repeatability effect is recommended by QIBA and termed QIBA-reproducibility herein. Reproducibility that excludes repeatability effect is popular in Gauge R&R studies and termed Gauge-reproducibility (19) herein. The following reproducibility metrics were calculated: QIBA-reproducibility SD ( $\sqrt{{\sigma }_T^2+{\sigma }_{ST}^2+{\sigma }_E^2}$), reproducibility coefficient (RDC=2.77 $\sqrt{{\sigma }_T^2+{\sigma }_{ST}^2+{\sigma }_E^2}$), and Gauge-reproducibility SD ( $\sqrt{{\sigma }_T^2+{\sigma }_{ST}^2}$).

RESULTS

Participants

41 participants (26 females) were recruited from UCSD’s NAFLD Research Center and those willing to participate were enrolled. The mean age was 55 (F: 59; M: 48) years old and the age range was 27–72 (F: 31–72; M: 27–68) years old. The mean body mass index (BMI) was 30.1 kg/m², and the BMI range was 17.6–51.5 kg/m². The 20 Group A participants included 7 men and 13 women with a mean BMI of 30.1 kg/m² (range: 21.7–40.7 kg/m²) and mean age of 56 y (range: 31–72 y). The 21 Group B participants included 8 men and 13 women with a mean BMI of 30.1 kg/m² (range: 17.6–51.5 kg/m²) and mean age of 53 y (range: 27–71 y). 34 of the 41 participants had MRI-PDFF measured within 0 to 277 days (mean: 20 days) of US; mean MRI-PDFF was 14.3%, and the MRI-PDFF range was 3.2–40.0%. This MRI-PDFF range is comparable to a previous study with 204 participants (1). 35 participants had clinical-care liver biopsy within 1 to 283 days (mean: 70 days) of US and with the following distribution of histology-determined steatosis grades: 0: 2, 1: 18, 2: 12, and 3: 3. The MRI-PDFF and histology-determined steatosis grade are presented to help characterize the participant cohort but were not included in subsequent analysis. The MRI-PDFF values show that the participant cohort covers a wide range of hepatic fat fractions. The histology-determined steatosis grades also show the broad steatosis spectrum of the study participants.

AC and BSC Measurement Results

Twelve single-image AC and 12 single-image logBSC measures were computed per participant. Boxplots (Figure 4(ab)) of all the single-image AC and logBSC measures were grouped by participant ID and ordered by BMI to provide an overview of the distribution and variability of the measures. Visual inspection of the boxplots revealed that the within-participant variability was much smaller than the between-participant variability for both AC and logBSC, indicating good overall repeatability and reproducibility for the two parameters. AC and logBSC values did not appear to be correlated with the BMI; nor was any correlation observed between the within-participant variability and the BMI. Therefore, participant BMI did not seem to affect the AC and BSC outcomes.

Figure 4.

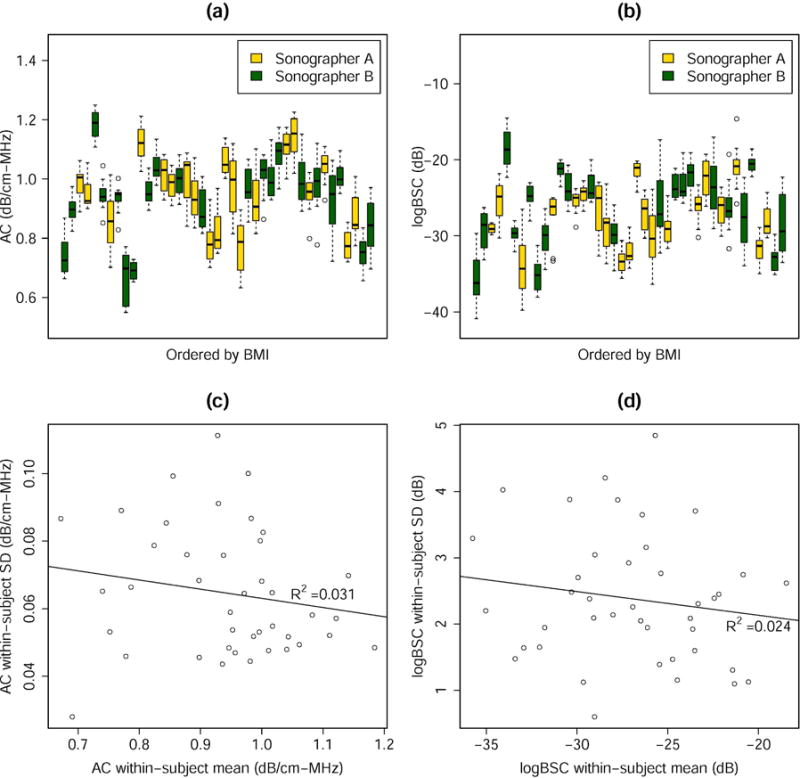
Summary plots for the AC and logBSC results. The boxplots show the single-image measures of (a) AC and (b) logBSC for all transducers, trials and images, as ordered by participant BMI. The standard deviation versus the mean scatter plots show no linear correlation between the standard deviation and the mean of (c) AC and (d) logBSC.

The within-participant SD for the single-image measures were plotted against the participant means in Figure 4(c–d). No statistically significant linear correlation between the mean and SD was observed, suggesting that the absolute AC and logBSC levels would be unlikely to affect the repeatability and reproducibility results. Therefore, the repeatability and reproducibility results did not have to be reported at specified AC and logBSC levels.

Overall, the mean of measured AC was 0.94 dB/cm-MHz and of measured logBSC was −27.0 dB for the 41 participants. The average within-participant SD in measured AC was 0.06 dB/cm-MHz and in measured logBSC was 2.4 dB, with a CV of 6.9% for AC; CV was not applicable for logBSC. The CV value for AC was a small number that indicated good repeatability and reproducibility. Notice that CV was presented here for completeness. While still useful, this measure was not as relevant when the SD is not correlated with the mean.

Between-image Repeatability of Single-image Measures

The between-image repeatability was assessed independently under various measurement conditions (i.e., sonographer-transducer-trial combinations) using the model described in Equation (1). For each condition, there were 20 or 21 participants and three replicate measures (three images) per participant. The estimated between-participant SD, between-image repeatability SD, RC, ICC(1,1) and ICC(1,3) were summarized in Table 2 for each measurement condition. The estimates under different conditions were similar, with ICC(1,1) > 0.9 for most conditions, and ICC(1,3) > 0.95 for all conditions. The ICCs of AC were close to those of the logBSC.

Table 2.

Between-image Repeatability Estimates for Single-image AC and BSC Measures Obtained under Various Conditions, Calculated Using the One-way Random Effects Model.

Conditions			Summary Statistics for AC (Unit: dB/cm-MHz)					ICC Estimates for AC
Participant Group*	Transducer	Trial ID	Mean	Range	Between-participant SD (95% CI)	Between-image repeatability SD (95% CI)	RC (95% CI)	ICC(1, 1) (95% CI)†	ICC(1, 3) (95% CI)‡
A	4C1	1	0.94	[0.69, 1.21]	0.13 (0.10, 0.19)	0.04 (0.03, 0.05)	0.12 (0.10, 0.15)	0.91 (0.82, 0.96)	0.97 (0.93, 0.99)
A	4C1	2	0.94	[0.63, 1.18]	0.14 (0.10, 0.20)	0.03 (0.03, 0.04)	0.09 (0.08, 0.12)	0.94 (0.89, 0.98)	0.98 (0.96, 0.99)
A	6C1HD	1	0.97	[0.75, 1.23]	0.11 (0.08, 0.16)	0.03 (0.03, 0.04)	0.09 (0.07, 0.11)	0.92 (0.84, 0.96)	0.97 (0.94, 0.99)
A	6C1HD	2	0.96	[0.72, 1.21]	0.12 (0.09, 0.18)	0.04 (0.03, 0.05)	0.10 (0.09, 0.13)	0.92 (0.83, 0.96)	0.97 (0.94, 0.99)
B	4C1	1	0.93	[0.69, 1.25]	0.13 (0.10, 0.19)	0.04 (0.03, 0.05)	0.11 (0.09, 0.14)	0.91 (0.83, 0.96)	0.97 (0.93, 0.99)
B	4C1	2	0.93	[0.66, 1.14]	0.12 (0.09, 0.18)	0.04 (0.03, 0.05)	0.10 (0.08, 0.13)	0.92 (0.84, 0.96)	0.97 (0.94, 0.99)
B	6C1HD	1	0.93	[0.58, 1.18]	0.14 (0.11, 0.21)	0.05 (0.04, 0.07)	0.15 (0.12, 0.18)	0.88 (0.77, 0.94)	0.96 (0.91, 0.98)
B	6C1HD	2	0.93	[0.55, 1.22]	0.15 (0.12, 0.22)	0.05 (0.04, 0.06)	0.12 (0.10, 0.16)	0.92 (0.85, 0.96)	0.97 (0.94, 0.99)
Conditions			Summary Statistics for logBSC (Unit: dB)					ICC Estimates for logBSC
Participant Group*	Transducer	Trial ID	Mean	Range	Between-participant SD (95% CI)	Between-image repeatability SD (95% CI)	RC (95% CI)	ICC(1, 1) (95% CI)†	ICC(1, 3) (95% CI)‡
A	4C1	1	−28.18	[−39.77, −20.17]	4.40 (3.26, 6.51)	1.67 (1.37, 2.13)	4.62 (3.79, 5.91)	0.87 (0.76, 0.94)	0.95 (0.90, 0.98)
A	4C1	2	−28.16	[−39.23, −20.32]	4.40 (3.30, 6.47)	1.18 (0.97, 1.52)	3.28 (2.69, 4.20)	0.93 (0.87, 0.97)	0.98 (0.95, 0.99)
A	6C1HD	1	−27.29	[−34.26, −19.67]	3.55 (2.66, 5.23)	1.01 (0.83, 1.29)	2.78 (2.29, 3.56)	0.93 (0.85, 0.97)	0.97 (0.95, 0.99)
A	6C1HD	2	−26.38	[−34.97, −14.63]	4.20 (3.14, 6.19)	1.25 (1.02, 1.60)	3.45 (2.84, 4.42)	0.92 (0.84, 0.96)	0.97 (0.94, 0.99)
B	4C1	1	−27.26	[−35.71, −16.82]	4.53 (3.42, 6.58)	1.19 (0.98, 1.51)	3.28 (2.71, 4.17)	0.94 (0.87, 0.97)	0.98 (0.95, 0.99)
B	4C1	2	−27.44	[−40.90, −19.07]	5.23 (3.96, 7.60)	1.24 (1.02, 1.58)	3.44 (2.84, 4.37)	0.95 (0.89, 0.98)	0.98 (0.96, 0.99)
B	6C1HD	1	−25.73	[−38.08, −17.00]	5.18 (3.90, 7.54)	1.54 (1.27, 1.96)	4.27 (3.52, 5.43)	0.92 (0.84, 0.96)	0.97 (0.94, 0.99)
B	6C1HD	2	−25.48	[−37.36, −14.49]	5.48 (4.12, 7.98)	1.66 (1.37, 2.11)	4.61 (3.80, 5.86)	0.92 (0.84, 0.96)	0.97 (0.94, 0.99)

Note:

^*Participant group A and B represent participants scanned by Sonographers A and B, respectively.

^†ICC(1, 1) and the 95% CI were calculated using the ‘irr’ package in R using the one-way ANOVA model, ‘agreement’ type, and ‘single’ unit.

^‡ICC(1, 3) and the 95% CI were calculated using the one-way ANOVA model, ‘agreement’ type, and ‘average’ unit.

The between-image repeatability represented a very short-term repeatability; adjacent images were acquired around 15 seconds apart. The participant stayed on the scanning table and was not repositioned. This is a more idealized repeatability test. The between-image repeatability SD was much lower than the between-participant SD. As a result, the ICC values were high, showing excellent short-term repeatability for both AC and logBSC.

Theoretically, the repeatability measures could be different under different conditions. For example, transducer X might have better repeatability than transducer Y, etc. That was why the repeatability measures were analyzed separately for different conditions. The fact that ICC values were high for all conditions suggest that the short-term repeatability was excellent for all conditions examined. The similar ICC values between different conditions indicated that the short-term repeatability did not depend on which of the two transducers was used, or on which of the two sonographers performed the scan, etc.

Also, the robustness of the statistical model was demonstrated by the observation that the between-participant SD estimate was similar among all conditions.

Between-trial Repeatability of Single-image and Three-image Measures

The between-trial repeatability was assessed independently for various measurement conditions (i.e., sonographer-transducer combinations) using the model described in Equation (1). For single-image measures, the data from the first image of the three images in an acquisition sequence were used when the one-way random effects model was applied. Therefore, there were 20 or 21 participants and two replicate measures (i.e., two trials) per participant for each sonographer-transducer combination, regardless of whether single-image or three-image measures were assessed. The repeatability estimates were summarized in Table 3. For the single-image measures, the estimated ICC(1,1) for between-trial repeatability was greater than 0.7 for most conditions, and ICC(1, 2) was greater than 0.8 for most conditions. The ICCs estimated from three-image measures were higher by up to 0.10 compared to those estimated from single-image measures.

Table 3.

Between-trial Repeatability Estimates for Single- and Three-image AC and BSC Measures Obtained under Various Conditions, Calculated Using the Two-way Random Effects Model.

Conditions			Summary Statistics for AC (Unit: dB/cm-MHz)					ICC Estimates for AC
Participant Group	Transducer	# Images Averaged	Mean	Range	Between-participant SD (95% CI)	Between-trial Repeatability SD (95% CI)	RC (95% CI)	ICC(1, 1) (95% CI)	ICC(1, 2) (95% CI)
A	4C1	1	0.94	[0.66, 1.18]	0.12 (0.07, 0.19)	0.08 (0.06, 0.12)	0.23 (0.18, 0.34)	0.67 (0.34, 0.85)	0.80 (0.50, 0.92)
		3	0.94	[0.67, 1.16]	0.12 (0.08, 0.19)	0.06 (0.05, 0.09)	0.16 (0.13, 0.24)	0.81 (0.59, 0.92)	0.90 (0.74, 0.96)
A	6C1HD	1	0.97	[0.73, 1.23]	0.10 (0.06, 0.16)	0.07 (0.05, 0.09)	0.18 (0.14, 0.26)	0.71 (0.40, 0.87)	0.83 (0.57, 0.93)
		3	0.97	[0.73, 1.21]	0.11 (0.07, 0.16)	0.05 (0.04, 0.08)	0.15 (0.11, 0.21)	0.80 (0.56, 0.91)	0.89 (0.72, 0.95)
B	4C1	1	0.93	[0.69, 1.25]	0.12 (0.08, 0.18)	0.05 (0.04, 0.08)	0.15 (0.12, 0.22)	0.83 (0.63, 0.93)	0.91 (0.78, 0.96)
		3	0.93	[0.69, 1.24]	0.12 (0.08, 0.17)	0.05 (0.04, 0.07)	0.14 (0.11, 0.20)	0.84 (0.66, 0.93)	0.91 (0.79, 0.96)
B	6C1HD	1	0.93	[0.56, 1.20]	0.13 (0.09, 0.20)	0.08 (0.06, 0.11)	0.21 (0.17, 0.31)	0.74 (0.48, 0.89)	0.85 (0.64, 0.94)
		3	0.93	[0.56, 1.21]	0.13 (0.09, 0.20)	0.07 (0.05, 0.09)	0.18 (0.14, 0.26)	0.81 (0.59, 0.92)	0.89 (0.74, 0.96)
Conditions			Summary Statistics for logBSC (Unit: dB)					ICC Estimates for logBSC
Participant Group	Transducer	# Images Averaged	Mean	Range	Between-participant SD (95% CI)	Between-trial Repeatability SD (95% CI)	RC (95% CI)	ICC(1, 1) (95% CI)	ICC(1, 2) (95% CI)
A	4C1	1	−28.17	[−39.23, −20.65]	3.64 (1.87, 5.88)	3.12 (2.39, 4.51)	8.65 (6.62, 12.50)	0.58 (0.20, 0.81)	0.73 (0.33, 0.89)
		3	−28.17	[−37.75, −20.76]	3.85 (2.52, 5.90)	2.26 (1.73, 3.27)	6.27 (4.79, 9.05)	0.74 (0.46, 0.89)	0.85 (0.63, 0.94)
A	6C1HD	1	−26.55	[−34.26, −14.63]	3.49 (2.24, 5.39)	2.18 (1.67, 3.15)	6.04 (4.62, 8.72)	0.72 (0.42, 0.88)	0.84 (0.59, 0.93)
		3	−26.83	[−34.40, −17.89]	3.50 (2.37, 5.33)	1.85 (1.42, 2.67)	5.13 (3.92, 7.41)	0.78 (0.53, 0.91)	0.88 (0.70, 0.95)
B	4C1	1	−27.31	[−38.54, −16.82]	4.64 (3.25, 6.93)	2.23 (1.72, 3.19)	6.19 (4.76, 8.84)	0.81 (0.60, 0.92)	0.90 (0.75, 0.96)
		3	−27.35	[−39.88, −17.51]	4.47 (3.14, 6.66)	2.10 (1.61, 3.00)	5.81 (4.47, 8.31)	0.82 (0.61, 0.92)	0.90 (0.76, 0.96)
B	6C1HD	1	−25.46	[−36.95, −15.91]	4.41 (2.64, 6.85)	3.25 (2.50, 4.65)	9.01 (6.93, 12.87)	0.65 (0.32, 0.84)	0.79 (0.48, 0.91)
		3	−25.61	[−37.20, −15.14]	4.46 (2.80, 6.87)	3.03 (2.33, 4.32)	8.38 (6.45, 11.98)	0.69 (0.38, 0.86)	0.81 (0.55, 0.92)

The between-trial repeatability is a test-retest repeatability. This is a more clinically meaningful repeatability because the participants were repositioned (left the table and returned) between trials. The ICC values showed good between-trial repeatability if only a single image was acquired and analyzed to yield the AC and logBSC, and excellent between-trial repeatability if 3 images were used to yield the AC and logBSC. It is not surprising that averaging the results from three images improved the between-trial repeatability.

Similar to the between-image repeatability, the between-trial repeatability did not appear to be affected by the examined experimental conditions (transducer and sonographer) except the number of images used, as indicated by the similar ICC values between different transducers and sonographers.

Comparing Tables 2 and 3, the between-participant SD estimates were similar. The between-participant SD estimate in Table 2 was obtained using the one-way random effects model, whereas the same estimate in Table 3 was obtained using the two-way random effects model. The observation that the two models yielded similar between-participant SD estimates served as a corroboration of the data and algorithm.

The between-trial RC of single-image measures (Table 3) was approximately twice as large as the between-image RC (Table 2), suggesting better repeatability in the very short-term repeat condition without participant repositioning than in the test-retest condition with participant repositioning. Participant repositioning therefore appeared to adversely affect the repeatability, possibly because it is more difficult to scan the same region of the liver as the participant was repositioned. In other words, the liver might not be a perfectly homogenous tissue in terms of AC and logBSC estimates.

The between-trial RC of three-image measures was approximately 1.5 times as large as the between-image RC. The averaging appeared to have shortened the gap between the very short term and the test-retest repeatabilities.

Between-transducer Reproducibility of Single-image and Three-image Measures

The between-transducer reproducibility was assessed using the two-way random effects model described in Equation (2). Participants and transducers were the two main random effects, and the trials were the replicates. For analysis based on single-image measures, only the data from the first image of the three images in an acquisition sequence were used. The two-way random effects model yielded the between-transducer reproducibility estimates shown in Table 4. Additionally, between-trial repeatability without differentiating the transducers was also obtained as a result of the model.

Table 4.

Transducer Reproducibility Estimates for Single- and Three-image AC and BSC Measures Obtained under Various Conditions, Calculated Using the Two-way Random Effects Model.

Conditions		Summary Statistics for AC (Unit: dB/cm-MHz)
Participant Group	# Images Averaged	Mean	Range	Between-participant SD (95% CI)	QIBA-reproducibility SD (95% CI)	Gauge-reproducibility SD	Between-trial Repeatability SD (95% CI)	RDC (95% CI)
A	1 3	0.95	[0.66, 1.23]	0.11 (0.07, 0.16)	0.08 (0.07, 0.62)	0.03	0.08 (0.06, 0.10)	0.23 (0.20, 1.70)
		0.96	[0.67, 1.21]	0.10 (0.07, 0.16)	0.07 (0.06, 0.55)	0.05	0.06 (0.05, 0.07)	0.21 (0.17, 1.52)
B	1 3	0.93	[0.56, 1.25]	0.13 (0.09, 0.19)	0.07 (0.06, 0.08)	0	0.07 (0.06, 0.09)	0.18 (0.16, 0.23)
		0.93	[0.56, 1.24]	0.13 (0.09, 0.18)	0.06 (0.05, 0.09)	0	0.06 (0.05, 0.07)	0.16 (0.14, 0.26)
Conditions		Summary Statistics for BSC (Unit: dB)
Participant Group	# Images Averaged	Mean	Range	Between-participant SD (95% CI)	QIBA-reproducibility SD (95% CI)	Gauge-reproducibility SD	Between-trial Repeatability SD (95% CI)	RDC (95% CI)
A	1 3	−27.36	[−39.23, −14.63]	3.56 (2.50, 5.39)	2.91 (2.51, 36.6)	1.09	2.69 (2.21, 3.45)	8.05 (6.94, 101)
		−27.50	[−37.75, −17.89]	3.46 (2.42, 5.26)	2.56 (2.18, 30.2)	1.51	2.07 (1.70, 2.64)	7.09 (6.04, 84.7)
B	1 3	−26.39	[−38.54, −15.91]	4.63 (3.45, 6.81)	2.90 (2.49, 41.9)	0.78	2.79 (2.30, 3.55)	8.02 (6.90, 116)
		−26.48	[−39.88, −15.14]	4.58 (3.42, 6.70)	2.68 (2.30, 39.4)	0.63	2.60 (2.15, 3.31)	7.42 (6.38, 109)

The QIBA-reproducibility SD estimates that included the transducer effects and the between-trial repeatability effects shown in Table 4 were close to the between-trial repeatability presented in Tables 3 and 4, and consequently, the RDC estimates in Table 4 were close to the RC estimates in Table 3. The closeness in the estimates between the QIBA-reproducibility and the between-trial repeatability indicated that the transducers did not contribute significantly to the overall variability in the AC and logBSC measures. The variability caused by transducers alone was described by the Gauge-reproducibility, and the estimated Gauge-reproducibility SD values were lower than the between-trial repeatability SD values for all cases shown in Table 4. These results showed excellent between-transducer reproducibility, that is, the transducer did not contribute significantly to the measurement variability.

The between-participant SD and between-trial repeatability shown in Table 4 were close to those shown in Table 3, demonstrating consistency in the results obtained from different analyses. In Table 3, the between-participant SD and between-trial repeatability had to be estimated separately for the two transducers, whereas in Table 4, the transducer effect became a model parameter.

DISCUSSION

QUS imaging is being increasingly investigated as an inexpensive, objective and noninvasive method of diagnosing diseases and monitoring treatments using widely available clinical US systems. For QUS to gain wide acceptance, R&R must be demonstrated. Some of the key elements of R&R include very-short-term repeatability (between image), on-and-off-table repeatability (between trial), and reproducibility between different transducers, operators, manufacturers, measurement site in the liver, etc. While it is hard to quantify R&R across all the conditions in a single study, some elements believed important to the R&R in human subjects of QUS measures were examined.

Good to excellent overall R&R was demonstrated for AC and BSC measures obtained from 41 participants with known or suspected NAFLD. To better understand the implications of the results, potential sources of variation in AC and BSC measures were examined. Technically, AC and BSC were spatially averaged in the right liver lobe. Repeatability error has two sources: A) intrinsic error of the measurement methods, and B) biological variability. Error source A can be assessed by acquiring data from a spatially homogenous, liver-mimicking physical phantom. A previous phantom-based study (16) showed that error source A was low: repeatability SD was less than 0.02 dB/cm-MHz for AC, and 0.6 dB for logBSC. In the human studies herein, both sources contribute to the repeatability error, which may explain why the between-image repeatability observed (repeatability SD was between 0.03 to 0.05 dB/cm-MHz for AC and between 1 and 2 dB in logBSC) is somewhat worse than the phantom results. Error source B may result from liver heterogeneity or technical difficulty of scanning a human being. One way to address the effect of liver heterogeneity is to acquire multiple images and average together the measures. Hence both single-image measures and three-image measures were assessed. Additional images may be used if better repeatability is desired, but the optimum number is yet to be determined. As a reference, 10 repeated measures are commonly used for liver stiffness assessment by acoustic radiation force impulse (ARFI) (20) and transient elastography (15).

The between-image repeatability assesses the very-short-term repeatability in a more controlled condition to help understand the sources of repeatability error. However, the between-image repeatability is less clinically demanding because the images shared the same acoustic window and target area of the liver with minimal transducer repositioning as well as the same phantom scan, plus the participant was not repositioned. In comparison, the between-trial repeatability may be more relevant to clinical practice.

Good to excellent ICC values were observed for between-trial repeatability. ICC (1,1) for the three-image measures was greater than 0.8 for most cases and ICC (1,3) for the three-image measures was in the range 0.85–0.9 for most cases. These ICC values demonstrate that the majority portion of the overall variability originates from the between-participant variability rather than the between-trial variability when the measurements are acquired using the same transducer.

In addition to good repeatability, good transducer reproducibility was also observed, with QIBA-reproducibility SD only slightly greater than the between-trial repeatability SD. The error introduced by transducer was lower than the repeatability error, as was also observed in the phantom study (16). These AC and BSC measurement techniques were designed to remove the system and operator dependencies by scanning a calibrated phantom, which explains the low variability introduced by transducers in both the phantom and in vivo human studies.

QUS R&R measures are comparable to or better than other imaging modalities for liver assessment. For example, an overall ICC of 0.68 was reported for MR elastography used for assessing liver stiffness (21). ARFI was shown to have an ICC between 0.7 and 0.9 for liver fibrosis assessment (22). Another method for liver fibrosis assessment, transient elastography (Fibroscan), has an excellent overall inter-observer reproducibility with a reported ICC up to 0.96 (23). However, the reproducibility of transient elastography depends on the liver fibrosis stage (ICC=0.6 for fibrosis stage ≤1, and ICC=0.99 for fibrosis stage ≥2) (24).

The focus of this R&R study was precision rather than accuracy. A thorough analysis of the accuracy is the topic of future studies. The accuracy is briefly discussed herein in two perspectives: 1) accuracy of measuring the AC and BSC using the reference phantom technique, and 2) diagnostic accuracy of using AC and BSC to quantify liver steatosis.

The reference phantom technique has been used in QUS research for over two decades. It was originally proposed by Yao et al. (25). Portions of our previously published phantom data (16) are summarized as follows to demonstrate the accuracy of the reference phantom technique. The AC and BSC of two additional phantoms P4 and P6 (CIRS, Inc., Norfolk, VA) were measured with the reference phantom technique and compared with the independently calibrated AC and BSC values for P4 and P6. The AC and BSC were calibrated using a broadband insertion loss method (26) and a planar reference method (27), respectively. The independent calibration techniques have been validated by two inter-laboratory measurement studies sponsored by American Institute of Ultrasound in Medicine (26, 28). Two sonographers (A and B) each repeatedly scanned three phantoms (P2, P4, and P6) using two transducers (4C1 and 6C1HD) on the Siemens S3000 ultrasound scanner. A total of 60 data sets were acquired (A with 4C1: 11, A with 6C1HD: 10, B with 4C1: 20, and B with 6C1HD: 19). Each data set consisted of a set of scans of P2, P4, and P6 all under the same settings, while the settings varied across different data sets. Figure 5 shows boxplots of the AC and BSC for P4 and P6 measured using the reference phantom technique with P2 as the reference. The boxplots were grouped with sonographer and transducer on the same graph. Also presented in the boxplots were two independent calibrations performed in September 2015 (designated as cal1) and June 2016 (designated as cal2), respectively. Each calibration represented the average of repeated calibrations performed by multiple operators. Excellent agreement was observed between the AC and BSC from the reference phantom technique and those from the two independent calibrations. Also, excellent agreement was observed between the two independent calibrations performed 9 months apart, implying stability of the phantom acoustic properties.

Figure 5.

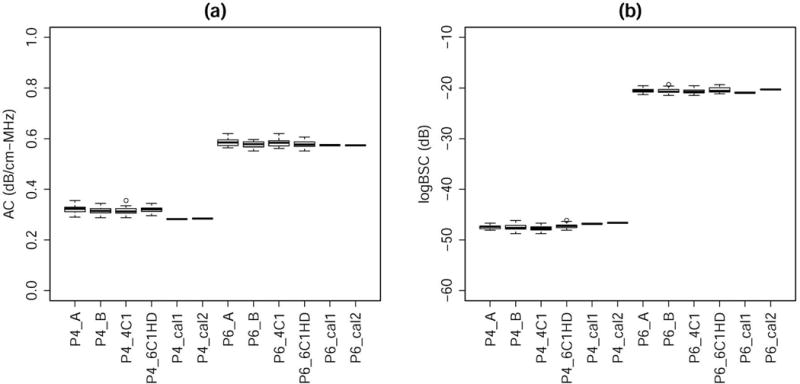
Boxplots of the (a) AC and (b) logBSC for P4 and P6 measured using the reference phantom technique with P2 as the reference and those independently calibrated in September 2015 and June 2016. Each calibration represented the average of repeated calibrations performed by multiple operators. The reference phantom technique results were grouped with sonographer and transducer on the same graph.

The diagnostic accuracy of using AC and BSC to quantify hepatic steatosis can be found from two published studies (1, 3) but are the focus of ongoing research. The results are briefly summarized as follows. The accuracy of BSC in the diagnosis and quantification of hepatic steatosis was assessed in (1) using MRI-PDFF as a reference. BSC was shown to be correlated with MRI-PDFF (Spearman ρ = 0.80; P < .0001). The area under the curve value for using BSC to detect NAFLD was 0.98 (95% confidence interval, 0.95–1.00; P < .0001) in the training group. In the training and validation groups, the optimal BSC cut-off value detected NAFLD with 93% and 87% sensitivity, 97% and 91% specificity, 86% and 76% negative predictive values, and 99% and 95% positive predictive values, respectively. In the other study (3), the diagnostic performance of AC and BSC was assessed for predicting histology-confirmed steatosis grade. The raw and cross-validated steatosis grading accuracies were 61.7% and 55.0%, respectively, for AC, and 68.3% and 68.3%, respectively, for BSC. The accuracy of AC and BSC for predicting steatosis grade was shown to be higher than conventional ultrasound image interpretation (51.7% accuracy).

The accuracy of BSC measurement could be affected by subcutaneous fat. However, the subcutaneous fat did not appear to significantly affect the diagnostic accuracy of BSC as high accuracy was demonstrated in (1) and (3) without taking into account the effect of subcutaneous fat. Nevertheless, future studies should address the effect of subcutaneous fat to improve the BSC measurement accuracy, possibly by adopting an approach similar to that described in (29). The subcutaneous fat does not affect the AC measurement as determined by the physical principles underlying the AC measurement algorithm; local attenuation, rather than the attenuation above the liver, is being measured by the technique.

An important limitation of the described QUS technology is that it requires an external phantom and offline processing. Also, obtaining and working with RF data is challenging. Research is ongoing to streamline the workflow, with more manufacturers providing RF capabilities. We envision ultimate development of internally calibrated real-time QUS technology, which will facilitate its clinical translation. Another limitation of our study was the small sample size, which precluded analysis of some factors that may affect precision. We assessed some but not all components of variability, and future research is needed to assess other components including scanner and sonographer reproducibility. This study was done at a single site and external multiple-site validation of our results is needed.

In conclusion, hepatic AC and BSC measures using a reference phantom technique on a clinical scanner are repeatable and transducer-reproducible in adults with known or suspected NAFLD. Further research is needed to evaluate additional factors that might affect the variability of the measurements.