Mental Health Risk Adjustment with Clinical Categories and Machine Learning

Abstract

Objective

To propose nonparametric ensemble machine learning for mental health and substance use disorders (MHSUD) spending risk adjustment formulas, including considering Clinical Classification Software (CCS) categories as diagnostic covariates over the commonly used Hierarchical Condition Category (HCC) system.

Data Sources

2012–2013 Truven MarketScan database.

Study Design

We implement 21 algorithms to predict MHSUD spending, as well as a weighted combination of these algorithms called super learning. The algorithm collection included seven unique algorithms that were supplied with three differing sets of MHSUD‐related predictors alongside demographic covariates: HCC, CCS, and HCC + CCS diagnostic variables. Performance was evaluated based on cross‐validated R ² and predictive ratios.

Principal Findings

Results show that super learning had the best performance based on both metrics. The top single algorithm was random forests, which improved on ordinary least squares regression by 10 percent with respect to relative efficiency. CCS categories‐based formulas were generally more predictive of MHSUD spending compared to HCC‐based formulas.

Conclusions

Literature supports the potential benefit of implementing a separate MHSUD spending risk adjustment formula. Our results suggest there is an incentive to explore machine learning for MHSUD‐specific risk adjustment, as well as considering CCS categories over HCCs.

In health insurance, risk selection refers to the exploitation of unpriced variation in risk, either by insurance consumers or by insurers, which can interfere with efficient market performance (Newhouse 1996). In regulated health insurance markets, risk selection is principally mitigated via the use of risk adjustment. The goal of risk adjustment is to pay plans so that insurers are incentivized to compete for enrollees based on providing the best care with respect to quality and efficiency, rather than competing for the lowest risk individuals. Risk adjustment controls for differences in health care spending at the individual level, typically by utilizing age–sex information and health status or diagnosis‐based information. The effectiveness of the risk adjustment system relies on the accurate prediction of health care spending to redistribute funds based on the health of the enrollees in the insurer's plans. Given the large, complex claims data used for risk adjustment, parametric ordinary least squares (OLS) may be limited in how well it can search for relationships among variables and make predictions.

As one example, the federal risk adjustment program for the Health Insurance Marketplaces uses OLS and includes covariates related to age–sex categories, disease diagnosis, and select disease interactions (Kautter et al. 2014). The diagnosis variables are aggregated based on the Department of Health and Human Services Hierarchical Condition Category (HCC) system. These HCCs correspond to clusters of diagnostic conditions and are created by mapping thousands of ICD‐9 codes. Not all underlying diagnoses recorded in the claims data are used in an HCC‐based risk adjustment formula, and only certain interaction relationships are considered for various competing reasons (Montz et al. 2016; Ellis, Martins, and Rose 2018). Another prominent example is the Medicare Advantage risk adjustment system, which uses similar regression methods and HCC classifications (Pope et al. 2011).

The ACA mandates coverage of mental health and substance use disorders (MHSUD) at parity with coverage of other services (Garfield et al. 2011). However, evidence from older insurance markets similar to the Marketplaces suggests that the provisions might not be sufficient to deter underserving individuals with MHSUD (McGuire and Sinaiko 2010; McGuire et al. 2014). According to Montz et al. (2016), the federal risk adjustment system recognizes only about 20 percent of MHSUD enrollees as individuals with elevated risk and pays plans accordingly, when the remaining 80 percent of MHSUD enrollees have higher than average spending without other HCCs that compensate for their higher spending. One reason for this is that some ICD‐9 codes associated with MHSUD do not map to an HCC included in the federal model. The Montz et al. paper used Clinical Classification Software (CCS) categories‐based mapping of ICD‐9 codes where every ICD‐9 links to a CCS category by design and was able to capture individuals with MHSUD more comprehensively. For example, less than one‐third of individuals in the alcohol‐related disorders CCS group also map to an HCC in 2012, and the average MHSUD spending in this group was over $3,000. The CCS categories were developed by the Agency for Healthcare Research and Quality and have been used in risk adjustment formulas in the past (Ash et al. 2003).

The proportion of individuals with MHSUD who are not recognized by the ACA risk adjustment system and the under compensation of these enrollees is concerning for several reasons. First, in 2013, mental health spending topped the list of most expensive health conditions in the United States with total annual spending of $201B (Roehrig 2016). Second, it has also been established that individuals with MHSUD, recognized and unrecognized by the risk adjustment system, have more than double the average annual total health care spending compared to those without (McGuire and Sinaiko 2010; Montz et al. 2016). This difference in total spending is greater than the cost of MHSUD, which suggests that individuals with MHSUD have higher health care needs beyond just the need for mental health care. Montz et al. also found that, even when accounting for payments triggered by all comorbidities in the Marketplace risk adjustment formula, the unrecognized group was undercompensated by 21 percent. Individuals with MHSUD clearly have elevated risk, and failing to recognize 80 percent of this subpopulation may provide health plans with incentives to select against MHSUD individuals and jeopardize the functioning of the Marketplaces if plans are not adequately compensated for the average individual with MHSUD. Even if portions of the ACA are repealed, any regulated individual health insurance market will likely require risk adjustment of plan payments.

Current risk adjustment systems in the United States consider MHSUD spending together with general health spending. However, there has been substantial interest in the field for a separate MHSUD formula. Individuals with MHSUD can be systematically targeted against enrollment in risk adjustment systems that fail to predict spending accurately and reimburse plans accordingly (Ettner et al. 1998). By separating MHSUD risk adjustment payments, all individuals in the sample have at least one diagnosis, improving the ability to accurately identify average costs. A risk adjustment formula specifically for MHSUD would be similar to the approach sometimes taken in employer‐sponsored insurance markets and in Medicaid managed care, where spending for MHSUD conditions is “carved‐out” into a separate contract due to the higher risk and cost (Frank et al. 1996). The social health insurance system in the Netherlands also includes two separate formulas for short‐term and long‐term mental health care (van Kleef et al. 2018).

Literature on methods for prediction of MHSUD spending is relatively sparse, with few studies contextualizing MHSUD spending for risk adjustment. A review article that looked at 16 published cost prediction studies related to mental health care found that there are a number of methodological challenges that have yet to be addressed (Jones et al. 2007). One of the key limitations has been the lack of cross‐validation, which should be routine. Predicting health care spending is generally challenging because the distribution of spending is heavily right skewed, and this is especially true in the case of MHSUD because the majority of the population have no MHSUD spending in a year. Most studies contend that if the goal is prediction of spending, a one‐part OLS model using raw costs performs consistently as well as or better than two‐part models or those using log‐transformed models (Dunn, Mirandola, and Amaddeo 2003; Jones et al. 2007; Ellis, Martins, and Rose 2018). It is notable that none of the MHSUD studies explored nonparametric machine learning methods that can more easily accommodate nonlinear relationships. Super learner is a nonparametric ensembling machine learning algorithm, established in the statistics literature, and was recently demonstrated to perform better than OLS for risk adjustment of total health spending (Rose 2016).

We investigated whether machine learning can improve on OLS methods for MHSUD spending risk adjustment. Performance was evaluated based on cross‐validated R ² and predictive ratios (PRs), which are ratios of predicted spending to observed spending for subgroups. We developed a risk adjustment function specifically for individuals with MHSUD using super learning, the first machine learning‐based formula for MHSUD spending risk adjustment ever created. A second major goal of this study was to examine the predictive performance of CCS‐based categories versus HCCs to capture diagnosis information in our MHSUD risk adjustment function.

Methods

Data

The data for this analysis came from Truven MarketScan's Commercial Claims and Encounters database, which contains individual‐level claims for enrollees insured by health plans and large employers (Adamson, Chang, and Hansen 2008). We created a sample of 1,700,856 individuals continuously enrolled in the years 2012–2013 and further identified 212,837 individuals with MHSUD diagnoses that were included in our MHSUD sample.

To identify enrollees and related costs, we focused only on MHSUD inpatient services and outpatient service‐related costs, excluding prescription drugs because it is difficult to accurately attribute drug prescriptions to MHSUD versus other conditions (Montz et al. 2016). We defined individuals as having a MHSUD in 2012 if they had at least one inpatient or outpatient principal MHSUD diagnosis based on ICD‐9 codes. According to this classification, there were 15,414 individuals that had an MHSUD diagnosis during an inpatient visit and 207,848 individuals that had an MHSUD diagnosis during an outpatient visit. There were 10,425 individuals that were in both groups.

To calculate MHSUD spending, we summed over outpatient and inpatient MHSUD spending. Inpatient MHSUD spending for an individual was calculated by adding the payments for services that were associated with a major diagnostic category of “mental disease and disorders” and “alcohol/drug use and alcohol/drug induced organic mental disorders.” The outpatient MHSUD spending for an individual was calculated by adding the payments for services where either the provider codes or the primary diagnosis ICD‐9 codes were associated with an MHSUD. The provider codes included for this categorization were “mental mealth and chemical dependency,” “mental health facilities,” “chemical dependency treatment center,” “mental health and chemical dependency day care,” “psychiatry,” “psychiatric nurse,” “therapists – supportive,” “therapists – alternative,” and “psychologist.” During an outpatient visit, a provider other than those in the aforementioned categories might diagnose an enrollee with an MHSUD. Thus, we also included payments for services where the primary diagnosis was an ICD‐9 code associated with MHSUD, regardless of the provider.

MHSUD spending and total spending were calculated for 2013, and the predictor variables represent 2012 data; thus, we focus on prospective risk adjustment. To predict MHSUD spending, we used a combination of demographic and diagnostic covariates. The demographic covariates were age, sex, employer classification, employment status and industry, and geographic region. A total of 15 CCS categories and 9 HCCs were used to create diagnostic indicator variables. Because we defined our MHSUD sample as those with a MHSUD diagnosis based on ICD‐9 codes, each individual was associated with at least one CCS category, but this was not true for HCCs. All categorical variables in our dataset were converted to indicator variables, resulting in a total of 55 predictors in our dataset.

Statistical Analysis Procedure

The goal of this analysis was to generate the best predicted values for MHSUD spending Y, given demographic and diagnostic covariates X, while also considering the policy‐relevant issue of payment by spending subgroups. We formalized the measure of errors in prediction by using a loss function. Although health care spending data are usually right skewed (many individuals with moderate health care costs and a few high spenders with large costs), the squared loss error function is commonly used in risk adjustment, and the one we employ here. We return to alternative loss function approaches in our discussion section.

Risk adjustment generally uses parametric regression; it is easy to understand, implement, and interpret. However, parametric regressions make strong assumptions, including in the strict specification of the relationships between the outcome and predictors, and we may wish to consider approaches that make fewer assumptions. We selected a set of additional algorithms that have different methods of searching for relationships among variables compared to OLS.

Penalized regression methods (including LASSO, elastic nets, and ridge regression) tackle issues related to many possibly colinear covariates by shrinking the coefficients of some variables toward (or to exactly) zero (Friedman, Hastie, and Tibshirani 2001). This can lead to more parsimonious regressions that, in the context of risk adjustment, may be less susceptible to upcoding by insurers (Rose 2016). Polynomial regression splines relax the assumptions of OLS by allowing for local piecewise functions of the predictors (Friedman 1991), which may capture additional nuances between variables that OLS misses. Random forests average over many decision trees that split the predictor space into nonoverlapping regions, sequentially increasing the homogeneity of the observations for the outcome in those regions (Breiman 2001). Neural networks define the relationship between the predictors and the outcome by a series of interconnected nodes (Hornik, Stinchcombe, and White 1989). Both random forests and neural networks may find nonlinearities, such as interactions between predictors; OLS would not include without prespecification. For more details on these and other statistical learning methods, we guide interested readers to Friedman, Hastie, and Tibshirani (2001) and James et al. (2013).

While we could have performed k‐fold cross‐validation of the algorithms described above, and simply selected the algorithm with the smallest cross‐validated mean squared error, we chose to go one step further and select the best weighted average of these algorithms. The best weighted average may perform better than the best single algorithm. We therefore implemented the super learner, which is an ensemble learning method that allows us to perform this task with optimal finite and asymptotic performance. To estimate the optimal weight vector for the super learner, we regressed the outcome Y on the cross‐validated predicted values for each algorithm, restricting the family of weighted combinations to a convex combination. This results in a coefficient for each algorithm in our collection, many of which will be zero. It has been shown that this procedure generates a prediction function with the smallest mean squared error (van der Laan, Polley, and Hubbard 2007; van der Laan and Rose 2011). To obtain predicted values from the super learner for the original dataset or a new dataset, we fit each algorithm on the full dataset and combine these predicted values with the estimated weights. To evaluate the super learner, we obtained cross‐validated predicted values by performing k‐fold cross‐validation on the entire super learner procedure.

Our implementation of the super learner also involved additional layers of variable selection that will apply to all algorithms, even those that do not inherently perform variable selection. Thus, the super learner incorporated variable selection as a way to compare multiple variable sets. The cross‐validated metrics for algorithms considering subsets of variables can then be evaluated in comparison to each other and the full covariate set. These subsets of covariates can be user defined or selected using common variable selection algorithms such as LASSO or random forests. If a machine learning technique is used, the screening steps are done within the k‐fold cross‐validation to fairly evaluate performance. In addition to the full covariate set with demographic information and diagnostic information from CCS categories and HCCs, we included two subsets of covariates in combination with demographic information: diagnostic information from CCS categories and diagnostic information from HCCs.

Seven algorithms (OLS, LASSO, ridge, elastic nets, adaptive splines, random forests, and neural networks) were included with all three versions of the covariate sets, for a total of 21 algorithms. We used the R statistical programming language for implementation, with ten‐fold cross‐validation, relying on the SuperLearner package (Polley et al. 2016). Our primary analysis focused on implementing this super learner in our MHSUD sample, but we also analyzed the full sample.

Evaluation Metrics

Cross‐validated R ² and cross‐validated PRs were our basis of evaluation for the algorithms. These are typical metrics for risk adjustment, with R ² being the most common. We used cross‐validated versions of these metrics to more accurately assess out‐of‐sample performance, but note that most evaluations of risk adjustment are not performed with cross‐validated metrics, despite being recommended. The cross‐validated R ² is given by $R^2=1-\left[{\sum }_{i=1}^N{(Y_i-{\widehat{Y}}_i)}^2/{\sum }_{i=1}^N{(Y_i-{\overline{Y}}_i)}^2\right]$, where N is the sample size, Y _i are the observed outcome values, and ${\widehat{Y}}_i$ are the cross‐validated predicted outcome values. We also calculated the relative efficiency (RE) for each algorithm, which we defined as the ratio of cross‐validated R ² for an algorithm to the cross‐validated R ² for the super learner. The PRs are computed as the ratio of mean cross‐validated predicted spending to the mean observed spending in each quintile of the cross‐validated predicted spending for each algorithm. A PR of 1 suggests that the mean predicted spending for that group is equal to the mean observed spending. In general, PRs between 0.90 and 1.10 are considered reasonable prediction accuracy (Kautter et al. 2014).

Results

A summary of variables used in the analysis is presented in Table 1. The demographic (age, sex, employment, and geographic location), diagnostic (HCC and CCS), and spending summaries were calculated for both the MHSUD sample and the full sample. The distributions of all demographic variables, except sex, were similar between the MHSUD population and the full population. A larger proportion of females (59 percent) appeared in the MHSUD population. While the average MHSUD spending is modest, the average total spending for those with MHSUD diagnoses is about twice that for the full population. The difference in average total spending between the two groups exceeds the average MHSUD spending. This suggests that, on average, individuals with MHSUD incur higher medical costs, and the excess cost goes beyond just the cost of MHSUD.

Table 1.

Summary of Variables in Truven MarketScan Samples

Variables	MHSUD Sample N = 212,837	Full Sample N = 1,700,856
Average total spending	$8,301	$4,181
Average MHSUD spending	$743	$131
Age	42	41
Female (%)	59	49
Active employment status (%)	73	79
Employee classification (%)
Salary	26	30
Hourly	27	30
Industry (%)
Services	21	18
Manufacturing, durable goods	18	19
Transportation, communications, utilities	16	16
Finance, insurance, real estate	11	12
Region (%)
Northeast	15	14
North Central	27	24
South	38	43
West	20	19
HCC (%)
Major depressive and bipolar disorders	19	2
Drug dependence	2	<1
CCS (%)
Mood disorders	40	5
Anxiety disorders	36	4
Screening and history of MHSUD codes	18	2
Adjustment disorders	13	2
Attention‐deficit/conduct/disruptive behavior	8	1

There were nine categories each for employment classification and employment status and 11 industries represented in the dataset. There were 9 MHSUD HCCs and 15 MHSUD CCS categories in total. These variables have been summarized for this table after grouping into larger categories, and only those categories with the largest percentages are presented. The additional categorizations are for the representation of summary statistics only and are not retained in our super learner analysis. Less than 1% of the population fell in each of the HCCs excluded from the table. Less than 10% of the population fell in each of the CCS categories excluded from the table.

Figure 1 shows the distribution of age and sex within each CCS category. The proportion of males exceeds those of females in almost all age groups in some CCS categories, such as alcohol‐related disorders and impulse control disorders. In other CCS categories, including mood disorders and anxiety disorders, the proportion of females exceeds those of males across all ages. When examining all MHSUD together, the proportion of females is higher than males in almost every age group. The only age group where the proportions are similar is 21–25. The distribution peaks for males around age 22, as does the distribution for females, but females have a second larger peak that occurs around age 50.

Figure 1.

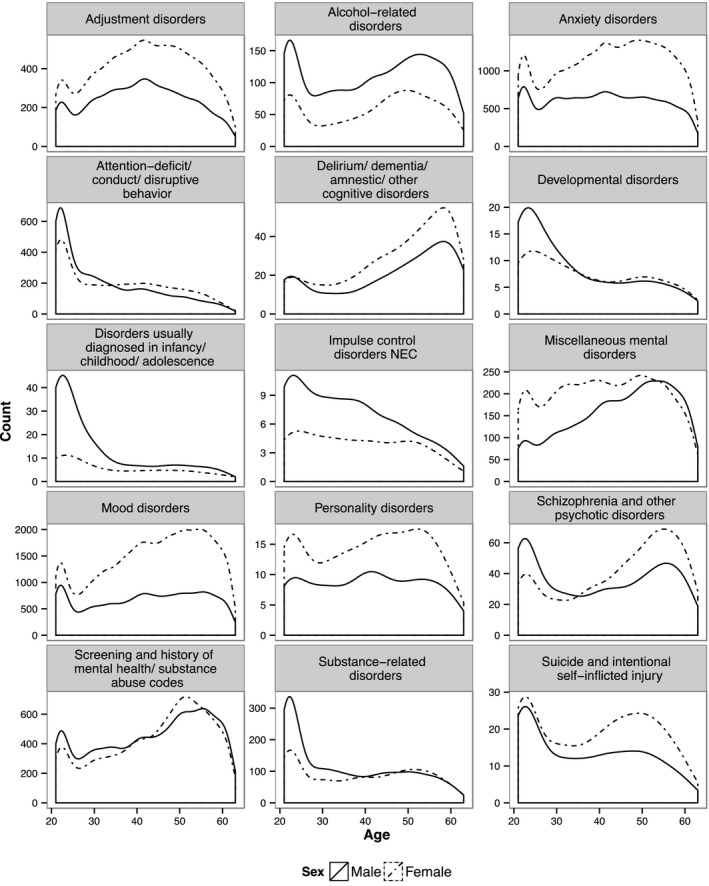
Distribution of Individuals with MHSUD by Age, Sex, and CCS Category

We explored the correlation between HCCs and CCS categories given their different ICD‐9 mapping systems. There is not high positive correlation within HCCs or CCS categories: the largest correlation across HCCs is between drug psychosis and schizophrenia (0.26), and the largest positive correlation across CCS groups is between schizophrenia/other psychotic disorders and screening/history of substance abuse codes (0.16). (See Web Figure S1 in Appendix SA2 for a complete heatmap of correlation results.) In terms of correlation between HCCs and CCS categories, HCCs tend to be most correlated with a single CCS, but not all of the CCS groups are well correlated with an individual HCC. (See Web Table S2 in Appendix SA2 for detailed results.)

The final super learner prediction function is a combination of algorithms defined by the weights listed in Figure 2. For prediction of MHSUD spending, the super learner had the highest cross‐validated R ². Random forests with the full set of covariates perform nearly as well as the super learner with a RE = 0.97. The regressions (OLS, LASSO, ridge, and elastic nets) have the next best performance (RE = 0.88), and the adaptive spline is substantially worse (RE = 0.64). Neural network has the worst performance across all variable sets and algorithms and has a cross‐validated R ² of 0.3 percent for the full covariate set. What remains consistent is that, within each algorithm (other than neural networks), the cross‐validated R ² is higher when the CCS variable set is used rather than the HCC variable set. (See Web Table S1 in Appendix SA2 for expanded results.) This supports the idea that for prediction of MHSUD spending, the information contained in the HCCs is not sufficient.

Figure 2.

Super Learner Weight, Cross‐Validated (CV) R ² and Relative Efficiency (RE) in MarketScan MHSUD Sample by Covariate Set

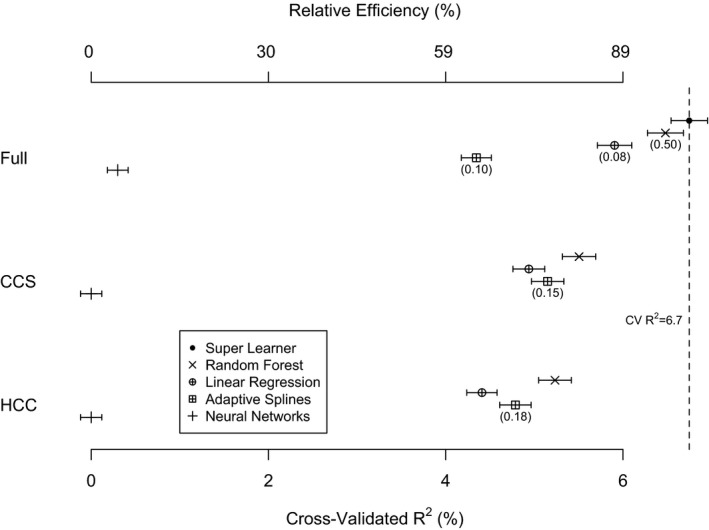
• Note: Elastic nets, LASSO, and ridge are omitted from the plot due to similarity to linear regression results. RE = CV R ²(algorithm)/CV R ²(SuperLearner). Numbers in parentheses indicate the weight in the super learner function; algorithms with no number received a weight of zero.

Figure 3 shows the cross‐validated PRs for MHSUD spending by quintile with the [0.90, 1.10] interval shaded. The PRs are close to 1 for all quintiles of the super learner. For the four regressions and the adaptive splines, the PRs were extremely low in the first quintile. The PRs in the second quintile for the regressions are still not close to 1, but this stabilizes after the third quintile. The adaptive splines have stable PRs close to 1 in quintiles 2 to 5. Some PRs are <0 because the algorithm is underpredicting for low spenders, including sometimes predicting negative costs. (When negative predicted values are bounded to zero, these PRs remain low, although not negative.) The random forests have stable PRs close to 1 for all quintiles, although overpredicting in the first quintile. The neural networks have PRs near 1 for all quintiles; however, this is due to this algorithm simply predicting values close to the mean for each observation.

Figure 3.

Predictive Ratios by Quintile for Predicted MHSUD Spending

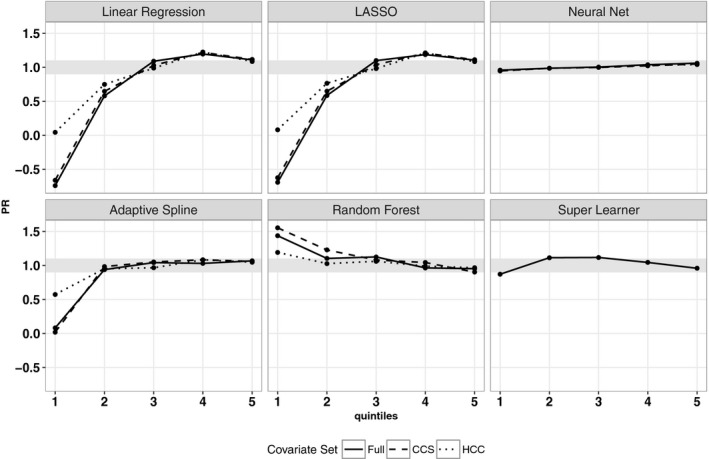
• Note: Elastic nets and ridge are omitted from the plot due to similarity to LASSO and linear regression results.

We also display the distribution of differences in predicted MHSUD spending for selected algorithms compared to the super learner in Figure 4. The distributions for random forests and adaptive splines are closely centered around 0, which demonstrates that for most of the observations, the predictions from the two algorithms are similar to those of the super learner. In contrast, the distribution for neural networks has the widest spread and is right skewed. The four regressions have slightly left‐skewed distributions. The poor performance of the adaptive splines with respect to cross‐validated R ², yet strong performance when looking at PRs and distribution of differences, can be explained by a single outlier value. Adaptive splines overpredict spending for one observation by approximately 150 times, which drives down its cross‐validated R ². This highlights the well‐known problem in risk adjustment of relying on a single metric for the evaluation of fit.

Figure 4.

Differences in Predicted MHSUD Spending Compared to Super Learner

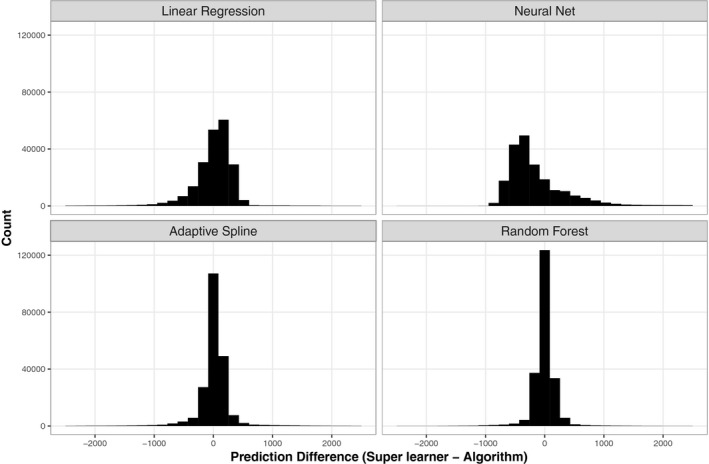
• Note: Elastic nets, LASSO, and ridge are omitted from the plot due to similarity to linear regression results. All predicted values represent those obtained using the full covariate set.

Results in our analysis of the full sample were similar: super learner and random forests were the top performers, and the best cross‐validated R ² for a single algorithm was obtained by the random forest with full covariate set. Each algorithm was slightly worse in the full sample based on cross‐validated R ², except for adaptive splines, which was substantially worse, with cross‐validated R ² that rounded to 0.0 percent. The PR patterns in the full sample mirrored those in the MHSUD sample for all algorithms.

Discussion

In this study, we introduced a nonparametric machine learning framework to predict MHSUD spending for individuals with MHSUD (as defined by CCS diagnoses) to develop a separate MHSUD risk adjustment function. We used cross‐validated metrics to evaluate the prediction performance of all the algorithms considered. Cross‐validation gives a fair evaluation of algorithm performance, particularly in the presence of algorithms that are prone to overfitting. We found that the super learner improved on OLS in terms of cross‐validated R ² and PRs. In fact, super learner performed better than all linear regressions considered in our study. Furthermore, we demonstrated that nonlinear algorithms, such as random forests, provided nontrivial improvements compared to linear regressions. This suggests there may be complex nonlinear relationships and interactions in our data that parametric regressions were not able to capture.

It is worth noting that the cross‐validated R ² values for most of our algorithms were generally low. Prediction of mental health care spending is difficult, and diagnosis‐based risk adjustment functions have an average R ² of 6.7 percent (Hermann, Rollins, and Chan 2007), where most studies did not use cross‐validation. R ² values based on fitting all observations tend to be higher than cross‐validated R ² values. Thus, 6.7 percent likely overestimates the performance that would be obtained with pervasive cross‐validation. The super learner crossed‐validated R ², which was the highest of all algorithms we considered, was 6.7 percent for MHSUD spending. However, the noncross‐validated R ² for the super learner was 9.0 percent, an improvement of 2.3 percentage points (or 34 percent higher) compared to the performance reported in the previous literature. We also found that our cross‐validated R ² values in the sample containing individuals with and without MHSUD were similar to the MHSUD sample and in fact were better in the MHSUD sample. Thus, it may not be necessary to train a MHSUD‐specific risk adjustment formula on the larger sample containing individuals with and without MHSUD.

The fact that random forests was the best single algorithm is a significant finding as well. Previous work implementing super learner to predict total spending found that although super learner minimized the cross‐validated risk, the best single algorithm was still a linear regression (Rose 2016). Moreover, other risk adjustment studies beyond that paper have explored various regressions but, to our knowledge, have not considered or compared regression to random forests. The performance of the random forests improved on linear regression by about 10 percent, which is notable for a risk adjustment prediction function. These results suggest that there is an incentive to explore machine learning algorithms for risk adjustment.

A major finding of this study was the higher cross‐validated R ² of the algorithms using CCS categories as diagnostic variables compared to the algorithms using HCCs alone, indicating they are more predictive of MHSUD spending. The approach we used to evaluate the predictive performance of the HCCs and CCS categories also demonstrates a process for variable selection within the framework of super learner. This framework can also be used in conjunction with screening algorithms like random forests (on the basis of variable importance) and LASSO (on the basis of nonzero coefficients) to find a more parsimonious prediction function (Rose 2016; Rose, Bergquist, and Layton 2017). This has been done in the context of a risk adjustment function for total spending, where the results showed that a random forests‐screened version of the variables retains similar predictive performance in terms of cross‐validated R ² (Rose 2016). This type of variable screening could be applied in the context of MHSUD risk adjustment as well.

There are a few limitations in our methodology. Firstly, we included a small set of algorithms in our collection and many used the default tuning parameter settings, which may not be optimal. An expanded approach would be to include a much larger set of algorithms with a range of tuning parameter specifications. While the objective of this paper was to identify whether machine learning had the potential to outperform OLS for MHSUD spending, a larger set of algorithms is a natural extension of this work. Secondly, we did not account for prescription drug costs because we are not able to deterministically link prescription drugs with MHSUD and to avoid complications regarding how we define our population of individuals with MHSUD. Had we included drug costs in our analysis, the spending for each individual would be larger and there would be increased variation in costs between individuals. While this could have impacted our cross‐validated R ², we do not have any prior belief that this would disproportionately impact our results. Finally, we used a database of commercially insured enrollees to create our prediction functions. While these enrollees are generally ineligible to obtain insurance through the Marketplaces, the MarketScan database is used by HHS to calibrate risk adjustment formulas for the Marketplaces, and several studies for evaluating ACA risk adjustment use these data (Kautter et al. 2014; Centers for Medicare Medicaid Services 2016; Montz et al. 2016).

There are a number of other natural extensions. For example, we could implement a two‐part version of super learner where the first part predicts whether an individual is likely to have MHSUD and the second part calculates the expected spending given that the individual has MHSUD. We could also consider log transform or square root transform of the spending variable as has been done in the literature (Montez‐Rath et al. 2006; Ellis, Martins, and Rose 2018). Although our research suggested that data with raw costs should suffice when the goal is prediction, we could certainly assess this with a two‐part approach and transformed costs. Additionally, we could study other loss functions, such as the quasi‐log‐likelihood for bounded continuous outcomes.

These results strengthen our scientific knowledge about the ability to improve MHSUD spending predictions using nonparametric machine learning and differing diagnostic variable definitions. We found that both super learning and individual machine learning approaches can improve MHSUD spending predictions compared to standard practice, which is parametric regression. This had not been explored previously in the literature. We also see that CCS categories are more predictive of MHSUD spending than HCCs alone, which is an important and novel finding. Although we approached the issue in the context of the ACA, there are over 50 million health care enrollees in the United States that are part of a health plan that uses risk adjustment. The results of this study therefore have broader implications for general risk adjustment.

Supporting information

Appendix SA1: Author Matrix.

Table S1: Super Learner Weight, Cross‐Validated (CV) R ², and Relative Efficiency (RE) for Competitive Algorithms in MarketScan MHSUD Sample.

Table S2: HCCs and Single Most Highly Correlated CCS Category.

Figure S1: Heatmap of Correlation for HCCs and CCS Categories.