Plasmonic thin film InP/graphene-based Schottky-junction solar cell using nanorods

Graphical abstract

Abstract

Herein, the design and simulation of graphene/InP thin film solar cells with a novel periodic array of nanorods and plasmonic back-reflectors of the nano-semi sphere was proposed. In this structure, a single-layer of the graphene sheet was placed on the vertical nanorods of InP to form a Schottky junction. The electromagnetic field was determined using solving three-dimensional Maxwell's equations discretized by the finite difference method (FDM). The enhancement of light trapping in the absorbing layer was illustrated, thereby increasing the short circuit current to a maximum value of 31.57 mA/cm² with nanorods having a radius of 400 nm, height of 1250 nm, and nano-semi sphere radius of 50 nm, under a solar irradiation of AM1.5G. The maximum ultimate efficiency was determined to be 45.8% for an angle of incidence of 60°. This structure has shown a very good light trapping ability when graphene and ITO layers were used at the top and as a back-reflector in the proposed photonic crystal structure of the InP nanorods. Thence, this structure improves the short-circuit current density and the ultimate efficiency of 12% and 2.7%, respectively, in comparison with the InP-nanowire solar cells.

Introduction

Solar cells, which convert solar energy into electrical energy with remarkable conversion efficiencies, are attractive candidates for renewable [1], endless and clean power sources [2], [3]. Meanwhile, thin solar cells are a very important class of photovoltaics and have recently become the subject of intense research, commercialization, and development efforts due to their high efficiency and low cost. Commonly, the film thickness is equivalent to two microns or less, and is used in absorptive materials devices [4]. Light trapping is one of the methods of increasing light absorption in thin film solar cells, due to multiple reflection within the absorbing layers [5], [6], [7]. Light-trapping can be achieved by the formation of a wavelength-scale texture on the substrate and by depositing thin layers of the solar cell on it [8]. Compared with the generally used Si, indium phosphide (InP) has a direct band gap of 1.34 eV [9], [10], which is located in the broad range of the solar energy spectrum [11]. InP solar cells are very desirable as space solar cells [12]. Graphene is the first substance discovered with a 2D atomic crystal [13], [14], having a honeycomb lattice structure. Graphene has a high carrier mobility [15], remarkable conductivity, and transparency [11]. It has great potentials for applications in the making of novel optoelectronic and electronic devices [16], [17], [18], [19], [20]. As a result of its special characteristics, graphene is an ideal electrode for use in thin solar film cells [11]. The graphene-semiconductor Schottky junction offers a new platform for photovoltaic devices. A Schottky junction is created if the work function difference between the metal and the semiconductor is large enough and the semiconductor carrier density is moderate or low [1]. In addition, the fabrication of Schottky junctions has the benefit of low-cost and simplicity [2].

Recently, Schottky junction solar cells have been made with a single layer of graphene on Si substrate, so that graphene behaves as a metal [21]. Graphene-based Schottky junction solar cells have been displayed on various substrates such as CdS [22], CdSe [22], Si [22] and InP [11] with power conversion efficiencies ranging from 0.1 up to 2.86%. Miao et al. [22] demonstrated a power conversion efficiency of 8.6% for a doped graphene/n—Si Schottky junction solar cell. Shi et al. [21] have shown a TiO₂-G-Si solar cell showed excellent device parameters including an open-circuit voltage of 0.612 V, a fill factor of 72%, and an incident photon to electron conversion efficiency of up to 90% across the visible spectrum. Wang et al. [11] demonstrated a graphene/thin film InP Schottky junction. The proposed solar cell was shown power conversion efficiency of 3.3% [11].

In this article, a novel InP-based graphene-Schottky junction solar cell, composed of InP-nanorods is proposed. A thin layer of silver is deposited on one side of the nanorods with the semispherical surface serving as a back-reflector with a single layer of graphene on top of the InP nanorods, to improve the optical properties of the proposed solar cell. The indium tin oxide (ITO) and graphene layers on top of the nanorods and silver layer on the bottom of the solar cell structure form an optical waveguide which facilitates light trapping. The proposed solar cell architecture increases the light absorption, the short-circuit current density and the ultimate efficiency overall incident wavelengths in the solar spectrum from 400 to 920 nm.

Material and methods

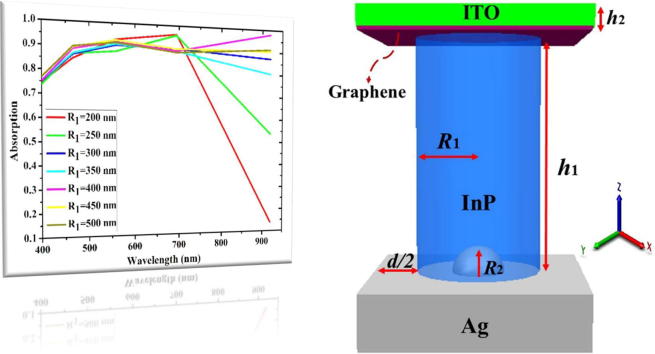
The layer stack of the graphene-InP Schottky junction solar cell is shown in Fig. 1. This structure is periodic in the x and y directions. The specifications of layers are Indium phosphide (InP) nanorods with a height of h₁ and a radius of R₁, nano-semi sphere silver with a radius of R₂ grown on a silver-coated substrate, a single layer of the graphene sheet, an anti-reflective layer of ITO on top of a graphene layer with the thickness of h₂. The edge-to-edge distance between the nanorods of InP is equal to d.

Fig. 1.

Three dimensional (3D) schematics view of the InP-based graphene Schottky junction solar cell.

To obtain a realistic solar cell performance, the spectrum of AM 1.5G is utilized to determine the wavelength dependent absorption (A(λ)) over the sunlight electromagnetic spectrum. The relation between the incident power, P_in (λ), output power, P_out (λ), and A(λ) are given as [23]:

$$A(\lambda )=\frac{P_{\text{in}}(\lambda )-P_{\text{out}}(\lambda )}{P_{\text{in}}(\lambda )}$$ (1)

This helps to calculate the weighted absorption of < A_w> within the wavelength range of λ₁ and λ₂ [24], [25], [26]:

$$\langle A_{\text{w}}\rangle =\frac{{\int }_{{\lambda }_1}^{{\lambda }_2}A(\lambda )\psi (\lambda )d\lambda }{{\int }_{{\lambda }_1}^{{\lambda }_2}\psi (\lambda )d\lambda }$$ (2)

Here, ψ(λ) is the incidence solar flux per unit wavelength and λ₁=400 nm and λ₂ = 920 nm (λ₂ = 920 nm-corresponding to the band edge for InP) are assumed. Short-circuit current density (J_sc) can also be calculated [27] as

$$J_{\text{SC}}=\frac{e}{\mathit{hc}}{\int }_{{\lambda }_1}^{{\lambda }_2}\lambda A(\lambda )\psi (\lambda )d\lambda$$ (3)

Wherever h, c, and e are the Planck constant, the speed of light in vacuum space and the electron charge density, respectively. The short circuit current is proportional to the number of incident photons at the top of the bandgap; it is considered that all photons are absorbed to generate the electron-hole pairs and each photo-generated carrier can reach the electrodes [28], [29], [30]. The finite difference method (FDM) is used to determine the electromagnetic fields (optical fields) propagated through the structure. In this method, Maxwell’s equations are discretized in the solar cell structure.

To evaluate the optical absorption performance of the photovoltaic, the ultimate efficiency ($\eta$) is calculated, which is described as the efficiency of the solar cell as the temperature approaches 0 K, when each photon with energy higher than the bandgap energy generates an electron-hole pair [31], [32].

$$\eta =\frac{\frac{2\pi {\mathit{hAQ}}_s}{{\lambda }_g}}{P_{\mathit{in}}}$$ (4)

$$\eta =\frac{{\int }_0^{{\lambda }_{\text{g}}}A(\lambda )\psi (\lambda )\frac{\lambda }{{\lambda }_{\text{g}}}d\lambda }{{\int }_0^{{\lambda }_{\text{g}}}\psi (\lambda )d\lambda }$$ (5)

Which ${\lambda }_{\text{g}}$ and $Q_s$ are the wavelength corresponding to the bandgap wavelength of absorption layer and the number of quanta of wavelength shorter than ${\lambda }_{\text{g}}$ incident per unit area per unit time.

Results and discussion

In the wavelength range between 400 and 920 nm, the normalized absorption A(λ) as a function of wavelength is shown in Fig. 2, for different radii of InP nanorods. By increasing the radius of nanorods from 200 to 500 nm, the optical absorption of the proposed structure can be greatly enhanced at the IR (Infrared Radiation)-wavelength. The use of a silver nano-semi sphere as a back reflector creates localized surface plasmons on the silver nano-structures. Thus, under appropriate conditions, this structure effectively reflects the incident optical power.

Fig. 2.

Absorption as a function of wavelength for different radius of InP nanorods (R₂ = 50 nm, d = 100 nm, h₁ = 1000 nm, and h₂ = 65 nm).

The thickness of the anti-reflection coating layer of ITO must satisfy the relation h₂ = λ/4n, where λ and n are the wavelength and refractive index of the anti-reflection coating layer, respectively. The thickness of ITO was determined as 65 nm at a wavelength of 510 nm with a reflective index of 1.93. By considering the nano-semi sphere radius of 50 nm, the distance between adjacent nanorods of 100 nm, and height of nanorods of 1000 nm, the weighted absorption as a function of the radius of nanorods determined is shown in Fig. 3(a). Meanwhile, the short-circuit current density as a function of the radius of nanorods is depicted in Fig. 3(b). The maximum value of the short current circuit and the weighted absorption was obtained at a radius of about R₁ = 400 nm, due to the maximum reflectance at the nanorod/air interface. As can be observed in Fig. 3, the absorbed optical power increased with increase in the radius of the nanorods (R₁ < 400 nm) because more optical power entered the InP-nanorods. For the radius of nanorods higher than 400 nm, the trapped optical power became reduced as a result of the decrease in the path length of the reflected optical power.

Fig. 3.

(a) Weighted absorption 〈A_w〉 and (b) short current circuit density (J_sc) as a function of R₁ (R₂ = 50 nm, d = 100 nm, h₁ = 1000 nm, and h₂ = 65 nm).

Another variable parameter for increasing the trapping of light in this structure is the distance between the InP nanorods (d). The gap between the nanorods is changed from 50 to 200 nm to determine the absorption and short-circuit current density (see Fig. 4) by assuming R₁ = 400 nm and h₁ = 1000 nm while the remaining parameters are kept constant. Fig. 4 is shown that the maximum values of the short circuit current density of 31 mA/cm² and the weighted absorption of 0.92, occurred at a distance of 75 nm between nanorods. It can be observed that the guiding light decreases within the InP-nanorods as the gap between the nanorods increases in the solar cell structure. By increasing the gap between the InP nanorods, the spatial distribution density of InP-nanorods decreased and consequently, light trapping reduced in the InP nanorods.

Fig. 4.

(a) Weighted absorption 〈A_w〉 and (b) short circuit current density (J_sc) versus d (R₂ = 50 nm, R₁ = 400 nm, h₁ = 1000 nm, and h₂ = 65 nm).

In the next step, the weighted absorption and short-circuit current density were also determined for the various heights of InP nanorods while R₁ = 400 nm and d = 75 nm were kept constant. The maximum short circuit current density of 31.36 mA/cm² was obtained at h₁ = 1250 nm. By increasing the height of the InP nanorods above 1250 nm (h₁ = 1250 nm), the weighted absorption and the short-circuit current became reduced because less optical power reached the nano-semi sphere and was reflected back, thus reducing the light trapping (see Fig. 5(a) and (b)). The weighted absorption of the solar cell without the nano-semi sphere was also determined for the various heights of InP nanorods which causes less light trapping (Fig. 5(a)). Also, the extinction spectrum of the plasmonic nano-semi sphere (defined as the sum of absorption cross-section and scattering cross-section) is shown in Fig. 5(c) and is in good agreement with Fig. 5(a) and (b).

Fig. 5.

(a) Weighted absorption 〈A_w〉, (b) short circuit current density (J_sc) as a function of h₁ (R₂ = 50 nm, R₁ = 400 nm, d = 75 nm, and h₂ = 65 nm), and (c) the extinction spectra of plasmonic nano-semi sphere.

The angle of incidence on the solar cell plays an important role in light trapping to have a maximum propagation length inside the structure. Fig. 6 is shown the short circuit current density (J_Sc) for different angles of incidence of the incoming light for R₁ = 400 nm, d = 75 nm, and h₁ = 1250 nm. The short circuit current density reaches a minimum value at an angle of 30° with respect to the normal incidence and then increases at an incident angle of 60° (J_SC = 31.57 mA/cm²). The scattered light has a maximum propagation length through the solar cell structure at the angle of 60°, results in maximum light trapping, while it reaches to a minim value at the angle of 30°.

Fig. 6.

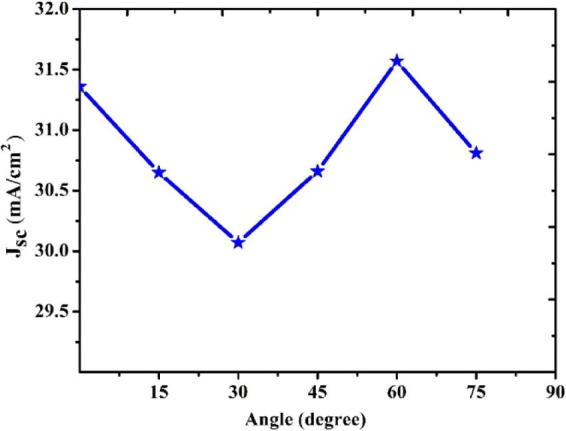
Short circuit current density (J_sc) against different angles of incidence of the incoming light (R₂ = 50 nm, R₁ = 400 nm, d = 75 nm, h₁ = 1250 nm, and h₂ = 65 nm).

Ultimate efficiency is the best estimate of the optical performance of the solar cell. Ultimate efficiency was calculated for different angles of incidence of the incoming light for R₁ = 400 nm, d = 75 nm, and h₁ = 1250 nm (see Fig. 7). It was observed that the maximum value of ultimate efficiency is 45.8% at an incident angle of 60°.

Fig. 7.

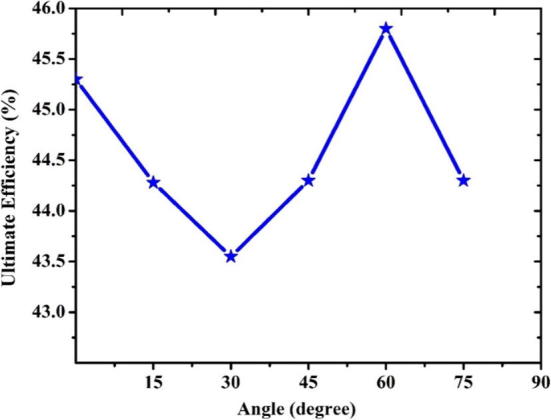
The ultimate efficiency for different angles of incidence of the incoming light (R₂ = 50 nm, R₁ = 400 nm, d = 75 nm, h₁ = 1250 nm, and h₂ = 65 nm).

In the design of thin film solar cells, light trapping is important, so as to increase light absorption. Light trapping occurs due to the presence of ITO and graphene on top and silver at the bottom of the structure. Also, the nanorod photonic crystal structure and plasmonic back-reflectors are an attractive solution to the light trapping of long wavelength photons leading to enhanced light absorption in the periodically structured device. The structure of the anti-reflection coating surface (ITO) is very effective in repressing reflection loss, for example, short circuit current density is with and without the use of ITO 31.57 mA/cm² and 29.43 mA/cm² for an incident angle of 60°, R₁ = 400 nm, d = 75 nm, and h₁ = 1250 nm. Therefore, after coating ITO, the solar cell has shown a much-reduced light reflection in the same wavelength spectrum.

The lateral propagation of the wave on the graphene surface can be observed in the Poynting vector plot as shown in Fig. 8. The Poynting vector on the graphene surface is shown through all angles, thereby increasing the path length of photons within the absorber layer. The graphene-InP interface enhances the surface reflectivity.

Fig. 8.

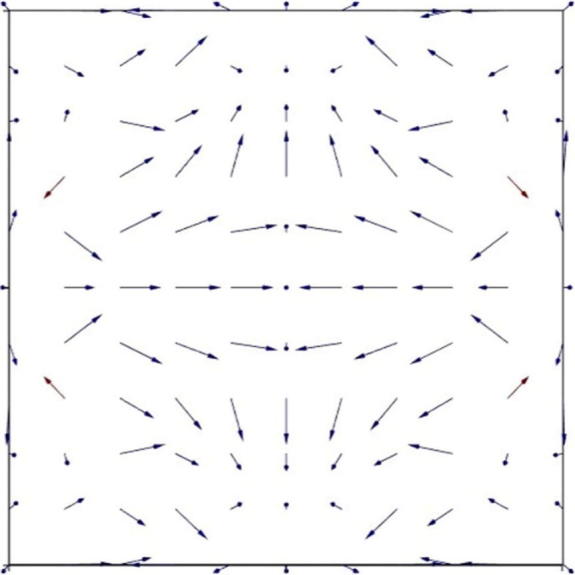
Poynting vector in the surface of graphene (R₂ = 50 nm, R₁ = 400 nm, d = 75 nm, h₁ = 1000 nm and h₂ = 65 nm).

The main advantage of the proposed solar cell in respect to the InP-based nanowire [12], [33], [34] (without a back-reflector and graphene layers) is higher than the short-circuit current density and the ultimate efficiency of 3.37 mA/cm² and 2.7%, respectively.

Conclusions

In this paper, a novel graphene/InP Schottky junction solar cell with a periodic array of nanorods with a back-reflector of nano-semi sphere silver and using an ITO layer of the anti-reflection coating was simulated. 3D simulations were based on a finite difference method (FDM) to determine absorption, the weighted absorption, the short-circuit current, and ultimate efficiency. It was found that an optimized geometry with R₁ = 400 nm, d = 75 nm, h₁ = 1250 nm, R₂ = 50 nm and an incident angle of 60° would absorb 400 nm up to 920 nm wavelength of sunlight, obtaining the short-circuit current density and the ultimate efficiency of 31.57 mA/cm² and 45.8%, respectively. Therefore, this design demonstrates a considerable reduction in absorbing layer thickness with respect to the planar InP-based solar cell.

Conflict of interest

The authors have declared no conflict of interest.

Compliance with Ethics Requirements

This article does not contain any studies with human or animal subjects.