Abstract
Background and Purpose
Development of combination therapies has received significant interest in recent years. Previously, a two‐receptor one‐transducer (2R‐1T) model was proposed to characterize drug interactions with two receptors that lead to the same phenotypic response through a common transducer pathway. We applied, for the first time, the 2R‐1T model to characterize the interaction of noradrenaline and arginine‐vasopressin on vasoconstriction and performed inter‐species scaling to humans using this mechanism‐based model.
Experimental Approach
Contractile data were obtained from in vitro rat small mesenteric arteries after exposure to single or combined challenges of noradrenaline and arginine‐vasopressin with or without pretreatment with the irreversible α‐adrenoceptor antagonist, phenoxybenzamine. Data were analysed using the 2R‐1T model to characterize the observed exposure–response relationships and drug–drug interaction. The model was then scaled to humans by accounting for differences in receptor density.
Key Results
With receptor affinities set to published values, the 2R‐1T model satisfactorily characterized the interaction between noradrenaline and arginine‐vasopressin in rat small mesenteric arteries (relative standard error ≤20%), as well as the effect of phenoxybenzamine. Furthermore, after scaling the model to human vascular tissue, the model also adequately predicted the interaction between both agents on human renal arteries.
Conclusions and Implications
The 2R‐1T model can be of relevance to quantitatively characterize the interaction between two drugs that interact via different receptors and a common transducer pathway. Its mechanistic properties are valuable for scaling the model across species. This approach is therefore of significant value to rationally optimize novel combination treatments.
Abbreviations
- 2R‐1T
two‐receptor one‐transducer
- AIC
Akaike information criterion
- AVP
arginine‐vasopressin
- CH
receptor density in human vessels
- CR
receptor density in rat vessels
- E/[A]
concentration‐effect
- Emax
maximum effect
- FIH
first‐in‐human
- GOF
goodness‐of‐fit
- IIV
inter‐individual variability
- K
the total transducer amount at half‐maximal effect
- KAVP
affinity of AVP on V1A receptors
- KHS
Krebs–Henseleit solution
- KNA
affinity of noradrenaline on α1A‐adrenoceptors
- mAVP/K
maximum transducer amount that AVP can produce normalized by K
- mNA/K
maximum transducer amount that noradrenaline can produce normalized by K
- nAVP
Hill slope index of AVP transduction pathway
- nH
Hill slope index of E/[A] curve
- nM
Hill slope index of the common transduction pathway
- nNA
Hill slope index of noradrenaline transduction pathway
- PBZA
phenoxybenzamine effect on α1A‐adrenoceptors
- PBZM
phenoxybenzamine effect on the common transducer
- pEC50
midpoint location of E/[A] curve
- RSE
relative standard error
- SMA
small mesenteric artery
- VPC
visual predictive check
Introduction
The increasing availability of targeted therapeutic agents has raised interest in rationally developing combination therapies associated with improved efficacy profiles or reduction of side effects (Fitzgerald et al., 2006; Al‐Lazikani et al., 2012). However, the identification and characterization of optimal drug combination regimens are not straightforward. Mathematical approaches to characterize pharmacological interactions between drugs have shown to be of significant relevance to address this challenge (Jonker et al., 2005; Danhof et al., 2007; Van Hasselt and Van Der Graaf, 2015; Gabrielsson et al., 2016; Koch et al., 2016).
The interaction of two agonists that lead to a single phenotypic response through different receptors and a common transduction pathway is one common type of drug–drug interaction. For such an interaction, a theoretical mechanism‐based model was proposed three decades ago (Leff, 1987). According to the geometry of the agonist concentration‐effect (E/[A]) curve, this two‐receptor one‐transducer (2R‐1T) model can account for phenomena like threshold amplification and potentiation and predicts the conditions under which they will occur (Christ and Jean‐Jacques, 1991; Gerthoffer, 1996). Previously, a model based on these principles was used to describe the effect of a single agonist acting simultaneously at two different receptors linked to a common transduction pathway (Van der Graaf et al., 1996). Scaramellini then extended this model to allow for the interacting agonists to have E/[A] curves with different slopes (Scaramellini et al., 1997). This approach provides a framework that can describe another mechanism of drug–drug interaction besides other commonly used mechanism‐based methodologies that focus primarily on the effect of two drugs acting on one receptor (Koch et al., 2016). However, there is still a lack of research on the application of this framework.
Experimental models for drug‐induced vasoconstriction have been extensively used to quantitatively investigate agonist–agonist interactions (Prins et al., 1992; Cohen and Schenck, 2000; Lemos et al., 2002; Segarra et al., 2002; Streefkerk et al., 2003). In the present study, we focused on the pharmacological interaction between http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=2168) and http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=484. Noradrenaline and AVP are two endogenous molecules involved in cardiovascular regulation as well as being used as clinical therapeutic agents to constrict blood vessels. Noradrenaline is a typical treatment for septic shock where AVP can be added with the intent of raising blood pressure or decreasing noradrenaline dosage (Dellinger et al., 2013). We assessed if the previously described theoretical 2R‐1T framework can be used to characterize the interaction between noradrenaline and AVP on blood vessel contraction. Rat small mesenteric artery (SMA) was chosen as the model system, for which it is known that vasoconstriction induced by AVP and noradrenaline is associated with the http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=366 (Stam et al., 1998) and the http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=22 (Stam et al., 1999; Pérez‐Rivera et al., 2007), respectively, involving a common transduction pathway (Mauger et al., 1984). Furthermore, we also investigated if the mechanism‐based basis of the 2R‐1T model can be utilized to allow for translational inter‐species scaling to humans. As far as we know, the present paper is the first account of an application of the 2R‐1T model and its use in translational pharmacology.
Methods
Animals
All animal care and experimental protocols were approved by the local Animal Experiments Committee, under the Dutch National Experiments on Animals Act. Animal studies are reported in compliance with the ARRIVE guidelines (Kilkenny et al., 2010; McGrath and Lilley, 2015), and United States NIH guidelines. Male Wistar rats, a commonly used rat strain in pharmacological studies, were obtained from Harlan, Zeist, The Netherlands.
Rat small mesenteric artery (SMA) preparation
Male Wistar rats (250–350 g, 6–12 weeks) were anaesthetized (sodium pentobarbitone, 60 mg·kg−1, i.p.) and killed by cervical dislocation. The mesentery was removed and placed in ice‐cold modified Krebs–Henseleit solution (KHS) of the following composition (mM): NaCl 119.0, NaHCO3 25.0, KCI 4.7, KH2PO4 1.2, MgSO4 1.2, glucose 5.5, CaCl2 2.5, and EDTA 0.026. Arterial trees were dissected and cleared from surrounding adipose tissue. From each arterial tree, a ring segment (~2 mm in length) was mounted in a myograph (J.P. Trading, Aarhus, Denmark) with separated 6 mL organ baths containing modified KHS at 37°C. The KHS was continuously gassed with 95% O2 and 5% CO2, as described previously (Mulvany et al., 1977). Tissue responses were measured continuously as changes in isometric force.
Following a 30 min stabilization period, the internal diameter of each vessel was set to a tension equivalent to 0.9 times the estimated diameter at 100 mmHg effective transmural pressure (I100 = 200–300 μm) according to the standard procedure of Mulvany & Halpern (Mulvany et al., 1977). After a further 30 min stabilization period, the preparations were challenged five times with noradrenaline (10 μM) with washouts after each challenge. The presence of the endothelium was confirmed by adding with 10 μM of methacholine after the first challenge and tissues which responded with less than 60% relaxation were rejected. The contraction induced by the fifth noradrenaline challenge was regarded as a calibration contraction in the experiment, relative to which all subsequent responses were expressed. This normalization eliminated absolute contractile power differences between vessel segments that result from for example smooth muscle content of the segments.
In all experiments, 60 min prior to construction of each agonist E/[A] curve, a mixture of http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=2286 (30 μM), http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=565 (6 μM) and http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=956 (R(+)‐7‐chloro‐8‐hydroxy‐3‐methyl‐1‐phenyl‐2,3,4,5‐tetrahydro‐1H‐3‐benzazepine hydrochloride; 10 nM) were added to the KHS to block neuronal uptake, β1/β2‐adrenoceptors and dopamine D1 receptors respectively (Stam et al., 1999).
Experimental design
In general, SMAs were exposed in vitro to single or combined challenges of noradrenaline and AVP in varying concentrations, with or without pretreatment with http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=7268, a non‐selective irreversible α‐adrenoceptor blocker which also has a possible effect on calcium channels (Gengo et al., 1984; McPherson et al., 1985).
Interaction experiments without receptor inactivation
Concentration dependent contraction of rat SMA induced by noradrenaline or AVP in the absence or presence of the other drug was investigated according to the paired and single E/[A] curve protocols developed previously for noradrenaline (Stam et al., 1999) and AVP (Stam et al., 1998) respectively. Initial noradrenaline E/[A] curves were first obtained (n = 19) and were followed by 30 min washing and further equilibration for another 45 min. Subsequently, threshold contractions that amounted about 5, 10 or 25% of the maximum of the initial E/[A] curves were induced by AVP through increasing drug concentrations in small steps until desired contraction level was reached. After stabilization of the threshold contraction, second noradrenaline E/[A] curves were obtained. AVP E/[A] curves with no threshold contraction or with threshold contractions induced by noradrenaline that amounted about 5, 10 or 25% of the calibration contraction were obtained as described above but from separate vessel segments (n = 18).
Interaction experiments with prior receptor inactivation
In another set of experiments, the interaction between noradrenaline and AVP on the contraction of rat SMA was also assessed after pretreating the vessel segments with phenoxybenzamine. Prior to the interaction experiments, the vessel segments (n = 8) were pretreated with phenoxybenzamine (3 nM) for 5 min and were then washed eight times during a 30 min period and equilibrated for 45 min. Subsequently, the E/[A] curves of noradrenaline with or without a threshold contraction induced by AVP that amounted about 10% of the calibration contraction were produced as described earlier. Randomization and blinding were not applicable as this is not an intervention study.
Data analysis
Model development
Scaramellini and co‐workers presented a theoretical 2R‐1T model which provides a quantitative framework to interpret the interaction between two agonists, A1 and A2, which bind to two different receptors, R1 and R2, respectively, and produce a common intracellular mediator M leading to a pharmacological effect E (Figure 1) (Scaramellini et al., 1997). For the current research, we analysed the experimental data of noradrenaline and AVP with the 2R‐1T model. The estimation of model parameters and associated uncertainty/confidence intervals was based on simultaneous fitting of all individual data. The data and statistical analysis comply with the recommendations on experimental design and analysis in pharmacology (Curtis et al., 2018).
Figure 1.
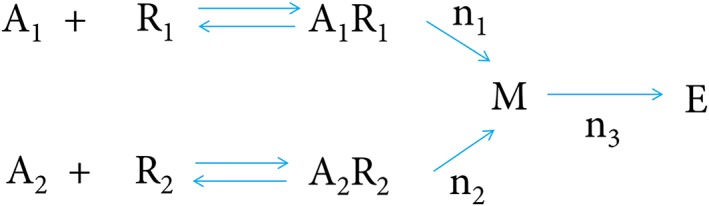
2R‐1T model structure (Scaramellini et al., 1997).
The 2R‐1T model assumes that the intracellular mediators [M]NA and [M]AVP amount depend on drug concentrations and have the algebraic form of a Hill equation (Equations (1) and (2)). The pharmacological effect E is derived by [M]Tot, the summation of mediator concentrations (Equation (3)), also according to the Hill equation (Equation (4)). Our experiments also included the addition of a third drug, phenoxybenzamine. To account for this inhibitor, two additional terms PBZ A and PBZ M were included (Equations (1) and (3)), representing the irreversible blockade effect on α1A‐adrenoceptors and the inhibition effect on the common transducer respectively:
| (1) |
| (2) |
| (3) |
Here, m NA and m AVP represent the maximum transducer amount that noradrenaline and AVP can produce, respectively and can be considered to represent receptor density, [NA] and [AVP] represent the concentrations of these two drugs, n NA and n AVP represent the Hill slope index of the two separated transduction pathways, K NA and K AVP represent the noradrenaline and AVP concentrations that produce half‐maximal amount of [M] NA and [M] AVP, which can be considered as the affinities of noradrenaline and AVP on α1A‐adrenoceptors and V1A receptors respectively. We considered both estimating K NA and K AVP, and fixing these parameters to the published values, identified as 4.27 μM (Nyborg and Bevan, 1988) and 0.24 nM (Bockman et al., 1992) respectively. PBZ A and PBZ M were both constrained to values between 0 and 1. In the absence of phenoxybenzamine, PBZ A and PBZ M were both set to be 1 as the receptor or transducer is intact. Finally, the E/[A] relationship for noradrenaline and AVP was characterized with Equation (4):
| (4) |
Here, E max represents the maximum possible system effect, K represents the amount of [M] tot at half‐maximal value of E, and n M represents the Hill slope index of the common transduction pathway. The absolute value of K is unidentifiable, and was therefore fixed to 1, which means both numerator and denominator of Equation (4) were divided by K. Thus, the estimates of m NA and m AVP could be expressed as m NA /K and m AVP /K .
A mixed‐effect modelling approach was applied to account for inter‐individual variability (IIV). Parameter estimate was performed through the first order conditional estimation method with interaction (FOCEI), implemented in nonlinear mixed‐effect modelling software NONMEM, version 7.3.0 (ICON Development Solutions) (Keizer et al., 2013). IIV was estimated for m NA /K, m AVP /K and E max with Equation (5), where Pi represents the parameter of each experiment, P tp represents typical value of the parameter, and η represents the IIV which was assumed to be log‐normally distributed with mean of 0 and variance of ω2. IIV of K NA and K AVP were also estimated while fixing the corresponding typical values as literature values. Residual error was characterized with additive error model with Equation (6), where Y obs_i represents observations, Y pred_i represents predictions, and ε represents the residual error which was also assumed to log‐normally distributed with mean of 0 and variance of σ2.
| (5) |
| (6) |
Precision of parameter estimates, which was reflected by relative standard error (RSE) of parameters, and the Akaike information criterion (AIC) were regarded as the criteria to assess the goodness‐of‐fit (GOF) of model. Standard GOF plots and a visual predictive check (VPC) were also used to assess the model performance (Nguyen et al., 2017).
Translation to human contractile data
We investigated the extrapolation of the model to human data by adjusting parameters m NA /K and m AVP /K according to the difference in receptor density of α1A‐adrenoceptors and V1A receptors between rat and human vessels (Eq. (7)), while K NA and K AVP were kept unchanged:
| (7) |
Here, P H and P R represent parameter m NA /K and m AVP /K for human and rat respectively, and C H and C R respectively represent the receptor density in human and rat vessels. C H and C R were reported respectively as 61.6 fmol·mg−1 of protein (Yamada et al., 1994) and 101 fmol·mg−1 of protein (Faber et al., 2001) for α1A‐adrenoceptors and 36 fmol·mg−1 of protein (Serradeil‐Le Gal et al., 1995) and 52 fmol·mg−1 of protein (Vågnes et al., 2004) for V1A receptors, making the ratio C H /C R 0.61 and 0.69 for α1A‐adrenoceptors and V1A receptors respectively.
Drug induced E/[A] curves in human were derived from published data where human renal arterial rings were challenged ex vivo with noradrenaline with or without small concentrations of AVP (0.1 and 0.03 nM) (Segarra et al., 2002). The data points were digitized by WebPlotDigitizer, version 3.11 (http://arohatgi.info/WebPlotDigitizer/app/). The scaled model performance was assessed by comparing the result of 500 simulations with observed human data. The predictive performance of the model without any scaling for receptor density was also assessed as a comparison.
Contractile responses in the human study were expressed relative to a response to 100 mM KCl, the relative level of which differs from that of the calibration contraction (i.e. the response to 10 μM noradrenaline) used in our rat experiment. Therefore, to make the scaled model predictions be comparable with the human data, the simulation results were adjusted through being multiplied by the human contraction response induced by 10 μM noradrenaline, which was 150% of the response to 100 mM KCl.
Sensitivity analysis was performed to evaluate the effects of receptor density ratios and drug affinity values on the scaled model predictions respectively. The C H /C R ratio of α1A‐adrenoceptors and V1A receptors as well as K NA and K AVP were set as 0.5‐fold, onefold and twofold of the original values, respectively, and the prediction results were assessed by plotting population prediction results together with the human experimental data where human vessels were challenged with noradrenaline and 0.1 nM of AVP.
Materials
[Arg8] vasopressin, cocaine hydrochloride, methacholine bromide, l‐noradrenaline hydrochloride, phenoxybenzamine hydrochloride and timolol maleate were purchased from Sigma, Zwijndrecht, the Netherlands. SCH 23390 were purchased from Research Biochemicals Incorporated, Natick, USA. Noradrenaline was dissolved in stoichiometric ascorbic acid solution. Methacholine and phenoxybenzamine were dissolved in ethanol, and the final amount of ethanol in organ bath was <1‰ which causes no extra relaxation on the vessel segments (Ru et al., 2008). All other drugs were dissolved in distilled water.
Nomenclature of targets and ligands
Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY (Harding et al., 2018), and are permanently archived in the Concise Guide to PHARMACOLOGY 2017/18 (Alexander et al., 2017).
Results
Effects of noradrenaline, AVP and phenoxybenzamine on contraction
Noradrenaline caused concentration‐dependent contractions of SMAs (Figure 2A). Individual E/[A] curves were fitted to the Hill equation as described in Stam et al. (1998, 1999) to obtain estimates of midpoint location (pEC50 = −log (EC50) and Hill slope (nH). Threshold contractions that amounted to 5.5 ± 0.6% (mean ± SD, n = 4), 12.4 ± 2.3% (n = 8) and 28.4 ± 4.2% (n = 7) of the calibration contraction were induced by 0.13 ± 0.1, 0.08 ± 0.03 and 0.09 ± 0.08 nM AVP respectively. The three threshold contractions to AVP caused a >twofold flattening of the control noradrenaline E/[A] curves [nH changed from 2.67 ± 0.67 (n = 19) to 1.04 ± 0.17, 0.81 ± 0.10 and 0.75 ± 0.06, respectively], and a leftward shift of up to ~fourfold (pEC50 changed from 6.57 ± 0.23 to 6.89 ± 0.29, 7.16 ± 0.32 and 7.15 ± 0.38, respectively), without changing the maximum response (Figure 2A).
Figure 2.
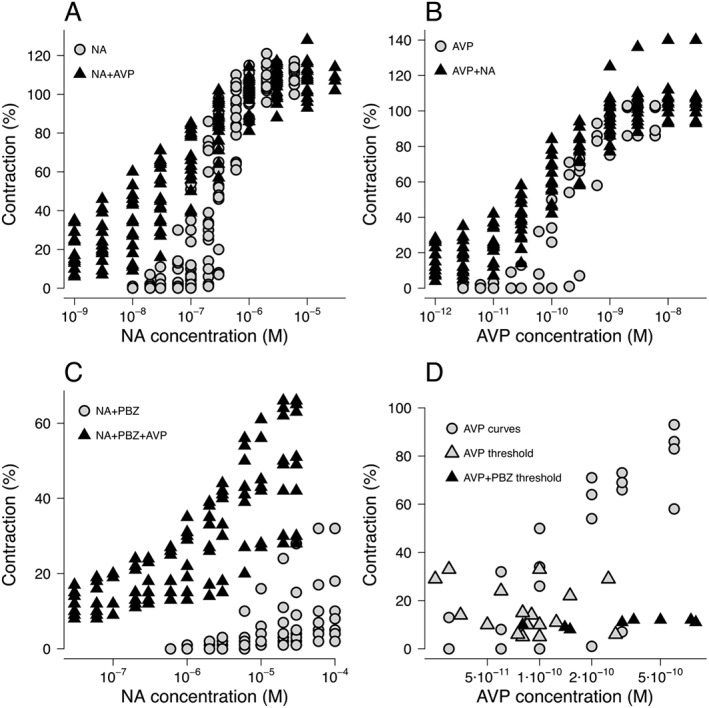
Concentration dependent contraction curves induced by (A) noradrenaline (NA) in the absence of AVP (n = 19) and presence of AVP (n = 19, concentration range from 0.025 to 0.275 nM); (B) AVP with absence of noradrenaline (n = 4) and presence of noradrenaline (n = 14, concentration range from 30 to 280 nM); and (C) noradrenaline with absence of AVP (n = 8) and presence of AVP (n = 8, concentration range from 0.08 to 0.8 nM) while 3 nM phenoxybenzamine (PBZ) was present. (D) E/[A] curves induced by AVP without thresholds (n = 4) and the threshold contractions induced by AVP without (n = 14) or with (n = 8) pretreatment with 3 nM phenoxybenzamine. When phenoxybenzamine was present, higher AVP concentration was needed to reach the same contraction level as when phenoxybenzamine was absent. Responses were expressed as percentages of the contraction induced by the fifth previous noradrenaline (10 μM) challenge.
AVP also caused concentration‐dependent contractions of SMAs (Figure 2B). Pre‐incubating with 0.07 ± 0.05 (n = 4), 0.08 ± 0.03 (n = 5) and 0.21 ± 0.08 (n = 5) μM noradrenaline produced threshold contractions that amounted to 6.0 ± 2.2, 11.2 ± 1.6 and 24.0 ± 3.2% of the calibration contraction respectively. The three threshold contractions to noradrenaline also caused a >twofold flattening of the AVP E/[A] curves compared to control [nH changed from 2.31 ± 1.4 (n = 4) to 1.08 ± 0.17, 0.85 ± 0.17 and 0.83 ± 0.08, respectively], and a leftward shift of up to ~3.5‐fold (pEC50 changed from 9.71 ± 0.32 to 9.96 ± 0.18, 10.22 ± 0.26 and 9.87 ± 0.28, respectively), without changing the maximum response (Figure 2B). The reported n numbers were used only for data display and calculation of SD and not for any statistical comparison.
Pretreating with phenoxybenzamine reduced the maximum noradrenaline‐induced contraction from 111 ± 4.8 to 10 ± 10.3% (n = 8) and caused a rightward shift of the noradrenaline E [A] curves (Figure 2C). When AVP was added, the noradrenaline E/[A] curves were potentiated and flattened with maximum contraction increased to 49 ± 15.1% (n = 8) (Figure 2C).
In addition to the well‐established inhibitory effect of phenoxybenzamine on noradrenaline (Van der Graaf and Stam, 1999), when plotting AVP‐induced E/[A] curves together with AVP‐induced threshold contractions with or without presence of phenoxybenzamine, the combination of AVP with phenoxybenzamine also appeared to be associated with an inhibitory effect (Figure 2D).
Model development and evaluation
In their theoretical paper, Scaramellini et al. (1997) demonstrate that the 2R‐1T model predicts a variety of patterns of agonist E/[A]‐curve location and slope changes induced by the presence of another agonist. Our data (leftward shift, flattening and no change in maximum response) are entirely consistent with the scenario for two full agonists which share a common transduction pathway with a steep slope. We therefore developed our further analysis of the data on the basis of this 2R‐1T model framework.
The parameter estimates obtained after fitting the experimental data to the 2R‐1T model are shown in Table 1. Two models were considered. In Model 1, all parameters were estimated but the RSEs of m AVP /K and K AVP were >100%, indicating that the information our experimental data provided could not support precise estimation of these parameters. Nonetheless, K NA could be estimated with better precision (RSE = 26%) and was close to the previously reported values (Nyborg and Bevan, 1988). Other parameters were estimated with acceptable precision (RSE < 25%). After fixing the typical value of K NA and K AVP to published values while estimating corresponding IIV (Model 2), all model parameters could be estimated with greater precision (RSE ≤ 20%). The AIC of Model 2 was 3777 and was 22 lower than that of Model 1, which was 3799, indicating that Model 2 had better GOF than Model 1. Therefore, the model with fixed K NA and K AVP was selected to characterize our experimental dataset. Model evaluation results of Model 2 are shown in Figures 3 and 4. Both population predictions and individual predictions were comparable to the observations (Figure 3A, B), and no trends were observed in the conditional weighted residuals (Figure 3C). The VPC plots (Figure 4), where model simulations were plotted together with observed data points for different dose regimens, showed that most observations could be adequately covered within the 97.5th and 2.5th percentiles of model simulations, and the 50th percentiles of observations could mostly fit within the 95% confidence intervals of the 50th percentiles of simulations, although wider simulation confidence intervals were shown in Figure 4C, E, F due to the fewer curves involved in the corresponding scenarios. Using the developed model, the interactions between noradrenaline and AVP concentrations on contraction can be visualized using a response surface plot (Figure 5).
Table 1.
Parameter estimates of the model where K NA and K AVP were not fixed (Model 1) and where K NA and K AVP were fixed (Model 2)
| Model 1 | Model 2 | |||||
|---|---|---|---|---|---|---|
| Estimates | RSE% | IIV (CV%) | Estimates | RSE% | IIV (CV%) | |
| Parameter | ||||||
| m NA /K (−) | 8.35 | 13.2 | 34.8 | 7.56 | 8.3 | 25.5 |
| n NA (−) | 0.658 | 4.7 | – | 0.665 | 3.8 | – |
| m AVP /K (−) | 8.59 | 189.8 | 44.3 | 1.75 | 6.9 | 27.0 |
| n AVP (−) | 0.495 | 14.5 | – | 0.690 | 7.1 | – |
| K NA (10−6 M) | 5.65 | 26.4 | – | 4.27 FIX | – | 51.6 |
| K AVP (10−9 M) | 18.1 | 478.5 | – | 0.24 FIX | – | 91.2 |
| E max (%) | 105 | 2.0 | 9.0 | 108 | 1.4 | 8.0 |
| n M (−) | 3.77 | 5.4 | – | 3.75 | 5.3 | – |
| PBZ A | 0.120 | 24.1 | – | 0.132 | 20.4 | – |
| PBZ M | 0.585 | 14.9 | – | 0.557 | 11.6 | – |
| Residual errors | ||||||
| ADD (SD, %) | 4.66 | – | – | 4.53 | – | – |
ADD, additive error; CV, coefficient of variation; IIV, inter‐individual variability.
Figure 3.
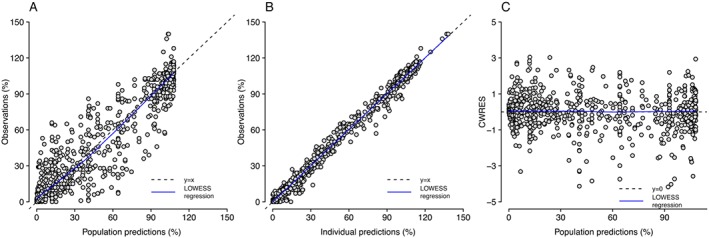
GOF plots for the final model, including observations versus population predictions (A), observations versus individual predictions (B), and conditional weighted residual errors (CWRES) versus population predictions (C). Locally weighted scatterplot smoothing (LOWESS) regression lines were also plotted.
Figure 4.
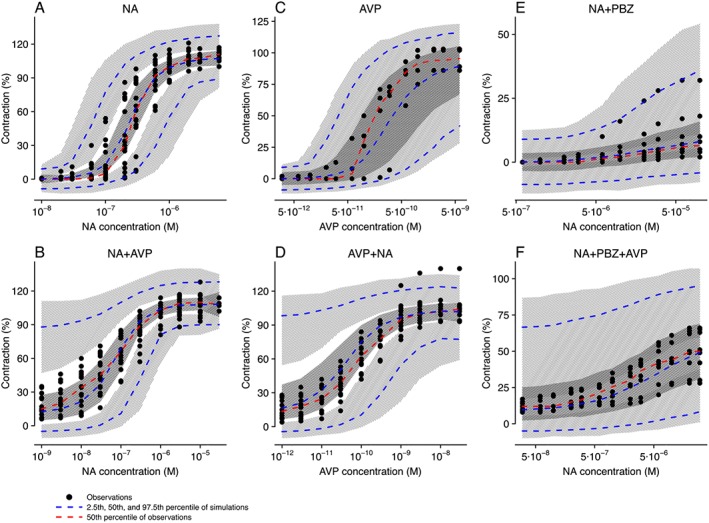
Visual predictive check of the final model stratified on different dose regimens: (A) noradrenaline (NA) only; (B) noradrenaline with fixed concentrations of AVP; (C) AVP only; (D) AVP with fixed concentrations of noradrenaline; (E) noradrenaline only when phenoxybenzamine (PBZ) was added; (F) noradrenaline with fixed concentrations of AVP when phenoxybenzamine was added. Light grey hatching represents 95% confidence interval of the 2.5th and 97.5th percentile of simulations, and dark grey hatching represents 95% confidence interval of the 50th percentile of simulations.
Figure 5.
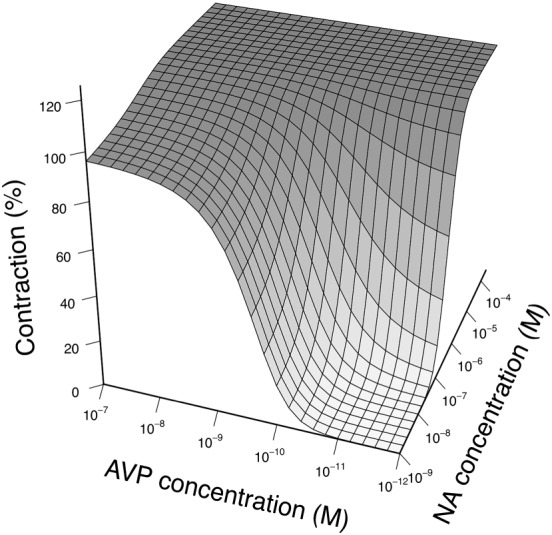
Response surface plot for the predicted contraction of different combinations of noradrenaline (NA) and AVP as predicted by the developed 2R‐1T model.
The extent of phenoxybenzamine inhibitory effects were also estimated in the model. It was identified that the addition of 3 nM phenoxybenzamine reduced the noradrenaline‐induced contractions by 92.6% and reduced AVP‐induced contractions by 44.3%.
Prediction of the contractile response of human vessels
According to the simulation results, the model derived from rat experimental data could not successfully capture experimental data for human renal arteries assuming a 1–1 cross‐species translation with identical parameters (Figure 6A, B). However, after adjusting m NA /K and m AVP /K by accounting for the differences in receptor density between species, human data were shown to be adequately described by the model (Figure 6C, D).
Figure 6.
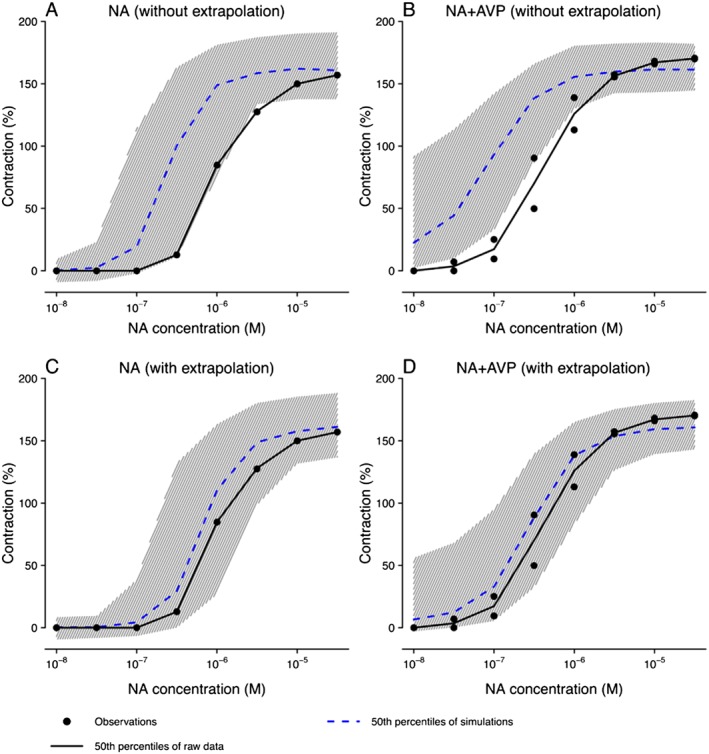
Prediction of human vasoconstriction data under challenging with noradrenaline (NA) only (A and C) and noradrenaline with two different concentrations of AVP (0.1 and 0.03 nM) (B and D), based on the model without extrapolation (A and B) and with scaled receptor capacities, where the scaling term on m NA /K and m AVP /K were 0.61 and 0.69 respectively (C and D). Grey hatching represents 95% confidence interval of the 50th percentile of simulations.
The results of sensitivity analysis showed that compared with changing drug affinity values, a change in receptor density ratio appeared to have a greater overall effect on 2R‐1T model scaling results. Half reduction or a twofold increase of original α1A‐adrenoceptor C H /C R ratio, as well as a twofold increase of original V1A receptor C H /C R ratio resulted in apparently inferior prediction of human data (Figure 7), while half reduction of original V1A receptor C H /C R ratio only slightly changed the accuracy of predictions. In contrast, halving original K NA or K AVP values resulted in less accurate predictions, while doubling original K NA or K AVP values affected the scaling results less (Figure 8).
Figure 7.
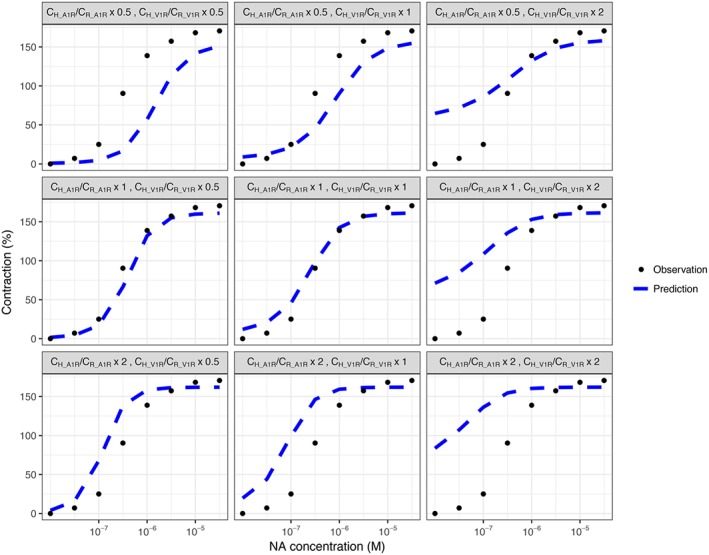
Sensitivity analysis for evaluating the effects of receptor density ratios (C H / C R) on the scaled model predictions. The C H /C R ratio of α1A‐adrenoceptors and V1A receptors were set as 0.5‐fold, onefold and twofold of the original using values. Population predictions were plotted together with the human experimental data where human vessels were challenged with noradrenaline (NA) and 0.1 nM of AVP.
Figure 8.
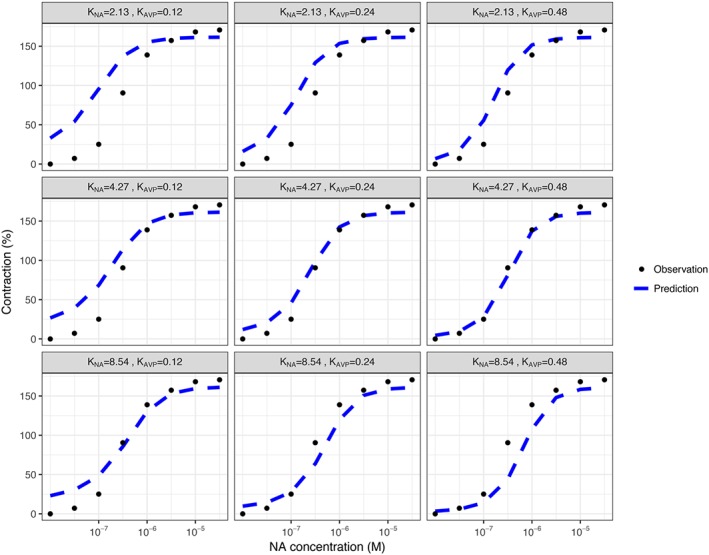
Sensitivity analysis for evaluating the effects of drug affinity values on the scaled model predictions. The K NA and K AVP were set as 0.5‐fold, onefold and twofold of the original using values. Population predictions were plotted together with the human experimental data where human vessels were challenged with noradrenaline (NA) and 0.1 nM of AVP.
Discussion
The previously proposed 2R‐1T model provides an attractive quantitative framework to characterize drug–drug interactions in a mechanism‐based fashion. Unlike other commonly used mechanism‐based modelling methodologies (Koch et al., 2016), the 2R‐1T model allows the description of the interaction between two agonists acting on different receptors. Meanwhile, in comparison with fully mechanistic ordinary differential equation models that concern complex receptor bindings and underlying signalling pathways (Bianconi et al., 2012), the 2R‐1T model is simpler to be implemented as less prior knowledge is required. In this study, we have shown that this model can indeed be used to successfully describe the interaction between two agonists of interest that share a common transduction pathway and scale to human, using a case example for contractile responses induced by noradrenaline and AVP.
The 2R‐1T model structure assumes the combination effect was derived by the summation of mediator concentrations, which matches the pharmacological mechanisms of noradrenaline and AVP‐induced vasoconstriction. The estimates of m NA /K and m AVP /K were much larger than 1, indicating that the concentrations of transducer ([M]NA and [M]AVP) produced by noradrenaline or AVP are able to reach saturation of the E/[A] curves. This is consistent with the fact that although the contractions of rat SMA induced by noradrenaline and AVP were mutually potentiated, the maximum effects (E max) induced by either drug alone or in combination were similar (Figure 2). Estimates of n NA and n AVP indicated that the slope of transducer production for noradrenaline and AVP was similar. The slope change of noradrenaline or AVP E/[A] curves that occurred when the other drug produced a certain level of threshold could be captured by the estimate of n M, as was shown in the simulation results of the initial theoretical model (Scaramellini et al., 1997).
As there is no irreversible antagonist available for V1A receptors (Lolait et al., 2018), the E/[A] curves required to estimate K AVP and m AVP /K were not obtained, which was considered to be the main reason why K AVP (RSE = 478.5%) and m AVP /K (RSE = 189.8%) could not be estimated with acceptable accuracy (Table 1, Model 1). Therefore, the value of K NA and K AVP was ultimately fixed according to published values. The reported value of K NA in rat SMA was identified as 0.66–4.27 μM (Nyborg and Bevan, 1988; Oriowo et al., 1989; Van der Graaf and Stam, 1999) and that of K AVP was identified as 0.16–1.25 nM (Lariviere et al., 1989, 1988; Gopalakrishnan et al., 1991; Bockman et al., 1992). Besides the values we applied, using other identified values to fit the data showed to have inferior GOF results (AIC increased by 1 to 114). Therefore, the values of K NA and K AVP were finally set as 4.27 μM (Nyborg and Bevan, 1988) and 0.24 nM (Bockman et al., 1992), respectively, to fit our experimental data.
The use of a mixed‐effect model was of particular relevance to account for the IIV of the data as it may lead to bias in parameter estimates if the variance between individual vessel segments were not considered appropriately. The IIV of the maximum effect was small, while for m NA /K, mAVP /K, K NA and K AVP it was more pronounced, which was considered to primarily account for the variability among observations. The IIV of PBZ A and PBZ M was too small to be identified, thus they were not included in our model. This population analysis approach also allowed us to analyse all individual data simultaneously which dealt with the unequal number of E/[A] curves for noradrenaline and AVP result from the paired and single curve protocols effectively.
The effect of phenoxybenzamine was characterized by two independent terms, which respectively refers to (i) the inactivation effect on α1A‐adrenoceptors and (ii) the inhibition effect on the common signal transducer for both noradrenaline and AVP stimulus to account for phenoxybenzamine caused contraction decrease for both noradrenaline and AVP. This is in accordance with the underlying mechanism that phenoxybenzamine as a non‐selective irreversible α‐adrenoceptor blocker has well‐established inhibitory effect on noradrenaline through α1A‐adrenoceptors (Van der Graaf and Stam, 1999), and phenoxybenzamine was also reported previously to have an inhibition effect on calcium channels (Gengo et al., 1984; McPherson et al., 1985) and calmodulin (Conant et al., 2003). These latter mechanisms were considered to contribute to phenoxybenzamine inhibition of AVP‐induced contraction shown in Figure 2D as well as on noradrenaline, as calcium is a common signal transducer of noradrenaline and AVP (Mauger et al., 1984). This current approach resulted in a significantly better fit of the overall data (AIC decreased 8.7) comparing with only using one term to describe the effect of phenoxybenzamine. The results shown in GOF and VPC plots confirmed the satisfactory fit and predictive performance of our model.
The main limitation of our study is inherent to the in vitro assay system used and the fact that measurements were only obtained at (pseudo) steady‐state conditions, which does not take into account the role of time‐dependent changes in pharmacokinetics and pharmacodynamics and feedback mechanisms present in intact in vivo models. In addition, receptor binding kinetics (de Witte et al., 2016) and receptor turnover (Dua et al., 2015) were not considered in the current 2R‐1T model, because no evidence was observed for slow‐onset or (de)sensitization of the effect (Van der Graaf et al., 1996; Stam et al., 1999, 1998; Van der Graaf and Stam, 1999). Also, we did not explore the effect of repeated dosing in the current study. Of course, such mechanistic elements could be added when new data emerges that underpin the development of more advanced versions of the 2R‐1T model.
We further demonstrated that the 2R‐1T model allows inter‐species extrapolation from rat to humans, indicating that our approach can be applied in translational research. The initial significant discrepancy between observed human data and the corresponding predictions from the model without scaling, which assumed identical parameters for rat and human, suggested an important pharmacological difference between species. Relative differences in receptor density of blood vessels and drug affinities were considered to be the most likely causes of this difference. The reported range of noradrenaline and AVP affinity for α1A‐adrenoceptors and V1A receptors were from 0.40–1.58 μM (Perez et al., 2018) and 0.50–3.16 nM (Lolait et al., 2018) respectively in humans and from 0.66–4.27 μM and 0.16–1.25 nM respectively in rats. As the ranges of affinity values for human and rats overlap, K NA and K AVP were kept unchanged during scaling. Receptor density values, which were demonstrated to have greater influence on the inter‐species scaling of 2R‐1T model from sensitivity analysis, were derived from previous reports where the studies were mostly performed on aortic tissue, which was the closest related tissue where we could identify density data. An additional suitable receptor density value for V1A receptors was also identified as 325 fmol·mg−1 of protein for five 8‐week‐old rats and 45 fmol·mg−1 of protein for four 12‐week‐old rats (Lariviere et al., 1989), the mean of which is 201 fmol·mg−1 of protein. When applying this mean value, the model scaling results did not change dramatically, as shown by the sensitivity analysis that the reduction of the V1A receptor C H /C R ratio did not greatly affect the accuracy of scaling model predictions. On the basis of our current finding, the potential clinical value of this model structure on scaling from adults to paediatrics based on age‐dependent expression of α1A‐adrenoceptors and V1A receptors could be further investigated. The applicability of such a system–pharmacology approach to explaining differences between hERG‐mediated QTC prolongation in adults and neonates on the basis of model‐predicted differences in target expression levels, which were consistent with experimentally derived mRNA levels in patients (Moric‐Janiszewska et al., 2011), has been recently demonstrated (Gotta et al., 2016).
In conclusion, we have shown, for the first time, that the 2R‐1T model can be applied to characterize the interaction between two clinically relevant agonists acting at different receptors but producing effects through a converging transduction pathway. Our data (leftward shift, flattening and no change in maximum response) are entirely consistent with the theoretical predictions made by Scaramellini et al. (1997) for two full agonists which share a common transduction pathway with a steep slope. As pointed out by these authors, their 2R‐1T model may not be universally applicable and is undoubtedly an oversimplification of receptor transduction pathways, but our first experimental validation provided support for its validity. We therefore propose that this simple quantitative systems pharmacology model structure provides a translational framework to mechanistically interpret and predict drug–drug interactions and is of significant value to rationally optimize novel combination treatments. We believe this is fully in line with the new 2017 European Medicines Agency guideline on nonclinical and clinical aspects of first‐in‐human (FIH) and early clinical trials, which puts more emphasis on the better use of preclinical data to guide rational dose selection of FIH studies (Ponzano et al., 2018; Van der Graaf and Benson, 2018).
Author contributions
All authors contributed to manuscript writing. An.Y. and Ak.Y. performed the data analysis. W.B.S. and P.v.d.G. designed and performed the experiments. J.G.C.v.H. and P.v.d.G. supervised this work.
Conflict of interest
The authors declare no conflicts of interest.
Declaration of transparency and scientific rigour
This http://onlinelibrary.wiley.com/doi/10.1111/bph.13405/abstract acknowledges that this paper adheres to the principles for transparent reporting and scientific rigour of preclinical research recommended by funding agencies, publishers and other organisations engaged with supporting research.
Acknowledgements
This work was supported by the IMI TransQST consortium. We also would like to thank Dr Viji Chelliah (Certara QSP) for help with receptor expression data mining.
Yin, A. , Yamada, A. , Stam, W. B. , van Hasselt, J. G. C. , and van der Graaf, P. H. (2018) Quantitative systems pharmacology analysis of drug combination and scaling to humans: the interaction between noradrenaline and vasopressin in vasoconstriction. British Journal of Pharmacology, 175: 3394–3406. 10.1111/bph.14385.
References
- Al‐Lazikani B, Banerji U, Workman P (2012). Combinatorial drug therapy for cancer in the post‐genomic era. Nat Biotechnol 30: 679–692. [DOI] [PubMed] [Google Scholar]
- Alexander SPH, Christopoulos A, Davenport AP, Kelly E, Marrion NV, Peters JA et al (2017). The Concise Guide to PHARMACOLOGY 2017/18: G protein‐coupled receptors. Br J Pharmacol 174: S17–S129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bianconi F, Baldelli E, Ludovini V, Crinò L, Flacco A, Valigi P (2012). Computational model of EGFR and IGF1R pathways in lung cancer: a systems biology approach for translational oncology. Biotechnol Adv 30: 142–153. [DOI] [PubMed] [Google Scholar]
- Bockman CS, Jeffries WB, Pettinger WA, Abel PW (1992). Reduced contractile sensitivity and vasopressin receptor DOCA‐salt hypertension. Am J Physiol 262: H1752–H1758. [DOI] [PubMed] [Google Scholar]
- Christ GJ, Jean‐Jacques M (1991). Mutual‐effect amplification of contractile responses elicited by simultaneous activation of α‐1 adrenergic and 5‐hydroxytryptamine2 receptors in isolated rat aorta. J Pharmacol Exp Ther 256: 553–561. [PubMed] [Google Scholar]
- Cohen ML, Schenck K (2000). Contractile responses to sumatriptan and ergotamine in the rabbit saphenous vein: effect of selective 5‐HT 1F receptor agonists and PGF 2α. Br J Pharmacol 131: 562–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conant AR, Shackcloth MJ, Oo AY, Chester MR, Simpson AWM, Dihmis WC (2003). Phenoxybenzamine treatment is insufficient to prevent spasm in the radial artery: the effect of other vasodilators. J Thorac Cardiovasc Surg 126: 448–454. [DOI] [PubMed] [Google Scholar]
- Curtis MJ, Alexander S, Cirino G, Docherty JR, George CH, Giembycz MA et al (2018). Experimental design and analysis and their reporting II: updated and simplified guidance for authors and peer reviewers. Brit J Pharmacol 175: 987–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danhof M, de Jongh J, De Lange ECM, Della Pasqua O, Ploeger BA, Voskuyl RA (2007). Mechanism‐based pharmacokinetic‐pharmacodynamic modeling: biophase distribution, receptor theory, and dynamical systems analysis. Annu Rev Pharmacol Toxicol 47: 357–400. [DOI] [PubMed] [Google Scholar]
- de Witte WEA, Danhof M, van der Graaf PH, de Lange ECM (2016). In vivo target residence time and kinetic selectivity: the association rate constant as determinant. Trends Pharmacol Sci 37: 831–842. [DOI] [PubMed] [Google Scholar]
- Dellinger RP, Levy MM, Rhodes A, Annane D, Gerlach H, Opal SM et al (2013). Surviving sepsis campaign: international guidelines for management of severe sepsis and septic shock, 2012. Intensive Care Med 39: 165–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dua P, Hawkins E, and van der Graaf PH (2015). A tutorial on target‐mediated drug disposition (TMDD) models 324–337. [DOI] [PMC free article] [PubMed]
- Faber JE, Yang N, Xin X (2001). Expression of α‐adrenoceptor subtypes by smooth muscle cells and adventitial fibroblasts in rat aorta and in cell culture. J Pharmacol Exp Ther 298: 441–452. [PubMed] [Google Scholar]
- Fitzgerald JB, Schoeberl B, Nielsen UB, Sorger PK (2006). Systems biology and combination therapy in the quest for clinical efficacy. Nat Chem Biol 2: 458–466. [DOI] [PubMed] [Google Scholar]
- Gabrielsson J, Gibbons FD, Peletier LA (2016). Mixture dynamics: combination therapy in oncology. Eur J Pharm Sci 88: 132–146. [DOI] [PubMed] [Google Scholar]
- Gengo PJ, Yousif F, Janis RA, Triggle DJ (1984). Interaction of phenoxybenzamine with muscarinic receptors and calcium channels. Biochem Pharmacol 33: 3445–3449. [DOI] [PubMed] [Google Scholar]
- Gerthoffer WT (1996). Agonist synergism in airway smooth muscle contraction. J Pharmacol Exp Ther 278: 800–807. [PubMed] [Google Scholar]
- Gopalakrishnan V, Xu YJ, Sulakhe PV, Triggle CR, McNeill JR (1991). Vasopressin (V1) receptor characteristics in rat aortic smooth muscle cells. Am J Physiol 261: H1927–H1936. [DOI] [PubMed] [Google Scholar]
- Gotta V, Yu Z, Cools F, van Ammel K, Gallacher DJ, Visser SAG et al (2016). Application of a systems pharmacology model for translational prediction of hERG‐mediated QTc prolongation. Pharmacol Res Perspect 4: e00270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harding SD, Sharman JL, Faccenda E, Southan C, Pawson AJ, Ireland S et al (2018). The IUPHAR/BPS Guide to PHARMACOLOGY in 2018: Updates and expansion to encompass the new guide to IMMUNOPHARMACOLOGY. Nucleic Acids Res 46: D1091–D1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonker DM, Visser SAG, Van der Graaf PH, Voskuyl RA, Danhof M (2005). Towards a mechanism‐based analysis of pharmacodynamic drug‐drug interactions in vivo. Pharmacol Ther 106: 1–18. [DOI] [PubMed] [Google Scholar]
- Keizer RJ, Karlsson MO, Hooker A (2013). Modeling and simulation workbench for NONMEM: tutorial on Pirana, PsN, and Xpose. CPT Pharmacometrics Syst Pharmacol 2: 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilkenny C, Browne W, Cuthill IC, Emerson M, Altman DG (2010). Animal research: reporting in vivo experiments: the ARRIVE guidelines. Br J Pharmacol 160: 1577–1579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch G, Schropp J, Jusko WJ (2016). Assessment of non‐linear combination effect terms for drug–drug interactions. J Pharmacokinet Pharmacodyn 43: 461–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lariviere R, Baribeau J, St‐Louis J, Schiffrin EL (1989). Vasopressin receptors and inositol trisphosphate production in blood vessels of spontaneously hypertensive rats. Can J Physiol Pharmacol 67: 232–239. [DOI] [PubMed] [Google Scholar]
- Lariviere R, St‐Louis J, Schiffrin EL (1988). Vascular binding sites and biological activity of vasopressin in doca‐salt hypertensive rats. JHypertension 6: 211–217. [DOI] [PubMed] [Google Scholar]
- Leff P (1987). An analysis of amplifying and potentiating interactions between agonists. J Pharmacol Exp Ther 243: 1035–1042. [PubMed] [Google Scholar]
- Lemos VS, Côrtes SF, Silva DMR, Campagnole‐Santos MJ, Santos RAS (2002). Angiotensin‐(1‐7) is involved in the endothelium‐dependent modulation of phenylephrine‐induced contraction in the aorta of mRen‐2 transgenic rats. Br J Pharmacol 135: 1743–1748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lolait S, Bichet D, Bouvier M, Chini B, Gimpl G, Guillon G, et al (2018) Vasopressin and oxytocin receptors: V1A receptor. IUPHAR/BPS Guide to PHARMACOLOGY. Available at http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=366 (accessed 2018 Feb 25).
- Mauger J‐P, Poggioli J, Guesdon F, Claret M (1984). Noradrenaline, vasopressin and angiotensin increase Ca{+2+} influx by opening a common pool of Ca{+2+} channels in isolated rat liver cells. Biochem J 221: 121–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGrath JC, Lilley E (2015). Implementing guidelines on reporting research using animals (ARRIVE etc.): new requirements for publication in BJP. Br J Pharmacol 172: 3189–3193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPherson GA, Krstew E, Malta E (1985). Effects of phenoxybenzamine on responses to some receptor agonists and calcium in vitro. Clin Exp Pharmacol Physiol 12: 455–464. [DOI] [PubMed] [Google Scholar]
- Moric‐Janiszewska E, Głogowska‐Ligus J, Paul‐Samojedny M, Wȩglarz L, Markiewicz‐Łoskot G, Szydłowski L (2011). Age‐ and sex‐dependent mRNA expression of KCNQ1 and HERG in patients with long QT syndrome type 1 and 2. Arch Med Sci 7: 941–947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulvany MJ, Halpern W, Mulvany MJ, Halpern W (1977). Contractile properties of small arterial resistance vessels in spontaneously hypertensive and contractile properties of small arterial resistance vessels in spontaneously hypertensive and normotensive rats. Circ Res 41: 19–26. [DOI] [PubMed] [Google Scholar]
- Nguyen T, Mouksassi M‐S, Holford N, Al‐Huniti N, Freedman I, Hooker A et al (2017). Model evaluation of continuous data pharmacometric models: metrics and graphics. CPT Pharmacometrics Syst Pharmacol 6: 87–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyborg NC, Bevan JA (1988). Increased α‐adrenergic receptor affinity in resistance vessels from hypertensive rats. Hypertension 11: 635–638. [DOI] [PubMed] [Google Scholar]
- Oriowo MA, Bevan JA, Bevan RD (1989). Variation in sensitivity of six cat and six rat arteries to norepinephrine can be related to differences in agonist affinity and receptor reserve. J Pharmacol Exp Ther 251: 16–20. [PubMed] [Google Scholar]
- Pérez‐Rivera AA, Hlavacova A, Rosario‐Colón LA, Fink GD, Galligan JJ (2007). Differential contributions of α‐1 and α‐2 adrenoceptors to vasoconstriction in mesenteric arteries and veins of normal and hypertensive mice. Vascul Pharmacol 46: 373–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez D, Bond RA, Bylund DB, Eikenburg DC, Hieble JP, Hills R, et al (2018) Adrenoceptors: α1A‐adrenoceptor. IUPHAR/BPS Guide to PHARMACOLOGY. Available at http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=22 (accessed 2018 Feb 25).
- Ponzano S, Blake K, Bonelli M, Enzmann H, on behalf of the European Medicines Agency Committee for Human Medicinal Products First‐in‐Human Guideline Drafting Group (2018). Promoting safe early clinical research of novel drug candidates: a European Union regulatory perspective. Clin Pharmacol Ther 103: 564–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prins BA, Weber MA, Purdy RE (1992). Norepinephrine amplifies angiotensin II‐induced vasoconstriction in rabbit femoral artery. J Pharmacol Exp Ther 262: 198–203. [PubMed] [Google Scholar]
- Ru XC, Qian LB, Gao Q, Li YF, Bruce IC, Xia Q (2008). Alcohol induces relaxation of rat thoracic aorta and mesenteric arterial bed. Alcohol Alcohol 43: 537–543. [DOI] [PubMed] [Google Scholar]
- Scaramellini C, Bennett G, Leff P (1997). Analysis of agonist–agonist interactions: the crucial influence of curve shape. J Pharmacol Toxicol Methods 37: 167–178. [DOI] [PubMed] [Google Scholar]
- Segarra G, Medina P, Vila JM, Chuan P, Domenech C, Lluch S (2002). Increased contraction to noradrenaline by vasopressin in human renal arteries. J Hypertens 20: 1373–1379. [DOI] [PubMed] [Google Scholar]
- Serradeil‐Le Gal C, Herbert JM, Delisee C, Schaeffer P, Raufaste D, Garcia C et al (1995). Effect of SR‐49059, a vasopressin V_1a_ antagonist, on human vascular smooth muscle cells. AmJPhysiolHeart CircPhysiol 268: H404–H410. [DOI] [PubMed] [Google Scholar]
- Stam WB, Van der Graaf PH, Saxena PR (1999). Analysis of α1L‐adrenoceptor pharmacology in rat small mesenteric artery. Br J Pharmacol 127: 661–670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam WB, Van der Graaf PH, Saxena PR (1998). Characterization of receptors mediating contraction of the rat isolated small mesenteric artery and aorta to arginine vasopressin and oxytocin. Br J Pharmacol 125: 865–873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Streefkerk JO, Pfaffendorf M, Van Zwieten PA (2003). Vasopressin‐induced facilitation of adrenergic responses in the rat mesenteric artery is V1‐receptor dependent. Auton Autacoid Pharmacol 23: 35–41. [DOI] [PubMed] [Google Scholar]
- Vågnes BØB, Hansen FH, Christiansen REF, Gjerstad C, Iversen BM (2004). Age‐dependent regulation of vasopressin V1a receptors in preglomerular vessels from the spontaneously hypertensive rat. Am J Physiol Renal Physiol 286: F997–F1003. [DOI] [PubMed] [Google Scholar]
- Van der Graaf P, Benson N (2018). The role of quantitative systems pharmacology (QSP) in the design of first‐in‐human trials. Clin Pharmacol Ther. 10.1002/cpt.1145. [DOI] [PubMed] [Google Scholar]
- Van der Graaf PH, Shankley NP, Black JW (1996). Analysis of the effects of α1‐adrenoceptor antagonists on noradrenaline‐mediated contraction of rat small mesenteric artery. Br J Pharmacol 118: 1308–1316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Graaf PH, Stam WB (1999). Analysis of receptor inactivation experiments with the operational model of agonism yields correlated estimates of agonist affinity and efficacy. J Pharmacol Toxicol Methods 41: 117–125. [DOI] [PubMed] [Google Scholar]
- Van Hasselt JGC, Van Der Graaf PH (2015). Towards integrative systems pharmacology models in oncology drug development. Drug Discov Today Technol 15: 1–8. [DOI] [PubMed] [Google Scholar]
- Yamada S, Suzuki M, Tanaka C, Mori R, Kimura R, Inagaki O et al (1994). Comparative study on α1‐adrenoceptor antagonist binding in human prostate and aorta. Clin Exp Pharmacol Physiol 21: 405–411. [DOI] [PubMed] [Google Scholar]


