Exploring the denatured state ensemble by single-molecule chemo-mechanical unfolding: the effect of force, temperature and urea

Abstract

While it is widely appreciated that the denatured state of a protein is a heterogeneous conformational ensemble, there is still debate over how this ensemble changes with environmental conditions. Here, we use single-molecule chemo-mechanical unfolding, which combines force and urea using the optical tweezers, together with traditional protein unfolding studies to explore how perturbants commonly used to unfold proteins (urea, force and temperature) affect the denatured state ensemble. We compare the urea m-values, which report on the change in solvent accessible surface area for unfolding, to probe the denatured state as a function of force, temperature and urea. We find that while the urea- and force-induced denatured states expose similar amounts of surface area, the denatured state at high temperature and low urea concentration is more compact. To disentangle these two effects, we use destabilizing mutations that shift the Tm and Cm. We find that the compaction of the denatured state is related to changing temperature as the different variants of acyl-coenzyme A binding protein have similar m-values when they are at the same temperature but different urea concentration. These results have important implications for protein folding and stability under different environmental conditions.

Graphical abstract

Introduction

Protein folding is predicted to be a very heterogeneous process with vast conformational space available for the protein to sample [1–4]; this complex energy landscape is often depicted as a funnel where a multitude of possible unfolded states are fed through many parallel pathways towards the native state [1, 5–7]. There is debate, however, over the degree of heterogeneity on this landscape. For instance, does the unfolded state depend drastically on the environmental conditions [2, 8–10]? If so, the different environmental conditions seen within the cell have the potential to greatly affect protein stability [11, 12]. Moreover, since traditional studies of protein stability employ perturbants, such as chemical denaturant, temperature and force, to unfold proteins, it is important to understand if and how they alter the denatured state ensemble [13–16].

Small angle X-ray scattering (SAXS) measurements consistently indicate that the radius of gyration of the denatured state does not change with chemical denaturant concentration and single-molecule Forster resonance energy transfer (smFRET) indicates that the expansion of the denatured state changes with chemical denaturant concentration and temperature [17–23]. While simulations help to reconcile these seemingly conflicting results [24–26], the discrepancy highlights the importance of using multiple experimental techniques and the need for new techniques to fully characterize the denatured state ensemble and how it changes under different environmental conditions.

Recently, we developed an approach we term single-molecule chemo-mechanical unfolding, which combines chemical denaturant and mechanical force using optical tweezers, to characterize heterogeneity in the protein-folding process [27]. We used chemo-mechanical unfolding to resolve a conflict about the heterogeneity in protein-folding trajectories – do proteins fold through one pathway or many parallel pathways? We harnessed the fact that the effect of urea on the kinetics of a folding reaction (m^‡-value) is a reflection of the change in conformation of the transition state. By monitoring the urea-dependence of unfolding as a function of force we were able to observe and characterize different transition state ensembles, demonstrating that a simple single-domain protein can fold through multiple pathways and that force, point mutations, and urea can shift the flux between these pathways. Here, we use single molecule chemo-mechanical unfolding to explore the top of the protein-folding funnel. Instead of looking at the unfolding rate, we now quantify the effect of denaturant (urea) on the folding stability (lnK_UF) using force, urea and temperature to perturb this equilibrium and populate the unfolded state.

The effect of urea on the equilibrium stability of a protein is quantified in terms of an m-value, which reports on the difference in solvent accessible surface area (ASA) between the native and denatured state [28–30]. Although the native state is not a static structure, heterogeneity in the native state tends to involve small-scale fluctuations that do not significantly affect ASA [31, 32]. Therefore, the native-state ASA is unlikely to change significantly under different conditions and we rationalize that any difference in the effect of urea will be a reflection of a change in the denatured-state ensemble. Simulations using the molecular transfer model and experiments using hydrogen exchange kinetics to probe structure support this hypothesis [33, 34]. While ASA will not detect all conformational changes [26, 35], m-values provide a particularly versatile probe of the unfolded state because they can be measured in conjunction with different types of protein folding experiments (force spectroscopy, thermal and denaturant melts).

Here, we use Acyl CoA-binding protein (ACBP) as a model protein to explore the denatured state under different conditions. ACBP folds and unfolds at experimentally measurable rates at forces near 15 pN and therefore we can monitor the folding equilibrium at relatively high force [36]. Moreover, previous work has found evidence for residual structure in the ACBP denatured state, which raises the possibility that this structure may change under different conditions [37, 38].

We determine urea m-values for force-, urea- and temperature-induced denaturation of ACBP. We find that the m-value decreases at high temperature, suggesting that the temperature-induced denatured state is significantly more compact than the urea- or force-induced denatured state. However, we do not find any evidence for changes in the denatured state ensemble under the force and denaturant conditions we studied. We compare our results to other experimental and theoretical work exploring the denatured state ensemble. Previous studies exploring the unfolded state using techniques such as SAXS, FRET and NMR have focused on the denaturant- or temperature-induced unfolded state [10, 17, 18, 20, 22, 24, 39–43]. Using m-values, we have, for the first time, been able to compare force-, denaturant-, and temperature-induced denatured states.

Results

m-Values quantify effect of urea on folding equilibrium

Thermodynamic m-values (m) describe how the change in free energy for unfolding (ΔG_U) depends on denaturant concentration [44]. The urea m-value is given by Equation 1:

$$\Delta {\text{G}}_{\text{U}}=\Delta {\text{G}}_{\text{U}}{}^{0\text{M}\text{urea}}-m[\text{urea}]$$ Equation 1

where ΔG_U^{0M urea} is the free energy for unfolding in the absence of urea and [urea] is the molar concentration of urea. Below, we harness different methods for measuring m-values while using force, urea and temperature to unfold the protein ACBP.

ACBP is an 86-residue, single domain protein that is known to fold in a two-state process [45–47]. Recent mechanical unfolding studies have shown that ACBP is mechanically stable and both unfolding and refolding can be monitored at relatively high forces (~15 pN) when pulled between residues 46 and 86 with an optical trap [36]. Therefore, for force-induced studies, we used the variant ACBP M46C/I86C, where cysteines have been introduced to create pulling points via the attachment of DNA handles (Fig. 1).

Figure 1.

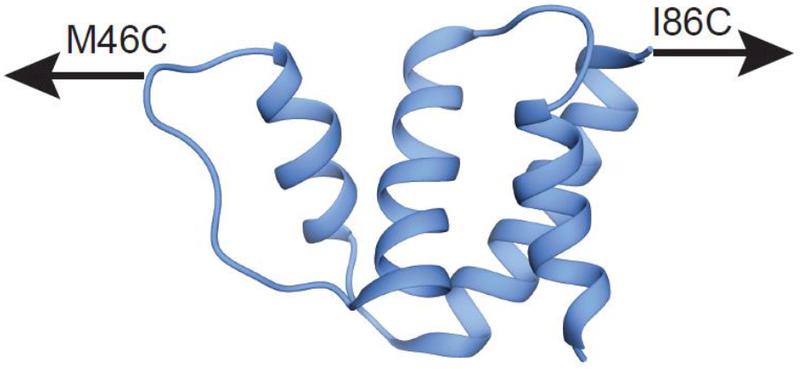
Structure of ACBP (Protein Data Bank code 1NTI) showing the pulling points used in single molecule optical trap experiments to explore the role of force.

Urea m-Values and force-induced unfolding

First, we measured the ACBP M46C/I86C m-value in the absence of force using standard equilibrium urea denaturation at 25°C, monitoring the CD signal at 222 nm as a function of urea (Fig. 2a). The data were fit with a two-state, linear extrapolation model (see methods) with a resulting m-value (average of four separate denaturation studies) of 1.22 ± 0.01 as shown in Table 1.

Figure 2.

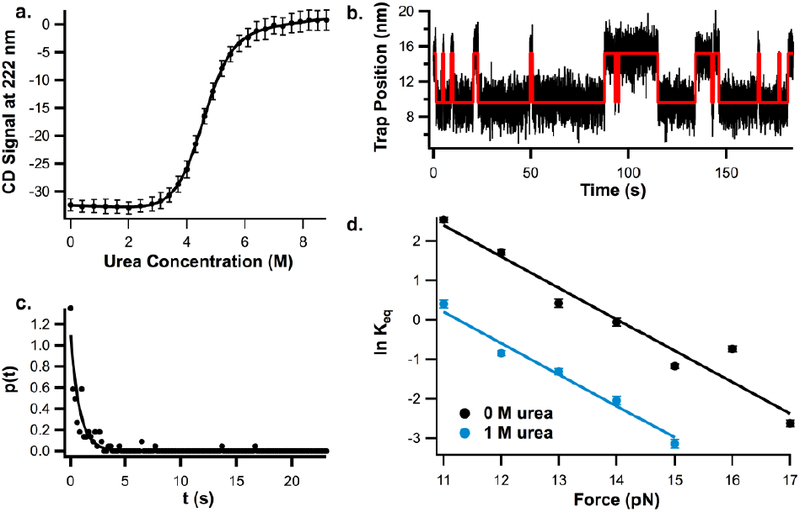
a. Representative urea melt for ACBP M46C/I86C at 25°C in 100 mM Tris, 250 mM NaCl, 1 mM TCEP, pH 7 buffer, b. Sample trace of ACBP hopping between the unfolded and folded state at 14 pN in 0M urea, red line indicates HMM fit overlayed over data. c. Example of probability distribution used to calculate ACBP folding and unfolding rates from hopping data collected on optical tweezers (from unfolding data at 16 pN in 0M urea), d. Plot of natural log of K_eq vs force for ACBP M46C/I86C determined from constant-force hopping experiments in the same buffer with 0M urea and 1M urea.

Table 1.

m-Values from urea- and force-denaturation experiments with ACBP M46C/I86C in 100 mM Tris, 250 mM NaCl ,1mM TCEP, pH 7 buffer.

Experiment	Conditions*	m (kcal mol−1 M−1)
Urea Melt	4.6 M Urea, 0 pN Force,	1.22 ± 0.01**
	25°C
Constant	0–1 M Urea, 11–17 pN	1.30 ± 0.12***
Force	Force, 25°C
Hopping

^*For urea melt, the reported urea concentration is the Cm

^**Uncertainty determined from standard error of four independent measurements

^***Reported uncertainty is uncertainty of fit

To apply force, we used single molecule mechanical unfolding with an optical trap. We attached DNA handles to the cysteines in ACBP M46C/I86C as described in methods. Using force-feedback mode in the optical tweezers, the protein was held at constant forces ranging from 11 to 17 pN and the trap position (which is proportional to extension) was monitored as the protein hopped between the folded and unfolded state (Fig. 2b). A hidden Markov model [48] was used to identify the transitions between states (red line on Fig. 2b) and determine the dwell time in each state. The resulting distributions of dwell times were fit to determine the folding and unfolding rate (Fig. 2c, see methods and supplemental information). We determined ΔG_U from the ratio between the folding and unfolding rates (k_f and k_u) using equation 2:

$$\Delta {\text{G}}_{\text{U}}=-{\text{RTInk}}_{\text{eq}}=-\text{RTIn}(k_u/k_f)$$ Equation 2

where K_eq is the equilibrium constant for unfolding, T is temperature, and R is the gas constant. As expected, ΔG_U, shows a linear dependence on force over the measure force range (11–17 pN).

To determine the urea m-value under force, we measured ΔG_U as a function of force in the presence of 1M urea (Fig. 2d); the difference between ΔG_U^{0M Urea} and ΔG_U^{1M urea} is the reported m-value. The force dependence at 0M urea and 1M urea are parallel, indicating that the m-value does not change significantly with force. We fit the data globally as described in methods to determine the m-value for force-induced unfolding (Table 1) at this relatively high force. The resulting m-value at high force is within error of the m-value calculated in the absence of force indicating that urea affects both processes similarly. The relatively large uncertainty in this m-value compared to standard equilibrium denaturation studies is due to the fact that this value is derived from single-molecule measurements.

Urea m-Values and temperature-induced unfolding

To explore how temperature affects the urea m-value, we collected temperature- and urea-denaturation melts for ACBP. Here, we used wild type ACBP (WT ACBP), which is cysteine-free, to avoid temperature-dependent complications. As for ACBP M46C/I86C, we collected four WT ACBP urea melts at 25°C (Fig. 3a) and report the average m-value in Table 2.

Figure 3.

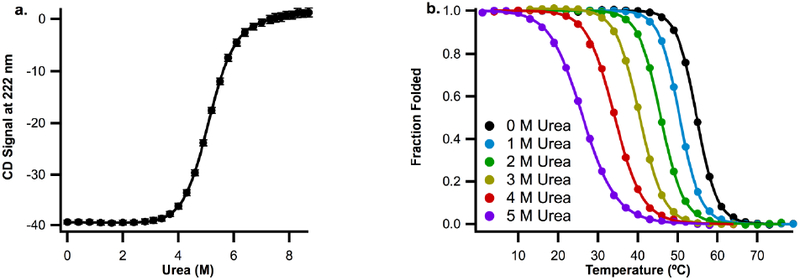
a. Representative urea denaturation curves for wild-type ACBP at 25°C in 50mM Potassium Phosphate, pH 7 buffer, b. Plots of fraction folded protein vs temperature for wild-type ACBP in the same buffer with 0, 1, 2, 3, 4, and 5 M urea.

Table 2.

m-Values from urea and thermal denaturation experiments with WT ACBP in 50 mM Potassium Phosphate pH 7 buffer.

Experiment	Conditions*	m** (kcal mol−1 M−1)
Urea Melt	4.9 M Urea, 25°C, 0 pN	1.28 ± 0.02
	Force
Thermal Melt	0–1 M Urea, 52.7°C, 0 pN	1.09 ± 0.01
	Force
Thermal Melt	1–2 M Urea, 48.1°C, 0 pN	1.13 ± 0.01
	Force
Thermal Melt	2–3 M Urea, 43.1°C, 0 pN	1.13 ± 0.01
	Force
Thermal Melt	3–4 M Urea, 37.3°C, 0 pN	1.24 ± 0.01
	Force
Thermal Melt	4–5 M Urea, 30.1°C, 0 pN	1.27 ± 0.02
	Force

^*For urea melt, the reported urea concentration is the Cm

^**Uncertainties determined from standard error of four independent measurements

Next, we monitored the CD signal at 222nm as a function of temperature in buffer containing 0–5 M urea. The resulting curves (Fig. 3b) were fit as described in methods. Using these fits, ΔG_U can be accurately determined at temperatures near the melting transition temperature (T_m) where there is a significant population of both folded and unfolded protein (i.e. fraction folded is not zero or one). m-values were calculated by comparing ΔG_U from two melting curves collected at different urea concentrations at a temperature that falls in the transition region for both curves (to ensure transition regions align, we do not compare melting curves with a urea concentration difference greater than 1M). The resulting m-values and respective temperatures are reported in Table 2.

The m-value determined at 30.1°C from thermal melts collected at 4 and 5 M urea is the same within error (1.27 ± 0.02) as the m-value determined from the urea melt (1.28 ± 0.02, Cm = 4.9 M urea, 25°C). These m-values, determined using different experimental methods but under similar environmental conditions, agree well, supporting the validity of using both techniques to determine m-values.

On the other hand, there is a statistically significant 15% difference between the m-value for urea-induced unfolding (1.28 ± 0.02) and the m-value determined from comparing thermal melts at 0 and 1M urea (1.09 ± 0.01), which was determined at a significantly higher temperature (52.7°C) and lower urea concentration than that determined from the urea melt. As urea concentration in the temperature melts is increased (and so unfolding temperature is decreased), the m-value approaches the m-value measured from urea melts. Therefore, the m-value is dependent on environmental conditions.

To explore this trend further, we carried out urea-denaturation studies at temperatures ranging from 25 to 53°C (Fig. 4a). Fitting these denaturation curves individually requires both an upper and lower baseline, which is impossible to obtain at high temperature where the protein is already partially unfolded in the absence of urea. Therefore, we fit the data globally as described in methods.

Figure 4.

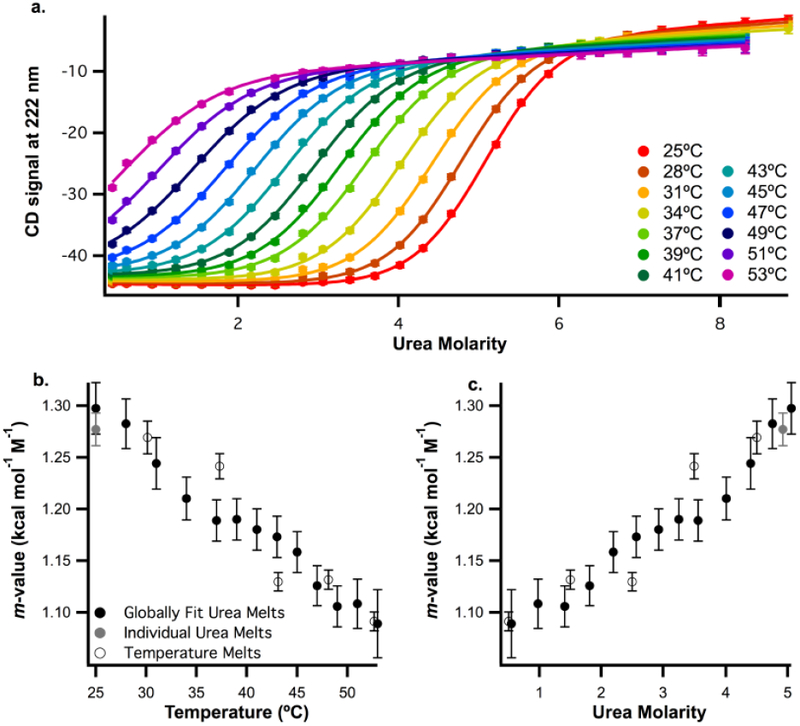
a. Wild-type ACBP urea denaturation profiles at temperatures ranging from 25 to 53°C in 50mM Potassium Phosphate, pH 7 buffer. CD signal at 222 nm is plotted as a function of urea molarity. Data were globally fit as described in methods, b. Plot of m-values collected from different experiments against temperature. Open circles indicate m-values calculated from temperature melts at different urea concentrations (Fig. 3a). Black and grey circles indicate data collected from urea melts at different temperatures. Black circles represent data from the globally fit melts in Figure 4a. Grey circles represent data from four replicates of a urea melt at 25°C collected using a titrator (Fig. 3a). c. The same m-values from Fig. 4b plotted against urea concentration (symbols have the same meaning). For urea melts, the urea concentration is the midpoint denaturation concentration (the Cm). For temperature melts, the urea concentration is the average urea concentration from the melts used to calculate the m-value.

Together, the fits of these thermal and urea denaturation studies (data in Figs. 3 and 4a), result in m-values determined at a range of temperatures and urea concentrations by three different methods – individual fits of urea melts, global fits of urea melts at different temperatures and global fits of temperature melts at different [urea]. All of these m-values are plotted as a function of temperature (Fig. 4a) and urea concentration (Fig. 4b). The globally fit urea melts (black circles) are consistent with both the individually fit m-values from urea melts (grey circles) and temperature melts (open circles), supporting the validity of the global fits. Moreover, the m-values determined from temperature melts and urea melts under similar conditions are quite close, again validating our ability to measure m-values using both temperature and urea.

There is a well-defined trend where the urea m-value decreases with temperature and increases with urea concentration. Therefore, it is clear that the m-value depends on environmental conditions; however, it is not clear if this change in m-value is due to changing the urea concentration, the temperature, or both since they are changing simultaneously in each set of experiments.

To help resolve this issue, two destabilized ACBP mutants (Y28N and Y73A) [49] were created in order to shift the measured Tm at each [urea] (or Cm at each temperature). As before, we measured urea m-values for these variants as a function of temperature and urea concentration using the three different approaches (urea denaturation at different temperatures (Fig. 4a, b), thermal denaturation at 0 and 1M urea (Sup. Fig. 4c, d), and independently fit urea melts (Sup. Fig. 4a, b)). The m-values as a function of temperature and urea are shown in Figures 5c and 5d. The plots for all three mutants as a function of temperature (Fig. 5c) align while the plots as a function of urea concentration (Fig. 5d) do not. Therefore, m-values for the ACBP mutants measured at the same temperature, but different urea concentrations, are similar. These data suggest that the noted trend in m-values is a result of the change in temperature, not the [urea].

Figure 5.

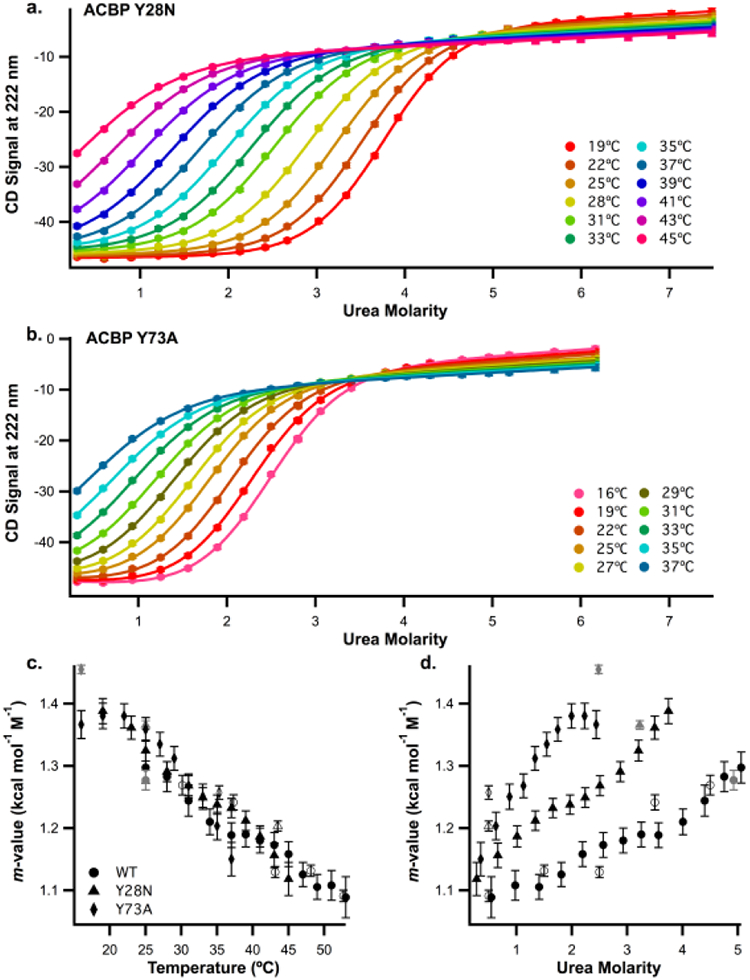
a. ACBP Y28N urea denaturation profiles at temperatures ranging from 19 to 45°C in 50mM Potassium Phosphate, pH 7 buffer, b. ACBP Y73A urea denaturation profiles at temperatures ranging from 16 to 37°C in same buffer. For a and b, CD signal at 222nm is plotted as a function of urea molarity. Data were globally fit as described in methods, c. Plots of m-values collected from different experiments versus temperature for ACBP WT (circles), Y28N (triangles) and Y73A (diamonds). Data from globally fitting temperature melts at different temperatures (Fig 4a, 5a, 5b) are represented by black symbols, data from urea denaturations replicated four times (Fig.3a, Sup. Fig. 4a, b) are represented by grey symbols and data from thermal denaturation at different urea concentrations (Fig. 3bm Sup. Fig 4c, d) are represented by open symbols, d. Plot of the same m-values shown in (c) as a function of urea concentration (symbols and colors have the same meaning). For urea melts, the urea concentration is the midpoint denaturation concentration (the Cm). For temperature melts, the urea concentration is the average urea concentration from the melts used to calculate the m-value.

Discussion

Using m-values to probe the denatured state

The effect of chemical denaturants on the free energy associated with a conformational change reflects the amount and type of solvent accessible surface area buried or exposed (ΔASA) [28–30]. Thus, m-values are a useful probe of processes like protein folding that involve large-scale conformational changes – proteins that bury more surface area upon folding have larger m-values. Changes in a protein’s m-value under different conditions imply a change in the ΔASA = ASA (native state) – ASA (denatured state). Since the conformation of the native state is relatively homogeneous and robust, changes in environmental conditions are unlikely to affect the native state ASA. The denatured state, on the other hand, is highly heterogeneous so different denatured state ensembles may well have different ASA values. Therefore, any difference in m-value (and thus ΔASA) for protein folding should reflect a difference in the surface area exposed in the denatured state.

Urea and force produce a more extended denatured state than temperature

Our results with ACBP indicate that the urea-induced and force-induced unfolded states are similar: the m-values from urea melts and constant-force hopping experiments are the same within error (Table 1). Of note, the m-value measured in the force-unfolding experiments is constant over the range of forces studied here: the denatured state does not change with force. Using the worm-like chain model (Fig. 6), which models the unfolded polypeptide as function of force [50, 51], the extension of unfolded ACBP will increase from 8.6 to 9.5 nm over the 11–15 pN range studied here (where the maximum possible extension (contour length) is 14.4 nm and the distance between residues 46 and 86 in the crystal structure for ACBP is 3.8 nm [36]). Our results suggest that there is no detectable change in ASA over this ~10% change in extension. Perhaps at these relatively high extensions, ASA is already maximally exposed so increasing extension will not change the m-value.

Figure 6.

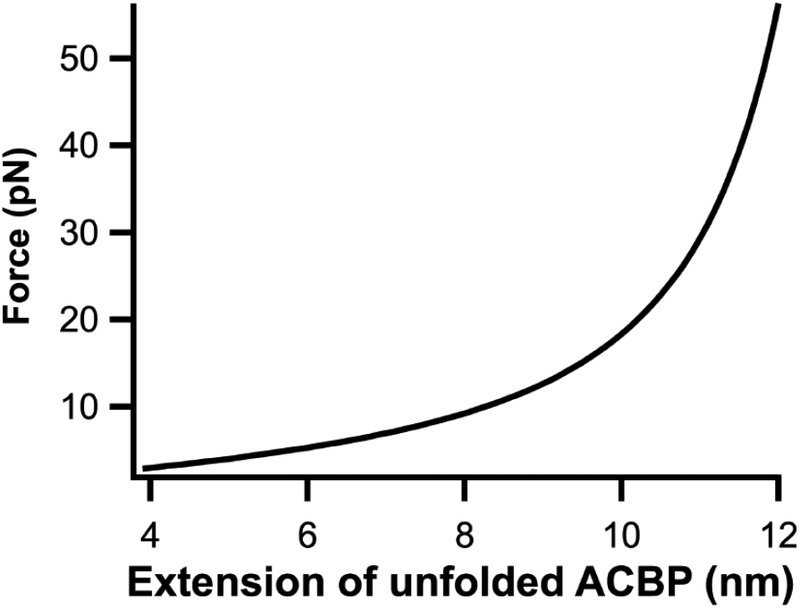
Plot of force vs extension for ACBP calculated using the worm-like chain model with a contour length of 14.4 nm and persistence length of 0.7 nm.

In contrast, m-values decrease in magnitude as temperature is increased and urea concentration is decreased (Table 2), indicating that the denatured state is more compact under these high-temperature and low-urea conditions. To disentangle these two conditions, we used destabilizing mutations that altered the transition regions for this protein. ACBP mutants at the same urea concentration but different temperatures can have different denatured state ensembles (Fig. 5d): the denatured state ensemble becomes more compact as temperature increases. On the other hand, ACBP mutants at the same temperature have denatured state ensembles with similar ASA exposure even when the urea concentration is different (Fig. 5c). Therefore, the denatured state ensemble appears to be independent of urea concentration.

The mutational analysis also supports our hypothesis that differences in m-value can be interpreted as differences in the ASA of the denatured state ensemble. Previous work has shown it is possible to have a breakdown in the two-state approximation near the Tm [52], which would lower the measured m-value near the Tm. This does not appear to be the case for our studies. The single-site variants we study modulate the Tm of the protein, yet the temperature-dependent m-values overlap, indicating that the reduction in m-value is not due to presence of an intermediate near the Tm.

These results suggest that temperature induces a denatured state that is fundamentally different from the denatured state induced by urea or force. Urea unfolds proteins because it favors conformations that expose more ASA [28, 30] while force induces unfolding by favoring more extended conformations [16, 53]; both of these denaturants might be expected to promote denatured states that expose more ASA. Temperature, however, unfolds proteins by altering the entropy-enthalpy compensation that dictates the free energy for unfolding [54, 55]. Thus, temperature-induced denaturation is not directly related to the amount of ASA exposed in unfolding. While the urea- and force-induced denatured states are more similar to extended chains, the temperature-induced denatured state appears more compact and perhaps molten-like [56]. Indeed, hydrogen exchange studies on thermally denatured RNase A show no protection of amide protons despite evidence for residual structure, suggestive of a molten-globule type state [40].

Comparison to trends in m-value with temperature for other proteins

Temperature dependent urea m-values have been noted for other proteins [5762]: these changes are summarized in Table 3 (see supplemental Fig. 6 for plots of m-value vs temperature). Like ACBP, the m-values for HPr, FKPB12 and the lac DNA binding domain clearly decrease with temperature, but the percent changes in m-value are different for each protein. For the Notch ankyrin domain, the m-value decreases with temperature nonlinearly: at low temperatures the slope is much smaller. For CT AcP and RNase T1, there is no clear trend—the m-values do not appear to change in a systematic way with respect to temperature. These different effects are expected based on our suggestion that the temperature dependent changes in m-values are a result in changes in ΔASA for unfolding. If, on the other hand, our data were the result of a temperature dependence of the proportionality constant between the m-value and ΔASA (change in the thermodynamics of the interaction of urea with the protein), the m-value changes would be independent of the protein studied.

Table 3.

Trends in urea m-values with respect to temperature for different proteins

Protein	$\frac{dm}{dT}$ (cal mol−1 M−1 °C −1)	Folding m at 25°C (kcal mol−1 M−1)	Percent change in m per degree Celcius (°C −1)**
WT ACBP	−7.33 ± 0.40	1.28 ± 0.02	−0.587 ± 0.033
HPr [59]	−5.4 ± 1.3	1.19 ± 0.06	−0.453 ± 0.026
Lac DNA binding domain [57]	−1.02 ± 0.22	0.4490 ± 0.0108	−0.227 ± 0.049
FKBP12 [58]	−8.0 ± 2.0	1.7 ± 0.6	−0.47 ± 0.20
CT AcP [60]	−3.0 ± 4.7	1.5 ± 0.1	−0.20 ± 0.31
RNase T1 [61]	2.6 ± 1.8	1.20 ± 0.05	0.22 ± 0.15
Notch ankyrin domain [62]*	Non-linear decrease

^*Precise m-values not available, plots of m-value vs temperature given in ref 62.

^**Percent change in m-value obtained by dividing values in row 2 by values in row 3 of this table

The different magnitudes of effects seen for these different proteins suggest that the denatured state and how it responds to the environment are highly dependent on protein sequence. These conclusions are consistent with smFRET experiments on intrinsically disordered proteins which also suggest that the degree of compaction of the thermally denatured state varies from protein to protein and depends on the proportion of hydrophobic and hydrophilic residues [23]. Computational studies from the Pappu lab also suggest that the conformation of denatured proteins is sequence-dependent and that expansion of denatured proteins is primarily related to the interaction of the solvent with different protein side chains [63, 64]. The change in m-value with both temperature and [urea] has not been explored for other proteins in the same systematic way that we have done ACBP, so it is not known if the trends for other proteins are more correlated with temperature or with [urea].

Relating chemo-mechanical unfolding data to the FRET vs SAXS debate

Although much work has been done to explore how the denatured state ensemble changes under different environmental conditions, there are often conflicts between the conclusions given by different techniques. A great example of this is the classic FRET vs SAXS debate described below. Chemo-mechanical unfolding provides another technique that can give a fuller picture of the denatured state ensemble and help resolve remaining discrepancies.

When proteins are diluted from high to low denaturant concentration, time-resolved SAXS experiments do not show a change in structure of the denatured state with urea concentration [18, 20, 22]. This is consistent with our data suggesting that the ASA of the denatured state does not depend on urea concentration. On the other hand, studies of the FRET efficiency of the denatured state ensemble show an increase in distance between labeled sites in the denatured state ensemble as urea concentration is increased and a decrease in distance as temperature is increased [10, 17, 21, 23, 24, 39]. While this collapse with temperature is consistent with our data showing a decrease in m-value with temperature, the increase in distance with urea seems to be inconsistent our ACBP data and with SAXS data. To resolve this discrepency, Borgia et al computationally generated an ensemble of denatured states and used a Bayesian reweighting procedure to achieve agreement with SAXS and smFRET data at different chemical denaturant concentrations [24]. They found that both SAXS and smFRET data are consistent with an expansion of the denatured state as chemical denaturant is added but because different techniques probe different aspects of the denatured state ensemble, some techniques may appear to show more expansion than others. For instance, the radius of gyration probed in SAXS experiments changes little relative to the distance probed in smFRET experiments. Song et al support this argument with simulations showing that radius of gyration need not be correlated with FRET efficiency [25]. Therefore, it is also possible that the distance between labeled sites can increase without a significant change in ASA, which is why we do not see a change in ACBP m-value with urea concentration. Indeed, simulations and experiments comparing sensitivities of different experimental measurements of polypeptide dimensions show that distances from FRET are more sensitive than radii of gyration from SAXS, which are more sensitive than ASA values [26, 35].

Comparison to theoretical studies of the denatured state ensemble

The above example makes it clear that the combination of experiments and simulations is necessary to fully understand the denatured state ensemble. There have been several theoretical studies attempting to simulate the effects of urea, force, and temperature on the denatured state. Simulations by Stirnemann et al perturb ubiquitin unfolding with force and urea and find that the force-unfolded structure of ubiquitin is significantly more extended than the urea-unfolded structure, which seems to contradict our result that urea and force induce similar denatured states [14]. However, in order to completely unfold ubiquitin on a computationally-accessible time scale they performed their simulations at 550K. As we have shown, high temperature can induce a more compact denatured state so the difference they see may be related to temperature rather than urea.

The molecular transfer model was developed to simulate the effect of denaturants on protein folding and generally predicts that the denatured state is more compact at low denaturant concentrations [34, 65, 66]. Simulations by O’Brien et al using the molecular transfer model show that the denatured state for protein L exposes more ASA (and so has a higher m-value) as urea concentration increases up to approximately 3 M urea, where ASA becomes independent of urea concentration [34]. This is inconsistent with our data in Figure 4c, showing that ACBP variants have the same m-value at different urea concentrations. At 37°C, the midpoint urea unfolding concentration (Cm) is 3.57 ± 0.08 for WT ACBP, 1.66 ± 0.03 for ACBP Y28N and 0.36 ± 0.02 for ACBP Y73A, yet all variants have approximately the same m-value. Therefore, even below 3 M urea, the ACBP m-value is independent of urea concentration. However, analysis of m-values measured for variants of barnase suggest that unlike ACBP, the barnase m-value is [urea] dependent [67]. Therefore, it is possible that, like the temperature dependence, the urea dependence of the m-value is sequence dependent.

Implications for the Linear Extrapolation Method

Chemical denaturant melts are typically analyzed using the linear extrapolation method (LEM, Eq. 1), where ΔG is assumed to depend linearly on denaturant concentration with a slope defined as the m-value [44]. In a typical denaturant melt, the information used to determine this slope comes from the transition region where we can see the population of folded and unfolded protein change with denaturant concentration [13]. The m-value determined in this region is used to extrapolate to ΔG in the absence of denaturant, assuming a constant m-value. Since it is difficult to probe the folding process without adding a denaturant, this assumption is rarely tested.

Our data, supports the assumption of the LEM that the m-value does not change with denaturant concentration. We find that m-values measured using force at low urea concentration are the same as m-values measured in the absence of force at higher urea concentration and that m-values measured for variants of ACBP at the same temperature and different urea concentrations are similar (Fig. 5c). This is consistent with native state hydrogen exchange experiments where ΔG_HX is determined as a function of low urea concentration and found to be the same as ΔG determined using the LEM [68, 69].

Implications for protein folding in vivo

In sum, our work reveals that the ACBP denatured state changes with some environmental conditions (temperature) but not others (urea concentration, force). This has broad implications for the behavior of proteins in the crowded, heterogeneous cellular environment and for how proteins respond to stress. For instance, in some cases, the cellular environment has been noted to stabilizes protein native structure while in other cases it has a destabilizing effect [12, 70–73]. This change in stability may be related to a difference in the structure of the denatured state under cellular conditions.

Force is an important variable in many cellular processes including protein folding. For instance, protein folding itself can generate force as the protein exits the ribosome exit tunnel [74] and force is applied to unfold proteins during proteasomal degradation [75, 76]. The forces applied in physiological processes are similar to the forces applied here (tens of piconewtons) [53]. Our data suggest that these physiologically relevant forces do not significantly perturb the denatured state.

Proteins are also exposed to a wide range of small molecules in the cell, ranging from denaturants like urea and guanidinium chloride to stabilizing osmolytes like trehalose and glycine betaine [11, 77]. We find that denaturant concentration does not significantly affect the ASA of the denatured state—future work will explore the effect of osmolytes and crowding agents.

Our data suggest that when cells are exposed to higher temperatures, denatured proteins bury more ASA. If the buried surface is aggregation prone, this response could lower the probability of aggregation. Therefore, it is possible the proteins have evolved to bury surface area during temperature stress.

Conclusions

In conclusion, we have shown that chemo-mechanical unfolding is a useful tool to probe heterogeneity in both protein-folding pathways and the protein denatured state. By combining different perturbants like force, urea and temperature, we can access and characterize new aspects of the protein energy landscape. In this work, we have shed light on the longstanding debate of whether the denatured state ensemble changes with environmental conditions. We find that for ACBP, the denatured state changes with temperature but not force or urea. Comparison to other work reveals that effects of temperature and urea may be sequence dependent. Chemo-mechanical unfolding provides a tool to explore this sequence dependence as well as effects of other perturbants on the denatured state.

Materials and Methods

Protein Expression and Purification

Wild Type bovine ACBP [78] and the mutants studied here were expressed in Escherichia coli strain Rosetta/pLysS, using the pET28a vector with insertion of the ACBP gene into the NdeI and HindIII sites. This adds an N-terminal His Tag, which was not removed in these studies. Mutations were introduced using QuikChange site-directed mutagenesis. Cells were grown at 37°C until the OD₆₀₀ reached 0.6–08. Expression was then induced using 1 mM IPTG and the cells were incubated for three more hours. Cells were harvested by centrifugation and resuspended in buffer. For ACBP M46C/I86C, 100 mM Tris 250 mM NaCl 1 mM TCEP pH 7 buffer was used, for all other variants 50 mM potassium phosphate pH 7 buffer was used. After lysis by sonication, all variants were purified over HisPur Ni-NTA Superflow resin and eluted with buffer containing 250 mM immidazole. The resulting elutions were further purified using gel-filtration chromatography with a Hi-Load Superdex-75 16/60 column on a GE Healthcare AKTA purification system.

Optical Tweezers

DNA handles were attached to ACBP M46C/I86C as described previously [79]. Experiments were conducted using an optical tweezers instrument described in previous studies [51, 80, 81]. The optical trap is made of two coaxial, counter-propagating lasers holding a 3.2 μm, anti-digoxigenin coated bead at the focus. This bead is tethered via the DNA-protein-DNA chimera to a 2.1 μm streptavidin-coated bead, which is held on a micropipette via suction. The micropipette is stationary, and the trapped bead is manipulated by steering the optical trap, which samples data at 1 kHz and has a spring constant of ~0.08 pN/nm.

Determining urea m-values under mechanical force

To monitor the equilibrium between the folded and unfolded ACBP, the protein was held using constant-force-feedback mode as described previously [82]. These experiments were performed at a range of forces where folding and unfolding could be observed in 0 and 1M urea. By monitoring extension as a function of time, the protein was observed to hop between the folded and unfolded state. For each force and urea condition, at least six different tethers were used to collect at least 70 folding and unfolding transitions. These experiments were performed in 100 mM Tris 250 mM NaCl pH 7 buffer.

The hopping data were averaged to 50 Hz and fit using a hidden Markov Model (HMM) analysis to identify transitions [48]. See supplemental Fig. 1 for an example of this analysis workflow. The resulting dwell times were divided into bins of width Δt where t is a time that is at least 20% of the time constant τ for the dataset. The probability for each bin was determined by dividing the number of events in that bin by the overall number of events. The probability density p(t) was determined by dividing this probability by Δt. Probability density values were plotted against the midpoint t of the bin (supplemental Fig. 2) and fit to Eq. 3 to determine rates.

$$\text{p}(\text{t})=k{e}^{-k\text{t}}$$ Eq. 3

Folding rates (kf) were determined by fitting dwell times in the unfolded state and unfolding rates (k_u) were determined by fitting dwell times in the folded state. Supplemental figure 3 shows plots of the folding and unfolding rates. The unfolding equilibrium constant K_eq was determined from the ratio k_u/k_f.

The natural logarithm of K_eq was plotted against force for 0M urea and 1M urea hopping data (Fig 2d). The urea dependence of ΔG (-RTlnK_eq) is quantified by the m-value according to Eq. 1. The force dependence is quantified by the x-value using Eq. 4:

$$\Delta {\text{G}}_{\text{U}}=\Delta {{\text{G}}_{\text{U}}}^{\text{0pN\hspace{0.17em}Force}}+{\text{F}}^{*}x$$ Eq. 4

where ΔG_U ^{0pN Force} is the ΔG_U value in the absence of force. We can combine equations 1,2 and 4 to create Eq. 5, which describes the urea and force dependence of lnK_eq:

$$-{\text{RTInk}}_{\text{eq}}=-{\text{RTInk}}_{\text{eq}}{}^{0\text{pn\hspace{0.17em}Force},0\text{M\hspace{0.17em}urea}}+m[\text{urea}]+{\text{F}}^{*}x$$ Eq. 5

where RTlnK_eq^{0pN Force, 0M urea} is the extrapolated equilibrium constant in the absence of force and urea. Igor Pro v6.22a was used to globally fit the lnK_eq vs Force plots for both 0M and 1M urea data sets to Eq. 5, fixing lnK_eq^{0pN Force}’^{0M urea}, m and x to be the same for both data sets. The resulting x-values are within error of the values obtained when fitting the 0M and 1M urea data separately.

Determining urea m-values from urea melts

Urea melts were collected by monitoring the circular dichroism (CD) signal at 222nm as a function of urea using samples with approximately 2uM protein in a 1cm pathlength cuvette. For most variants, melts were performed in 50 mM Potassium Phosphate pH 7 buffer. For ACBP M46C/I86C, TCEP was required to prevent disulfide bonds. TCEP interacts with potassium phosphate buffer [83] so these melts were performed in 100 mM Tris, 250 mM NaCl, 1mM TCEP, pH 7 buffer. Urea melts at 25°C for WT ACBP, ACBP M46C/I86C and ACBP Y28N and 16°C for ACBP Y73A were collected on an Aviv model 410 spectrophotometer using a Microlab 500 series titrator to vary the urea concentration. Samples were stirred for two minutes before data were collected by averaging the signal for 60 seconds. Four replicates of each titrator melt were collected. For all urea melts, CD signal was plotted as a function of urea and fit to determine ΔG_U ^{0M urea} and the m-value using Equation 6:

$$S_{obs}=\frac{S_{N,}{H}_{2}O+{\beta }_N[urea]+(S_{D,}{H}_{2}O+{\beta }_D[urea])e^{(-\Delta G^{0Murea}-m[urea])/RT}}{1+e^{(-\Delta G^{0Murea}-m[urea])/RT}}$$ Eq 6

where S_obs is the observed signal, β_D and β_Ν are the slopes of the denatured and native baseline signals, and S_D,H2O and Sn,h2o are the denatured and native protein signals in the absence of urea (intercepts of the native and denatured baselines).

Determining urea m-values from temperature melts

Temperature melts were performed by monitoring the circular dichroism (CD) signal at 222nm as a function of temperature using an Aviv model 430 spectrophotometer. Data were collected in a 1cm pathlength cuvette with samples containing approximately 2uM protein. All temperature melts were performed in 50 mM potassium phosphate, pH 7 buffer with urea concentrations varying from 0–5 M for WT ACBP and 0–1M for ACBP Y28N and ACBP Y73A. We use potassium phosphate buffer for these experiments because its pH does not depend on temperature. Samples were allowed to equilibrate for three minutes at each temperature before data were collected by averaging the signal for 60 seconds. An external thermistor probe was used to verify that the temperature equilibration time was sufficient. Four replicates of each melt were collected.

Plots of CD signal vs temperature were created and fit to determine Tm, the temperature where the protein is half folded and half unfolded, and S, the slope of ΔG_U against temperature [84]. This fitting method makes the approximation that ΔG_U varies linearly with temperature, which is valid in the region near the Tm (see plots of ΔG vs temperature in sup. Fig 5). This means we can accurately determine ΔG_U only at temperatures near Tm. Because different melts were collected at slightly different urea concentrations, fraction folded was calculated using the fit parameters and used to create Fig. 3a.

To determine urea m-values from temperature melts, we compare two sets of melts collected at urea concentrations that differ by 1M. We don’t compare melts that differ by more than 1M because the transition regions differ in temperature too much to calculate ΔG_U values at a temperature near Tm for both melts. For each m-value calculation, we determine the average of the two Tm values from the different sets of melts and calculate ΔG_U at that temperature for each set. The m-value is the difference in ΔG_U values divided by the difference in urea concentration (d ΔG_U/d[urea]). ΔG_U and Tm values used in these calculations are the average of the values determined from four replicates melts in each set of conditions.

Determining urea m-values from global analysis of urea melts at different temperatures

Data for urea melts collected at different temperatures that were globally analyzed (Figs. 4 and 5) were collected on an Aviv model 430 spectrophotometer. Melts were performed in 50 mM Potassium Phosphate, pH 7 buffer with samples containing approximately 2 uM protein in a 1 cm pathlength cuvette. For WT ACBP, ACBP Y28N and ACBP Y73A, samples at different urea concentrations were prepared manually by mixing 0M urea and high urea protein stocks in different ratios. For each different urea concentration sample, CD signal at 222 was monitored at at least 12 different temperatures below the Tm in 0M urea. Samples were equilibrated and data were collected as described above for temperature melts

The CD signal was plotted against urea concentration for each temperature (Fig 4a, 5a,b). To fit the data, equation 6 was modified by replacing S_N,H2Owith a term to describe the temperature dependence of the lower baseline to create Equation 7:

$$S_{obs}=\frac{S_{N,H_{2}O}^{25°C}+{\beta }_{S_{N,H_{2}O}}(T-25)+{\beta }_N[urea]+(S_{D,}{H}_{2}O+{\beta }_D[urea])e^{(-\Delta G^{0Murea}-m[urea])/RT}}{1+e^{(-\Delta G^{0Murea}-m[urea])/RT}}$$ Eq 7.

In this equation, S_N,H2O^25°C is the lower baseline signal in the absence of urea at 25°C and β_SN,H2O is the slope of this lower baseline signal with respect to temperature. Data were globally fit by linking all lower baseline parameters between plots at different temperatures. Additionally, urea melts at temperatures where the plots had a sufficient lower baseline to fit alone were fit individually using equation 6. If the ΔG and m-values from individual fits were not within error of the values obtained from global analysis the melts were removed from the global analysis.

Highlights.

• Does the protein denatured state ensemble change with environmental conditions?

• The effect of urea on folding is used to probe the structure of the denatured state ensemble.

• Force and urea induce similar denatured states.

• Temperature induces a more compact denatured state.