Long-range temporal correlations reflect treatment response in the electroencephalogram of patients with infantile spasms

Abstract

Infantile spasms syndrome is an epileptic encephalopathy in which prompt diagnosis and treatment initiation are critical to therapeutic response. Diagnosis of the disease heavily depends on the identification of characteristic electroencephalographic (EEG) patterns, including hypsarrhythmia. However, visual assessment of the presence and characteristics of hypsarrhythmia is challenging because multiple variants of the pattern exist, leading to poor inter-rater reliability. We investigated whether a quantitative measurement of the control of neural synchrony in the EEGs of infantile spasms patients could be used to reliably distinguish the presence of hypsarrhythmia and indicate successful treatment outcomes. We used autocorrelation and Detrended Fluctuation Analysis (DFA) to measure the strength of long-range temporal correlations in 21 infantile spasms patients before and after treatment and 21 control subjects. The strength of long-range temporal correlations was significantly lower in patients with hypsarrhythmia than control patients, indicating decreased control of neural synchrony. There was no difference between patients without hypsarrhythmia and control patients. Further, the presence of hypsarrhythmia could be classified based on the DFA exponent and intercept with 92% accuracy using a support vector machine. Successful treatment was marked by a larger increase in the DFA exponent compared to those in which spasms persisted. These results suggest that the strength of long-range temporal correlations is a marker of pathological cortical activity that correlates with treatment response. Combined with current clinical measures, this quantitative tool has the potential to aid objective identification of hypsarrhythmia and assessment of treatment efficacy to inform clinical decision-making.

1. Introduction

Infantile spasms (IS) is a potentially devastating form of epilepsy characterized by epileptic spasms and often accompanied by a chaotic electroencephalographic (EEG) pattern known as hypsarrhythmia (Pavone et al. 2013). In contrast with the low amplitude, mixed frequency activity of normal awake EEG (Fig. 1a), classic hypsarrhythmia is defined by multi-focal, independent epileptiform discharges on a disorganized background activity with asynchronous large amplitude slow waves (Fig. 1b) (Stamps et al. 1959). There are also several variants of hypsarrhythmia that include episodes of voltage attenuation, burst-suppression patterns, increased interhemispheric synchronization, and hyperactive epileptiform foci (Hrachovy et al. 1984). Quantifying the presence and severity of hypsarrhythmia is nontrivial, as these variants exhibit drastically different power and spectral characteristics (Lux and Osborne 2004; Hussain et al. 2015). For example, Hussain et al. showed that the inter-rater reliability for hypsarrhythmia identification is unacceptably low, with kappa less than 0.5 (2015). This can impede accurate diagnosis and evaluation of short-term treatment response for patients with IS. Therefore, quantitative measurements of hypsarrhythmia are needed to improve the accuracy, objectivity, and reliability of these assessments (Hussain et al. 2015). Improving these methods may also reduce the time between diagnosis and successful treatment, a factor that has been shown to be related to improved developmental outcome (Riikonen 2010).

Fig. 1.

Example EEG traces. a Awake EEG from control patient containing no epileptic activity. b Awake EEG from an infantile spasms patient with hypsarrhythmia

As opposed to hypsarrhythmia, which is qualitatively described as a “chaotic” pattern, it is known that EEG activity in a healthy human brain possesses scale-free structure over multiple time scales (Linkenkaer-Hansen et al. 2001). Neural data has been shown to exhibit amplitude modulations on a power-law scale, in which the power in the amplitude envelope y is related to its frequency f by: $y=\frac{1}{f^{\alpha }}$, with a scaling constant α termed the Hurst parameter (Linkenkaer-Hansen et al. 2001). The power-law scaled nature of amplitude fluctuations in EEG data gives rise to long-range temporal correlations in the time series (Stadnitski 2012).

The autocorrelation is one of the simplest methods to assess long-range temporal structure in time series data. It has been used to characterize periodic phenomena in childhood absence seizures (Babloyantz and Destexhe 1986) and to perform automatic detection of neonatal seizures (Liu et al. 1992). However, the autocorrelation function often provides a noisier estimate of the decay of temporal correlations than more complex methods (Smit et al. 2011). The noise level in these calculations can be reduced by using techniques that are based on random walk theory rather than analyzing the time series directly (Kantelhardt et al. 2001). Specifically, detrended fluctuation analysis (DFA) has been shown to be robust to certain nonstationarities in positively correlated signals, such as discontinuities due to artifact removal, and it is appropriate for use on shortened data segments (Chen et al. 2001; Hardstone et al. 2012). Both of these factors directly affect the stability of the autocorrelation. Thus, we used both the autocorrelation and DFA to characterize the long-range temporal dependence in EEG data associated with infantile spasms before and after treatment. We hypothesized that the presence of infantile spasms and hypsarrhythmia would disrupt long-range temporal correlations in the EEG and that a response to treatment would be associated with the return of temporal correlations to normal levels.

2. Methods

2.1. EEG Data Recording

Scalp EEG data was recorded from infantile spasms and control patients using Nihon-Kohden acquisition hardware and software in the Epilepsy Monitoring Unit at the Children’s Hospital of Orange County (CHOC). Nineteen scalp EEG electrodes recorded neural activity, placed according to the 10–20 international electrode placement system. Data were sampled at 200 Hz with electrode impedances below 5 kOhms. A clinical pediatric epileptologist at CHOC (DS) retrospectively collected the datasets from the electronic medical record and stored them in an encrypted database. Approval to perform this study was obtained from the CHOC Institutional Review Board.

We gathered EEG and clinical data for 21 infantile spasms patients. Two separate recordings were collected during wakefulness (median recording duration: 22.1, IQR 19.4–24.1 minutes). The first recording was performed at the time of the infantile spasms diagnosis prior to treatment (median age: 6.3, IQR 5.2–8.1 months), and the second was done after treatment initiation to assess response (median time to second recording: 29, IQR 19–42.25 days). The data was clipped without reviewer knowledge of treatment status or outcome. Awake EEG was chosen for analysis because EEG characteristics vary significantly across different sleep stages. The pre-treatment EEGs of all 21 patients exhibited findings consistent with hypsarrhythmia. In three patients, this pattern occurred intermittently, whereas in the other 18 it was consistently present.

We also collected data for 21 control subjects of a similar age distribution (median age: 7, IQR 5.75–11.25 months). In this group, neurologists had ordered routine EEGs for suspected neurological abnormalities due to trauma or atypical behavior, but later classified the EEG as normal. These recordings contained both sleep and awake data, and the sections of wakefulness were selected for analysis (median recording duration: 12.2, IQR 10.1–16.3 minutes). Additional exclusion criteria for control patients in this study included a history of epilepsy, abnormal developmental history, abnormal video-EEG telemetry monitoring, and known neurological conditions.

2.2. Data pre-processing

The EEG data were re-referenced to a linked-ear montage and divided into narrow frequency bands using FIR filters for the delta (1–3 Hz), theta (4–7 Hz), alpha (8–12 Hz), and beta (13–30 Hz) ranges. Epileptologists at CHOC marked and removed artifacts due to eye blinks, muscle activity, movement, poor electrode contact, and periods of photic stimulation prior to analysis.

2.3. The autocorrelation function

We calculated the autocorrelation of the amplitude envelope of infantile spasms patients with and without hypsarrhythmia in the Cz electrode. Electrode Cz was chosen because it is minimally affected by muscle and eye movement artifacts. The amplitude envelope was extracted from the bandpass-filtered data by applying the Hilbert transform and calculating the magnitude of the analytic signal. We then calculated the autocorrelation using a biased cross-correlation of the envelope at all possible time lags, normalized to correlation values between 0 and 1. To assess the significance of temporal correlations in the data, we compared the result of the autocorrelation to surrogate data that was created by shuffling the Fourier phases of the original envelope. We calculated the time lag at which each patient autocorrelation function failed to exceed the 95^th percentile of the surrogate data. This represented the time lag at which the correlations in the time series were not significantly different from chance levels.

2.4. Detrended Fluctuation Analysis

Detrended Fluctuation Analysis (DFA) was implemented using the following algorithm, adapted from Hardstone et al. (2012):

First, the amplitude envelope was extracted from each channel by similar methods used in the autocorrelation calculation. We then subtracted the mean of the amplitude envelope and computed the cumulative sum of the signal to create the signal profile. This signal profile was divided into equally-sized windows with 50% overlap. Within each window, we performed a linear fit of the signal profile, subtracted the fit from the time series, and calculated the standard deviation of the detrended signal. After computing the standard deviations of the detrended signal for all windows of that size, we recorded the median standard deviation for that window size. This process was repeated for logarithmically-spaced window sizes from 3 seconds to 25 seconds in length.

When the median standard deviations are plotted on a logarithmic scale against the log-spaced window sizes, the result is linear with slope α (Fig. 2). This slope is a direct estimation of the Hurst parameter and indicates the strength of the temporal correlations present in the time series (Hardstone et al. 2012). The slope of the resultant DFA plot varies between 0 and 1.0. Exponents less than 0.5 designate anti-correlated signals, while positively correlated signals have an exponent greater than 0.5, indicating strong long-range temporal correlations. Uncorrelated signals, such as white noise, result in a DFA exponent of 0.5.

Fig. 2.

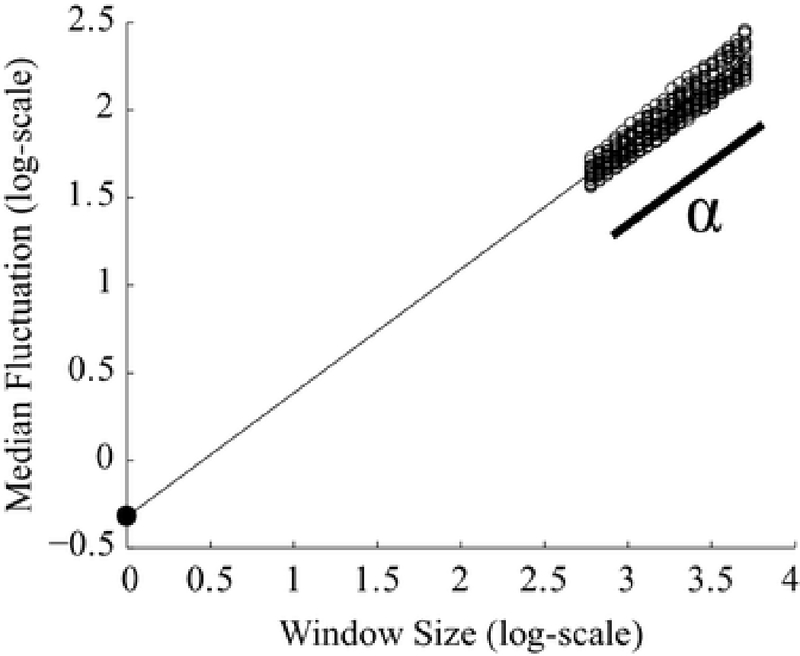
Example DFA plot. The DFA exponent, α, is the slope of the linear fit of the average of all channels. Each channel’s median fluctuation value (standard deviation of the detrended signal) is plotted as a circle for each window size. Window size is measured in data points. The intercept is calculated as the theoretical fluctuation value when the logarithm of the window size equals zero, represented by the filled dot on the y-axis

We averaged α from all individual channels to obtain a single value approximating the strength of long-range temporal correlations in the EEG, as individual channels within a subject exhibited consistent slopes (Fig. 2). The intercept of the DFA plot was calculated from the linear fit of the channel average by extrapolating on the logarithmic plot to find the fluctuation value when window size was one sample, the value at which the logarithm of the window size equals zero. (Fig. 2, filled black dot).

Note that DFA has been shown to robustly measure temporal dependence in positively-correlated signals, even when the data contains discontinuities due to artifact removal (Chen et al. 2001). Although DFA has been criticized by several groups in this regard (Bardet and Kammoun 2008; Bryce and Sprague 2012), their concerns are often aimed at the generalizability of the technique to all signal nonstationarities. We use the method under the careful assumption that neural signals are positively correlated and we use sufficiently long window sizes to mitigate the uncertainty of the measure in small data segments. Other forms of the algorithm increase the largest window size to 1/10 of the signal length (Hardstone et al. 2012), but the use of large windows can cause a piecewise linear result with one or more “cross-over” points, requiring special analysis techniques (Chen et al. 2001; Ferree and Hwa 2003). Therefore, we set the smallest window size to 3 seconds and the largest window size to 25 seconds to maintain consistent linearity at all window sizes (mean SSE: 0.0017 +/− 0.0042).

2.5. Support Vector Machine Classification

To quantify our ability to distinguish between patients with and without hypsarrhythmia, we trained one-dimensional and two-dimensional support vector machines (SVM). The one-dimensional SVM imposes a simple threshold, while the two-dimensional SVM optimizes a linear classifier to separate the two groups. To train the SVM, we randomly selected half of the subjects with hypsarrhythmia (n=25) and half of the subjects without hypsarrhythmia (both spasms and control patients, n=38) and used the MATLAB function “svmtrain”. We then tested the classifier with the remainder of the data using the MATLAB function “svmclassify”. The number of correct classifications, the sensitivity, and specificity were recorded over 1000 iterations of randomly-selected training and testing datasets.

2.6. Amplitude histogram calculation

We quantified the amplitude variation for each EEG, as hypsarrhythmia is defined as a high-amplitude pattern. We calculated amplitude histograms of the broadband (0.5–55 Hz) bandpass-filtered data for all patients, as follows: For each 1-second window of data, we recorded the amplitude as the difference between the maximum and minimum voltage in the Cz electrode. We then binned the resulting amplitudes into a histogram consisting of 50 bins with occurrences represented as a fraction of the total number of windows in the dataset.

2.7. Effect of amplitude and standard deviation on DFA parameters

To gain insight into how basic characteristics of the EEG data, including amplitude and standard deviation, affect the DFA measurement, we performed simulations using pink noise. Pink noise was generated at 200 Hz for 20 minutes to match the characteristics of our EEG dataset. After bandpass filtering, the amplitude envelope was extracted by performing the Hilbert transform and calculating the magnitude of the analytic signal.

We then measured the DFA exponent and intercept of the simulated signal, using scaling factors to independently vary the amplitude and variance of the envelope. The 1000 scaling factors were linearly-spaced values from 1 to 100. To vary the overall amplitude, we calculated the mean value of the amplitude envelope, multiplied the mean by the scaling factor, and added this constant to the original envelope (Fig. 3, green line). To scale the variance, we first subtracted the mean from the original amplitude envelope, multiplied the zero-mean signal by the scaling factor, and added the original mean value back into the signal (Fig. 3, blue line). For each scaling factor, DFA was performed on all three envelopes: the original envelope, the envelope with increased amplitude, and the envelope with increased variance.

Fig. 3.

Example amplitude envelope traces used in simulated EEG filtered in the alpha band. The red line is the original extracted amplitude envelope from a simulated EEG signal. The green and blue lines depict the original envelope scaled with increased amplitude and variance, respectively

3. Results

3.1. Hypsarrhythmia is associated with weaker long-range temporal correlations

In the beta frequency band, the EEGs of patients without hypsarrhythmia exhibited stronger autocorrelation values over all time lags when compared to data with hypsarrhythmia (Fig. 4a). Both patient groups showed significant correlations over longer time lags than surrogate data (Fig. 4a), but the autocorrelation of data without hypsarrhythmia remained significantly higher than surrogate data over longer time lags (Wilcoxon rank-sum: p<0.01, z = −2.58, Fig. 4b). Results in other frequency bands were not significant (data not shown). The differences in the beta band motivated further investigation into how hypsarrhythmia disrupts temporal structure in EEG. Note, however, that we were unable to directly compare to the autocorrelation functions for the control group, as the control subject EEG data was often shorter and contained both sleep and wakeful states. The autocorrelation measurement is negatively impacted by the discontinuities created by concatenating the awake segments, and it was not possible to extract uninterrupted segments of awake data of sufficient length to directly compare the autocorrelation functions of the three groups.

Fig. 4.

EEG data with hypsarrhythmia is associated with decreased temporal correlations in the beta frequency band when calculated with autocorrelation. a The median normalized autocorrelation function of the amplitude envelope in patients with hypsarrhythmia (red, n=25), patients without hypsarrhythmia (blue, n=17), and surrogate data (green, n=42). The respective shaded areas represent data between the 25^th and 75^th quantile of individual autocorrelation functions. The black line indicates the 95^th quantile of the surrogate data used as the threshold of significance for patient data. b Boxplots of the distribution of lag times at which individual patient autocorrelation functions were no longer significant, for patient data with (red) and without (blue) hypsarrhythmia. Patients with intermittent hypsarrhythmia are included in the hypsarrhythmia boxplot

Thus, further quantification and a comparison with control data warranted the use of detrended fluctuation analysis to more robustly characterize the strength of long-range temporal correlations in the data. First, we compared DFA exponents of patients with hypsarrhythmia to those without, regardless of whether the data was collected before or after treatment. Recall that some patients did not respond to treatment and still had hypsarrhythmia in the post-treatment EEG (4 out of 21 patients, see Table 1). Patients with hypsarrhythmia exhibited lower DFA exponents than control subjects in all frequency bands (Fig. 5, Wilcoxon rank-sum test: p<0.0125 corrected for multiple comparisons, average z = −3.74). Patients without hypsarrhythmia had significantly greater DFA exponents than patients with hypsarrhythmia in the theta (p<0.0125, z = −3.31), alpha (p<0.0125, z = −2.92), and beta (p<0.0001, z = −3.92) bands. There was no significant difference between patients without hypsarrhythmia and control patients in any frequency band (Fig. 5).

Table 1. Infantile Spasms Patient Clinical Information.

Clinical information for 21 infantile spasms patients.

Patient Number	Age at Treatment Initiation (months)	Spasms Etiology	Medication	Time between Onset of Spasms and Treatment (days)	Treatment Response
					Hypsarrhythmia Resolved	Spasms Resolved
1	12.0	Cortical Malformation	VGB	35	No	No
4	5.5	Neonatal HIE	ACTH	7	Yes	Yes
5	8.7	Unknown, Prematurity, Diffuse Cerebral Atrophy	ACTH	4	Yes	Yes
6	6.8	Tuberous Sclerosis	VGB	4	Yes	Yes
8	4.5	Dysmorphic, likely genetic	ACTH	14	Yes	No
9	6.0	Neurofibromatosis Type I	ACTH	3	Yes	No
10	4.5	Unknown	ACTH	10	Yes	No
11	7.9	Paroxysmal Bifunctional Protein Deficiency	ACTH	7	Yes	Yes
13	3.7	GBS Ventriculitis and hydrocephalus	VGB	7	No	No
16	6.6	CDKL5 Mutation	ACTH, VGB	23	Yes	No
18	18.3	Unknown	ACTH	270	Yes	Yes
19	4.9	Neonatal HIE	ACTH	8	Yes	Yes
20	6.3	Unknown	ACTH	30	Yes	Yes
22	7.7	Unknown	ACTH	30	Yes	Yes
25	7.7	Tuberous Sclerosis	VGB	7	Yes	No
28	6.0	Chromosome 8 Abnormality & Stroke	ACTH	4	Yes	Yes
29	5.8	Lissencephaly & Pachygyria	ACTH	5	Yes	Yes
30	5.3	Lissencephaly	ACTH	90	No	No
31	19.4	Bacterial Meningoencephalitis	ACTH	90	Yes	No
32	9.0	Prematurity and Left-sided IVH	ACTH	4	Yes	Yes
34	4.9	Unknown	ACTH	28	No	No

Acronyms are defined as follows: HIE = hypoxic-ischemic encephalopathy, WM = white matter, GBS = Group B streptococcus, ACTH = adrenocorticotropic hormone, and VGB = vigabatrin.

Fig. 5.

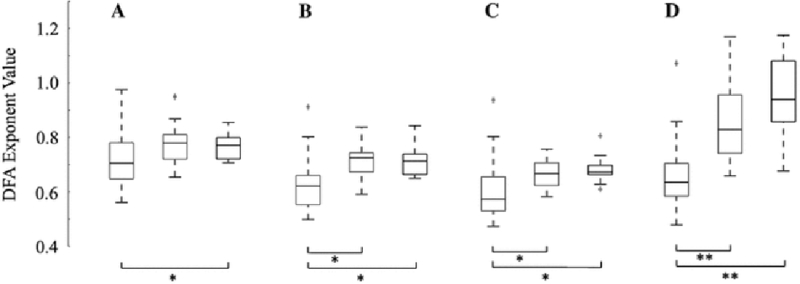
Hypsarrhythmia is associated with lower values of the DFA exponent (* = p<0.0125, ** = p<0.0001). Results are shown for a delta band (z = −2.54), b theta band (z = −3.64), c alpha band (z = −3.77), and d beta band (z = −5.03). Z-values report significance between hypsarrhythmia and controls. The red box designates hypsarrhythmia (n=25), blue indicates no hypsarrhythmia (n=17), and black represents control patients (n=21). Patients with intermittent hypsarrhythmia are included in the hypsarrhythmia boxplot

3.2. DFA parameters enable classification of patients with and without hypsarrhythmia

DFA analysis results in a straight line that is characterized by both its slope (exponent) and y-intercept (Fig. 2). The DFA exponent measures how the amplitude envelope is modulated over time, whereas the DFA intercept is a function of the standard deviation of the amplitude envelope (see Fig. 9d). When these two quantities were plotted against one another, we saw a separation between subjects with hypsarrhythmia (Fig. 6, red and pink circles) and those without hypsarrhythmia (Fig. 6, blue and black circles), regardless of treatment status (pre- or post-treatment). We note a strong negative correlation between the DFA intercept and DFA exponent in our data, despite the fact that they are derived from independent properties of the signal (Fig. 6).

Fig. 9.

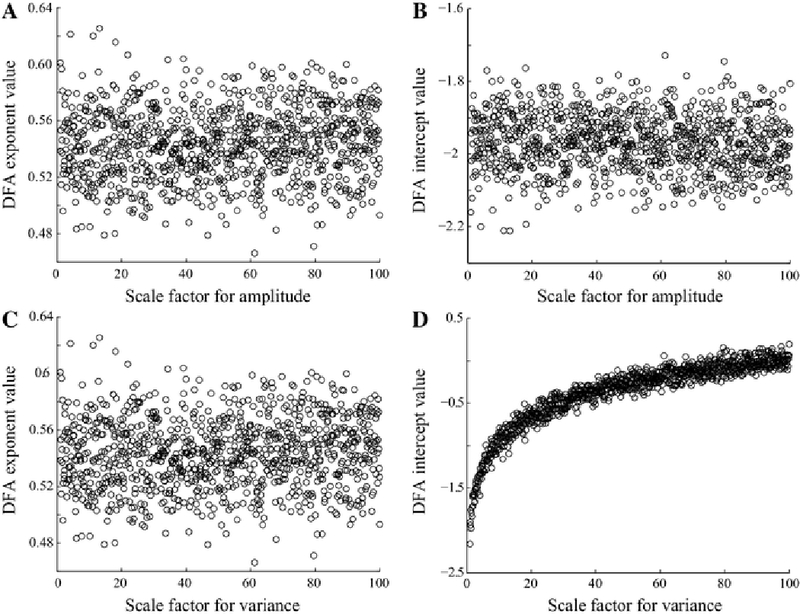
DFA results based on 1/f distributed noise filtered into the alpha band (8–12 Hz). a DFA exponent does not vary with increasing amplitude. b DFA intercept does not vary with increasing amplitude. c DFA exponent does not vary with increasing envelope variance. d DFA intercept varies logarithmically with increasing envelope variance

Fig. 6.

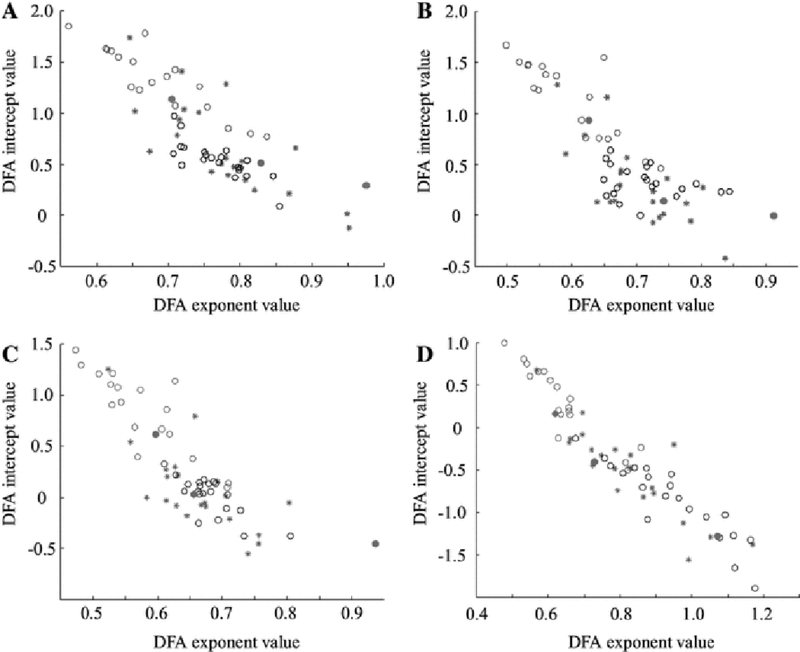
A plot of DFA exponent versus DFA intercept results in separation of patients with hypsarrhythmia from those without, enabling classification. Red open circles designate hypsarrhythmia pre-treatment and magenta closed circles indicate intermittent hypsarrhythmia pre-treatment. The red and blue stars indicate hypsarrhythmia and no hypsarrhythmia post-treatment, respectively. Black open circles represent control subjects. Results are shown for the a delta, b theta, c alpha, and d beta frequency bands

We used a support vector machine to quantify our ability to classify patients with and without hypsarrhythmia. The SVM was trained first using only the DFA exponent as input (the one-dimensional case based on a simple threshold for the exponent), and then with both the exponent and intercept as inputs (the linear, two-dimensional case). When the data were classified using only the DFA exponent, the highest classification accuracy was 80.9%, based on the beta frequency band, with 80% sensitivity and 81% specificity (Table 2). When the intercept was added as a parameter, the mean classification accuracy, sensitivity, and specificity increased an average of 11% in all categories. Using both parameters as input, we achieved a maximum classification accuracy of 92% in the delta band with 92% sensitivity and 91% specificity (Table 2).

Table 2.

Support Vector Machine Classification of Hypsarrhythmia

Frequency Band	Classification Accuracy		Sensitivity		Specificity
	Exponent only	Exponent and Intercept	Exponent only	Exponent and Intercept	Exponent only	Exponent and Intercept
Delta	69.1%	91.6%	62.95%	91.86%	73.77%	91.06%
Theta	77.6%	86.8%	67.52%	77.30%	85.27%	93.37%
Alpha	78.0%	88.9%	64.11%	74.27%	87.64%	98.99%
Beta	80.9%	82.9%	79.62%	75.90%	80.62%	88.24%

3.3. The change in the DFA exponent reflects treatment response

Successful treatment of infantile spasms is defined by both a resolution of hypsarrhythmia and a cessation of clinical spasms. In our dataset, 10 of the 21 patients were classified as “non-responders” because they still exhibited clinical spasms after the administered treatment. Four of those 10 patients had persistent hypsarrhythmia following treatment.

Based on the results in Section 3.1, we expected a group-wise increase in strength of long-range temporal correlations due to the resolution of hypsarrhythmia in 17 subjects (see also Fig. 5). An analysis of pair-wise measurements in the theta and beta bands of pre- and post-treatment datasets showed that a significant number of responders exhibited an increase in strength of long-range temporal correlations after treatment (Wilcoxon left-tailed sign-rank test: p<0.01), whereas non-responders did not (Fig. 7b and 7d).

Fig. 7.

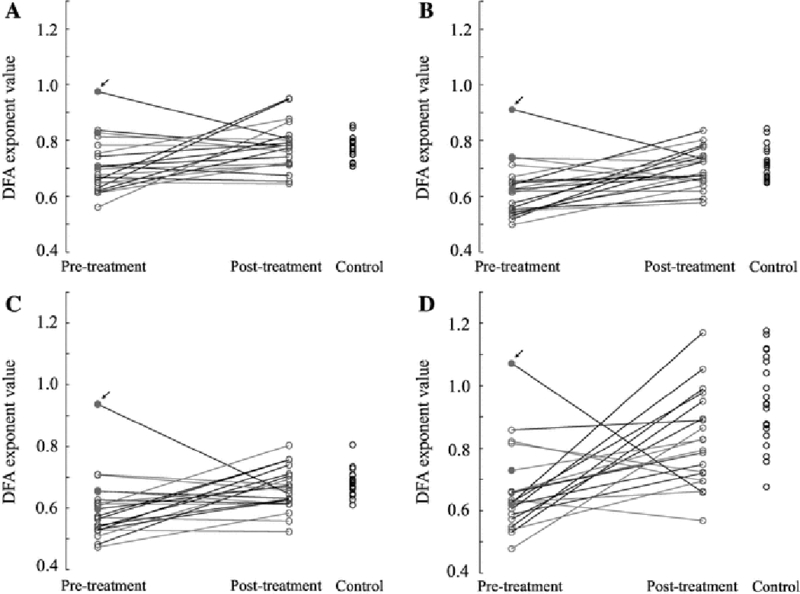
Greater increases in DFA exponent in the beta band are associated with treatment success. Data is shown for patients with hypsarrhythmia (red open circles), patients with intermittent hypsarrhythmia (magenta closed circles), patients without hypsarrhythmia (blue open circles), and control subjects (black open circles). The black lines indicate that the patient was a responder who had a resolution of hypsarrhythmia and spasms after treatment. The magenta lines represent patients that were non-responders with persistent spasms after treatment. The small black arrows indicate outlier patient 18 (see Discussion). Results are shown for the a delta, b theta, c alpha, and d beta frequency bands

In the beta band, responders had a greater increase in strength of long-range temporal correlations after treatment than non-responders (Fig. 7d). The median post-treatment DFA exponent in the beta band of responders was not significantly different from the median value for the control patients (Wilcoxon rank-sum: p=0.4509, z = −0.75). However, the non-responder post-treatment median exponent was significantly lower than the control patient median exponent (Wilcoxon rank-sum: p<0.001, z = −3.44) (Fig. 7d). Accounting for the DFA intercept induces further separation between responders and non-responders (Supplementary Fig. 1). These results suggest that the change in the DFA exponent may reflect the clinical response to treatment, rather than just the presence or absence of hypsarrhythmia.

3.4. Interpretation of DFA exponent and intercept relative to basic EEG characteristics

Because the long-range temporal correlation measurement integrates information over many time scales, it is informative to interpret the DFA parameters relative to basic characteristics of the EEG that can be visually assessed by the human eye and are used for clinical diagnosis. For example, hypsarrhythmic EEG is clinically defined as a high amplitude signal, so pre-treatment EEGs with hypsarrhythmia have a much higher amplitude than post-treatment EEGs without hypsarrhythmia. Indeed, our calculation of amplitude histograms in patient EEGs revealed a decrease in amplitude after treatment, consistent with a resolution of hypsarrhythmia in most cases (17 out of 21 patients) (Fig. 8). To investigate how this change in amplitude affected the analysis of temporal correlations, we performed DFA on simulated data with varying amplitude characteristics. We modulated both the overall amplitude value as well as the variance of the amplitude envelope (Fig. 3). Our simulations confirmed that the DFA exponent is robust to variations in the amplitude of the signal (Fig. 9a and 9c). The DFA intercept is also independent from the EEG amplitude (Fig. 9b), but it exhibits a logarithmic relationship to the scaled amplitude variance (Fig. 9d, see also Fig. 3, blue line).

Fig. 8.

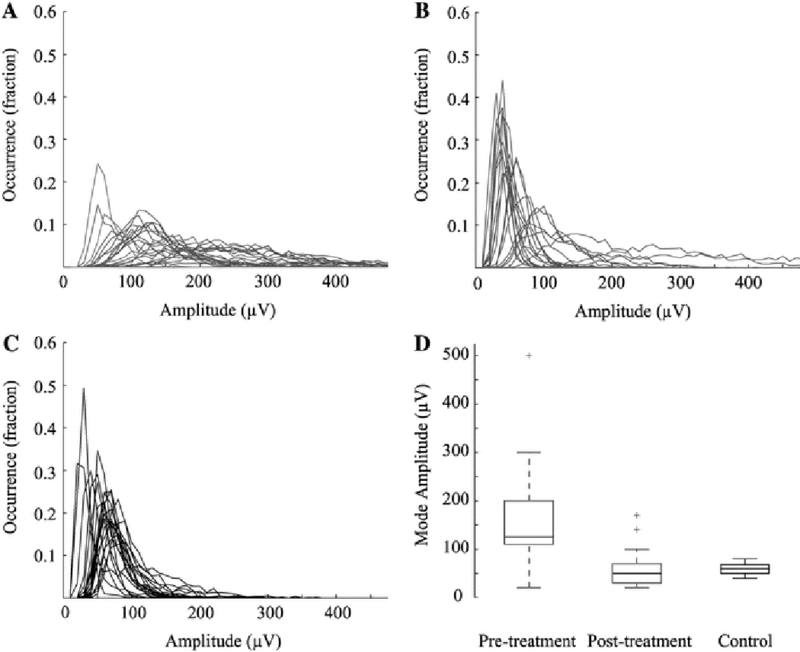
Histograms of EEG amplitude. The count in each bin is represented as a fraction of the total number of occurrences. Histograms for a pre-treatment, b post-treatment and c control patients. Red lines designate patients with hypsarrhythmia, magenta for patients with intermittent hypsarrhythmia, blue for patients without hypsarrhythmia, and black indicates control patients. d Boxplot of the mode amplitude values for all pre-treatment (red), post-treatment (blue), and control patients (black). Pre-treatment boxplot includes patients with intermittent hypsarrhythmia, and post-treatment boxplot includes patients that had persistent hypsarrhythmia and spasms after treatment

4. Discussion

In this study, we demonstrated a relationship between infantile spasms and hypsarrhythmia and the strength of long-range temporal correlations in the developing brain. Consistent with the idea that long-range temporal correlations reflect the brain’s normal functional control of synchrony, we found that the strength of correlations in the EEGs of infantile spasms patients were weaker than those seen in healthy brains. Using the DFA parameters, the presence of hypsarrhythmia could be classified with up to 92% accuracy. We further found that successful treatment caused the strength of long-range temporal correlations to return to the level of control patients, with responders exhibiting a significantly greater increase in exponent values than non-responders. These results suggest that the strength of long-range temporal correlations may not only be an indicator of hypsarrhythmia, but also reflect treatment response.

Researchers and clinicians have tried to quantify various characteristics of hypsarrhythmia in an attempt to ameliorate the subjectivity of the assessment (Sue et al. 1997). Some groups have attempted to quantitatively describe the underlying functional and neuronal network that facilitates hypsarrhythmia through EEG-fMRI (Siniatchkin et al. 2007), source analysis methods (Japaridze et al. 2013), and detection of fast oscillations (Kobayashi et al. 2015). Though the hypsarrhythmia signal is often empirically described as “chaotic,” with the term describing the signal’s disorganized appearance (Pavone et al. 2013), the mathematical definition of chaos and signal nonlinearity has been explored in several forms of epilepsy (Babloyantz and Destexhe 1986; Van Putten and Stam 2001; Kannathal et al. 2014). In hypsarrhythmia, an inter-ictal phenomenon, the deviation from stochastic behavior was greater than in control data, but not as nonlinear as seen during seizure periods (Van Putten and Stam 2001). Our results correspondingly indicate that temporal structure reliably exists in hypsarrhythmia, although it is disrupted as an effect of the disease.

DFA has been used to show that the scaling properties of the EEG change when a patient experiences a stroke, enabling accurate detection of stroke by EEG in the absence of MRI (Hwa and Ferree 2004). In a study of epilepsy, long-range temporal correlations measured by DFA in depth electrodes and subdural EEG were shown to be stronger when in close proximity to the epileptogenic zone (Parish et al. 2004; Monto et al. 2007). Similar to our results, the effects of proximity to the seizure onset zone and treatment were the most prevalent in the beta frequency band (Monto et al. 2007). However the pathogenic zone in that study showed elevated levels of long-range temporal correlations (Monto et al. 2007), whereas our results showed weaker correlations in the untreated, pathologic state. Under the interpretation of DFA as measuring the functional self-control of the underlying network of the brain, we associated weaker temporal correlations with an inability to self-regulate the amplitude modulations necessary for healthy processing over long time scales.

The classification accuracy of infantile spasms patients in this study indicates that the strength of long-range temporal correlations measured with DFA is highly differentiable in patients with and without hypsarrhythmia. We used a support vector machine to classify patients in this study to simulate how this measure might perform if used in a clinical environment. Because the training and testing procedures used in the SVM are independent of one another, the classification accuracy indicates how well new data would be categorized in the clinic based on data from a cohort of patients from a prior study. While our dataset is quite small, the high accuracy, sensitivity, and specificity are promising, and they support future investigation on the use of DFA in hypsarrhythmia identification for both diagnosis and treatment evaluation.

An assessment of long-range temporal correlations, by definition, analyzes longer temporal scales than typical time-frequency analyses. Because human reviewers are only able to visualize several seconds of EEG data at a time, a measure of control of the neural network over long time frames is a novel way to probe the severity of infantile spasms and hypsarrhythmia. Additionally, our quantitative measurement of long-range temporal correlations in these patients is unique in that we are assessing the ability of the neural network to regulate its own activity. The results of our simulations with pink noise indicate that DFA captures more complex characteristics of the EEG with greater clinical relevance than amplitude alone: the changes in DFA parameters after treatment are not influenced by large decreases in amplitude, but rather are secondary to alteration of the neuronal activity that underlies spasms and hypsarrhythmia.

Although there were slight increases in DFA exponents in the other frequency bands following successful treatment, the increases were most significant in the beta band. We hypothesize this may be the case for several reasons. First, studies show that high amplitude beta activity is a predominant EEG feature in healthy infants (Ebersole and Pedley 2003). Secondly, paroxysmal fast activity (PFA) and focal or lateralized beta activity are commonly seen in infantile spasms and other epileptic syndromes (Hooshmand et al. 1980; Wu et al. 2008). In addition, some of the medications prescribed for patients with IS, such as barbiturates and benzodiazepines, are often associated with an increase in beta activity (Ebersole and Pedley 2003). Although beta activity is more prevalent in the spasms cases, the lower pre-treatment DFA exponents indicate that the activity is less correlated over long time scales. Thus, the stronger correlations seen after successful treatment may indicate that the brain has reestablished normal beta amplitude fluctuations associated with this stage of development.

There are several important limitations to the current study. Data collection was retrospective, which led to a variable amount of time between pre-treatment and post-treatment EEGs and an inability to precisely control the dataset lengths. The relatively small number of patients included in this study is an effect of the rarity of the disease and precluded comparative analysis of antiepileptic medication and etiology of spasms. Although the diverse etiology of patients is a limitation of the current study, the surprising consistency of the strength of temporal correlations across both focal and generalized etiologies promotes the use of DFA as a potential widespread diagnostic tool in this disease. Additionally, though others have reported differences in the strength of long-range temporal correlations as a function of age (Smit et al. 2011), we found no significant correlation between age and DFA exponent in the control patients in our study (Supplementary Fig. 2). We believe this is due to the narrow age distribution of the control patients (median age: 7 months, IQR 5.75–11.25 months). Lastly, we tested only one epileptic syndrome, so it remains unknown whether the change in the strength of long-range temporal correlations is specific to infantile spasms or is a general marker for differentiating neuropathologies from normal cortical function.

In our dataset, there were several outliers that may have impacted our results, and these correspond to some of the confounding factors known to affect successful treatment. For example, patient 18 responded to treatment, but had a much higher pre-treatment DFA exponent than post-treatment, a pattern that was different than all other responders in the dataset (see small black arrows in Fig. 7). This patient, as well as three others, had a large time delay between spasms onset and the initiation of treatment (Table 1), a factor known to be associated with worse developmental outcomes (Riikonen 2010).

These limitations and gaps in knowledge necessitate further investigation into the effects of other clinical factors that confound the assessment of long-range temporal correlations in patients with infantile spasms. A prospective study with a much larger dataset will be required to assess how temporal structure is affected by factors such as therapy type and spasms etiology. As this study focused on analyzing the strength of temporal correlations in pre- and post-treatment EEG with respect to the presence of hypsarrhythmia and correlation with initial treatment response, larger prospective studies may elucidate changes in the EEG temporal structure associated with specific epileptic encephalopathies as well as their relationship to long-term outcome.