Temporal Evolution of Brain Functional Connectivity Metrics: Could 7 Min of Rest be Enough?

Abstract

Unaccounted temporal dynamics of resting-state functional connectivity (FC) metrics challenges their potential as biomarkers for clinical applications in neuroscience. Here we studied the scan time required to reach stable values for various FC metrics including seed-voxel correlations and spatial independent component analyses (sICA), and for the local functional connectivity density (lFCD), a graph theory metric. By increasing the number of time points included in the analysis, we assessed the effects of scan time on convergence of accuracy, sensitivity, specificity, reproducibility, and reliability of these FC metrics. The necessary scan time to attenuate the effects of the temporal dynamics by 80% varied across connectivity metrics and was shorter for lFCD (7 min) than for FC (11 min) or for sICA (10 min). Findings suggest that the scan time required to achieve stable FC is metric-dependent, with lFCD being the most resilient metric to the effects of temporal dynamics. Thus, the lFCD metric could be particularly useful for pediatric and patient populations who may not tolerate long scans.

Introduction

“Resting-state” functional magnetic resonance imaging (rfMRI) provides the opportunity to study brain functional connectivity (FC) over periods of several minutes, in the presence of temporal changes in the degree of vigilance, arousal and attention, functional states supported by different brain networks (Mason et al. 2007; Doucet et al. 2012; Shirer et al. 2012; Liu and Duyn 2013). In recent years, rfMRI has attracted the attention of the neuroimaging community because it is a simple yet innovative noninvasive technique that allows data sharing, does not require explicit task performance, and holds potential as a biomarker for clinical applications in neurology and psychiatry (Biswal et al. 2010).

A large majority of the published rfMRI studies assume stationary conditions over the scan length (Van Dijk et al. 2010) and are based on relatively short (5–10 min) acquisition (Biswal et al. 2010). However, there is emerging evidence that significant temporal variability in rfMRI metrics (Chang and Glover 2010; Handwerker et al. 2012; Hutchison et al. 2013b; Allen et al. 2014) undermines the reliability of the static rfMRI metrics. This temporal variability suggests a dynamic rather than a stationary nature for rfMRI metrics (Hutchison et al. 2013a) and could in part reflect dynamic properties of the brain network topology necessary for context-dependent coordination of neuronal populations (Zalesky et al. 2014). For example, significant temporal variability was detected in lateral parietal and cingulate cortices and in the default-mode network (DMN) using the popular sliding-window approach (Chang and Glover 2010; Kiviniemi et al. 2011; Allen et al. 2014). Moreover, time-varying rfMRI signals have been correlated with dynamic electrophysiological signals in the brain (Magri et al. 2012; Tagliazucchi et al. 2012; Chang et al. 2013). Despite the profound impact of rfMRI on neuroscience, its temporal dynamics creates significant within-subject variability that limits the potential of rfMRI metrics as clinical biomarkers in psychiatry/neurology (Hutchison et al. 2013a). Thus, the need to characterize both the static and the dynamic components of rfMRI metrics and the required scan time length to achieve stable static measures (Birn et al. 2013) is urgent.

The reliability of brain FC measures as a function of scan time ranges from moderate to high (Shehzad et al. 2009; Thomason et al. 2011; Braun et al. 2012; Guo et al. 2012; Li et al. 2012; Wang et al. 2013; Tomasi and Volkow 2014) and could benefit from longer scanning times. Specifically, the reproducibility and reliability of the correlation between fMRI signals in different regions-of-interest (ROIs) was shown to increase as a function of scan length, reaching a plateau after 13 min of rfMRI data (Birn et al. 2013; Gonzalez-Castillo et al. 2014). Nonetheless, the optimal scan time might be metric-dependent. For instance, an automated machine-learning classifier required 15 min of rfMRI data to differentiate individual patterns from a group of subjects (Anderson et al. 2011). Though longer scanning sessions might reduce the impact of temporal variability, the resulting rfMRI patterns could be prone to motion artifacts (Power et al. 2012; Van Dijk et al. 2012), and could increase the likelihood of sleep during the scan, which is a serious confound for rfMRI measures (Horovitz et al. 2009; Gonzalez-Castillo et al. 2014).

Although the influence of scan time has been properly quantified for ROI measures of FC (Birn et al. 2013; Gonzalez-Castillo et al. 2014), the influence of scan time has not been studied for graph theory metrics of brain connectivity such as the local functional connectivity density (lFCD) (Tomasi and Volkow 2010), or other rfMRI measures such as those resulting from spatial independent component analysis (sICA). Since various metrics are being used to assess brain FC, it is important to quantify the impact of scan time for different metrics with different benchmark criteria.

The relatively long rfMRI sessions (14.4 min) from the open access Human Connectome Project (HCP) database have high spatiotemporal resolution (2-mm isotropic, 0.72 s) and are ideal for studying the effect of scan length on rfMRI measures. Based on the saturating exponential increases in test–retest reliability with scan length observed in prior studies (Birn et al. 2013; Gonzalez-Castillo et al. 2014), we hypothesized that longer rfMRI scanning would increase the accuracy, reproducibility, and reliability of FC metrics as well as their gray matter (GM) sensitivity and specificity. Specifically, these increases would follow different saturating exponential curves with scan time for different rfMRI metrics, which would reach their respective plateaus at different scan times.

We mapped the temporal evolution of 3 different rfMRI metrics over a 14.4-min time interval on the fMRI data sets from 40 healthy adults using an expanding-window approach with fixed expanding steps of 36 s (50 time points), increasing in total length from 72 to 864 s (23 steps). Specifically, we assessed the effect of scan time on brain-wide lFCD (Tomasi and Volkow 2010) measures, on the connectivity of the DMN extracted by sICA (McKeown and Sejnowski 1998), and seed-voxel correlations from an important rfMRI hub at the occipito-parietal junction (Biswal et al. 1995). For all metrics, we quantified reproducibility, accuracy, and reliability as well as GM sensitivity and specificity. An exponential saturation model was used to assess the optimal scanning time for lFCD, sICA, and seed-voxel correlations. Since lFCD, sICA, and seed-voxel correlations reflect different underlying phenomena, we hypothesized that accuracy, sensitivity, specificity, reproducibility, and reliability will reach their asymptotic values at different time scales for lFCD, sICA, and seed-voxel correlations.

Materials and Methods

Subjects

No experimental activity with any involvement of human subjects took place at the author's institutions. High spatiotemporal resolution data sets were drawn from the publicly available repository of the WU-Minn HCP Q1 data release (http://www.humanconnectome.org/). The HCP participants (n = 40; age: 31 ± 3 years; 31 females) provided written informed consent and were scanned on a 3.0 T Siemens Skyra (Siemens) unit with a 32-channel head coil according to procedures approved by the IRB at Washington University in St. Louis's. Additional data sets with conventional spatiotemporal resolution were drawn from the 1000 Functional Connectome Project (FCP; http://fcon_1000.projects.nitrc.org/)(Biswal et al. 2010), and from the Consortium for Reliability and Reproducibility (CoRR; http://fcon_1000.projects.nitrc.org/indi/CoRR/html/)(Zuo et al. 2014). The FCP participants (n = 40; age: 22 ± 3 years; 31 females) were randomly selected from the Cambridge sample. They provided written informed consent and were scanned on a 3.0 T Siemens Trio unit with a 12-channel head coil according to procedures approved by the IRB at Harvard University or Partners Healthcare. The CoRR participants (n = 30; age: 24 ± 3 years; 15 females) were those in the HNU1 sample (Chen et al. 2015). They provided written informed consent and were scanned on a GE MR750 3.0 Tesla scanner (GE Medical Systems) with an 8-channel head coil according to procedures approved by the IRB of the Center for Cognition and Brain Disorders (CCBD) at Hangzhou Normal University (HNU).

Data Sets

Human Connectome Project

A gradient-echo-planar (EPI) sequence with multiband factor 8, repetition time (TR) 720 ms, echo time (TE) 33.1 ms, flip angle (FA) 52°, 104 × 90 matrix size, 72 slices and 2 mm isotropic voxels (Smith et al. 2013; Uğurbil et al. 2013) was used to acquire rfMRI time series with 1200 time points while the participant relaxed with their eyes open. A fixation cross was presented through a projector on a dark screen in a darkened room. Scans were repeated twice, using different phase encoding directions (LR and RL) in each of the two sessions (REST1 and REST2). One hundred and sixty “resting-state” time series with 1200 time points collected over 864 s and 2 -mm-isotropic voxels covering the whole brain were used in this study. The “minimal preprocessing” data sets (rfMRI_REST*_hp2000_clean.nii) were used, which included gradient distortion correction, rigid-body realignment, field-map processing, spatial normalization to the stereotactic space of the Montreal Neurological Institute (MNI), high pass filtering (1/2000 Hz frequency cutoff) (Glasser et al. 2013), independent component analysis-based de-noising (Salimi-Khorshidi et al. 2014), and brain masking. In addition, the HCP's gray and white matter parcellations of each subject's brain structural scans (wmparc.2.nii.gz) were used to assess the GM specificity and sensitivity of the rfMRI metrics.

FCP-Cambridge

An EPI sequence with TR/TE = 3000/30 ms, FA 85°, 72 × 72 matrix size, 47 slices (interleaved acquisition; no gap between slices) and 3-mm isotropic voxels was used to acquire rfMRI time series with 119 time points while the participants relaxed with their eyes open during the 6 min rfMRI scan. A multiecho T1-weighted magnetization-prepared gradient-echo image (multiecho MP-RAGE) pulse sequence (TR = 2200 ms, inversion time (TI) = 1100 ms, TE = 1.54 ms for image 1 to 7.01 ms for image 4, FA = 7°, 1.2 × 1.2 × 1.2 mm³, and field of view [FOV] = 230) was used to acquire high-resolution anatomical brain images.

Consortium for Reliability and Reproducibility-HNU

An EPI sequence with TR/TE = 2000/30 ms, FA 90°, 64 × 64 matrix size, 43 slices (interleaved acquisition; no gap between slices), and 3.4-mm isotropic voxels was used to acquire rfMRI time series with 300 time points while the participant relaxed with their eyes open during the 10 min rfMRI scans. A T1-weighted Fast Spoiled Gradient echo (FSPGR: TR = 8.1 ms, TE = 3.1 ms, TI = 450 ms, FA = 8°, FOV = 256 × 256 mm, matrix = 256 × 256, voxel size = 1.0 × 1.0 × 1.0 mm³, 176 sagittal slices) was used to acquire high-resolution anatomical brain images.

Image Preprocessing for FCP and HNU Data Sets

The FreeSurfer (version 5.3.0) software package (http://surfer.nmr.mgh.harvard.edu) was used to automatically segment the anatomical MRI scans into cortical and subcortical GM structures (Fischl et al. 2002). The first 4 time points of the rfMRI time series were removed to avoid nonequilibrium effects in the blood-oxygenation-level-dependent (BOLD) signal. Then, the University of Oxford's Center for Functional Magnetic Resonance Imaging of the Brain (FMRIB) Software Library (FSL version 5.0; http://www.fmrib.ox.ac.uk/fsl) was used for image realignment (to correct for head motion with MCFLIRT, Motion Correction using FMRIB's Linear Image Registration Tool), and for spatial normalization to the MNI152 template with 3-mm isotropic voxels (using FLIRT, the FMRIB's Linear Image Registration Tool) (Jenkinson et al. 2002; Smith et al. 2004). The interactive data language (IDL, ITT Visual Information Solutions) was used for 0.01 Hz frequency cutoff high pass filtering.

Head Motion

Framewise displacements, FD, were computed for every time point from head translations and rotations, using a 50 mm radius to convert angle rotations to displacements. The mean FD was not different for the REST1 (0.17 ± 0.05 mm; mean ± standard deviation) and REST2 (0.18 ± 0.05 mm) sessions or for the LR (0.17 ± 0.05 mm) and RL (0.18 ± 0.05 mm) phase encoding directions (P > 0.24; paired t-test). Scrubbing was implemented in IDL to remove time points excessively contaminated with motion. Specifically, time points were excluded if the temporal derivative root means squared variance (DVARS) of the BOLD signal, DVARS > 0.5% and FD > 0.5 (Power et al. 2012). The number of time points removed per time series by scrubbing was not significantly different for REST1 (0.5 ± 1.1; mean ± SD) and REST2 (0.8 ± 1.1) or for LR (0.5 ± 1.2) and RL (0.8 ± 1.1) (P > 0.12, t-test).

Expanding Window

To quantify the effect of scan time on lFCD, seed-voxel correlations, and sICA, we constructed a set of rfMRI data sets with increasing scan length from the original rfMRI data. lFCD, seed-voxel correlations, and sICA were computed independently for each scan length. In order to limit the effect of spurious connectivity fluctuations, the shortest time window had 100 image time points (72 s) (Leonardi and Van De Ville 2015; Zalesky and Breakspear 2015). Note that according to Zalesky and Breakspear, nonstationary fluctuations in FC can be detected with short temporal windows (>40 s) while maintaining nominal control of false positives (Zalesky and Breakspear 2015). In the subsequent steps, the window was expanded 50 image time points (36 s) compared with that of the previous one and the metrics were recalculated. This was repeated until the temporal window covered the full time series. Thus, a total of 23 (HCP), 15 (CoRR-HNU), or 8 (FCP-Cambridge) temporal windows with N_i = 72s/TR + 36s/TR × i time points were extracted from each rfMRI timeseries. lFCD, seed-voxel correlations, and sICA were computed for each window length, subject, session, and phase encoding direction.

Local Functional Connectivity Density

The lFCD at every voxel in the brain was computed as the number of elements in the local FC cluster using a “growing” algorithm (Tomasi and Volkow 2010). The Pearson correlation was used to assess the strength of the FC, R_ij, between voxels i and j in the brain, and a high correlation threshold R_ij > 0.5, was selected to ensure significant correlations between time-varying signal fluctuations at P_FWE < 0.05, corrected, for all temporal windows (lFCD_HT). A voxel (x_j) was added to the list of voxels functionally connected with x₀ only if it was adjacent to a voxel that was linked to x₀ by a continuous path of functionally connected voxels and R_0j > 0.5. This calculation was repeated for all brain voxels that were adjacent to those that belonged to the list of voxels functionally connected to x₀ in an iterative manner until no new voxels could be added to the list. lFCD was additionally computed using a less conservative correlation threshold R_0j > 0.3 (lFCD_LT; P < 0.003, uncorrected, for all temporal windows) to address potential effects of threshold selection in the performance of the lFCD metric.

Seed-voxel Correlation

The local maximum of the lFCD at the occipito-parietal junction, which is the location of the strongest lFCD hub in the brain, was used as cubic seed (125 voxels; 1 mL) for seed-voxel correlations. Specifically, Pearson correlation was used to compute the strength of the FC_max between time-varying signals at the seed location and those in other brain voxels, and the Fisher's z-transformation was used to normalize the step-distributed correlation coefficients. The FC patterns corresponding to four additional bilateral seed regions (cubic; volume 125 voxels) were computed in a similar way for each rfMRI data set to assess potential effects of seed location on the performance of the FC metric. Specifically, the MNI coordinates of the bilateral dorsolateral prefrontal cortex (PFC; left: −50, 20, 34 mm; right: 46, 14, 43 mm) and inferior parietal cortex (IPC; left: −52, −49, 47 mm; right: 52, −46, 46 mm) seeds were extracted from literature (Vincent et al. 2008). To represent subcortical regions we used seeds in the dorsolateral caudal putamen (DCP; left: −28, 1, 3 mm; right: 28, 1, 3 mm) (Di Martino et al. 2008) and the thalamus (THA; −12, −19, 8 mm; right: 12, −19, 8 mm) (Tomasi and Volkow 2011a).

Spatial Independent Component Analyses

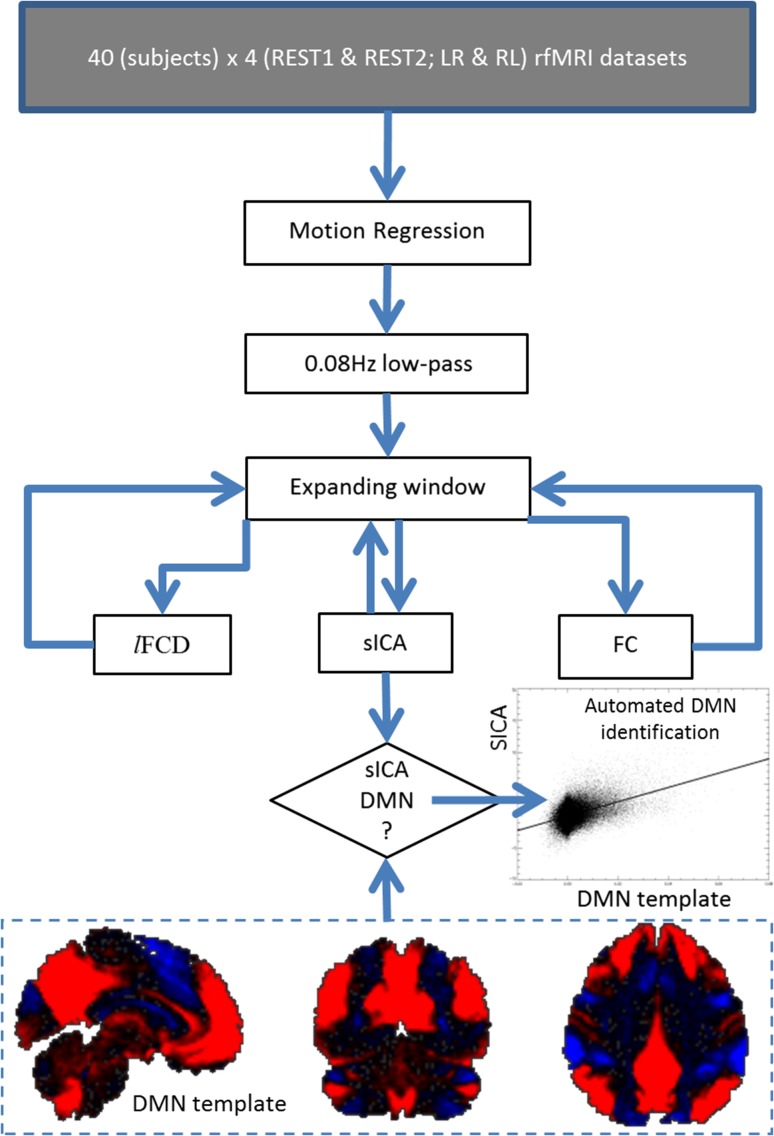
The sICA maps (melodic_IC.nii) provided with the HCP data set (Salimi-Khorshidi et al. 2014) were used to extract a reference DMN template for the group (Fig. 1). Specifically, a sICA component map that best fitted the pattern classically associated with the DMN was identified upon visual inspection for 10 random subjects (Biswal et al. 2010). These maps were averaged to create a preliminary DMN template. Then, an automated DMN identification approach was used to identify the DMN in the “melodic_IC.nii” maps in 260 randomly selected subjects from the HCP database. Specifically, the Pearson product-moment correlation between the preliminary DMN template and “melodic_IC.nii” maps was computed in MATLAB (MathWorks, Inc.) and the sICA component with the highest correlation (i.e. highest spatial overlap) with the DMN template was selected as the component representing the DMN. These 260 DMN maps were then averaged to create the final DMN template.

Figure 1.

Image processing pipelines. Dynamic lFCD, sICA, and FC maps with 2-mm isotropic resolution and 91 × 109 × 91 voxels were computed for each subject, session, and phase encoding direction using 160 HCP data sets with low-pass filtered “minimally preprocessed” data (Glasser et al. 2013) from the Q1 release and an expanding-window approach (see text). The DMN template (bottom) used for automated DMN identification reflects the average of 260 DMN maps and shows the standard DMN pattern (red) and its anticorrelated network (blue) superimposed on the human brain (black).

In order to examine the effect of length of resting-state scans on the DMN, we segmented the data for each run and phase encoding direction using our expanding-window approach and extracted the DMN using sICA as implemented in FSL by restricting the maximum number of independent components (IC#) to 250 (sICA₂₅₀). Specifically, in each iteration, the data were low-pass filtered (~0.08 Hz) and the multivariate exploratory linear decomposition into independent components (MELODIC) toolbox of the FSL package was used to extract sICA components (Salimi-Khorshidi et al. 2014). The spatial loading map for each sICA component was compared against the predefined DMN template using an algorithm for automated component identification (Fig. 1). Specifically, the Pearson product-moment correlation between the DMN template and component loadings maps was computed in MATLAB and the sICA component with the highest correlation with the DMN template was selected as the component representing the DMN for a given temporal window, for each subject, each session, and each phase encoding direction. In addition, a similar approach with a maximum IC# of 50 was used to assess potential effects of MELODIC parameters on the performance of the sICA-DMN metric (sICA₅₀).

Pipelines

Three pipelines were implemented (Fig. 1). Multilinear regression was used to minimize motion-related fluctuations in the MRI signals (Tomasi and Volkow 2010), and standard 0.08 Hz low-pass filtering was used to remove magnetic field drifts and minimize physiologic noise of high-frequency components. Then the dynamic rfMRI metrics (lFCD, sICA, and seed-voxel correlation) were computed using the expanding-window approach as described above. Spatial smoothing was not used in order to preserve the high spatial resolution of the original data sets. All dynamic metrics were computed in the whole brain.

Accuracy, Sensitivity, Specificity, Reproducibility, and Reliability

We used five benchmarks to quantify the effect of scan time on a given connectivity metric, X(t) (strength of lFCD, sICA, or FC):

“Accuracy,” the similarity between patterns from time series of different lengths, assesses the Pearson correlation across subjects between spatial map of X(t_full), computed from the full-length time series, and spatial map X(t) computed from a given temporal window:

$$\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}(t)=\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}[X^{\left\{j\right\}}(t_{\mathrm{f}\mathrm{u}\mathrm{l}\mathrm{l}}),X^{\left\{j\right\}}(t)],\left\{j\right\}:\mathrm{set}\mathrm{of}\text{subjects}.$$ (1)

“Sensitivity” is a true positive rate that gauges the proportion of X within GM for each temporal window by summing X within GM voxels:

$$\mathrm{S}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{t}\mathrm{y}(t)=\frac{\sum _{i\in \{\mathrm{G}\mathrm{M}\}}{X}_i(t)}{\sum _{i\in \{\mathrm{b}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\}}{X}_i(t)}.$$ (2)

“Specificity,” the proportion of white matter voxels with low connectivity, is a true negative rate that gauges the proportion of white matter voxels with X(t) lower than its whole-brain average for each temporal window.

$$\mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}(t)=\frac{\sum _{i\in \{\mathrm{W}\mathrm{M}\}}ϵ(t)}{\sum _{i\in \{\mathrm{W}\mathrm{M}\}}1},ϵ=\{\begin{array}{c}1\mathrm{i}\mathrm{f}{X}_i(t)\le \frac{1}{N}\sum _{k\in \{\mathrm{b}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\}}{X}_k(t),\\ 0\mathrm{i}\mathrm{f}{X}_i(t)>\frac{1}{N}\sum _{k\in \{\mathrm{b}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\}}{X}_k(t)\mathrm{.}\end{array}$$ (3)

The FreeSurfer's gray and white matter parcellations were used for these purposes:

“Reproducibility” estimates the similarity of the X(t) patterns from two independent sessions for each subject at a given time point.

$$\mathrm{R}\mathrm{e}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{i}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}(t)=1-\frac{1}{N}\sum _{i\in \mathrm{b}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}^N\mathrm{a}\mathrm{b}\mathrm{s}\left(\frac{{X_i}^{\mathrm{R}\mathrm{E}\mathrm{S}\mathrm{T}1}(t)-{X_i}^{\mathrm{R}\mathrm{E}\mathrm{S}\mathrm{T}2}(t)}{{X_i}^{\mathrm{R}\mathrm{E}\mathrm{S}\mathrm{T}1}(t)+{X_i}^{\mathrm{R}\mathrm{E}\mathrm{S}\mathrm{T}2}(t)}\right),$$ (4)

“Reliability” was determined for each temporal window and each voxel using two-way mixed single measures intraclass correlation (Shrout and Fleiss 1979),

$$\mathrm{I}\mathrm{C}{\mathrm{C}}_{3,1}(t)=\frac{\mathrm{B}\mathrm{M}\mathrm{S}(t)-\mathrm{E}\mathrm{M}\mathrm{S}(t)}{\mathrm{B}\mathrm{M}\mathrm{S}(t)+(k-1)\mathrm{E}\mathrm{M}\mathrm{S}(t)},$$ (5)

Specifically, each subject's measurement (X at each voxel) is assumed to be a random sample from a population of measurements. Case 3 (fixed effects) was selected because the measures were obtained in two different sessions (k = 2, REST1 and at REST2; “the raters”), which are the only sessions of interest. Previous test–retest reliability studies on FC have also used Case 3. In this work, ICC was based on single measurements in order to be consistent with previous test–retest reliability studies. Thus, ICC(3,1) was mapped in the brain in terms of between-subjects (BMS) and residuals (EMS) mean square values computed for each voxel using the IPN MATLAB toolbox (www.mathworks.com/matlabcentral/fileexchange/22122-ipn-tools-for-test-retest-reliability-analysis) and the X maps corresponding to REST1 and REST2 sessions (k = 2). Note that ICC(3,1) coefficients range from 0 (no reliability) to 1 (perfect reliability).

$$\begin{array}{c}\mathrm{B}\mathrm{M}\mathrm{S}(t)=\frac{1}{n-1}{\sum _{j=1}^n\left(\sum _{i=1}^k{X}_{ij}(t)-\frac{1}{n}\sum _{j=1}^n\sum _{i=1}^k{X}_{ij}(t)\right)}^2\hfill \\ \begin{array}{cc}EMS(t)=& \frac{1}{\left(n-1\right)\left(k-1\right)}\sum _{i=1}^k[\sum _{j=1}^n{\left(X_{ij}(t)-\frac{1}{k}\sum _{i=1}^k{X}_{ij}(t)\right)}^2\hfill \\ & -\left(\sum _{j=1}^n{X}_{ij}(t)-\frac{1}{k}\sum _{j=1}^n\sum _{i=1}^k{X}_{ij}(t)\right)]\end{array}\hfill \end{array}$$ (6)

Statistical Methods

The exponential model $Y\left(t\right)=Y_0+A(1-{\mathrm{e}}^{-t/t_0})$ with 3 free adjustable constants: time constant (t₀), which captures the time of convergence of a given benchmark (accuracy, sensitivity, specificity, reproducibility, or reliability) to its equilibrium, the static amplitude (Y₀), which represents the minimum value of the benchmark (i.e. at 72 s, the length of the first temporal window), and the dynamic amplitude (A), which represents the potential benchmark gain (i.e. for t = ∞), was used to assess the asymptotic behavior of the benchmarks of X(t). The fitting constant t₀ was used to test the hypothesis “sensitivity, specificity, reproducibility, accuracy, and reliability will achieve their asymptotic values faster for lFCD patterns than for sICA or FC patterns” at P < 0.05 using two sample t-tests.

Results

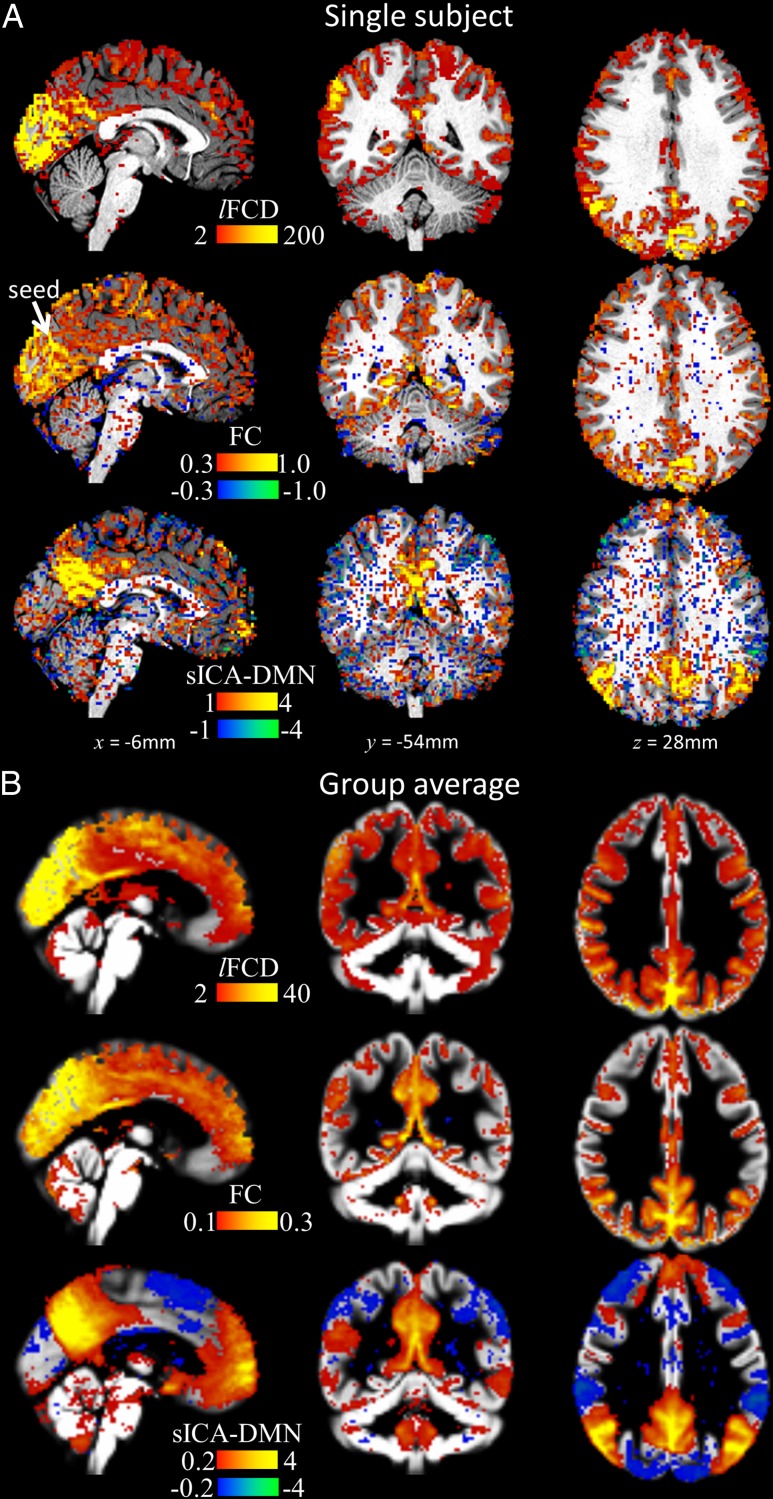
Figure 2 shows exemplary patterns of the 3 metrics for an individual (Fig. 2A) and for the group average (Fig. 2B). As expected, all three connectivity metrics delineated more precisely their final patterns as the length of the windows increased. Whereas the lFCD_HT pattern had high signal-to-noise and fitted tightly the GM in all subjects (Tomasi et al. 2015), the FC_max and sICA₂₅₀ patterns of the DMN were noisier and overlapped significantly both gray and white matter (Fig. 2A). The group average patterns for FC_max and sICA₂₅₀, however, did not overlap significantly with white matter regions (Fig. 2B). Note this work does not focus on the similarities and differences between these patterns. Instead, we quantified the evolution of the individual patterns with scan time in terms of five different time-varying benchmarks. Overall, these whole-brain average benchmarks did not differ for LR and RL phase encoding directions for any of the rfMRI metrics, and increased exponentially with the length of the temporal window (goodness of exponential fit: χ_ν² < 0.001; see Supplementary Figures).

Figure 2.

(A) Exemplary FC patterns from full-length time series from a randomly chosen individual superimposed on the subjects’ T1-weighted MRI for lFCD, FC (seed: lFCD hub at the occipito-parietal junction; arrow) and DMN from sICA. (B) Average patterns across 40 subjects, 2 sessions, and 2 phase encoding directions, superimposed on three orthogonal views of a GM template of the human brain.

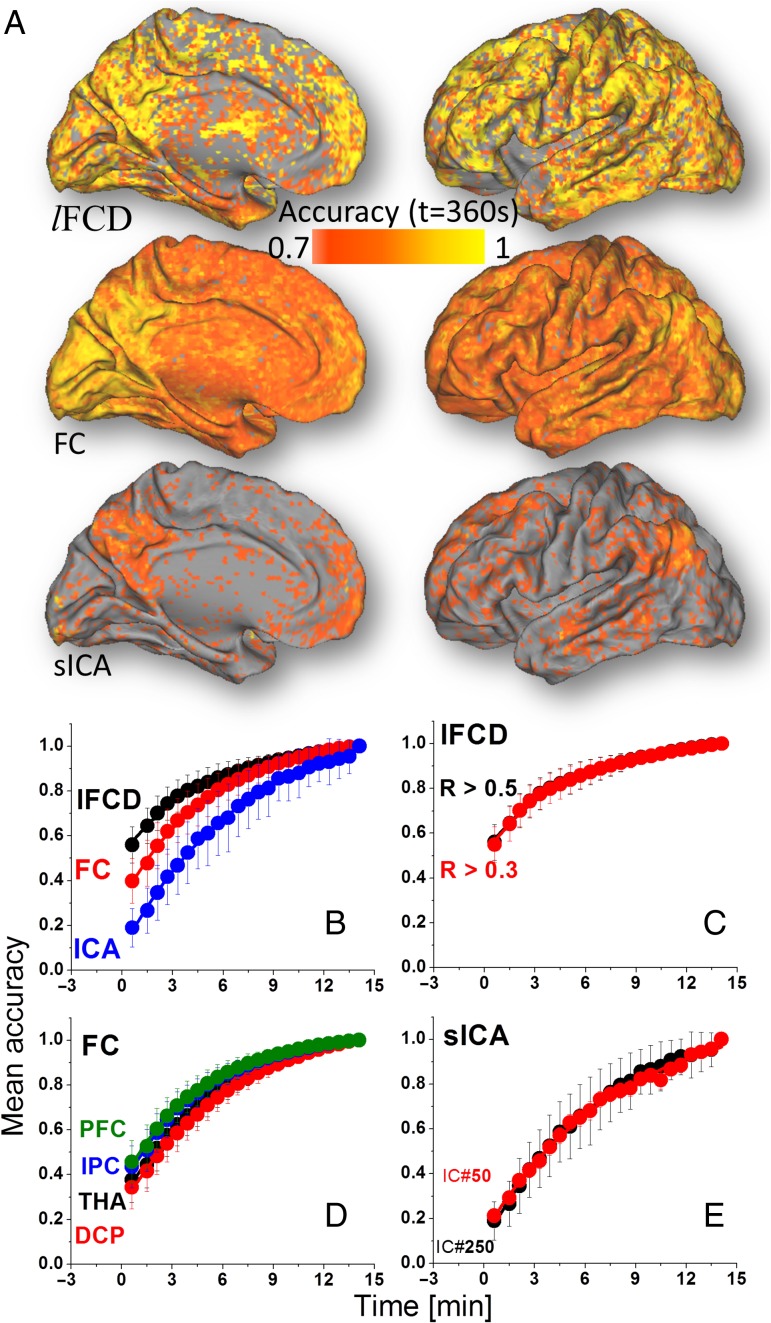
Accuracy

The whole-brain average accuracy converged faster to its maximum value for lFCD and FC from cortical seeds (t₀ < 5.2 min) than for sICA (t₀ > 7.4 min; P < 0.005; Fig. 3B, Table 1). Differences in convergence time between lFCD_LT and lFCD_HT, or between FC from different seed regions, or between sICA₂₅₀ and sICA₅₀ were not statistically significant (Fig. 3C–E). Y₀ was larger for lFCD than for FC or for sICA and for FC than for sICA (P < 0.0002). A was larger for sICA than for FC or for lFCD, and for FC than for lFCD (P < 0.0001). In addition, A was larger for the FC_DCP than for FC_max, FC_IPC, and FC_PFC (P < 0.05).

Figure 3.

(A) Spatial distribution of the accuracy computed across subjects at t = 6 min, independently for each metric (lFCD, FC, sICA). Whole-brain average accuracy as a function of time for: lFCD, FC, and sICA (B); lFCD_HT (R > 0.5) and lFCD_LT (R > 0.3) (C); seed-voxel correlations for seed regions in THA, DCP, IPC, and dorsolateral PFC (D); and for sICA-DMN maps computed using 50 and 250 maximum independent components (E). Average values computed across two rfMRI sessions (REST1 and REST2) and two phase encoding directions (LR and RL). Bars reflect standard errors.

Table 1.

Average parameters of the exponential model, $Y\left(t\right)=Y_0+A\left(1-{\mathrm{e}}^{-t/t_0}\right)$, for accuracy, sensitivity, specificity, reproducibility, and reliability of lFCD, seed-voxel correlations (FC), and sICA with scan time

Metric	Accuracy	Sensitivity	Specificity	Reproducibility	Reliability
t0(min)
lFCDHT	4.9 ± 0.3a	4.0 ± 1.6	1.9 ± 0.2	1.8 ± 0.1	2.8 ± 0.2
lFCDLT	4.7 ± 0.2a	2.5 ± 0.2	1.7 ± 0.1	2.6 ± 0.2b	3.1 ± 0.3
lFCDshort	3.5 ± 0.2	2.3 ± 0.8	1.7 ± 0.3	1.7 ± 0.1	2.2 ± 0.4
FCmax	5.2 ± 0.3	4.9 ± 0.5	8.1 ± 1.8	10.8 ± 7.9	7.5 ± 2.4
FCTHA	6.0 ± 0.6	6.5 ± 2.3	9.3 ± 2.8	12.3 ± 3.8	9.5 ± 2.6
FCDCP	6.8 ± 0.4	6.6 ± 1.5	21.7 ± 12.5	15.9 ± 8.1	13 ± 8
FCIPC	4.9 ± 0.9	4.7 ± 1.2	7.8 ± 2.6	7.6 ± 0.6	5.6 ± 0.6
FCPFC	4.8 ± 0.4	4.8 ± 0.9	6.4 ± 1.6	8.6 ± 2.1	6.0 ± 1.2
sICA250	7.4 ± 0.9	3.9 ± 0.9	25 ± 9	3.1 ± 0.5	4.1 ± 1.0
sICA50	7.0 ± 0.6	3.5 ± 0.4	17 ± 12	3.1 ± 0.1	3.9 ± 0.3
Y0
lFCDHT	0.52 ± 0.02	0.63 ± 0.02	0.90 ± 0.02	0.46 ± 0.01	0.12 ± 0.04
lFCDLT	0.51 ± 0.03	0.58 ± 0.02	0.86 ± 0.02	0.38 ± 0.01	0.10 ± 0.04
lFCDshort	0.51 ± 0.03	0.62 ± 0.03	0.89 ± 0.02	0.45 ± 0.01	0.10 ± 0.02
FCmax	0.31 ± 0.04	0.43 ± 0.01	0.66 ± 0.01	0.28 ± 0.01	0.01 ± 0.01
FCTHA	0.29 ± 0.04	0.42 ± 0.01	0.64 ± 0.01	0.29 ± 0.01	0.00 ± 0.01
FCDCP	0.26 ± 0.03	0.42 ± 0.01	0.63 ± 0.01	0.28 ± 0.01	0.00 ± 0.03
FCIPC	0.34 ± 0.04	0.43 ± 0.01	0.67 ± 0.01	0.29 ± 0.01	0.01 ± 0.01
FCPFC	0.37 ± 0.04	0.43 ± 0.01	0.67 ± 0.01	0.30 ± 0.01	0.02 ± 0.01
sICA250	0.0 ± 0.1	0.42 ± 0.01	0.65 ± 0.01	0.25 ± 0.01	0.00 ± 0.01
sICA50	0.10 ± 0.04	0.42 ± 0.01	0.65 ± 0.07	0.25 ± 0.01	0.00 ± 0.03
A
lFCDHT	0.50 ± 0.03	0.09 ± 0.01	0.08 ± 0.01	0.43 ± 0.01	0.34 ± 0.08
lFCDLT	0.55 ± 0.03	0.09 ± 0.01	0.09 ± 0.01	0.43 ± 0.01	0.34 ± 0.08
lFCDshort	0.51 ± 0.03	0.23 ± 0.01	0.12 ± 0.02	0.30 ± 0.04	0.34 ± 0.09
FCmax	0.74 ± 0.05a	0.09 ± 0.01	0.15 ± 0.01	0.08 ± 0.04	0.31 ± 0.07
FCTHA	0.79 ± 0.06	0.09 ± 0.01	0.18 ± 0.04	0.13 ± 0.03	0.43 ± 0.07
FCDCP	0.85 ± 0.05	0.06 ± 0.01	0.21 ± 0.09	0.10 ± 0.04	0.45 ± 0.25
FCIPC	0.70 ± 0.03a	0.08 ± 0.01	0.16 ± 0.03	0.10 ± 0.01	0.41 ± 0.01
FCPFC	0.67 ± 0.04a	0.09 ± 0.01	0.16 ± 0.01	0.11 ± 0.01	0.42 ± 0.01
sICA250	1.0 ± 0.1	0.05 ± 0.01	0.10 ± 0.02	0.06 ± 0.01	0.20 ± 0.01
sICA50	0.99 ± 0.03	0.05 ± 0.01	0.07 ± 0.03	0.06 ± 0.01	0.23 ± 0.01

Note: The high (HT) and low (LT) correlation thresholds used for the computation of the lFCD maps were 0.5 and 0.3, respectively. The lFCD was computed for the full length (14.4 min) as well as for first 7 min (short) of the rfMRI data sets. Seed-voxel correlation maps (FC) were computed for the 5 different seed regions: the strongest lFCD hub at the occipito-parietal junction (max); THA [MNI coordinates: left (−12, −19, 8) mm; right (12, −19, 8) mm]; DCP [MNI coordinates: left (−28, 1, 3) mm; right (28, 1, 3) mm]; IPC [MNI coordinates: left (−52, −49, 47) mm; right (52, −46, 46) mm]; dorsolateral PFC [MNI coordinates: left (−50, 20, 34) mm; right (46, 14, 43) mm]. Seed volume: 1 mL (125 voxels). Two different sICA were performed using 250 and using 50 independent components.

^aFC < FC_DCP (P < 0.05).

^blFCD > lFCD_short (P < 0.05).

Sensitivity

The whole-brain average sensitivity approached its maximum value at similar rate for lFCD, FC, and sICA (t₀ ~5 min; Fig. 4B, Table 1). t₀ was longer for lFCD_LT than for lFCD_HT (Fig. 4C), but did not differ across seed regions (for FC) or between sICA₂₅₀ and sICA₅₀ (Fig. 4D,E). Sensitivity was predominately static for all metrics (Y₀ ≫ A; P < 10^–4). Y₀ was larger for lFCD than for FC or for sICA (P < 10^–5), and for FC than for sICA (P < 0.05).

Figure 4.

(A) Spatial distribution of the GM sensitivity of the FC metrics (lFCD, FC, and sICA) computed across subjects at t = 6 min. Whole-brain average sensitivity as a function of time for: lFCD, FC, and sICA (B); lFCD_HT (R > 0.5) and lFCD_LT (R > 0.3) (C); seed-voxel correlations for seed regions in THA, DCP, IPC, and dorsolateral PFC (D); and for sICA-DMN maps computed using 50 and 250 maximum independent components (E). Average values computed across two rfMRI sessions (REST1 and REST2) and two phase encoding directions (LR and RL). Bars reflect standard errors.

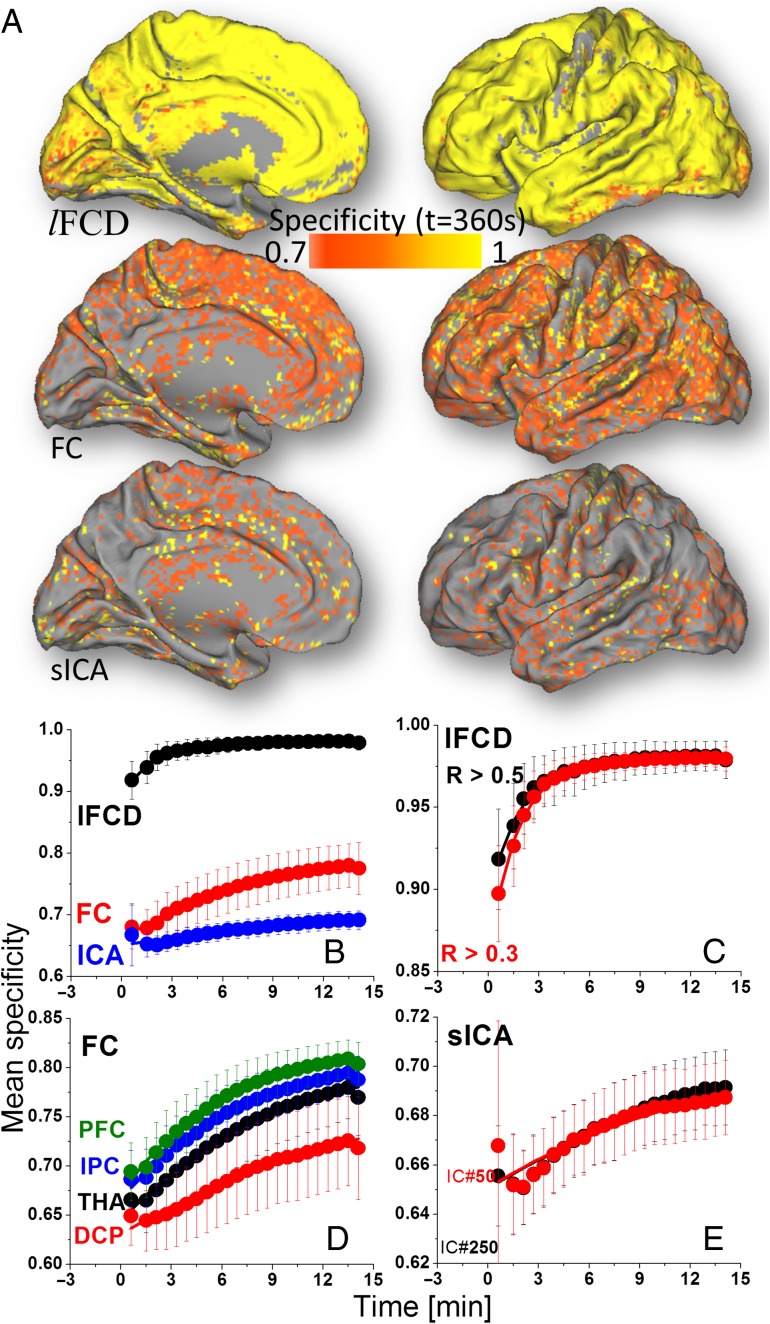
Specificity

The convergence of the whole-brain average specificity was faster for lFCD (t₀ ~1.8 min) than for FC or for sICA (t₀ > 6.4 min, P < 0.0001; Fig. 5B and Table 1). t₀ did not differ significantly between lFCD_HT and lFCD_LT, between different seed regions (for FC), or between sICA₂₅₀ and sICA₅₀ (Fig. 5C–E). Specificity was predominately static for all metrics (Y₀ ≫ A; P < 10^–4). Y₀ was larger for lFCD than for FC or for sICA (P < 10^–6) and for FC than for sICA (P < 0.05). A was larger for FC than for lFCD or for sICA (P < 0.001) and for lFCD than for sICA (P < 0.015).

Figure 5.

(A) Spatial distribution of the GM specificity computed across subjects at t = 6 min for each of the metrics (lFCD, FC, and sICA). Whole-brain average specificity as a function of time for: lFCD, FC, and sICA (B); lFCD_HT (R > 0.5) and lFCD_LT (R > 0.3) (C); seed-voxel correlations for seed regions in THA, DCP, IPC, and dorsolateral PFC (D); and for sICA-DMN maps computed using 50 and 250 maximum independent components (E). Average values computed across two rfMRI sessions (REST1 and REST2) and two phase encoding directions (LR and RL). Bars reflect standard errors.

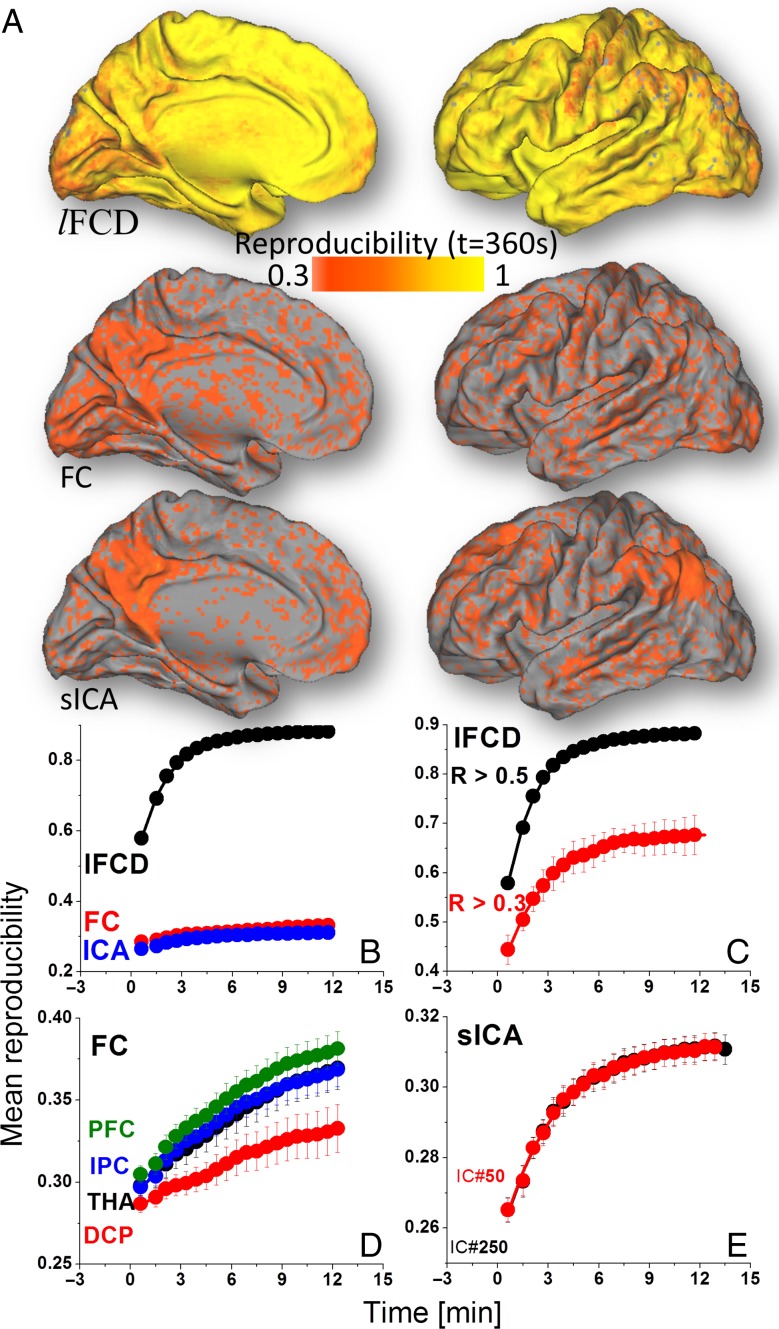
Reproducibility

The convergence of the whole-brain average reproducibility was faster for lFCD (t₀ ~2 min) than for sICA (t₀ ~4 min, P < 0.009; Fig. 6B and Table 1); t₀ was shorter for lFCD and sICA than for FC. Particularly, this effect was statistically significant for the THA, IPC, and PFC seeds (P > 0.01). t₀ was longer for lFCD_LT than for lFCD_HT (Fig. 6C). t₀ did not differ significantly across seed regions (for FC) or between sICA₂₅₀ and sICA₅₀ (Fig. 6D,E). Y₀ and A were larger for lFCD than for FC or for sICA (P < 10^–6).

Figure 6.

(A) Spatial distribution of the reproducibility across subjects at t = 6 min for each of the metrics (lFCD, FC, and sICA). Whole-brain average reproducibility as a function of time for: lFCD, FC, and sICA (B); lFCD_HT (R > 0.5) and lFCD_LT (R > 0.3) (C); seed-voxel correlations for seed regions in THA, DCP, IPC, and dorsolateral PFC (D); and for sICA-DMN maps computed using 50 and 250 maximum independent components (E). Average values computed across two rfMRI sessions (REST1 and REST2) and two phase encoding directions (LR and RL). Bars reflect standard errors.

Reliability

The convergence of the whole-brain average reliability did not differ significantly for lFCD than for sICA or for FC (P > 0.07; t₀ ~6 min; Fig. 7B and Table 1). Similarly, t₀ did not differ between lFCD_LT and lFCD_HT, across seed regions (for FC), or between sICA₂₅₀ and sICA₅₀ (Fig. 7C–E). Y₀ was larger for lFCD than for FC or for sICA (P > 0.01; Fig. 7B and Table 1).

Figure 7.

(A) Spatial distribution of the ICC(3,1) computed at t = 6 min for each of the functional connectivity metrics (lFCD, FC, and sICA) Whole-brain average reliability as a function of time for: lFCD, FC, and sICA (B); lFCD_HT (R > 0.5) and lFCD_LT (R > 0.3) (C); seed-voxel correlations for seed regions in THA, DCP, IPC, and dorsolateral PFC (D); and for sICA-DMN maps computed using 50 and 250 maximum independent components (E). Average values computed across two rfMRI sessions (REST1 and REST2) and two phase encoding directions (LR and RL). Bars reflect standard errors.

Effect of scan length

We aimed to assess potential effects of scan length on the benchmarks. Thus, using the same methodology we estimated sensitivity and specificity for shorter and longer scans. Specifically, lFCD_HT^short and FC_max^short were computed from the first 7 min of each rfMRI data sets, and lFCD_HT^long and FC_max^long were derived from 56.6 min long time series obtained from temporal concatenation of the BOLD signal maps corresponding to the 4 rfMRI (LR, RL, sessions 1 and 2) HCP data sets, as well as from 60 min long time series obtained from temporal concatenation of the BOLD signal maps corresponding to the first 6 (out of 10) rfMRI CoRR-HNU data sets. For lFCD convergence time did not differ significantly (2.3 ± 0.8 and 1.7 ± 0.3 min; t₀ for sensitivity and specificity, respectively) for the short than for the full length (14.4 min) rfMRI data sets. However, for lFCD_long the exponential model for sensitivity and specificity did not fit accurately the sensitivity and specificity benchmarks (see Supplementary Figures), suggesting detrimental effects of temporal concatenation in the computation of lFCD_long. Similarly for FC_max, convergence time did not differ significantly (3.6 ± 0.5 and 10 ± 2 min; t₀ for sensitivity and specificity, respectively) for short than for the 14.4 min rfMRI data sets. However, for FC_max from long rfMRI data sets the time-varying sensitivity and specificity exhibited artifacts and had low dynamic range (see Supplementary Figures).

Effect of Spatiotemporal Resolution

Since multiband EPI is still a novel technique and many groups use different MRI acquisition parameters, we studied the impact of MRI data acquisition parameters on t₀ for specificity and sensitivity using two different rfMRI data sets collected with conventional EPI: FCP-Cambridge (3 mm spatial and 3 s temporal resolution; 6 min acquisition time) and CoRR-HNU (3.4 mm spatial and 2 s temporal resolution; 10 min acquisition time). Overall, sensitivity and specificity for lFCD and FC were significantly higher for multiband EPI (HCP) than for standard EPI (FCP-Cambridge or CoRR-HNU) data sets (P < 0.0001). For lFCD, t₀ was not significantly different for the HCP than for FCP-Cambridge (2.5 ± 1.6 and 0.6 ± 0.4 min; t₀ for sensitivity and specificity, respectively) or CoRR-HNU (1.9 ± 1.9 and 2.2 ± 0.6 min) data sets (Fig. 8). For FC, however, t₀ was poorly quantified for the FCP-Cambridge (125 ± 177 and 87 ± 157 min; t₀ for sensitivity and specificity, respectively) and CoRR-HNU (320 ± 446 and 15 ± 2 min; specificity) data sets.

Figure 8.

Whole-brain average sensitivity (left) and specificity (right) for lFCD (black) and FC (red) as a function of time computed from FCP-Cambridge (top) and CoRR-HNU (bottom) rfMRI data sets. Bars reflect standard errors.

Discussion

FC metrics are highly dynamic (Chang and Glover 2010; Tomasi et al. 2016) and have a neurophysiological origin (Tagliazucchi et al. 2012). Image acquisition protocols that minimize the temporal variability of the connectivity patterns could facilitate the development of imaging biomarkers of healthy brain function and their disruption by brain diseases. This is the first study to contrast the effect of scan time on 3 different rfMRI metrics: lFCD, sICA, and FC, as assessed by ICC(3,1) test–retest reliability and four understudied additional performance benchmarks: accuracy, reproducibility, sensitivity, and specificity. We found that the necessary rfMRI scan time to attenuate the overall effects of the temporal dynamics on these five parameters by 80% or more varied across connectivity metrics and was shorter for lFCD (4.5 ± 1.5 min) than for FC or sICA (13.2 ± 4.2 min).

Static (or minimal) accuracy was significantly higher for lFCD (>51%) than for FC or sICA (<37%). Short time windows (<7 min) attenuated the temporal variability of the lFCD patterns by 80% (i.e. achieved 80% dynamic accuracy) but less so for FC (70%) or for sICA (60%). Thus, longer scan windows were necessary for FC (9 ± 1 min) and for sICA (12 ± 1 min) to achieve 80% dynamic accuracy. This finding is consistent with prior studies on the stabilization of graph theory metrics after 5 min of BOLD signal acquisition (Whitlow et al. 2011). Our findings are also consistent with the exponential attenuation of the average root-mean-square deviations (RMSD) of temporal correlations as a function of scan length (Birn et al. 2013). Specifically, Birn et al. studied the effect of scan length on the strength of the correlations between rfMRI signals from 18 spherical ROIs. They found that RMSD decreased with scan time and suggested that 8 min of scan time is necessary to sufficiently reduce RMSD. When we fitted a mono exponential decay model to their data we found that a scan length of 8.5 min was needed to attenuate the RMSD by 80%. Our findings are also consistent with the exponential saturation of the similarity between FC matrices as a function of scan length (Gonzalez-Castillo et al. 2014). Specifically, they found that similarity increased with scan time and suggested that 10 min of scan time is necessary to optimize within-subject reproducibility of whole-brain connectivity patterns. When we fitted the exponential model to their data, we found that a scan length of 6.8 min was needed to attenuate the temporal variability of the similarity index by 80%.

This is the first study to assess the effect of scan length on the sensitivity and the specificity of connectivity metrics. Short time windows efficiently attenuated the temporal variability of the sensitivity index by 80% for lFCD (5 ± 1 min) and sICA (5 ± 1 min), but longer windows were necessary for FC (9 ± 1 min). For lFCD, short scanning (<3 min) can efficiently attenuate the temporal variability of the specificity index by 80%, but much longer scanning (>17 min) may be necessary to achieve similar attenuations for FC and sICA. Overall, the high specificity and sensitivity of the lFCD reflect its precise GM localization (Tomasi et al. 2015).

Between-session reproducibility was also significantly higher for lFCD than for FC and sICA, and the temporal variability in the reproducibility of the patterns decreased faster for lFCD than for FC and SICA. To attenuate the temporal variability of the reproducibility index by 80% relatively short temporal windows (3 ± 1 min) were necessary for lFCD, but longer windows were required for FC (18 ± 3 min) and sICA-DMN (5 ± 1 min). The slower convergence of the reproducibility index for FC is consistent with the exponential attenuation of the mean difference between ROI-based FC measures as a function of scan length (Anderson et al. 2011). Specifically, when we fitted a mono exponential decay model to the single-subject data by Anderson et al., we found that a scan length of 15 min was needed to attenuate the dynamic differences in FC by 80%. Our reproducibility data suggest that graph theory metrics may be less prone to temporal dynamics than other connectivity metrics (FC and SICA) (Chang and Glover 2010; Van Dijk et al. 2010).

The average ICC(3,1) in cortical GM was significantly higher for lFCD than for FC and sICA. Overall, our findings are consistent with moderate to high reliability of the FC indices (Shehzad et al. 2009; Thomason et al. 2011; Braun et al. 2012; Faria et al. 2012). Whereas short time windows (<5 min) effectively attenuated the temporal variability of the reliability by 80% for lFCD, longer windows were necessary for FC (>9 min) and sICA (>6 min). The slower convergence of the reliability of the FC is consistent with previous reports (Birn et al. 2013) as estimated from the authors’ data (t₀ = 8 ± 2 min).

Resting-state fMRI has a potential as a biomarker of brain function that can be applied in medical diagnosis (Buckner et al. 2013; Castellanos et al. 2013). Whereas the nonstationarity of the connectivity patterns (Chang and Glover 2010) appears to have biological significance (Handwerker et al. 2012; Hutchison et al. 2013a, 2013b; Allen et al. 2014; Calhoun et al. 2014), the temporal dynamics should be critically considered in the development of biomarkers for neuropsychiatric disorders, particularly for protocols that use short imaging times (<6 min). Convergence time is metric-dependent and a function of the benchmark used to characterize convergence (e.g. sensitivity, reproducibility, etc.).

Overall the present study suggests that lFCD, a graph theory metric that gauges the local degree of connectivity, is more resilient to the effects of temporal dynamics than standard FC metrics such as FC and sICA, which could explain the high sensitivity of lFCD to brain disorders. We and others have shown that lFCD hubs in posterior parietal and occipital cortices (Tomasi and Volkow 2010, 2011b) are influenced by age (Tomasi and Volkow 2012b), gender (Tomasi and Volkow 2011c), stimulant drugs (Konova et al. 2015), fluid reasoning capacity (Lang et al. 2015), brain development (Tomasi and Volkow 2014), and dopamine signaling (Tian et al. 2013; Li et al. 2016). Thus, FCD mapping is being increasingly utilized to assess brain function at rest in neuropsychiatric populations. For instance, recent studies showed that lFCD hubs are disrupted in attention deficit hyperactivity disorder (Tomasi and Volkow 2012a), cocaine addiction (Konova et al. 2015), alcohol intoxication and abuse (Zhang et al. 2015; Shokri-Kojori et al. 2016), Alzheimer's disease (Sui et al. 2015), nonepileptic seizures (Ding et al. 2014), schizophrenia (Tomasi and Volkow 2014; Zhuo et al. 2014; Chen et al. 2015; Liu et al. 2015), post-traumatic stress disorder (Zhang et al. 2016), major depression (Zhang et al. 2016; Zou et al. 2016), congenital blindness (Qin et al. 2015), myopia (Zhai et al. 2016), amblyopia (Wang et al. 2014), traumatic axonal injury (Caeyenberghs et al. 2015), hepatic encephalopathy (Qi et al. 2015), tinnitus (Han et al. 2015), and other brain disorders.

Because fatigue, drowsiness, sleepiness, and movement all increase with scan time, it is unknown whether metrics computed from 14.4 min rfMRI data sets equals ground truth. This study does not identify significant t₀-differences between lFCD_short (7 min) and lFCD_HT (14.4 min) for any of the benchmarks. Similarly, findings were not driven by the parameters used in the computation of the metrics. Specifically, t₀-estimations were not significantly different for lFCD_HT (R > 0.5) and lFCD_LT (R > 0.3), or for seed-voxel correlations computed from different seed regions (FC_THA, FC_DCP, FC_IPC, FC_PFC, and FC_max), or for sICA-DMN patterns computed using different maximum numbers of components (sICA₅₀ and sICA₂₅₀). The decreased sensitivity for lFCD_long (57.6 min) and the longer t₀ of the sensitivity and specificity benchmarks for FC_long suggest that there may be limitations in our approach for modeling temporal evolution of connectivity metrics in concatenated rfMRI data sets.

lFCD is an ultrafast data-driven graph theory metric that quantifies the local degree, the size of the local network cluster functionally connected to each brain network node (Tomasi and Volkow 2010). We have shown that lFCD hubs in posterior parietal and occipital cortices (Tomasi and Volkow 2011b) have high metabolic cost (Tomasi et al. 2013) and exhibit pronounced temporal variability (Tomasi et al. 2016). MRI data sets with higher spatiotemporal resolution (2-mm isotropic; 0.72 s) have demonstrated high accuracy for hub localization, and high GM specificity and sensitivity (Tomasi et al. 2015). In part, this reflects the high temporal resolution achieved by multiband EPI, which allows significant attenuation of spurious connectivity in white matter by 0.01–0.08 Hz band-pass filtering. The more pronounced partial volume effects and less effective physiologic noise removal at lower spatiotemporal resolution of CoRR-HNU and FCP-Cambridge data sets could explain the lower dynamic range (A) of specificity and sensitivity for CoRR-HNU and FCP-Cambridge than for HCP. This also affects accurate quantification of t₀ for these data sets.

Thus, high spatiotemporal resolution FCD is a powerful voxelwise data-driven tool for exploring the brain connectome. In contrast to seed-voxel correlation analysis (Biswal et al. 1995), data-driven FCD is ideal for exploratory analyses because it does not rely on a priori hypotheses and quantifies the strength of the local FC hubs in just a few minutes/subject (Tomasi and Volkow 2010). However, the fact that lFCD requires shorter scan time does not mean that FC and sICA are less appropriate to use in clinical research than lFCD because they provide complementary information and may reflect nonidentical physiological phenomena. In this respect, a recent study showed that resting functional networks derived from sICA predicted an individual's brain fMRI activation patterns to different tasks (Tavor et al. 2016), which as on now has not been shown for FCD.

Overall this study suggests that 7–10 min scanning could result in stable static rfMRI biomarkers. However, development of dynamic biomarkers such as those reflecting the dynamics of the “state of mind” of each patient may require longer scanning times. The resilience of the lFCD metric to temporal dynamics makes it ideal for FC studies in pediatric and patient populations who may not tolerate long scans.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/

Funding

Data were provided by (1) the Human Connectome Project, WU-Minn Consortium (PIs: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research and by the McDonnell Center for Systems Neuroscience at Washington University, (2) The Consortium for Reliability and Reproducibility (CoRR), and (3) The 1000 Functional Connectome Project, with financial support from the National Institute of Health and the National Natural Science Foundation of China (NSFC). This work was accomplished with support from the National Institutes of Alcohol Abuse and Alcoholism (Y1AA-3009).