Gain Control in the Auditory Cortex Evoked by Changing Temporal Correlation of Sounds

Abstract

Natural sounds exhibit statistical variation in their spectrotemporal structure. This variation is central to identification of unique environmental sounds and to vocal communication. Using limited resources, the auditory system must create a faithful representation of sounds across the full range of variation in temporal statistics. Imaging studies in humans demonstrated that the auditory cortex is sensitive to temporal correlations. However, the mechanisms by which the auditory cortex represents the spectrotemporal structure of sounds and how neuronal activity adjusts to vastly different statistics remain poorly understood. In this study, we recorded responses of neurons in the primary auditory cortex of awake rats to sounds with systematically varied temporal correlation, to determine whether and how this feature alters sound encoding. Neuronal responses adapted to changing stimulus temporal correlation. This adaptation was mediated by a change in the firing rate gain of neuronal responses rather than their spectrotemporal properties. This gain adaptation allowed neurons to maintain similar firing rates across stimuli with different statistics, preserving their ability to efficiently encode temporal modulation. This dynamic gain control mechanism may underlie comprehension of vocalizations and other natural sounds under different contexts, subject to distortions in temporal correlation structure via stretching or compression.

Introduction

Sounds in the natural world exhibit variations in their temporal statistical structure. Different acoustic scenes are composed of sounds with temporal modulations under variable statistical constraints, and this variation in the TC statistics serves as a cue for discrimination and identification of natural sounds (Attias and Schreiner 1997; Escabi et al. 2003; Singh and Theunissen 2003; Geffen et al. 2011; McDermott and Simoncelli 2011; McDermott et al. 2013; Gervain et al. 2014). The correlation of amplitude modulations over time determines a highly salient qualitative property of sound: the slowly changing howl of wind blowing through an open window has a high temporal correlation (TC), whereas the rapidly changing rustle of wind blowing though leaves exhibits a relatively low TC. Communication sounds, including speech, contain important components across a range of temporal scales (Rosen 1992; Poeppel 2003). In particular, the temporal structure of human vocalizations plays a role in speech comprehension: degrading temporal, but not spectral information impairs speech comprehension (Remez et al. 1981; Shannon et al. 1995). Therefore, it is critical to identify how neurons in the auditory stream encode and represent sounds across varying TC statistics to elucidate the neuronal mechanisms for hearing both environmental and communication sounds.

Our present knowledge of neuronal mechanisms of encoding of the vast range of sounds at different TCs remains limited. Human brain imaging studies found that sounds with different temporal modulation properties differentially activated regions of the auditory cortex, suggesting a hierarchical scheme of sensitivity to TC in sounds. In Heschl's gyrus, containing the primary auditory cortex, studies have identified sensitivity to sounds with increasingly rapid modulations (Zatorre and Belin 2001; Schonwiesner et al. 2005). The superior temporal sulcus, containing higher order auditory cortices, exhibited sensitivity to sounds with lower temporal modulations (Boemio et al. 2005). Further, areas downstream of the auditory cortex, including the superior temporal gyrus and auditory association cortex, but not the primary auditory areas, exhibited differential activation by sounds with varying TC (Overath et al. 2008). The goal of our study was to identify the neuronal coding strategies in the primary auditory cortex for sounds with varying TC using electrophysiological recordings in rodents to isolate spiking activity.

As the BOLD signal is thought to be driven by elevation of the average neuronal activity over large populations of neurons (Logothetis and Wandell 2004), a number of coding strategies in the primary auditory cortex would be consistent with the imaging results. While exhibiting on average uniform activity across all neurons, subpopulations of neurons in the auditory cortex may preserve information about TC of sounds leading to differential activation in downstream areas. Just as neurons have been found to adapt with the statistical distribution of sound intensity and contrast (Dean et al. 2005, 2008; Rabinowitz et al. 2011; Watkins and Barbour 2011), they may also adapt to the TC structure of the stimuli thereby maximizing the dynamic range for their responses and providing information about TCs to downstream areas. Alternatively, different neurons may be tuned to stimuli with specific TC structure, resulting in uniform responses when averaged across neurons. Here, we tested whether and how neurons in the auditory cortex responded to sounds with varying temporal correlation and whether they exhibited adaptation in response to such variation.

To determine the mechanisms of sensitivity and responsiveness to sounds with varying temporal correlation TC, we recorded the activity of A1 neurons in awake rats while presenting dynamic chord stimuli with varying TC. We designed these stimuli to preserve the spectral complexity found in natural scenes, while permitting systematic variation in temporal statistics (Overath et al. 2008). Consistent with human imaging studies, we found that varying TC of sounds did not change the overall response of A1 in terms of the mean population firing rate. As an underlying mechanism of this stability, we revealed that A1 neurons adapted to increasing stimulus TC by decreasing stimulus response gain. Expanding on prior findings on gain control of stimulus intensity and spectrotemporal contrast (Rabinowitz et al. 2011), these results show that gain control in A1 compensates for a wider range of sound statistics and identifies the mechanisms for sensitivity to sounds with varying TC structure, that are likely essential in natural sound processing.

Methods

Animals

All procedures were approved by the Institutional Animal Care and Use Committee of the University of Pennsylvania. Subjects in all experiments were adult male Long-Evans rats. Rats were housed in a temperature- and humidity-controlled vivarium on a reversed 24-h light–dark cycle with food and water provided ad libitum.

Surgery

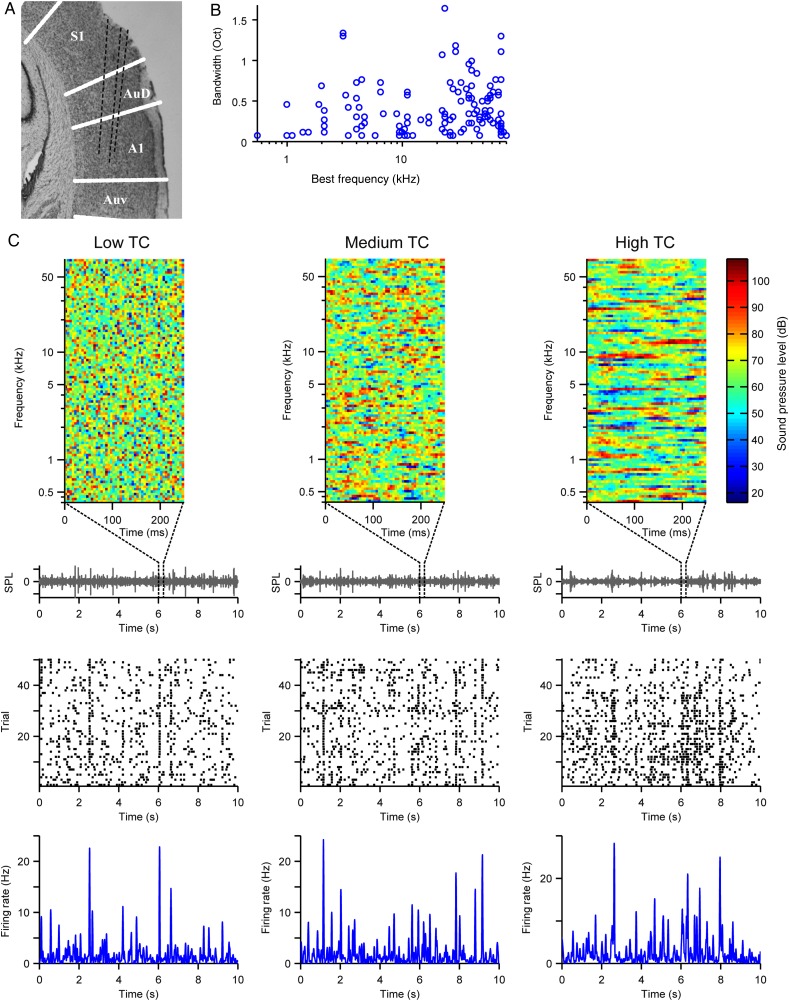
Adult male Long-Evans rats (N = 7, 12–21 weeks) were implanted with a chronic custom-built 6-tetrode drive as previously described (Otazu et al. 2009; Carruthers et al. 2013, 2015; Blackwell et al. 2015). Briefly, rats were anesthetized with a mixture of ketamine (60 mg/kg body wt, IP) and dexmedetomidine (0.25 mg/kg, IP). Buprenorphine (0.1 mg/kg, SC) was used as an operative analgesic, with ketoprofen (5 mg/kg, SC) as postoperative analgesic. The animal's head was secured in a stereotactic frame, and the temporal muscle was recessed. Craniotomy and durotomy were performed over A1. Eight tetrodes housed in a custom-built microdrive were lowered in the brain, and the microdrive was attached to the skull with dental cement (Metabond) and dental acrylic. Each tetrode consisted of 4 polyimide-coated nichrome wires (Kanthal Palm Coast, wire diameter of 12 μm) twisted together and was controlled independently with a turn of a screw. Two screws (1 reference and 1 ground) were inserted in the skull at a location distal from the craniotomy. The tetrodes were positioned 4.0–6.0 mm posterior to bregma and 7.0 mm left of the midline and covered with agar solution (3.5%). During the recording, the microdrive was connected via a custom-built interface board to a headstage (Neuralynx). The electrodes were gradually advanced below the brain surface in daily increments of 40–50 μm to ensure recorded units were unique. Targeting of the electrodes to the primary auditory cortex (A1) was verified on the basis of their position in relation to brain surface blood vessels, stereotaxic coordinates, and histological reconstruction of the electrode tracks and confirmed by identifying the frequency response function of the recorded units as previously described (Carruthers et al. 2013) (Fig. 1A). The recorded units' best frequency (frequency of the tone that elicited the highest firing rate) and tuning width spanned the range of rat hearing (n = 118, Fig. 1B) and was consistent with previous studies on the response properties of units in A1 (Sally and Kelly 1988; Polley et al. 2007; Carruthers et al. 2013, 2015).

Figure 1.

Recording neuronal spiking activity from primary auditory cortex (A1). (A) Reconstruction of primary auditory cortex showing tetrode traces in black dashed lines and cortical area borders in white lines. (B) Distribution of the best frequency and bandwidth of recorded units. (C) Top row: 100 ms sample of the amplitude envelope across each frequency for each stimulus TC level. Below, waveforms of the repeated 10 s stimuli, from which each sample is extracted. Center row: Spike raster from a single neuron in response to 50 repeats of each stimulus TC level. Bottom row: Mean firing rate PSTH of response to each stimulus TC level. Left column: low TC. Center column: medium TC. Right column: high TC.

Stimulus Construction

All stimuli were created in Matlab (MathWorks) and sampled at 400 kHz and 32-bit resolution. A set of temporally correlated dynamic random chord stimuli (CDRC) (Linden et al. 2003) was constructed similarly to stimuli in previous studies (Overath et al. 2008), adapted to the rat hearing range (Fig. 1C). This stimulus was designed to measure the spectrotemporal receptive field of neurons under different statistical regimes by fitting a linear–nonlinear model (Fig. 3B). One hundred amplitude modulated pure tones, of logarithmically spaced frequencies from 400 Hz to 70 kHz, were superimposed. The amplitude envelope was generated as following: for the uncorrelated (low TC, r = 0) stimulus, the amplitude modulations of each frequency were drawn independently from a normal distribution over 5 ms time frames. For the correlated (medium TC and high TC) stimuli, the amplitude within each successive frame was generated to ensure correlation with the previous frame, according to the Pearson's correlation coefficient of r = 0.67 for medium TC or r = 0.90 for high TC (Fig. 1C). To generate the frequency amplitude envelope matrix, the first column at time 0 was generated with a random set of values drawn from a Gaussian distribution (mean = 40 dB, standard deviation = 8.7 dB). Each subsequent frame was generated as follows:

$$S_i=S_{i-1}\times p+g(1-p^2{)}^{0.5}$$ (1)

where S_i−1 is a vector of the amplitude values of the previous frame, p is r/10, and g is a vector of random values drawn from the same Gaussian distribution. After generating each frame, the correlation coefficient between the adjacent frames was calculated to ensure that it was r ± 0.01. Frames that violated this condition were rejected and recalculated with a new g. Likewise, frames were also rejected if they contained values >3 standard deviations to prevent sound clipping. The final matrix S was rescaled to an average of 65 and standard deviation of 15 dB. Each frequency amplitude envelope was resampled to 400 kHz with linear spline interpolation to smooth amplitude transitions. Respective amplitude envelopes were multiplied by sine waves of each frequency and added together to produce the final signal. For all TC values, the stimuli had the same average intensity and standard deviation of the amplitudes within each spectral band. A 5 ms cosine squared ramp was applied to the beginning and end of each stimulus. The correlation coefficients used correspond to the window length of 5, 20, or 80 ms for a correlation reduction to r = 0.2. These values were chosen to be smaller, similar, or greater than a typical temporal width of a spectrotemporal receptive field of the recorded neurons.

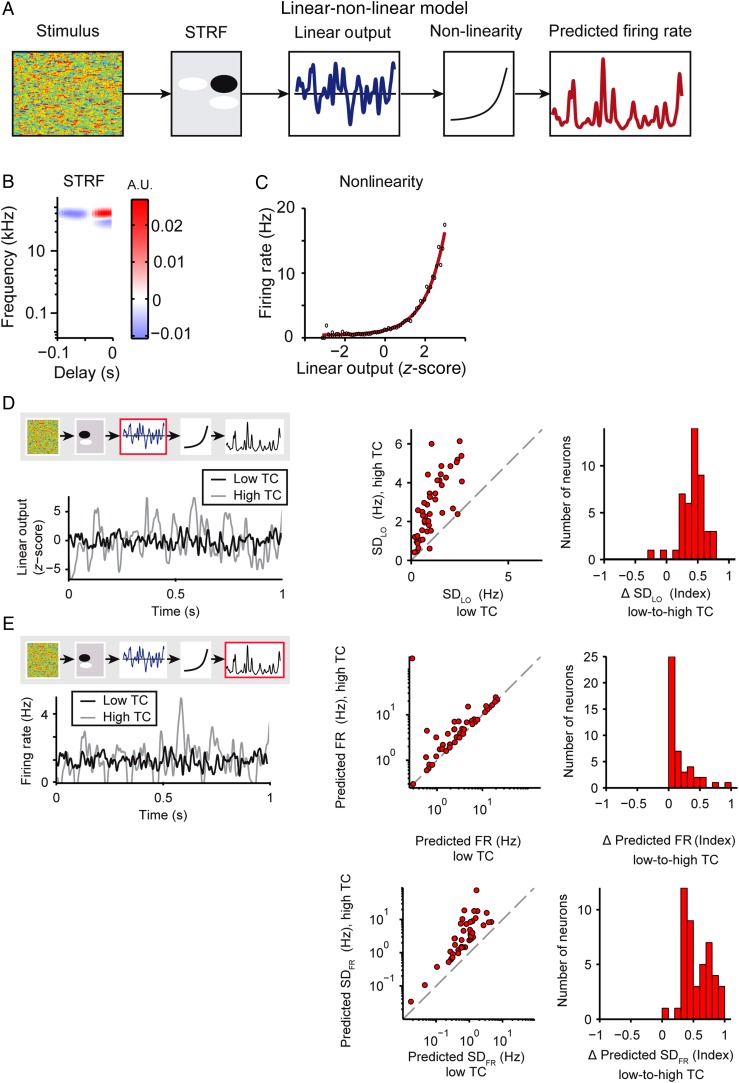
Figure 3.

Predicted increase in neuronal responses with increased stimulus TC. (A) Linear–nonlinear model diagram illustrating how the model predicts the firing rate in response to input stimulus: Amplitude modulation envelope of the stimulus is convolved with the linear filter (STRF) to produce the linear output, (Equation 2), which is subject to a transfer function (exponential fit to the nonlinearity) to generate the predicted firing rate for the neuron (Equation 3). (B) Sample STRF. (C) Sample nonlinearity (red: exponential fit, black: data). (D,E) Model predictions for responses to low or high stimulus TC levels. Left panels: Example of model outputs fitted to a single neuron's TC stimulus response properties. The red box in the model diagram highlights the feature being analyzed. Middle: Single neuron responses. Right: Population histogram of the change in predicted response with increased stimulus TC. (D) Standard deviation of the linear output (SD_LO, Equation 2) of the low TC model in response to low or high TC stimuli. (E) Predicted mean firing rate (top) and standard deviation (bottom) (Equation 3) of the low TC model in response to low versus high TC stimuli. Fit to low TC responses: black; fit to high TC responses: gray. Here and below: unity line: gray dashed.

Using the method described above, 3 sets of stimuli were created: short, long, and alternating. Short and long stimuli consisted of a single CDRC stimulus at each TC level, 10 s and 10 min long, respectively. Alternating stimuli consisted of a sequence of CDRC stimuli, at 2 TC levels (low/medium, medium/high, and low/high), alternating every 2 s. For each alternating stimulus, an amplitude envelope matrix was created in which r changed between 2 selected values every 200 frames (2 s). To ensure that amplitude power was sampled evenly across frequencies at each time frame, 1 vector from the matrix was time shifted by a 4 s interval and applied to each frequency. Examples of these stimuli as provided as Supplementary Materials (TClow.mp3, TCmed.mp3, and TChigh.mp3).

Stimulus Delivery

Acoustic stimuli were output from the computer via a National Instruments 16-bit high sampling rate data card (NIDAQ model NI PCIe-6353), pre-amplified, and delivered via a magnetic speaker (MF-1, Tucker-Davis Technologies) positioned above the recording chamber. The speaker output was calibrated using a Bruel and Kjaer 1/4-inch free-field microphone type 4939 positioned at the location of the animal's ear. The microphone was used to record speaker output of repeated white noise bursts and tone pips between 400 and 80 000 Hz. From these measurements, the speaker transfer function and its inverse were computed. The input to the microphone was adjusted using the inverse of the transfer functions previously described (Carruthers et al. 2013), such that the speaker output 70-dB sound pressure level relative to 20 µPa (SPL) tones within 3 dB between 400 and 80 000 Hz. Spectral and temporal distortion products were found to be >50 dB below the SPL of the fundamental. All stimuli were presented at 400-kHz sampling rate. The narrow recording chamber was custom-designed to minimize acoustic distortions. The chamber was positioned inside a sound-proof acoustically isolated double-walled room.

Experimental Design

The rat was implanted with an electrode microdrive and was trained to sit still in the recording chamber. Animals were monitored via video recording for their level of arousal, following methods previously developed in the laboratory (Aizenberg and Geffen 2013; Carruthers et al. 2013; Aizenberg et al. 2015; Blackwell et al. 2015; Carruthers et al. 2015; Mwilambwe-Tshilobo et al. 2015). The chronically implanted microdrive was connected via a cable to the Neuralynx digital acquisition system. The rat was exposed to stimuli for <4 h and given a 15 min break to drink water every 1.5 h. A stimulus designed to map the frequency response function of the recorded units, consisting of 50 tones, each 50 ms long, between 400 and 80 000 Hz, logarithmically spaced, at 70 dB, was presented first. The same set of stimuli was played in the following order: 1 repeat of a long CDRC stimulus at each TC, 50 repeats of each short CDRC stimulus at each TC, 1 repeat of each alternating CDRC stimulus. After stimulus presentation, each tetrode was advanced by 40 μm.

Neural signals were acquired from the 24 implanted electrodes with a Neuralynx Cheetah system. The neuronal signal was filtered between 0.6 and 6.0 kHz, digitized, and recorded at 32-kHz rate. Spikes were clustered into single-unit and multi-unit clusters with Plexon Offline Spike Sorter software. Single units were isolated using a stringent set of criteria as previously described (Aizenberg and Geffen 2013; Carruthers et al. 2013; Aizenberg et al. 2015; Blackwell et al. 2015; Carruthers et al. 2015; Natan et al. 2015): Single-unit clusters contained <1% of spikes within a 1.0 ms interspike interval, and the spike waveforms had to form a visually identifiable distinct cluster in a projection onto a 3-dimensional subspace (Otazu et al. 2009; Bizley et al. 2010; Brasselet et al. 2012).

Measurement of Neuronal Response Properties to the Stimulus

Mean Firing Rate

To avoid drift effects, the mean firing rate was measured from responses to the alternating TC stimuli, between 1 and 2 s after TC transition, and pooled across 900 TC alternation cycles per stimulus. To test for changes in firing rate between different TC levels for each neuron, we compared the mean firing rate across TC cycles across neurons, using the paired sign rank test to assay the significance (α = 0.05).

Linear–Nonlinear Model

To compute the spectrotemporal receptive field and the instantaneous nonlinearity, the neuronal responses at steady state (at least 200 ms following stimulus onset) to the 10 m long stimulus were fitted to a linear–nonlinear model (Fig. 3B). The linear–nonlinear model consisted of a linear component, corresponding to the spectro-temporal receptive field (STRF), followed by a static rectifying nonlinearity (Baccus and Meister 2002; Linden et al. 2003; Woolley et al. 2005; Geffen et al. 2007; Carruthers et al. 2013). The linear output (LO) is given by:

$$LO(t)=\sum _{f^{\mathrm{\prime }}=0}^{F-1}\sum _{t^{\mathrm{\prime }}=0}^{M-1}\text{STRF(}{f}^{\mathrm{\prime }},t^{\mathrm{\prime }})s(f^{\mathrm{\prime }},t-t^{\mathrm{\prime }})$$ (2)

and the predicted firing rate by:

$$R(t)=N[LO(t)]$$ (3)

where STRF is an M by F matrix; F is the number of frequency bins, and M is the number of temporal bins; and $N(x)$ is the instantaneous nonlinearity. The standard deviation of the linear output (SD_LO) is computed by taking the standard deviation of LO(t) over time.

STRF Parameters

STRFs were estimated as the optimal linear filter between the spiking response and the frequency amplitude envelope. Ridge regression was applied to normalize the filter by the stimulus autocorrelation function (Theunissen et al. 2001; Baccus and Meister 2002; Escabi et al. 2003; Geffen et al. 2007), after which the filter was smoothed by applying a 2-dimensional Gaussian filter with standard deviation of 1.5 bins (7.5 ms and 0.15 octaves in the temporal and spectral domains, respectively). STRF was denoised, by setting all values outside of a significant positive cluster of pixels to 0. Negative clusters were not included in the analysis, because including them did not improve firing rate prediction accuracy and did not appear to systematically change with TC. To determine the significance of the cluster, the z-score of pixels was computed relative to the baseline values from an STRF generated with scrambled spike trains, using Stat4ci toolbox (Chauvin et al. 2005). From STRF, the center time, duration, center frequency, and bandwidth of the positive cluster were measured (Woolley et al. 2006; Shechter and Depireux 2007; Schneider and Woolley 2010). To measure temporal parameters of the receptive field, the positive portion of the cluster-corrected STRF over the positive lobe was averaged across frequencies and fitted with a 1-dimensional Gaussian. Because we only examine the positive lobe of the STRF and not the entire STRF, we assumed that the positive lobe of the STRF was linearly separable in frequency and time. Center time and duration were defined as the center and twice the standard deviation of the Gaussian fit to the temporal STRF profile, respectively. Likewise, to measure spectral parameters, STRF was averaged across time over the positive lobe and fitted with a 1-dimensional Gaussian. Center frequency and bandwidth were defined as the center and 2× standard deviation of the Gaussian fit, respectively.

Nonlinearity

The nonlinear component of the linear–nonlinear model was computed as the transfer function between the linear prediction from the cluster-corrected STRF and the actual firing rate (Baccus and Meister 2002; Geffen et al. 2007; Carruthers et al. 2013) and fitted to exponential or logistic functions, $N(x)$:

$$N_1(x)=a+b\times e^{xc}$$ (4)

$$N_2(x)=\frac{L}{1+e^{-k(x-x_0)}}$$ (5)

Where a, b, c, L, k, and x₀ are free variables. Firing rate offset was defined as the firing rate at the average linear output $(N_1(x)=0)$ along the exponential nonlinearity fit. Gain was defined as the slope between 2 points along the exponential (Equation 4): One point at the average linear output and the other at the linear output 2 standard deviations greater than the average, thus the slope between $N_1(x)=0and2$. Steepness was defined as the variable k (Equation 5).

Fano Factor

The Fano factor was defined as the firing rate variance divided by the mean firing rate (Marguet and Harris 2011). The Fano factor was measured from responses to the alternating stimulus, at 1 to 2 s after TC transition for each TC level.

Signal to Noise Ratio

Signal was defined as the variance of the firing rate over time, averaged over trials. Noise was defined as the variance of the firing rate over trials, averaged over time (Geffen et al. 2009). The signal to noise ratio (SNR) was measured from responses to the alternating stimulus, at 1 to 2 s after TC transition for each TC level.

Prediction Quality of the Linear–Nonlinear Model

The prediction quality of the model was measured as the correlation coefficient between the predicted firing rate from the linear–nonlinear model and the measured firing rate. The model was fitted on responses to the long stimulus and tested for prediction quality on responses to the repeated short stimulus.

Adaptation Time Constant

Two post-stimulus time histograms (PSTH), one for each TC level, were computed from the mean firing rate over time between TC transitions (every other 2 s) for each alternating TC stimulus (Asari and Zador 2009). PSTHs were smoothed with a Gaussian filter with a standard deviation of 50 ms (10 frames). A decaying exponential function was fitted from the peak of the absolute value of the initial response (between 25 and 250 ms), to the end of the PSTH as:

$$y(t)=c+k\times e^{-t/\tau }$$ (6)

Where c is the adapted firing rate, k is the magnitude of the initial response, and τ is the adaptation time constant.

Neuron Selection Criteria for Analysis

Out of 180 single units recorded, 118 displayed measurable tuning properties (Fig. 1). Only those with demonstrable stimulus response to each TC level (mean SNR >0.22 across low, medium, and high TC) were included for analysis of firing rate, SNR, Fano factor, and nonlinearity slope, steepness, and offset (n = 45, Figs 2–5 and 8; n = 37, Fig. 6). Only units with a minimally stable STRF (at least one shared significant positive pixel between STRFs generated from low, medium, and high TC) were included in analysis of STRFs (n = 30, Fig. 7). To measure adaptation, only units with demonstrable adaptation (variance differing significantly between the initial 25–250 ms and final 500 ms after both transitions, unpaired 1-tailed t-test, α = 0.001) were included (n = 51, Fig. 9).

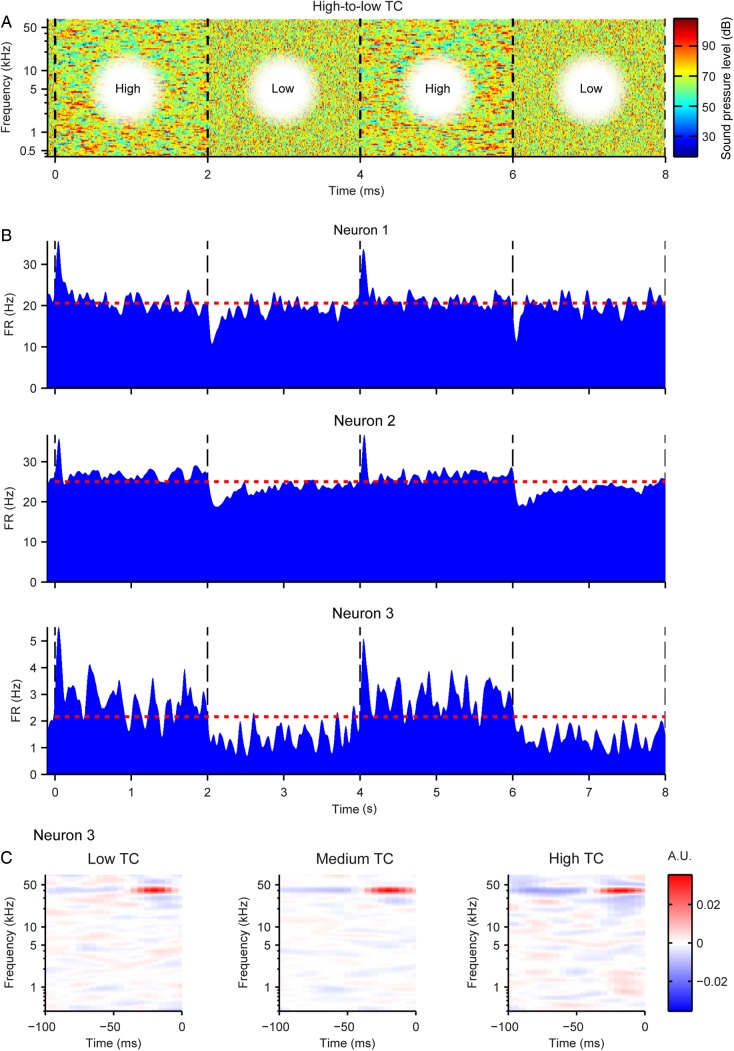
Figure 2.

Properties of neuronal spiking in response to varied TC levels. (A) Top: 8 s sample of the stimulus amplitude envelope for the alternating low-to-high TC stimulus. Transitions between TC levels occurred every 2 s (black dashed lines). (B) Mean firing rate PSTHs from 3 representative neurons aligned to the TC level transitions every 8 s. (C) STRFs from Neuron 3 in response to low, medium, and high TC levels.

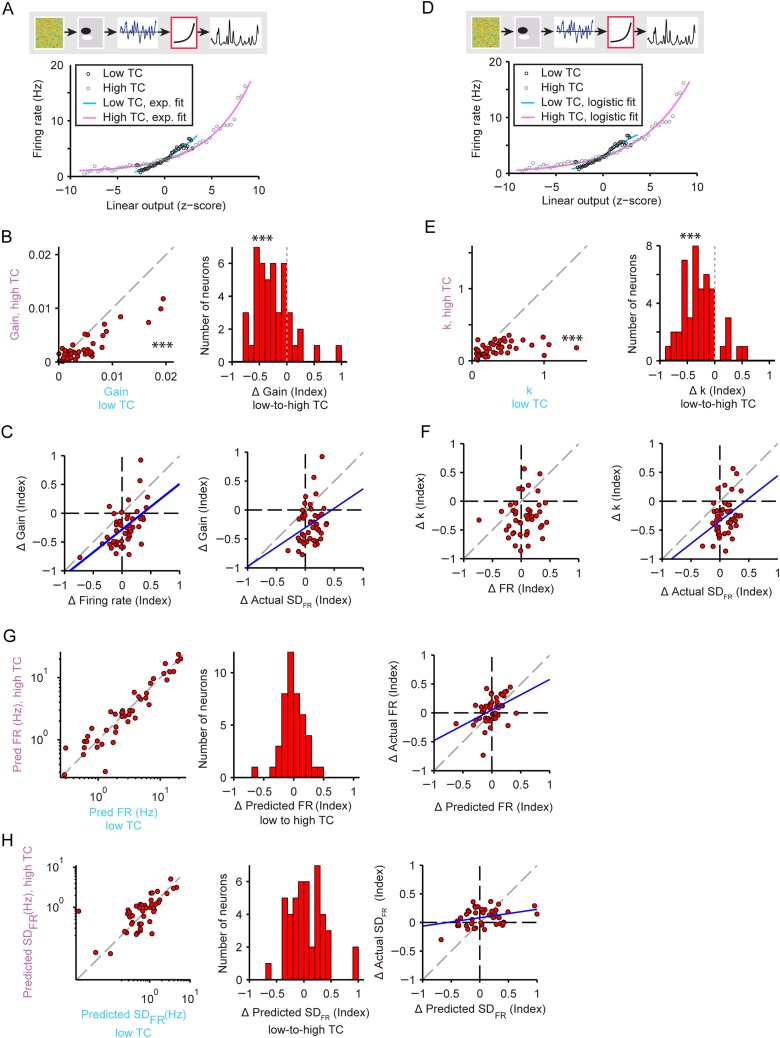
Figure 5.

Gain adaptation in neuronal responses to stimuli with increased temporal correlation. (A) Exponential nonlinearity fitted to the actual firing rate response to low versus high TC stimuli. Gain is measured through a linear fit to the exponential. Cyan: low TC fit, Magenta: high TC fit. Responses to low TC stimulus: black circles; responses to high TC stimulus: gray circles. (B) Gain measurements for high versus low TC stimuli. Left: individual neurons, right: histogram of change in the gain. Stars indicate that gain was higher for low TC than for high TC stimuli (left panel) and that gain decreased upon transition from high to low TC stimuli (right panel). (C) Change in the gain versus the change in the firing rate (left) or the standard deviation of the firing rate (right). (D, E, F) Same as in (A), (B), (C) but with logistic nonlinearity fit. Gain is measured as the steepness parameter k in Equation 5. (G) Predictions for the firing rate based on models fitted to high versus low TC stimulus. Left: individual neurons. Center: histogram of the index of change of the predicted firing rate with increasing TC. Right: actual versus predicted change in firing rate. (H) Predictions for the standard deviation of the firing rate based on models fitted to high versus low TC stimulus. Panels same as in G.

Figure 8.

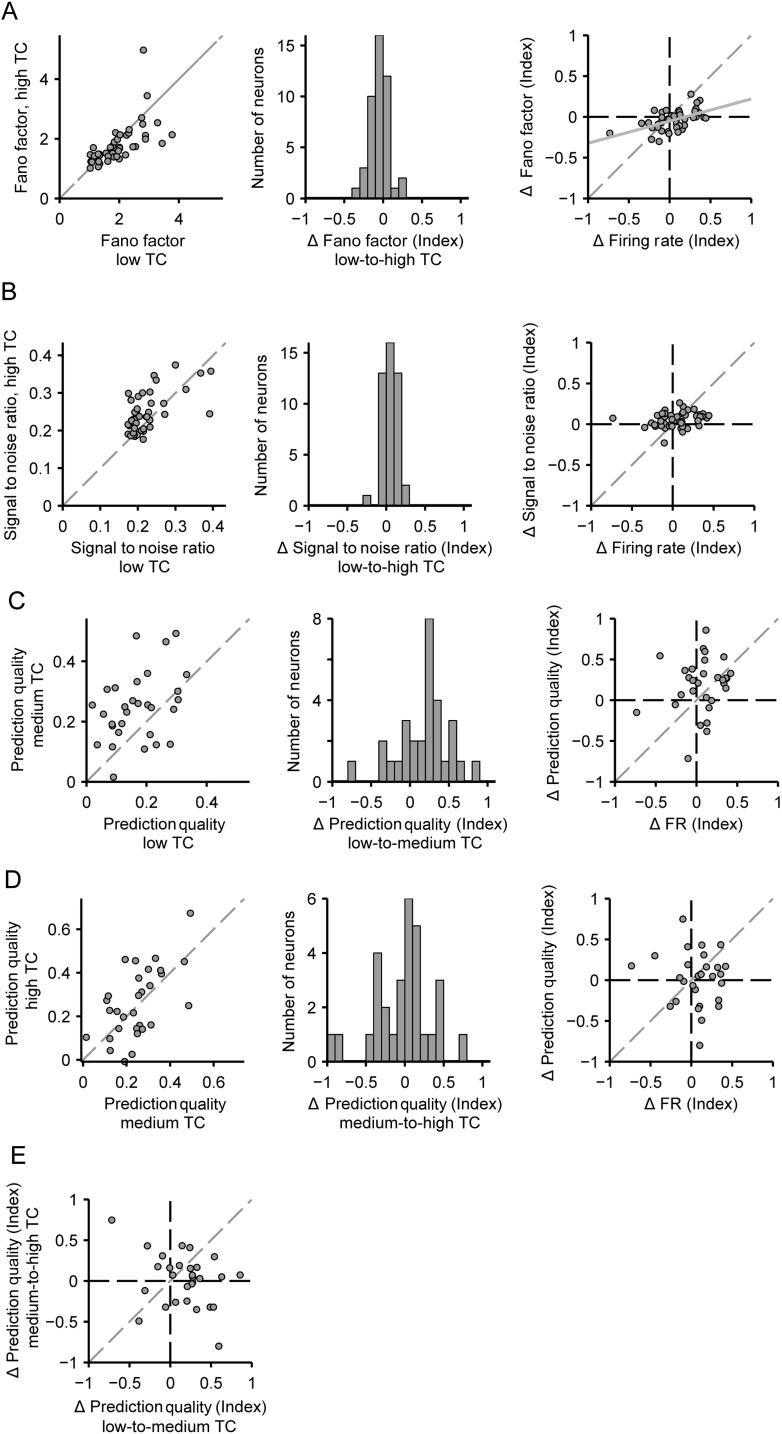
Improved encoding efficiency with increases in temporal correlation. (A) Fano factor of each neuron for low versus high stimulus TC. (B) Signal-to-noise ratio of each neuron for low versus high stimulus TC. (C) Prediction quality of each neuron for low versus medium stimulus TC. (D) Prediction quality of each neuron for medium versus high stimulus TC. Left, middle, and right panels as in Figure 6B–D. (E) Index of change in prediction quality from low-to-medium stimulus TC versus medium-to-high stimulus TC for each neuron. Plot axes as in D, left right panel.

Figure 6.

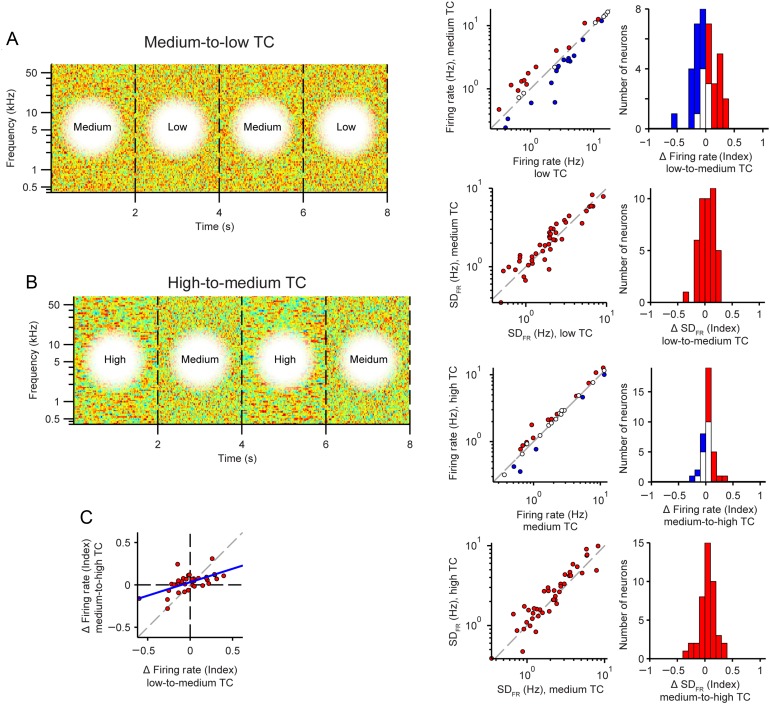
Neuronal firing rates in response to intermediate TC-level changes. (A) Transition from low to medium TC. (B) Transition from medium to high TC. (A, B) Left: Stimulus envelope, as in Figure 5A. Right: Change in mean firing rate (top) and standard deviation of the firing rate (bottom) from low to high TC stimulus. Axes and colors same as in Figure 4B,C. (C) Correlation between change in mean firing rate for medium-to-low and high-to-medium TC stimuli.

Figure 7.

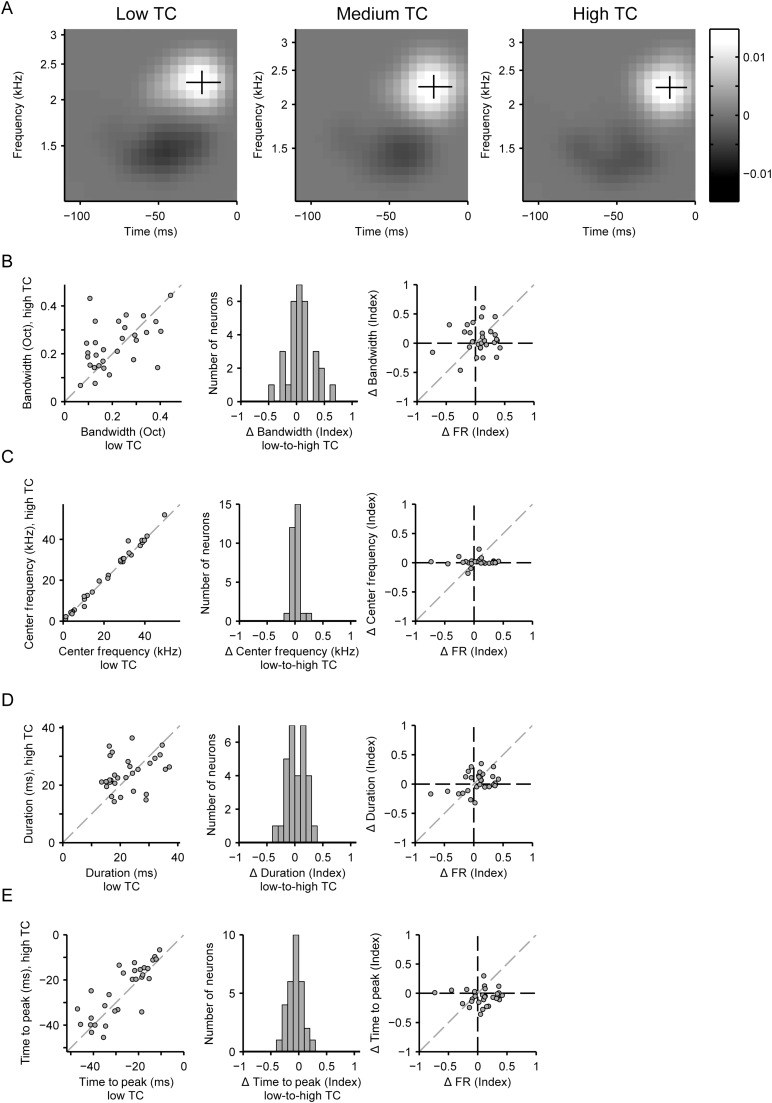
Neuronal spectrotemporal receptive fields remain stable across varying temporal correlation levels. (A) Spectrotemporal receptive field (STRF) of a neuron in response to low (left), medium (middle), and high (right) stimulus TC levels. Excitatory lobe: white, inhibitory lobe: black. Excitatory lobe bandwidth: vertical line. Excitatory lobe duration: horizontal line. The intersection of the black lines marks the excitatory lobe center frequency and time to peak. (B–E) Analysis of model parameters (positive lobe of the linear filter) in response to high-to-low stimulus TC levels for each neuron. (B) Frequency bandwidth. (C) Center frequency. (D) Duration. (E) Time to peak. (B–E) Left: Single neuron data. Center: Population histogram. Right: Correlation between the change in the STRF parameter versus the change in the firing rate with increased TC.

Figure 9.

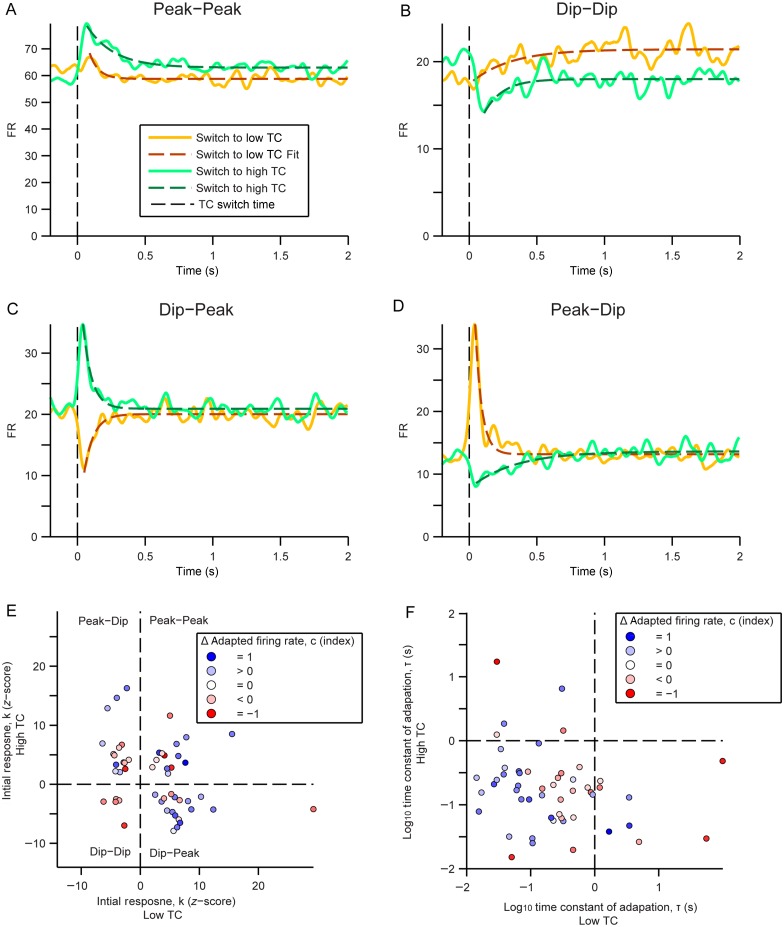
Heterogeneous responses to abrupt changes in stimulus TC. (A–D) Example PSTHs of the average firing rate of neurons with the transition from one TC level to another centered at time 0. Transitions from high to low TC and its adaptation fit (decaying exponential function, Equation 6) are in orange and dashed dark orange lines, respectively. Transitions from low to high TC and its adaptation fit are in green and dashed dark green lines, respectively. (A) A neuron that displays a peak in firing rate after either transition. (B) A neuron that displays a dip in firing rate after either transition. (C) A neuron that displays a dip in firing rate after transition to low TC and a peak in firing rate after transition to high TC. (D) A neuron that displays a peak in firing rate after transition to low TC and a dip in firing rate after transition to high TC. (E) Z-score of the initial response (k) after transition to low versus high TC. Each neuron is represented by a circle and its fill color indicates the index of change in adapted firing rate (c). (F) Time constant (τ) of the firing rate adaptation after the initial response to the low versus to the high stimulus TC. Each neuron is represented as in E.

Statistical Tests

The correlation coefficient (r) and correlation P values were computed as Pearson's correlation coefficient following a standard MATLAB routine. The index of change, Δ (index), was used to compute differences between lower and higher TC levels for several parameters:

$$\mathrm{\Delta }=\frac{\text{T}{\text{C}}_h-\mathrm{T}{\text{C}}_l}{\text{T}{\text{C}}_h+\text{T}{\text{C}}_l}$$ (7)

Where TC_h and TC_l represent the parameter value during the lower and higher of 2 stimulus TC levels. Significant differences and P values of these parameters between stimulus TC levels were reported based on the index of change as calculated using single sample Student's t-test (unless noted otherwise) with standard MATLAB routines. In calculating population mean percent changes, outliers were removed if they exceeded the sample mean ± 5 standard deviations. Mean ± standard error of the mean was reported unless stated otherwise.

Results

Neurons in A1 are sensitive to the temporal modulation rate in the acoustic structure of sounds, but how this sensitivity is affected by the overall statistics of the stimulus is unknown. Here, we tested the effect of changes in the range of temporal modulation statistics on encoding of temporally modulated sounds by neurons in A1. We presented a series of spectrotemporally complex acoustic stimuli to awake rats and recorded the responses of neurons in their primary auditory cortex. The stimuli consisted of a library of correlated dynamic random chords (CDRC) with different temporal correlation structure (Fig. 1C), presented either separately for each TC level, or in alternating block design (TC level changed every 2 s). Each CDRC was composed of 100 tones, and the amplitude of each tone varied over time. In the uncorrelated (low TC, r = 0) stimulus, the amplitude of each tone within the chord was chosen at random every 5 ms. For the intermediate and high TC stimuli, the amplitude of tones in a chord depended on the amplitude in the preceding chords, according to the correlation coefficient of that CDRC (r = 0.67 and r = 0.9, respectively). Stimuli with different TC values (low, medium, and high) evoked precise time-locked responses in A1 neurons (Fig. 1C).

Adaptation in A1 Neurons to Changed TC of the Stimulus

Upon transition to a different TC value of the stimulus, A1 neurons typically responded by a brief increase or a decrease in their mean firing rate, followed by relaxation to a steady firing rate. The responses of 3 representative neurons to an alternating high-to-low TC stimulus are depicted in Figure 2. In the stimulus, TC level alternates every 2 s. Note that upon transition from low TC to high TC, the firing rate consistently increased and then gradually decreased to a steady-state level; whereas upon transition from high to low TC level, there was a transient decrease in the firing rate following by a gradual increase (Fig. 2A,B). These firing rate profiles are characteristic of neurons undergoing adaptation to a statistical change in the stimulus (Dean et al. 2005, 2008; Hosoya et al. 2005; Chen et al. 2010; Rabinowitz et al. 2011). Interestingly, not only did the firing rate adapt between TC levels, but also the spectro-temporal receptive field remained constant during isolated stimuli of different TC levels (Fig. 2C). Such adaptation is thought to facilitate efficient coding in neuronal circuits, by bringing the dynamic range of the response closer to the dynamic range of the stimulus (Barlow 1961). We next investigated whether over the recorded neuronal population, the responses of neurons exhibited adaptation to stimulus TC, and if so, what mechanism might be responsible for it.

Expectation for an Increase in Neuronal Responses to Stimuli with Higher Temporal Correlation

Neuronal responses to CDRC in A1 are typically modeled by a linear–nonlinear model, which consists of a linear term that takes into account the stimulus history, and an instantaneous nonlinearity, which rectifies the output. Under the linear–nonlinear model, the linear component of the neuronal response is modeled as the spectrotemporal receptive field (STRF, Fig. 3B). Prior to nonlinear rectification, the convolution of the stimulus with the STRF generates an estimate of the stimulus input strength to the model, termed the linear output (Equation 2). The nonlinear component is the instantaneous transfer function from the STRF's linear output to the observed firing rate of the neuron (Fig. 3C). We designed the stimuli using a random composition of the signal within each frequency band, which allowed for fitting stimulus responses to the linear–nonlinear model. To establish an expectation for how response properties would change without gain control, we used the linear–nonlinear-model fits to estimate the change in mean and standard deviation of the firing rate in response to low and high TC stimuli. Under the linear–nonlinear model, the dynamic range of the linear prediction for each neuron can be characterized by the standard deviation of the linear output (Equation 2, SD_LO). We found that between low and high TC, SD_LO increased by a factor of 2.8 (difference 183 ± 20%, P = 5.6e−19, n = 45, Fig. 3D). An implementation of the full linear–nonlinear model, fitted on the response to the low TC stimulus (Equation 3), also predicted a 1.5-fold increase in the mean firing rate and a 6-fold increase in the standard deviation of the firing rate (SD_FR) compared with the responses to low TC stimulus (FR: difference 53 ± 17%, P = 1.42e−5; SD_FR: difference 497 ± 110%, P = 5.1e−21; n = 45, Fig. 3E, SD_FR reflects the dynamic range of the response). Therefore, we expected a dramatic increase in the range of the firing rate of neurons in response to the high TC stimulus.

Change in the Temporal Correlation of the Stimulus Evokes Gain Control in A1 Neurons

Analysis of the recorded neuronal responses to stimuli with varying TC levels (Fig. 4A) revealed that changes in the firing rate and its standard deviation were much lower than those predicted by the linear–nonlinear model, pointing to an adaptation process. For the low-to-high TC level transition (between 1 and 2 s after TC transition), there were no significant changes in the mean firing rate (P = 0.95, n = 45, Fig. 4B), and there was only a small difference in SD_FR (−26 ± 6%, P = 1.9e−4, Fig. 4C). These changes in FR were significantly smaller than would have been expected from predicted SD_LO (P = 1.7e−12, Fig. 4D, left) or predicted FR (P = 0.025, Fig. 4D, right). Likewise, the observed changes in the SD_FR were significantly smaller than expected from predicted SD_LO (P = 4.0e−13, Fig. 4E, left) or SD_FR (P = 3.2e−15, Fig. 4E, right). These results support the hypothesis that A1 neurons adapt to the temporal dynamic range of the inputs, thus preserving the ability to efficiently encode stimuli under varying statistical constraints without changing the activity level.

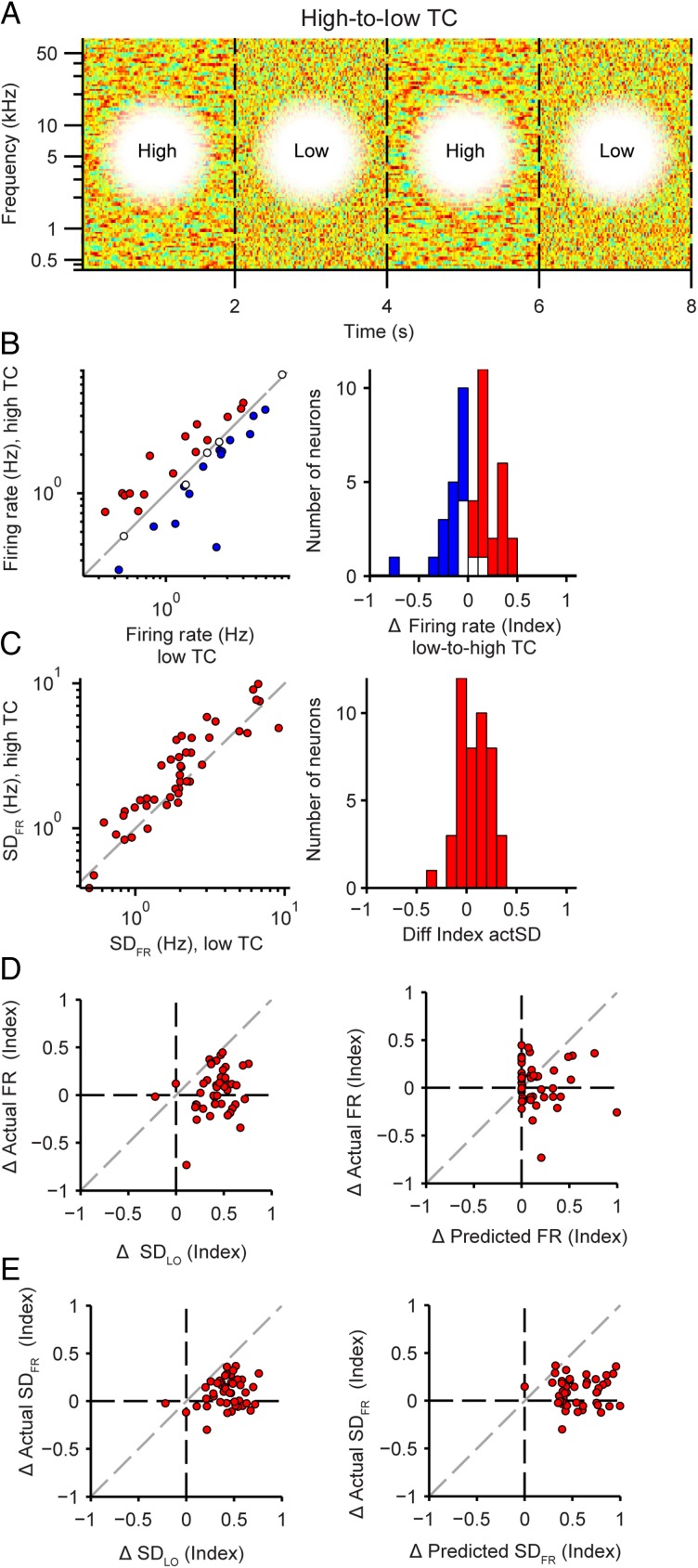
Figure 4.

Adaptation in neuronal responses to stimuli with increased temporal correlation. (A) Stimulus amplitude envelope, as in Figure 1C, for the alternating high–low TC stimulus. (B) Mean neuronal firing rate to high TC versus low TC stimulus. Left: single neuron responses, right: histogram of population responses (blue: significant decrease, red: significant increase; white: not significant). (C) Standard deviation of the firing rate to high TC versus low TC stimulus. Panels same as in (B). (D) Actual versus predicted change in the mean firing rate. Left: prediction based on standard deviation of the linear output. Right: prediction based on full linear–nonlinear model. (E) Actual versus predicted change in standard deviation of the firing rate. Panels same as in D.

Next we wanted to understand which parameters of neuronal responses contributed to the preservation of the firing rate and SD_FR over time. The gain of the nonlinearity has been previously shown to be involved in the firing rate adaptation to acoustic contrast and amplitude (Rabinowitz et al. 2011). We predicted that to reduce or eliminate a change in firing rate following change in stimulus TC, the gain should decrease with higher TC to fully or partly compensate for the increased synaptic input, as predicted by SD_LO. We independently estimated the linear–nonlinear model to responses to either low or high TC stimuli, fitting an exponential function (Equation 4) to the nonlinearity (Fig. 5A). Indeed, across the population, the gain was significantly lower for higher TC stimuli (−31 ± 9%, P = 1.4e−5, n = 45, Fig. 5B). The change in gain exhibited significant positive correlation with the change in firing rate (r = 0.54, P = 1.3e−4) and change in SD_FR (r = 0.30, P = 0.048), that is, neurons that displayed no change or reduced firing rate or standard deviation for higher stimulus TC exhibited stronger gain reductions (Fig. 5C). Fitting the nonlinearity with a logistic function (Fig. 5D) preserved the results: the parameter controlling the steepness of the slope of the nonlinearity, k, decreased with higher TC of the stimulus (−28 ± 10%, P = 8.2e−7, n = 45, Fig. 5E). The change in steepness also correlated with the change in SD_FR (r = 0.37, P = 0.012), although not the change in firing rate (P = 0.33) (Fig. 5F). When we re-fitted the model on responses to the higher TC stimulus, thereby incorporating the gain changes, the firing rate and SD_FR did not change from low to high TC (FR: P = 0.42; SD_FR: P = 0.27; Fig. 5G,H). Also, there was no longer a discrepancy between the change in predicted versus actual firing rate magnitude and standard deviation (FR: not significant, P = 0.44; SD_FR: not significant, P = 0.35). Furthermore, the correlation between the predicted and expected changes in the firing rate and its standard deviation were improved (FR: r = 0.47, P = 0.0012; SD_FR: r = 0.33, P = 0.027; Fig. 5G,H) compared with nonsignificant correlation between the prediction of the model based on low TC responses, which lacked gain adaptation (Fig. 4D,E). Together these results suggest that changes in gain reflect adaptation in neuronal responses.

We examined the changes in the firing rate offset of the nonlinearity as an analog for a shift in baseline firing rate between TC conditions. If the observed effects were due primarily to gain adaptation, we would not expect the nonlinearity offset to change significantly across conditions. Indeed, across the neuronal population, offset did not change between lower and higher TC stimuli (P = 0.42). Since the baseline firing rate does not change across the population, it is unlikely to contribute to compensation for increased SD_LO. However, changes in offset were correlated with changes in firing rate (r = 0.40, P = 0.0058). For individual neurons, underlying offset firing may explain some of the change in firing rate exhibited upon stimulus TC transitions.

Transitions from low TC to medium TC and from medium TC to higher TC led to similar adaptation in FR and its standard deviation (Fig. 6). There was no difference in the mean firing rate or its standard deviation for low-to-medium transitions (FR: P = 0.50; SD_FR: P = 0.13; n = 37, Fig. 6A). For medium-to-high transitions, there was no change in firing rate (FR: P = 0.84) and a small change in SD_FR (SD_FR: 16 ± 5%, P = 0.011, n = 37, Fig. 6B). We note that individual neurons exhibited significant changes in their firing rates, with some neurons increasing and some decreasing their responses to higher TC stimuli. The firing rate changes between responses for low-to-medium and medium-to-high TC transitions were correlated (n = 37, r = 0.60, P = 7.5e−5, Fig. 6C), suggesting that firing rate responses to TC-level changes are monotonic with TC level.

Our results thus far demonstrate that neurons in the primary auditory cortex exhibit adaptation to changes in temporal correlation of the stimulus. The mean firing rate does not change significantly and its standard deviation increases only slightly upon transition from low to high temporal correlation, whereas a large change would have been expected on the basis of the spectrotemporal receptive field of these neurons. The measured adaptation in the firing rate can primarily be attributed to the change in the slope of the nonlinear response function, corresponding to the gain of neuronal responses.

Spectrotemporal Dynamics of Neuronal Responses Are Unaffected by Stimulus TC

Changes in the gain of neurons due to adaptation are commonly accompanied by changes in the receptive fields of neurons (Baccus and Meister 2002; Nagel and Doupe 2006). For example, in the visual system, the time course of the receptive fields of ganglion cells becomes slower with a decrease in contrast (Baccus and Meister 2002). The spectrotemporal density of tone pips in an auditory stimulus has also been shown to affect the receptive fields of neurons in the inferior colliculus (Blake and Merzenich 2002; Kvale and Schreiner 2004). Changes in the receptive field shape and size could potentially modulate the neurons response properties. Therefore, to determine whether the changes in the receptive field explain differences in the firing rate between different temporal correlation levels, we quantified 4 aspects of the recorded STRFs under each condition (Fig. 7A): peak response time, temporal duration, center frequency, and frequency bandwidth. Only units containing a significant positive cluster-corrected lobe in the STRF for both low and high TC models, that spatially overlapped, were included in this analysis.

Interestingly, we found no systematic changes in the temporal or spectral profile of STRFs with an increase in TC. There were no significant changes in the bandwidth, center frequency, and duration of the STRF positive lobe (P = 0.14, P = 0.32, and P = 0.28, respectively, n = 30), nor were there significant correlations between the change in these parameters and changes in firing rate (P = 0.68, P = 0.74, P = 0.051, respectively) (Fig. 7B–D). Although there was a small reduction in the time-to-peak (−2.3 ± 1.3 ms, P = 0.018, Fig. 7E), this change was smaller than the 5 ms time frame of acoustic envelope modulation. In addition, changes in time-to-peak were not correlated with changes in firing rate (P = 0.99). Taken together, we did not find a systematic change in the receptive field that can explain the pattern of change in the firing rate with an increasing temporal correlation.

Adaptation to Temporal Correlation Leads to More Efficient Information Processing

The efficient coding hypothesis posits that matching the stimulus response dynamic range to the dynamic range of the stimulus improves the efficiency of coding (Barlow 1961; Fairhall et al. 2001; Schwartz and Simoncelli 2001; Vinje and Gallant 2002). We hypothesized that the gain modulation observed above serves to maintain encoding efficiency under different TC conditions. We quantified encoding efficiency using 3 measures: the SNR, the Fano factor, and prediction quality, and compared them for different TC levels.

The Fano factor provides a quantification of the variability in neuronal responses to the stimulus (Churchland et al. 2011). An effect of adaptation, consistent with the efficient coding hypothesis, would result in a decrease in the Fano factor. In fact, we found that the Fano factor decreased with increased TC (−5.1 ± 3.6%, P = 0.029, n = 45, Fig. 8A). Changes in Fano factor were also significantly correlated with changes in firing rate (r = 0.52, P = 2.8e−4).

The SNR gives a measure of how strongly the response variability is used to encode the stimulus (Geffen et al. 2009). Consistent with the efficient coding hypothesis, an effect of adaptation should be an increase in SNR (Baccus and Meister 2002). Indeed we found that SNR increased between low and high TCs (13 ± 3.1%, P = 3.1e−4, n = 45), and changes in SNR were not correlated with changes in firing rate (P = 0.10) (Fig. 8B). This suggests that populations of A1 neurons encode stimuli of higher TC with less noise.

The prediction quality is a measure of how well the linear–nonlinear model captures the response properties of each neuron (Woolley et al. 2005; Schneider and Woolley 2010; Carruthers et al. 2013). It can be affected by the dynamic range of the stimulus, as well as the precision and variability of the response. We compared the prediction quality of the linear–nonlinear model for responses to the low, medium, and high TC stimuli (n = 30, Fig. 8C–E). Over the population, prediction quality was lowest for low TC stimuli, and highest for medium and high TC stimuli (prediction quality = 0.17 ± 0.02, 0.24 ± 0.02, 0.26 ± 0.03, respectively). Between the 2 lowest TC levels, prediction quality was significantly greater for medium TC stimuli (108 ± 43%, P = 0.0062, Fig. 8C). Comparing medium to high stimulus TC, there was no significant change in prediction quality (P = 0.076, Fig. 8D). Neither prediction quality comparison (low-to-medium or medium-to-high) showed correlation with firing rate changes associated with different TC levels (P = 0.33, 0.87, respectively, Fig. 8C–D). Together, these results show that increasing the TC of the stimulus improves encoding. However, prediction quality does not continue to increase with increased TC. In fact, across the population, there is no correlation between increased prediction quality from low to medium TC versus medium to high TC (P = 0.073, Fig. 8E).

Interestingly, the correlation time window (Overath et al. 2008) of the medium TC stimulus (20 ms) most closely matches the temporal duration of the STRF (22 ± 1 ms). Therefore, the typical spectrotemporal response properties of A1 neurons, at least in rats, may be best suited to encode amplitude fluctuations occurring within the medium TC stimuli and contribute to more efficient encoding for this TC level. Furthermore, this implies that the time course of adaptation likely scales with encoding time of cortical neurons, and neurons with different encoding times (such as found in other cortical auditory fields (Polley et al. 2007)) may adapt to different TC stimuli.

Dynamics of Firing Rate Adaptation to Changes in Temporal Correlation

Examining the time course of firing rate change after a transition in the stimulus temporal correlation can be informative about the neuronal mechanism that underlies the firing rate adaptation (Asari and Zador 2009). We averaged the neuronal responses to a nonrepeating sequence of CDRCs, whose TC alternated between high and low, triggered on the low-to-high or high-to-low transitions, and examined the dynamics of the firing rate over several hundred milliseconds following the transition. Upon transition to a higher or lower TC regime, neurons (34% of recorded neurons) displayed either a transient increase (peak) or decrease (dip) in their firing rate over about 100 ms. If neurons followed the linear–nonlinear model and used gain adaptation, they would uniformly exhibit a peak in firing rate upon transition to higher TC, and a dip upon transition to low TC. In contrast, all combinations of initial responses were observed: peaks for both transition (Peak–Peak, Fig. 9A), dips for both transition (Dip–Dip, Fig. 9B), and peak for one and dip for another (Dip–Peak or Peak–Dip, Fig. 9C–D, also see Fig. 2A), as characterized by the z-score of their initial response. Across the population (n = 51), there is some correlation with each neuron's adaptation profile and its changes in adapted firing rate (represented by c in the adaptation model, Fig. 9E): All Dip–Dip neurons exhibit decreased firing rate in response to higher TC. Also, most Dip–Peak neurons exhibit increased firing rate in response to higher TC. However, the Dip–Peak and Peak–Peak populations did not exhibit a consistent change in responses to stimuli with different TC.

Our results demonstrate substantial heterogeneity in the initial response to a transition between high and low TCs. Similar heterogeneity was observed in the time constants that characterize the time scale of the adaptation of the baseline firing rate from the peak to baseline (Fig. 9F). For the majority of cells, the time constants fell below 1 s (Fig. 9F), which is consistent with previously observed time course for gain control in both the inferior colliculus and the auditory cortex (Dean et al. 2008; Rabinowitz et al. 2011). Neurons that increased their firing rate in response to high TC had shorter time constants of adaptation. This suggests that there are multiple processes in place that determine the initial response to TC transition, and that these processes are in some cases distinct from those determining the baseline firing rate change.

Combined, we found that over the neuronal population, there was no significant change in the neuronal steady-state firing rates with increase in TC. A prediction for the response strength of neurons to these stimuli was that neurons would exhibit higher firing rates to stimuli with higher TC. Analysis of specific response components revealed that the firing rate adaptation could be attributed to the change in the neuronal stimulus-driven, nonlinear response gain rather than neuronal spectrotemporal receptive fields. The change in the gain was part of an active adaptation mechanism, triggered by the transition in the stimulus to an increased or decreased TC.

Discussion

Dynamic gain control is ubiquitous in neuronal systems (Shapley and Victor 1978; Smirnakis et al. 1997; Brown and Masland 2001; Chander and Chichilnisky 2001; Baccus and Meister 2002; Chung et al. 2002; Kohn and Movshon 2003; Kvale and Schreiner 2004; Dean et al. 2005, 2008; Nagel and Doupe 2006; Chen et al. 2010; Rabinowitz et al. 2011). From the point of view of efficiency of neuronal coding, dynamic gain control permits increased information transmission by matching the dynamic range of responses to the dynamic range of the stimulus (Barlow 1961; Fairhall et al. 2001; Schwartz and Simoncelli 2001; Vinje and Gallant 2002). Neurons in the auditory cortex exhibit tuning to the temporal modulation structure of acoustic stimuli (Lu et al. 2001; Miller et al. 2002; Linden et al. 2003; Woolley et al. 2005; Ter-Mikaelian et al. 2007). This tuning, however, has previously been measured using stimuli with fixed temporal correlation structure. We found that changes in the temporal correlation of a broadband acoustic signal evoked gain control in neuronal responses in the primary auditory cortex. This gain control mechanism affected the nonlinear component of the response, improving stimulus encoding. Interestingly, unlike in other sensory modalities (Baccus and Meister 2002), the temporal response parameters of neurons were not affected by the temporal statistics of the stimulus.

Cortical Contribution to Temporal Gain Control

Gain adaptation has previously been observed in the auditory cortex in response to sounds with varying intensity and contrast (Rabinowitz et al. 2011), as well as to transitions between different types of sounds (Asari and Zador 2009). Responses of neurons in the inferior colliculus have also been shown to exhibit adaptation to sound contrast (Blake and Merzenich 2002; Kvale and Schreiner 2004; Dean et al. 2005, 2008). Gain adaptation to stimulus contrast in the auditory cortex is therefore likely a combination of processing that takes place at the more peripheral processing stages as well as within the cortex, at the level of inhibitory-excitatory neuronal circuits. The dynamic gain control in response to temporal correlation observed in the present study may be driven by a similar mechanism as the previously observed gain control to changes in sound contrast (Chen et al. 2010; Rabinowitz et al. 2011). Indeed, when the stimulus is projected on the receptive field of the neuron, despite its normalization for intensity and standard deviation, it produces signals with increasing dynamic range for higher TCs (Fig. 5A). As the spectrotemporal receptive field can be thought of as approximating processing performed prior to integration of the inputs by the A1 neuron, the stimulus with an increased TC provides higher dynamic range of inputs to the A1 neuron, much like a stimulus with an increased intensity contrast. This is due to the specific properties of the temporal integration time course of the spectrotemporal receptive fields of A1 neurons. Therefore, the observed gain control likely extends to a range of higher order statistics beyond the lower order features, such as intensity, contrast, and temporal correlation.

We observed that for some neurons, responses increased with increasing TC (Fig. 4)—therefore, gain control did not lead to complete adaptation, preserving information about TC in the mean firing rate of the neurons. These effects are consistent with those observed previously in response to an increase in sound contrast, where the firing rate of neurons increases with contrast, but is subject to incomplete gain control (Rabinowitz et al. 2011). Interestingly, the effects of gain control for changes from high to low TC, and vice versa, were heterogeneous for a subpopulation of neurons. Some neurons that lowered their firing rate to low TC exhibited a transient increase in firing rate upon transition to high TC (Fig. 9). The nonlinear component of the linear–nonlinear model is thought to reflect the spiking nonlinearity at the level of cortical neurons. Therefore, this observation supports the argument for contribution of intra-cortical mechanisms to gain adaptation, at least in some of the neurons (in which the sign of firing rate change upon transition is inconsistent with the prediction of the linear–nonlinear model). Remarkably, we did not find a significant effect on the timing and spectral bandwidth of the receptive fields of the neurons. A circuit that uses synaptic depression or facilitation in implementing gain control would likely result in a change in temporal response properties of the neurons (Abbott et al. 1997; Chance et al. 1998) and therefore is not supported by the present observations. Furthermore, the measured time scale of gain control in A1, with time constants of adaptation below 1 s for most neurons (Fig. 9F), is greater than the time course of adaptation measured in the inferior colliculus, corresponding to the time constants of tens of milliseconds (Dean et al. 2008). Therefore, while a major component of adaptation may be inherited from earlier auditory areas to the cortex, intra-cortical mechanisms also seem to play an important role.

Relation to Previous Studies

Neurons in A1 exhibit both time-locked and sustained responses to sounds that were modulated at different temporal rates: neurons responded to fast sounds with a sustained response, encoding the click rate in their mean firing rate; and to slower temporal fluctuation with synchronized spiking discharges, phase-locked to the modulations (Lu et al. 2001). In the present study, we did not observe such a dichotomy in responses; the change from time-locked to sustained responses would have been reflected in a change in the temporal component of the neuronal spectrotemporal receptive field. Here, we did not identify a systematic change in the temporal component of the STRF (Fig. 6). This inconsistency may be due to the difference in stimuli between different studies: we implemented a novel approach to examining the effect of temporal fluctuation rates on A1 responses by systematically changing the statistical structure of the broadband stimulus. It is plausible that the time scales of the stimulus modulation that were used in this study differed from those used previously. Furthermore, using a spectrotemporally more complex stimulus decreased the synchronization versus firing rate dichotomy, as the responses were likely driven by an integration of onset and sustained acoustic cues.

Our results provide for a potential link between two earlier studies in humans: one identifying differential activation in the human auditory cortex by stimuli with varying temporal modulation rates (Boemio et al. 2005) and the other using a similar stimulus design to ours that found differential activation of the areas downstream in the auditory cortex, including the superior temporal gyrus and auditory association cortex (Overath et al. 2008). The BOLD signal may average out the heterogeneous changes in the neuronal spiking responses (Logothetis and Wandell 2004). Our findings provide support for this explanation for 2 reasons. The momentarily high responses that are produced at the transition from low to high temporal correlation are likely too fast to be detected by the BOLD signal that integrates the inputs over hundreds of seconds. The gain control mechanism that we observed may normalize the responses that the BOLD signal picks up. At the same time, since some neurons are inhibited by the increase in TC, while others are excited, the averaged population activity is also less affected. In contrast, the downstream areas may convert the heterogeneous changes in the firing rates of A1 neurons into an increase in their firing activity, and therefore, their responsiveness may be detected by the BOLD signal.

Consequences for Processing of Speech and Communication Signals

Temporal modulations at different time scales have been shown to correspond to different aspects of the speech signal (Rosen 1992; Poeppel 2003; Hickok and Poeppel 2007). The faster fluctuations denote the fine structure of speech, while the slower fluctuations refer to periodicity and envelope (Rosen 1992). Signals at different temporal scales contribute information about different aspects of segmental and prosodic cues in speech perception. Our results suggest that at the level of A1, the neuronal resources devoted to any single scale are equalized, as the neuronal firing rates are stable across a range of TCs.

Furthermore, the auditory system shows remarkable invariance to temporal stretching and compressing of acoustic signals: compressing speech up to 2-fold does not lead to an impairment in speech comprehension (Beasley et al. 1980; Ahissar et al. 2001). The neuronal mechanisms that would enable such invariance have been hypothesized to produce a code that also stretches and compresses with changes in the stimulus statistics. Our results do not support such transformation, as the receptive fields of neurons do not change with temporal correlation of the stimulus. Therefore, they are expected to produce differential responses to sounds that are stretched or compressed, consistent with our previous measurements of responses to rat vocalizations and emergent properties of invariant representation within the auditory cortex (Carruthers et al. 2013, 2015).

To summarize, we found that neurons in the primary auditory cortex exhibited gain control to changes in the temporal correlation statistics of acoustic stimuli. This adaptation allows neurons to maintain their mean firing rates under different stimulus regimes, while increasing or preserving the information that neurons can transmit about the stimulus.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/.

Funding

This work was supported by R01DC014479 and R03DC013660 from NIH NIDCD to M.N.G., Klingenstein Award in the Neurosciences to M.N.G., Human Frontiers in Science Foundation Young Investigator Award to M.N.G., Pennsylvania Lions Foundation Hearing Research grant to M.N.G., Penn Medicine Neuroscience Center Pilot Award to M.N.G., Behavioral and Cognitive Neuroscience Training grant to R.G.N., and Complex Scene Perception IGERT grant to I.M.C. M.N.G. is the recipient of the Burroughs Wellcome Career Award at the Scientific Interfaces.