Abstract
The kinetics of lithium diisopropylamide (LDA) in tetrahydrofuran under non-equilibrium conditions are reviewed. These conditions correspond to a class of substrates in which the rates of LDA aggregation and solvation events are comparable to the rates at which various fleeting intermediates react with substrate. Substrates displaying these reactivities, by coincidence, happen to be those that react at tractable rates on laboratory timescales at −78 °C. In this strange region of non-limiting behavior, rate-limiting steps are often poorly defined, sometimes involve deaggregation and at other times include reaction with substrate. Changes in conditions routinely cause shifts in the rate-limiting steps, and autocatalysis is prevalent and can be acute. The studies are described in three distinct portions: (1) methods and strategies used to deconvolute complex reaction pathways, (2) the resulting conclusions about organolithium reaction mechanisms, and (3) perspectives on the concept of rate limitation reinforced by studies of LDA in tetrahydrofuran at −78 °C under non-equilibrium conditions.
Graphical abstract
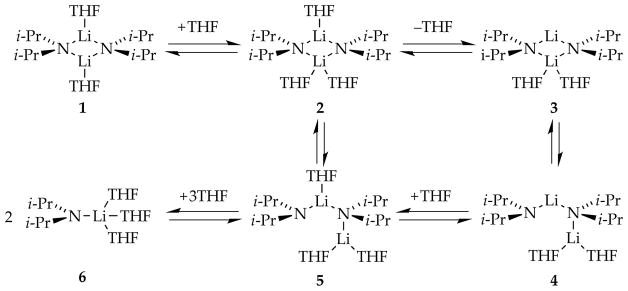
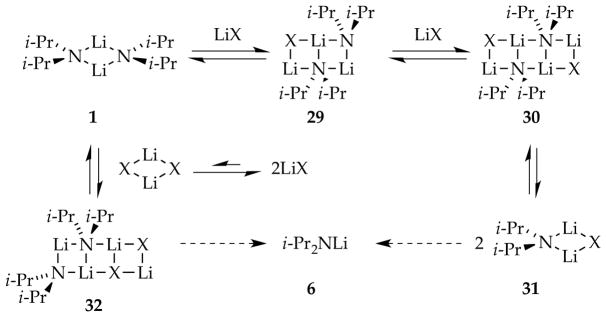
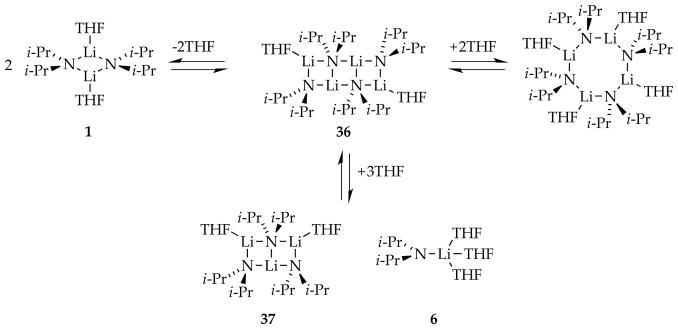
Lithium diisopropylamide (LDA), a highly reactive and selective Brønsted base, stands among the most prominent reagents in organic synthesis.1 A survey of 500 total syntheses revealed that LDA is the most commonly used reagent.2 In the world of structural and mechanistic organolithium chemistry in which solvent-dependent aggregation and mixed aggregation impart enormous structural and mechanistic complexity,3 LDA has appeal for the study of structure–reactivity relationships owing to its relative structural simplicity: it exists exclusively as disolvated dimers in most coordinating solvents.4 That said, tetrahydrofuran (THF)-mediated deaggregation of LDA, depicted in Scheme 1 (1–6), exemplifies only a few of the many structural forms that can occur fleetingly in solution at full equilibrium. Include the plethora of possible mixed aggregates formed from LDA and other lithium salts (LiX), and it is clear that even the simplest organolithium reagent offers the potential for breathtaking mechanistic complexity.5
Scheme 1.
Simplified deaggregation of LDA dimer to monomer. Reproduced from ref 8e. Copyright 2011 American Chemical Society.
This review of the chemistry of LDA is our second. The first described investigations that probed mechanistic pathways—nearly a dozen amide–solvent stoichiometries in the rate-limiting transition states—that become available when LDA solvated by standard coordinating solvents reacts with various electrophiles.6,7 We thought we were nearing a logical end point, but that proved to be premature. We had assiduously avoided studying metalations at −78 °C based on the misguided notion that dry ice–acetone baths would provide inadequate temperature control. Reevaluating this bias, we discovered an extraordinary coincidence that forms the foundation of this review: LDA-mediated metalations in THF at −78 °C—conditions that are of singular importance in organic synthesis—occur at nearly the rates at which the aggregates in Scheme 1 exchange. The resulting mechanistic complexity proved high even by organolithium standards, and the effort expended to understand metalations under such non-equilibrium conditions would have been difficult to justify for reagents of lesser importance. This base was the iconic LDA, however.
Eight publications form the core of this second review.8 LDA, however, is only one part of a three-part story. Section 1 is a tutorial that delineates the methods and tactics used to untangle the interwoven mechanistic pathways, in particular, when rate-limiting steps routinely change. These strategies and principles are generally applicable to the deconvolution of complex ensembles of mechanisms. Section 2 summarizes the specifics of LDA-mediated metalations under non-equilibrium conditions. Rather than re-adjudicating the cases, we merely summarize observations that are of potential interest to mechanistic organolithium and synthetic chemists. Section 3 focuses on seemingly simple notions of rate limitation emanating from rate studies that may be counterintuitive and possibly even difficult to accept. We begin by illustrating why this particular subset of LDA-mediated metalations is so strange.
Background
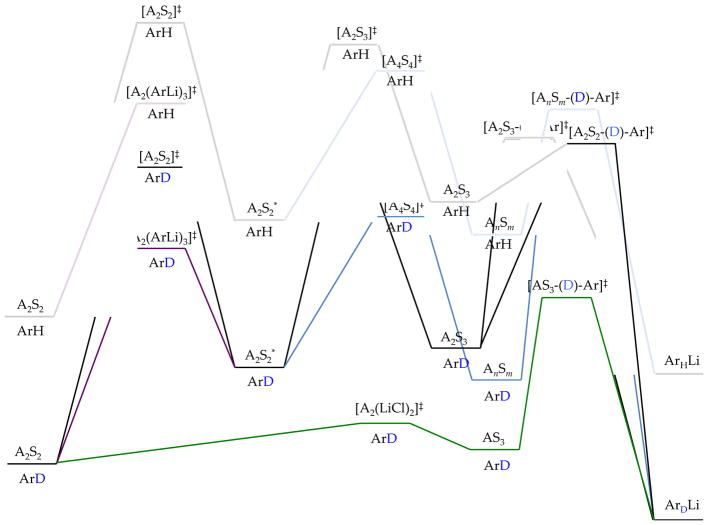
LDA-mediated metalations as well as all other organolithium reactions can be described using three scenarios (Figure 1). The dimensionless concept of reactivity in Figure 1 can be construed as the reaction temperature required to monitor a reaction on laboratory timescales using standard kinetic methods. Complexity, also a dimensionless entity, will become clear in the forthcoming description of scenario 3.
Figure 1.
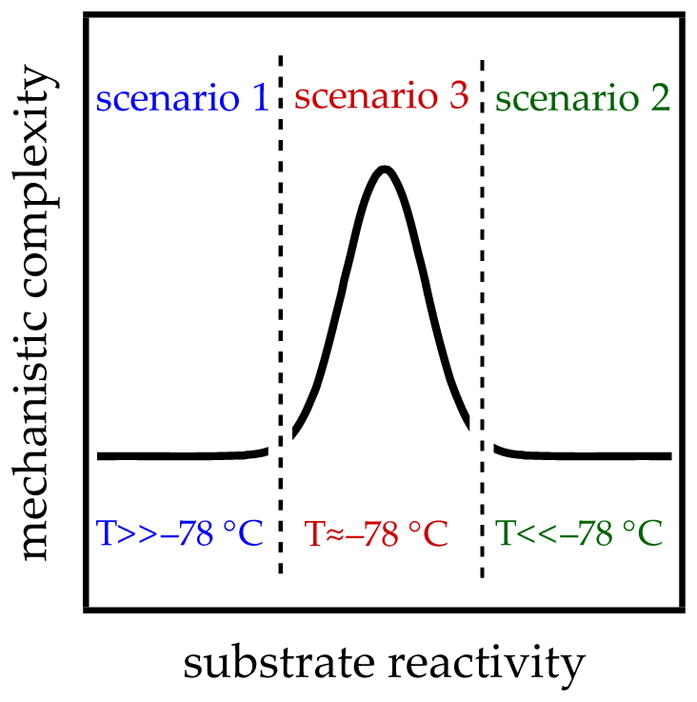
Abstract depiction of mechanistic complexity in the limit of fast aggregate exchange (
 ), aggregate non-exchange (
), aggregate non-exchange (
 ), and non-equilibrium aggregate exchange (
), and non-equilibrium aggregate exchange (
 ).
).
Scenario 1: Fast aggregate exchange
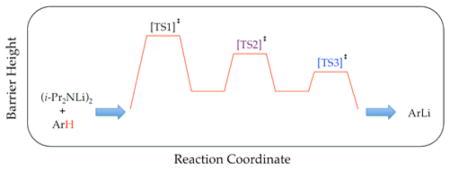
In the limit that all aggregates rapidly equilibrate on the timescales of subsequent metalations, the mechanistic course of a reaction is dictated by the lowest barrier of the LDA-mediated proton transfer (Scheme 2). We rely heavily on the shorthand shown in the inset in Scheme 2 to simplify forthcoming discussions. For example, A2S2 refers to a disolvated dimer such as 1, [A2Sn*] connotes a spectroscopically invisible dimer of solvation number n, and [A2Sn(ArH)]‡ corresponds to a transition structure for the metalation of an arene, ArH, of A2Sn(ArH) stoichiometry. LDA/THF-mediated metalations of relatively unreactive substrates are comfortably monitored from −55 °C to room temperature. Substrates necessarily undergo rate-limiting proton transfers, which display large (sometimes very large) primary kinetic isotope effects (KIEs).9 Although the multitude of substrate-solvent combinations have revealed almost a dozen stoichiometrically distinct monomer- and dimer-based mechanisms,6 one or two mechanisms usually dominate for any given substrate–solvent combination.
Scheme 2.
Reactions of LDA via parallel pathways
Scenario 2: Aggregate non-exchange
In the limit that an organolithium reagent reacts with substrate rapidly relative to the rate that aggregates exchange, only the observable aggregates are available to react (Scheme 3). (Solvent exchanges may remain rapid on the reaction timescales.) After seminal studies by McGarrity and co-workers10,11 using rapid injection NMR spectroscopy, Reich12 investigated a number of organolithium reactions under conditions in which two or more aggregates are observable at the non-exchange limit. The rates were fast, and the requisite temperatures were typically much lower than −100 °C. Although the technical challenges of carrying out these reactions were considerable, the rate studies were simple: they measured the relative rates at which each observable form disappears. Fleeting intermediates were not germane.
Scheme 3.
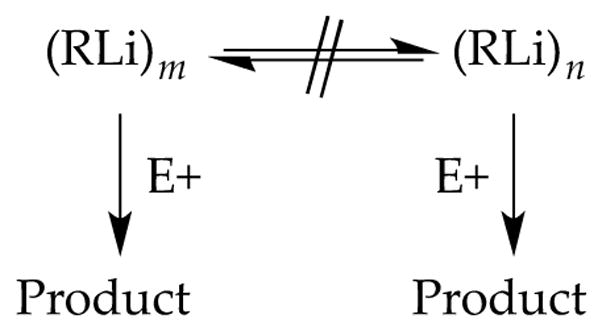
Reactions of aggregates that do not exchange.
Scenario 3: Non-equilibrium aggregate exchange
There is a fateful level of substrate reactivity—a narrow temperature range required to monitor reactions on normal laboratory timescales—at which the barriers to LDA aggregate–aggregate exchanges are comparable to the barriers that fleeting structural forms react with substrates. Imagine that the equilibria in Scheme 1 are not fully established on the timescales of a metalation. In this non-limiting regime, the rate-limiting steps often become poorly defined with an affiliated spike in mechanistic complexity (Figure 1). Moreover, any of the fleeting intermediates could react with substrate via rate-limiting deaggregation, substrate complexation, or proton transfer (Scheme 4). The most viable mechanism for proton transfer could lie behind an insurmountable barrier to deaggregation.
Scheme 4.
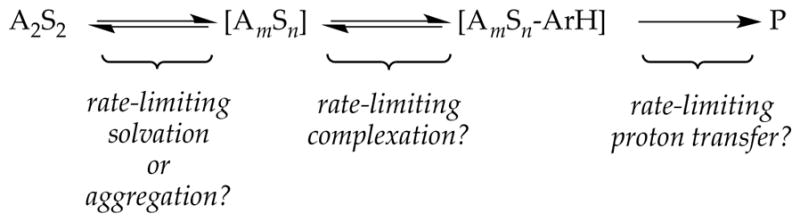
Rate limiting aggregation, complexation or proton transfer.
With an irony that will be lost on few, this fateful twilight zone corresponding to scenario 3 for LDA/THF-mediated metalations is centered on substrates that react on laboratory timescales (half-lives of minutes) at −78 °C. Under this non-limiting regime, rate-limiting deaggregations are commonplace. Traces of LiX—particularly LiCl—catalyze reactions at parts per million levels with marked changes in mechanisms, rates, and rate laws. LDA generated in situ from LiCl-contaminated n-butyllithium can have reactivities that are >100 times that of LiCl-free commercial LDA. Traces of added Et3N-HCl bring commercial LDA to parity with LDA generated in situ. Unlike metalations in scenario 1 in which unreactive LDA–LiX mixed aggregates are autoinhibiting,6 the resulting LiX salts cause autocatalysis under scenario 3. Plots of substrate concentration versus time display unusual curvatures in place of standard first- or second-order decays. Reactions can manifest rate-limiting deaggregations in which, paradoxically, the rates depend on the choice of substrate but not on their concentrations (manifesting linear decays). Simple isotopic substitution can completely change the mechanism and affiliated rate law. Relentlessly shifting rate-limiting steps resulting from seemingly inconsequential changes in reaction conditions, although confounding at the outset, proved pivotal in unlocking insights into the reaction mechanisms and nuances of rate limitation.
1. Methods and Strategies
LDA-mediated reactions under conditions in which observable and fleeting forms are at full equilibrium (Scenario 1) are easily examined using traditional kinetic methods based on the equilibrium approximation with flooding techniques13 or the method of initial rates.14 These strategies were summarized in our 2007 review.6 Non-equilibrium kinetics are more demanding, however. In this section, we provide a tutorial on our methods and strategies as well as some foundational principles of rate limitation that are easily overlooked or misunderstood. Throughout the review, illustrative simulations are used rather than the actual raw data with fits. The mathematics underlying the simulations are archived in supporting information.
1.1. Analytical Tools
A combination of 6Li, 15N, and 19F NMR spectroscopies4,15,16 and in situ IR spectroscopy17 were used to determine the solvation and aggregation states of observable intermediates and monitor reaction rates. Isotopic labeling shows whether a proton transfer is rate limiting but, as our results demonstrate, offers far more than that. The method of initial rates assumes special importance because substrate decays often deviate from first order. Numerical methods are critical owing to pervasive non-limiting behaviors.
The importance of synergies cannot be overstated. Synthetic organic and physical organic chemistries together underpin this review. Classical and numerical kinetics methods are used in tandem to tease apart complex mechanisms. Kinetics and density functional theory (DFT) computational methods18 are mutually supportive: the computational methods offer insights that can elude experimental observations, whereas the rate data constrain the computational methods to address precise questions and comparisons.
1.2. Saturation Kinetics
Plots of initial rates or pseudo-first-order rate constants (kobsd) versus the concentration of a substrate or other reagent can show first-order (or higher-order) dependence at low concentration and independence at high concentration. These so-called saturation kinetics are illustrated in Figure 2. Saturation behavior emerges in two mathematically interchangeable but chemically distinct ways.
Figure 2.
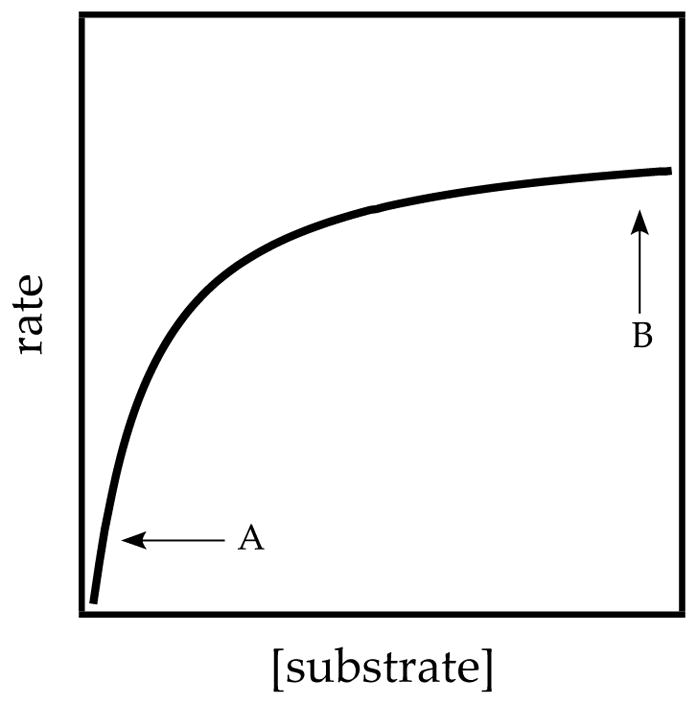
Saturation kinetics. A and B correspond to regions of substrate-concentration-dependent and substrate-concentration-independent regions.
The most prevalent origin of saturation kinetics is akin to that in Michaelis–Menten enzyme kinetics,19 in which the catalyst is uncomplexed by the “substrate” at low substrate concentrations and becomes fully saturated, forming an observable substrate–catalyst complex, at high concentrations (eqs 1 and 2).20
Saturation Kinetics Case 1: Shifting Ground State (Michaelis–Menten Kinetics)
| (1) |
| (2) |
Saturation Kinetics Case 2: Shifting Rate-Limiting Step
| (3) |
| (4) |
An alternative, far less common form of saturation kinetics occurs when the change in substrate concentration is accompanied by a shift in the rate-limiting step (eqs 3 and 4).21 Saturation occurs as the substrate concentration becomes sufficiently high to trap the fleeting intermediate efficiently. Note that cases 1 and 2 are mathematically interchangeable yet mechanistically unrelated. Case 2-type saturation dominates our investigations of non-equilibrium kinetics.
1.3. What Defines a Rate-Limiting Step?
Consider a variation of case 2 using a mechanism for the A2S2-mediated metalation of ArH via a fleeting (high-energy) isomeric form, [A2S2*], to give ArLi (eq 5). The rate law is described by eq 6. To maintain focus on rate limitation, we chose an example that does not require formal deaggregation, additional solvation, or explicit substrate complexation. Rate limitation can be considered from a number of perspectives as follows.
| (5) |
| (6) |
Rate limitation is dictated by barrier heights (Figure 3). Proton transfer is rate limiting when its barrier is high relative to that of deaggregation (Figure 3; red). Conversely, zdeaggregation is rate limiting when the proton transfer barrier is low relative to that of deaggregation (Figure 3; blue).
- The proton transfer in eq 5 can be viewed as being dictated by the fate of fleeting intermediate A2S2* by placing it in the context of the rate law (eq 6). If A2S2* readily returns to starting material and only rarely proceeds to product—if k2[ArH] ≪ k−1—then A2S2–A2S2* equilibrium is fully established, and the relatively infrequent proton transfer limits the rate (see Figure 3; red). The rate law in eq 6 reduces to eq 7, showing first-order dependence on substrate. Loss of ArH versus time follows a simple first-order decay (Figure 4, curve A). By contrast, if the proton transfer is fast relative to reaggregation—if k2[ArH] ≫ k−1—intermediate A2S2* is converted to product each time it forms (Figure 3; blue). The rate law reduces to eq 8 and shows zeroth-order substrate dependence (Figure 4; blue).
(7) (8) The substrate concentration dependence transitioning from first to zeroth order is manifested in plots of substrate concentration versus time. At low substrate concentration, the proton transfer is rate-limiting and manifests a standard exponential decay (Figure 4, curve A). At high substrate concentrations, the zeroth-order substrate dependencies display linear decays (Figure 4, curve B). Moreover, linear decays of ArH are independent of initial concentration (Figure 5 and eq 8). Slight curvatures arise at depleting concentrations of ArH as the proton transfer begins to limit the rate (see Figure 5).
Figure 3.
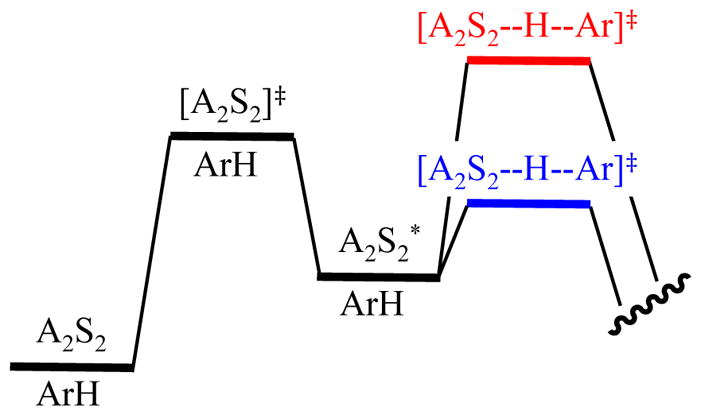
Reaction coordinate diagram for a dimer-based metalation showing rate-limiting proton transfer (red) and rate-limiting deaggregation (blue).
Figure 4.
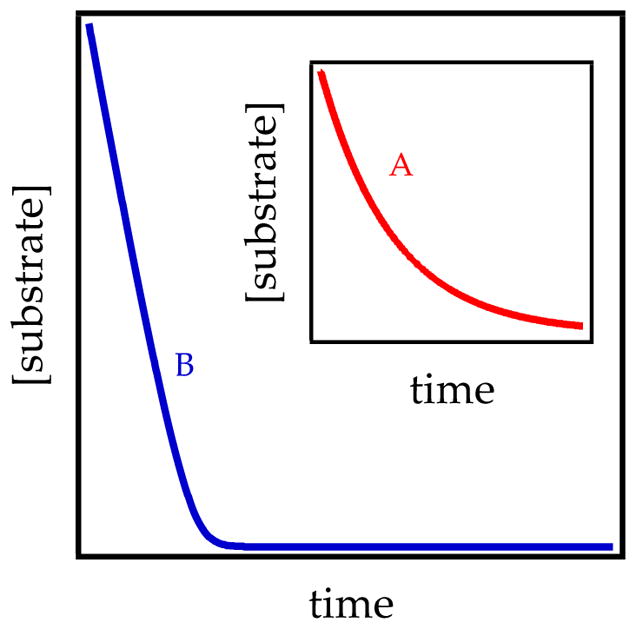
Decays of substrate ArH according to eqs 5 and 6 assuming rate-limiting proton transfer (k2[ArH]/k−1 = 0.1; curve A) and rate-limiting deaggregation (k2[ArH]/k−1 = 10; curve B).
Figure 5.
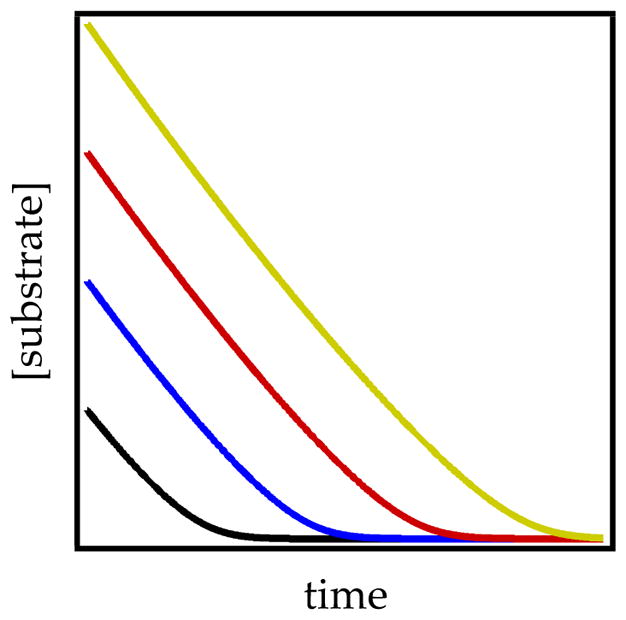
Zeroth-order decays at various initial starting concentrations of ArH showing parallel decays and the onset of rate-limiting proton transfer (curvatures) at low ArH concentration.
There is an awkward non-limiting region in which the barriers for deaggregation and proton transfer are comparable. Fleeting intermediate A2S2* proceeds to product and back to starting material with equal fidelity: k2[ArH] ≈ k−1. This phenomenon occurs in the highly curved (fall-off) region of Figure 2. The rate law in eq 6 does not reduce to a simple limiting form, and the resulting profile resembles an exponential decay but does not fit a first-order function. This non-limiting behavior is prevalent in metalations by LDA/THF at −78 °C.
Throughout the sections below, we cite instances of shifting rate-limiting steps.21,22 Saturation behaviors are central to these observations. In principle, a rate-limiting deaggregation obscures critical post-rate-limiting steps. In practice, many strategies allow us to peer over or beyond the horizon (vide infra).
1.4. Comments on Reaction Coordinate Diagrams
Thermochemical depictions of reaction coordinates such as those in Figure 3 are popular pedagogical tools of introductory chemistry courses. We find them useful to discuss non-equilibrium kinetics as well, but they are fraught with risk. Several basic principles must be adhered to for meaningful discussion.
(1) All energy levels must be fully balanced
Energy levels must share a common empirical formula. The balancing can be left implicit to eliminate clutter but at great peril.
(2) Reaction coordinate diagrams necessarily represent a single snapshot of a dynamic picture
Changes in reaction parameters—concentration, temperature, or substrate—cause the relative energies to change, and energies change continuously as a reaction proceeds. Despite some drawbacks, these reaction variables offer control over the energies. Raising the LDA concentration, for example, lowers the barriers of the more highly aggregated intermediates and transition structures relative to those of the less aggregated forms. Lowering the THF concentration raises the energies of more highly solvated forms relative to those of less solvated forms. Deuteration introduces zero-point energy (ZPE) contributions in all minima as well as in the often overlooked transition states.
(3) Discussion of mechanism is dangerous at the murky interface where prose meets thermochemistry
Bear with us as we try to avoid taking excessive linguistic liberties.
1.5. Multidimensionality of Rate Laws
Much the way reaction coordinate diagrams are slices of a complex picture, rate laws do not reflect a single scenario. The case of saturation kinetics arising from a shifting reaction order in one species (such as the substrate in Section 1.2), for example, is often affiliated with shifting orders in other species. Thus, reaction orders for all other species must be measured at the two limits corresponding to rate-limiting proton transfer and rate-limiting deaggregation. We frequently determine the orders in LDA at different THF concentrations to track THF-concentration-dependent changes in mechanism. In cases in which catalysis is involved (vide infra), detailed rate studies—full rate laws—with and without catalyst are imperative. Non-equilibrium kinetics are so sensitive to changes in conditions that even an isotopic substitution (vide infra) ostensibly used to measure a simple KIE demands an autonomous rate law. Similar to other multidimensional imaging techniques, probing a complex mechanism requires multiple slices through the data.
1.6. Serial versus Parallel Pathways
We often observe instances in which two aggregation events appear to be competing for rate limitation as evidenced by non-integer LDA orders;6,8 competing dimer- and tetramer-based aggregation events akin to those in Section 2.8 are emblematic. A composite LDA order between first and second order implicates two pathways of comparable barriers either in series (Figure 6) or in parallel (Figure 7). Increasing LDA concentration stabilizes the more highly aggregated tetramer-based transition structure relative to the dimer-based transition structure. In the serial case (Figure 6), tetramer stabilization causes the dimer-based barrier to be rate limiting and the rate law to converge on dimer-like dependencies (rate = k[A2S2]1[S]1). By contrast, in the parallel sequence (Figure 7), analogous lowering of the tetramer-based barrier diverts the chemistry through the tetramer-based pathway with an affiliated tetramer-like rate law (rate = k[A2S2]2[S]1).
Figure 6.

Thermochemical picture for two barriers in series. Solvents and LDA needed to balance the stoichiometries have been omitted.
Figure 7.
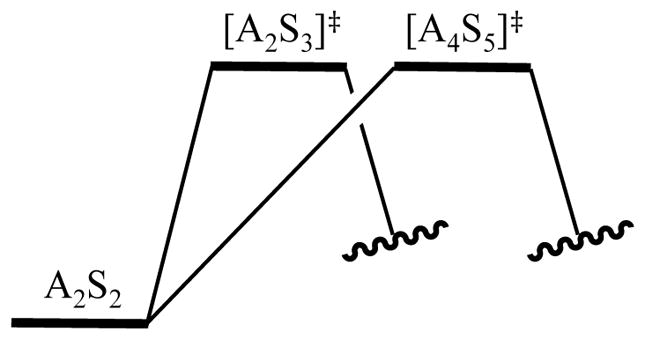
Thermochemical picture for two barriers in parallel. Solvents and LDA to balance the stoichiometries have been omitted.
1.7. Autocatalysis
LDA/THF-mediated metalations at −78 °C under non-equilibrium conditions are markedly autocatalytic: the reactions are accelerated by the products formed.23,24 Autocatalysis has two critical prerequisites: (1) the reaction must be susceptible to catalysis, and (2) the product must be a catalyst. We have documented autocatalysis as well as LDA-mediated metalations that fail to autocatalyze because one of the two prerequisites was not satisfied.8
Autocatalysis is detectable in decays of substrate versus time (Figure 8). Low levels cause a slight straightening (curve B) relative to a first-order decay (curve A). Autocatalysis by ArLi formation during during an ortholithiation, for example, offsets the deceleration owing to the loss of ArH titer. Beware that mild autocatalysis (curve B) is easily confused with superimposed first- and zeroth-order decays (Figure 4). Stronger autocatalysis (curve C) can be equally confusing. For example, in our first detailed study (see Section 2.1), autocatalysis produced nearly perfect linear decays that were not zeroth order.8a We routinely probe for mild autocatalysis using a standard control experiment. At the end of an experiment using excess organolithium reagent, a second aliquot of substrate is added. Autocatalysis is evidenced by acceleration relative to the first aliquot. Pronounced autocatalysis, by contrast, appears as sigmoidal decays (Figure 8, curve D, inset). Even mild autocatalysis affords sigmoidal curvature when superimposed on an otherwise zeroth-order decay.
Figure 8.
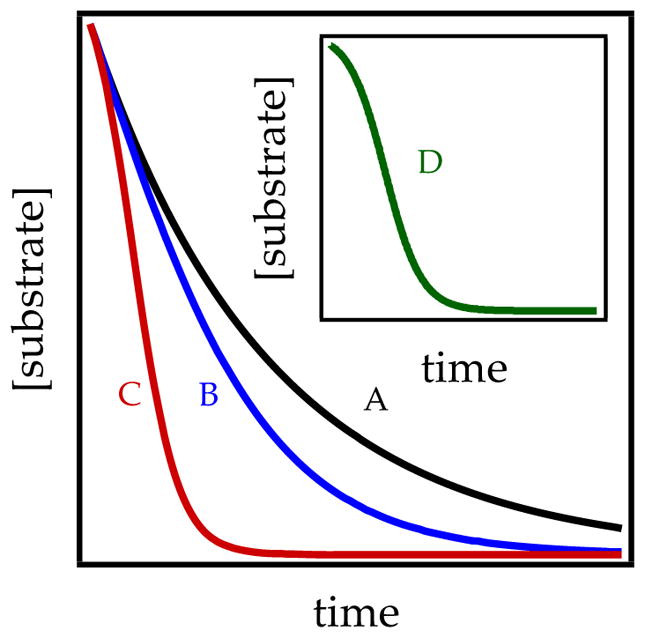
Varying degrees of autocatalysis superimposed on first-order decays: curve A, none; curve B, mild; curve C, medium; curve D, strong.
1.8. Salt Effects and Saturation Kinetics
What processes are the various LiX salts catalyzing? In a word, deaggregation. Several steps in the deaggregation shown in Scheme 1 are susceptible to catalysis, but usually the net effect is to shift the rate-limiting step from LDA deaggregation to proton transfer. Figure 9 illustrates initial rates versus catalyst concentration showing first- and second-order saturation kinetics. (Both have been observed.) It might be tempting to invoke Michaelis–Menten-like behavior in which LDA and LiX form a reactive mixed aggregate that becomes the observable form at saturation, but saturation is attained at low LiX concentration (often <5%) relative to the concentration of LDA.
Figure 9.
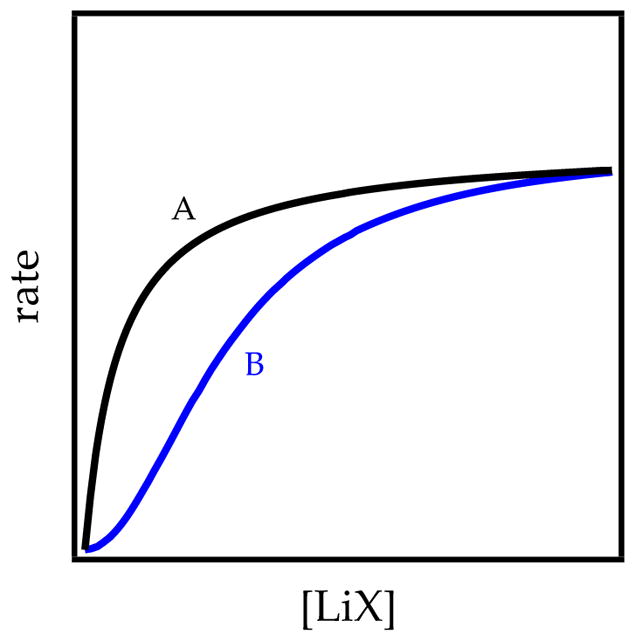
Simulation of catalysis showing first-order (curve A) and second-order (curve B) saturation kinetics.
Catalysis of dimer-to-monomer conversion is the most prevalent salt effect under non-equilibrium conditions (eq 9) and, thus, is used emblematically here. The rate law is described by eq 10. We have overtly excluded the THF dependencies on both the uncatalyzed and catalyzed deaggregation for this illustration. The algebraic complexity in eq 10 stemming from deaggregation and the requisite use of the quadratic equation disappears in the various limits (eqs 11–13).
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
In the absence of catalyst, a rate-limiting deaggregation manifests a first-order dependence on A2S2 owing to an [A2S2]‡ rate-limiting transition structure and a zeroth-order substrate dependence (Figure 5). The rate law reduces to the simplest form (eq 11). Adding low concentrations of LiX causes acceleration reflected by k1+kcat[LiX] while the deaggregation remains rate limiting (eq 12). The mechanistic details of catalysis (including THF and catalyst concentration dependencies) are ascertained by taking a slice of the multidimensional rate law (see Section 1.5), but we bypass them here. At high catalyst concentrations (although <5% in most cases), the pre-equilibrium becomes fully established, and additional catalysis has no effect on the measured rate of metalation (eq 13). The mechanism at saturation includes a rate-limiting proton transfer and is probed by ascertaining the LDA and THF concentration dependencies. One would expect to find no isotope effect in the absence of catalyst (kH/kD = 1.0) and a substantial isotope effect at full catalysis (kH/kD ≫ 1.0). That story proves more complex (Section 1.13.)
Figure 10 underscores additional points. Strong and weak catalysis are represented by curves A and B, respectively. Although a less effective catalyst requires higher loading, the limiting rate at saturation is the same. Fully established aggregate–aggregate equilibration affords rates that are independent of catalyst structure. The commonality of rates shows a commonality in the intermediates. Curve C, by contrast, shows an altogether different metalation rate at full saturation. The catalyst that produces curve C is necessarily catalyzing a deaggregation that differs from those in curves A and B. The rate laws measured at the plateaus reveal the differences.
Figure 10.
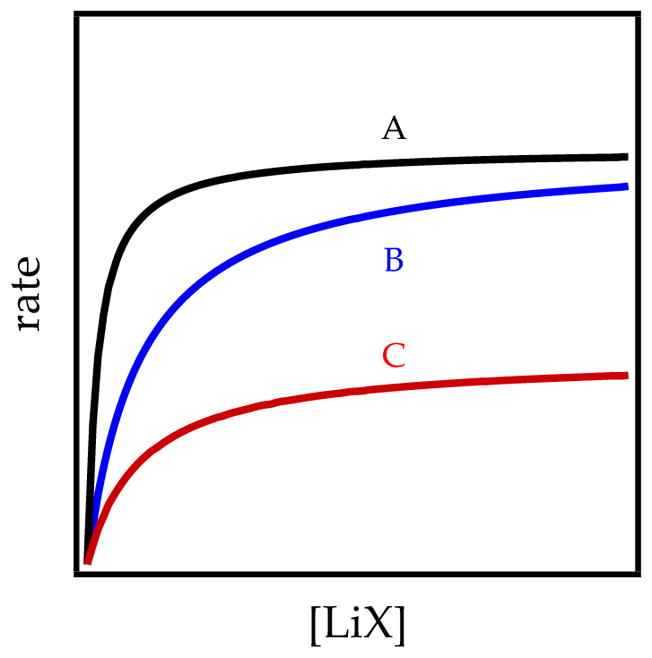
Saturation behavior for LiX catalysts. Curve A is a strong catalyst, curve B is a weak catalyst, and curve C corresponds to catalysis of a different deaggregation step than those of curves A and B.
1.9. Catalysis: Acceleration versus Rate Limitation
LiX catalysts serve two seemingly related roles: accelerating a reaction by catalyzing an otherwise rate-limiting deaggregation and shifting the rate-limiting step from deaggregation to proton transfer. It goes without saying that catalyzing a slow (rate-limiting) deaggregation—(k−1 + kcat[LiX]) in eq 9—accelerates that reaction. However, recall that rate limitation is determined by the fate of the fleeting intermediate (ASm* in eq 9). In the absence of catalyst, monomer proceeds to product with high efficacy—k−1[ASm*] ≪ k2[ArH]—rendering deaggregation rate limiting. By contrast, the LiX catalyst shifts the rate-limiting step to the proton transfer by accelerating the reaggregation of LDA monomer to dimer such that (k−1 + k−cat)[ASm*] ≫ k2[ArH]. In short, catalyzing the forward step—the deaggregation—accelerates the reaction, whereas catalyzing the reverse step—the reaggregation—shifts the rate-limiting step.
1.10. Peering beyond Rate-Limiting Steps
In principle, rate-limiting deaggregation renders all subsequent steps, including the critical proton transfers, invisible to scrutiny. The discussion to this point, however, shows that this is not altogether true. For years, we chose to study sluggish substrates to ensure that the reaction with LDA was slow, and the various aggregated forms were in full equilibrium. In essence, we were shifting the rate-limiting step by attenuating the proton transfer rate. The catalysis described above shows how under non-equilibrium conditions, we can reduce the barrier to deaggregation, revealing the previously concealed proton transfer. (Recall the caveat in Section 1.4 that the barriers visualized in reaction coordinate diagrams are anything but constant.) Changing THF concentration can lower the barrier to any THF-dependent step relative to those that are not dependent. Deuteration alters the relative barriers to metalations and deaggregations in ways that are discussed separately below. Finally, a variety of competitions allow us to probe reactions of substrates with post-rate-limiting fleeting intermediates without lowering or bypassing the obstructing barrier.
1.11. Relative Rate Law
Whereas the rate law provides the stoichiometry of the transition state relative to the reactants, a relative rate law provides the stoichiometries of transition structures relative to one another. For example, the relative proportions of two products might be independent of LDA concentration and linearly dependent on THF concentration, which shows that the two product-determining transition structures differ by a single THF ligand. The relative rate law assumes special importance for documenting the origins of minor impurities or selectivities when the influence of the minor pathway on the rates cannot be measured directly.8d,25
Relative rate laws also provide useful insights about non-equilibrium kinetics in which the key proton transfers of regioselective orthometalations occur in post-rate-limiting steps. Whereas measuring the observable metalation rates versus THF and LDA concentration reveals the stoichiometry of the rate-limiting deaggregation, the dependencies on the product distribution reflect the relative solvation and aggregation states of the competing post-rate-limiting metalations. This notion of relative rate law is similar to the principles underlying competitive and intramolecular isotope effects.
1.12. Isotope Effects: Variants
The most common application of deuterium substitution in rate studies is to confirm a rate-limiting proton transfer,9 but isotope effects are even more powerful for probing complex mechanisms. Their utility in studying LDA-mediated metalations under conditions of shifting rate-limiting steps proved far more central than we imagined. In this section, we explore three types of KIEs that are often erroneously considered interchangeable.9e Section 1.16 considers nuances that we did not fully appreciate at the outset.
(1) Intermolecular Isotope Effects
The most standard isotope effect is to measure rate constants for protonated and deuterated substrates (ArH and ArD) independently (eq 14) to afford a KIE emblematic of rate-limiting proton transfer. The disappearance of substrate over time will follow first-order decays with very different rates. In the event of a rate-limiting deaggregation and post-rate-limiting proton transfer (eq 8), kH/kD will be equal to 1.0. According to the saturation curve in Figure 2, kH/kD ≫ 1.0 at low ArH (ArD) concentrations, and kH/kD = 1.0 at high concentrations. An isotope effect of unity will likely show linear (zeroth order) decays for ArH and ArD that are superimposable. Analogously, under catalyzed conditions (Figure 9), low catalyst loading affords a kH/kD ≈ 1.0, and at high loadings (saturation), kH/kD ≫ 1.0.
| (14) |
(2) Intramolecular Isotope Effects
A mixed isotopologue in which symmetry-equivalent sites are protonated and deuterated is used to measure an intramolecular isotope effect by analyzing the isotopic content of quenched products (eq 15).26 The merit of the intramolecular isotope effect is that regardless of whether the proton transfer is rate limiting or post-rate limiting, the isotopically sensitive selectivity will be manifested by a preference for proton rather than deuterium extraction. Moreover, an intermolecular isotope effect of unity and a large intramolecular isotope effect confirm a post-rate-limiting proton transfer.
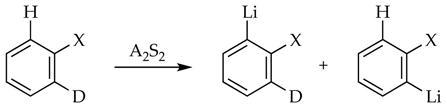 |
(15) |
(3) Competitive Isotope Effects
Isotope effects measured when two substrates compete in a single vessel (eq 16) show similarities to, but are not interchangeable with, intramolecular and intermolecular isotope effects. They seem straightforward because they involve monitoring of the isotopic content of the starting materials and products in quenched products. They also risk misinterpretation, however.
| (16) |
In the event of rate-limiting proton transfer, both ArH and ArD disappear via first-order decays and display large kH/kD values mirroring the intermolecular isotope effect. A rate-limiting deaggregation and post-rate-limiting proton transfer, by contrast, produce what we call biphasic kinetics (Figure 11 and Scheme 5).8c,f,g The fleeting AmSn* intermediate is efficiently and selectively scavenged by ArH and shows the characteristic zeroth-order linear decay discussed in Section 1.3. The induction period for ArD loss occurs because ArD does not appreciably scavenge AmSn* until ArH has been consumed, after which the slopes of ArD and ArH decay are comparable (kH/kD ≈ 1). The curvature arising from the dilution of ArH is often acutely more visible in the decay of the much less efficient trapping by ArD. Deuteration shifts the rate-limiting step.
Figure 11.
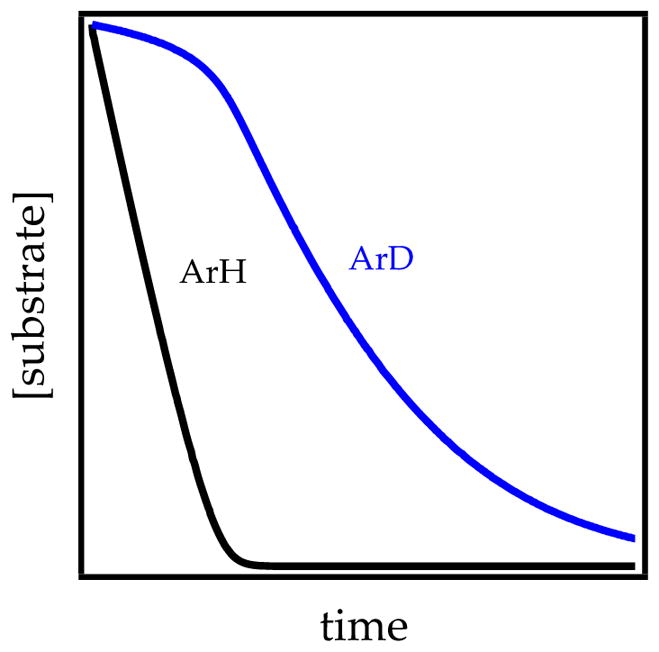
Plot showing preferential metalation of ArH over ArD corresponding to kH/kD = 24.
Scheme 5.
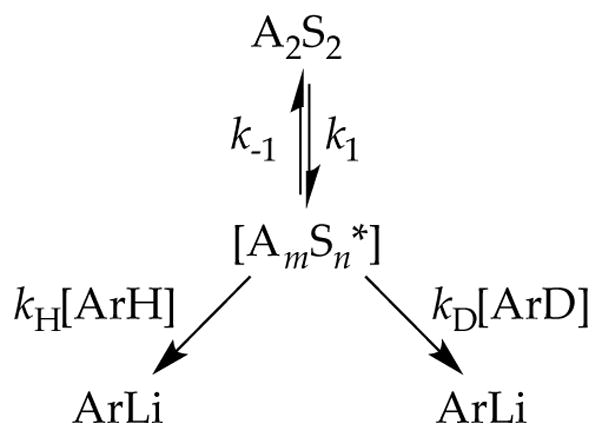
Post-rate-limiting proton transfer leading to biphasic kinetics (Figure 11). Reproduced from ref 8f. Copyright 2013 American Chemical Society.
1.13. Isotope Surrogates
In one case study described below, LDA reacts via a 1,4-addition rather than a proton transfer (see Section 2.3), and in this and many other instances, a detailed mechanistic study lacks the probative power of primary deuterium isotope effects (Chart 1). One might be tempted to turn to secondary deuterium isotope or heavy-atom isotope effect9 strategies similar to those of Singleton and co-workers,27 but the appeal of these approaches is attenuated (for us at least) by the complexity of the system. Although not for purists, an alternate strategy that is seriously underutilized is the use of surrogates.
Imagine varying the size of the R groups in Chart 1 enough to perturb reactivity but insufficiently to impart mechanistic change. In the 1,4-addition example below, we used n-alkyl and cyclohexyl and, by coincidence, imposed a relative reactivity of 7:1 (the value often associated with primary KIEs). The analog of the intermolecular isotope effect showed superimposable zeroth-order decays of the two substrates consistent with a rate-limiting deaggregation. The analog of the competitive isotope effect—monitoring the loss of the two concurrently—revealed relative rates of 7 along with biphasic kinetics (as in Figure 11), which are both consistent with a structurally sensitive post-rate-limiting addition. How would one confirm the presumed absence of a deep-seated mechanistic change with the change in substituent? The relative rate law (see Section 1.11) would largely put that issue to rest.
1.14. Role of Substrate Complexation
Along the reaction coordinate, the substrate probably complexes to a fleeting intermediate, which is followed by proton transfer (eq 17). The mechanism has several possibilities, each affording a different limiting scenario as follows.
| (17) |
The proton transfer corresponding to k3 is rate limiting (k3 ≪ k−2). This reaction is a standard metalation with aggregates (at least those shown) at full equilibrium as described in our previous review.6
The second step corresponding to substrate complexation is rate limiting with a subsequent rapid proton transfer. This sequence would manifest all the trappings of a normal metalation including a first-order dependence on substrate, but no intermolecular isotope effect would occur (kH/kD = 1.0). As described, there would be a large intramolecular isotope effect but no competitive isotope effect because the product distribution is dictated by an isotopically insensitive complexation step. Biphasic kinetics would not be observed.
In a third scenario in which the substrate is involved (even assists), a rate-limiting deaggregation followed by post-rate-limiting metalation would be difficult to distinguish from scenario ii. If, unlike in scenario ii, substrate exchange is fast before proton transfer, a large competitive isotope effect in conjunction with biphasic kinetics is observed. This scenario was observed during fluoropyridine metalations (see Section 2.6).
We are reminded that the three types of KIEs offer powerful probes of rate limitation as well as post-rate-limiting proton transfers. There is great risk in presuming that they are equivalent.
1.15. Isotope Effects: Roles of ZPE
The simplest (two-body) analysis of primary deuterium isotope effects shows that the rate differential emanates from the ZPE of ArD in the ground state, which is retained in all steps preceding the proton transfer but disappears in the transition state for proton transfer (Figure 12).9 We use [A2S2--H--Ar]‡ to keep the discussion stoichiometrically simple. It is widely held that KIEs maximize at a kH/kD of approximately 7 at 25 °C and at a kH/kD of up to 20 if adjusted to −78 °C. Notably, a KIE is implicitly an inherent property of the substrate and independent of the mechanism of proton abstraction. Additional vibrations coupled to the vibration becoming the reaction coordinate are invoked to account for mechanism-dependent KIEs.
Figure 12.

Two-body model showing the role of ZPE as a determinant of a primary KIE.
How does deuteration shift the rate-limiting step? It is tempting to assume that the barrier to transfer is higher, but the two-body model says that cannot be. By including a fleeting intermediate—A2S2* to maintain simplicity—we see that the ZPE retained in the deaggregation transition state causes the shift (Figure 13).
Figure 13.
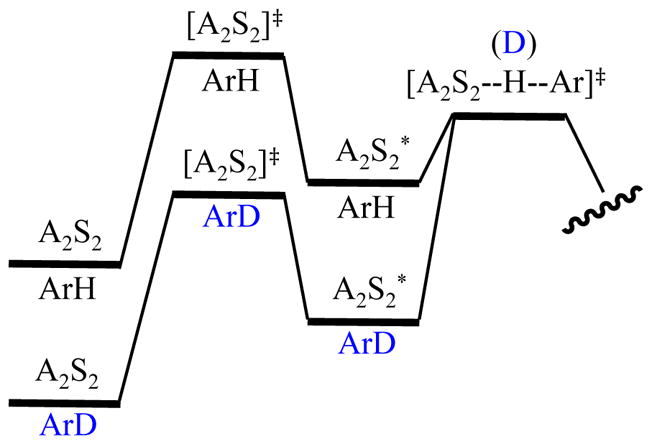
Contributions of isotopic substitution and ZPE to an intermolecular KIE and rate-limiting step using ArH and
 measured independently.
measured independently.
Consider the two additional isotope effects from the thermochemical perspective. Figure 14 shows that the intramolecular isotope effect has no differential ZPE at any point leading up to the proton transfer. The origin of kH/kD is the retention of stabilizing ZPE associated with the C–D bond that promotes the abstraction of the proton. Note that, at least in theory, proton and deuterium transfer could have different rate-limiting steps (deaggregation in the former and deuterium transfer in the latter.) The competitive isotope effect (Figure 15) is similar in that ZPE retained in the rate-limiting transition state dictates the relative rates and the step that is rate limiting. The relative roles of ground-state and transition-state ZPEs are easily overlooked.
Figure 14.
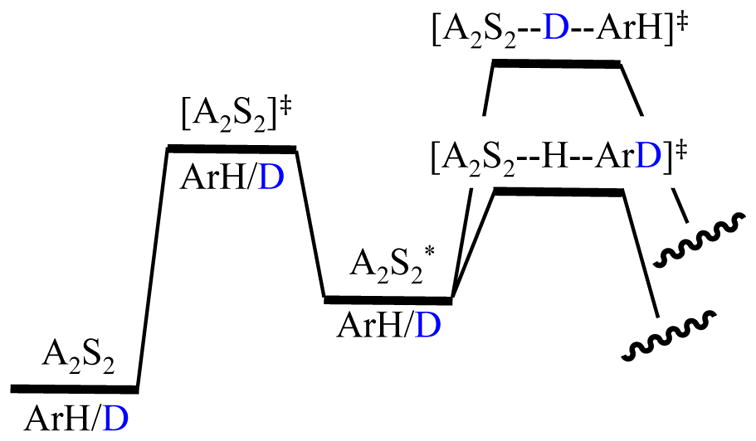
Contributions of isotopic substitution and ZPE to an intramolecular KIE on a monodeuterated substrate denoted
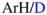 .
.
Figure 15.
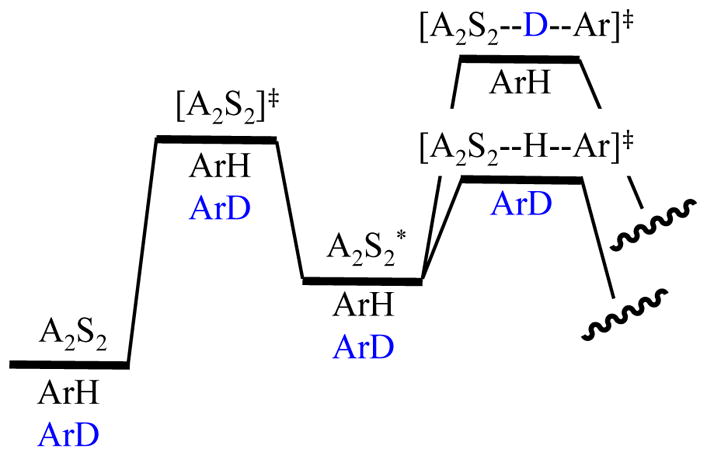
Contributions of isotopic substitution and ZPE to a competitive KIE using a mixture of ArH and
 . All ground and transition states contain all three components.
. All ground and transition states contain all three components.
1.16. Isotope Effects: Role of Tunneling
Organolithium-based metalations can manifest KIEs that exceed 50 for a variety of bases and conditions.8,28 A number of instances emerge in the LDA-mediated ortholithiations described in Section 2. Their magnitudes and considerable mechanism-dependent variations influence rate limitation markedly. To explain these isotope effects, we join the ranks of those who have invoked tunneling.9 We have little interest in discussing the origins of this predilection beyond noting that isotopically sensitive tunneling in the transition state favoring proton transfer (Figure 16) would work in concert with ZPE in a multiplicative relationship in the ground states to produce large KIEs.
Figure 16.
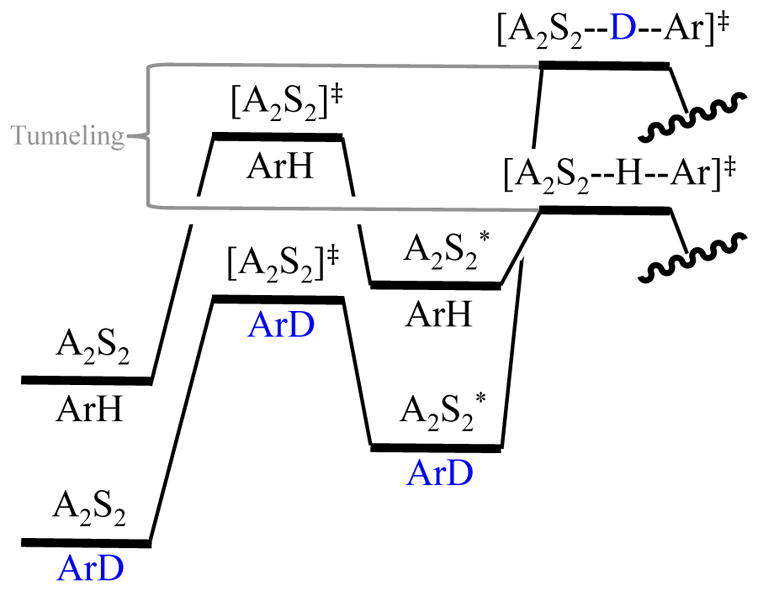
ZPE and tunneling as determinants of an intermolecular KIE and rate-limiting step.
2. Case Studies
This section describes studies showing how the rates of LDA aggregate exchanges influence reactivity and selectivity under non-equilibrium conditions. The studies are largely chronological, capturing the evolution of our understanding, and are placed in the context of the tutorial in Section 1 without re-adjudicating the cases.
We first detected strange rate behavior during the detailed rate studies of the LDA/THF-mediated lithiations of 16 imines.29 The most reactive imine—that requiring dry ice–acetone bath at −78 °C to monitor the rates—showed distorted decays in the form of an unusual lack of curvature within the first several half-lives (Figure 8). We noted it and ignored it. The ortholithiation of carbamates forced an attitude correction, which is where the story begins.
2.1. Arylcarbamate Lithiations
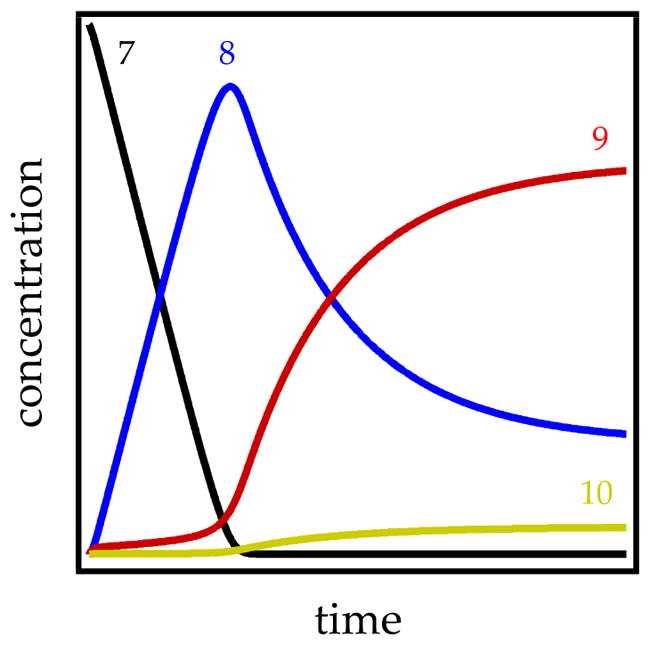
The metalation of carbamate 7 by LDA/THF at −78 °C under second-order conditions (1:1 ArH to base) followed an apparent first-order decay to the exclusion of observable mixed aggregates (eq 18).10a We appeared to have discovered the simplest organolithium reaction to date, but it should have followed a second-order decay. Pseudo-first-order conditions or any conditions with a modest excess of LDA paint an altogether different picture (Figure 17) in which linear loss of starting material and the formation of ArLi product is followed by the delayed appearance of mixed aggregates. The final mechanistic model is summarized in Scheme 6.
Figure 17.
Simulated plots of concentration versus time for the reaction of 7 (black trace) with lithium diisopropylamide in tetrahydrofuran at −78 °C. The functions derive from a mathematical model based on Scheme 6.
Scheme 6.
Mechanism of carbamate ortholithiation. Reproduced from ref 8a. Copyright 2008 American Chemical Society.
 |
(18) |
The decays proved paradoxical in that the linearity suggested a zeroth-order dependence on substrate (see Section 1.3), but the slopes were concentration-dependent (Figure 18) rather than parallel (Figure 5), which suggested an approximate first-order dependence. Changing the THF concentration or inserting a deuterium afforded sigmoidal behavior showing that autocatalysis was at play (see Section 1.7). The linearity stemmed from a remarkable coincidence in which an upwardly curving decay was precisely offset by downward curvature imparted by autocatalysis.
Figure 18.
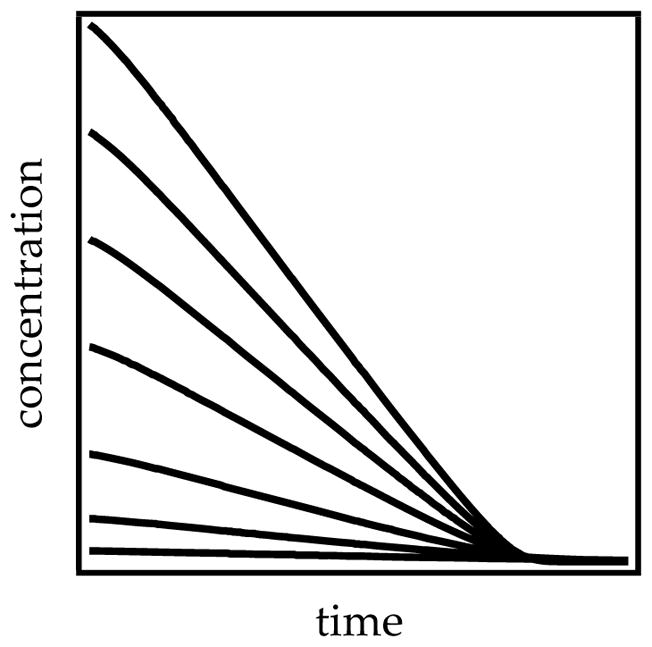
Simulations of plots showing concentration versus time for various initial concentrations of carbamate 7. The original paper simply displayed independent linear fits.8a
The mechanistic hypothesis in Scheme 6 underscores a number of oddities. An LDA-dimer-based metalation (step 1) affords cyclic mixed dimer 9 (step 1) and low concentrations (3%) of mixed dimer 10. However, LDA–ArLi mixed aggregates 9 and 10 are consumed rapidly by substrate and therefore persist only after carbamate 7 is completely consumed. Moreover, the 9–10 equilibrium (step 2) is not fully established on the timescale of the metalation (step 3); minor isomer 10 is far more reactive and can be selectively depleted with an aliquot of 7. Autocatalysis stemmed from the conversion of LDA dimer 1 to mixed dimers (step 4) via a mixed-trimer-based transition structure. The mathematical model based on Scheme 6 was effective at fitting data over a range of conditions. Moreover, the model was not “sloppy” (subject to large variations); many plausible models failed to fit the data.
The overarching themes of this first study are that aggregates are not rapidly (fully) equilibrating in THF at −78 °C on the laboratory timescales of the metalations, and catalysis by LiX is significant. We noted with some prescience, however, that the model was “vulnerable to revision.” Indeed, a small isotope effect within the range expected for a primary isotope effect was reinvestigated in the context of a subsequent study8d and shown to be a fraction of a much larger KIE because proton transfer was only partially rate limiting. Deuteration to measure kH/kD was, unbeknownst to us at the time, imparting fundamental mechanistic changes. Only in retrospect did we realize that the linear decays attributed to autocatalysis superimposed on an exponential decay also include contributions from a true zeroth-order term. We also noted, “it almost goes without saying that an autocatalytic organolithium reaction necessarily involves highly reactive mixed aggregates.” Although technically true, the mixed aggregates do not necessarily mediate proton transfer.23 Such retrospective adjustments to the models and experimental reinvestigations became the norm: each case study offered a more nuanced view and often prompted reevaluation of preceding work.
2.2. Ortholithiations: A Survey
As multiple investigators within our laboratory began exploiting a newfound confidence in −78 °C baths, strange rate behaviors began emerging, paradoxical ones at that. We had discovered during the carbamate lithiations that traces of LiCl markedly influence rates. A survey of a dozen arenes found that metalations of many, but not all, arenes are autocatalyzed and highly susceptible to LiCl catalysis.8b With LiCl catalysis, all metalations showed standard pseudo-first- or second-order decays. Subsequent studies showing catalysis by as little as 100 ppm LiCl eventually showed that multiply recrystallized LDA containing <0.02% LiCl was not pure enough,8b prompting us to modify a literature procedure to generate LiCl-free LDA.8c
On a practical level, rumors that commercially available LDA is inferior to LDA prepared from n-butyllithium were traced to the absence of LiCl in commercial LDA, which ironically is almost indistinguishable from analytically pure LDA. Deaggregation-limited lithiations using commercial LDA are markedly accelerated by generating traces of LiCl in situ (eq 19).31
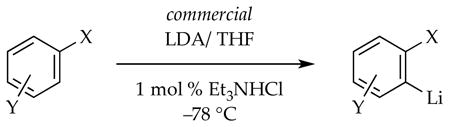 |
(19) |
The window of substrate reactivity in which the anomalies clustered was confusing at the time. Highly reactive and notably unreactive substrates were insensitive to catalysis, prompting us to create the progenitor to Figure 1. A half dozen other LiX salts accelerate ortholithiations from 2-fold to 300-fold. What we did not know at the time was that the salts do not necessarily catalyze the same process (vide infra).
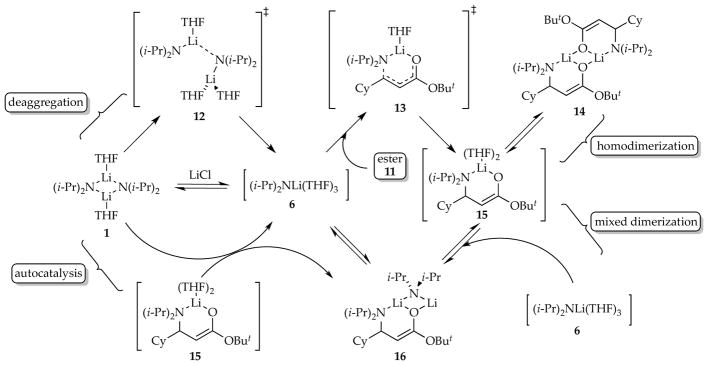
2.3. Conjugate Additions
As part of an attempt to study γ-deprotonations of unsaturated esters, we achieved clean 1,4-addition (eq 20)8c akin to that observed by Schlessinger and co-workers32 and exploited its synthetic potential for other lithium amides.33 The conjugate addition offered one of the more interesting probes into the non-equilibrium kinetics of LDA and confirmed that the effects transcend proton transfer.
 |
(20) |
Monitoring the 1,4-addition under pseudo-first-order conditions revealed new and unusual curvatures—Figure 19 is emblematic but only one of a multitude of flavors—that led to the mechanism shown in Scheme 7. The time dependencies shown in Figure 19 include a number of striking features: (1) the linear loss of starting material superficially akin to that noted in carbamate metalations proved to be true zeroth-order decay (see Section 1.3); (2) homodimeric enolate 14 overshoots its equilibrium population, reaching an apex at the point that starting ester 11 is consumed; (3) mixed dimer 16 formation appears to decelerated and then accelerate abruptly at that same point, eventually attaining an equilibrium population; and (4) the absence of an induction period shows that mixed dimer 16 is not uniquely the precursor to homodimer 14.
Figure 19.

Simulated time-dependent concentrations of ester 11, lithium diisopropylamide dimer 1, enolate homodimer 14, and mixed dimer 16. The functions are from the model described in Scheme 7.
Scheme 7.
Mechanism of 1,4-addition. Reproduced from ref 8c. Copyright 2010 American Chemical Society.
Rate and computational studies filled in the details in Scheme 7 and afforded the final model that fit multiple and highly variable time-dependent behaviors akin to those in Figure 19. The zeroth order in ester 11 was traced to a trisolvated-dimer-based rate-limiting deaggregation; 12 is one of several possibilities. Enolate monomer 15, formed via monosolvated-monomer-based transition structure 13, reacts with one of three species: (1) a second equivalent of 15 to form homodimer 14, (2) LDA monomer 6 to form mixed dimer 16, or (3) LDA dimer 1 to form mixed dimer 16 and regenerate LDA monomer 6. This third process is the source of low but detectable levels of autocatalysis. Owing to slow aggregate exchange and the rapid consumption of monomer 6, many of the species in Scheme 8 are not in fully established equilibria until ester 11 is consumed. A 100-fold acceleration by LiCl was traced to the facile equilibration of dimer 1 with highly reactive monomer 6, shifting the rate-limiting step to 1,4-addition rather than deaggregation and greatly simplifying the reaction coordinate.
Scheme 8.
Mechanism of carbamate ortholithiation. Reproduced from ref 8d. Copyright 2011 American Chemical Society.
The nature of catalyzed deaggregation unfolded slowly and had many subtleties, as described in Section 2.7. As noted in Section 1.7, autocatalysis has two immutable requirements: (1) the reaction must be susceptible to catalysis, and (2) the product must be a viable catalyst. In this case, enolate monomer 15 rather than, for example, dimer 14 appears to be the catalyst, but its concentrations remain too low to be highly autocatalytic. Homodimer 14 reenters the cycle via mixed dimer 16 but also quite slowly. Notably, the scenario in which LDA dimer (A2) is converted sequentially to mixed dimer (AX) and enolate homodimer (X2) is grossly oversimplified:
Also, whereas mixed dimer 16 reacts demonstrably faster than LDA homodimer 1, 16 does not appear to react directly with ester 11; it serves as a kinetically facile source of LDA monomer. This may have been the case for the LiCl mixed aggregates in the carbamate studies described in Section 2.1
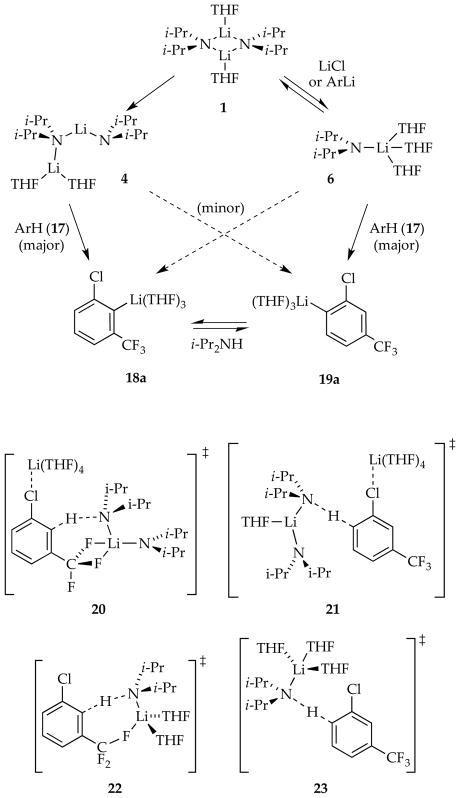
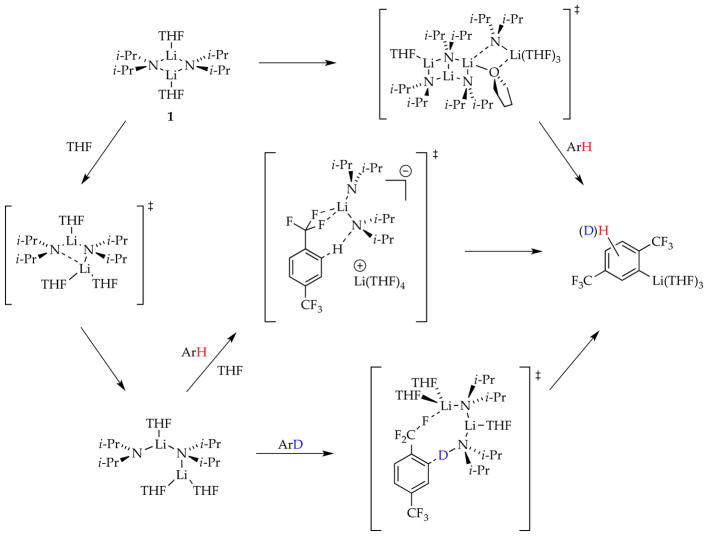
2.4. Ortholithiation of 1-Chloro-3-(trifluoromethyl)benzene
Another generic ortholithiation first reported by Schlosser (eq 21)34 manifests substrate-independent rates, shifting rate-limiting steps, autocatalysis, and LiCl catalysis—key hallmarks of a reaction under the auspices of rate-limiting aggregation events.8d
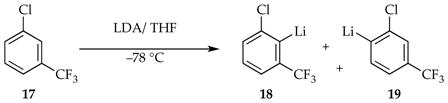 |
(21) |
The results from rate studies are summarized in Scheme 8. In the uncatalyzed lithiations, rate-limiting deaggregation occurs via an [A2S2]‡-based rate-limiting deaggregation rather than the [A2S3]‡ variant observed for the 1,4-additions. This reaction can only occur if the post-rate-limiting reaction for the ortholithiation and 1,4-addition occur from different intermediates that are not at equilibrium. Shifting rate-limiting steps by changing concentrations and using deuterated isotopologues with large and variable isotope effects (kH/kD = 30–60) showed that the dimer-based rate-limiting deaggregation event is followed by post-rate-limiting dimer-based lithiations differing by one THF ligand (suggested by DFT computations to be 20 and 21).
ArLi-derived autocatalysis or the markedly more efficient LiCl catalysis diverts the reaction through reversibly formed fleeting monomer 6 and monomer-based transition structures 22 and 23, thereby affording the opposite regioselectivity favoring 19a. The catalyst-independent regioselectivity implicates a common intermediate. It is ironic and amusing that aryllithium 18a is the major isomer of the dimer-based metalation and a 6-fold more effective autocatalyst than 19a, yet 18a then promotes the formation of 19a.
A complicating isomerization of 18a and 19a is superimposed on the non-equilibrium and equilibrium kinetics.35 The isomerization is mediated by diisopropylamine via LDA monomers as expected from the principle of microscopic reversibility.36 The conclusion section describes whimsical and contrasting views of the chemistry through the lenses of mechanistic organolithium and synthetic organic chemistry.
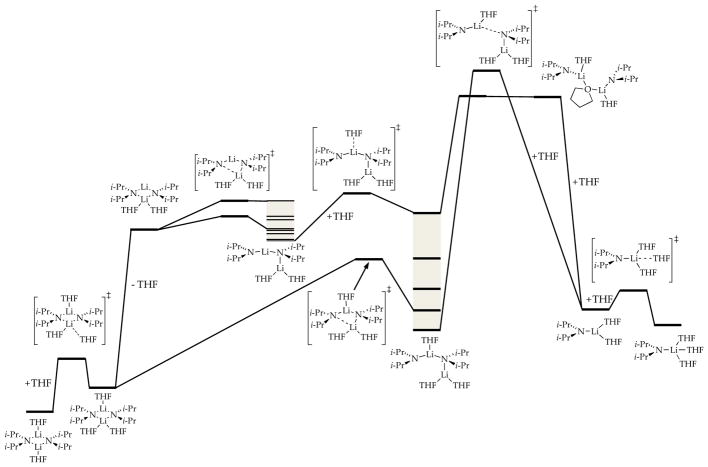
2.5. LDA Deaggregation: A Computational Study
The growing number of rate-limiting solvation or aggregation steps dictating metalation rates and selectivities prompted a detailed computational study of the conversion of LDA dimer 1 to monomer shown in Scheme 1.8e Figure 20 is the expanded version of Scheme 1 but with transition structures as well as ensembles of conformational isomers (shaded in gray) arising from rotations about the isopropyl groups. (Note that the rigorous equation balancing discussed in Section 1.4 is omitted to minimize clutter.) Of special note, the barriers crudely approximate a monotonic rise with the final fragmentation to monomers corresponding to the highest barrier. The shaded conformational ensembles spanning a broad energy range are entered and exited through “portals” via various conformers showing substantially different energies. We also introduced the notion that bridging THF ligands (24 and 25) may be important motifs in critical fragmentation steps (eq 22).37 To the best of our knowledge, this detailed analysis is the first for an organolithium deaggregation. It might have benefitted from the algorithmic methods for searching complex surfaces developed recently by Zimmerman and co-workers.38
Figure 20.
DFT-calculated mechanisms for the deaggregation of lithium diisopropylamide dimer to monomer. The shaded areas correspond to ensembles of discrete conformers. Reproduced from ref 8e. Copyright 2011 American Chemical Society.
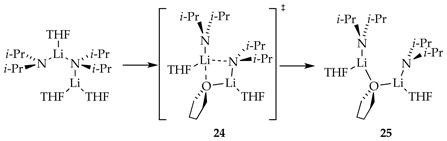 |
(22) |
The “washboard”-like surface in Figure 20 shows some analogy with examples in enzymology in which barriers of nearly equal energy are legion.39 With unreactive substrates in which all forms of LDA are at equilibrium (Figure 1, Scenario 1), all intermediates are accessible. Only a couple—often only one—dominate the reaction coordinate. However, if substrates react rapidly with fleeting intermediates in post-rate-limiting steps—if they react via barriers lower than those corresponding to aggregate–aggregate exchanges—fundamentally different mechanisms are separated by subtle factors.
Recall that during the metalations of 17, the monomer-based pathway made possible through catalysis was far more efficient than the dimer-based metalations dominating in the absence of catalysis. Even when deuteration causes dimer-based lithiations to involve rate-limiting proton transfer, more efficient monomer-based metalations are precluded by a barrier for final cleavage of dimer to monomer that is simply too high. In principle, even a conformational barrier could preclude access to an intermediate that might offer a more viable path for metalation. We do not take the energies in Figure 20 seriously, but exploring the process markedly shaped our thinking. Unbeknownst to us at the time, restricting our focus to only dimeric intermediates en route to monomers was an error (vide infra).
2.6. Ortholithiation of 2-Fluoropyridines
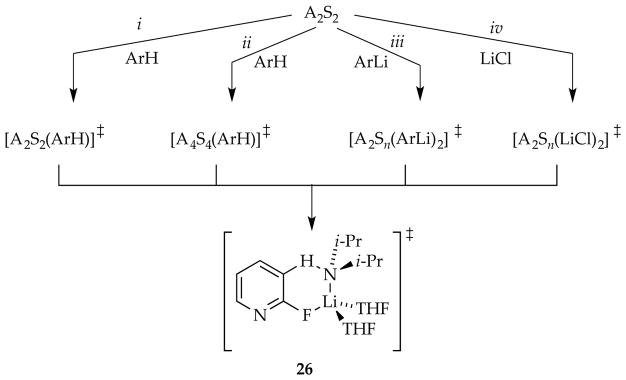
Lithiations of 2-fluoropyridines (eq 23)40,41 proved to be among the most challenging within the series because they revealed all of the trappings of non-equilibrium kinetics—autocatalysis, LiCl catalysis, rate-limiting and partially rate-limiting deaggregations (Scheme 9), strange time-dependent decays of substrates, and biphasic kinetics in the competitive KIE (see Section 1.12). It also included some subtleties that would not be understood until subsequent studies were completed.8g,h
Scheme 9.
Mechanism of 2-fluoropyridine ortholithiation. Reproduced from ref 8f. Copyright 2013 American Chemical Society.
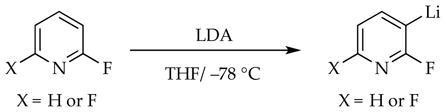 |
(23) |
Substrate-dependent rates accompanied by post-rate-limiting proton transfer (Scheme 9, path i) attest to either rate-limiting complexation or pyridine-assisted deaggregation (see Section 1.14). Moreover, the growing awareness that each substrate in the case studies offers unique probes of different portions of a very complex deaggregation surface was reinforced by evidence of a high-order dependence on LDA implicating a tetramer-based aggregation event (Scheme 9, path ii). The role of LDA tetramers resurfaces and is fleshed out in Section 2.9, augmented by additional experimental support. Autocatalysis by ArLi and catalysis by LiCl were traced to A2X2 mixed-tetramer-based mechanisms (paths iii and iv), which we discuss in the next section. Under full LiCl catalysis—at full saturation as shown in Figure 9 (see Section 1.8)—the metalation proceeds via disolvated-monomer-based transition structure 26, which is strongly supported computationally.
We had missed a critical part of the story. Previous evidence showed that autocatalysis by ArLi and catalysis by LiCl share common monomer-based intermediates. Pyridine lithiations offered evidence that the two salts catalyze different pathways (see Figure 10), but we did not fully understand the implications until we undertook studies of 1,4-difluorobenzene lithiations (vide infra).8g A discussion of ArLi-autocatalyzed and LiCl-catalyzed deaggregation proceeding via mixed tetramers segues to the next section describing our accumulated thoughts on the mechanism of catalysis.
2.7. Mechanism of Catalyzed Deaggregation
Our understanding of catalyzed deaggregation was assembled piecemeal and is presented as a single picture in this section. Rate studies were used to ascertain the stoichiometry of the rate-limiting transition structures for LiCl- and ArLi-catalyzed metalations. The mechanisms appear to be salt- and substrate-dependent. In some instances, a first-order dependence on LiX implicates an [A2X]‡ mixed trimer stoichiometry, whereas in others, an [A2X2]‡ mixed tetramer is suggested. The saturation kinetics discussed in Section 1.8 are the norm. Given assignments of ArLi as trisolvated monomers and a more limited understanding of LiCl structure, even solvation numbers were assigned, albeit tentatively. We consider two basic types of mechanisms for catalyzed deaggregation as follows.
Triple-ion-like species such as 27, with chloride playing a role as a highly dipolar ligand (Scheme 10), carry some appeal. We may have detected such a chloride adduct of lithium 2,2,6,6-tetramethylpiperidide years ago.42 A second-order dependence on LiCl suggested a complex gegenion, maybe a cationic triple ion.43 The bridging THF in computationally viable 28 is a motif that we find highly appealing as central to the final aggregate scission.
An alternative and potentially more general model involves intermediate three- and four-rung ladders (Scheme 11).44 This laddering could be considered a form of associative substitution. Whereas dissociating two high-energy monomers from a dimer carries an inherently high thermochemical penalty, dissociating a single monomer from the end of ladder 29 or 32 may be less costly.45 Alternatively, the facile dissociation of two mixed dimers (31) from ladder 30 also seems credible. This laddering model was examined computationally on several occasions.8g,h We return to it in the context of tetramer-based LDA chemistry.
Scheme 10.
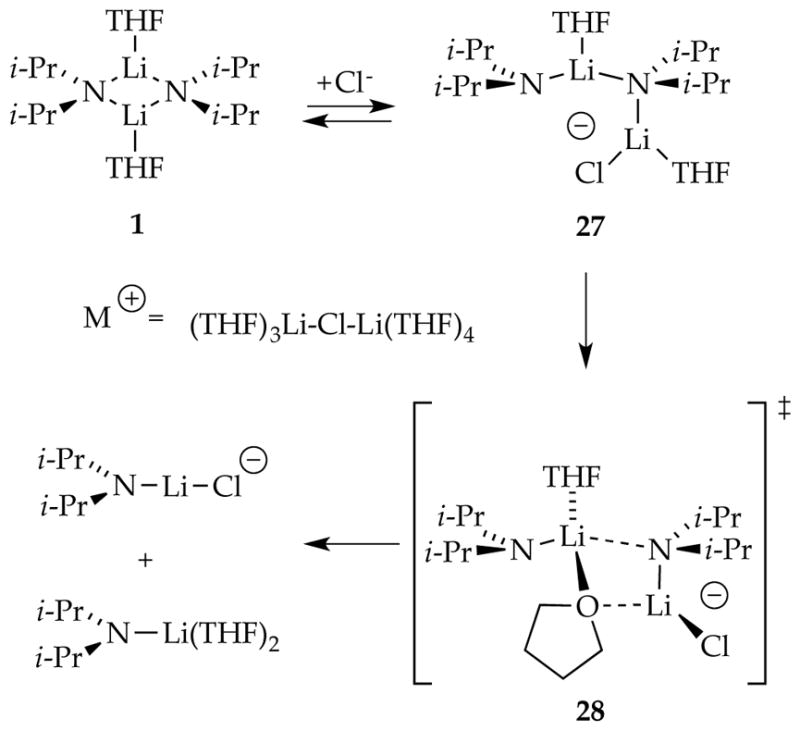
Lithium chloride-catalyzed LDA deaggregation via triple ions. Reproduced from ref 8f. Copyright 2013 American Chemical Society.
Scheme 11.
Lithium chloride-catalyzed LDA deaggregation via ladders. Reproduced from ref 8f. Copyright 2013 American Chemical Society.
2.8. Ortholithiation of 1,4-Difluorobenzene
The ortholithiation of 1,4-difluorobenzene (eq 24)46 underscored the ease with which rate-limiting steps can shift.8g Isotope effects played a prominent role in this process (see Sections 1.15 and 1.16). We also exploited reaction coordinate diagrams (Figure 21) to describe the various experimentally detectable barriers. Recall, however, that such diagrams are riddled with intellectual traps (see Section 1.4) in which any change in reaction conditions, including changes with percent conversion, alters the diagram. These diagrams are living, breathing depictions in which the version shown represents merely a snapshot. The implicit balancing of equilibria are omitted to minimize clutter, again placing the model at risk for misinterpretation.
Figure 21.
Snapshot of an experimentally determined reaction coordinate diagram for the metalation of 1,4-difluorobenzene (eq 24). Reproduced from ref 8g. Copyright 2014 American Chemical Society.
 |
(28) |
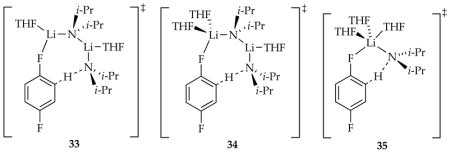
In the uncatalyzed variant, the previously detected rate-limiting deaggregation via disolvated dimer, [A2S2]‡, dominates. Autocatalysis by ArLi-catalyzed partial deaggregation allowed us to peer beyond this first barrier to observe a different rate-limiting aggregation event via a tetrasolvated tetramer, [A4S4]‡. The deuterated substrate in conjunction with large isotopic sensitivities in the transition states (see Section 1.16) revealed rate-limiting deuterium transfer via a combination of tri- and tetrasolvated dimers, [A2S2(ArD)]‡ and [A2S3(ArD)]‡, which guided by DFT computations, are depicted as 33 and 34, respectively. Lithium chloride, by contrast, catalyzes the deaggregation to monomer, affording rate-limiting monomer-based transition structure 35. In this study, a dimer-based proton transfer is observed because the more efficient monomer-based mechanism is unavailable in the absence of catalyst.
2.9. LDA Deaggregation Revisited: Role of Tetramers
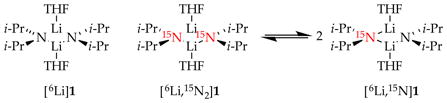
Dependencies of LDA significantly exceeding unity attest to the presence of tetramer-based rate-limiting steps. We must confess to having no idea that this scenario was even possible at the outset. After 30 years of studying the chemistry of LDA, we finally determined the rates and mechanisms of LDA subunit exchange by (1) analyzing the line shape of the coalescence of the 6Li triplet of [6Li,15N]LDA as a function of concentration, and (2) monitoring the rate at which [6Li]LDA and [6Li,15N]LDA form the mixed isotopologue on laboratory timescales (eq 25).8g In both instances, the data support a combination of dimer-to-monomer dissociative exchange (see Section 2.5 and eq 26) and dimer-to-tetramer associative exchange (eq 27). We offer the ladder-based pathway illustrated in Scheme 12 in which we have taken a few simplifying liberties. Computational support was challenging owing to the severe steric demands of the ladders that often subvert the DFT method, but we obtained a computationally viable sequence that may suffer from unnecessary complexity.8g
Scheme 12.
LDA deaggregation via tetrameric ladders. Reproduced from ref 8f. Copyright 2013 American Chemical Society.
 |
(25) |
| (26) |
| (27) |
The overall exchange rate showing half-lives of minutes at −78 °C was much slower than previously believed but was clearly predicted from the non-equilibrium conditions. The tetramer-based subunit exchange had a number of notable features. Associating two dimers to form tetrameric ladder 36 avoids the thermochemically challenging problem of generating two high-energy monomers via a single transition structure.47 A ladder fragment such as 37 can be viewed as a leaving group as well as the source of a second monomer. Moreover, the principle of microscopic reversibility36 suggests that the process in reverse—the aggregation of monomers to form dimers—proceeds via monomer–monomer self-association and the far less obvious sequential association of two monomers with LDA dimer 1 to form four-rung ladders followed by the dissociation to 2 equiv of 1. Last, we showed that, as expected, LiX salts such as LiCl accelerate the subunit exchange consistent with their influence on deaggregation-limited metalation rates.
2.10. Ortholithiation of 1,4-bis(Trifluoromethyl)benzene
Studies of the metalation in eq 2834 showed features similar to those of 1,4-difluorobenzene described in Section 2.8.8h
 |
(28) |
The results summarized in Scheme 13 reveal a combination of rate-limiting dimer- and tetramer-based aggregation events competing for dominance.48 With the aid of isotopic substitution to shift the rate-limiting steps, we showed that the dimer- and tetramer-based deaggregations are followed by dimer-based metalations. Unusually low levels of autocatalysis foreshadowed oddities.
Scheme 13.
Mechanism of LDA-mediated ortholithiation of bis(1,4-trifluoromethyl)benzene. Reproduced from ref 8h. Copyright 2015 American Chemical Society.
This final foray into non-equilibrium kinetics added one more jarring result to assure us that our understanding remains incomplete. We discovered that at −78 °C, LiCl had no measurable effect on the metalation rate (Figure 22, scenario 2). This result was unprecedented within the series. For obscure reasons, we examined the influence of LiCl at elevated temperature (−42 °C) and found that catalytic LiCl produced a small but still significant inhibition of the metalation—a factor of 2 (Figure 22, scenario 1). On first inspection, 5% catalyst imparting a 2-fold inhibition defies common sense given that inhibitors under equilibrium conditions are necessarily stoichiometric. The results became surreal when dropping the temperature to −95 °C revealed LiCl catalysis, albeit at muted levels (Figure 22, scenario 3).
Figure 22.

Plot of initial rate versus LiCl concentration showing catalyzed inhibition (scenario 1), no change in rate (scenario 2), and catalyzed acceleration (scenario 3).
How does one account for the influence of LiCl that ranges from catalyzed inhibition to catalyzed acceleration by merely adjusting the temperature? The key to constructing a model for catalyzed inhibition even as a proof of principle was noting the complex interplay between the LiCl-catalyzed monomer-based metalation and uncatalyzed dimer-based metalation. The critical portion of an otherwise complex mechanism and mathematical model is the reaction flux via the dimer-based metalation, which creates aryllithium and a low steady-state population of LDA monomer (AS3) that is rapidly scavenged by ArH (eq 29). We identified three limiting scenarios: (1) if the monomer population generated from the dimer-based metalation is below the equilibrium population, LiCl-catalyzed dimer-monomer equilibration increases the steady-state concentration to equilibrium levels and increases the reaction rate; (2) if the monomer population generated from the dimer is above the equilibrium population, LiCl catalysis accelerates the reaggregation to dimer with a consequent rate reduction (inhibition); and (3) if the monomer population generated from the dimer-based metalation is at the equilibrium population, LiCl-catalyzed monomer-dimer equilibration has no effect on the monomer population and thus no effect on the ortholithiation rate. These three conditions are met at −95 °C, −42 °C, and −78 °C, respectively. We find analogy of the catalyzed inhibition to photodesensitizers (fluoorescence quenchers) or anti-knock agents in gasoline to be useful constructs,49,50 as they are also non-equilibrium processes that can be influenced by an external agent (catalyst) to reestablish equilibria.
| (29) |
3. Rate Limitation: Some Additional Thoughts
Struggles to understand LDA-mediated reactions under non-equilibrium conditions underscored aspects of rate limitation that we either had thought about only superficially or worse, had no understanding of whatsoever. We failed to grasp, for example, the pragmatic consequences of ZPE and tunneling in transition states. In this final section, we present an eclectic mix of ideas tied together by rate limitation. Some will seem self-evident, whereas others may be counterintuitive.
3.1. Commensurate Barriers
The mechanistic complexity of the chemistry in this review stems from a series of activation barriers that are, energetically, nearly equivalent. This topic has received surprisingly little attention.22 Imagine, in the abstract, a surface that has, for the sake of discussion, a 10.0 kcal/mol barrier versus one with two sequential barriers of 10.0 kcal/mol each (Figure 23). Does fleeting intermediate I influence the reaction rate, or is the rate dictated by the energy of the highest barrier, which is 10.0 kcal/mol with or without I? In short, intermediate I imparts a two-fold rate suppression. Having overcome the first 10.0 kcal/mol barrier, I has a 50% probability of exiting to product. In fact, the rate suppression caused by n equal energy barriers is proportional to 1/n (supporting information). Thus, the existence of I makes the effective barrier >10 kcal/mol.
Figure 23.
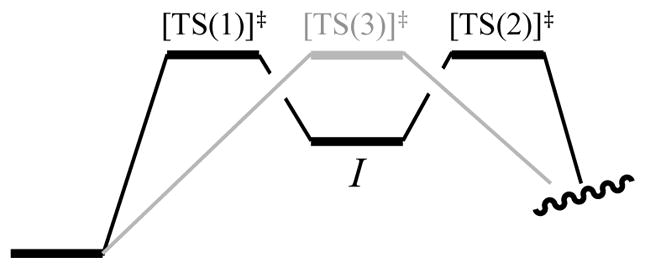
Superimposed single and double barriers of equal energies.
Now imagine that the second barrier is incrementally lower by 0.2 kcal/mol (Figure 24, top). Is the first barrier now rate limiting and the second barrier of no consequence? Again, the answer is no. The probability of I proceeding to product is now >50%, but the probability of returning to starting material remains significant (42% at 25 °C).
Figure 24.
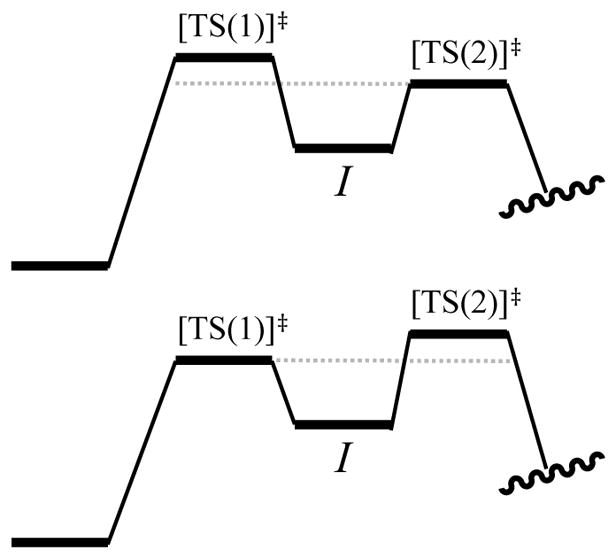
Double barriers in which the second barrier is slightly lower (top) and the first barrier is slightly lower (bottom).
It is less intuitive when the first barrier is slightly lower (Figure 24, bottom), but the rate suppression is identical whether the lower barrier precedes or succeeds the highest barrier. Given a series of barriers of similar but unique energies (eq 30), an expression for the effective barrier can be written (eq 31; supporting information). One should probably hope never to need this calculation.
| (30) |
| (31) |
3.2. Complex-Induced Proximity Effect
There is an exceedingly popular theory of ortholithiations and related directed metalations called the complex-induced proximity effect or CIPE.51 As the theory goes, pre-complexation of a substrate to a functional group brings the base and proton proximate, which facilitates the reaction (eq 32).
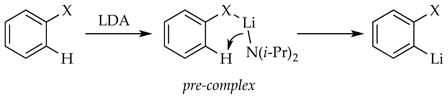 |
(32) |
We (and others) have challenged this theory at a foundational level and will now amplify our concerns.6,52 The arguments made were twofold to which we now add a third:
The energy required to proceed from the ground state to the rate-limiting transition state is a state function; it is path-independent. The existence of an intermediate en route does not affect the relative energies (which is fortunate for kineticists).
Should such a “pre-complex” be so stable as to become observable, the putative merits offered by proximity are offset by the lowering of the ground state with consequent increase in the overall barrier height.
We now add the scenario in which the barrier leading to the fleeting “pre-complex” is close to the barrier for proton transfer. Per the discussion in Section 3.1, the existence of the fleeting intermediate retards the metalation rate as much as twofold.
The notion that complexation facilitates a metalation has nothing to do with proximity. Metal–ligand interactions accelerate the metalation if, and only if, they stabilize the transition state for proton transfer.
3.3. Mixed Aggregation Effects and the Principle of Detailed Balance
The principle of detailed balance should, in our opinion, be one of the foundational principles emphasized in organic chemistry.53 It is especially useful when considering complex systems that otherwise defy intuition. The principle states that, given an ensemble of species at equilibrium (eq 33), each individual equilibrium is maintained.
| (33) |
If, for example, an additional equilibrium is attached by adding reagent X to afford CX (eq 34), the concentration of all species in the original equilibrium will diminish according to the principles of equilibrium.
| (34) |
The inhibition described in Section 2.10 arose from catalyzing an equilibrium that was not fully established in the absence of catalyst. Given an ensemble already at equilibrium, adding 5 mol % LiCl to form a 1:1 mixed aggregate would cause a 5 mol % concentration depletion of the original ensemble and an affiliated 5% reduction in the reaction rate, not 50%. Inhibition of systems at equilibrium are inherently stoichiometric. A corollary is that the attachment of an additional equilibrium to any of the species in the ensemble depletes all species in the ensemble: forming CX rather than BX or AX in no way attests to a mechanistic importance of C rather than A or B.
The principle of detailed balance offers insights into the consequences of heterogeneous media. It is tempting to infer that the rate of reaction of a partially soluble reagent or substrate will necessarily increase if one introduces an additive, X, that solubilizes the reagent (eq 35). The complexent could be a lithium salt, such as LiCl, added to form a soluble mixed aggregate or a polar solvent that may, but does not necessarily, coordinate directly to A. The concentration of the species denoted Asolution necessarily decreases with the formation of AXsolution. The reaction rate of A increases if, and only if, AX reacts without the dissociation of X. Thermochemically, dissolving a substrate is inherently stabilizing; the reactivity of that substrate will decrease unless the transition state is disproportionately stabilized.
| (35) |
3.4. Termolecular Reactions
In this final section, we pick a fight, and a risky one at that. We suggested earlier that LDA monomers reaggregate sequentially, associating two LDA monomers with a dimer to form a tetramer, which then dissociates to two dimers (see Section 2.9). We now ask the seemingly blasphemous question: can these three associate in a single step? The answer is no: assembling three fragments does not occur as a single-step—termolecular—reaction (eq 36) but rather proceeds through two sequential bimolecular reactions.
Try the following: ask a chemist why such three-component associations necessarily proceed via sequential bimolecular steps (eqs 37 and 38). The answer will, without fail in our experience, be some variant of “the probability of bringing three species together in one place to achieve termolecularity is simply too low.” In short, termolecular reactions via [A--B--C]‡ are widely accepted to be entropically disfavored. But is this true?
- termolecular
(36) - sequential bimolecular
(37) (38)
Using the principle of microscopic reversibility, consider the reaction in reverse: the dissociation of ABC via [AB--C]‡ is entropically favored as evidenced both experimentally and theoretically.54 Dissociation of ABC via [A--B--C]‡ should be entropically even more favored, should it not? Thus, scaled relative to ABC as a common reference point, [A--B--C]‡ is entropically favored relative to [AB--C]‡. In fact, unimolecular dissociation of a large n-mer to n-monomers would be stupendously favored entropically. [A--B--C]‡ is unfavorable because each partial bond represents significant enthalpic cost as the number of bonds rises. We add that, at the high-temperature limit, termolecular reactions would be highly favored and n-mers could indeed dissociate to n monomers unimolecularly.
Conclusion
Studies of LDA-mediated metalations under non-equilibrium conditions have provided a mechanistic complexity that rivals that of any homogeneous organometallic mechanism. The story unfolded owing to the efforts of a half dozen Ph.D. researchers. The big question is simple: was it worth it? A referee once suggested that such a question is inappropriate. To the contrary, that question should be asked of any scientific pursuit. We answer affirmatively and give five reasons: (1) the prominence of LDA in both academic and industrial organic synthesis easily justifies understanding its most intimate details; (2) probes of how LiX salts deaggregate are almost nonexistent; (3) partially and fully rate-limiting deaggregations and other non-equilibrium events have measurable consequences on the chemistry of LDA in THF at −78 °C; (4) such transitional regions of reactivity in which rates for key aggregation events and reactions of the fleeting structural forms with substrates necessarily exist for any organolithium reagent–solvent combination; and (5) the methods and strategies outlined in Section 1 are potentially generalizable to any complex mechanistic study. This review represents our last word on non-equilibrium kinetics as it pertains to the chemistry of LDA (or so we hope), but it is by no means the last word on the topic in the larger picture. Early results suggest that reactions of lithium enolates may be particularly influenced by the rates at which aggregates exchange, not just the existence of those aggregates.
Supplementary Material
Chart 1.

Reactions that do not involve proton transfer
Acknowledgments
We thank the National Institutes of Health (GM039764) for support.
Biography

Professor Collum finds his roots in organic synthesis but has been studying structure-reactivity relationships in organolithium chemistry for many years.
Footnotes
Notes
The authors declare no competing financial interests.
Supporting Information: Detailed protocols for graphical simulations and authors for reference 18. This material is available free of charge via the Internet at http://pubs.acs.org.
References and Footnotes
- 1.(a) Bakker WII, Wong PL, Snieckus V. Lithium Diisopropylamide. In: Paquette LA, editor. e-EROS Encyclopedia of Reagents for Organic Synthesis. John Wiley; New York: 2001. [Google Scholar]; (b) Eames J. Product Subclass 6: Lithium Amides. In: Snieckus V, editor. Science of Synthesis. 8a. Thieme; New York: 2006. p. 173. [Google Scholar]
- 2.Reich survey: http://www.chem.wisc.edu/areas/reich/syntheses/syntheses.htm
- 3.(a) Seebach D. Angew Chem Int Ed Engl. 1988;27:1624. [Google Scholar]; (b) Reich HJ. Chem Rev. 2013;113:7130. doi: 10.1021/cr400187u. [DOI] [PubMed] [Google Scholar]
- 4.Collum DB. Acc Chem Res. 1993;26:227. [Google Scholar]
- 5.Tchoubar B, Loupy A. Salt Effects in Organic and Organometallic Chemistry. VCH; New York: 1992. [Google Scholar]
- 6.Collum DB, McNeil AJ, Ramírez A. Angew Chem Int Ed. 2007;46:3002. doi: 10.1002/anie.200603038. [DOI] [PubMed] [Google Scholar]
- 7.The rate law provides the stoichiometry of the transition structure relative to that of the reactants: Edwards JO, Greene EF, Ross J. J Chem Educ. 1968;45:381.
- 8.(a) Singh KJ, Hoepker AC, Collum DB. J Am Chem Soc. 2008;130:18008. doi: 10.1021/ja807331k. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Gupta L, Hoepker AC, Singh KJ, Collum DB. J Org Chem. 2009;74:2231. doi: 10.1021/jo802713y. [DOI] [PMC free article] [PubMed] [Google Scholar]; (c) Ma Y, Hoepker AC, Gupta L, Faggin MF, Collum DB. J Am Chem Soc. 2010;132:15610. doi: 10.1021/ja105855v. [DOI] [PMC free article] [PubMed] [Google Scholar]; (d) Hoepker AC, Gupta L, Ma Y, Faggin MF, Collum DB. J Am Chem Soc. 2011;133:7135. doi: 10.1021/ja200906z. [DOI] [PMC free article] [PubMed] [Google Scholar]; (e) Hoepker AC, Collum DB. J Org Chem. 2011;76:7985. doi: 10.1021/jo2015642. [DOI] [PMC free article] [PubMed] [Google Scholar]; (f) Gupta L, Hoepker AC, Ma Y, Viciu MS, Faggin MF, Collum DB. J Org Chem. 2013;78:4214. doi: 10.1021/jo302408r. [DOI] [PMC free article] [PubMed] [Google Scholar]; (g) Liang J, Hoepker AC, Bruneau AM, Ma Y, Gupta L, Collum DB. J Org Chem. 2014;79:11885. doi: 10.1021/jo501392r. [DOI] [PMC free article] [PubMed] [Google Scholar]; (h) Liang J, Hoepker AC, Algera RF, Ma Y, Collum DB. J Am Chem Soc. 2015;137:6292. doi: 10.1021/jacs.5b01668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kohen Amnon, Limbach Hans-Heinrich., editors. Isotope effects in chemistry and biology. CRC Press; 2005. Bell RP. The Tunnel Effect in Chemistry. Chapman & Hall; New York: 1980. Carpenter BK. Determination of Organic Reaction Mechanisms. Wiley; New York: 1984. Caldin EF. Chem Rev. 1969;69:135.For an excellent discussion of the various isotope effects from a decidedly thermochemical perspective, see: Simmons EM, Hartwig JF. Angew Chem, Int Ed Engl. 2012;51:3066. doi: 10.1002/anie.201107334.
- 10.McGarrity JF, Ogle CA. J Am Chem Soc. 1985;107:1810. [Google Scholar]
- 11.(a) Thomas AA, Denmark SE. Science. 2016;352:329. doi: 10.1126/science.aad6981. [DOI] [PubMed] [Google Scholar]; (b) Bertz SH, Cope SK, Hardin RA, Murphy MD, Ogle CA, Smith DT, Thomas AA, Whaley TN. Organometallics. 2012;31:7827. [Google Scholar]
- 12.(a) Reich HJ. J Org Chem. 2012;77:5471. doi: 10.1021/jo3005155. [DOI] [PubMed] [Google Scholar]; (b) Jones AC, Sanders AW, Sikorski WH, Jansen KL, Reich HJ. J Am Chem Soc. 2008;130:6060. doi: 10.1021/ja8003528. [DOI] [PubMed] [Google Scholar]; (c) Plessel KN, Jones AC, Wherritt DJ, Maksymowicz RM, Poweleit ET, Reich HJ. Org Lett. 2015;17:2310. doi: 10.1021/acs.orglett.5b00650. [DOI] [PubMed] [Google Scholar]
- 13.Espenson JH. Chemical Kinetics and Reaction Mechanisms. 2. McGraw-Hill; New York: 1995. [Google Scholar]
- 14.Casado J, Lopez-Quintela MA, Lorenzo-Barral FM. J Chem Educ. 1986;63:450. [Google Scholar]
- 15.For a review of structural studies using 19F NMR spectroscopy, see: Gakh YG, Gakh AA, Gronenborn AM. Magn Reson Chem. 2000;38:551.McGill CA, Nordon A, Littlejohn D. J Process Anal Chem. 2001;6:36. doi: 10.1021/ac0102866.Espinet P, Albeniz AC, Casares JA, Martinez-Ilarduya JM. Coor Chem Rev. 2008;252:2180.
- 16.Review of 6Li NMR spectroscopy: Günther H. J Brazil Chem. 1999;10:241.
- 17.Rein AJ, Donahue SM, Pavlosky MA. Curr Opin Drug Discovery Dev. 2000;3:734.Eisenbeis SA, Chen R, Kang M, Barrila M, Buzon R. Org Process Res Dev. 2015;19:244., and references cited therein.
- 18.Frisch MJ, et al. GaussianVersion 3.09; revision A.1. Gaussian, Inc; Wallingford, CT: 2009. [Google Scholar]
- 19.Frey PA, Hegeman AD. Enzymatic Reaction Mechanisms. Chapter 2 Oxford University Press; New York: 2007. [Google Scholar]
- 20.(a) Kristian KE, Iimura M, Cummings SA, Norton JR, Janak KE, Pang K. Organometallics. 2009;28:493. [Google Scholar]; (b) Yi CS, Zeczycki TN, Lindeman SV. Organometallics. 2008;27:2030. [Google Scholar]; (c) Wijeratne GB, Corzine B, Day VW, Jackson TA. Inorg Chem. 2014;53:7622. doi: 10.1021/ic500943k. [DOI] [PubMed] [Google Scholar]
- 21.(a) Schneider KJ, van Eldik R. Organometallics. 1990;9:1235. [Google Scholar]; (b) Byers PK, Canty AJ, Crespo M, Puddephatt RJ, Scott JD. Organometallics. 1988;7:1363. [Google Scholar]; (c) Jordan RF, Norton JR. J Am Chem Soc. 1982;104:1255. [Google Scholar]; (d) Belt ST, Grevels FW, Klotzbücher WE, McCamley A, Perutz RN. J Am Chem Soc. 1989;111:8373. [Google Scholar]; (e) Brown TL, Bellus PA. Inorg Chem. 1978;17:3726. [Google Scholar]; (f) Minniti D, Alibrandi G, Tobe ML, Romeo R. Inorg Chem. 1987;26:3956. [Google Scholar]; (g) Durak LJ, Lewis JC. Organometallics. 2013;32:3153. [Google Scholar]
- 22.(a) Dumesic JA. J Catalysis. 1999;185:496. [Google Scholar]; (b) Campbell CT. J Catalysis. 2001;204:520. [Google Scholar]; (c) Dumesic JA. J Catalysis. 2001;204:525. [Google Scholar]; (d) Meskine H, Matera S, Scheffler M, Reuter K, Metiu H. Surface Science. 2009;603:1724. [Google Scholar]; (e) Campbell CT. Topics in Catalysis. 1994;1:353. [Google Scholar]; (f) Stegelmann C, Andreasen A, Campbell CT. J Am Chem Soc. 2009;131:8077. doi: 10.1021/ja9000097. [DOI] [PubMed] [Google Scholar]; (g) Barański A. Solid State Ionics. 1999;117:123. [Google Scholar]; (g) Kozuch S, Shaik S. Acc Chem Res. 2011;44:101. doi: 10.1021/ar1000956. [DOI] [PubMed] [Google Scholar]
- 23.(a) Besson C, Finney EE, Finke RG. J Am Chem Soc. 2005;127:8179. doi: 10.1021/ja0504439. [DOI] [PubMed] [Google Scholar]; (b) Besson C, Finney EE, Finke RG. Chem Mater. 2005;17:4925. doi: 10.1021/ja0504439. [DOI] [PubMed] [Google Scholar]; (c) Huang KT, Keszler A, Patel N, Patel RP, Gladwin MT, Kim-Shapiro DB, Hogg N. J Biol Chem. 2005;280:31126. doi: 10.1074/jbc.M501496200. [DOI] [PubMed] [Google Scholar]; (d) Huang Z, Shiva S, Kim-Shapiro DB, Patel RP, Ringwood LA, Irby CE, Huang KT, Ho C, Hogg N, Schechter AN, Gladwin MT. J Clin Invest. 2005;115:2099. doi: 10.1172/JCI24650. [DOI] [PMC free article] [PubMed] [Google Scholar]; (e) Tanj S, Ohno A, Sato I, Soai K. Org Lett. 2001;3:287. doi: 10.1021/ol006921w. [DOI] [PubMed] [Google Scholar]; (f) Barrios-Landeros F, Carrow BP, Hartwig JF. J Am Chem Soc. 2008;130:5842. doi: 10.1021/ja711159y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.(a) Bissette AJ, Fletcher SP. Angew Chem Int Ed. 2013;52:12800. doi: 10.1002/anie.201303822. [DOI] [PubMed] [Google Scholar]; (b) Espenson JH. Chemical Kinetics and Reaction Mechanisms. 2. McGraw-Hill; New York: 1995. p. 190. [Google Scholar]
- 25.Houghton MJ, Huck CJ, Wright SW, Collum DB. J Am Chem Soc. 2016;138:10276. doi: 10.1021/jacs.6b05481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Adam W, Krebs O, Orfanopoulos M, Stratakis M, Vougioukalakis GC. J Org Chem. 2003;68:2420. doi: 10.1021/jo0266240. and references cited therein.
- 27.Gonzalez-James OM, Kwan EE, Singleton DA. J Am Chem Soc. 2012;134:1914. doi: 10.1021/ja208779k. and references cited therein.
- 28.(a) Ma Y, Breslin S, Keresztes I, Lobkovsky E, Collum DB. J Org Chem. 2008;73:9610. doi: 10.1021/jo801410s. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Rennels RA, Rutherford JL, Collum DB. J Am Chem Soc. 2000;122:8640. [Google Scholar]; (c) Anderson DR, Faibish NC, Beak P. J Am Chem Soc. 1999;121:7553. [Google Scholar]; (d) Meyers AI, Mihelich ED. J Org Chem. 1975;40:3158. [Google Scholar]
- 29.Liao S, Collum DB. J Am Chem Soc. 2003;125:15114. doi: 10.1021/ja030409z. [DOI] [PubMed] [Google Scholar]
- 30.We discuss the varieties of salt effects on reaction rates in ref 6c.
- 31.Barr D, Snaith R, Wright DS, Mulvey RE, Wade K. J Am Chem Soc. 1987;109:7891. [Google Scholar]
- 32.Herrman JL, Kieczykowski GR, Schlessinger RH. Tetrahedron Lett. 1973;15:2433. [Google Scholar]
- 33.Davies SG, Smith AD, Price PD. Tetrahedron: Asymmetry. 2005;16:2833. [Google Scholar]
- 34.Mongin F, Desponds O, Schlosser M. Tetrahedron Lett. 1995;37:2767. [Google Scholar]
- 35.(a) Mongin F, Schlosser M. Tetrahedron Lett. 1997;38:1559. [Google Scholar]; (b) Cottet F, Schlosser M. Eur J Org Chem. 2004:3793. [Google Scholar]
- 36.The principle of microscopic reversibility must be applied with caution: Blackmond DG. Angew Chem Int Ed. 2009;48:2648. doi: 10.1002/anie.200804566.Krupka RM, Kaplan H, Laidler KJ. J Chem Soc, Faraday Trans. 1966;62:2754.Chandrasekhar S. Res Chem Intermed. 1992;17:173.Burwell RL, Pearson RG. J Phys Chem. 1966;70:300.
- 37.Representative examples of structurally characterized bridging THF ligands: Pratt LM, Merry A, Nguyen SC, Quanb P, Thanh BT. Tetrahedron. 2006;62:10821.Clegg W, Liddle ST, Mulvey RE, Robertson A. Chem Commun. 1999:511.Boche G, Boie C, Bosold F, Harms K, Marsch M. Angew Chem Int Ed. 1994;33:115.Daniele S, Drost C, Gehrhus B, Hawkins SM, Hitchcock PB, Lappert MF, Merle PG, Bott SG. J Chem Soc, Dalton Trans. 2001:3179.Chivers T, Fedorchuk C, Parvez M. Inorg Chem. 2004;43:2643. doi: 10.1021/ic0352755.Briand GG, Chivers T, Parvez M. J Chem Soc, Dalton Trans. 2002:3785.
- 38.Zimmerman PM. J Computational Chem. 2015;36:601. doi: 10.1002/jcc.23833. [DOI] [PubMed] [Google Scholar]
- 39.(a) Lonsdale R, Harvey JN, Mulholland AJ. Chem Soc Rev. 2012;41:3025. doi: 10.1039/c2cs15297e. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Bahnson BJ, Klinman JP. Methods Enzymol. 1995;249:373. doi: 10.1016/0076-6879(95)49042-6. [DOI] [PubMed] [Google Scholar]; (c) Hong YJ, Tantillo DJ. Nature Chem. 2009;1:384. doi: 10.1038/nchem.287. [DOI] [PubMed] [Google Scholar]
- 40.(a) Schlosser M. Angew Chem Int Ed. 2005;44:376. doi: 10.1002/anie.200300645. [DOI] [PubMed] [Google Scholar]; (b) Schlosser M, Rausis T. Eur J Org Chem. 2004:1018. [Google Scholar]; (c) Kuethe JT, Zhong Y-L, Alam M, Alorati AD, Beutner GL, Cai D, Fleitz FJ, Gibb AD, Kassim A, Linn K, Mancheno D, Marcune B, Pye PJ, Scott JP, Tellers DM, Xiang B, Yasuda N, Yin J, Davies IW, editors. Tetrahedron. 2009;65:5013. [Google Scholar]; (d) Güngör T, Marsais F, Queguiner G. J Organomet Chem. 1981;215:139. [Google Scholar]
- 41.(a) Fort Y. e-EROS Encyclopedia of Reagents for Organic Synthesis. John Wiley & Sons; NewYork: 2001. 2-Fluoropyridine. [Google Scholar]; (b) Bhardwaj P, Forgione P. e-EROS Encyclopedia of Reagents for Organic Synthesis. John Wiley & Sons; NewYork: 2001. 2,6-Difluoropyridine. [Google Scholar]
- 42.Romesberg FE, Collum DB. J Am Chem Soc. 1994;116:9198. [Google Scholar]
- 43.(a) Evans WJ, Broomhall-Dillard RNR, Ziller JW. J Organomet Chem. 1998;569:89. [Google Scholar]; (b) Klingebiel U, Tecklenburg B, Noltemeyer M, Schmidt-Baese D, Herbst-Irmer R. Z Naturforsch B Chem Sci. 1998;53:355. [Google Scholar]
- 44.Mulvey RE. Chem Soc Rev. 1991;20:167. [Google Scholar]
- 45.For examples of lithium amide mixed ladders, see: Williard PG, Hintze MJ. J Am Chem Soc. 1987;109:5539.Mair RS, Clegg W, O’Neil PA. J Am Chem Soc. 1993;115:3388.Engelhardt LM, Jacobsen GE, White AH, Raston CL. Inorg Chem. 1991;30:3978.Williard PG, Hintze MJ. J Am Chem Soc. 1987;109:5539.
- 46.For an example of the butyllithium-based ortholithiation of arene 1, see: Coffer PK, Dillon KB, Howard JAK, Yufit Dmitry S, Zorina NV. J Chem Soc, Dalton Trans. 2012;41:4460. doi: 10.1039/c2dt12369j.
- 47.Tetrameric lithium amide ladders: Armstrong DR, Barr D, Clegg W, Mulvey RE, Reed D, Snaith R, Wade K. J Chem Soc, Chem Commun. 1986:869.Gardiner MG, Raston CL. Inorg Chem. 1996;35:4047. doi: 10.1021/ic951251p.Vestergren M, Eriksson J, Hilmersson G, Hakansson M. J Organomet Chem. 2003;682:172.Boche G, Langlotz I, Marsch M, Harms K, Nudelman NES. Angew Chem. 1992;104:1239.
- 48.For crystallographically characterized examples of lithium amide ladder structures showing open-dimer-like subunits, see: Armstrong DR, Barr D, Clegg W, Hodgson SM, Mulvey RE, Reed D, Snaith R, Wright DS. J Am Chem Soc. 1989;111:4719.
- 49.(a) Lakowicz Joseph R. Principles of Fluorescence Spectroscopy. 3. Springer Science; New York, NY: 2006. [Google Scholar]; (b) Eftink MR. Fluorescence Quenching: Theory and Applications. In: Lakowicz Joseph R., editor. Topics in Fluorescence Spectroscopy. Vol. 2. Springer Science; New York, NY: 2002. [Google Scholar]
- 50.(a) Linteris GT, Rumminger MD, Babushok VI. Progress in Energy and Combustion Science. 2008;34:288. [Google Scholar]; (b) Casias CR, McKinnon JT. Combust Sci Technol. 1996;116–117:289. [Google Scholar]; (c) Benson SW. J Phys Chem. 1988;92:1531. [Google Scholar]
- 51.Whisler MC, MacNeil S, Snieckus V, Beak P. Angew Chem Int Ed. 2004;43:2206. doi: 10.1002/anie.200300590. [DOI] [PubMed] [Google Scholar]
- 52.For similar concerns about the language of the complex-induced proximity effect, see: van Eikema Hommes NJR, Schleyer PvR. Angew Chem Int Ed Engl. 1992;31:755.
- 53.Alberty RA. J Chem Educ. 2004;81:1206. [Google Scholar]
- 54.Anslyn EV, Dougherty DA. Modern Physical Organic Chemistry. University Science Books; Sausalito, California: 2006. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.