Super-resolution dipole orientation mapping via polarization demodulation

Abstract

Fluorescence polarization microscopy (FPM) aims to detect the dipole orientation of fluorophores and to resolve structural information for labeled organelles via wide-field or confocal microscopy. Conventional FPM often suffers from the presence of a large number of molecules within the diffraction-limited volume, with averaged fluorescence polarization collected from a group of dipoles with different orientations. Here, we apply sparse deconvolution and least-squares estimation to fluorescence polarization modulation data and demonstrate a super-resolution dipole orientation mapping (SDOM) method that resolves the effective dipole orientation from a much smaller number of fluorescent molecules within a sub-diffraction focal area. We further apply this method to resolve structural details in both fixed and live cells. For the first time, we show that different borders of a dendritic spine neck exhibit a heterogeneous distribution of dipole orientation. Furthermore, we illustrate that the dipole is always perpendicular to the direction of actin filaments in mammalian kidney cells and radially distributed in the hourglass structure of the septin protein under specific labelling. The accuracy of the dipole orientation can be further mapped using the orientation uniform factor, which shows the superiority of SDOM compared with its wide-field counterpart as the number of molecules is decreased within the smaller focal area. Using the inherent feature of the orientation dipole, the SDOM technique, with its fast imaging speed (at sub-second scale), can be applied to a broad range of fluorescently labeled biological systems to simultaneously resolve the valuable dipole orientation information with super-resolution imaging.

Introduction

Through specific labeling of biological molecules, fluorescence microscopy plays an important role in visualizing subcellular organelles. The fundamental physical dimensions of fluorescence include intensity (which reflects the fluorescence concentration), wavelength (absorption and emission spectrum), time (fluorescence decay lifetime) and polarization (which arises from the dipole orientation). Because the fluorescent dipole orientation reflects the direction of the targeted protein, fluorescence polarization microscopy (FPM) has been studied extensively by utilizing polarization modulation of excitation (linear dichroism)^{1, 2, 3} or analyzing fluorescence polarization (fluorescence anisotropy)^{4, 5, 6, 7} to measure the angle of a fluorophore—the fluorescent dipole orientation—so that the direction of the targeted protein may be resolved. Unfortunately, these polarization-based investigations are limited by the optical diffraction in conventional fluorescence microscopy.

Super-resolution microscopy has been developed to extend our vision beyond the diffraction limit⁸. The key to achieve super-resolution is the intensity On–Off modulation, either in a structured manner, such as stimulated emission depletion (STED)^{9, 10} or saturated structured illumination microscopy¹¹, or in a stochastic manner, such as (f) photo-activated localization microscopy (PALM)/stochastic optical reconstruction microscopy (STORM)^{12, 13, 14}. These methods largely rely on intensity modulation using different excitation wavelengths, often in association with temporal modulation. The wavelength dependency nature of these techniques critically requires the fluorescent labeling of a suitable fluorophore, thereby limiting the applications of super-resolution microscopy¹⁵.

In addition to fluorescence intensity, wavelength, and lifetime, the fourth dimension of fluorescence—polarization—can also provide intensity modulation without the restriction to specific fluorophores; its investigation in super-resolution microscopy is still in its infancy. Via fluorescent polarization modulation, Hafi et al¹⁶ recently developed a novel super-resolution technique through sparse deconvolution of polarization-modulated fluorescent images (SPoD). Because the fluorescent dipole is an inherent feature of fluorescence, and its polarization intensity can be easily modulated with rotating linear polarized excitation, the polarization-based super-resolution technique therefore holds great promise with regard to a wide range of biological applications due to its compatibility with conventional fluorescent specimen labeling. Although super resolution can be achieved, the dipole orientation information is lost during SPoD reconstruction. Recently, there has been an interesting debate regarding whether fluorescent polarization can be used to yield additional super-resolution information^{17, 18}.

Here, by fully exploring the advantages of fluorescent polarization, we present a new technique called super-resolution dipole orientation mapping (SDOM) to extract the dipole orientation information beyond super-resolution imaging. In SDOM, a polarization-variant model is established, in which the intensity determines the super-resolution microscopic image, while the phase determines the mutual dipole orientation of each super-resolved focal volume. The SDOM algorithm uses sparsity-enhanced deconvolution to estimate effective dipole intensity under polarization modulation and applies least-squares estimation to extract the dipole orientation, thus fully utilizing the polarization modulation information. The dipole orientation mapping, as a new dimension, can be superimposed onto the super-resolution image, in which the angle denotes the effective dipole orientation, and the length denotes the orientation uniform factor (OUF), which describes the confidence of the orientation distribution of local dipoles. With such valuable dipole orientation information, we reprocess the neural polarization modulation data set, and the membranes of the spine neck in the opposite direction show very different polarization angles. This result clearly shows that the polarization does provide further structural information on top of the super-resolution image, thereby providing a timely answer to the key question raised by the debate mentioned above.

Moreover, by taking advantage of the parallel dipole orientation modulation with a low-excitation light level, we demonstrate that SDOM performs at a temporal resolution as fast as 5 f.p.s., which allows live cell imaging to reveal the dynamic structural information of proteins. Because fluorescence polarization is widely applied in different biological research areas, such as septin dynamics in live yeast cells^{6, 19}, nuclear pore complexes^{20, 21}, and protein structure and function in cell membranes^{1, 2, 22, 23, 24, 25, 26}, our SDOM method bridges the gap between wide-field polarization imaging and super-resolution microscopy. We therefore anticipate widespread interest in and adoption of SDOM as a powerful tool to answer a wide variety of key biological questions.

Materials and Methods

Experimental design

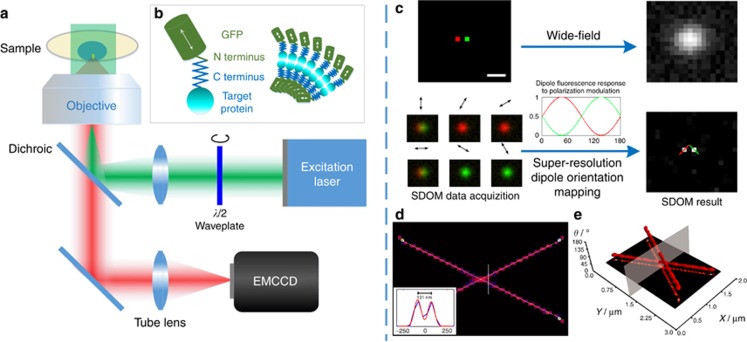
All organic fluorescent dyes and fluorescent proteins are dipoles, whose orientations are closely related to the structure of their labeled target proteins (Figure 1b)²⁰. Because both the excitation absorption and fluorescence emission of dipoles have polarization features, FPM has been widely used to study dipole orientation. SDOM is one type of FPM, working in the super-resolution region, and requires a series of fluorescence images from a wide-field epi-fluorescence illumination microscope under different angles of polarized excitation. Polarized excitation can be achieved by using a rotary half-wave plate that is synchronized to a camera (Figure 1a). There may exist multiple dipoles in the corresponding focal volume. Thus, the detected fluorescent anisotropic response is the integration of all of the fluorescent molecules’ dipole orientation contributions.

Figure 1.

Schematic diagram of SDOM. (a) SDOM is based on a wide-field epi-fluorescence illumination microscope. The rotary linear polarized excitation is realized by continuously rotating a half-wave plate in front of a laser. Then, the illumination beam is focused onto the back focal plane of the objective to generate uniform illumination with rotating polarization light. The series of fluorescence images excited from different angles of polarized excitation are collected by an EMCCD camera. As illustrated in the inset schematic figure (b), the fluorophores (such as GFP) are linked to the target protein via the C terminus (connected to GFP’s N terminus); the dipole angle of the fluorophore will reflect the orientation of the target protein. (c) Illustration of the principle of the SDOM super-resolution technique. Two neighboring fluorophores with 100 nm distance and different dipole orientations (pseudocolor in red and green) emit periodic signals excited by rotating polarized light. By rotating the polarization of excitation, the emission ratio between the two molecules is modulated accordingly, resulting in their separation in the polarization domain. The sparsity deconvolution can achieve a super-resolution image of effective dipole intensities under polarization modulation; with least-squares fitting, the dipole orientation can be determined. Arrows indicate the directions of dipole orientations. (d) The SDOM result of two intersecting lines, with arrows on top of the super-resolution image, illustrating the dipole orientation and OUF. (e) The corresponding data are represented in (X, Y, θ) coordinates, in which the XY plane is the super-resolved intensity image. From both d and e, we can see that as SDOM introduces a new dimension, the molecules that are not able to be resolved in the super-resolution intensity image can be completely separated in the dipole orientation domain. Scale bar=200 nm.

Unlike PALM/STORM^{12, 13}, 3B²⁷, SOFI²⁸ and so on, in which intensity fluctuation is achieved stochastically, intensity fluctuation in SPoD and SDOM is achieved through different dipole responses to polarized excitation; therefore, the demodulation algorithm is applied. In SDOM, effective dipole intensities under different polarized excitations are estimated via sparsity-enhanced de-convolution¹⁶ of polarization data within the point spread function (PSF). The polarization modulation, described by a cosine-squared (cos²) function, is then related to dipole orientation (Figure 1c) via least-squares estimation. Furthermore, we use OUF to evaluate the super-resolved dipole orientations.

Compared with the conventional FPM, where the neighboring fluorescent emitters cannot be discerned within the optical diffraction limit, SDOM, with super-resolution resolving power, analyzes polarization data from several fluorescent emitters under polarization excitation modulation by analyzing the distinct periodic oscillating fluorescence signals (Figure 1c).

The dipole orientation (polarization information) map can be either superimposed on top of the super-resolution image or demonstrated in a (X, Y, θ) coordinate system. For example, if we simulate two crossed lines with a dipole orientation difference of 90°, the image of orientation mapping and the (X, Y, θ) coordinate image will be as shown in Figure 1d and 1e, respectively. By providing the polarization as an additional dimension to the fluorescence intensity, the nearby fluorophores can be clearly discerned by using SDOM, as shown in Figure 1c and Supplementary Fig. S1. Figure 1d and 1e are the simulation results of two densely labeled intersecting lines with a uniform dipole orientation on each line. Figure 1d shows the orientation mapping image of SDOM, with a resolution of ~130 nm, from the intensity information. Shown in a (X, Y, θ) coordinate system, two lines with different dipole orientations can be completely separated.

Reconstruction algorithm of SDOM

The detected image I(r,θ) under illumination with a polarization angle θ is subject to Poisson distribution, with the photons reaching the sensor μ(r,θ) at each position r and polarization angle θ:

The ith emitting dipole at position r_i is described by intensity g₀(r_i) and orientation α_i. The effective photons emitted from each dipole are modulated by the polarization angle of illumination with a cosine-squared function f(θ,α_i)=cos²(α_i−θ), which is blurred by the PSF U(r) of the system. The entire imaging model can be described by Equation (2):

Here, the background b(r) is modeled as a polarization invariant within a short time. I₀(θ) is a polarization-dependent periodic correction factor of the non-uniform response of the entire optical system.

The purpose of the SDOM algorithm is to estimate both the intensity g₀(r_i) and the dipole orientation α_i. We denote g(r_i,θ) as the effective intensity under the illumination of polarization angle θ, which leads to g(r_i,θ)=g₀(r_i)f(θ,α_i). Thus, we can obtain

Because the effective intensity g(r_i,θ) considers polarization modulation information, as suggested by Hafi et al¹⁶, additional information is embedded in this model, which allows polarization super-resolution, benefitted also from a much sparser representation of the fluorescence intensity images.

Maximum a posteriori is applied to estimate g(r_i,θ) in this Poisson statistical model. g(r_i,θ) and b̃(r) are independently and identically distributed, respectively, with b̃(r) being the cosine transform of b(r) to accelerate the computation¹⁶. The blurred background usually varies slowly in space, the property of which can be achieved by requiring the sparsity of the cosine transform of b(r)¹⁶. Laplace (exponential) distribution can be applied to describe the prior sparsity of g(r_i,θ) andb̃(r)²⁹. We maximize the maximum a posteriori with

and obtain the optimization model: argmin L(g, b, I), where

After discretization, L is a multivariate function consisting of a convex smooth part and a convex non-smooth part. The fast iterative shrinkage-thresholding algorithm (FISTA) can be applied to achieve fast minimization³⁰. By integrating g(r_i,θ) with respect to θ, the intensity g₀(r_i) can be obtained, which is equivalent to the SPoD super-resolution image.

The orientation α_i could be extracted from the polarization-variant effective intensity g(r_i,θ) using least-squares curve fitting. Before that, because it is meaningless to calculate orientation in pixels without any dipoles, pixels containing no fluorescence signal can be marked on the super-resolution intensity image g₀(r_i). For pixels containing dipoles, each pixel could be affected by more than one dipole. Assume there are n dipoles influencing pixel i, with orientation α_j(α_j∈[0,π]) and the maximum number of photons M_j reaching pixel i. The polarization-variant intensity could be expressed as:

Through further calculation, Equation (6) could be re-written in the form of Equation (7):

For each pixel i, least-squares curve fitting could be applied to Equation (7) to estimate ᾱ_i. Instead of obtaining the orientation of each dipole, we calculated the ᾱ_i, which represents the average dipole orientation in pixel i. Supplementary Fig. S3 illustrates the summation of multiple dipoles. Dipoles with similar orientations show a strong mutual dipole, whereas when they distribute homogeneously the mutual dipole degrades such that it has a strong DC component (Supplementary Fig. S3a and S3b). Adjusted-R² is used to describe the quality of curve fitting and involves calculating R² after normalizing the fitted data to [0, 1]. To guarantee the correctness of orientation mapping, only pixels with relatively large adjusted-R² are orientation-mapped on the image.

Moreover, in Equations (6) and (7), A and B have the following analytic forms:

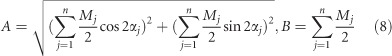where A is referred to as the orientation amplitude, which contains the dipole orientation signal; and B is referred to as the super-resolution translation, which contains the super-resolution signal. We define OUF as OUF=A/B to evaluate our result, and from Equation (8) we have 0≤OUF≤1. OUF describes the orientation uniformity of dipoles within a PSF area. Simulation in Supplementary Information describes how the divergence in orientation of dipoles can influence the OUF. In our orientation-mapped images, OUF is represented by the length of the arrow whose direction indicates the dipole orientation.

Optical setup and image acquisition

A 488-nm linear polarized continuous-wave laser (OBIS, Coherent, Santa Clara, CA, USA) is coupled to a polarization-maintaining optical fiber that is installed on a Nikon Ti-E motorized system (Nikon, Tokyo, Japan). A half-wave plate (450–650 nm, Union Optics, Wuhan, China) is mounted to a motorized rotary mount (G065117000, Qioptiq, Munich, Germany) to rotate the polarization of the incident laser. The rotation is monitored by using an infrared sensor and synchronized to an electron-multiplying charge-coupled device (EMCCD, Evolva Delta 512, Photometrics, Tucson, AZ, USA). A 60 × oil-immersion objective (numerical aperture=1.4, ApoPlan, Nikon) is used for epi-illumination and imaging. An additional 4 × relay lens (Nikon VM4X, Nikon) is used together with the Nikon 1.5 inner magnification (Nikon) to make the pixel size equal to 44.4 nm.

The excitation laser power is 20 W cm⁻² for actin samples and 100 W cm⁻² for live yeast samples. The exposure time of each image is 20 ms for actin samples and 100 ms for live yeast samples. The rotation speed of the half-wave plate is adjusted for 10 acquisitions during a polarization modulation cycle of 180°. The total number of measurements is 10 for actin samples and 20 for live yeast samples.

Sample preparation

The Saccharomyces cerevisiae yeast strain AGY169-pRS416-ScCdc12-conGFP:GEN(4D4) was a generous gift from Prof. Amy Gladfelter’s lab; it has four amino acids removed from the 3′ end of the septin Cdc12 and four amino acids removed from the 5′ end of the green fluorescent protein (GFP) with no linker between them. The S. cerevisiae yeast strain, with GFP-tagged nuclear pore protein Nic96, was obtained from a GFP-tagged budding yeast protein library³¹ purchased from Invitrogen (Thermo Fisher Scientific, Waltham, MA, USA).

To obtain the series of polarized fluorescence images for SDOM analysis, S. cerevisiae cells were grown in 3 ml of yeast extract-peptone-dextrose in 10-ml conical tubes and shaken at 30 °C for 10 h. The cells were refreshed for 2 h, and OD₆₀₀ was checked before the cells were collected via 1000 rpm of centrifuge. Then, the collected cells were re-suspended in yeast extract-peptone-dextrose, transferred to a slide, covered with a coverslip, sealed with VALAP and imaged.

Data analysis

The length of each arrow, labeled on each pixel, is proportional to the OUF value of each pixel. However, because the OUF of wide-field images is usually small, the lengths of arrows on these images are pre-magnified 2 × for easy visibility in this article.

To determine whether a pixel contains dipoles, a threshold based on global Otus’s method³² is used. This threshold is related only to which pixel should be fitted with dipole orientation and could be adjusted accordingly, which has no effect on the dipole orientation or OUF calculated.

The orientation mapped to the images of fluorescent beads, actin in fixed mammalian cells and septin in S. cerevisiae cells was calibrated carefully using polarizers and represents the true orientation of fluorescent dipoles. However, for images of a neuronal spine, we assumed that the orientation parallel to the horizontal direction is 0° and that the clockwise direction is positive in our simulation. Thus, the polarization angles labeled in these results are relative angles that may have a constant difference with real orientation.

The source code and manual of SDOM, together with parameters and details for SDOM reconstruction can be downloaded from: https://github.com/KarlZhanghao/SDOM.

Results and Discussion

Comparison between SDOM and SPoD

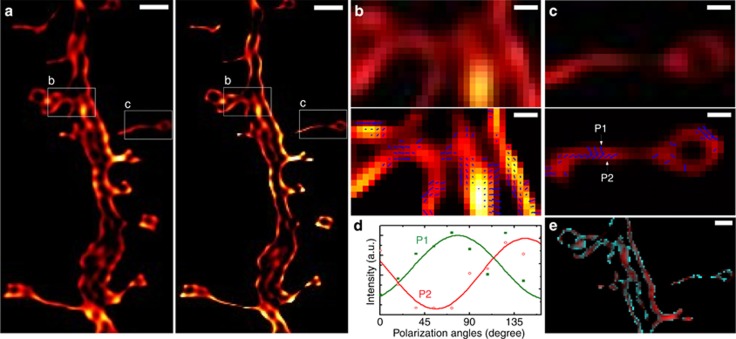
Through re-processing the data set presented in the SPoD method¹⁶, the comparable super-resolution image using our SDOM method was obtained as shown in Figure 2a (right); no information is lost due to over-deconvolution compared with the reported image using the SPoD method (Figure 2a, left). A significant advantage of SDOM is the achievement of a super-resolution image of fluorophore orientations. Zoomed-in SPoD and SDOM images of a dendritic spine neck in hippocampal neurons were compared (Figure 2b and 2c). Arrows in the SDOM image are used to map the dipole orientation, and their lengths are proportional to OUF. With the powerful capability of fluorophore orientation mapping, a heterogeneous distribution of dipole orientation on different borders of a dendritic spine neck can be revealed (Figure 2c), which may suggest the presence of a double membrane structure and a difference in the morphology of the fluorescent molecule orientation on the opposite side of the neck. When both the fluorescence intensity and fluorophore OUF are mapped using pseudocolor in the same image, we also find that the outer borders of the membrane usually have a larger OUF, while the inner parts have a larger intensity. As shown in Figure 2e, the outer border is rendered as cyan by the large OUF, while the inner remains red (small OUF is not shown). This is consistent with the fact that the orientations in the outer border are more uniform than those on the inner side because the fluorophores on the outer border are less influenced by fluorophores elsewhere. To determine the validity of the arrows labeled in the SDOM images, the modulation data of fluorescence intensity with polarization direction could be observed in each pixel (Figure 2d) via our purpose-programmed software (for details, see Supplementary Information). The fluorophore orientation can only be mapped when the adjusted-R² of the sinusoidal fitting of modulation data is sufficiently large.

Figure 2.

SPoD and SDOM comparison using the same neuron data set of Ref. 16. (a) Comparison of SPoD (left) and SDOM (right) images of dendritic spine neck in fEGFP membrane-labeled hippocampal neurons. (b,c) A close-up of the orientation mapping of dipoles from the corresponding boxed areas (upper panel, lower panel) in a; the directions of the dipoles are illustrated using arrows. (d) Fluorescence response to the polarization modulation of P1 and P2 in c, showing that these two points are almost perpendicular to each other with respect to dipole orientation. (e) Composite image of OUF (pseudocolor mapped in cyan) and fluorescent intensity data (pseudocolor mapped in red). Scale bar: (a) 1 μm, (b, c) 200 nm, (e) 500 nm.

SDOM of simulated data and fluorescent beads

Simulation is first performed on fluorescent beads, which are imaged thereafter to validate the SDOM method and to examine the accuracy of the dipole orientation mapping of fluorophores. First, simulation of two neighboring emitters, separated by a series of distances from 50 to 150 nm with various dipole orientations, is performed to test the super-resolution power of SDOM (Supplementary Fig. 1). We also generate a pattern of a 200-nm diameter circle for simulation (Figure 3a). In the wide-field image, the circle looks solid, while the SDOM reconstructed image reveals a hollow circle shape. The reconstructed dipole orientation map clearly recovers the radial arrangement, with a much larger OUF than the wide-field counterpart. We further image fluorescent beads with a diameter of ~500 nm in Figure 3b (F8888, Molecular Probes, Eugene, OR, USA). The rotational symmetric distribution of orientation mapping of fluorescent dipoles on the surface of 500 nm beads is also consistent with previous studies (Figure 3b)¹⁶.

Figure 3.

SDOM images of simulated data and fluorescent bead. (a) Wide-field (left) and SDOM result (right) of simulated ring structure with 200 nm diameter. The orientation of the fluorescent emitters is normal to the ring. (b) Experimental images of 500 nm hollow fluorescent beads using wide-field microscopy (left) and SDOM super-resolution microscopy (right). In comparison, the wide-field and SDOM fluorescence intensity results of the simulated 200 nm ring (c) and 500 nm diameter beads (d) are also shown. Scale bar: (a, b) 200 nm, (c, d) 500 nm.

Next, we verify the reliability of the orientation mapping of SDOM super-resolved images. Two neighboring emitters with a distance of 100 nm are simulated in large numbers and statistically analyzed (Supplementary Fig. 2d). After 100 repetitions, we can see from the diagram that the angle detection error is within 5° when two neighboring emitters have a 90° orientation difference. The angle detection error becomes larger when the difference of orientation becomes smaller. Overall, the angle detection error is within 10° when the neighboring emitters have a dipole angle difference of ≥30°.

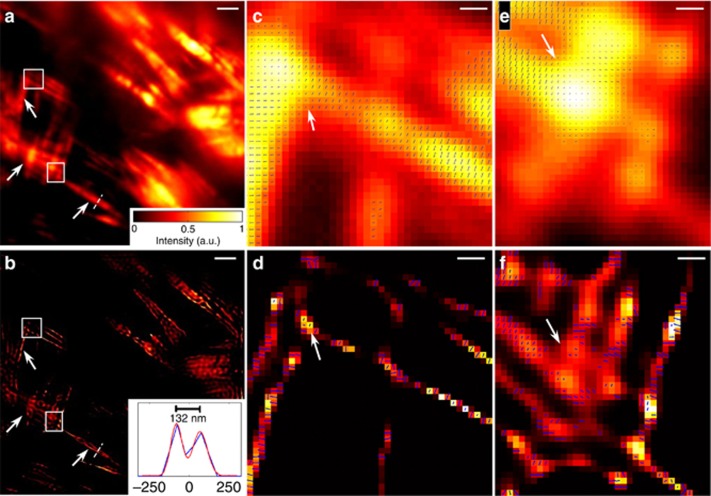
SDOM imaging of actin in fixed cells

The actin of a mouse kidney tissue slice labeled with Alexa Fluor 568 phalloidin (F-24630, Molecular Probes, Eugene, OR, USA) is investigated using the SDOM method; the fluorescence shows strong polarization. In the raw data, actin filaments of the same direction reach peak simultaneously, while filaments of different directions reach peaks at different polarization angles of the incident laser. Figure 4a shows the average intensity of 10 different fluorescence polarization-modulated images, being equivalent to that in the traditional wide-field image. Several neighboring filaments, indicated by arrows, could not be resolved by conventional microscopy but are distinguished by the super-resolved intensity image of SDOM (Figure 4b). In the intensity profile of Figure 4b, two filaments with a distance of 240 nm can be separated by SDOM, with 82 and 80 nm FWHM of each filament, calculated by double Gaussian fitting. Orientation mapping images using wide-field images (Figure 4c and 4e) and SDOM images (Figure 4d and 4f) are also compared. Because each single filament can be resolved in the SDOM images, the dipole orientation calculated is mostly influenced by fluorophores on the local filament. Thus, the fluorescent molecules with the same dipole orientation, or an isolated single-molecule, usually have a larger OUF, indicated by the lengths of the arrows. Because the OUFs in Figure 4c and 4e are very small, we have to magnify the OUF two-fold (which is proportional to the lengths of arrows labeled in the image), compared with the OUF in Figure 4d and 4f, so that it can be shown properly. We also find that in the SDOM images, the dipole orientation of fluorophores is mostly perpendicular to the direction of actin filaments, while in the wide-field images the orientation is nearly canceled by the different directions of actin filaments. This fact is consistent with the definition of OUF and strongly demonstrates the importance of super resolution in fluorescence polarization imaging.

Figure 4.

SDOM imaging of actin in fixed mammalian cells. Wide-field image (a) and SDOM image (b) of Alexa Fluor 568 phalloidin-labeled actin in fixed mouse kidney tissue cells. The diagram in b shows the intensity profile of the corresponding line indicated in a, b. (c, e) are zoomed-in wide-field orientation mapping images and (d, f) are zoomed-in SDOM images. Scale bar: (a, b) 2 μm, (c–f) 200 nm.

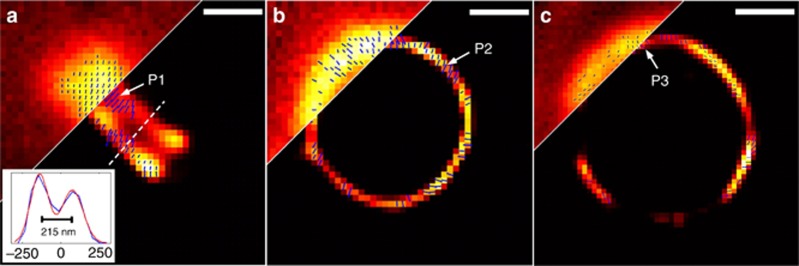
SDOM imaging of septin protein in live yeast cells

To test how well SDOM can be used in live cell imaging, the GFP-labeled septin protein (Cdc12) in S. cerevisiae cells^{6, 19, 33} is imaged. Septin is regarded as the fourth type of cytoskeleton³⁴ and shows strong fluorescence polarization as well. The cross-sectional view image (Figure 5a) and top-view image (Figure 5b) are orientation mapped with both wide-field images and SDOM reconstructed images, both of which are consistent with PolScope results¹⁹ but with higher resolution and higher OUF. The typical double-ring structure of the septin can be seen in the SDOM image; it cannot be distinguished in the wide-field image. The orientation mapped on the hourglass structure is consistent with PolScope results.¹⁹ To further illustrate how well SDOM can perform to detect the nucleus structure of live cells, the nuclear pore complex protein (Nic96) of S. cerevisiae cells, labeled with GFP, is also imaged using SDOM (Figure 5c); its fluorescent anisotropy was reported elsewhere²⁰.

Figure 5.

SDOM imaging of septin and nuclear pore complex protein in live yeast cells. (a) Orientation mapping images of GFP-labeled Cdc12 proteins in S. cerevisiae live cells (top view) with wide-field (upper-left) and SDOM (lower-right). (b) Cross-sectional view of GFP-labeled Cdc12. (c) Orientation mapping image of GFP-labeled nuclear pore protein, Nic96, in S. cerevisiae live cells. Scale bar=500 nm.

Limitation of our work

Although SDOM yields super-resolution information with orientation mapping, it has some limitations. For the SDOM results of S. cerevisiae live cells and the neuronal spine, some pixels containing a fluorescence signal cannot be mapped with orientation because the adjusted-R² is relatively small. Ideally, every pixel can be fitted with sinusoidal equations, even with a chaotic orientation distribution of dipoles within a PSF area. However, non-mapping can happen when the dipole orientation rapidly changes at a scale similar to that of image acquisition time or a high level of system noise (such as polarization distortion of the dichroic mirror, fluctuation of laser power and so on) buries the polarization modulation information. Moreover, in the SDOM algorithm, because the super-resolved orientation is mapped in two steps, that is, estimation of dipole intensity followed by estimation of dipole orientation, the error of the intensity estimation may be transferred to the orientation estimation. One-step orientation mapping may reduce the intermediate fitting error but will cause difficulty in formulating some criteria, such as OUF, to select robust orientations. Designing and establishing other algorithms to solve the orientation or orientation distribution at the super-resolution level will be part of our future work.

We should also note that the resolution of SDOM is related to the local distribution of dipole orientations. SDOM performs well with samples having similar dipole orientations rigidly attached to the subcellular structure, thus reflecting the underlying structure of the organelle. With densely labeled, homogenously orientated samples, SDOM can hardly resolve the polarization angle information due to the average of dipoles.

Conclusions

In 1995, the 2014 Nobel laureate Prof. Eric Betzig³⁵ proposed that super resolution can be obtained by separating neighboring molecules in different dimensions. Although various super-resolution techniques have been demonstrated based on fluorescence intensity with respect to wavelength (STED/PALM/STORM) and lifetime (pulsed and time-gated STED), the parameter of polarization, as the fourth dimension of fluorescence, has not been well-studied with respect to super-resolution techniques.

However, fluorescent dipole orientation is an important indicator of the underlying subcellular organelle structure and has been extensively studied in diffraction-limited microscopy, using fluorescence polarization techniques including linear dichroism^{1, 2, 3} and fluorescence anisotropy^{4, 5, 6}. The difference between the two techniques is that linear dichroism obtains the fluorescence polarization through excitation modulation with linearly polarized excitation light, while fluorescence anisotropy is obtained through the detection of polarized emission from fluorescent dipoles. Because fluorescence anisotropy is sensitive to the depolarization process, such as rotational diffusion or energy transfer², linear dichroism yields more accurate results with respect to the structure and functionality of the fluorescent molecules. In the past, fluorescence polarization was employed in the conventional microscopy setups, such as wide-field^{19, 36}, confocal^{2, 3}, two-photon excitation^{1, 23, 37, 38}, total internal reflection fluorescence²⁵ and fluorescence recovery after photobleaching^{22, 26}, to study protein structure and functions. Due to a large focal volume being limited by optical diffraction, all these techniques suffer from the same problem, that is, too many fluorophores within the focal volume may cancel the dipole orientation information.

The results presented here by using the SDOM method show the great advantage of mapping the dipole orientation information in a super-resolved manner once the super-resolution and fluorescence polarization methods work together. SDOM, using the same hardware setup and with advances in algorithms developed from its pioneering version, SPoD, developed by Hafi et al¹⁶, provides additional super-resolved information regarding the dipole orientation of fluorophores and reveals the structure and functionality of targeted subcellular organelles with greater detail. Here, we demonstrate that in both fixed cells and live cells, SDOM can yield dipole orientation information at super resolution. The fast imaging speed (at the second scale) also makes it possible to observe the dynamics of bioprocesses in live cells. Compared with traditional orientation mapping with wide-field images, SDOM not only provides higher resolution images but also fits the polarization-modulated data with a higher OUF, which makes the detection of orientation more robust to noise and the results more accurate with respect to local dipoles. Moreover, we show that super-resolution dipole orientation can bring us to a new level of understanding regarding biological systems, such as the perpendicular structure of actin, the radical orientation of the dipole on the Cdc12 septin protein and the inner-outer bilayer structure of the neuron axon membrane.

In this paper, we have demonstrated the SDOM super-resolution technique using both organic dyes and fluorescent proteins for a variety of biological specimens, such as a neuron, kidney slice and live yeast cell. It provides a completely new dimension—polarization—to super-resolution microscopy. Furthermore, with dipole orientation information at sub-diffractional resolution and a speed of 5 f.p.s., we believe that SDOM will attract immediate interest with regard to the super-resolution study of highly dynamic cellular processes. SDOM shows its advantages in comparing with the temporal resolution of PALM/STORM (at the level of several minutes) and the spatial resolution of SIM (>150 nm), which are not sufficient to fulfill expectations, and the power of STED (∼100 MW cm⁻²) may potentially inflict photodamage on the specimen. More importantly, SDOM is compatible with a wide range of conventional fluorescent dyes to yield super-resolution.