Skip to main content
PMC home page
Light, Science & Applications logoLink to Light, Science & Applications
. 2016 Jan 29;5(1):e16022. doi: 10.1038/lsa.2016.22

Repulsion of polarised particles from anisotropic materials with a near-zero permittivity component

Francisco J Rodríguez-Fortuño 1,*, Anatoly V Zayats 1
PMCID: PMC6059841  PMID: 30167119

Abstract

Reduction of adhesion and stiction is crucial for robust operation on nanomechanical and optofluidic devices as well as atom and molecule behaviour near surfaces. It can be achieved using electric charging, magnetic materials or light pressure and optical trapping. Here we show that a particle scattering or emitting in close proximity to an anisotropic substrate can experience a repulsive force if one of the diagonal components of the permittivity tensor is close to zero. We derive an analytic condition for the existence of such repulsive force depending on the optical properties of the substrate. We also demonstrate the effect using realistic anisotropic metamaterial implementations of a substrate. The anisotropic metamaterial approach using metal–dielectric and graphene–dielectric multilayers provides a tuneable spectral range and a very broad bandwidth of electromagnetic repulsion forces, in contrast to isotropic substrates.

Keywords: anisotropy, metamaterials, optical force, repulsion

Introduction

The concept of levitation of objects through action at a distance1 and the repulsion of particles from surfaces have great importance in nanotechnology, not only to reduce the unwanted adhesion and stiction of nanomechanical parts2,3 but also to achieve new functionalities in optofluidics and low friction devices4. Beyond trivial examples of repulsion of electric charges and magnetic poles or optical trapping in a focused laser beam, a specific permittivity and/or permeability of the material environment can be used to design electromagnetically facilitated forces. A magnet levitates above a superconductor which has a permeability µ = 0 and, thus, expels magnetic fields from its interior5,6. It has recently been shown that materials with a permittivity (ε) close to zero can be used for levitating an electric dipole7,8, since one of the defining characteristics of such ε-near-zero materials is the absence of electric displacement fields inside the material9. In the latter case, under the quasistatic approximation, valid when the dipole is very close to the surface, an electric dipole experiences an electromagnetic repulsive force away from a homogeneous isotropic substrate with complex relative permittivity ε, when the condition |ε|=|ε′+iε″|<1 is satisfied7. Such an isotropic ε-near-zero material can be implemented with natural materials near their (fixed) plasma frequencies7,10, but having |ε| ≈ 0 on demand at desired optical frequencies is challenging due to a limited range of available plasmonic materials and their losses at the plasma frequency11,12,13.

It has recently been shown that permittivity and permeability not commonly available in nature can be designed using metamaterials. The ε-near-zero properties discussed above have been achieved with both plasmonic and dielectric metamaterials and applied in a wide variety of applications such as phase front tailoring14,15,16, light supercoupling17,18,19,20,21,22, optical nanocircuits23, lensing24, cloaking25, nonlinearity enhancement26 and many others. Nevertheless, ε-near-zero properties have only recently been realised in the visible spectral range, requiring the use of very elaborate nanostructured three-dimensional metamaterials27,28 limited to micron-sized area samples and fixed light polarisations. At the same time, widely tuneable ε-near-zero behaviour is routinely achieved with anisotropic metamaterials with an effective permittivity tensor given by εeff = diag (εx,εy,εz) which can be fabricated in macroscopic-size implementations using nanowire composites29 or multilayered slabs30. Some components of the effective permittivity become close to zero at frequencies where the optical properties transition from conventional anisotropic to the so-called hyperbolic dispersion regime, when the real parts of εx = εy and εz have different signs26,31,32,33,34,35,36,37,38,39.

In this paper, we show that a particle with an induced electric dipole in near-field proximity to a uniaxial anisotropic substrate experiences a repulsive force if one of the components of permittivity is near-zero. We analytically derive the condition for repulsion and confirm the results with the exact electrodynamic calculations for specific examples of stacked slabs implementation of a metamaterial with metal or graphene multilayers. By dropping the requirement of an isotropic substrate, a much less stringent condition is sufficient to achieve repulsion of electromagnetic sources from an anisotropic material. This flexibility makes the proposed levitation suitable for experimental implementation with anisotropic ε-near-zero metamaterials40,41,42,43,44,45,46,47 at microwave and optical frequencies where both nanorod and multilayer composites of macroscopic sizes up to several centimetres are available48,49. The anisotropic metamaterials allow achieving a very broad spectral range where repulsive forces are induced, impossible with isotropic materials.

Materials and methods

We consider the electromagnetic force acting on an electric point dipole source with dipole moment p embedded in a medium with isotropic relative permittivity ε1 and located at a distance h above an arbitrary substrate. From the point of view of the dipole, oscillating at a given angular frequency ω, the knowledge of the substrate is entirely contained in the complex Fresnel reflection coefficients rp(kt) and rs(kt) for p- and s-polarisations, where 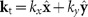Inline graphic is the transverse wave vector of the different spatial components of the dipole's fields. The vertical force acting on the dipole can be deduced from the Lorentz electromagnetic force acting on the oscillating charges of a dipole: the time-averaged force50,51 is 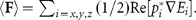Inline graphic By applying the spatial spectrum decomposition of the secondary fields of a dipole over a substrate (i.e., the reflected fields52), we obtain

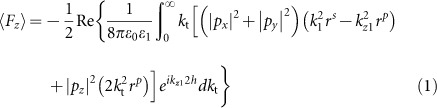graphic file with name lsa201622e7.jpg

where k1=k0n1=2πn1/λ0 is the wave vector in the upper medium, n1 is the medium refractive index, and 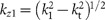Inline graphic. The only assumption made was the rotational symmetry of the reflection coefficients rp,s(kt)=rp,s(kt). The integral in Equation (1) effectively accounts for the force arising from the different spatial components of the reflected fields, spanning both the propagating kt ∈ [0,k1] and the evanescent kt ∈ [k1,∞] components. Equation (1) is an exact expression which is straightforward to numerically integrate. All the figures throughout the paper have been simulated using this exact formulation, but the initial discussion will focus on the quasistatic approximation, allowing analytical treatment in order to get an intuitive understanding of the phenomenon.

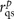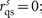The quasistatic approximation can be used when the dipole is very close to the surface of the uniaxial material h≪λ. In this case, the integral in Equation (1) is dominated by the integrand at very high values of kt≫k1, where the reflection coefficients approach constant limiting quasistatic values Inline graphic and Inline graphic the latter is zero in non-magnetic media since 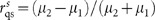Inline graphic. This approximation makes the integral analytically solvable, leading to a precise expression for the force at small heights over a non-magnetic medium7:

graphic file with name lsa201622e20.jpg

This force is typically attractive (〈Fz〉<0) towards the surface. However, a repulsive force (〈Fz〉>0) can be achieved if the condition 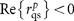Inline graphic can be realised.

Results and discussion

Dipole above uniaxial metamaterial

In the case of a uniaxial anisotropic substrate with the anisotropic permittivity εeff=diag(εx,εy=εx,εz) (Figure 1a), the p-polarised reflection coefficient is given by53,54,55

graphic file with name lsa201622e25.jpg

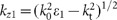where Inline graphic is the z-component of the wave vector in the upper space, while in the uniaxial substrate it is 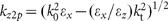Inline graphic for the extraordinary wave in the effective medium approximation. Assuming a non-absorbing superstrate (real ε1) and requiring the condition 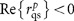Inline graphic, Equation (3) can be solved analytically for the repulsion of the dipole from the substrate:

graphic file with name lsa201622e29.jpg

This condition ensures the existence of the repulsive force 〈Fz〉>0 in the quasistatic approximation and provides a simple recipe for designing repulsive force for anisotropic substrates. It should be noted that if a dipole is placed in a medium with a high index material (e.g., water), repulsion is easier to achieve by using a lower-index isotropic dielectric as a substrate (Equation (4)). The real challenge, however, is to achieve repulsion in air or vacuum requiring |εx||εz|<1, which is the focus of this work. This is a much less strict requirement than for an isotropic substrate7 requiring |ε|<1. In particular, if one of the components of the permittivity tensor is close to zero, |εx|≈0 or |εz|≈0, the value of their respective counterpart components |εz| or |εx| can be high without affecting the condition for repulsion.

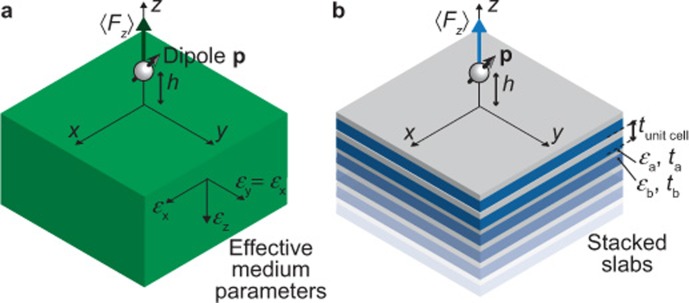
Figure 1.

Figure 1

Open in a new tab

Schematic diagram of a dipole above a uniaxial substrate. Electric dipole above a uniaxial anisotropic medium modelled with (a) effective medium theory and (b) stacked slabs implementation.

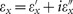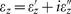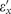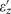The modulus operator in Equation (4) works on the complex relative permittivities Inline graphic and Inline graphic, so their imaginary part plays an important role. Nevertheless, since the condition given by Equation (4) is not a resonant phenomenon, realistic losses can be easily tolerated. Figure 2a maps the values of Inline graphic and Inline graphic for which repulsion is achieved for a dipole placed in air. To understand the role of losses, the repulsion condition is plotted for varying imaginary part (for simplicity, both permittivities are assumed to have equal imaginary parts 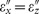Inline graphic). In the case of low losses, there exists a broad range of anisotropic permittivities where the repulsion force exists. 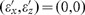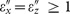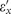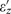With the increase of losses, the range of parameters becomes narrower around the point Inline graphic, so that for Inline graphic the condition |εx||εz|<1 is no longer satisfied in the quasistatic approximation for any real values of Inline graphic and Inline graphic.

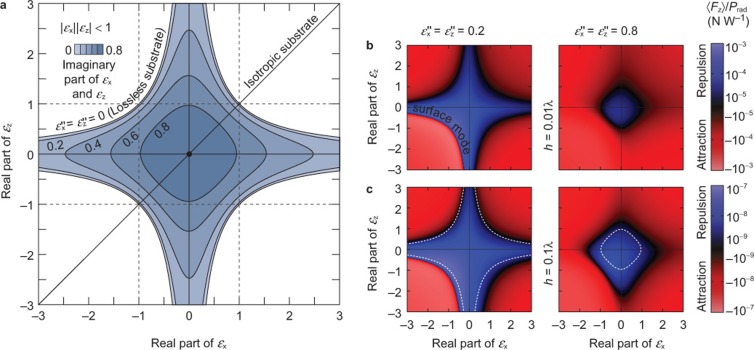
Figure 2.

Figure 2

Open in a new tab

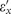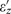Repulsive force dependence on the permittivity tensor components. (a) Parametric plot of the quasistatic repulsion condition (shaded area) for the particle in air |εx||εz|<1 as a function of the real parts of the permittivities Inline graphic and Inline graphic for different values of their imaginary parts 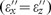Inline graphic. (b) Parametric plot of the exact vertical force calculated with Equation (1) for a vertically oriented dipole situated at a height h=0.01λ over a uniaxial substrate for two different values of losses. (c) Same as b but for a height h = 0.1λ, where the quasistatic condition does not apply. The permittivity range of the repulsive force is broader than in the quasistatic approximation shown with a dashed line.

The exact simulations using Equation (1) show that the repulsive force can be achieved in a broader range of parameters than estimated by the quasistatic condition (Figure 2b and 2c). However, for the increasing height h of the emitting dipole above the substrate, the force is reduced, following an h-4 dependence close to the substrate. Away from the substrate, the quasistatic limit (Equation (4)) does no longer exactly apply, and the condition for repulsion turns out to be relaxed, with slightly wider range of required permittivities. Also, notice in Figure 2b that a strongly enhanced force is observed near the surface mode resonance condition 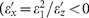Inline graphic when losses tend to zero), but this enhancement disappears completely with a slight increase in loss, due to its resonant nature. In contrast, the repulsive force near |εx||εz|≈0 is not resonant and robust to losses.

Dipole repulsion from multilayered metamaterial

As the next step, we consider a straightforward metamaterial implementation of the uniaxial metamaterial, consisting of stacked alternating slabs of two different materials (Figure 1b), one with relative permittivity 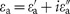Inline graphic and thickness ta, and the other with permittivity 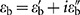Inline graphic and thickness tb. The total thickness of a unit cell is tunit cell=ta+tb, and the filling fraction of the first material is defined as fa=ta/tunit cell, while fb=1–fa. If the unit cell is sufficiently subwavelength, the metamaterial can be described as a homogeneous uniaxial medium (Figure 1a) with effective permittivities given by30

graphic file with name lsa201622e60.jpg

Thus, for a given value of filling fraction fa, the condition 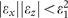Inline graphic can be mapped directly onto an equivalent condition for the materials’ permittivities of the multilayer εa and εb (Figure 3). This parametric plot allows straightforward design of the metamaterial to achieve repulsion in a given spectral range. As an example, we considered the case of the permittivities of silver (εa) and fused silica (εb)—the experimental values were taken from Refs. 56 and 57. By appropriately tuning the filling fraction of silver, different wavelength ranges can be selected to achieve a repulsive force, demonstrating the feasibility to adjust the metamaterial to work at any desired wavelength. For example, a stacked multilayer of silver and silica can achieve a repulsive force in the wide range between 600 nm and 700 nm by choosing a silver filling fraction of 0.1. For smaller thicknesses of the dielectric (larger fa), the requirements on the permittivity of metal are more stringently related to εa≈0, while for thicker dielectric layers (smaller fa), a very broad range of negative metal permittivities is acceptable to support repulsive force. The exact force (Equation (1)) calculated in the case fa=0.1 in the effective medium approximation is shown in Figure 3b, and agrees well with the analytically predicted wavelength range.

Figure 3.

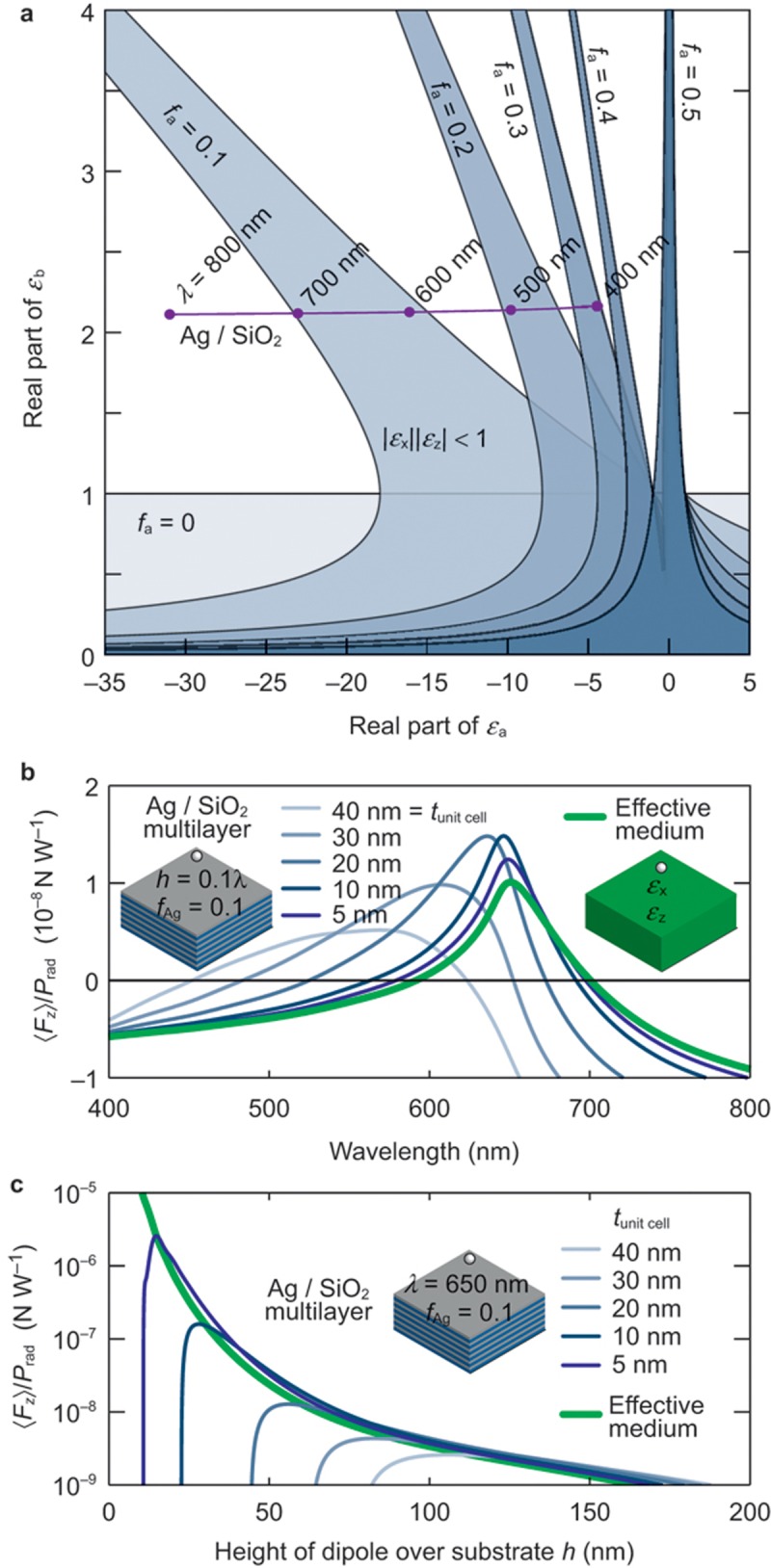
Figure 3

Open in a new tab

Repulsive force from metal–dielectric stacks. (a) Range of permittivities of the material constituents of the multilayer required to achieve repulsive force on the emitter in air in the effective medium approximation and neglecting material losses. Shaded areas correspond to the repulsive force for different filling fractions of the multilayer. If losses were increased, the shaded areas would become narrower and eventually disappear. Notice that when fa=0 (no material ‘a’), the repulsive condition becomes |εb|<1, corresponding to the known repulsion condition for an isotropic substrate. The horizontal line labelled Ag/SiO2 follows the permittivities of Ag and SiO2 layers at different wavelengths. (b) The spectral dependence of the force acting on a dipole at a height h=0.1λ above an Ag/SiO2 semi-infinite multilayered metamaterial with fAg=0.1 calculated using Equation (1) for different unit cell sizes, and for the equivalent homogeneous anisotropic effective medium. The low loss of silver in the visible spectral range56 Inline graphic allows the bandwidth of repulsion to almost match exactly that of the lossless case shown in a. (c) The height dependence of the force acting on a dipole at the wavelength of λ=650 nm. All other parameters are as in b.

In order to compare the effective medium theory predictions to the exact solutions for the multilayered composite, the reflection coefficient of the semi-infinite structure of stacked slabs in Equation (1) needs to be evaluated. The reflection coefficients of a multilayer can be analytically calculated using the well-known transfer-matrix method for 2N slabs (N unit cells) on a substrate55. The reflection coefficient of a semi-infinite stack of two alternating layers can be calculated as an eigenvalue problem55. We confirmed that, in all cases, increasing the number of unit cells converged towards the semi-infinite stack limit. As detailed in Ref. 55, the correspondence between the multilayered material and the equivalent effective medium breaks if the dipole is placed too close to the surface. In this case, the most rapidly decaying near fields dominate the force (large kt). For these kt, the evanescent fields decay so rapidly that they no longer “see” the stacked structure, and instead feel only the first material slab. In this case, the reflection coefficient approaches the quasistatic value of the reflection coefficient of the first interface between the superstrate ε1 and the first slab εa. Therefore, it is highly dependent on the material placed first55. Thus, in the quasistatic approximation kt→∞, valid when the dipole is very close to the semi-infinite stack, the dipole will only interact with the first interface (material εa), resulting in an attractive force (because |εa|>ε1) as shown in Figure 3c. The value of 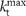Inline graphic for which the stack is a good approximation of the effective uniaxial medium can be increased if the unit cell of the multilayer is made smaller. Increasing the distance from the dipole to the surface attenuates the evanescent components with high 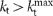Inline graphic. Thus, in order to achieve a repulsive force, we face a trade-off when using stacked slabs: either the dipole should be sufficiently far from the composite, so that only spatial components with fields that penetrate several layers dominate, or the unit cell is sufficiently thin to allow the strongly decaying near fields to penetrate several layers. This trade-off is clearly visible in Figure 3c. Nevertheless, in a reasonable range of small dipole heights and realistically big unit cells (Figure 3b), the force is repulsive and converges to that of the effective material model as the unit cell becomes smaller. Interestingly, the force is higher compared to the predictions of the effective medium model. For thicker unit cells, the force decreases but its bandwidth increases significantly (Figure 3b).

Increasing repulsion bandwidth

Isotropic ε-near-zero materials typically work in narrow bandwidths around specific frequencies. However, by properly engineering anisotropic metamaterials, we can achieve extremely large bandwidths of the anisotropic ε-near-zero property. The trend in Figure 3a for the repulsive force condition |εx||εz|<1 predicts an ever-increasing bandwidth as fa approaches zero and εb is close to 1. We will focus on achieving |εx|≈0 condition, which is sufficient to generate repulsive forces. The in-plane εx permittivity component of a stacked structure is simply the average of the constituent materials' permittivities, weighed by their filling fraction (Equation (5)). Therefore, near-zero εx can be easily achieved by combining positive (dielectric) with negative (metallic-like) permittivity materials, as shown above. In order to increase bandwidth, we consider two additional conditions: (i) a negative permittivity material εm with a very low filling fraction fm→0 (e.g., very thin films of a metal or other plasmonic material) and (ii) dielectric layers (filling fraction fd=1−fm) with a very low index εd≈1 (nanoporous polymer films of finely controllable thickness and low refractive indices close to 1 can be easily manufactured reproducibly and inexpensively, and are used as antireflection coatings58). From Equation (5), the condition |εx|<1 can be rewritten as |εdfd+εmfm|<1. Intuitively, the weighted average results in εx being lowered with respect to εd≈1, but not too much, thanks to the low filling fraction fm, resulting in |εx|<1. Importantly, the low filling fraction greatly reduces the frequency dispersion in εx, achieving a broad frequency range. We can describe this analytically as follows: the condition |εdfd+εmfm|<1 with εd≈1 can be rewritten as 1−2/fm<εm<1 (this inequality assumes a lossless metal, for simplicity of the argument, but the limiting case is also valid in the general lossy case, as shown later). As one can immediately see, when fm→0, the condition for |εx|<1 becomes simply εm(ω)<1, and such permittivity is ubiquitous in plasmonic materials for a wide range of frequencies. For Drude-like materials, the upper frequency bound is given approximately by the plasma frequency, while the lower frequency bound is limited in practice by the thinness of the negative permittivity material layer and by how close to 1 the permittivity εd of the dielectric slabs is. An analysis including losses yields the same conclusion: if we consider that εd≥1 is a lossless and dispersionless dielectric and 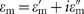Inline graphic, with 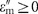Inline graphic, then the condition |εx|<1 can be written in terms of a required range of values for the real and imaginary parts of εm as follows:

graphic file with name lsa201622e114.jpg

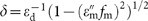where Inline graphic. In the limiting case of low filling factor fm→0, together with a low index dielectric εd=1, we obtain the simple condition 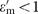Inline graphic described above, associated with very high bandwidths for plasmonic materials. This limiting case is true regardless of the losses since 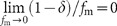Inline graphic when εd=1. In the general case, the existence of a lower and upper limit for 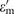Inline graphic determines a finite broad spectral range of repulsion, as seen in the following examples.

Figure 4a shows the repulsive force acting on a dipole above a structure of stacked thin gold films (experimental values of permittivity taken from Ref. 56) sandwiched between nanoporous polymer films58 (refractive index 1.05) with a very low metal filling fraction of 1/50, for different unit cell thicknesses, and compared to effective medium theory. The bandwidth of the ε-near-zero regime and the associated repulsive force is unusually large, spanning half the visible spectrum and most of the near infrared. In practice, the fabrication of extremely thin metallic films in a stack of nanoporous polymer can be challenging.

Figure 4.

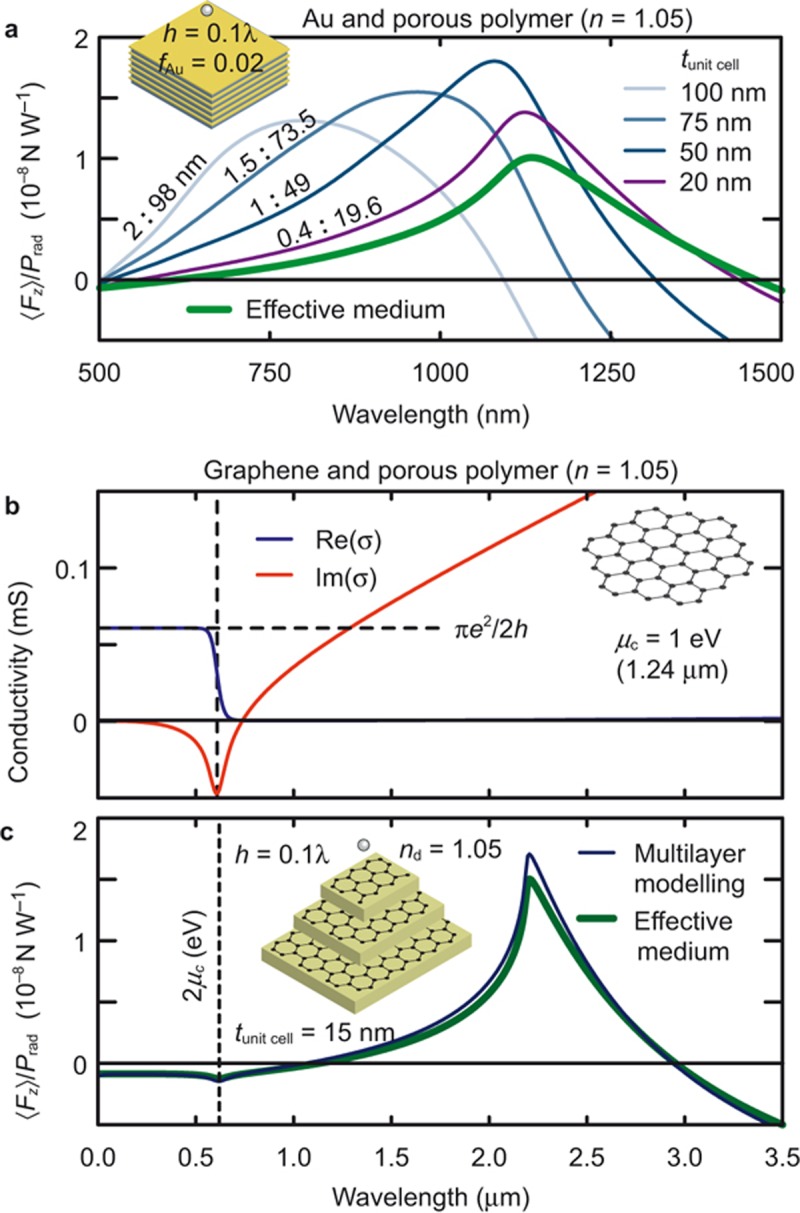
Figure 4

Open in a new tab

Repulsive forces with high bandwidth. (a) The spectra of the force acting on a vertical dipole at a height h=0.1λ above an Au/nanoporous polymer (n = 1.05) semi-infinite stack metamaterial with fAu = 0.02 = 1/50 for different unit cell sizes and for the equivalent homogeneous anisotropic effective medium. The thickness of gold and polymer slabs (in nm) is annotated for each plot. (b) The spectra of 2D sheet conductivity of a single sheet of graphene using the Kubo formula60,61, modelled with a scattering rate Γ=1.29 meV and chemical potential μc=1 eV. Regions of positive imaginary part of conductivity result in negative equivalent permittivity. (c) The spectra of the force acting on a dipole at a height h=0.1λ above a graphene/nanoporous polymer (n = 1.05) semi-infinite stack metamaterial for tunit cell = 15 nm and the effective medium approximation. The forces are calculated using Equation (1).

As an interesting solution to this problem, we suggest the use of graphene layers, known to be optically equivalent to extremely thin metal layers59 from zero frequency up to approximately ω<2μc/ħ, where μc is the chemical potential and ħ is the normalised Planck’s constant. The metallic character of graphene is realised when its sheet conductivity has a positive imaginary part59. In this regime, graphene is ideal to realise a vanishing filling fraction of negative permittivity material. Figure 4b depicts the sheet conductivity of a layer of graphene at room temperature, with a chemical potential of μc=1 eV. Graphene conductivity has been modelled using the Kubo formula60,61, which is known to fit well with experimental results. The scattering rate was set at Γ=1.29 meV, which is the highest value from Refs. 59,60,61, and the results do not depend strongly on the scattering rate. Figure 4c shows the corresponding repulsive force exerted on a dipole above a stack of such graphene layers, sandwiched between layers of 15 nm low-index nanoporous polymer films (n = 1.05). We can see a repulsive force in a wavelength range spanning a considerable part of the infrared spectrum (1.1−2.9 µm), which corresponds to a frequency range 100–270 THz. This constitutes a huge fractional bandwidth well beyond the possibilities of narrowband isotropic ε-near-zero materials, as discussed in detail below.

In the above considerations we modelled two-dimensional graphene using the approach described in the supplementary information of Ref. 59, summarised here. From Maxwell’s equation ∇×H=σvE−iωε0εE, a well-known equivalence between a conductor with volume conductivity σv and a dielectric with relative permittivity ε can be derived as ε=1+iσv/ωε0. A one-atom-thick system such as graphene does not have a well-defined volume conductivity, instead being characterised by a two-dimensional sheet conductivity, but both can be related if we consider a slab of conductor with thickness t in the z-direction. If t is sufficiently small (t≪λ) then E is approximately constant with z inside the slab, so the two-dimensional current density traversing a line element across the thickness of the slab is 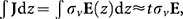Inline graphic equivalent to a sheet conductivity σ2D=σvt. This allows us to model graphene as a thin sheet of dielectric with a thickness-dependent permittivity given by ε=1+iσ2D/tωε0, in the limit of vanishing thickness. It follows that a negative real part in the equivalent permittivity (metallic character) is obtained when the sheet conductivity has a positive imaginary part. In graphene, the frequency up to which this metallic character is achieved is proportional to the chemical potential. As shown in Ref. 59, the thickness dependence in the optical properties cancels out for t→0 and the same behaviour as obtained by rigorous calculations using the sheet conductivity model of 2D graphene are recovered. With this model, we can easily calculate the reflection coefficient and forces for stacks of graphene layers and dielectrics in the same way as for metal–dielectric stacks. Using the same analytical transfer matrix method or the eigenvalue problem mentioned for semi-infinite stacks, we can consider any arbitrarily small thickness of graphene. We confirmed that the reflection coefficients and optical forces converged in all our results for the t→0 limit. In Figure 4c, we used a graphene thickness of 0.01 nm well inside the convergence region.

Comparison with isotropic ε-near-zero materials

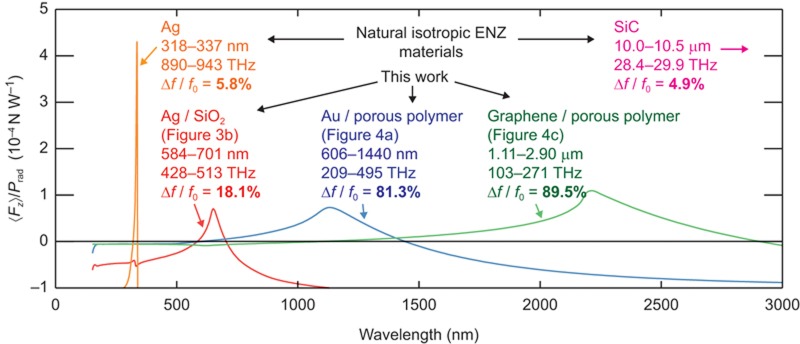
Some selected natural materials exhibit isotropic near-zero permittivity at their plasma frequencies or near permittivity resonances. Taking into account the required low loss conditions, repulsion can be observed for silver and silicon carbide at wavelengths of around 320 nm and 10 μm, respectively. This behaviour is fixed at a given wavelength and has a very narrow operating frequency bandwidth. Comparison of the metamaterial structures described above (with anisotropic ε-near-zero behaviour) and natural ε-near-zero materials, silver56 and hexagonal silicon carbide62, clearly shows the increased frequency range of the metamaterials (Figure 5). Changing the parameters of the anisotropic metamaterials, repulsion can be designed at any desired wavelength with a broad bandwidth.

Figure 5.

Figure 5

Open in a new tab

Comparison of repulsive force from isotropic and anisotropic ε-near-zero materials. Spectra of the force per unit radiated power acting on a vertical dipole situated at a height h=0.01λ above different ε-near-zero materials, including natural isotropic materials silver56 and silicon carbide62 and three anisotropic metamaterial realisations shown in Figures 3 and 4. Silicon carbide is represented only in labels (the related spectrum at around 10 µm is not shown in order not to obscure other spectra). The fractional bandwidth Δf/f0 is indicated, where Δf is the repulsion force bandwidth and f0 is the centre frequency of the repulsion force spectrum.

Isotropic and polarisation-independent ε-near-zero metamaterials have not been realised at optical frequencies so far. Implementations based on woodpile-type structures27 and on metal–dielectric stripes28 are remarkable examples of complex nanostructures with extreme optical parameters, but their ε-near-zero behaviour is polarisation dependent and fabrication is limited to microscopic sample sizes. In contrast, anisotropic implementations of ε-near-zero metamaterials can be fabricated with scalable fabrication techniques, such as multilayer deposition31,35,49 or electrochemical processing26,29,37,48, on macroscopic scales spanning squared centimetres. The practical (size and fabrication) and conceptual (tuneability of operation wavelength and bandwidth) advantage of using anisotropic ε-near-zero metamaterials is therefore evident for applications utilising repulsive optical forces.

Illumination of a polarisable particle

All the previous calculations assume an inherent radiating electric dipole source. Such a model can be applied to a variety of scenarios such as scattering from nanoparticles, dipole antennas, emitting quantum dots, molecules or atoms with transitions which can be adequately described by an electric dipole. In the case of dipole-like scattering from an illuminated small particle, the illuminating light will also exert a force on it and may influence the repulsion conditions. In order to account for this effect, we consider a nanoparticle with polarisability α placed at a location r0 at distance h over a surface, and illuminated with a plane wave (Figure 6a). An illuminating plane wave with electric field 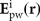Inline graphic is reflected by the surface, 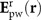Inline graphic, forming a standing wave 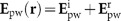Inline graphic. The dipole-like scattered field Es(r) of the polarized particle is also reflected by the surface, giving rise to the scattered-reflected fields 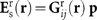Inline graphic, where 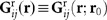Inline graphic is the Green function tensor of the scattered-reflected fields of a dipole over a surface52. The polarisation p of the particle is determined by the total incident electric field at r0, i.e. 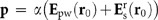Inline graphic. Since 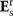Inline graphic itself depends on p, this equation has to be solved self-consistently giving 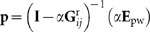Inline graphic, where I is the identity matrix. The matrix inversion is straightforward because 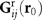Inline graphic is a diagonal tensor. Notice that the particle polarisation p tends to zero as the particle approaches the surface because the 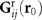Inline graphic diverge when h→0. The total vertical optical force acting on the dipole is given by 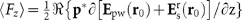Inline graphic, which can be divided into two terms 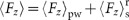Inline graphic corresponding to the gradient force due to the illuminating standing wave and the force due to the reflected dipolar scattering. The latter term corresponds to the force discussed in the previous sections. Both components of the force depend on the height of the particle with respect to the surface (Figure 6b).

Figure 6.

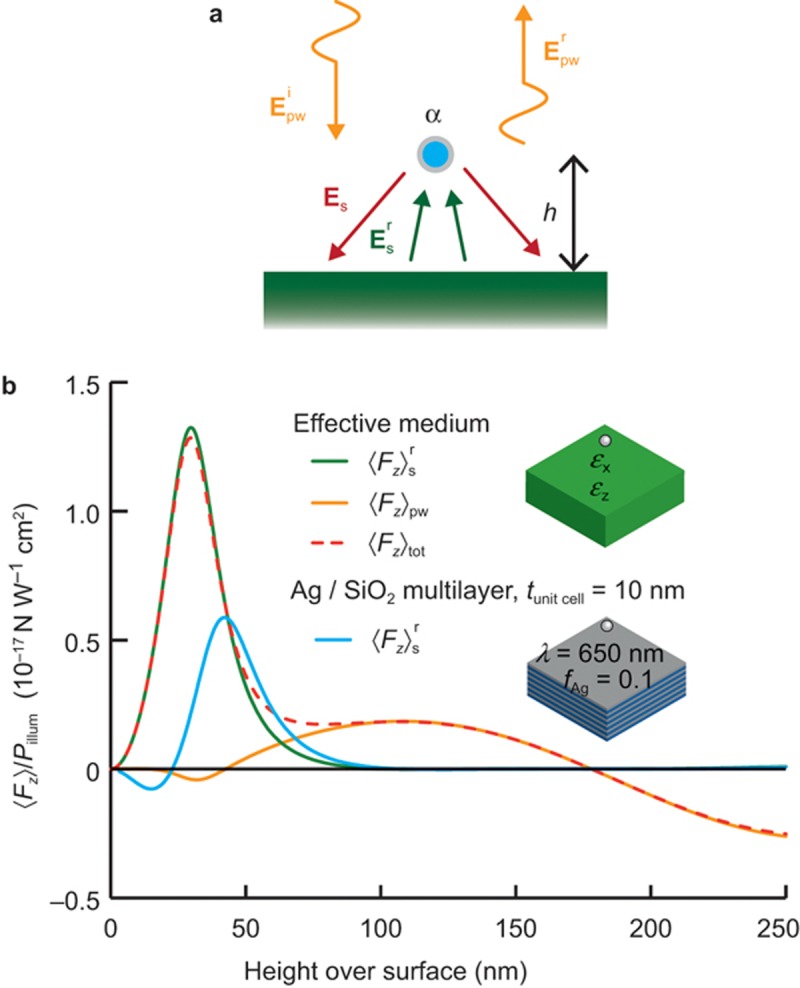
Figure 6

Open in a new tab

Repulsive forces on illuminated particle. (a) Schematic of a polarisable particle over a surface under plane wave illumination. (b) Different components of the vertical optical force acting on a polarisable particle over an Ag/SiO2 multilayer metamaterial (fAg=0.1) illuminated at a wavelength λ=650 nm at normal incidence with a power density of 1 W cm−2. Simulations with both the effective medium approximation and the semi-infinite multilayer structure (tunit cell=10 nm) are presented. The particle polarisability is (−3.92+2.37i)×10−32 C V−1 corresponding63 to a core-shell particle with SiO2 core (inner radius 27.1 nm) and Ag shell (outer radius 30 nm) designed to have a resonant polarisability near 650 nm. The 〈Fz〉pw component for the multilayer case is practically identical to that of the effective medium approximation and, therefore, not shown.

The repulsive force caused by the scattering 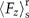Inline graphic dominates in the near-field region, as expected, while at larger distances the standing wave contribution dominates. This is valid for both the effective medium considerations and the stacked slabs implementation of the metamaterial. However, when the particle is too close to the surface of the stacked slabs, the effective medium approximation fails as the particle mainly “feels” the presence of the first layer only, and, therefore, the force is attractive as is typical for the |ε|>1 material of the top layer. The distance at which the force changes sign in the near-field can be controlled by appropriately changing the size of the unit cell of the metamaterial realisation. The observed repulsive forces are of the order of 10-14 N for illuminating intensities of 1 kW cm−2 (Figure 6b). Such intensity of illumination can be easily obtained using focusing with high numerical aperture objectives [e.g., 25 mW light focused on (50 µm)2].

Conclusions

We have shown that the condition for levitation of electromagnetic sources near an ε-near-zero material |ε|≈0 is greatly simplified if we allow the substrate to be anisotropic, by allowing the possibility that only one component of the permittivity tensor is near zero |εx||εz|≈0. This provides freedom for its design in all frequency domains, and readily available anisotropic ε-near-zero materials working at optical frequencies have already been demonstrated, with straightforward fabrication in wide areas up to several centimetres. The repulsion effect is non-resonant and insensitive to material losses. It is also tolerant to the effects of a finite unit cell in a metallo-dielectric stack: in fact, we showed that realistic metamaterial implementations (stacked slabs) not only do not degrade the performance, but actually can improve the repulsion bandwidth and strength compared to the effective medium theory. In addition, some natural crystals can behave as anisotropic ε-near-zero materials near the reststrahlen bands, typically in the mid-infrared spectral region64. Although the condition 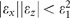Inline graphic is valid under the quasistatic approximation, we showed that taking retardation into account results in an even broader range of permittivity values that provide repulsion. All this amounts to a high robustness of the described repulsion effect. In stark contrast to the characteristic narrowband behaviour of natural isotropic ε-near-zero materials, we proposed a method to achieve an unusually wide bandwidth and tuneable spectral range of repulsion by using thin metallic film stacks or graphene stacks, sandwiched between low-index dielectrics.

Our calculations consider the force on a point electric dipole, thus the results should be applicable to small illuminated particles7,63,65 (scattering light in the Rayleigh limit), radiating fluorescent particles, quantum dots or radiating microwave antennas, where care should be taken to account for their size8. Importantly for applications, the described repulsive force on the dipole is a net force (averaged over a period of electromagnetic field oscillations), so the incoherence of radiation from fluorescent particles is not expected to be a problem as long as the coherence time is equal to several oscillations. Very interesting experiments and applications may involve reduced friction expected to occur on particles or atoms scattering near the proposed anisotropic metamaterials. Our calculations are purely classical, but in the optical regime, fluctuation-induced forces (Casimir/van der Waals) should be accounted for, and the wide bandwidth of repulsion presented opens the interesting possibility of a repulsive Casimir force for particles over these structures.

Authors’ contributions

FJR-F and AVZ have developed the concept. FJR-F has performed the simulations. Both authors have written the manuscript.

Acknowledgments

This work was supported, in part, by EPSRC (UK) and the ERC iPLASMM project (321268). AVZ acknowledges the support from the Royal Society and the Wolfson Foundation.

Note: Accepted article preview online 6 september 2015

Footnotes

The authors declare no competing financial interests.

References

  1. Brandt EH. Levitation in physics. Science 1989; 243: 349–355. [DOI] [PubMed] [Google Scholar]
  2. Maboudian R, Howe RT. Critical review: adhesion in surface micromechanical structures. J Vac Sci Technol B 1997; 15: 1–20. [Google Scholar]
  3. Tas N, Sonnenberg T, Jansen H, Legtenberg R, Elwenspoek M. Stiction in surface micromachining. J Micromech Microeng 1996; 6: 385–397. [Google Scholar]
  4. Munday JN, Capasso F, Parsegian VA. Measured long-range repulsive Casimir-Lifshitz forces. Nature 2009; 457: 170–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Hellman F, Gyorgy EM, Johnson DW, O’Bryan HM, Sherwood RC. Levitation of a magnet over a flat type II superconductor. J Appl Phys 1988; 63: 447–450. [Google Scholar]
  6. Tinkham M. Introduction to superconductivity. 2nd ed. New York: Dover Publications; 2004. [Google Scholar]
  7. Rodríguez-Fortuño FJ, Vakil A, Engheta N. Electric levitation using ϵ-near-zero metamaterials. Phys Rev Lett 2014; 112: 033902. [DOI] [PubMed] [Google Scholar]
  8. Krasikov S, Iorsh IV, Shalin A, Belov PA. Levitation of finite-size electric dipole over epsilon-near-zero metamaterial. Phys Status Solidi - Rapid Res Lett 2014; 8: 1015–1018. [Google Scholar]
  9. Alù A, Engheta N, Erentok A, Ziolkowski RW. Single-negative, double-negative, and low-index metamaterials and their electromagnetic applications. IEEE Antennas Propag Mag 2007; 49: 23–36. [Google Scholar]
  10. Naik GV, Kim J, Boltasseva A. Oxides and nitrides as alternative plasmonic materials in the optical range [Invited]. Opt Mater Express 2011; 1: 1090–1099. [Google Scholar]
  11. Monti A, Bilotti F, Toscano A, Vegni L. Possible implementation of epsilon-near-zero metamaterials working at optical frequencies. Opt Commun 2012; 285: 3412–3418. [Google Scholar]
  12. Sun L, Yu KW. Strategy for designing broadband epsilon-near-zero metamaterial with loss compensation by gain media. Appl Phys Lett 2012; 100: 261903. [Google Scholar]
  13. Zhou L, Song ZY, Huang XQ, Chan CT. Physics of the zeron̄ photonic gap: fundamentals and latest developments. Nanophotonics 2012; 1: 181–198. [Google Scholar]
  14. Enoch S, Tayeb G, Sabouroux P, Guérin N, Vincent P. A Metamaterial for Directive Emission. Phys Rev Lett 2002; 89: 213902. [DOI] [PubMed] [Google Scholar]
  15. Alù A, Silveirinha MG, Salandrino A, Engheta N. Epsilon-near-zero metamaterials and electromagnetic sources: tailoring the radiation phase pattern. Phys Rev B 2007; 75: 155410. [Google Scholar]
  16. Ziolkowski RW. Propagation in and scattering from a matched metamaterial having a zero index of refraction. Phys Rev E 2004; 70: 046608. [DOI] [PubMed] [Google Scholar]
  17. Alù A, Bilotti F, Engheta N, Vegni L. Metamaterial covers over a small aperture. IEEE Trans Antennas Propag 2006; 54: 1632–1643. [Google Scholar]
  18. Edwards B, Alù A, Young ME, Silveirinha MG, Engheta N. Experimental verification of Epsilon-near-zero metamaterial coupling and energy squeezing using a microwave waveguide. Phys Rev Lett 2008; 100: 033903. [DOI] [PubMed] [Google Scholar]
  19. Liu RP, Cheng Q, Hand T, Mock JJ, Cui TJ et al. Experimental demonstration of electromagnetic tunneling through an epsilon-near-zero metamaterial at microwave frequencies. Phys Rev Lett 2008; 100: 023903. [DOI] [PubMed] [Google Scholar]
  20. Silveirinha MG, Engheta N. Theory of supercoupling, squeezing wave energy, and field confinement in narrow channels and tight bends using ε near-zero metamaterials. Phys Rev B 2007; 76: 245109. [Google Scholar]
  21. Edwards B, Alù A, Silveirinha MG, Engheta N. Reflectionless sharp bends and corners in waveguides using epsilon-near-zero effects. J Appl Phys 2009; 105: 044905. [Google Scholar]
  22. Silveirinha MG, Engheta N. Tunneling of electromagnetic energy through subwavelength channels and bends using ε-near-zero materials. Phys Rev Lett 2006; 97: 157403. [DOI] [PubMed] [Google Scholar]
  23. Engheta N. Circuits with light at nanoscales: optical nanocircuits inspired by metamaterials. Science 2007; 317: 1698–1702. [DOI] [PubMed] [Google Scholar]
  24. Navarro-Cía M, Beruete M, Campillo I, Sorolla M. Enhanced lens by ε and μ near-zero metamaterial boosted by extraordinary optical transmission. Phys Rev B 2011; 83: 115112. [Google Scholar]
  25. Alù A, Engheta N. Achieving transparency with plasmonic and metamaterial coatings. Phys Rev E 2005; 72: 016623. [DOI] [PubMed] [Google Scholar]
  26. Wurtz GA, Pollard R, Hendren W, Wiederrecht GP, Gosztola DJ et al. Designed ultrafast optical nonlinearity in a plasmonic nanorod metamaterial enhanced by nonlocality. Nat Nanotechnol 2011; 6: 107–111. [DOI] [PubMed] [Google Scholar]
  27. Moitra P, Yang YM, Anderson Z, Kravchenko II, Briggs DP et al. Realization of an all-dielectric zero-index optical metamaterial. Nat Photonics 2013; 7: 791–795. [Google Scholar]
  28. Maas R, Parsons J, Engheta N, Polman A. Experimental realization of an epsilon-near-zero metamaterial at visible wavelengths. Nat Photonics 2013; 7: 907–912. [Google Scholar]
  29. Simovski CR, Belov PA, Atrashchenko AV, Kivshar YS. Wire metamaterials: physics and applications. Adv Mater 2012; 24: 4229–4248. [DOI] [PubMed] [Google Scholar]
  30. Schilling J. Uniaxial metallo-dielectric metamaterials with scalar positive permeability. Phys Rev E 2006; 74: 046618. [DOI] [PubMed] [Google Scholar]
  31. Poddubny A, Iorsh I, Belov P, Kivshar Y. Hyperbolic metamaterials. Nat Photonics 2013; 7: 948–957. [Google Scholar]
  32. Cortes CL, Newman W, Molesky S, Jacob Z. Quantum nanophotonics using hyperbolic metamaterials. J Opt 2012; 14: 063001. [Google Scholar]
  33. Podolskiy VA, Narimanov EE. Strongly anisotropic waveguide as a nonmagnetic left-handed system. Phys Rev B 2005; 71: 201101. [Google Scholar]
  34. Jacob Z, Alekseyev LV, Narimanov E. Optical hyperlens: far-field imaging beyond the diffraction limit. Opt Express 2006; 14: 8247–8256. [DOI] [PubMed] [Google Scholar]
  35. Liu ZW, Lee H, Xiong Y, Sun C, Zhang X. Far-field optical hyperlens magnifying sub-diffraction-limited objects. Science 2007; 315: 1686. [DOI] [PubMed] [Google Scholar]
  36. Salandrino A, Engheta N. Far-field subdiffraction optical microscopy using metamaterial crystals: theory and simulations. Phys Rev B 2006; 74: 075103. [Google Scholar]
  37. Kabashin AV, Evans P, Pastkovsky S, Hendren W, Wurtz GA et al. Plasmonic nanorod metamaterials for biosensing. Nat Mater 2009; 8: 867–871. [DOI] [PubMed] [Google Scholar]
  38. Kapitanova PV, Ginzburg P, Rodríguez-Fortuño FJ, Filonov DS, Voroshilov PM et al. Photonic spin Hall effect in hyperbolic metamaterials for polarization-controlled routing of subwavelength modes. Nat Commun 2014; 5: 3226. [DOI] [PubMed] [Google Scholar]
  39. Ginzburg P, Krasavin AV, Poddubny AN, Belov PA, Kivshar YS et al. Self-induced torque in hyperbolic metamaterials. Phys Rev Lett 2013; 111: 036804. [DOI] [PubMed] [Google Scholar]
  40. Cheng Q, Jiang WX, Cui TJ. Radiation of planar electromagnetic waves by a line source in anisotropic metamaterials. J Phys D Appl Phys 2010; 43: 335406. [Google Scholar]
  41. Zhou B, Cui TJ. Directivity enhancement to Vivaldi antennas using compactly anisotropic zero-index metamaterials. IEEE Antennas Wirel Propag Lett 2011; 10: 326–329. [Google Scholar]
  42. Cheng Q, Jiang WX, Cui TJ. Spatial power combination for omnidirectional radiation via anisotropic metamaterials. Phys Rev Lett 2012; 108: 213903. [DOI] [PubMed] [Google Scholar]
  43. He Q, Xiao SY, Li X, Zhou L. Optic-null medium: realization and applications. Opt Express 2013; 21: 28948–28959. [DOI] [PubMed] [Google Scholar]
  44. Sun L, Feng SM, Yang XD. Loss enhanced transmission and collimation in anisotropic epsilon-near-zero metamaterials. Appl Phys Lett 2012; 101: 241101. [Google Scholar]
  45. Feng SM. Loss-induced omnidirectional bending to the normal in ϵ-near-zero metamaterials. Phys Rev Lett 2012; 108: 193904. [DOI] [PubMed] [Google Scholar]
  46. Luo J, Xu P, Chen HY, Hou B, Gao L et al. Realizing almost perfect bending waveguides with anisotropic epsilon-near-zero metamaterials. Appl Phys Lett 2012; 100: 221903. [Google Scholar]
  47. Ma HF, Shi JH, Cai BG, Cui TJ. Total transmission and super reflection realized by anisotropic zero-index materials. New J Phys 2012; 14: 123010. [Google Scholar]
  48. Ginzburg P, Rodríguez-Fortuño FJ, Wurtz GA, Dickson W, Murphy A et al. Manipulating polarization of light with ultrathin epsilon-near-zero metamaterials. Opt Express 2013; 21: 14907–14917. [DOI] [PubMed] [Google Scholar]
  49. Rizza C, Di Falco A, Ciattoni A. Gain assisted nanocomposite multilayers with near zero permittivity modulus at visible frequencies. Appl Phys Lett 2011; 99: 221107. [Google Scholar]
  50. Nieto-Vesperinas M, Sáenz JJ, Gómez-Medina R, Chantada L. Optical forces on small magnetodielectric particles. Opt Express 2010; 18: 11428–11443. [DOI] [PubMed] [Google Scholar]
  51. Chaumet PC, Nieto-Vesperinas M. Time-averaged total force on a dipolar sphere in an electromagnetic field. Opt Lett 2000; 25: 1065–1067. [DOI] [PubMed] [Google Scholar]
  52. Novotny L, Hecht B. Principles of nano-optics. New York: Cambridge University Press; 2011. [Google Scholar]
  53. Lekner J. Reflection and refraction by uniaxial crystals. J Phys Condens Matter 1991; 3: 6121–6133. [Google Scholar]
  54. Saarinen JJ, Sipe JE. A Green function approach to surface optics in anisotropic media. J Mod Opt 2008; 55: 13–32. [Google Scholar]
  55. Kidwai O, Zhukovsky SV, Sipe JE. Effective-medium approach to planar multilayer hyperbolic metamaterials: strengths and limitations. Phys Rev A 2012; 85: 053842. [Google Scholar]
  56. Johnson PB, Christy RW. Optical constants of the noble metals. Phys Rev B 1972; 6: 4370–4379. [Google Scholar]
  57. Malitson IH. Interspecimen comparison of the refractive index of fused silica. J Opt Soc Am 1965; 55: 1205–1208. [Google Scholar]
  58. Walheim S, Schäffer E, Mlynek J, Steiner U. Nanophase-separated polymer films as high-performance antireflection coatings. Science 1999; 283: 520–522. [DOI] [PubMed] [Google Scholar]
  59. Vakil A, Engheta N. Transformation optics using graphene. Science 2011; 332: 1291–1294. [DOI] [PubMed] [Google Scholar]
  60. Hanson GW. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J Appl Phys 2008; 103: 064302. [Google Scholar]
  61. Gusynin VP, Sharapov SG, Carbotte JP. Magneto-optical conductivity in graphene. J Phys Condens Matter 2007; 19: 026222. [Google Scholar]
  62. Spitzer WG, Kleinman D, Walsh D. Infrared properties of hexagonal silicon carbide. Phys Rev 1959; 113: 127–132. [Google Scholar]
  63. Bohren CF, Huffman DR. Absorption and scattering of light by small particles. New York: John Wiley & Sons, Inc.; 1983. [Google Scholar]
  64. Falge HJ, Otto A. Dispersion of phonon-like surface polaritons on α-quartz observed by attenuated total reflection. Phys Status Solidi 1973; 56: 523–534. [Google Scholar]
  65. Shalin AS, Ginzburg P, Belov PA, Kivshar YS, Zayats AV. Nano-opto-mechanical effects in plasmonic waveguides. Laser Photon Rev 2014; 8: 131–136. [Google Scholar]

Articles from Light, Science & Applications are provided here courtesy of Nature Publishing Group

RESOURCES