Skip to main content
PMC home page
Light, Science & Applications logoLink to Light, Science & Applications
. 2016 Jan 1;5(1):e16003. doi: 10.1038/lsa.2016.3

High-efficiency surface plasmon meta-couplers: concept and microwave-regime realizations

Wujiong Sun 1, Qiong He 1,2, Shulin Sun 3,*, Lei Zhou 1,2,*
PMCID: PMC6059849  PMID: 30167110

Abstract

Surface plasmon polaritons (SPPs) and their low-frequency counterparts (i.e., spoof SPPs on artificial surfaces) have recently found numerous applications in photonics, but traditional devices to excite them (such as gratings and prism couplers) all suffer from problems of inherent low efficiency because the generated SPPs can decouple, returning to free space, and reflections at the device surface can never be avoided. Here, we propose a new SPP excitation scheme based on a transparent gradient metasurface and numerically demonstrate that it exhibits inherently high efficiency (~94%) because the designed meta-coupler suppresses both decoupling and surface reflections. As a practical realization of this concept, we fabricated a meta-coupler for operation in the microwave regime and performed near-field and far-field experiments to demonstrate that the achieved excitation efficiency for spoof SPPs reaches ~73%, which is several times higher than that achieved by other available devices in this frequency domain. Our findings can motivate the design and fabrication of high-performance plasmonic devices to harvest light–matter interactions, particularly those related to spoof SPPs in the low-frequency domain.

Keywords: metamaterial, metasurface, plasmonic coupler, surface plasmon polariton

Introduction

Surface plasmon polaritons (SPPs) are eigen electromagnetic (EM) waves bounded at certain dielectric/metal interfaces, with parallel wavevectors that are larger than the free-space value and EM fields that are highly confined near the interfaces1,2. Owing to their characteristics of local field enhancement and subwavelength confinement, SPPs have found many applications in photonics1,2, such as the enhancement of nonlinear3,4 and Raman effects5,6, chemical and bio-sensing7,8, plasmonic circuits9 and waveguides10,11, and subwavelength imaging12,13. Although natural SPPs do not exist at low frequencies (e.g., from the GHz to the middle infrared range), where the behavior of metals is too conductive, spoof SPPs can exist on certain artificial structured surfaces, and such spoof SPPS may find applications14,15,16,17,18,19,20 that are equally as numerous as those of their optical counterparts. To efficiently utilize SPPs and spoof SPPs, many couplers have been developed to convert incident propagating waves (PWs) into SPPs. However, the devices that are commonly used for this purpose, including prisms21,22,23 and grating couplers1,24,25,26, all suffer from low efficiency, which is inherent to such systems because the generated SPPs can also decouple back into PWs and initial reflections at the device surfaces are inevitable (see Figure 1a). Devices without translation symmetry (e.g., blade27,28 and defect29 couplers) possess even lower efficiencies because of the enhanced scattering at their sharp boundaries. In addition, some couplers (e.g., prism21,22,23 and blade27,28 couplers) are excessively bulky in size, making them inconvenient for integration into photonic devices.

Figure 1.

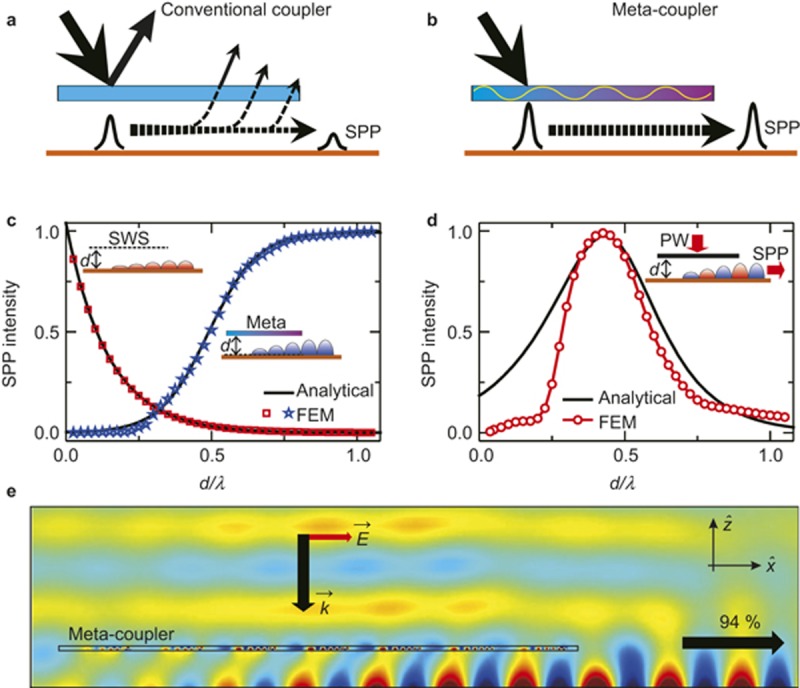
Figure 1

Open in a new tab

Device configuration, working principle, and coupling efficiency of the SPP meta-coupler. (a) Key factors that degrade the efficiencies of conventional SPP couplers (such as grating couplers and prism couplers): the initial reflection at the device surface and the decoupling from SPPs to free space. (b) Configuration of our SPP meta-coupler: a transparent gradient metasurface is placed at a distance d above the target plasmonic metal. The incident wave is first converted into a driven SW bound on the metasurface and is then resonantly coupled to the eigen SPP wave on the plasmonic metal. Neither reflection at the metasurface nor decoupling from the SPP to free space occurs. (c) FEM-stimulated intensities of SPP waves generated on the plasmonic metal versus the distance d in the excitation (red symbols) and scattering (blue symbols) processes compared with those calculated using the analytical formulas given in Equations (1) and (2) with k1= 210 m-1, α = 357.8, and k2=368 m-1 (lines). (d) Excited SPP intensities as a function of d when the meta-coupler is illuminated by an impinging wave with constant power, obtained via FEM simulations of the effective-medium model (symbols) and analytical calculations based on Equations (1) and (2) (line). (e) FEM-simulated (Hy) field distribution in the case of SPP excitation by our meta-coupler in an optimized configuration (with dc = 14.3 mm), showing that the highest SPP coupling efficiency is 94%. The εM(x) and μM(x) profiles are modified at the device corners and supercell boundaries to smooth the sharp discontinuities. In (c–e), the plasmonic metal (with εr = −4.33) supports an eigen SPP with kSPP = 1.14k0 at a working frequency of 9.2 GHz.

Recently, it was shown that a reflective gradient metasurface (a planar metamaterial consisting of designed EM units with tailored reflection phases) can convert a PW into a driven surface wave (SW) bounded on its surface with nearly 100% efficiency30. However, naively applying this concept to the design of an SPP coupler yields unsatisfactory results because the conversion efficiency decreases significantly as the width of incident beam increases31. The underlying physics of this phenomenon is that the driven SW generated is not an eigenmode of the gradient metasurface, and thus, it can experience significant scattering before coupling to an eigen SPP in the target system31. Other recently proposed metasurface-based SPP couplers32,33,34,35,36 also exhibit low efficiencies for similar reasons (i.e., decoupling and/or initial reflection).

In this article, we propose a new concept for realizing high-efficiency SPP couplers with deep-subwavelength thicknesses. Our device consists of a transparent gradient metasurface placed at a certain distance above the target plasmonic metal. This new device configuration resolves all previously identified issues that can degrade the PW-SPP conversion efficiency, and full-wave simulations of an ideal model predict an efficiency of 94%. As a practical realization, we designed and fabricated a realistic device operating in the microwave regime, and we performed both near-field (NF) and far-field (FF) experiments to demonstrate that our meta-coupler exhibits a spoof-SPP conversion efficiency of ∼73%, which is insensitive to the width of the incident beam. In particular, our experiments demonstrate that the performance of our meta-coupler is significantly higher than that achieved by any other available couplers (e.g., grating26 and blade28 couplers) in this frequency domain.

Materials and methods

New concept for realizing high-efficiency SPP excitation

As schematically shown in Figure 1a, the key factors that degrade the SPP coupling efficiency are the SPP decoupling effect and the reflection at the coupler surfaces. Such issues seem to be intrinsic to conventional couplers that exhibit lateral inversion symmetry (Supplementary Section 1). Inspired by our previous studies30,31, we here propose a new device configuration (Figure 1b) in which a slab of a transparent gradient metasurface (with a thickness dM much smaller than the working wavelength λ) serves as an SPP meta-coupler, which is placed at a distance d above the target plasmonic metal. To present quantitative arguments, we assume that the material properties of our meta-coupler are described by 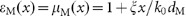Inline graphic, where ξ is the phase gradient and 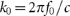Inline graphic (f0 and c are the working frequency and the speed of light in vacuum, respectively). To avoid excessively high values of εM and μM and for consistency with future practical design considerations, we introduce the super periodicity (L = 2π/ξ) to truncate the profiles of εM(x) and μM(x).

A careful analysis of the working principle of our meta-coupler indicates that the new device configuration has resolved all previously identified issues that can degrade the conversion efficiency. As a PW impinges on the meta-coupler at an incident angle θi, no initial reflection occurs because the meta-coupler is impedance-matched everywhere. Instead, a driven SW with a parallel wavevector kSW = k0 sin θi+ξ>k0 is induced on the surface of the meta-coupler, caused by the interference among the waves transmitted through the device at different local positions (Supplementary Section 2); this phenomenon can also be understood in terms of the generalized Snell’s law30,37. The driven SW can resonantly couple to an eigen SPP (with the parallel wavevector kSPP) on the bottom plasmonic metal when the condition kSPP = kSW is satisfied. The generated SPP wave cannot decouple back into a PW because the meta-coupler does not exhibit lateral inversion (x → −x) symmetry (Supplementary Section 2). Specifically, when the SPP wave couples back to the meta-coupler, the generated wave acquires an additional wavevector ξ, such that it becomes even more evanescent (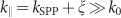Inline graphic) and thus cannot leave the interface. This is in stark contrast to previous schemes21,22,30,31, in which decoupling processes are always present. Moreover, the generated SPP no longer flows on the surface of the meta-coupler, and thus, the Bragg scattering by the periodic supercells on the metasurface is also significantly reduced, thereby solving the issue of beam-width dependence encountered in previous meta-couplers based on reflective metasurfaces30,31.

Let us now discuss how to achieve the highest possible PW-SPP conversion efficiency in this device configuration. The meta-coupler plays dual roles: (1) it mediates the coupling between the PW and SPP by generating a driven SW, and (2) it also weakly scatters the SPP by means of its lateral inhomogeneity. To understand the physics of the meta-coupler, we consider the following two independent processes. First, we replace the meta-coupler with a virtual surface wave source (SWS)30, 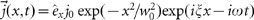Inline graphic (see the inset to Figure 1c. This virtual SWS can generate the same ‘driven SW’ that is induced by the meta-coupler illuminated by a normally incident Gaussian beam of waist width w0, but it does not scatter the generated SPP wave flowing on the plasmonic metal. This replacement is justified according to the argument presented in Ref. 27 (see Supplementary Section 2 for a detailed discussion). Numerical simulations based on the finite element method (FEM) reveal that the intensity I1 of the SPP generated on the plasmonic metal is a decreasing function of the distance d (red squares in Figure 1c), which can be perfectly modeled by the analytical formula postulated below:

graphic file with name lsa20163e5.jpg

where k1 is a fitting parameter that describes the decay rate of the evanescent wave. This expression has a clear physical meaning, because I1 should be proportional to the coupling strength between the driven SW and the eigen SPP and thus must follow an exponential function.

To study the second process, we replace the virtual SWS with the realistic inhomogeneous meta-coupler and study how the meta-coupler scatters an SPP wave that has already been launched on the plasmonic metal. FEM simulations indicate that the transmittance of the SPP wave, defined as I2/I1, is an increasing function of d (blue stars in Figure 1c), which can be well fitted by another postulated analytical formula:

graphic file with name lsa20163e6.jpg

where α and k2 are two additional fitting parameters. Equation (2) is also physically meaningful, as it exhibits the correct behaviors in two limits: the SPP wave exhibits a very small transmittance as d approaches zero (given that α is very large) and suffers only weak scattering 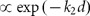Inline graphic when d is sufficiently large (see Supplementary Section 2).

Equations (1)–(2) not only provide a physical picture of the two competing processes (i.e., excitation and scattering) involved in our meta-coupler, but also suggest that a maximum SPP excitation efficiency can be achieved by carefully balancing these two effects. In a zero-order approximation, we can simply multiply the two expressions together to estimate the final SPP excitation efficiency (solid line in Figure 1d), where the efficiency is defined as the ratio between the power carried by the generated SPP and that carried by the impinging PW, and the result is found to agree very well with the result obtained via direct FEM simulations of the effective-medium model system (red circles in Figure 1d). Both calculations indicate that the highest SPP excitation efficiency can be obtained when d is fixed at a particular value dc. Figure 1e depicts the FEM-computed field pattern in a device with d = dc, for which the numerically calculated SPP coupling efficiency is found to be 94%.

Design and fabrication of an SPP meta-coupler

We now demonstrate the design presented in Figure 1 by means of a proof-of-concept experiment in the microwave regime. To fabricate the proposed meta-coupler, it is crucial to obtain a series of planar meta-atoms with a transmission amplitude of nearly 100% and a tailored transmission phase Φ that covers the entire 360° range. We find that an ABA sandwich structure, where A and B represent two ultra-thin layers of metamaterial (with thicknesses dA and dB, permittivities εA and εB and permeabilities μA = μB = 1), can support perfect transmission under normal incidence38,39,40 when the following condition is satisfied:

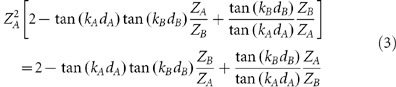graphic file with name lsa20163e8.jpg

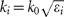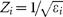where Inline graphic and Inline graphic, (i = A, B). Such a condition can be fulfilled with different combinations of materials and geometrical parameters. As an illustration, we present in Figure 2b the perfect transmission solutions (black solid line) in an εA versus εB diagram, with the other parameters fixed to f0 = 9.2 GHz, dA = 1.37 mm, and dB = 0.26 mm. Such a |t| = 1 line intersects with five representative equal-Φ lines (with a range of variation in Φ that covers the entire 360° space) at different positions. This is possible because the perfect transparencies in an ABA structure are governed by different mechanisms in different parameter regions of Figure 2b (Supplementary Section 4), such that the associated Φ varies within a very broad range. For example, whereas the scattering-cancelation mechanism is responsible for the transparency in the εA > 0, εB < 0 region38, the Fabry–Pérot resonance becomes the governing physics in the εA > 0, εB > 0 region. A large value of Φ is naturally expected when both εA and εB are large and positive (see Figure 2b). Considering other parameter freedoms (e.g., μA and μB), we expect that ABA structures can offer great flexibility in the design of the meta-atoms.

Figure 2.

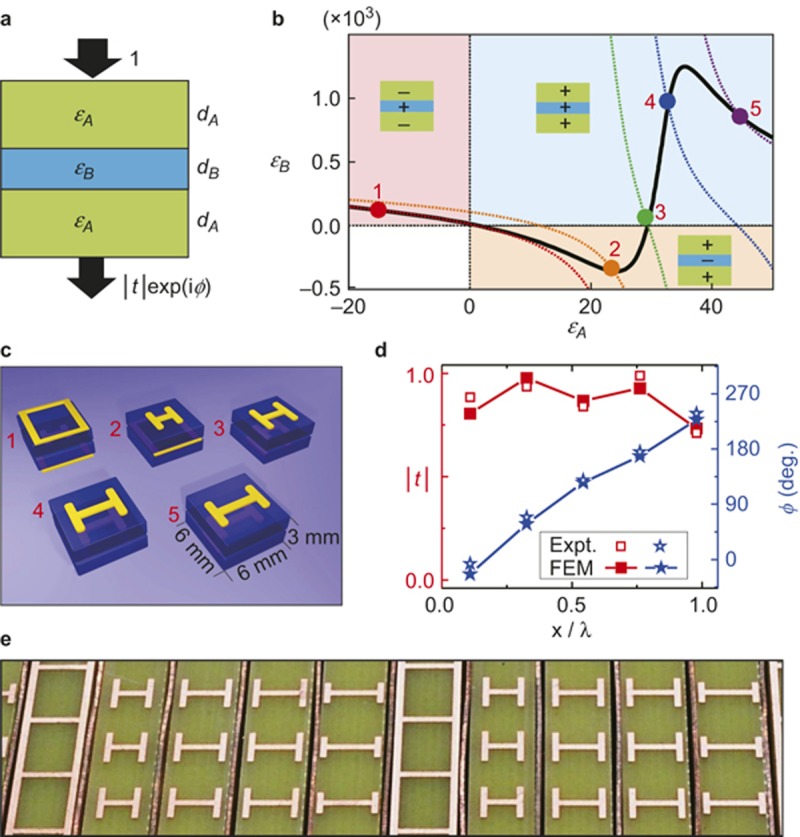
Figure 2

Open in a new tab

Model analysis and practical design of the meta-coupler. (a) The ABA structure, with a transmission coefficient of |t|exp(iΦ). (b) |t|= 1 line (black line) and five equal-Φ lines (red: Φ1 = 22°, orange: Φ2 = 94°, green: Φ3 = 166°, blue: Φ4 = 238°, purple: Φ5 = 310°) of the ABA structure (with μA = μB = 1, dA =1.37 mm, and dB =0.26 mm) in the εA−εB phase diagram. (c) Schematic diagrams of five designed meta-atoms, which are 6 × 6 mm2 ABA sandwich structures that consist of two identical metallic micro-structures of type A and another metallic micro-structure of type B separated by two 1.5-mm-thick dielectric spacers. (d) Measured and FEM-simulated transmission amplitudes (red squares, left axis) and phases (blue stars, left axis) of five slabs consisting of periodic arrays of different meta-atoms. (e) Image of part of the fabricated SPP meta-coupler. In the real sample, thin metallic sheets were inserted to separate two adjacent meta-atoms to reduce their mutual functional interferences.

These qualitative results motivated us to design five realistic meta-atoms with the structures shown in Figure 2c, where the metallic H-shaped structures and the mesh structures are used to obtain positive and negative ε values, respectively. The detailed structural parameters of these meta-atoms were chosen based on FEM simulations in which the NF couplings between neighboring metallic layers were fully taken into account (Supplementary Section 3). We then fabricated five samples based on these designs, each containing a periodic array of one of these meta-atoms, and performed microwave experiments to measure their transmission phases and amplitude spectra (Supplementary Section 3). At the central working frequency of f0 = 9.2 GHz, both the experiments and the FEM simulations indicate that these meta-atoms exhibit the desired transmission phases and high transmission amplitudes (Figure 2d). The transmission amplitudes do not reach 100%, however, primarily because of dielectric absorption and the inevitable fabrication errors that occur in such multilayered complex samples.

By arranging five meta-atoms sequentially in the x direction to form a supercell and then periodically replicating this supercell in two directions, we ultimately obtained the desired meta-coupler. Figure 2e shows an image of part of our fabricated meta-coupler (with a total size of 240 mm × 240 mm). Given that the length of each meta-atom is l = 6 mm and thus the length of a supercell is L = 5l = 30 mm, a simple calculation shows that the phase gradient of our meta-coupler is ξ = 2π/L = 0.94k0 at a frequency of f0 = 9.2 GHz. The fact that ξ < k0 implies that we must shine a PW at oblique incidence onto the meta-coupler to excite the desired SPP, which is helpful for distinguishing the specular reflection from the incident PW.

Results and discussion

Comparisons with other SPP couplers – near-field characterizations

Using the fabricated meta-coupler, we performed extensive experiments to demonstrate its ultra-high PW-SPP conversion efficiency. In the microwave regime, metals behave as perfect electric conductors and do not support natural SPPs. Therefore, we designed and fabricated a mushroom structure23 (see the inset to Figure 3b for its unit-cell geometry) that supported spoof SPPs to mimic a plasmonic metal. The FEM-simulated dispersion relation of the spoof SPPs on the mushroom structure is depicted as a solid red line in Figure 3b. To excite such spoof SPPs, we followed the scheme shown in Figure 1d to place our meta-coupler at an optimized distance dc =10 mm above the mushroom structure and then illuminated the meta-coupler with a PW incident at an angle of θi = 8°. We next placed a monopole antenna at a position 50 mm away from the coupler boundary to measure the local electric field of the SPP on the mushroom structure (Figure 3a). The open squares in Figure 3d illustrate how the measured SPP intensity (∝| Ez |2) varied as a function of frequency when the incident PW power was held constant. The measured SPP spectrum (open squares in Figure 3d) shows a pronounced peak at f0 = 9.2 GHz, where the resonant condition

graphic file with name lsa20163e11.jpg

is satisfied. To ensure that the measured |Ez| field indeed originated from the excited SPP wave, we performed NF scanning measurements30,41 to map the Re(Ez) field distribution on the ‘plasmonic metal’. The Re(Ez) pattern depicted in Figure 3c represents a very well-defined spoof SPP with a parallel wavevector of k‖ = 2π/λSPP = 216.7m−1, which is in good agreement with the theoretically calculated value (kSPP =210.3 m−1) at this frequency. Moreover, when we removed the meta-coupler from the mushroom structure and repeated the same measurement under the same illumination, we could not detect any signals on the mushroom structure.

Figure 3.

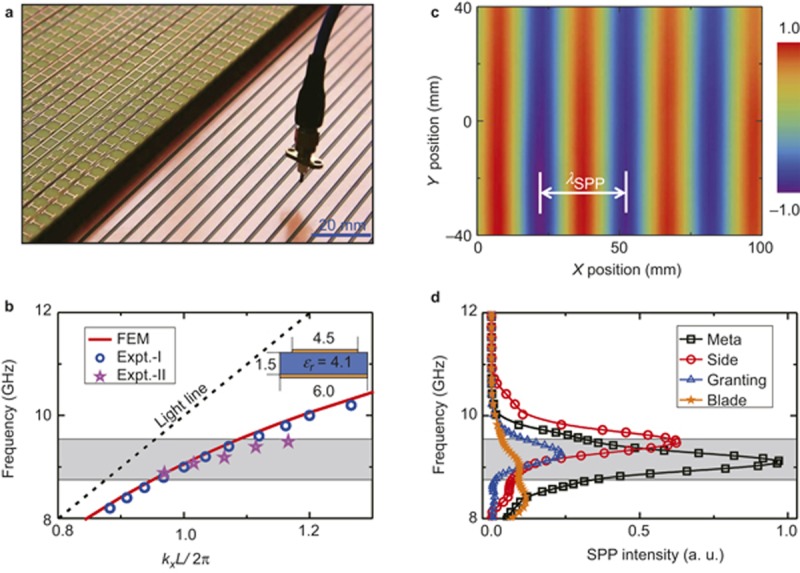
Figure 3

Open in a new tab

Near-field characterization of the meta-coupler. (a) Image of part of our experimental setup, in which the fabricated SPP coupler is placed at an optimized distance dc = 10 mm above the ‘plasmonic metal’. A monopole antenna is used to probe the SPP field distribution on the ‘plasmonic metal’. (b) Dispersion relation of the eigen SPP on the ‘plasmonic metal’, obtained via FEM simulations (solid line), direct near-field measurements (open circles) and retrieval from the SPP spectra (solid stars). The inset depicts the unit-cell geometry of the ‘plasmonic metal’, which consists of a metal stripe and a continuous metal separated by a dielectric spacer. All lengths are in units of mm. (c) Experimentally measured Re(Ez) field distribution on part of the ‘plasmonic metal’ when the meta-coupler is illuminated by an input propagating wave with a frequency of 9.2 GHz at an incident angle of θi = 8°. The origin (x = 0 position) is taken to be the point lying 60 mm from the coupler boundary. (d) Measured intensity spectra of the converted SPPs when different SPP couplers are placed at the same distance (10 mm) above the same ‘plasmonic metal’ and illuminated by the same input PW. The shaded region indicates the bandwidth of our meta-coupler, with boundaries defined by the condition that the SPP intensity decays to 1/ e of its maximum value.

Figure 3d shows that our meta-coupler exhibits a finite working frequency bandwidth (8.8–9.5 GHz), although it was designed for a target frequency of 9.2 GHz. This is because the meta-coupler is of finite size, and thus, the resonance condition given in Equation (3) need not be strictly satisfied. We retrieved the k|| values for the SPP waves excited at frequencies other than 9.2 GHz by means of the NF measurements and found that they agreed very well with the theoretical calculations (open circles in Figure 3b). Meanwhile, the peak SPP excitation frequency fP could also be tuned by changing the incident angle θi, in accordance with Equation (4); this behavior provided an alternative means of measuring the SPP dispersion relation. Assuming that ξ was insensitive to frequency, we experimentally studied how fP varied as a function of θi and then used Equation (4) to retrieve the SPP dispersion relation. The open stars represent the data obtained using this technique (see Supplementary Section 5 for the raw experimental data), which were found to agree well with both the FEM calculation and the direct NF characterization.

The performance of our meta-coupler is significantly superior to those of other available spoof-SPP couplers26,28,30 in the microwave regime. To ensure a fair comparison, we substituted a series of commonly used devices into our experimental setup in place of our meta-coupler and repeated the measurements in exactly the same configuration (with both the ‘plasmonic metal’ and the excitation PW unchanged). The other tested devices included a grating coupler, a blade coupler and a side coupler based on a reflective gradient meta-surface (see Supplementary Section 6 for the details of these devices). As shown in Figure 3d, the meta-coupler proposed in this paper exhibited the highest SPP excitation efficiency among all devices studied. In particular, the efficiency of our meta-coupler was found to be several times higher than those achieved by the grating and blade couplers. Compared with the side coupler, which already exhibits a reasonable conversion efficiency, the enhancement achieved by our meta-coupler is not as remarkable. However, the efficiency of the proposed meta-coupler is insensitive to the size of the wavefront of the input PW owing to its decoupling-free characteristics, whereas the efficiency achieved by the side coupler decreases significantly as the size of the input wavefront increases31, as demonstrated by our FEM simulations (Supplementary Section 7). Finally, we did not perform an experimental comparison with a prism coupler23 because such a device is extremely bulky in size, meaning that a comparison of such a device with the other ultra-thin devices considered here would not be very meaningful. However, numerical simulations (Supplementary Section 1) indicate that the performance of a prism coupler is much worse than that of our meta-coupler.

Efficiency of the meta-coupler—far-field characterizations

We now quantitatively examine the working efficiency of our meta-coupler by means of FF measurements. As schematically depicted in the inset to Figure 4a, three channels are available to transfer the energy of the impinging PW: scattering to the FF, absorption, and conversion into SPPs (including the desired mode to the right side and that to the left side arising from high-order diffraction). The SPP conversion efficiency can be quantitatively estimated using the formula η = 1− R − A, where R and A describe the scattered and absorbed energies, respectively. To experimentally determine R, we first rotated the receiver antenna to measure the angular power distributions for waves scattered to all possible directions at different frequencies. Figure 4a shows the normalized angular distributions of the scattered FF waves at two typical frequencies. Although the scattering was very strong dominated by specular reflection at a frequency of f = 8.2 GHz (outside the working frequency band of our meta-coupler), the scattering was very small at the working frequency of f = 9.2 GHz, implying that a significant amount of the impinging energy had been transferred into SPPs. To accurately determine R, we next integrated the scattered power over all directions and normalized this integrated value with respect to the total input power, which was obtained by following exactly the same procedure with the system replaced by a metallic plate of the same size.

Figure 4.

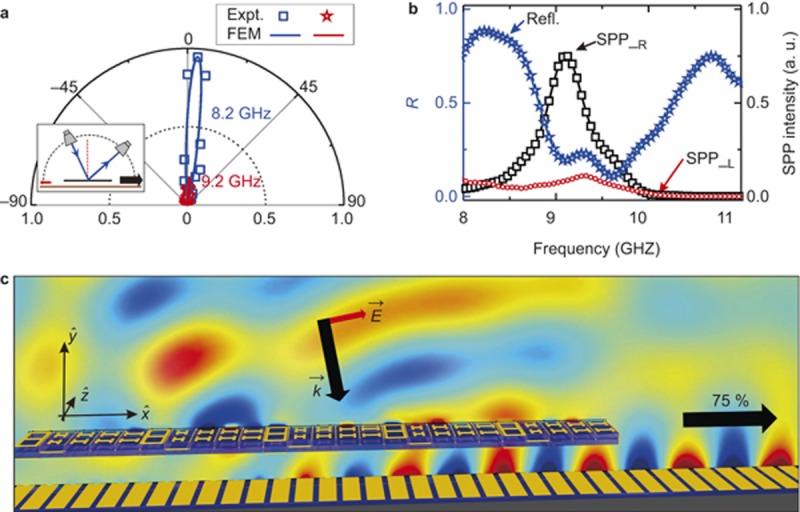
Figure 4

Open in a new tab

Far-field characterization of the meta-coupler. (a) Measured normalized angular distributions of scattered waves when the device is illuminated by input waves (at an incident angle of θi = 8°) at two frequencies, with the inset depicting a schematic illustration of our experimental setup. (b) Measured spectra of the integrated reflection (blue stars, left axis) and intensities of the excited SPPs (right axis) flowing to the right side (SPP_R, black squares) and left side (SPP_L, red circles) for our device illuminated by input beams with a fixed power. (c) FEM-simulated (Hy) field distribution for our device illuminated by an incident Gaussian beam at 9.2 GHz and θi = 8°. The SPP conversion efficiency, defined as the ratio between the power carried by the generated SPP flowing to the right side and that carried by the impinging wave, is found to be 75% based on the FEM-simulated field distribution.

The measured R spectrum is represented by open stars in Figure 4b, where a pronounced dip (R ∼ 20%) is observed at f0 = 9.2 GHz, coinciding very well with the peak in the measured right-side SPP intensity spectrum, which is re-plotted here (open squares). Although the absorption, A, is difficult to measure directly, we employed FEM simulations to obtain an approximate estimation of 4% (see Supplementary Section 3) at the working frequency. Finally, we note that the energy carried by the SPP wave flowing to the left side is non-negligible (red circles in Figure 4b); a simple calculation shows that the right-side SPP accounts for χ = 96% of the total SPP generated at the working frequency. Collecting all this information, we can use the formula ηR =(1 − R −A) χ to estimate that the SPP conversion efficiency of our device is 73% (with an error range of approximately ±2%) at the working frequency. This experimental value is quite close to the efficiency computed based on FEM simulations of realistic structures (75%), in which material absorption is fully taken into account (see Figure 4c for the FEM-computed field distribution). Although the demonstrated efficiency is already quite high, it can yet be further improved. For example, a more careful design could further enhance the overall transmission amplitude of the meta-coupler, which, in turn, could increase the final SPP conversion efficiency. In addition, using low-loss dielectric materials could also enhance the efficiency of our device by suppressing absorption.

Conclusions

We propose a new design concept for high-efficiency SPP couplers. The proposed device consists of a transparent gradient metasurface placed at an optimized distance above the target plasmonic metal. This new configuration resolves the key issues (i.e., initial reflection and SPP decoupling effects) encountered in previous SPP couplers that can degrade their efficiencies, resulting in an ideal working efficiency of ∼94%, as predicted by model calculations. As a practical realization of the proposed concept, we designed and fabricated a microwave spoof-SPP coupler and experimentally demonstrated that its working efficiency is ∼73%, which is much higher than those of all other available devices operating in this frequency domain. The presented device functions only for one polarization, but extensions to all-polarization SPP excitation are straightforward. Our novel concept can motivate the fabrication of high-performance plasmonic devices and applications related to spoof SPPs in the low-frequency regime ranging from the GHz to the middle infrared region. Although attempts to directly scale the present design to the optical regime might face fabrication challenges and inevitable issues of metal loss, recent remarkable advances in dielectric metasurfaces42,43 have enabled the possibility of realizing our concept in the high-frequency domain, and a simple design for λ = 1.55 μm is presented as a first example (Supplementary Section 8).

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Nos. 11474057, 11174055, 11204040, and 11404063), the MOE of China (B06011), and the Shanghai Science and Technology Committee (grant No. 14PJ1401200).

Note: Accepted article preview online 23 August 2015

Footnotes

Note: Supplementary information for this article can be found on the Light: Science & Applications' website (http://www.nature.com/lsa).

Supplementary Information

Supplementary Information
Click here for additional data file. (11.3MB, doc)

References

  1. Raether H.Surface Plasmons on Smooth and Rough Surfaces and on Gratings.Berlin: Springer; 1988. [Google Scholar]
  2. Barnes WL, Dereux A, Ebbesen TW. Surface plasmon subwavelength optics. Nature 2003; 424: 824–830. [DOI] [PubMed] [Google Scholar]
  3. Kim S, Jin J, Kim YJ, Park IY, Kim Y et al. High-harmonic generation by resonant plasmon field enhancement. Nature 2008; 453: 757–760. [DOI] [PubMed] [Google Scholar]
  4. Kauranen M, Zayats AV. Nonlinear plasmonics. Nat Photonics 2012; 6: 737–748. [Google Scholar]
  5. Kneipp K, Wang Y, Kneipp H, Perelman LT, Itzkan I et al. Single molecule detection using surface-enhanced Raman scattering (SERS). Phys Rev Lett 1997; 78: 1667–1670. [Google Scholar]
  6. Nie SM, Emory SR. Probing single molecules and single nanoparticles by surface-enhanced raman scattering. Science 1997; 275: 1102–1106. [DOI] [PubMed] [Google Scholar]
  7. Anker JN, Hall WP, Lyandres O, Shah NC, Zhao J et al. Biosensing with plasmonic nanosensors. Nat Mater 2008; 7: 442–453. [DOI] [PubMed] [Google Scholar]
  8. Zhang SP, Bao K, Halas NJ, Xu HX, Nordlander P. Substrate-induced Fano resonances of a plasmonic nanocube: a route to increased-sensitivity localized surface plasmon resonance sensors revealed. Nano Lett 2011; 11: 1657–1663. [DOI] [PubMed] [Google Scholar]
  9. Zia R, Schuller JA, Chandran A, Brongersma ML. Plasmonics: the next chip-scale technology. Mater Today 2006; 9: 20–27. [Google Scholar]
  10. Liu L, Han ZH, He SL. Novel surface plasmon waveguide for high integration. Opt Express 2005; 13: 6645–6650. [DOI] [PubMed] [Google Scholar]
  11. Bozhevolnyi SI, Volkov VS, Devaux E, Laluet JY, Ebbesen TW. Channel plasmon subwavelength waveguide components including interferometers and ring resonators. Nature 2006; 440: 508–511. [DOI] [PubMed] [Google Scholar]
  12. Fang N, Lee H, Sun C, Zhang X. Sub-diffraction-limited optical imaging with a silver superlens. Science 2005; 308: 534–537. [DOI] [PubMed] [Google Scholar]
  13. Gramotnev DK, Bozhevolnyi SI. Plasmonics beyond the diffraction limit. Nat Photonics 2010; 4: 83–91. [Google Scholar]
  14. Pendry JB, Martín-Moreno L, Garcia-Vidal FJ. Mimicking surface plasmons with structured surfaces. Science 2004; 305: 847–848. [DOI] [PubMed] [Google Scholar]
  15. Maier SA, Andrews SR, Martín-Moreno L, García-Vidal FJ. Terahertz surface plasmon-polariton propagation and focusing on periodically corrugated metal wires. Phys Rev Lett 2006; 97: 176805. [DOI] [PubMed] [Google Scholar]
  16. Williams CR, Andrews SR, Maier SA, Fernández-Domínguez AI, Martín-Moreno L et al. Highly confined guiding of terahertz surface plasmon polaritons on structured metal surfaces. Nat Photonics 2008; 2: 175–179. [Google Scholar]
  17. Gan QQ, Fu Z, Ding YJ, Bartoli FJ. Ultrawide-bandwidth slow-light system based on THz plasmonic graded metallic grating structures. Phys Rev Lett 2008; 100: 256803. [DOI] [PubMed] [Google Scholar]
  18. Yu NF, Wang QJ, Kats MA, Fan JA, Khanna SP et al. Designer spoof surface plasmon structures collimate terahertz laser beams. Nat Mater 2010; 9: 730–735. [DOI] [PubMed] [Google Scholar]
  19. Ng B, Wu JF, Hanham SM, Fernández-Domínguez AI, Klein N et al. Spoof plasmon surfaces: a novel platform for THz sensing. Adv Opt Mater 2013; 1: 543–548. [Google Scholar]
  20. Zhang HC, Liu S, Shen XP, Chen LH, Li LM et al. Broadband amplification of spoof surface plasmon polaritons at microwave frequencies. Laser Photon Rev 2015; 9: 83–90. [Google Scholar]
  21. Otto A. Excitation of nonradiative surface plasma waves in silver by the method of frustrated total reflection. Zeitschrift Phys 1968; 216: 398–410. [Google Scholar]
  22. Berini P. Long-range surface plasmon polaritons. Adv Opt Photonics 2009; 1: 484–588. [Google Scholar]
  23. Lockyear MJ, Hibbins AP, Sambles JR. Microwave surface-plasmon-like modes on thin metamaterials. Phys Rev Lett 2009; 102: 073901. [DOI] [PubMed] [Google Scholar]
  24. Lalanne P, Hugonin JP, Rodier JC. Theory of surface plasmon generation at nanoslit apertures. Phys Rev Lett 2005; 95: 263902. [DOI] [PubMed] [Google Scholar]
  25. López-Tejeira F, Rodrigo SG, Martín-Moreno L, García-Vidal FJ, Devaux E et al. Efficient unidirectional nanoslit couplers for surface plasmons. Nat Phys 2007; 3: 324–328. [Google Scholar]
  26. Akarca-Biyikli SS, Bulu I, Ozbay E. Resonant excitation of surface plasmons in one-dimensional metallic grating structures at microwave frequencies. J Opt A Pure Appl Opt 2005; 7: S159–S164. [Google Scholar]
  27. Saxler J, Rivas JG, Janke C, Pellemans HPM, Bolívar PH et al. Time-domain measurements of surface plasmon polaritons in the terahertz frequency range. Phys Rev B 2004; 69: 155427. [Google Scholar]
  28. Song ZY, Li X, Hao JM, Xiao SY, Qiu M et al. Tailor the surface-wave properties of a plasmonic metal by a metamaterial capping. Opt Express 2013; 21: 18178–18187. [DOI] [PubMed] [Google Scholar]
  29. Zayats AV, Smolyaninov II, Maradudin AA. Nano-optics of surface plasmon polaritons. Phys Rep 2005; 408: 131–314. [Google Scholar]
  30. Sun SL, He Q, Xiao SY, Xu Q, Li X et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat Mater 2012; 11: 426–431. [DOI] [PubMed] [Google Scholar]
  31. Qu C, Xiao SY, Sun SL, He Q, Zhou L. A theoretical study on the conversion efficiencies of gradient meta-surfaces. EPL 2013; 101: 54002. [Google Scholar]
  32. Lin J, Mueller JPB, Wang Q, Yuan GH, Antoniou N et al. Polarization-controlled tunable directional coupling of surface plasmon polaritons. Science 2013; 340: 331–334. [DOI] [PubMed] [Google Scholar]
  33. Miroshnichenko AE, Kivshar YS. Polarization traffic control for surface plasmons. Science 2013; 340: 283–284. [DOI] [PubMed] [Google Scholar]
  34. Rodríguez-Fortuño FJ, Marino G, Ginzburg P, O’Connor D, Martínez A et al. Near-field interference for the unidirectional excitation of electromagnetic guided modes. Science 2013; 340: 328–330. [DOI] [PubMed] [Google Scholar]
  35. Pors A, Nielsen MG, Bernardin T, Weeber JC, Bozhevolnyi SI. Efficient unidirectional polarization-controlled excitation of surface plasmon polaritons. Light Sci Appl 2014; 3: e197; doi:10.1038/lsa.2014.78. [Google Scholar]
  36. Huang LL, Chen XZ, Bai BF, Tan QF, Jin GF et al. Helicity dependent directional surface plasmon polariton excitation using a metasurface with interfacial phase discontinuity. Light Sci Appl 2013; 2: e70; doi:10.1038/lsa.2013.26. [Google Scholar]
  37. Yu NF, Genevet P, Kats MA, Aieta F, Tetienne JP et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 2011; 334: 333–337. [DOI] [PubMed] [Google Scholar]
  38. Zhou L, Wen WJ, Chan CT, Sheng P. Electromagnetic-wave tunneling through negative-permittivity media with high magnetic fields. Phys Rev Lett 2005; 94: 243905. [Google Scholar]
  39. Sun WJ, He Q, Hao JM, Zhou L. A transparent metamaterial to manipulate electromagnetic wave polarizations. Opt Lett 2011; 36: 927–929. [DOI] [PubMed] [Google Scholar]
  40. Song ZY, He Q, Xiao SY, Zhou L. Making a continuous metal film transparent via scattering cancellations. Appl Phys Lett 2012; 101: 181110. [Google Scholar]
  41. Ma HF, Cui TJ. Three-dimensional broadband and broad-angle transformation-optics lens. Nat Commun 2010; 1: 124. [DOI] [PubMed] [Google Scholar]
  42. Lin DM, Fan PY, Hasman E, Brongersma ML. Dielectric gradient metasurface optical elements. Science 2014; 345: 298–302. [DOI] [PubMed] [Google Scholar]
  43. Khorasaninejad M, Crozier KB. Silicon nanofin grating as a miniature chirality-distinguishing beam-splitter. Nat Commun 2014; 5: 5386. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (11.3MB, doc)

Articles from Light, Science & Applications are provided here courtesy of Nature Publishing Group

RESOURCES