Abstract
Extracting the light trapped in a waveguide, or the opposite effect of trapping light in a thin region and guiding it perpendicular to its incident propagation direction, is essential for optimal energetic performance in illumination, display or light harvesting devices. Here we demonstrate that the paradoxical goal of letting as much light in or out while maintaining the wave effectively trapped can be achieved with a periodic array of interpenetrated fibers forming a photonic fiber plate. Photons entering perpendicular to that plate may be trapped in an intermittent chaotic trajectory, leading to an optically ergodic system. We fabricated such a photonic fiber plate and showed that for a solar cell incorporated on one of the plate surfaces, light absorption is greatly enhanced. Confirming this, we found the unexpected result that a more chaotic photon trajectory reduces the production of photon scattering entropy.
Keywords: chaos, ergodicity, fiber, light-guiding plate, light harvesting, light trapping
Introduction
Light trapping and guiding in thin films combined with efficient light extraction or insertion in the direction orthogonal to the guiding one is essential to obtain energy-efficient light harvesting or emission. In this context, one is faced with two seemingly incompatible constraints—namely, to let as much light in or out as possible at any point on the guiding film surface while maintaining the light effectively trapped across the film. For several decades, in an attempt to maximize sunlight energy harvesting, researchers of thin film solar cells have been searching for the optimal system architecture to achieve the most effective light path ‘bending’ into the cell absorber layer1, 2. Many different approaches have already been explored. Texturing one or both surfaces of the film—in two or three dimensions—has been considered in several forms and instances. In organic cells, hexagonal arrays of nanocolumns3, 4 or nanoholes5 have been embossed in the active layer to increase light trapping by scattering.
Other thin film technologies, such as quantum dot solar cells, have used a light-trapping scheme with a nano-imprinted electrode capable of both diffracting light and collecting the photo-generated carriers6, 7, whereas in amorphous silicon solar cells, a whispering gallery light enhancement in nanospheres8, 9 has been used. Texturing the electrodes was also applied to organic cells using a periodic grating10, 11 or a random configuration12. Other approaches to increase the effective light path inside this type of cells have used plasmonic structures13. The presence of metallic nanoparticles increased the degree of light absorption and exciton dissociation14, 15. Different particle shapes have been used to enhance different parts of the spectra, such as nanocubes16 or oligomers17. In light-extracting devices with a similar configuration but a reverse direction of light flux—such as, for instance, in light-emitting diodes (LEDs)18 or displays19—adequate light energy management is another serious issue.
In films that are much thicker than the wavelength of the light, a random texturing of both film surfaces will produce a random distribution of light regardless of which direction the beam is coming from20, 21. This reduces the probability of escape once the light has been admitted inside the structure. One must take care, however, to introduce just the right amount of surface roughness required for ergodic behavior because even the slightest randomness may pose serious fabrication issues for the harvesting or illumination elements incorporated on them. This is why recent research efforts have aimed at achieving ergodicity within an ordered configuration: a metallic grating structure22, a pyramidal rear reflector23, 24, a microprism textured surface25, a V-shaped tandem device26, a V-groove surface texturing27 or an array of microlenses28 providing total internal reflection at the external device surface have been used to increase the amount of light that passes through the energy conversion layer. However, the goal of ergodic behavior could not be reached or demonstrated.
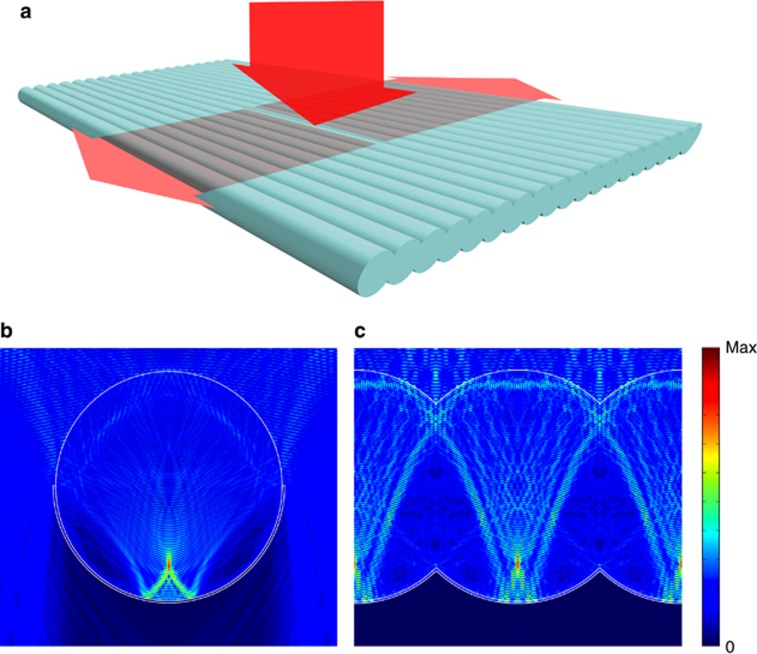
To achieve the goal of ergodicity within order, we propose a fundamentally new design based on a light-guiding plate formed by an array of interpenetrating fibers, shown schematically in Figure 1a. In such a photonic fiber plate (PFP), both front and back surfaces are equally textured. We define the cylinder interpenetration 𝓁/d as the ratio between the period of the array and the cylinder diameter. To evaluate the light-harvesting capacity of this PFP, we consider the case in which the back surface is covered by a multilayer nanostructure and a highly metallic reflective layer. We analyze the light propagation in this structure by implementing a full-wave vector numerical analysis that assumes a plane wave incident on the fiber array normally to the plane defined by the array. As observed in Figure 1b, when the plane wave is incident on an isolated fiber, equivalent to a non-interpenetrating fiber array, the incoming wave is focused toward the center of the fiber and interferes with the reflected wave, forming a fairly regular interference pattern with no apparent signs of light trapping. In contrast, when the cross-sections of the fibers overlap (𝓁/d<1), as observed in Figure 1c, the regular pattern breaks up into a more disordered pattern.
Figure 1.
Light trapping in a PFP. (a) Schematic drawing of light incidence and trapping in the PFP. Cross section of the electrical field distribution when a plane wave is incident, (b) on an isolated fiber and (c) on an array of intercalated fibers. Higher-intensity fields on the caustic coupling to the adjacent fibers are clearly visible in c. The numerical calculation was performed assuming an incident plane wave at λ=580 nm propagating normally to the axis of the fibers, whose diameters were set to 20 μm. In c, the period of the array was taken as 14.14 μm. In both configurations, the lower half of the fibers (n=1.46) was assumed to be coated by a dielectric multilayer characterized by the sequence of refractive indexes and thicknesses given in the caption of Figure 4. To better visualize the light trapping in the PFP, the imaginary part of the refractive index was assumed to be zero for all layers. Finally, on the bottom, a perfect electric conductor was introduced as a perfect mirror.
Part of the light intensity distribution of the caustic in one fiber connects to a whispering gallery mode (WGM) on the top interface of the adjacent fibers. Thus, the opening between fibers allows for an effective trapping of the incident light. In addition, polygonal interference patterns with widely varying orientations are observed across the bulk of the fiber array. This indicates that light is not just propagating back and forth between the top and bottom interfaces, as is essentially the case for isolated fibers, but rather in all directions, leading to the desired ergodic behavior.
Materials and methods
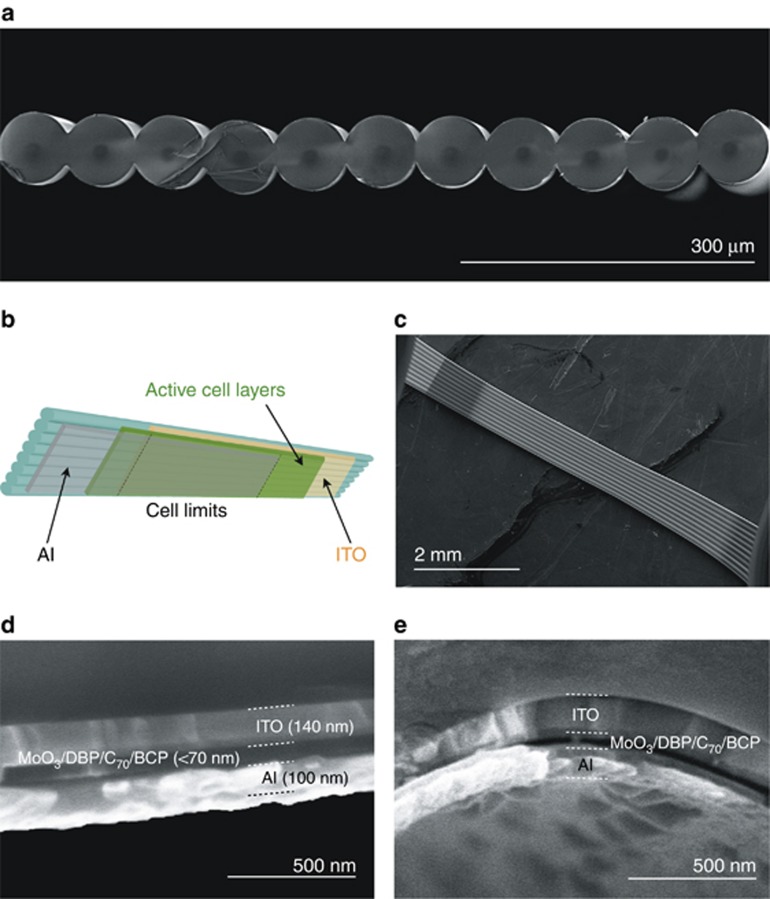
We implemented an experimental demonstration of light trapping and absorption in arrays of intercalated fibers by fabricating a PFP composed of a number of standard optical fibers ranging from 10 to 15. To reach the desired degree of interpenetration between adjacent fibers, the fibers were laid against each other, heated and pulled simultaneously. Details of the procedure followed to obtain the fiber array whose cross section is shown in Figure 2a can be found in section SI1 of the Supplementary Information. In contrast to a configuration with a random texturization of the surface, the smooth surface of the periodic fiber array allows for the deposition of high-quality layered devices such as a thin film solar cell (Figure 2b and 2c). Details of the evaporation of a small-molecule organic solar cell when using the fiber array as the substrate are given in section SI2 of the Supplementary Information. The architecture of the fabricated solar cell, shown in Figure 2d and 2e, incorporates a junction of a 10 nm Tetraphenyldibenzoperiflanthene (DBP) layer and a 40 nm C70 layer as donor and acceptor materials, respectively. The conformal and high-quality layer deposition at the central part of any given fiber and at the intersection between two adjacent fibers is show in Figure 2d and 2e, respectively. Changes in layer thickness (if any) are at the nanometric scale.
Figure 2.
Fabricated PFP solar cells. (a) SEM cross-section image of a fabricated array containing 11 fibers of 70-μm diameter. The average interpenetration parameter is 𝓁/d∼0.95. (b) Schematic drawing of a solar cell deposited on the PFP where the different layers are the transparent conducting electrode ITO (yellow); the hole-transporting layer MoO3, the bilayer junction of DBP/C70 and the electron transporting layer BCP (green); the Al back contact (gray). (c) SEM image of a PFP where an organic solar cell was deposited on one side of the plate. The changes in the gray tone are indicative of the different cell layers. SEM cross-section images of the cell layers, (d) at the bottom of a given fiber and (e) at the intersection in between two adjacent fibers. From the top edge of d and e, one can see the glass fiber and the ITO layer (140 nm), followed by a darker zone corresponding to the semiconductor organic junction (~50 nm) and finally a brighter layer corresponding to the back Al contact (100 nm). All such layers, including the buffer layers (not visible in the image) were conformal with the curvature of the fibers in both regions d and e. BCP, Bathocuproine; ITO, Indium tin oxide.
Results and discussion
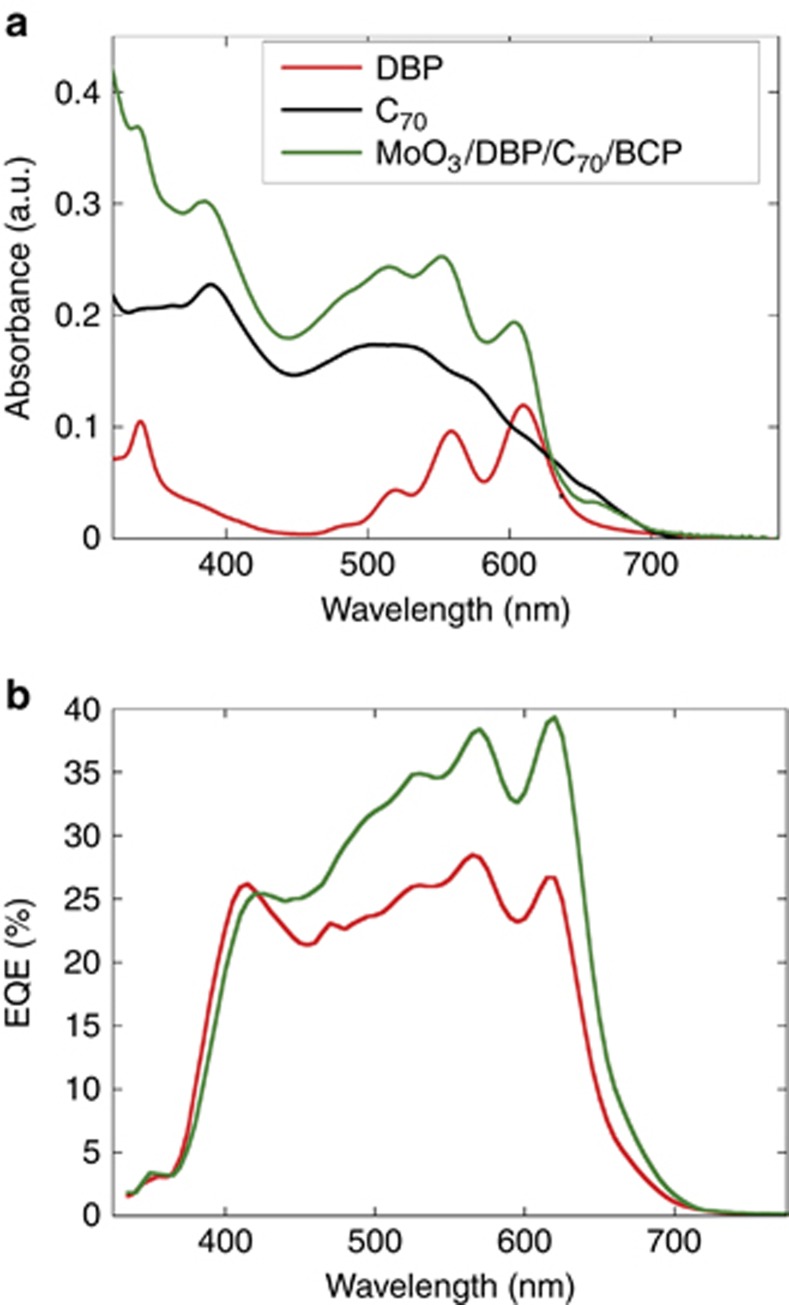
The nanometric thicknesses of the active layers, which are necessary for optimal exciton separation and charge collection, limit the effective light harvesting by the DBP/C70 junction, whose absorbance is shown in Figure 3a. The level of light trapping in the PFP that can compensate for such a small thickness of the junction can be determined by evaluating the performance of the solar cell relative to the same cell deposited on a flat glass substrate. The light-harvesting capacity of the cell evaporated on the PFP substrate was determined by first measuring the current density versus the applied voltage on the cell. A comparison of the measured photovoltaic parameters (given in Table 1) to the reference cell deposited on a flat substrate indicate a 34% increase in short circuit current or, equivalently, in light-harvesting capacity. In addition, it is important to note that as observed in Table 1, deposition of the cell on the PFP does not imply any relevant change in the photovoltaic (PV) parameters more directly linked to the electrical performance of the solar device, such as the fill factor (FF) or the open circuit voltage (VOC). On average, only a 6% decrease was observed in the FF, whereas for the VOC, even slightly better values could be obtained for cells on the PFP relative to cells on flat substrates. The efficiency in converting incident photons to collected charges can be further investigated by measuring the external quantum efficiency, shown schematically in Figure 3b. This measurement confirms an increase larger than 30% in light harvesting by the fiber array relative to the planar configuration.
Figure 3.
Absorption and charge collection enhancement. (a) Absorbance of a 10-nm layer of DBP (red), a 40-nm layer of C70 (black) and the active plus buffer layers in the cell architecture (green). (b) Measured EQE of a PFP organic solar cell (green) compared with a planar one (red line) with the same architecture depicted in Figures 2b and 4a. EQE, External quantum efficiency.
Table 1. Cell performance (J–V measurements).
| PV parameters cell type | Voc (mV) | FF (%) | Jsc (mA cm−2) | Efficiency (%) |
|---|---|---|---|---|
| PFP | 850.9±10.5 | 52.2±4 | −4.9±0.4 | 2.19±0.03 |
| Planar | 837.6±9.2 | 55.9±3 | −3.7±0.2 | 1.72±0.15 |
| Percentage change | +1.6% | −6.5% | +34% | +27% |
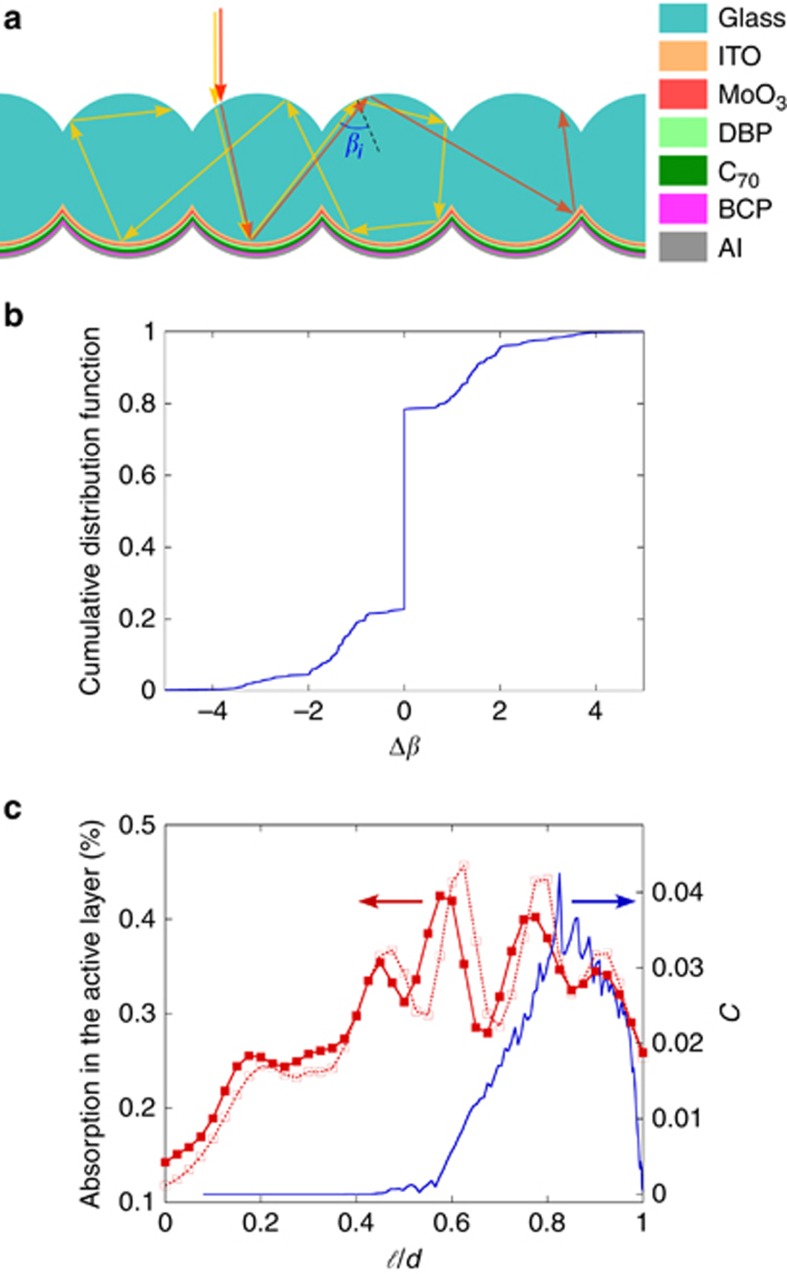
To gain further insight into the nature of photon propagation leading to enhanced absorption in the PFP, we consider the trajectory followed by normally incident photons (Figure 4a). Such photons follow a ballistic ray trajectory unambiguously determined by Fresnel laws of reflection and refraction. Elementary geometrical considerations show that consecutive bounces (labeled by j) within the same fiber preserve the angle of internal reflection βj:
Figure 4.
Chaotic photon trajectories in the PFP. (a) The chaotic character in the photon trajectory is schematically shown by considering slightly different incident positions rapidly leading to completely distinct paths. Here a change in the incidence corresponds to a lateral displacement of the ray without any angle change. Note that inside the fourth fiber, ray trajectory 1 follows a regular sequences of reflections akin to whispering gallery modes until crossing the gap connecting the fourth with the third fibers, at which point it undergoes a sudden change in reflection angle Δβ≠0. (b) CDF of the change in Δβ over a long series of computed ray segments, all produced by the same incident ray. The jump at Δβ=0 indicates that most of the ray trajectory is regular, and the observed chaos is of the intermittent type. The CDF depends on a single geometrical parameter, the ratio 𝓁/d between the array period and the fiber diameter (here: 0.92). (c) Full-wave simulation of absorption in the active layer at 580 nm (solid red squares) and at 585 nm (empty red squares). The lines are a guide for the eye. WGM injection parameter, measuring the efficiency of the coupling between a normally incoming plane wave and WGM inside the PFP (blue solid line). Values of 𝓁/d larger than 1 correspond to disjoined cylinders. In b and c, ray-optics computations were performed at 580 nm. The indexes of the different layers in the structure used from the top ITO to the bottom: all layers in the order shown on the right hand side of a are 1.83+0.007i, 2.05+0.0i, 2.06+0.57i, 2.19+0.40i, 1.71+0.003i and 1.01+7.03i. The layer thicknesses used were, from ITO to Al, 140, 8, 10, 40, 8 and 100 nm, respectively. To correctly visualize light trapping in the PFP when using the full-wave simulation, we set all dielectric refractive indexes to be purely real, except for the absorbing layers, in which the imaginary part was set to 0.001.
As noted above, when 𝓁/d <1, there is an opening through which photons can pass directly from one fiber to the next. When this occurs, βj changes abruptly, with high sensitivity to the initial point of incidence for a given photon. This is similar to a mechanical billiard made of a single, truncated cylindrical cell with a periodic boundary, which was proven to be chaotic29. Hence, the photons follow chaotic trajectories, and the system is optically ergodic. To verify this statement, we computed ray trajectories until the light intensity I was attenuated by a factor of 10−15. With the large set of ray segments so generated, we studied the statistics of Δβ. Dividing the range of allowed values into steps of 0.01, we determined the cumulative distribution function (CDF) F(Δβ). The result, plotted in Figure 2b, is found to be independent of the initial conditions, which clearly establishes ergodicity with respect to the geometrical variables denoting the incidence position and the angle of reflection. Another important feature is the discontinuity found in F(Δβ) at Δβ=0. From this jump, we infer that a large portion of the ray trajectory (~60% for that particular value of 𝓁/d) is regular; that is, the chaos encountered here is intermittent. In other words, most of the ray trajectory is composed of regular segments, separated by brief, abrupt changes. Furthermore, within the regular part, the angle βj may be larger in absolute value than the critical angle for total internal reflection. When this occurs, light rays are trapped in a WGM of the fiber array for several reflections without escape losses. Examples of ray trajectories are given in Figure 4a. This simple ballistic approach, with the modification that for each optical incidence on the boundary both reflection and refraction are possible, clearly illustrates that ergodic trapping in such a PFP combines the attributes of chaos and whispering gallery. Indeed, changing the initial incident ray and computing a distinct statistical ensemble of ray segments by ray-tracing yields the same CDF, which demonstrates ergodicity. Note that in contrast to the WGMs found in high-Q spheres30 or toroids31, 32 used in sensing33 applications, the whispering gallery propagation in the PFP is generally low-Q and interrupted each time the photon trajectory crosses the intersection plane between adjacent fibers.
From what precedes, it appears important to quantify the degree of coupling into such WGMs from a normally incident plane wave. To this end, we ran a large number of ray simulations, all starting with a normally incident ray and with initial positions uniformly distributed over a spatial period of the PFP. We then computed the average sum of intensities in ray segments such that Δβ=0 and that |βi|>βc=arcsin(1/n), where n is the refractive index contrast between the PFP and the air:
This injection coefficient C depends on the interpenetration parameter 𝓁/d. As observed in Figure 4c, the coupling has a broad maximum around 𝓁/d= 0.8 and vanishes for small values of 𝓁/d and as 𝓁/d → 1. This conforms to the limit 𝓁 → 0 corresponding to a flat PFP, whereas when 𝓁 → d, the fibers that make up the PFP become isolated. This non-monotonic dependence of the PFP light-trapping capacity with 𝓁/d was also corroborated by implementing full-wave finite-element method simulations. Specifically, to characterize such light confinement, we considered an active layer with a very small artificial absorption value (Im(n)=0.001) and set to zero the imaginary part of the refractive index for all other layers. Because the parameter C is defined only in the ray-optic limit, we monitored the coupling instead through the absorption inside the active layers as a function of 𝓁/d, for λ=580 nm. The resulting curve, shown in Figure 4c, confirms the non-monotonic behavior. The wider width of the absorption curve can be qualitatively explained by the fact that contrary to C, the absorption does not vanish in either the flat or the separated cylinder limits for the substrate. In addition, the full-wave vector simulations yield an oscillatory dependence on the overlap parameter. This feature, not captured by the ray optics calculation, results from an interferometric enhancement of the field inside the cylinders. Indeed, we note that the diameter used in the wave simulations is only 20 μm, whereas the ray-optics analysis corresponds to the strict limit λ/d → 0. The interferometric origin of the modulation is confirmed by the slight shift observed in such a modulation when the absorption is computed at 585 nm instead of 580 nm (cf. Figure 4c).
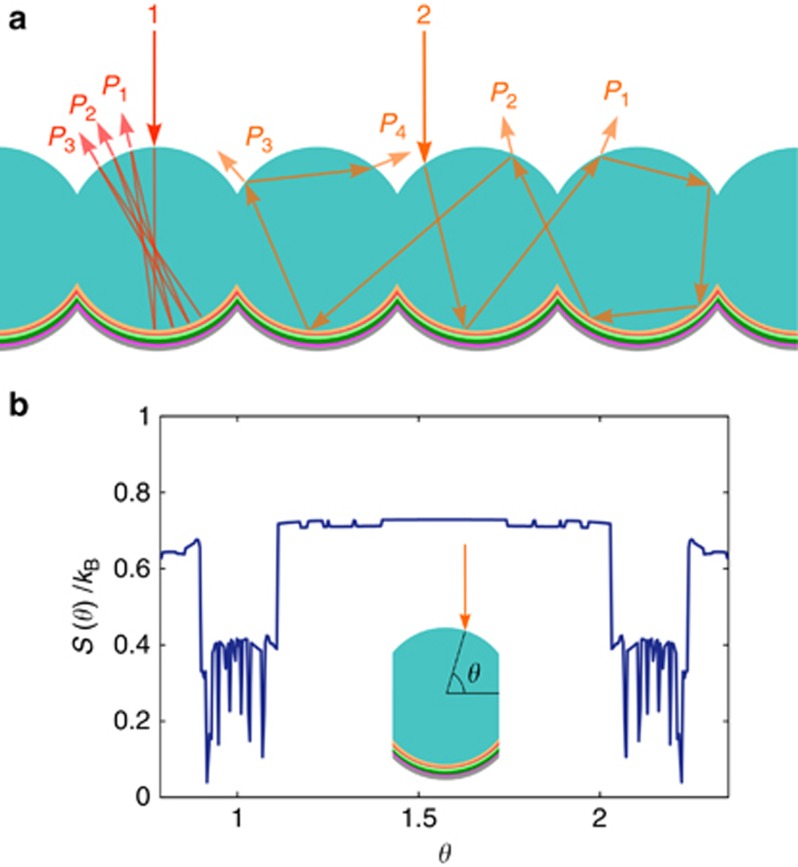
As shown schematically in Figure 4a, the incident position for a given photon at the top interface of the fiber array unambiguously determines the absorption probability for that photon. However, the absorption probability of a photon incident at a nearby position cannot be predicted based on the trajectory of the first photon (Figure 4a). Here we consider that a change in incidence corresponds to a lateral displacement of the incident photon trajectory. However, similar unpredictability would be found if an angular change in the trajectory were to be applied. Such chaotic character in the photon propagation provides a scattering character in an ordered periodic configuration, which does not undermine the whispering gallery trapping inherent to the circular configuration used. The end result is that photons following chaotic trajectories have higher chances of being absorbed, leading to an unexpected decrease in entropy production for a given photon. Indeed, before a given photon hits the PFP, its state is known with perfect certainty, so the entropy is initially zero. Once that photon enters the fiber array, it follows a well-defined ray trajectory within the array with a given number of escape channels (Figure 5a). Denoting the probability for that photon to escape via the ith channel as Pi (i = 1, 2,…), we can define a scattering Gibbs entropy per photon S(θ)as
Figure 5.
Scattering entropy. (a) Two different photon trajectories corresponding to photons entering the fiber array in different angular locations. Photons may either be absorbed at the bottom multilayer or escape the array in a new direction when hitting the top interface with a nonzero probability Pi. (b) Entropy generated per photon as a function of the incident position θ. Photons that fall on the array in the vicinity of the fiber intercalation (around θ=1 and θ=2 above) reside for a longer time inside the array. As a result, they have a larger probability to be absorbed, so the uncertainty of their final state is reduced, and the production of entropy lowered. Inset: schematic drawing showing the angle indicating the ray incident position.
where P0 is the overall probability of absorption through the bottom interface, kB is Boltzmann’s constant, and θ is the incidence coordinate shown in the inset of Figure 5b. Note that the above expression only represents the entropy production in the system associated with light trapping. Other processes that result from the absorption of photons, such as re-emission of light or heat dissipation, also generate entropy34, 35, 36 but are not discussed here. Using a ray tracing code, the above expression of the entropy can easily be calculated. Alternative definitions of entropy such as Kolmogorov–Sinay entropy, used to characterize other chaotic optical processes37, have a less immediate implementation here. Indeed, the dimension of the phase space increases each time a ray is refracted at the silica–air interface. Figure 5b displays the calculated scattering entropy as a function of θ. In the vicinity of θ=π/2, the entropy is nearly constant; it is nearly equal to the value associated with a flat geometry. However, there is a sharp transition at θ<1.1 rad and θ>2.03 rad, where the entropy production undergoes an abrupt drop and becomes a non-smooth function of θ. This marks the transition at which the rays enter the gap between adjacent cylinders immediately after the first reflection at the bottom interface. The rapid changes in S(θ) are evidence of the chaotic sensitivity to initial conditions. Besides, the drop in S(θ) indicates that despite the chaotic nature of photon propagation in the fiber array, there is less uncertainty regarding the final state of the photons compared with the flat configuration. Indeed, they are trapped for relatively long times into whispering gallery trajectories and therefore have greater probability to be collected at the bottom interface. Hence, the region of low value of S(θ) indicates efficient trapping.
The intermittent chaotic propagation described above provides a good qualitative explanation for the enhanced absorption by the active materials from the solar cell deposited on the backside of the PFP shown in Figure 3b. However, in the experimental implementation, there are several additional subtleties that increase the difficulty of reaching an accurate quantitative prediction of the measured increase in light-harvesting capacity. For instance, in the bilayer junction used, the exciton generation distribution in the direction perpendicular to the layered architecture is greatly affected by the wavelength of the incident photon. In other words, blue-shifted photons may generate a larger quantity of excitons in the C70 layer, whereas red-shifted photons are more likely to be absorbed by the DBP layer. The high vacuum evaporation procedure used for the deposition of the active layers over a non-flat substrate, such as the fiber array, may result in nanometric variations in the thicknesses of such layers. Indeed, in the central part of the fiber, the layers may be slightly thicker than in the neighborhood of the fiber intersection. The final orientation of DBP molecules may be significantly different on the PFP substrate leading to a birefringence, which may significantly alter the DBP layer refractive index. In addition, as observed in Figure 3a, the degree of fiber interpenetration increases as one moves away from the center of the array. All such effects should be incorporated in a model aiming at a quantitative description of the external quantum efficiency.
Conclusions
In this work, we propose a fundamentally novel light propagation regime that enables the effective trapping of light incident orthogonally to the plane defined by a novel trapping plate design. We show that the incident light trajectory can be effectively bended and remain intermittently trapped in interrupted guided trajectories within the plate. This paradoxical combination of light perpendicularly incident to the PFP plane and of trapping within that same guide is the result of intermittent chaotic light propagation in an array of parallel interpenetrated optical fibers. A similar behavior can only be achieved by introducing a randomization of the surface, which would lead to strong limitations in the implementation of well-structured devices. In the fiber array configuration we propose, we have incorporated a solar cell and experimentally demonstrated that the light-harvesting capacity of the cell can be increased by more than 30%. To a large extent, the increased absorption capacity of the PFP results from photons following chaotic trajectories, which have higher chances of being absorbed. This leads to the unexpected result that the presence of chaos implies a lower increase in the scattering entropy. In addition, we have demonstrated that the fabrication of well-ordered devices can be conducted without detrimental effects on the parameters that determine the electrical performance of such a device. Finally, the interest in the novel light-guiding mechanism we propose well exceeds photovoltaics and may contribute to many relevant applications in future illumination systems, displays or wearable devices. For instance, our approach may have a significant impact on portable display devices incorporating edge-lit LED guiding plates for LCD illumination where <5% of the emitted light reaches the user’s eye. In such systems, the guidance across the plate must compete with very homogenous light extraction. The effective 90° light bending and trapping of the PFP may markedly improve such poor light management, resulting in a drastic reduction in the power consumption of such illumination or display systems.
Author contributions
MM fabricated the PFP; MM, LGG, PR-G and JP fabricated and measured the solar cells. MM, with the assistance of PR-G, deposited the ITO electrode on the PFP. JB-A developed the full-wave theory and performed the corresponding numerical simulations. GK developed the theory and performed ray tracing numerical simulations. GK and JM wrote the manuscript with the assistance of all other authors. JM conceived the concept of PFP and planned and coordinated all the work.
Acknowledgments
MM, PR-G and JM acknowledge financial support from the Spanish MINECO (Severo Ochoa Program, grant no. SEV-2015-0522), the MINECO and the Fondo Europeo de Desarrollo Regional FEDER (grant no. MAT2014-52985-R), the Fundacio Privada Cellex, and from the EC FP7 Program (ICT-2011.35) under grant no. NMP3-SL-2013-604506. GK is a Research Associate of the Fonds de la Recherche Scientifique—FNRS (Belgium). GK thanks Thomas Gilbert for useful comments. JB-A acknowledges financial support from the Spanish MINECO/FEDER (grant no. MAT2015-66128-R). LGG and JP acknowledge financial support from the Spanish MINECO (grant no. ENE2014-56237-C4) and Mexico’s grant program CONACyT.
Footnotes
Note: Supplementary Information for this article can be found on the Light: Science & Applications’ website(http://www.nature.com/lsa).
The authors declare no conflict of interest.
Supplementary Material
References
- Kroll M, Fahr S, Helgert C, Rockstuhl C, Lederer F et al. Employing dielectric diffractive structures in solar cells–a numerical study. Phys Status Solidi A 2008; 205: 2777–2795. [Google Scholar]
- Brongersma ML, Cui Y, Fan SH. Light management for photovoltaics using high-index nanostructures. Nat Mater 2014; 13: 451–460. [DOI] [PubMed] [Google Scholar]
- Ko DH, Tumbleston JR, Zhang L, Williams S, DeSimone JM et al. Photonic crystal geometry for organic solar cells. Nano Lett 2009; 9: 2742–2746. [DOI] [PubMed] [Google Scholar]
- Liu YC, Kirsch C, Gadisa A, Aryal M, Mitran S et al. Effects of nano-patterned versus simple flat active layers in upright organic photovoltaic devices. J Phys D: Appl Phys 2013; 46: 024008. [Google Scholar]
- Hsiao YS, Chien FC, Huang JH, Chen CP, Kuo CW et al. Facile transfer method for fabricating light-harvesting systems for polymer solar cells. J Phys Chem C 2011; 115: 11864–11870. [Google Scholar]
- Adachi MM, Labelle AJ, Thon SM, Lan XZ, Hoogland S et al. Broadband solar absorption enhancement via periodic nanostructuring of electrodes. Sci Rep 2013; 3: 2928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mihi A, Beck FJ, Lasanta T, Rath AK, Konstantatos G. Imprinted electrodes for enhanced light trapping in solution processed solar cells. Adv Mater 2014; 26: 443–448. [DOI] [PubMed] [Google Scholar]
- Grandidier J, Callahan DM, Munday JN, Atwater HA. Light absorption enhancement in thin-film solar cells using whispering gallery modes in dielectric nanospheres. Adv Mater 2011; 23: 1272–1276. [DOI] [PubMed] [Google Scholar]
- Yao Y, Yao J, Narasimhan VK, Ruan ZC, Xie C et al. Broadband light management using low-Q whispering gallery modes in spherical nanoshells. Nat Commun 2012; 3: 664. [DOI] [PubMed] [Google Scholar]
- Na SI, Kim SS, Jo J, Oh SH, Kim J et al. Efficient polymer solar cells with surface relief gratings fabricated by simple soft lithography. Adv Funct Mater 2008; 18: 3956–3963. [Google Scholar]
- Nalwa KS, Park JM, Ho KM, Chaudhary S. On realizing higher efficiency polymer solar cells using a textured substrate platform. Adv Mater 2011; 23: 112–116. [DOI] [PubMed] [Google Scholar]
- Yu X, Yu XM, Zhang JJ, Hu ZY, Zhao GS et al. Effective light trapping enhanced near-UV/blue light absorption in inverted polymer solar cells via sol–gel textured Al-doped ZnO buffer layer. Sol Energ Mater Sol Cells 2014; 121: 28–34. [Google Scholar]
- Atwater HA, Polman A. Plasmonics for improved photovoltaic devices. Nat Mater 2010; 9: 205–213. [DOI] [PubMed] [Google Scholar]
- Wu JL, Chen FC, Hsiao YS, Chien FC, Chen P et al. Surface plasmonic effects of metallic nanoparticles on the performance of polymer bulk heterojunction solar cells. ACS Nano 2011; 5: 959–967. [DOI] [PubMed] [Google Scholar]
- Lu LY, Luo ZQ, Xu T, Yu LP. Cooperative plasmonic effect of Ag and Au nanoparticles on enhancing performance of polymer solar cells. Nano Lett 2013; 13: 59–64. [DOI] [PubMed] [Google Scholar]
- Wang XN, Zhu HJ, Xu YM, Wang H, Tao Y et al. Aligned ZnO/CdTe core-shell nanocable arrays on indium tin oxide: synthesis and photoelectrochemical properties. ACS Nano 2010; 4: 3302–3308. [DOI] [PubMed] [Google Scholar]
- Pastorelli F, Bidault S, Martorell J, Bonod N. Self-assembled plasmonic oligomers for organic photovoltaics. Adv Optical Mater 2014; 2: 171–175. [Google Scholar]
- David A, Hurni CA, Aldaz RI, Cich MJ, Ellis B et al. High light extraction efficiency in bulk-GaN based volumetric violet light-emitting diodes. Appl Phys Lett 2014; 105: 231111. [Google Scholar]
- Chen YY, Chang RS. Partial polarization of direct LED backlight module. J Display Technol 2015; 11: 360–366. [Google Scholar]
- Yablonovitch E. Statistical ray optics. J Opt Soc Am 1982; 72: 899–907. [Google Scholar]
- Yu ZF, Raman A, Fan SH. Fundamental limit of nanophotonic light trapping in solar cells. Proc Natl Acad Sci USA 2010; 107: 17491–17496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tvinstedt K, Tang Z, Inganäs O. Light trapping with total internal reflection and transparent electrodes in organic photovoltaic devices. Appl Phys Lett 2012; 101: 163902. [Google Scholar]
- Cao WR, Myers JD, Zheng Y, Hammond WT, Wrzesniewski E et al. Enhancing light harvesting in organic solar cells with pyramidal rear reflectors. Appl Phys Lett 2011; 99: 023306. [Google Scholar]
- Labelle AJ, Thon SM, Masala S, Adachi MM, Dong HP et al. Colloidal quantum dot solar cells exploiting hierarchical structuring. Nano Lett 2015; 15: 1101–1108. [DOI] [PubMed] [Google Scholar]
- Esiner S, Bus T, Wienk MM, Hermans K, Janssen RAJ. Quantification and validation of the efficiency enhancement reached by application of a retroreflective light trapping texture on a polymer solar cell. Adv Energy Mater 2013; 3: 1013–1017. [Google Scholar]
- Zhou YH, Zhang FL, Tvingstedt K, Tian WJ, Inganäs O. Multifolded polymer solar cells on flexible substrates. Appl Phys Lett 2008; 93: 033302. [Google Scholar]
- Cho C, Kim H, Jeong S, Baek SW, Seo JW et al. Random and V-groove texturing for efficient light trapping in organic photovoltaic cells. Sol Energy Mater Sol Cells 2013; 115: 36–41. [Google Scholar]
- Myers JD, Cao WR, Cassidy V, Eom SH, Zhou RJ et al. A universal optical approach to enhancing efficiency of organic-based photovoltaic devices. Energy Environ Sci 2012; 5: 6900–6904. [Google Scholar]
- Bunimovich LA. On the ergodic properties of nowhere dispersing billiards. Commun Math Phys 1979; 65: 295–312. [Google Scholar]
- Vollmer F, Arnold S. Whispering-gallery-mode biosensing: label-free detection down to single molecules. Nat Methods 2008; 5: 591–596. [DOI] [PubMed] [Google Scholar]
- He LN, Özdemir ŞK, Zhu JG, Kim W, Yang L. Detecting single viruses and nanoparticles using whispering gallery microlasers. Nat Nanotechnol 2011; 6: 428–432. [DOI] [PubMed] [Google Scholar]
- Lu T, Lee H, Chen T, Herchak S, Kim JH et al. High sensitivity nanoparticle detection using optical microcavities. Proc Natl Acad Sci USA 2011; 108: 5976–5979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soria S, Berneschi S, Brenci M, Cosi F, Nunzi CN et al. Optical microspherical resonators for biomedical sensing. Sensors 2011; 11: 785–805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruppel W, Wurfel P. Upper limit for the conversion of solar energy. IEEE Trans Electron Devices 1980; 27: 877–882. [Google Scholar]
- Markvart T. Solar cell as a heat engine: energy–entropy analysis of photovoltaic conversion. Phys Status Solidi A 2008; 205: 2752–2756. [Google Scholar]
- De Vos A. Thermodynamics of Solar Energy Conversion. Berlin: Wiley-VCH; 2008. [Google Scholar]
- Hagerstrom AM, Murphy TE, Roy R. Harvesting entropy and quantifying the transition from noise to chaos in a photon-counting feedback loop. Proc Natl Acad Sci USA 2015; 112: 9258–9263. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.