Skip to main content
NCBI home page
Light, Science & Applications logoLink to Light, Science & Applications
. 2016 Dec 2;5(12):e16177. doi: 10.1038/lsa.2016.177

Concealing arbitrary objects remotely with multi-folded transformation optics

Bin Zheng 1,2,3,✝, Hamza Ahmad Madni 1,2,3,✝, Ran Hao 2, Xianmin Zhang 2, Xu Liu 1, Erping Li 2,*, Hongsheng Chen 1,2,3,*
PMCID: PMC6059891  PMID: 30167134

Abstract

An invisibility cloak that can hide an arbitrary object external to the cloak itself has not been devised before. In this Letter, we introduce a novel way to design a remote cloaking device that makes any object located at a certain distance invisible. This is accomplished using multi-folded transformation optics to remotely generate a hidden region around the object that no field can penetrate and that does not disturb the far-field scattering electromagnetic field. As a result, any object in the hidden region can stay in position or move freely within that region and remain invisible. Our idea is further extended in order to design a remote illusion optics that can transform any arbitrary object into another one. Unlike other cloaking methods, this method would require no knowledge of the details of the object itself. The proposed multi-folded transformation optics will be crucial in the design of remote devices in a variety of contexts.

Keywords: multi-folded, object independent, remote cloaking, transformation optics

Introduction

The ingenious theory of transformation optics proposed by Pendry et al.1 gives the ability to control electromagnetic waves. Due to this extraordinary feature, transformation optics has many applications, such as cloaking devices2, 3, 4, 5, 6, superlenses7, 8, 9 antennas10 etc. Among them, the most attractive is a cloaking device that can direct light to propagate smoothly around an object, making it disappear for the viewers1, 2, 3, 4, 5, 6. Since the transformation-based cloak was firstly proposed, extensive theoretical and experimental works have been developed to demonstrate the functionality of this interesting device11, 12, 13, 14, 15, 16, 17, 18, 19, 20. An important feature of this invisibility cloak is that the object should be enclosed by the cloaking shell, such that no incident wave can penetrate into the hidden region.

In order to hide an object at a distance, Lai et al.21 proposed the ‘anti-object’ concept22, a complementary ‘image’ object that cancels the scattering field generated by a pre-specified object. Based on this method, a scheme for illusion optics23 was further introduced to generate the illusion of transforming one object into another one. A key feature of a remote cloak is that it does not require the cloak shell to enclose the object. However, unlike the original cloak that can hide any arbitrary object1, Lai’s remote devices are designed for a particular object with known shape, size, and position. Therefore, the cloak can operate only for a specific object, and a little change in its position can destroy the exact restoration and cancellation of the optical path of the incident wave. Another approach to remote cloaking was investigated to design active exterior cloaks24 that require advance knowledge of the phase information and of the incoming probing wave. In (Ref. 25, 26), Milton and Nicorovici et al proposed an external cloak that can hide a countable set of dipoles with the help of a cylindrical superlens. However, that cloak can only work in the quasistatic limit for polarizable lines. In short, a remote cloaking device that can hide any arbitrary object is still elusive.

In this Letter, we propose the design for a remote cloaking device that requires no knowledge of the hidden object’s shape and material. Our designing technique is based on multi-folded transformation optics27 to remotely produce a hidden region into which the incoming electromagnetic waves cannot penetrate, and that does not alter the far-field scattering field. Therefore, the device can still rendered invisible even with the existence of such hidden region. Most importantly, the proposed device is not based on the ‘anti-object’ concept and the hidden object is not restricted to move within a certain range of the hidden region to avoid affecting the outer boundary field pattern. Our new designed device has no physical attachment with the hidden object so any object inside the hidden range can move freely. We further extend this idea to design an object-independent remote illusion optics that remotely creates the illusion of any object in this hidden region looking like another object. Full-wave finite element simulations validate the expected behavior of our proposed device.

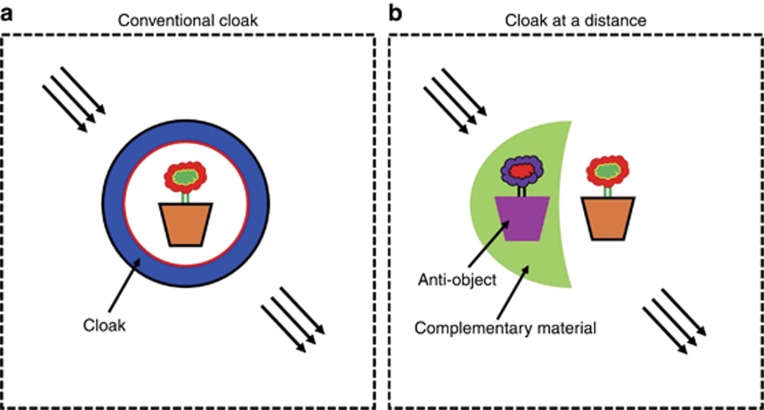
Figure 1a shows the schematics of a conventional cloak1 that conceals an object inside the cloak region without altering the incoming field. This is achieved using a coordinate transformation to create a hole in the center such that no fields can penetrate inside the cloak but the outside field remains unaltered. Therefore, any object inside the cloak is invisible to the outside observers. A conventional remote cloaking21, instead, cloaks a pre-specified object outside of the cloaking shell by using the ‘anti-object’ concept. The idea is illustrated in Figure 1b, where an object with constitutive parameters ε(r) and μ(r) is placed in free space (on the right), and a complementary image object with negative constitutive parameters Inline graphic is embedded in the complementary media (on the left). As a consequence, the object and the complementary media with anti-object cancel the scattering field generated by the object and the object becomes undetectable.

Figure 1.

Figure 1

Open in a new tab

Illustration of the ideal conventional cloak and the anti-object remote cloaking device. (a) A conventional cloak1 is used to conceal the hidden object with its cloaking shell, so that the hidden object is not penetrated by EM waves. (b) An object dependent remote cloaking device proposed by Lai et al.21 is based on the ‘anti-object’ concept, which is used to conceal the object outside of the cloaking shell, in which a complementary media embedded with a complementary image of the cloaked object is used to cancel the scattering effect of the actual cloaked object.

Materials and methods

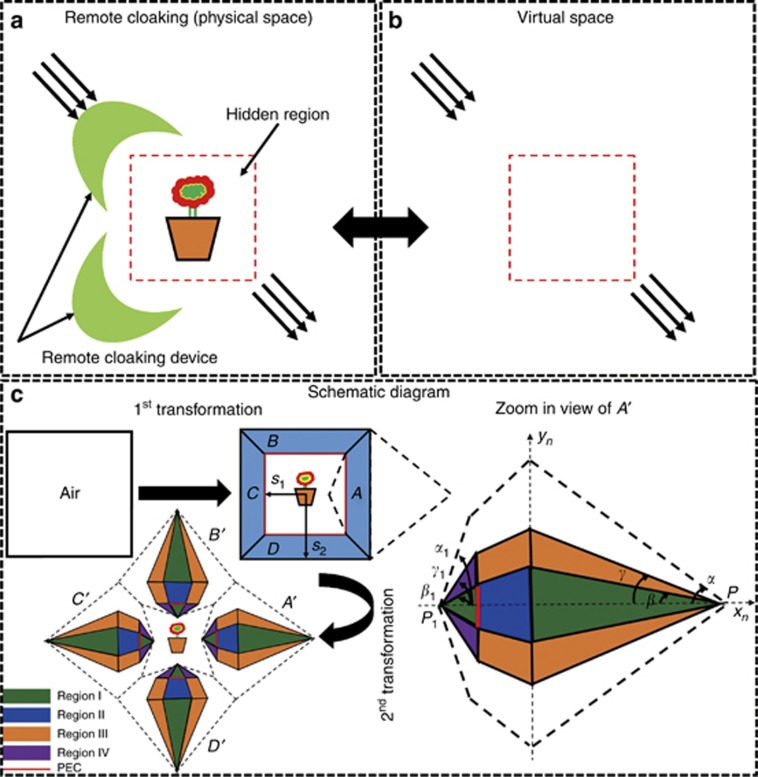
Unlike the methods mentioned above, in this paper we aim to create a hidden region at a distance, so that any object moving inside this hidden region can be invisible, as shown in Figure 2a. Therefore, this remote cloaking device is object-independent. Here, as an example, the remote cloaking device is made of two elements that create a hidden region, but the same method can be extended to an arbitrary number of elements. Figure 2b depicts the effect of this object-independent remote cloaking device in free space. The figure shows the equivalent virtual space created by the device and how the wave can propagate through the cloak without any perturbations. Figure 2c illustrates the schematic diagram of our proposed remote cloaking device with two transformation steps. In the first step, a square shaped space filled with air placed in the virtual space (x,y,z) is transformed into a conventional cloak (light blue segments). In the next step, the cloak is divided into four segments (delimited by dashed lines and denoted A, B, C and D); the second transformation function on each segment is used to compress the whole segment as A′, B′, C′ and D′, respectively, so that the cloak is open and does not require enclosing the hidden object. As shown in Figure 2c, each segment is further divided into four regions. For example, segment A’ contains the region I (green), represented by (x1,y1,z1), region II (dark blue), denoted by (x2,y2,z2), region III (orange), denoted by (x3,y3,z3), and region IV (purple) denoted by (x4,y4,z4). A zoomed-in view of the proposed system, clarifying the design methodology, is presented at the most right side of Figure 2c. Consequently, we compress the complete black dashed lined area into the region I and region II. It should be noticed that the material parameters of region II are obtained from the conventional square cloak. Thereafter, a folded transformation is used to compensate the discontinuity due to the compressing coordinate transformation. In this case, the regions III and IV are obtained with different parameters at different folding ranges. The materials in these two regions are complementary materials that have been used to compensate some space in the lens design7. xn, yn and zn indicate the coordinate system of each region, where n=1, 2, 3 and 4.

Figure 2.

Figure 2

Open in a new tab

Schematic diagram of the proposed object independent remote cloaking device. (a) One or several remote devices can be used to realize the hidden region in the real space. For comparison, the equivalent virtual space generated by such device remains similar to that of an ideal cloak (b). (c) Schematic diagram of the proposed remote cloaking device, based on two steps. At the first step the virtual space is transformed into a closed square cloak with four different segments (here labeled A, B, C and D) and then a multi-folded transformation method is applied on each part to make it a remote cloaking device. As an example, after applying the second transformation function, segment A turns into A′, which is composed of four different regions. Zoom in view used to clearly visualize the different regions of each part in reference to the derivation in the main text. PEC, perfect electric conductor.

For the first step shown in Figure 2c, the constitutive parameters of the conventional cloak are obtained from (Ref. 6), the resulting permittivity and permeability tensors for the segment A of the conventional square cloak can be expressed as:

graphic file with name lsa2016177e1.jpg

with

graphic file with name lsa2016177e2.jpg

The half of the side lengths of the inner and outer square are s1 and s2 respectively (see Figure 2c).

In the next step, we apply the second transformation as shown in Figure 2c. It should be noted that although here we use a square shaped cloak as an example, the method can be applied to cloaks of any shapes19, 20. We take the segment A′ as an example (the other three segments B′, C′ and D′ can be analyzed in a similar way due to the symmetry of the cloak), the transformation equations of the regions I and II in the Cartesian coordinates are given

graphic file with name lsa2016177e3.jpg

where κ=tan β/tan α. The constitutive parameters for the regions I and II are obtained from the Jacobian transformation matrix as follows:

graphic file with name lsa2016177e4.jpg
graphic file with name lsa2016177e5.jpg

Moreover, the folded transformations are applied to the regions III and IV. Taking the orange area in the first quadrant as an example in region III, leads to the transformation equation:

graphic file with name lsa2016177e6.jpg

where τ=tan γ=( tan α +tan β)/2 and P is the intersection point of all the regions at the horizontal-axis. The material parameters of the complementary material for this region are:

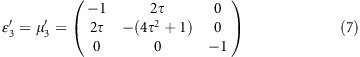graphic file with name lsa2016177e7.jpg

Similarly, taking the purple area in the second quadrant as an example in region IV, gives the transformation equation and the constitutive parameters:

graphic file with name lsa2016177e8.jpg
graphic file with name lsa2016177e9.jpg

where τ1=tan γ1=(tan α1 +tan β1)/2 and P1 is the coordinate value along the x-axis. The other parts of these complementary regions transform in a similar way, that for brevity we do not write in this Letter. In addition, due to the symmetry of the cloak, the permittivity and permeability tensors of the other domains i.e. B′, C′ and D′ can be obtained by rotating all of the corresponding tensors shown above by π/2, π, and 3π/2, respectively.

In short, we apply a second step transformation to the conventional enclosed cloak design. By compressing the different segments, the hidden region is open to the outer space and the cloaking device can work remotely. Folded transformations are also applied to satisfy the boundary continuity. A detailed general transformation function is described in the Supplementary Material.

Results and discussion

The following section summarizes the full wave simulations of the proposed remote cloaking device by adopting the scattered transverse electric (TE) mode with a frequency of 3 GHz and by using the 2D finite element simulator (COMSOL). For the closed square cloak, the simulation uses the following parameters: s1=0.075 m and s2=0.1 m, the compression ratio κ=0.8 with α=45°, γ=42° and β=38.66° for the regions I and II. Additionally, τ=0.9 with the same α, γ and β in the region III and τ1=2.7 with α1=71.57°, γ1=69.68° and β1=67.38° for a different folding range of region IV.

The material parameters for each region in segment A′ are shown in Figure 3. It should be noted that all the parameters are transformed into the diagonal form. For region I, all the parameters are homogeneous, positive and anisotropic, as shown in Figure 3a. For regions III and IV, as a consequence of the folding transformation, all the parameters are negative and highly anisotropic, as shown in Figures 3b and 3c. For region II, since it is obtained from applying the second transformation to the conventional square cloak, all the parameters are inhomogeneous and highly anisotropic. Figure 3d shows the distribution of the parameters in region II. For εv or μv, an inset shows a color bar range of the distribution with x from 0.075 to 0.078 m. The white dotted line represents the position of the x-axis in region II and a plot of the parameters along this line is also shown in Figure 3d.

Figure 3.

Figure 3

Open in a new tab

The material parameters for the simulated structures in segment A′. (a) Parameters of region I. (b) Parameters of region III. (c) Parameters of region IV. (d) Parameters distribution of the region II and the parameters in the line along the x-axis.

In Figure 4, we consider the electric field components of the wave for objects of different shape and compare the field behaviors for each with and without the remote cloaking device. In Figure 4a, a perfect electric conductor (PEC) circle with a radius of 0.03 m is placed in the air and is subjected to a plane wave. In this case, the field is scattered. In Figure 4b, the remote cloaking device is used to cloak the PEC circle. It can be seen that the scattering field caused by the PEC circle (visible in Figure 4a) is well minimized by the open cloaking device and the PEC circle becomes invisible. It should be noted that, although the remote cloaking device is open, the center field region it creates is a hidden region that no wave can penetrate, and therefore, any change of the objects does not affect the performance of the cloak. In order to verify this, we changed the hidden object to be a PEC square, and a dielectric star shaped object with ε0=5 and μ0=1, respectively. The results shown in Figures 4c–4f illustrate that the scattering caused by these different objects can be well minimized by the same remote object-independent cloak. Figures 4g–4i show the calculated far field differential RCS via different azimuthal angles for all the three cases. The blue lines represent the RCS with the bare object, while the red lines represent the RCS with the cloak. The results show that for different objects, the scattering is much larger without the cloaking device than with the cloaks, especially for the forward scattering. Moreover, for different objects with the external cloaking device, the RCS are the same, which is a proof of the object independence of our cloaking device.

Figure 4.

Figure 4

Open in a new tab

Comparison of the total electric field distributions in 2-D TE scattering mode for both an object alone and the same object beside the object independent remote cloaking device. (a) The incoming TE wave is impinging a PEC circular shaped object along the x-direction, producing large scattering, while in (b) the object independent remote cloaking device reduces the scattering effect, achieving to cloak the circle. Similarly, the scattering of a PEC square shaped object in (c) and a dielectric star of ε0=5 and μ0=1 in (e) are reduced in (d) and (f) respectively. This figure validates the object independency concept of the proposed device. (g–i) The comparison of the calculated far field differential RCS via different azimuthal angles. RCS, radar cross section.

The required parameters for regions III and IV have double negative values for both the permittivity and permeability as described by Equation (7) and Equation (9). This will lead to loss and dispersions. In the following, we show how the material dispersion will influence the cloaking effect. For the ease of discussion, we use a Drude model for permittivity and a Lorentz model for permeability:

graphic file with name lsa2016177e10.jpg
graphic file with name lsa2016177e11.jpg

where Γe and Γh are damping constants for the electric and magnetic field, respectively, while F is the filling ratio. From previous works28, it can be seen that Γh/ω0 can reach values as low as 10−3. In low frequencies, the damping constant can be further reduced29. Accordingly, in our simulation we choose Γe=Γh=1e7 Hz and F=0.5, at the working frequency of 3 GHz. Different ωp and ωo are also chosen separately to satisfy the required negative values in the working frequency. The reduction of the total RCSs by this cloaking device compared with the bare object via different frequencies is shown in Figure 5. It is evident that the dispersion will affect the cloaking performance very much and that the cloak can only work in a small frequency band.

Figure 5.

Figure 5

Open in a new tab

Reduction of the total RCS by the simulated cloaking device for different frequencies with the assumed dispersion model.

To further show how the loss will influence the cloaking effect, we make simulations with some loss in the ideal parameters. The frequency is set to be 3 GHz and we use ε=εr(1 + iδ) and μ=μr(1 + iδ) for the region III and IV, where εr and μr are the ideal parameters from Equation (7) and Equation (9). δ is the loss tangent for the negative values in region III and IV. For the dispersion model mentioned above, the magnitude of the loss tangent is δ=0.001. Since the first double negative metamaterial has been experimentally realized30, many successive studies have been done to minimize the loss28, 31. The loss of the metamaterials can be further reduced by adding some gain elements32, 33. In the simulation, we set the loss tangent to be 0.0001, 0.001, 0.01 and 0.1, respectively. The total field distributions with different loss tangents are shown in Figure 6. The calculated far field differential RCSs via different azimuthal angles with different losses compared to those of the bare object are also provided in each figure. One can see that a big loss will destroy the cloaking effect, leading to a forward scattering even higher than that of the bare object, but the performance is still acceptable when the loss is relatively small.

Figure 6.

Figure 6

Open in a new tab

Total field distribution of the cloaking device and differential RCS with different loss tangents of (a) δ=0.0001, (b) δ=0.001, (c) δ=0.01 and (d) δ=0.1.

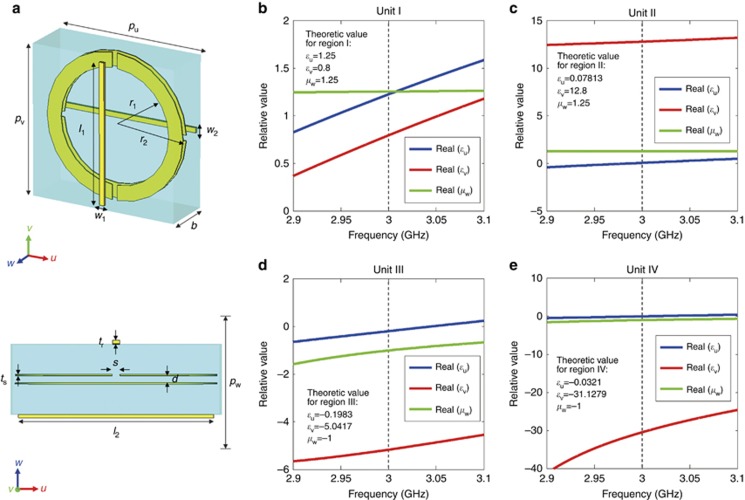
To realize such an external cloaking device will be a big challenge due to its complicated parameters, especially for regions III and IV that have negative and highly anisotropic values for both permittivity and permeability. Here we propose a possible metamaterial structure that could be used to mimick the parameters of the cloaking device. We take the transverse magnetic polarization as an example. The related constitutive parameters in the simulation are ε1u=1.25, ε1v=0.8, μ1w=1.25, ε3u=−0.1983, ε3v=−5.0417, μ3w=−1 and ε4u=−0.0321, ε4v=−31.1279, μ4w=−1 for region I, III and IV, respectively. Region II is inhomogeneous; choosing the position at x=0.08 m and y=0 m as an example we get ε2u=0.07813, ε2v=12.8, μ2w=1.25. The structure is shown in Figure 7a, which is composed of split-ring resonators (SRRs) and metal rods together. With the dimensions and parameters described in the Figure caption, we can get the parameters shown in Figures 7b–7e. The retrieved results match well with the required parameters at the frequency of 3 GHz. This therefore demonstrates the possibility of realization of our cloaking device.

Figure 7.

Figure 7

Open in a new tab

(a) The designed unit cell. The periodicity of the unit in the u-v plane is pu=pv=9.35 mm and it is repeated along the w-axis with a period of pw=5.11 mm. The substrate has thickness b=3.2 mm. Two copper SRRs have d=400 μm and ts=60 μm. Two copper rods perpendicular to each other are on both sides. By adjusting the unit structure, the retrieved parameters will fit the requirement, as shown in b–d. (b) Retrieved parameter of unit I. The permittivity of the substrate is εsub=10 while r1=1.87 mm, r2=2.18 mm, s=780 μm, w1=100 μm, l1=9350 μm, w2=30 μm, l2=9350 μm and tr=60 μm. (c) Retrieved parameter of unit II. The permittivity of the substrate is εsub=10 while r1=1.87 mm, r2=2.18 mm, s=780 μm, w1=620 μm, l1=8920 μm, w2=200 μm, l2=9350 μm and tr=30 μm. (d) Retrieved parameter of unit III. The permittivity of the substrate is εsub=2.1 while r1=3.58 mm, r2=4.52 mm, s=21 μm, w1=600 μm, l1=9349.2 μm, w2=53 μm, l2=9350 μm and tr=150 μm. (e) Retrieved parameter of unit IV. The permittivity of the substrate is εsub=2.1 while r1=3.58 mm, r2=4.52 mm, s=21 μm, w1=600 μm, l1=9349.4 μm, w2=141 μm, l2=9350 μm and tr=30 μm. At the frequency of 3 GHz, the real part of the retrieved parameters are: ε1u=1.23, ε1v=0.79 and μ1w=1.25 for unit I, ε2u=0.073, ε2v=12.78 and μ2w=1.30 for unit II, ε3u=−0.196, ε3v=−5.17 and μ3w=−1.01 for unit III, ε4u=−0.032, ε4v=−30.48 and μ4w=−1.00 for unit IV, respectively.

This multi-folded transformation optics method can be similarly extended to design remote illusion optics. The real space of object-independent illusion optics is illustrated in Figure 8a. In this scenario, the remote device, embedded with the compressed object selected for the illusion, is used to create the hidden region. Figure 8b demonstrates the illusion effect created by the illusion device. In general, any object (here a flower is shown as an example) inside the hidden region will turn into another object, e.g., a stick. The schematic diagram of the proposed illusion optics is shown in Figure 8c. This device is based on the remote cloaking device discussed earlier, with the addition of an illusionary object embedded inside the remote cloaking device. Here, as an example, we used a dielectric stick as embedded object. The stick is first transformed and adjusted into the segment B of the conventional cloak, and further compressed in the second transformation step with the same equation as regions I and II for segment B′ of the proposed remote cloaking device.

Figure 8.

Figure 8

Open in a new tab

Schematics of an object independent illusion device that remotely transforms the image of one object (a flower) into another object (a stick). (a) The flower (any object) is free to move inside the hidden region surrounded by the remote illusion device in real space. (b) The stick (or any object used for illusion) in the illusion space. (c) Designing methodology of the remote illusion device in real space. The remote illusion device is based on the remote cloaking device (Figure 2) with some minor addition such as a stick (or any object) embedded into the cloak region B, originally transformed from virtual space. Next, the stick (or any object) is further compressed to the B′ region while maintaining the same domain.

Figure 9a–9f is the simulation result that demonstrates the functionality of the remote illusion device in transforming one image into another. In Figure 9a, a dielectric flower with εf=3 and μf=1 is placed at the center, with a plane wave incident from left to right. Figure 9b shows the scattering pattern of the flower with the remote illusion device placed beside it, while Figure 9c shows the scattering pattern of a dielectric stick of 0.02 m with εs=5 and μs=1. Comparing the field patterns of Figure 9a–9c, it is evident that the remote illusion device makes the flower behave like if there were a stick. Furthermore, the device is omnidirectional. For example, Figure 9d–9f shows the simulated results when the propagation direction of the incident plane wave is rotated by π/4. The material parameters and functionality in Figure 9d–9f are the same as in Figure 9a–9c, respectively. One can see that the scattering pattern of Figure 9e is identical to Figure 9f, which is a proof that the proposed remote illusion device is without any limitation of incident wave’s direction. It is important to realize that, since the center region we created is a hidden region, the object to be transformed is not limited to be made of dielectric materials. This shows that the remote illusion device can be applied to any arbitrary object.

Figure 9.

Figure 9

Open in a new tab

The numerical demonstration of remotely transforming the image of a dielectric flower with εf=3 and μf=1 into a stick with εs=5 and μs=1 through an object independent remote illusion device under an incident TE plane wave propagating from left (a–c) and top left (d–f). (a) Scattering behavior of the dielectric flower. (b) Scattering behavior of the dielectric flower besides the object independent remote illusion device, identical to that of the dielectric stick as shown in (c). (d–f) The incident plane wave is rotated by π/4 with respect to the objects and the remote illusion device. The scattering pattern of (e) is exactly the same as that of (f).

Conclusions

We proposed a new recipe to remotely conceal any arbitrary object by applying multi-folded transformation optics. This remote device can hide any object from a certain distance and it can be used to remotely change the field pattern of one object into that of another one. The hidden object can move freely inside the hidden region created by the proposed device, and it can change shape, without requiring the cloak to create different anti-objects for each different structure. Due to the material dispersed, the device we proposed is still limited to a small frequency band. Still, the multi-folded transformation method will be very helpful to design many other remote devices such as remote waveguides, remote antennas, sensors etc., that will be very useful in future microwave and optical applications.

Acknowledgments

The authors thank P. Rebusco for critical reading and editing of the manuscript. This work was sponsored by the National Natural Science Foundation of China under Grants No. 61625502, No. 61322501, No. 61574127, No. 61575174, No. 61601408, No. 61550110245 and No. 61275183, the Top-Notch Young Talents Program of China, the Program for New Century Excellent Talents (NCET-12-0489) in University, the Fundamental Research Funds for the Central Universities and the Innovation Joint Research Center for Cyber-Physical-Society System. B. Zheng acknowledges the support of the Postdoctoral Science Foundation of China under Grant No. 2015M581930.

Footnotes

Note: Supplementary Information for this article can be found on the Light: Science & Applications’ website (http://www.nature.com/lsa).

Supplementary Material

Supplementary Information
Click here for additional data file. (1.1MB, doc)

References

  1. Pendry JB, Schurig D, Smith DR. Controlling electromagnetic fields. Science 2006; 312: 1780–1782. [DOI] [PubMed] [Google Scholar]
  2. Cai WS, Chettiar UK, Kildishev AV, Shalaev VM. Optical cloaking with metamaterials. Nat Photonics 2007; 1: 224–227. [Google Scholar]
  3. Li JS, Pendry JB. Hiding under the carpet: a new strategy for cloaking. Phys Rev Lett 2008; 101: 203901. [DOI] [PubMed] [Google Scholar]
  4. Leonhardt U, Tyc T. Broadband invisibility by non-euclidean cloaking. Science 2009; 323: 110–112. [DOI] [PubMed] [Google Scholar]
  5. Alù A, Engheta N. Multifrequency optical invisibility cloak with layered plasmonic shells. Phys Rev Lett 2008; 100: 113901. [DOI] [PubMed] [Google Scholar]
  6. Rahm M, Schurig D, Roberts DA, Cummer SA, Smith DR et al. Design of electromagnetic cloaks and concentrators using form-invariant coordinate transformation of the Maxwell’s equations. Photon Nanostr Fundam Appl 2008; 6: 87–95. [Google Scholar]
  7. Pendry JB, Ramakrishna SA. Near-field lenses in two dimensions. J Phys: Condens Matter 2002; 14: 8463–8479. [Google Scholar]
  8. Kildishev AV, Narimanov EE. Impedance-matched hyperlens. Opt Lett 2007; 32: 3432–3434. [DOI] [PubMed] [Google Scholar]
  9. Yan M, Yan W, Qiu M. Cylindrical superlens by a coordinate transformation. Phys Rev B 2008; 78: 125113. [Google Scholar]
  10. Luo Y, Zhang JJ, Chen HS, Huangfu JT, Ran LX. High-directivity antenna with small antenna aperture. Appl Phys Lett 2009; 95: 193506. [Google Scholar]
  11. Schurig D, Mock JJ, Justice BJ, Cummer SA, Pendry JB et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006; 314: 977–980. [DOI] [PubMed] [Google Scholar]
  12. Leonhardt U. Optical conformal mapping. Science 2006; 312: 1777–1780. [DOI] [PubMed] [Google Scholar]
  13. Chen HS, Zheng B, Shen L, Wang HP, Zhang XM et al. Ray-optics cloaking devices for large objects in incoherent natural light. Nat Commun 2013; 4: 2652. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Leonhardt U. Optical metamaterials: invisibility cup. Nat Photonics 2007; 1: 207–208. [Google Scholar]
  15. Yan W, Yan M, Ruan ZC, Qiu M. Coordinate transformations make perfect invisibility cloaks with arbitrary shape. New J Phys 2008; 10: 043040. [Google Scholar]
  16. Ruan ZC, Yan M, Neff CW, Qiu M. Ideal cylindrical cloak: Perfect but sensitive to tiny perturbations. Phys Rev Lett 2007; 99: 113903. [DOI] [PubMed] [Google Scholar]
  17. Xi S, Chen HS, Wu BL, Kong JA. One-directional perfect cloak created with homogeneous material. IEEE Microw Wirel Compon Lett 2009; 19: 131–133. [Google Scholar]
  18. Li W, Guan JG, Sun ZG, Wang W, Zhang QJ. A near-perfect invisibility cloak constructed with homogeneous materials. Opt Express 2009; 17: 23410–23416. [DOI] [PubMed] [Google Scholar]
  19. Diatta A, Guenneau S. Non-singular cloaks allow mimesis. J Opt 2011; 13: 024012. [Google Scholar]
  20. Chen HS, Zheng B. Broadband polygonal invisibility cloak for visible light. Sci Rep 2012; 2: 255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lai Y, Chen HY, Zhang ZQ, Chan CT. Complementary media invisibility cloak that cloaks objects at a distance outside the cloaking shell. Phys Rev Lett 2009; 102: 093901. [DOI] [PubMed] [Google Scholar]
  22. Chen HY, Chan CT. ‘Cloaking at a distance’ from folded geometries in bipolar coordinates. Opt Lett 2009; 34: 2649–2651. [DOI] [PubMed] [Google Scholar]
  23. Lai Y, Ng J, Chen HY, Han DZ, Xiao JJ et al. Illusion optics: the optical transformation of an object into another object. Phys Rev Lett 2009; 102: 253902. [DOI] [PubMed] [Google Scholar]
  24. Zheng HH, Xiao JJ, Lai Y, Chan CT. Exterior optical cloaking and illusions by using active sources: A boundary element perspective. Phys Rev B 2010; 81: 195116. [Google Scholar]
  25. Milton GW, Nicorovici NAP. On the cloaking effects associated with anomalous localized resonance. Proc R Soc A 2006; 462: 3027–3059. [Google Scholar]
  26. Nicorovici NAP, Milton GW, McPhedran RC, Botten LC. Quasistatic cloaking of two-dimensional polarizable discrete systems by anomalous resonance. Opt Express 2007; 15: 6314–6323. [DOI] [PubMed] [Google Scholar]
  27. Han TC, Qiu CW, Tang XH. An arbitrarily shaped cloak with nonsingular and homogeneous parameters designed using a twofold transformation. J Opt 2010; 12: 095103. [Google Scholar]
  28. Rudolph SM, Pfeiffer C, Grbic A. Design and free-space measurements of broadband, low-loss negative-permeability and negative-index media. IEEE T Antenn Propag 2011; 59: 2989–2997. [Google Scholar]
  29. Pendry JB, O’Brien S. Very-low-frequency magnetic plasma. J Phys: Condens Matter 2002; 14: 7409–7416. [Google Scholar]
  30. Smith DR, Padilla WJ, Vier DC, Nemat-Nasser SC, Schultz S. Composite medium with simultaneously negative permeability and permittivity. Phys Rev Lett 2000; 84: 4184–4187. [DOI] [PubMed] [Google Scholar]
  31. Lapine M, Shadrivov IV, Kivshar Y. Wide-band negative permeability of nonlinear metamaterials. Sci Rep 2012; 2: 412. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wuestner S, Pusch A, Tsakmakidis KL, Hamm JM, Hess O. Overcoming losses with gain in a negative refractive index metamaterial. Phys Rev Lett 2010; 105: 127401. [DOI] [PubMed] [Google Scholar]
  33. Ye DX, Chang KH, Ran LX, Xin H. Microwave gain medium with negative refractive index. Nat Commun 2014; 5: 5841. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (1.1MB, doc)

Articles from Light, Science & Applications are provided here courtesy of Nature Publishing Group

RESOURCES