Angle-selective perfect absorption with two-dimensional materials

Abstract

Two-dimensional (2D) materials have great potential in photonic and optoelectronic devices. However, the relatively weak light absorption in 2D materials hinders their application in practical devices. Here, we propose a general approach to achieve angle-selective perfect light absorption in 2D materials. As a demonstration of the concept, we experimentally show giant light absorption by placing large-area single-layer graphene on a structure consisting of a chalcogenide layer atop a mirror and achieving a total absorption of 77.6% in the mid-infrared wavelength range (~13 μm), where the graphene contributes a record-high 47.2% absorptivity of mid-infrared light. Construction of such an angle-selective thin optical element is important for solar and thermal energy harvesting, photo-detection and sensing applications. Our study points to a new opportunity to combine 2D materials with photonic structures to enable novel device applications.

Introduction

Two-dimensional (2D) materials such as graphene and transition-metal dichalcogenide have generated significant recent interest in photonics and optoelectronics owing to their unique properties for light–matter interactions^{1, 2, 3, 4, 5}. To exploit these properties for device applications, significant recent efforts have focused on combining these 2D materials with photonic structures, such as dielectric waveguides^{2, 6, 7, 8, 9, 10, 11, 12, 13}, plasmonic structures^{3, 14, 15, 16, 17} or photonic crystals^{18, 19, 20, 21, 22, 23, 24, 25, 26, 27}. Such combinations of 2D materials with photonic structures have led to the demonstration of near-complete absorption in single-layer graphene^{22, 23, 27}, as well as modulators^{6, 7, 11, 12, 13, 25}, detectors^{8, 9, 10, 28, 29, 30, 31, 32, 33} and lasers²⁴.

In this study, we consider a particularly simple geometry of a photonic structure incorporating a 2D material. The geometry, shown in Figure 1a, consists of a single layer of 2D material separated from a mirror by a dielectric spacer layer. This geometry has been previously used to enhance the absorption in a graphene layer of normal incident light³⁴, but the demonstrated enhancement is rather limited. Here, we theoretically prove that such a structure provides a universal mechanism for achieving perfect absorption in the 2D material. In this geometry, for any standard 2D material in the wavelength range, in which the material has some loss, there always exists an angle of incidence, at which the absorption of the 2D material reaches unity. Therefore, the simple geometry in Figure 1a can function as an angle-selective perfect absorber. Experimentally, we have shown that the geometry in Figure 1a can lead to a total absorption exceeding 77% in the mid-infrared wavelength range, in which the absorption in single-layer graphene exceeds 47%.

Figure 1.

Decay rates and critical coupling. (a) Schematic of a structure consisting of a 2D material, separated from a mirror (light gray) by a dielectric spacer layer (dark gray). As an example, the 2D material is a single-layer graphene. (b) External and internal decay rates of the structure as a function of angle of incidence. The external decay rate (γ_e, blue line) and internal decay rate (γ_i, red line) are evaluated from Equations (7) and (8), respectively. (c) Calculated mid-infrared absorptivity of the structure, for varying angles of incidence. (d) Calculated peak absorptivity as a function of angle of incidence. In b, c and d, the structure consists of single-layer graphene separated from a PEC layer by a 1.9-μm-thick dielectric layer with a refractive index of 2.1. The graphene is assumed to have a Fermi energy of −500 meV with a mobility of 750 cm² V⁻¹ s⁻¹. In b, c and d, s-polarization is considered. PEC, perfect electric conductor.

The construction of an angle-selective thin optical element has been of emerging interest recently owing to its importance for solar and thermal energy harvesting^{35, 36, 37} as well as photo-detection³⁸. Thus, our work points to a new opportunity of combining 2D materials with photonic structures to enable novel device applications. The demonstrated angle-selective perfect absorption in the infrared wavelength range alone can also be important for sensing applications¹⁷.

Materials and methods

Fabrication of the structure

The bare structure is deposited atop a polished silicon wafer. A 200-nm-thick chromium adhesion layer is first deposited using electron beam evaporation, followed by 200 nm of gold. After cleaning the surface of the Au/Cr/Si substrate, a Ge₂₃Sb₇S₇₀ chalcogenide layer ~1.9 μm thick is deposited on top using standard single-source thermal evaporation.

A single layer of graphene is grown by chemical vapor deposition on copper foil and transferred onto the structure with the standard Poly(methyl methacrylate) (PMMA) process³⁹. After baking at 120 °C for 5 min, the PMMA is dissolved by soaking the sample in acetone for 6 h and acetic acid for 3 h. Chemical doping⁴⁰ is then performed by applying nitric acid vapor on the graphene layer. We control the doping of the graphene layer by varying the duration of nitric acid vapor treatment. Two samples were fabricated with 5-min doping time and 40-s doping time, respectively.

Characterization of the structure

At infrared wavelengths from 400 cm⁻¹ to 2500 cm⁻¹, a Fourier transform infrared spectrometer (Nicolet 6700, Thermo Fisher Scientific, Waltham, MA, USA) is used to characterize the reflectance of the samples, with a gold film used as a reflectance standard, as shown in Figure 2c–2e. Because the structure is planar, from the measured reflectance R, absorptivity A can be calculated by A=1−R. A variable-angle reflection accessory (Seagull, Harrick Scientific, Pleasantville, NY, USA) equipped with KRS-5 substrate-based wire grid polarizer (Seagull FTIR polarizer, Harrick Scientific) allows for specular reflectance measurement at varying angles of incidence. The measurement sampling step in wave number is 1.9 cm⁻¹. Nitrogen purging is performed for the FTIR and the variable-angle reflection accessory during the measurement.

Figure 2.

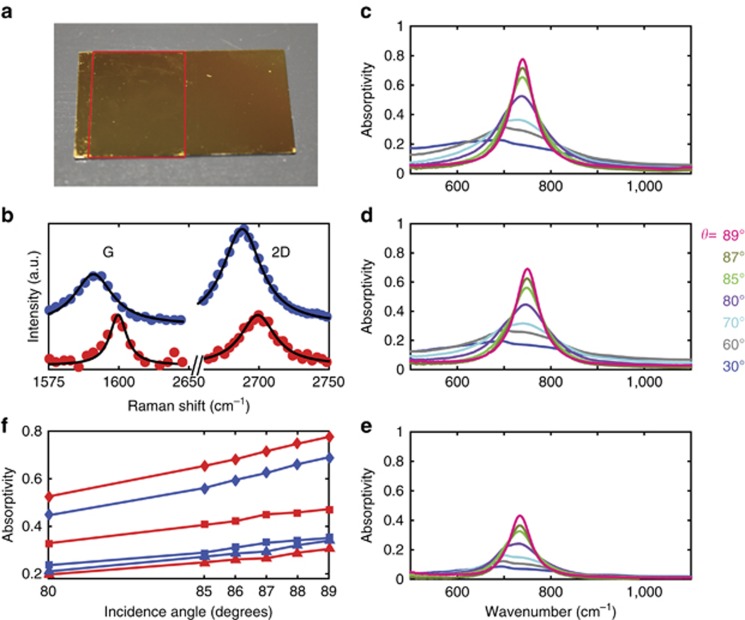
Device and experimentally measured absorptivity. (a) Photo of the structure. It consists of a doped single layer of graphene separated from a gold reflector by a 1.9-μm-thick Ge₂₃Sb₇S₇₀ ChG layer. Here, the red rectangle denotes the region that is coated with graphene. (b) Raman spectra for two structures with different graphene layers with different doping levels. The experimental spectra are shown as dots, and Lorentzian fittings are shown as black lines. The Raman spectra are vertically displaced for clarity. The graphene with 5-min (red dots) and 40-s (blue dots) doping durations are estimated to have Fermi energy E_F of −500 meV and −300 meV, respectively (see the Supplementary Information). (c–e) Measured angle-resolved absorptivity for structures. (c) The case of graphene at E_F=−500 meV. (d) The case of graphene at E_F=−300 meV. (e) The case of a bare structure without graphene. (f) Peak absorptivities for the whole structure (diamonds), the absorption inside graphene (squares) and parasitic absorption (triangles). Red and blue lines denote graphene with E_F=−500 meV and E_F=−300 meV, respectively. c–f are for s-polarization.

Raman measurement of samples is performed using a laser with a 514-nm wavelength, which is the same wavelength of the laser used in Ref. 41. The Raman measurement in both doping cases is performed at five randomly selected locations on each structure.

Extraction of absorption in single-layer graphene

The external decay rate γ_e results from the resonance mode of the bare structure. The internal decay rate results both from material loss inside the single-layer graphene γ_i,G and parasitic loss γ_i,P inside the metal and spacer layers. Using the coupled mode theory^{42, 43}, the absorptivity of the bare structure is:

and the absorptivity of the structure with graphene is:

Here, we have assumed that the resonance frequency ω₀ remains unchanged with the introduction of the graphene layer. From Equations (1) and (2), by comparing the measured absorptivities of the structures with and without graphene, decay rates can be obtained, and the absorption in the graphene layer and the remaining structure can be extracted. The absorption in graphene is:

and the parasitic absorption is:

Graphene conductivity in intraband transition regime

The conductivity of doped graphene in the intraband regime⁴⁴ can be described as:

where the Drude weight, and the relaxation rate, 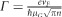. Here, Fermi velocity⁴⁵, v_F≈10⁶ ms⁻¹, carrier density, n is related to Fermi energy, E_F by 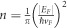, and μ_G is the carrier mobility. In the intraband transition regime, for s-polarization, the internal decay rate of graphene can then be expressed as:

where α is the fine structure constant. We observe that the internal decay rate increases with increasing Fermi energy, |E_F|. For a fixed Fermi energy and resonance frequency, as a function of mobility, the maximal internal decay rate is 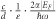when .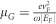

Results and discussion

We consider the theoretical condition for perfect light absorption in the 2D material with the structure shown in Figure 1a. For simplicity, we assume that all layers except the 2D material is lossless and that the bottom mirror has 100% reflectivity. Such a structure supports a resonance with light trapped in the dielectric layer owing to the reflections at its top and bottom surfaces. The resonance mode amplitude can decay either through external radiation through the top surface, as characterized by an external decay rate γ_e, or by the absorption in the 2D material, as characterized by an internal decay rate γ_i. Complete absorption in the 2D material layer can be reached when the critical coupling condition γ_e=γ_i is satisfied.

We consider first the s-polarization, whose electric field is perpendicular to the plane of incidence. The external decay rate γ_e of the resonance mode can be derived as (see the Supplementary Information for a detailed derivation):

where c is the velocity of light, d is the thickness of the spacer layer, ε is the relative permittivity of the spacer layer, and θ is the angle of incidence. The internal decay rate due to the absorption in the 2D material can be derived as (see the Supplementary Information):

where σ is the 2D conductivity of the 2D material, and 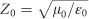is the vacuum impedance.

For a large group of 2D materials in the interband transition regime^{46, 47}, the 2D conductivity, σ is related to the fine structure constant 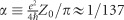. Graphene⁴⁶, for example, has , whereas semiconductor nanomembranes⁴⁷ have 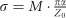, where M, an integer, is the number of allowed transitions at a given transition energy. In either case, at normal incidence θ=0, from Equations (7) and (8), we have 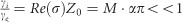, where M=1 for graphene. Hence, critical coupling cannot be reached at normal incidence, owing to the smallness of the fine structure constant. For intraband transition, the form of σ is more complicated. Nevertheless, the condition Re(σ)Z₀<<1 is still satisfied, and hence one also cannot reach critical coupling in this geometry at θ=0.

However, notice that γ_i is independent of θ, whereas γ_e reaches zero at θ=π/2. Therefore, there is always a critical angle of incidence θ_c, at which critical coupling is satisfied.

In the cases considered here, where Re(σ)Z₀<<1, the critical angle can be determined as:

and is close to 90°. For graphene or semiconductor nanomembranes in the interband transition regime,

where M=1 for graphene. Therefore, we see that the critical angle is directly related to the fine structure constant in this regime.

As an example, in Figure 1, we consider a single layer of graphene atop a structure consisting of a 1.9-μm-thick dielectric layer with a refractive index of 2.1 atop a perfect electric conductor layer. The graphene has a Fermi energy of −500 meV and a mobility of 750 cm² V⁻¹ s⁻¹. The structure supports a resonance in the mid-infrared wavelengths. Figure 1b shows the external and internal decay rates of the structure. At normal incidence, we indeed see γ_e(0)>>γ_i(0). As the angle of incidence increases, Figure 1c shows that critical coupling is achieved at θ_c≈88.4°, where the structure transitions from over-coupling to under-coupling (Figure 1b). The angular dependence of the peak absorptivity is shown in Figure 1d. Around the critical angle, the peak absorptivity is sensitive to the angle of incidence.

We now experimentally demonstrate our concept by showing large angle-selective enhancement of mid-infrared light absorption in single-layer graphene. In our experiment, we place a single layer of chemically doped graphene atop a structure consisting of a 1.9-μm-thick Ge₂₃Sb₇S₇₀ chalcogenide glass (ChG) layer backed by a gold reflector, as shown in Figure 2a. Here, Ge₂₃Sb₇S₇₀ ChG has relatively weak absorption at mid-infrared wavelengths. It also has a low refractive index^{48, 49, 50} of ~2.1, which is important for reducing the absorption loss inside the metal reflector.

From Equation (9), we see that the same structure can provide complete absorption for different 2D materials with different 2D conductivity σ. To demonstrate this, we use two different graphene layers with different doping levels. We chemically dope graphene by applying nitric acid vapor and achieve two doping levels by doping graphene for 5 min and 40 s, respectively. Figure 2b shows the Raman spectra of the graphene for the two cases. The single symmetric 2D peak in the Raman spectra confirms that it is single-layer graphene⁵¹. For different doping, the G and 2D peaks of the Raman spectra shift. Using the experimentally determined relation between the doping level and the positions of G and 2D peaks from Ref. 41, the Fermi energy E_F for the graphene with 5-min and 40-s doping are estimated to be −500 meV and −300 meV, respectively (see the Supplementary Information).

The measured angle-resolved absorptivity for the structures with and without graphene are shown in Figure 2c–2e. We consider s-polarization. In Figure 2c, for the graphene with E_F=−500 meV, the peak absorptivity increases with increasing angle of incidence and reaches 77.6% at an 89° angle of incidence. For the graphene with E_F=−300 meV (Figure 2d), the peak absorptivity reaches 69% at an 89° angle of incidence. In contrast, the bare structure without graphene exhibits much smaller absorptivity (Figure 2e), and the peak absorptivity is only 43.1% at an 89° angle of incidence. The absorption in the bare structure results from parasitic loss inside the gold reflector and the ChG layer. We see that the same structure can be used to enhance the absorption for two different graphene layers at different doping levels.

Figure 2f shows the absorption in graphene (squares), the parasitic absorption (triangles) and the total absorptivity (diamonds). The absorption in graphene and the parasitic absorption are obtained from experimental results using coupled mode theory formulas. We note that the absorption in graphene is not simply equal to the difference between the peak absorptivities for the structures with and without graphene. For both cases, the absorption in graphene dominates the parasitic absorption. For the structure with the graphene at E_F=−500 meV, at an 89° angle of incidence, the absorption in graphene is 47.2%, and parasitic absorption is 30.4%. For the structure with the graphene at E_F=−300 meV, at an 89° angle of incidence, the absorption in graphene and parasitic absorption are 35.1% and 34%, respectively. Figure 2f also shows that as the doping level of graphene increases, the absorption in graphene increases while the parasitic absorption decreases, which is consistent with the coupled mode theory (see Equations (3) and (4)).

The demonstrated 47.2% light absorption in the single-layer graphene is a significant enhancement of mid-infrared light absorption in single-layer graphene. Previously, the highest experimentally demonstrated mid-infrared light absorption in graphene was 30% from Ref. 16, by nanopatterning a graphene layer into a graphene nanodisk array. Our achieved absorption enhancement is substantially higher than previously experimentally demonstrated mid-infrared light absorption in single-layer graphene^{15, 16, 52, 53, 54} yet is realized using a simpler structure. Our scheme is also compatible with chemical and biological sensing applications¹⁷, in which the molecules must have contact with the 2D material.

Using an experimentally characterized complex refractive index of Ge₂₃Sb₇S₇₀ and tabulated optical constants of Au⁵⁵, numerical calculation shows that the structure with E_F=−500 meV graphene can achieve near-complete absorption, in which light is predominantly absorbed by graphene (see the Supplementary Information). This calculated absorptivity is higher than the measured result in Figure 2. The difference between the two can be well explained by considering a typical angular spread of the probing light in the measurement system (see the details in the Supplementary Information). Therefore, we expect that our fabricated device may already achieve critical coupling, in which the majority of absorption is in the graphene.

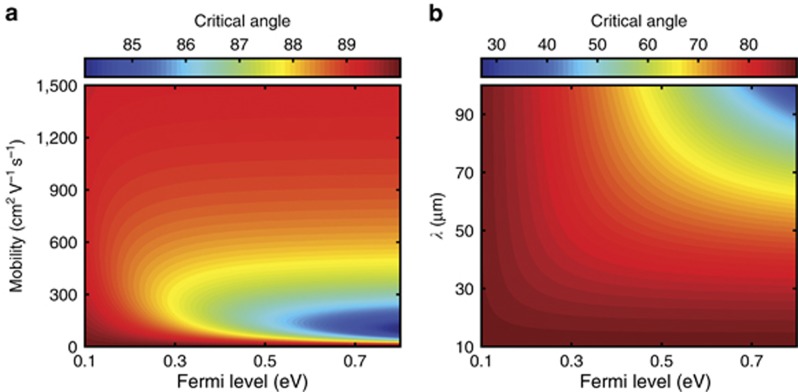
Our approach has the significant advantage that the same structure can provide critical coupling for different 2D materials with different properties. The specific material properties of the 2D materials often cannot be precisely controlled in an experiment and are rather characterized only after the device is fabricated. This presents an experimental challenge for other resonant enhancement approaches to enhance light absorption in 2D materials, owing to the stringent requirement for the critical coupling to achieve perfect resonant absorption. In contrast, our approach provides a simple enhancement approach that can work with 2D materials as prepared. As an example, in the case of graphene considered here, the conductivity σ_G of graphene due to intraband transition depends on doping level and mobility. Regardless of these properties of graphene, there is always an angle of incidence, at which critical coupling is met. In Figure 3a, we show the critical angle as a function of Fermi level and mobility. Here, the structure includes a 1.9-μm-thick spacer layer with a refractive index of 2.1.

Figure 3.

Calculated critical angle for different graphene properties and wavelengths. (a) Calculated critical angle as a function of graphene Fermi level and mobility. The structure consists of a graphene layer on top, a 1.9-μm-thick dielectric layer with a refractive index of 2.1 in the middle and a PEC layer on the back. (b) Calculated critical angle as a function of graphene Fermi level and resonance wavelengths. The structure consists of a graphene layer on top, a dielectric layer with a refractive index of 2.1 in the middle and a PEC layer on the back. The graphene has a mobility of 750 cm² V⁻¹ s⁻¹. In a and b, s-polarization is considered. PEC, perfect electric conductor.

The critical angle depends on the conductivity of the 2D material and is not necessarily large. Figure 3b shows the critical angle for different doping levels and resonance wavelengths, with the mobility of graphene of 750 cm² V⁻¹ s⁻¹. We observe that the critical angle can be as small as 30° at far infrared, owing to increasing conductivity of graphene at longer wavelengths. In addition, for quasi-2D thin films with tuned thickness, the critical angle can be quite small.

Although we discuss the s-polarized case above, angle-selective perfect absorption in a 2D material can be generalized to p-polarization in a geometry consisting of a 2D material separated from a perfect magnetic conductor mirror^{56, 57} by a lossless spacer. In this case, the external and internal decay rates are 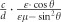and 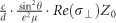, respectively (see the Supplementary Information for derivation). Here, σ_⊥ is the 2D conductivity of the 2D material in the vertical direction, and the spacer material has a relative permittivity ε and relative permeability μ. For small 2D conductivity, the critical angle in p-polarization can be described as 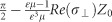(see the Supplementary Information).

Conclusions

In conclusion, we report a general and robust mechanism for achieving angle-selective perfect light absorption in 2D material by placing it on a dielectric spacer layer backed by a mirror. In this geometry, for any standard 2D material in the wavelength range, in which the material experiences loss, we theoretically prove that there always exists an angle of incidence, at which light is completely absorbed in the 2D material. Experimentally, we show high light absorption in single-layer graphene by placing it on a Ge₂₃Sb₇S₇₀ chalcogenide layer backed by a mirror, achieving a total absorption of 77.6% at a wavelength of ~13 μm, in which the graphene contributes a record-high 47.2% absorptivity in the mid-infrared wavelength range. Our approach also has the significant advantage that the same structure can provide angle-selective perfect absorption for different 2D materials with different properties, and we experimentally show angle-selective absorption enhancement on the same structure using graphene with different doping levels. Because our approach does not involve the nanopatterning process, it is robust and can be scaled to large areas with a high yield. Our approach provides a robust platform, on which to achieve angle-selective perfect absorption in 2D materials. Construction of such an angle-selective thin optical element is important for applications ranging from solar and thermal energy harvesting and photo-detection, to chemical and biological sensing. Our results open new avenues for combining 2D materials with photonic structures to enable novel device applications.

Author contributions

LZ, ZY, XW and SF envisioned and implemented the experimental studies and wrote the manuscript. LZ performed the theoretical analysis, FTIR measurement and numerical analysis. HL, JH, LZ and ZY deposited the chalcogenide and gold layers. FL and XW deposited, transferred and chemically doped the graphene layers. LZ, FL and XW performed Raman spectroscopy of the samples. All authors discussed the data and commented on the manuscript. ZY, XW and SF supervised the project.