Nonlinear terahertz devices utilizing semiconducting plasmonic metamaterials

Abstract

The development of responsive metamaterials has enabled the realization of compact tunable photonic devices capable of manipulating the amplitude, polarization, wave vector and frequency of light. Integration of semiconductors into the active regions of metallic resonators is a proven approach for creating nonlinear metamaterials through optoelectronic control of the semiconductor carrier density. Metal-free subwavelength resonant semiconductor structures offer an alternative approach to create dynamic metamaterials. We present InAs plasmonic disk arrays as a viable resonant metamaterial at terahertz frequencies. Importantly, InAs plasmonic disks exhibit a strong nonlinear response arising from electric field-induced intervalley scattering, resulting in a reduced carrier mobility thereby damping the plasmonic response. We demonstrate nonlinear perfect absorbers configured as either optical limiters or saturable absorbers, including flexible nonlinear absorbers achieved by transferring the disks to polyimide films. Nonlinear plasmonic metamaterials show potential for use in ultrafast terahertz (THz) optics and for passive protection of sensitive electromagnetic devices.

Introduction

The advent of active and tunable metamaterials (MMs) introduced a new path toward controlling light-matter interactions with the possibility to impact photonic applications spanning from microwave to visible frequencies¹. Nonlinear MMs represent an important class of active electromagnetic composites that can potentially pave the way to produce tailored nonlinear optical phenomena such as harmonic generation or self-focusing². Pioneering prominent examples of nonlinear MMs have been demonstrated in the microwave region where nonlinear lumped circuit elements were used³. At infrared frequencies, field enhancement plasmonic MMs provide an important route toward creating enhanced nonlinear composites^{4, 5, 6, 7}.

Optically responsive materials at terahertz (THz) frequencies have also been demonstrated in the past decade through judicious MM design^{8, 9, 10}. This includes the creation of dynamically tunable MM devices employing optical, mechanical or electrical control methods^{1, 11, 12, 13, 14, 15}. Nonlinear THz MMs have also been demonstrated^{16, 17, 18, 19, 20}. The majority of tunable and nonlinear THz MMs have incorporated semiconductors into the active region of split ring resonators to enable dynamic tuning of the electromagnetic response^{13, 14, 21, 22}. It is also possible to exclusively employ semiconductors to create plasmonic devices at THz and infrared frequencies^{23, 24, 25}. The plasma frequency of semiconductors can be tuned by adjusting the doping level, providing a path toward THz plasmonic semiconductor MMs (PSMM)^{26, 27, 28, 29}. The response of PSMM can be tailored via structure and geometry and can be modulated using, as examples, electric, magnetic and thermal stimuli. Importantly, semiconductors exhibit large nonlinearities at THz frequencies^{30, 31, 32, 33, 34, 35, 36} enabling (as demonstrated below) nonlinear plasmonics and providing a key capability for future terahertz circuits and systems^{6, 37}.

We have created PSMMs using n-doped InAs (n-InAs) thin films patterned into disk arrays that are resonant at THz frequencies. As is well known, the plasmonic response of a particle arises from dielectric confinement. This results in a resonant response that is determined by the geometry and the carrier concentration with the quality of the resonance determined by the scattering rate or, in the case of semiconducting plasmonic particles, the mobility. Thus, n-InAs is an attractive plasmonic material at THz frequencies because of the high mobility (~20 × 10³ cm² V⁻¹ s⁻¹) and ability to control the resonance frequency through doping. Further, as we demonstrate, InAs disks exhibit a strong nonlinear response. In particular, high-field terahertz nonlinear transmission measurements reveal that the disk plasmon resonance exhibits a nonlinear response arising from field-induced intervalley scattering of conduction band electrons to a low-mobility satellite valley. We utilized these nonlinear PSMMs to create both saturable absorbers (SAs) and optical limiters (OLs) by incorporating a ground plane to create a perfect absorber geometry including flexible absorbers created via transfer of the InAs arrays to polyimide.

Materials and methods

Fabrication

For our studies, 2-μm-thick n-InAs films were grown via molecular beam epitaxy (MBE) with a Si doping concentration of 10¹⁷ cm⁻³ on a 500-μm-thick semi-insulating (SI) GaAs substrate. A 100-nm-thick Ti mask layer was patterned on the film using a lift-off technique. Next, an InAs film on a 1 × 1 cm² die was etched thoroughly using reactive ion etching with a gas mixture of H₂, CH₄ and Ar. The Ti mask was then etched away in HF solution. For the perfect absorbers on GaAs substrates, this procedure was followed by polyimide spin coating and curing, and 150 nm gold evaporation.

To fabricate flexible absorbers with no substrate, we used a transfer patterning technique. Thin films of 2-μm-thick n-doped InAs were grown by MBE on a 500 nm AlAsSb sacrificial layer on semi-insulating GaAs substrate. Subsequent to growth, the InAs film was patterned and etched into disks with a hexagonal symmetry (D=60 μm, P=72.7 μm), using a citric acid/H₂O₂ solution down. The exposed area of the sacrificial layer was then etched away using a 5% HF solution; at this step, the InAs disks remained attached to the GaAs substrate by unexposed AlAsSb. Next, polyimide was spin-cast and cured, and Cr/Au/Ti layers were deposited on the polyimide as a dual-purpose ground plane and etchmask. Subsequently, 28 μm diameter etch holes were formed by RIE of the polyimide layer and wet etching of the InAs, resulting in the disks acquired a ring shape. To complete the transfer of the InAs rings to polyimide, the AlAsSb sacrificial layer underneath the InAs rings was etched away in a 5% HF bath. After 2 h of etching, the polyimide was peeled off from the GaAs substrate. A final citric acid dip was made to remove compound residues from the surface. Due to anisotropic wet etching of InAs, the fabricated rings possessed a long axis diameter of 64 μm and a short axis diameter of 60 μm. An explanatory figure showing fabrication steps for flexible PSMMs can be seen in Supplementary Fig. S1.

THz-TDS

The THz-time-domain spectroscopy (TDS) setup makes use of the tilted-pulse-front technique to generate THz pulses from a LiNbO₃ crystal (see Supplementary Fig. S2). The THz pulses used in this experiment were ~1 ps in duration with a maximum electric field strength of ~300 kV cm⁻¹. The field strength incident on the sample is controlled through a pair of linear polarizers. Example time-domain measurements of the PSMM and SI-GaAs reference are presented in Supplementary Fig. S3.

Simulations

In our simulations, we used the Drude response for n-InAs with the following parameters: N_d=1e17 cm⁻³, ε_∞=12.25, m_eff=0.023, and μ=3.5e3–1.9e4  cm² V⁻¹ s⁻¹. The SI-GaAs substrate is assumed to have a relative dielectric constant of 12.94 with a frequency independent loss tangent of 0.006. A unit cell and a reference sample were simulated in the time domain and the results were obtained in the same manner as in the experiments (for example, by Fourier transforming the time-domain data and performing a Fresnel analysis in the frequency domain). To include nonlinearities caused by intervalley scattering, we used a variable mobility and effective mass in our Drude model of InAs. By varying the relationship between mobility and effective mass, we were able to account for the field-dependent collision frequency. Supplementary Tables S1 and S2 in the Supplementary Information provide the mobilities and effective masses used to model each nonlinear device.

Results and discussion

A PSMM composed of 70-μm-diameter n-InAs disks with 100 μm hexagonal lattice periodicity was fabricated as shown in Figure 1a and 1b. The geometry was formed by dry etching of a 2-μm-thick n-InAs film grown on SI-GaAs using MBE³⁸. Our samples were doped to 10¹⁷ cm⁻³, as shown in Figure 2, to obtain a strong plasmonic response at ~0.8 THz. The band structure, depicted in Figure 1c plays an important role in the plasmonic response. At low electric fields, the free electrons reside predominantly in the Γ-valley and exhibit a small effective mass and high mobility. The oscillator strength of the plasmon resonance can, in principle, be modified at high electric fields through intervalley scattering or impact ionization^{30, 31, 32, 33, 34, 35} (Figure 1c). For example, efficient intervalley scattering (Γ→L) would result in a damping of the plasmon resonance because of the considerably larger effective mass and reduced mobility of carriers in the L-valley.

Figure 1.

Nonlinear plasmonic semiconductor metamaterial. (a) Schematic view of InAs disk array on semi-insulating GaAs. (b) SEM image of the fabricated PSMM: InAs film thickness: 2 μm, SI-GaAs substrate thickness=500 μm, disk diameter D=70 μm, periodicity P=100 μm. (c), Band diagram of InAs showing potential inter- and intra-band transitions triggered by high THz fields (for example, ballistic acceleration, impact ionization and intervalley scattering). Abbreviation: SEM, scanning electron microscope.

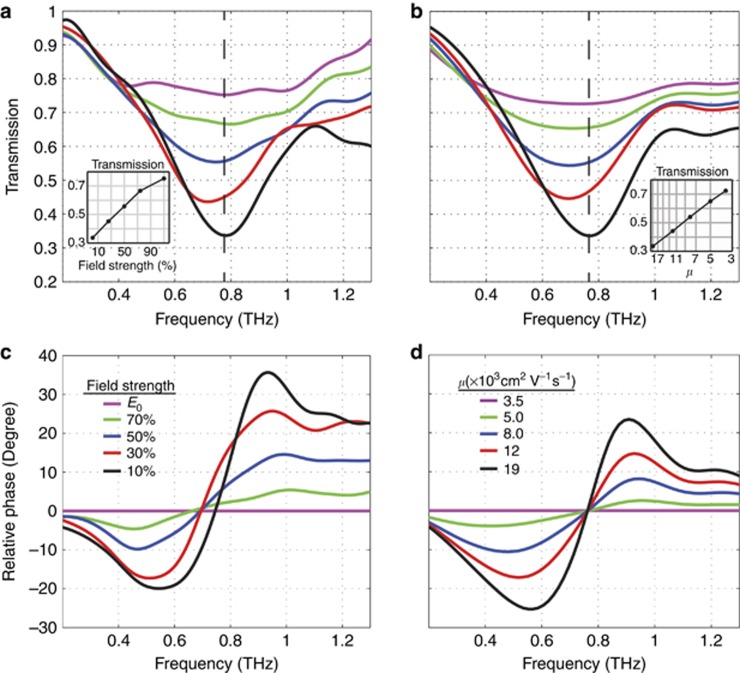
Figure 2.

Transmission spectra of the nonlinear PSMM. (a) Measured transmission amplitude of PSMM shown in Figure 1 for various THz field strengths. Inset shows the change in transmission as a function of field strength at the resonance frequency of 0.77 THz. (b) Simulated transmission amplitude as a function of InAs mobility with N_d=1 × 10¹⁷ cm⁻³, μ=3.5 × 10³–1.9 × 10⁴ cm² V⁻¹ s⁻¹, ε_∞=12.25, m_eff=0.023–0.035. Inset shows the change in transmission as a function of InAs mobility (unit: × 10³  cm² V⁻¹ s⁻¹) at the resonance frequency of 0.77 THz. (c, d) Corresponding measured and simulated transmission phases normalized with respect to the phase at the highest field strength and the lowest electron mobility.

High-field THz-TDS was employed to characterize the samples utilizing tilted-pulse-front generation in lithium niobate^{39, 40}. Figure 2a shows the measured PSMM plasmon resonance as a function of frequency at various incident field strengths with an estimated maximum around E₀≈300 kV cm⁻¹. At the lowest field (0.1E₀, the black curve in Figure 2a), a plasmon resonance is evident at 0.77 THz with a transmission of ~35%. With increasing field strength there is an increase in the transmission associated with plasmon damping. At the highest field strength (E₀, the purple curve in Figure 2a) the transmission has increased to ~75%, an increase of 40% in comparison to the low-field case. Figure 2c shows the corresponding phase as a function of frequency (relative to the phase at the highest field strength). The largest phase shift (between the lowest and highest fields) at ~0.9 THz was 35° at 1.2 THz (well above resonance) it has decreased to ~22°. The observed damping is consistent with THz electric field-induced intervalley scattering (Γ→L), resulting in a decrease in the average electron mobility⁴¹.

To gain insight into the nonlinear response of the InAs disks, we modeled the PSMMs using CST Microwave Studio (Framingham, MA, USA) utilizing the Drude model to describe the electromagnetic response of InAs (see Supplementary Information for details). In agreement with experiment, the simulated resonant response at ~0.77 THz corresponds to the dipolar plasmonic mode of the disk structure. To simulate the increased carrier scattering, we decreased the electron mobility, which results in a quenching of the plasmon oscillator strength in agreement with experiment (Figure 2b). This interpretation is consistent with intervalley scattering, leading to coexisting populations of electrons in the Γ and L valleys, which yields an average effective mobility as indicated in Figure 2d. Specifically, our simulations are consistent with a decrease in the effective mobility from 19 × 10³  cm² V⁻¹ s⁻¹ to 3.5 × 10³  cm² V⁻¹ s⁻¹ on increasing the field from 0.1E₀ to E₀. Ignoring effects due to nonparabolicity, impact ionization, and scattering to the X-valley, and assuming the Γ and L-valleys have constant mobilities of 20 × 10³ and 20  cm² V⁻¹ s⁻¹, respectively, the observed change is consistent with greater than 50% of the carriers being transferred to the L-valley. In the experimental data, there is also a slight shift in the resonance frequency; we attribute this shift to the decrease in the plasma frequency caused by an increase in effective mass arising from band nonparabolicity and transfer to the L-valley at high fields⁴². This effect is well-captured in the simulations by increasing the effective electron mass (m_eff=0.023→0.035) in the Drude model.

The ability to fabricate MMs from semiconductor resonators opens up vast opportunities for creating nonlinear active devices. In the following, we demonstrate nonlinear absorbers (that is, SAs and OLs). Similar devices operating in the infrared currently find practical use in ultrafast optics, mode locking and sensor/eye protection^{43, 44}. Indeed, bulk semiconductors can show a nonlinear absorption of THz light due to several electronic nonlinear processes^{45, 46, 47}. However, using semiconductors in a MM perfect absorber geometry⁴⁸ provides additional control over the nonlinearity, absorption strength, frequency and modulation depth, reducing the device thickness in comparison to an unpatterned semiconductor device.

Perfect absorption phenomenon in MM absorbers can be explained in terms of impedance matching of MM effective parameters⁸ or in terms of interference of the reflected light from resonator and ground plane layers⁴⁹. The highest absorbance is achieved over a narrow range of optimized conditions, with the absorbance becoming weaker (or stronger) as the MM properties are modified. Thus, as the properties of the PSMM layer are altered due to nonlinearities the optimal absorbance conditions change. PSMM absorbers can be designed such that the highest absorbance occurs at either low fields or at high fields, resulting in SAs or OLs, respectively.

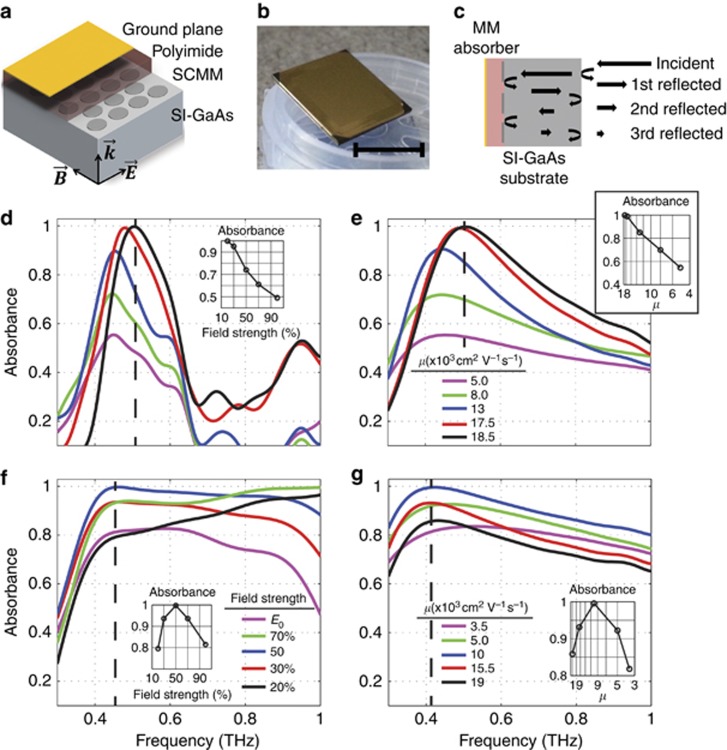
PSMMs in a hexagonal array (70 μm diameter and 90 μm periodicity) were made into absorbers by spin coating a polyimide layer followed by physical evaporation of a gold ground plane as additional steps to PSMM fabrication (Figure 3a and 3b). The PSMM geometry was chosen to obtain a resonance at ~0.5 THz, which is close to the peak of our THz high-field source, thereby providing the largest possible THz field for this nonlinear proof-of-principle demonstration. Two optimized thicknesses were used for the polyimide spacer layer; for the SA and OL, the thicknesses of the polyimide spacer layers were 18 μm and 40 μm, respectively. The SA is designed to maximize the absorption at low-field strengths by taking advantage of the high carrier mobility n-InAs. The OL is optimized to increase the absorption at higher field strengths where the effective electron mobility is decreased. Importantly, these devices are thinner than a quarter wavelength at the peak absorption frequency of 0.46 THz (for example, λ/4≈160 μm in free space and 45 μm in GaAs).

Figure 3.

Nonlinear PSMM absorbers. (a) Schematic view of the PSMM absorber layers. (b) A fabricated PSMM device view from the ground plane side with 1 cm² active area (scale bar=1 cm). (c) Schematic representation of the etalon reflections in the GaAs substrate. Measurements and corresponding simulation results for (d, e) the SA with 18-μm-thick polyimide layer and (f, g) OL with 40-μm-thick polyimide layer, respectively. d, f share the same legend. Insets show the absorbance trends as a function of field strength and electron mobility (μ) at the frequencies indicated by the dashed lines (mobility unit: × 10³  cm² V⁻¹ s⁻¹).

The ground plane prevents illumination from the front side and has zero transmission. Thus, the reflection from the absorbers was measured from the bare GaAs side of the device at near-normal incidence. This is shown schematically in Figure 3c. The absorber acts as a Fabry–Perot etalon and produces multiple time resolved THz pulses in the TDS reflection signal. The first reflected pulse is directly from the front surface of the substrate and contains no information about the PSMM absorption. To determine the absorption of the active layer of the PSMM absorber (that is, the internal absorbance), we windowed the data to isolate second reflected pulse, which corresponds to the first reflection from the device layer (see Supplementary Information). As a reference, a sample composed of a SI-GaAs substrate, polyimide spacer and the ground plane was used. Utilizing the second reflected pulses from both the device and the reference provides a normalized measure of the internal absorbance. We followed the same procedure for the full wave electromagnetic simulations using a time-domain transient solver.

The measurement and simulation results are shown in Figure 3d–3g for the SA and OL absorbers. The absorbance for each device was calculated by subtracting the reflectance from unity (A=1−|E_reflected|²), since the transmission through the ground plane was negligible. For the SA, the absorbance at the resonant frequency of 0.5 THz was 97.5% at low fields (0.2E₀, the black curve in Figure 3d). With increasing field strength, the absorbance monotonically decreases. At the full strength of the THz beam (E₀, the purple curve in Figure 3d), the absorbance was reduced to 49%. Thus, between 0.2 and 1.0 E₀, a modulation of nearly 50% was obtained. The inset of Figure 3d shows the change in the absorbance as a function of field strength.

The measurement results for the OL are shown in Figure 3f. The absorbance was 80% at low fields (0.2E₀, the black curve in Figure 3f). As the field strength is increased (0.5E₀, the blue curve in Figure 3f), the absorbance increased to ~99%. Further increasing the field strength up to E₀, the absorbance dropped back to 80%, indicating that the optimal OL effect for this particular device occurred at 0.5E₀. The inset of Figure 3f clearly shows the nonlinear modulation of the absorbance at 0.46 THz. This reveals a limitation of the present device in that it exhibits optical limiting behavior up to a certain field value (0.5E₀), after which it degrades. Another consequence of using a thicker spacer layer in the OL was the observed broadband absorption. This is mainly because of a second absorption mode arising around 1 THz whose tail merged with the fundamental absorption mode. While the modulation was much smaller for the OL in comparison to the SA, these results nonetheless reveal that it is possible to create both SAs and OLs from nonlinear MMs.

We note that it is possible to improve the optical limiting capabilities of PSMM with alternative designs. Optimization of the MM geometry (see Supplementary Information for an improved OL design example—Supplementary Fig. S7) substantially improves the modulation depth and increases the maximum field at which optical limiting behavior is maintained. There are, of course, inherent limitations that exist due the intrinsic properties of the semiconductor. For example, secondary nonlinear processes such as impact ionization may take place at even higher fields resulting in a degradation of the absorption.

As in Figure 2, the nonlinear response of the PSMM absorbers were modeled using the Drude response of n-InAs, with both the mobility and effective mass used as variable parameters (see Supplementary Table S1). The overall trends in the simulated absorbances (Figure 3e and 3g) are in good agreement with the measurements. The origin of the differences in resonances between experiment and simulation arise from several sources. In particular, for the high-field THz reflectance measurements, it is difficult to remove artifacts arising from scattering, and slight deviations in the fabricated structures were not captured in the simulations.

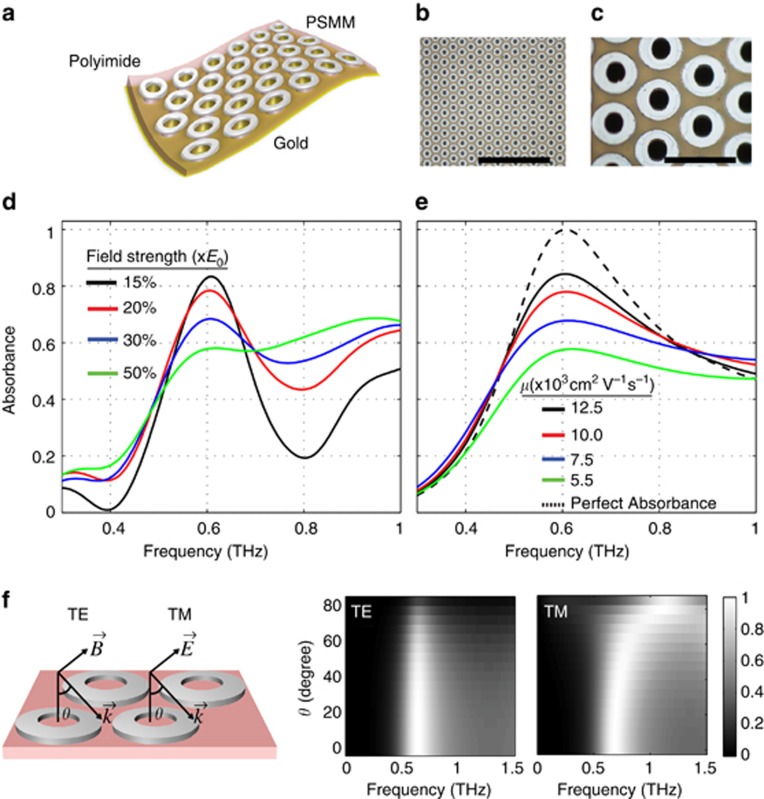
While the PSMM absorbers with a GaAs substrate demonstrate the feasibility of creating MM SAs and OLs, it is desirable to eliminate the substrate to achieve real perfect absorption (that is, to eliminate the first surface reflection from the substrate). Transfer printing techniques have recently been developed making it possible to transfer semiconductors onto flexible materials with the aid of a sacrificial layer⁵⁰. We have fabricated substrate-free PSMM absorbers using n-InAs film grown on an AlAsSb sacrificial layer grown via MBE on a SI-GaAs substrate (Figure 4a–4c). To facilitate etching based lift-off of the InAs, we used ring shaped resonators with holes that extend through the ground plane creating a perforated sheet. Although this perforated structure is not optimal for perfect absorbers, the diameter of the holes is much smaller than the resonance wavelength and the transmission through them is negligibly small. Moreover, tests were conducted by placing the samples on gold mirrors, ensuring zero transmission. A gold mirror was also used as a reference.

Figure 4.

PSMM absorber on flexible substrate. (a) Representative sketch of the flexible semiconductor-based metamaterial absorber. (b) Microscope image of the fabricated flexible absorber (scale bar=500 μm). (c) Close-up image of the rings. Rings have 30 μm outer and 15 μm inner radius on average with 72.7 μm hexagonal symmetry (scale bar=100 μm). (d) Terahertz-time-domain spectroscopy measurements showing the absorbance for increasing field strength. (e) Simulated absorbance spectra for Drude models with varying mobility and effective mass. (f) Simulated absorbance spectra of substrate-free absorber as a function of incidence angle (θ) for TE and TM polarized THz light.

This substrate-free device was optimized to act as a SA; it exhibited an 83% resonant absorbance peak at 0.15E₀ and ~0.6 THz (the black curve in Figure 4d). The absorbance dropped to 58% at 0.5E₀ field strength (the green curve in Figure 4d). The maximum absorption did not reach unity due to fabrication imperfections (for example, the fabricated polyimide thickness came out 4 μm thinner than the designed thickness of 29 μm). Further, defects were formed on the InAs film during the transfer printing, which potentially decreased the carrier mobility. Nonetheless, absorption saturation of ~25% was successfully demonstrated. The simulation results are shown in Figure 4e (see Supplementary Table S2 for the model). The dashed line in Figure 4e shows the designed maximum absorbance available for a thicker, better optimized polyimide layer and for the expected mobility of a defect-free InAs film.

One of the design concerns of MM absorbers is the dependence of the absorption on the incidence angle (θ) and incident polarization (ϕ). Due to complications with the high-field optical setup for oblique angles, we investigated these scenarios for the substrate-free PSMM absorber via simulation. The simulated θ and ϕ dependence of the substrate-free PSMM absorber are shown in Figure 4f. For TE polarized light, there was a slight absorption degradation for θ>45°, while for TM polarized light absorption was maintained over a wide range of angles with a slight shift to higher frequencies.

Conclusions

Our results suggest that PSMMs are of potential use in applications that include ultrafast THz optics and as protective layers from strong resonant electromagnetic fields. The ability to create flexible nonlinear devices further facilitates applications since these PSMMs can conformally adhere to curved surfaces. PS resonators complement existing metallic structures, such as split ring resonators, providing alternative fabrication strategies to create active materials with reduced local field enhancement and correspondingly higher damage thresholds. Geometries other than disk and ring arrays (for example, dimers or bowties) can also be employed to obtain useful functionality. Finally, the doping level and defect density in InAs can be engineered to control the resonance frequency, strength and response time of MM devices. In principle, even higher mobility materials (for example, InSb or two-dimensional electron gases) will yield even sharper plasmonic resonances.

Author contributions

RDA, XZ, SRB and HRS developed the idea. SRB and SJM performed InAs material growth. HRS and GRK performed electromagnetic simulations and optimizations. HRS, KF and XZ fabricated the device. JZ built the measurement setup and conducted the measurements. RDA, XZ and SRB supervised the project. HRS, GRK, XZ and RDA wrote the paper. All authors contributed to understanding of the physics and revised the paper.